Неопределенная форма
В исчислении обычно можно вычислить предел суммы, разности, произведения, частного или степени двух функций, взяв соответствующую комбинацию отдельных пределов каждой соответствующей функции. Например,
и то же самое для других арифметических операций; это иногда называют алгебраической предельной теоремой . Однако некоторые комбинации конкретных предельных значений не могут быть вычислены таким способом, и знание предела каждой функции в отдельности недостаточно для определения предела комбинации. Говорят, что в этих конкретных ситуациях предел принимает неопределенную форму , описываемую одним из неформальных выражений.
где каждое выражение обозначает предел функции, построенной как арифметическая комбинация двух функций, пределы которых соответственно стремятся к или как указано. [1]
Предел, принимающий одну из этих неопределенных форм, может стремиться к нулю, может стремиться к любому конечному значению, может стремиться к бесконечности или может расходиться, в зависимости от конкретных задействованных функций. Предел, однозначно стремящийся к бесконечности, например не считается неопределенным. [2] Этот термин был первоначально введен Коши учеником Муаньо в середине XIX века.
Наиболее распространенным примером неопределенной формы является частное двух функций, каждая из которых сходится к нулю. Эту неопределенную форму обозначают . Например, как подходы соотношения , , и пойти в , , и соответственно. В каждом случае, если подставить пределы числителя и знаменателя, результирующее выражение будет , что является неопределенным. В этом смысле может принимать значения , , или , путем соответствующего выбора функций для подстановки в числитель и знаменатель. Фактически можно найти пару функций, для которых пределом является любое конкретное заданное значение. Еще более удивительным, возможно, является то, что частное двух функций может фактически расходиться, а не просто расходиться до бесконечности. Например, .
Итак, тот факт, что две функции и сходиться к как приближается к некоторой предельной точке недостаточно для определения предела
Такую же форму неопределенной формы может иметь выражение, возникающее иными способами, чем применение алгебраической предельной теоремы. Однако некорректно называть выражение «неопределённой формой», если выражение сделано вне контекста определения пределов.Примером может служить выражение . Оставлено ли это выражение неопределенным или оно определено как равное , зависит от области применения и может различаться у разных авторов. Подробнее читайте в статье Ноль в степени нуля . Обратите внимание, что и другие выражения, включающие бесконечность, не являются неопределенными формами .
Некоторые примеры и не примеры
[ редактировать ]Неопределенная форма 0/0
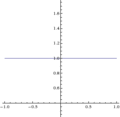
[ редактировать ]- Рис. 1: у = x / x
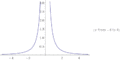
- Рис. 2: у = x 2 / x
- Рис. 3: у = грех х / х
- Рис. 4: у = х - 49 / √ х - 7 (для х = 49)
- Рис. 5: у = a x / x где a = 2
- Рис. 6: у = х / х 3
Неопределенная форма особенно распространен в исчислении , поскольку часто возникает при оценке производных с использованием их определения в терминах предела.
Как упоминалось выше,
пока
Этого достаточно, чтобы показать, что является неопределенной формой. Другие примеры этой неопределенной формы включают:
и
Прямая замена числа, которое подходы к любому из этих выражений показывают, что эти примеры соответствуют неопределенной форме , но эти пределы могут принимать множество разных значений. Любое желаемое значение для этой неопределенной формы можно получить следующим образом:
Значение также можно получить (в смысле расходимости на бесконечность):
Неопределенная форма 0 0
[ редактировать ]Следующие пределы иллюстрируют, что выражение представляет собой неопределенную форму:
Таким образом, в целом, зная, что и недостаточно для оценки предела
Если функции и являются аналитическими в , и является положительным для достаточно близко (но не равно) к , то предел будет . [3] В противном случае используйте преобразование из таблицы ниже, чтобы оценить предел.
Выражения, не являющиеся неопределенными формами
[ редактировать ]Выражение обычно не рассматривается как неопределенная форма, потому что, если предел существует, то нет никакой двусмысленности относительно его значения, поскольку оно всегда расходится. В частности, если подходы и подходы затем и можно выбрать так, что:
- подходы
- подходы
- Предел не существует.
В каждом случае абсолютное значение подходы , и поэтому частное должны расходиться, в смысле расширенных действительных чисел (в рамках проективно расширенной действительной линии пределом является беззнаковая бесконечность во всех трёх случаях [4] ). Аналогично любое выражение вида с (включая и ) не является неопределенной формой, поскольку частное, порождающее такое выражение, всегда будет расходиться.
Выражение не является неопределенной формой. Выражение полученное в результате рассмотрения дает предел при условии, что остается неотрицательным, так как подходы . Выражение аналогично эквивалентно ; если как подходы , предел получается как .
Чтобы понять, почему, позвольте где и Взяв натуральный логарифм обеих частей и используя мы поняли это это означает, что
Оценка неопределенных форм
[ редактировать ]Прилагательное неопределенное не означает , что предела не существует, как показывают многие приведенные выше примеры. Во многих случаях алгебраическое исключение, правило Лопиталя для манипулирования выражением и вычисления предела можно использовать или другие методы.
Эквивалент бесконечно малого
[ редактировать ]Когда две переменные и сходятся к нулю в одной и той же предельной точке и , они называются эквивалентными бесконечно малыми (экв. ).
Более того, если переменные и таковы, что и , затем:
Вот краткое доказательство:
Предположим, что существуют две эквивалентные бесконечно малые величины и .
Для оценки неопределенной формы , можно использовать следующие факты об эквивалентных бесконечно малых (например, если x становится ближе к нулю): [5]
Например:
Во 2-м равенстве где по мере того, как y становится ближе к 0, и используется где используется в 4-м равенстве, а используется в пятом равенстве.
Правило больницы
[ редактировать ]Правило Лопиталя — общий метод оценки неопределенных форм. и . Это правило гласит, что (при соответствующих условиях)
где и являются производными от и . (Обратите внимание, что это правило не распространяется на выражения , и т. д., поскольку эти выражения не являются неопределенными формами.) Эти производные позволят выполнить алгебраическое упрощение и в конечном итоге оценить предел.
Правило Лопиталя можно применить и к другим неопределенным формам, предварительно применив соответствующее алгебраическое преобразование. Например, чтобы оценить форму 0 0 :
Правая часть имеет вид , поэтому к нему применимо правило Лопиталя. Обратите внимание, что это уравнение справедливо (пока определена правая часть), поскольку натуральный логарифм (ln) является непрерывной функцией ; не имеет значения, насколько хорошо себя ведут и может (а может и не быть) до тех пор, пока является асимптотически положительной. (область логарифмов — это совокупность всех положительных действительных чисел.)
Хотя правило Лопиталя применимо к обоим и , одна из этих форм может быть более полезна, чем другая в конкретном случае (из-за возможности последующего алгебраического упрощения). Между этими формами можно переключаться, преобразуя к .
Список неопределенных форм
[ редактировать ]В следующей таблице перечислены наиболее распространенные неопределенные формы и преобразования для применения правила Лопиталя.
| Неопределенная форма | Условия | Преобразование в | Преобразование в |
|---|---|---|---|
| / | — | ||
| / | — | ||
См. также
[ редактировать ]- Определенный и неопределенный
- Деление на ноль
- Расширенная строка действительных чисел
- Неопределенное уравнение
- Неопределенная система
- Неопределенный (переменный)
- Правило больницы
Ссылки
[ редактировать ]Цитаты
[ редактировать ]- ^ Варберг, Перселл и Ригдон (2007) , с. 423, 429, 430, 431, 432.
- ^ Вайсштейн, Эрик В. «Неопределенный» . mathworld.wolfram.com . Проверено 2 декабря 2019 г.
- ^ Луи М. Ротандо; Генри Корн (январь 1977 г.). «Неопределенная форма 0 0 . Журнал Mathematics 50 ( 1): 41–42. doi : 10.2307/2689754 . JSTOR 2689754 .
- ^ «Неопределенное и неопределенное в математике» . www.cut-the-knot.org . Проверено 2 декабря 2019 г.
- ^ «Таблица эквивалентных бесконечно малых» (PDF) . Программное обеспечение Vaxa .
Библиографии
[ редактировать ]- Варберг, Дейл Э.; Перселл, Эдвин Дж.; Ригдон, Стивен Э. (2007). Исчисление (9-е изд.). Пирсон Прентис Холл . ISBN 978-0131469686 .
![{\displaystyle {\begin{aligned}\lim _{x\to c}{\bigl (}f(x)+g(x){\bigr)}&=\lim _{x\to c}f( x)+\lim _{x\to c}g(x),\\[3mu]\lim _{x\to c}{\bigl (}f(x)g(x){\bigr )}& =\lim _{x\to c}f(x)\cdot \lim _{x\to c}g(x),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/400168377cf61fda5b98b48170717381000c608f)
















































































![{\displaystyle {\begin{aligned}\lim _{x\to 0}{\frac {1}{x^{3}}}\left[\left({\frac {2+\cos x}{3 }}\right)^{x}-1\right]&=\lim _{x\to 0}{\frac {e^{x\ln {\frac {2+\cos x}{3}}} -1}{x^{3}}}\\&=\lim _{x\to 0}{\frac {1}{x^{2}}}\ln {\frac {2+\cos x} {3}}\\&=\lim _{x\to 0}{\frac {1}{x^{2}}}\ln \left({\frac {\cos x-1}{3}} +1\right)\\&=\lim _{x\to 0}{\frac {\cos x-1}{3x^{2}}}\\&=\lim _{x\to 0}- {\frac {x^{2}}{6x^{2}}}\\&=-{\frac {1}{6}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c77dd026051c68e8a3ae139a8a19259a5ba4ae15)




























