Плитка Амманн А1

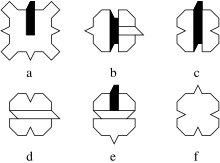
В геометрии плитка Ammann A1 представляет собой плитку из 6 частей, из набора прототипов показанного справа. Их нашел в 1977 году Роберт Амманн . ^{[ 1 ]} Амманн был вдохновлен плитками Робинсона , которые были найдены Робинсоном в 1971 году. Плитки А1 — один из пяти наборов плиток, обнаруженных Амманном и описанных в книге «Плитки и узоры» . ^{[ 2 ]}

Набор плиток A1 является апериодическим , ^{[ 2 ]} т.е. они замощают всю евклидову плоскость , но только без создания периодического замощения .

Генерация через сопоставление

Четыре поколения увеличивающихся патчей, составленных из прототипов A1.

Два варианта продолжения синего участка в левом верхнем углу для мозаики A1 в горизонтальном направлении и два дополнительных варианта в вертикальном направлении. Разобранный вид для лучшей видимости.

Прототайлы представляют собой квадраты с углублениями и выступами по бокам и углам, которые заставляют мозаику образовывать образец идеального двоичного дерева , продолжающегося бесконечно. Маркировка на плитках на рисунках подчеркивает эту иерархическую структуру , однако носит лишь иллюстративный характер и не представляет собой дополнительных правил сопоставления , поскольку об этом уже заботятся углубления и выступы.

Однако мозаика, полученная таким способом, не уникальна, даже с точки зрения изометрий евклидовой группы , например, сдвигов и вращений . Переходя к следующему поколению, у человека есть выбор. На рисунке слева начальный участок в левом верхнем углу, выделенный синим цветом, может быть продлен либо зеленой, либо красной плиткой, которые являются зеркальными отражениями друг друга и экземпляров прототипа, помеченного b . Дальше есть еще два варианта в том же духе, но с прототипом e . Остальная часть следующего поколения затем фиксируется. Если кто-то отклонится от шаблона следующего поколения, он столкнется с конфигурациями, которые не будут совпадать глобально, по крайней мере, на каком-то более позднем этапе.

Выбор закодирован бесконечными словами из $\Sigma ^{\omega }$ для алфавита $\Sigma =\{g,r\}$ , где g указывает на зеленый выбор, а r — на красный. ^{[ 3 ]} Они находятся в биекции к множеству Кантора и, таким образом, их мощность является континуумом . Не все варианты приводят к замощению плоскости. Например, если вы придерживаетесь только зеленого выбора, вы заполните только нижний правый угол плоскости. существует достаточно общее и бесконечно много изменений, Однако если между g и r одно из них покроет всю плоскость. В результате остается бесчисленное множество различных мозаик A1, причем все они обязательно непериодические. Поскольку существует только счетное количество возможных евклидовых изометрий, которые учитывают квадраты, лежащие в основе плиток, чтобы связать эти различные мозаики, существует несчетное количество мозаик A1 даже с точностью до изометрий.

Кроме того, мозаика A1 может иметь разломы (также называемые коридорами ), уходящие в бесконечность . Это дополнительно увеличивает количество возможных мозаик A1, но мощность остается такой же, как у континуума . Обратите внимание, что коридоры позволяют поворачивать некоторую часть с иерархией двоичного дерева по сравнению с другими такими частями.

Часть мозаики А1 с разломами. Разломы удлинены по сравнению с частями двоичного дерева для лучшей видимости.

Дальнейшие фотографии

Участок пятого поколения плитки Amman A1.

См. также

Ссылки

^ Гарднер, Мартин (2001), Колоссальная книга по математике , WW Norton & Company, стр. 76, ISBN 978-0393020236
^ Jump up to: ^а ^б Грюнбаум, Бранко и Шепард, Джеффри К. (1986). Плитки и узоры . Нью-Йорк: WH Freeman. ISBN 978-0-7167-1194-0 .
^ Грюнбаум, Бранко ; Шепард, Джеффри Колин (1987). Плитки и узоры . Нью-Йорк: WH Freeman. п. 528ф. ISBN 0-7167-1193-1 .

[ColMath-1] Гарднер, Мартин (2001), Колоссальная книга по математике , WW Norton & Company, стр. 76, ISBN 978-0393020236

[gs-2] Jump up to: ^а ^б Грюнбаум, Бранко и Шепард, Джеффри К. (1986). Плитки и узоры . Нью-Йорк: WH Freeman. ISBN 978-0-7167-1194-0 .

[gs2-3] Грюнбаум, Бранко ; Шепард, Джеффри Колин (1987). Плитки и узоры . Нью-Йорк: WH Freeman. п. 528ф. ISBN 0-7167-1193-1 .

[ 1 ]

[ 2 ]

[ 3 ]