Оценка плотности

Демонстрация оценки плотности с использованием оценки плотности ядра : Истинная плотность представляет собой смесь двух гауссиан с центрами вокруг 0 и 3, показанную сплошной синей кривой. В каждом кадре из распределения, показанного красным, генерируется 100 выборок. В центре каждой выборки серым цветом нарисовано ядро Гаусса. Усреднение гауссиан дает оценку плотности, показанную пунктирной черной кривой.

В статистике оценка плотности вероятности или просто оценка плотности — это построение оценки на основе наблюдаемых данных ненаблюдаемой основной функции плотности вероятности . Ненаблюдаемая функция плотности рассматривается как плотность, согласно которой распределяется большая популяция; данные обычно рассматриваются как случайная выборка из этой совокупности. ^[1]

Используются различные подходы к оценке плотности, включая окна Парцена и ряд методов кластеризации данных , включая векторное квантование . Самая базовая форма оценки плотности — это масштабированная гистограмма .

Пример

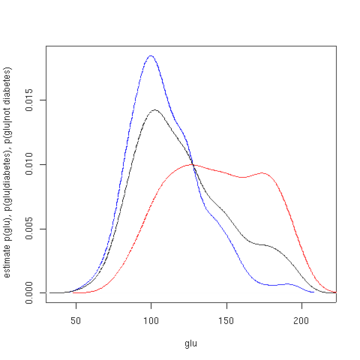
Мы рассмотрим записи заболеваемости сахарным диабетом . Следующее цитируется дословно из описания набора данных :

Популяция женщин в возрасте не менее 21 года, индейцев Пима , проживающих недалеко от Финикса, штат Аризона, была проверена на сахарный диабет в соответствии с критериями Всемирной организации здравоохранения . Данные были собраны Национальным институтом диабета, заболеваний органов пищеварения и почек США. Мы использовали 532 полные записи. ^[2]^[3]

В этом примере мы строим три оценки плотности для «glu» ( в плазме концентрации глюкозы ), одна зависит от наличия диабета,второй при условии отсутствия диабета, а третий не при условии диабета.Затем оценки условной плотности используются для построения вероятности диабета, зависящей от «глу».

Данные «glu» были получены из пакета MASS. ^[4] языка программирования R. Внутри Р, ?Pima.tr и ?Pima.te дать более полный отчет о данных.

Среднее значение «glu» в случаях диабета составляет 143,1, а стандартное отклонение — 31,26.Среднее значение «glu» в случаях отсутствия диабета составляет 110,0, а стандартное отклонение — 24,29.Из этого мы видим, что в этом наборе данных случаи диабета связаны с более высоким уровнем «глю».Это станет понятнее благодаря графикам оцененных функций плотности.

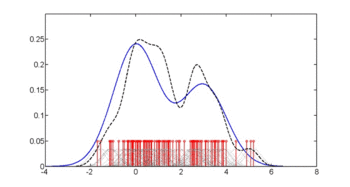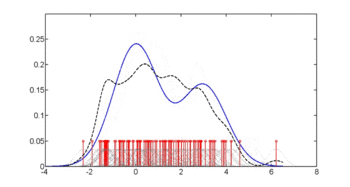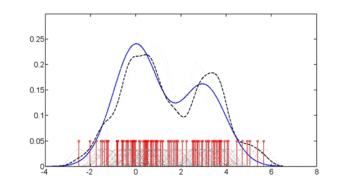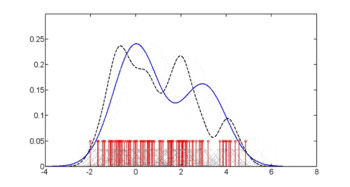
На первом рисунке показаны оценки плотности p (glu | диабет=1), p (glu | диабет=0) и p (glu).Оценки плотности представляют собой оценки плотности ядра с использованием ядра Гаусса. То есть функция плотности Гаусса помещается в каждую точку данных, а сумма функций плотности вычисляется по диапазону данных.

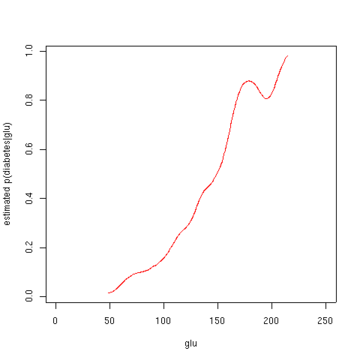
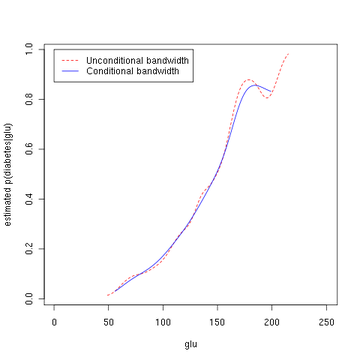
Из плотности «глю», обусловленного диабетом, мы можем получить вероятность диабета, обусловленного «глю», с помощью правила Байеса . Для краткости слово «диабет» обозначается сокращенно «дб». в этой формуле.

p({\mbox{diabetes}}=1|{\mbox{glu}})={\frac {p({\mbox{glu}}|{\mbox{db.}}=1)\,p({\mbox{db.}}=1)}{p({\mbox{glu}}|{\mbox{db.}}=1)\,p({\mbox{db.}}=1)+p({\mbox{glu}}|{\mbox{db.}}=0)\,p({\mbox{db.}}=0)}}

На втором рисунке показана предполагаемая апостериорная вероятность p (диабет = 1 | glu). Из этих данных следует, что повышенный уровень «глу» связан с диабетом.

Применение и цель

Очень естественным использованием оценок плотности является неформальное исследование свойств данного набора данных. Оценки плотности могут дать ценное представление о таких особенностях, как асимметрия и мультимодальность данных. В некоторых случаях они приведут к выводам, которые затем можно будет считать самоочевидно верными, тогда как в других все, что они сделают, — это укажут путь к дальнейшему анализу и/или сбору данных. ^[5]

Важным аспектом статистики часто является представление данных клиенту с целью объяснения и иллюстрации выводов, которые могли быть получены другими способами. Оценки плотности идеально подходят для этой цели по той простой причине, что они довольно легко понятны нематематикам.

Дополнительные примеры, иллюстрирующие использование оценок плотности в исследовательских и презентационных целях, включая важный случай двумерных данных. ^[7]

Оценка плотности также часто используется при обнаружении аномалий или обнаружении новизны : ^[8] если наблюдение находится в регионе с очень низкой плотностью населения, оно, скорее всего, будет аномалией или новинкой.

В гидрологии гистограмма и расчетная функция плотности данных об осадках и расходе рек, проанализированные с помощью распределения вероятностей , используются для понимания их поведения и частоты появления. ^[9] Пример показан на синем рисунке.

Оценка плотности ядра

В статистике (KDE) — это оценка плотности вероятности применение сглаживания ядра для оценки плотности вероятности , то есть непараметрический метод оценки функции плотности вероятности на случайной величины основе ядер в качестве весов . KDE решает фундаментальную проблему сглаживания данных, когда выводы о совокупности делаются на основе конечной выборки данных . В некоторых областях, таких как обработка сигналов и эконометрика, его также называют методом окна Парцена-Розенблатта в честь Эмануэля Парцена и Мюррея Розенблатта , которым обычно приписывают независимое создание его в его нынешней форме. ^[10]^[11] Одним из известных применений оценки плотности ядра является оценка условных классов предельных плотностей данных при использовании наивного байесовского классификатора , что может повысить точность его прогнозирования. ^[12]

См. также

Ссылки

^ Альберто Бернаккья, Симоне Пиголотти, Самосогласованный метод оценки плотности, Журнал Королевского статистического общества, серия B: Статистическая методология, том 73, выпуск 3, июнь 2011 г., страницы 407–422, https://doi.org/10.1111 /j.1467-9868.2011.00772.x
^ «Диабет у индийских женщин Пима - документация R» .
^ Смит, Дж.В., Эверхарт, Дж.Э., Диксон, В.К., Ноулер, В.К. и Йоханнес, Р.С. (1988). Р. А. Гринс (ред.). «Использование алгоритма обучения ADAP для прогнозирования возникновения сахарного диабета» . Материалы симпозиума по компьютерным приложениям в медицинской помощи (Вашингтон, 1988) . Лос-Аламитос, Калифорния: 261–265. ПМК 2245318 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ «Функции поддержки и наборы данных для Венейблса и МАССЫ Рипли» .
^ Сильверман, BW (1986). Оценка плотности для статистики и анализа данных . Чепмен и Холл. ISBN 978-0412246203 .
^ Калькулятор распределений вероятностей и функций плотности.
^ Джефф Х., Гивенс (2013). Вычислительная статистика. Уайли. п. 330. ISBN 978-0-470-53331-4 .
^ Пиментел, Марко А.Ф.; Клифтон, Дэвид А.; Клифтон, Лей; Тарасенко, Лионель (2 января 2014 г.). «Обзор обнаружения новизны». Обработка сигналов . 99 (июнь 2014 г.): 215–249. дои : 10.1016/j.sigpro.2013.12.026 .
^ Иллюстрация гистограмм и функций плотности вероятности.
^ Розенблатт, М. (1956). «Замечания о некоторых непараметрических оценках функции плотности» . Анналы математической статистики . 27 (3): 832–837. дои : 10.1214/aoms/1177728190 .
^ Парзен, Э. (1962). «Об оценивании функции плотности вероятности и режима» . Анналы математической статистики . 33 (3): 1065–1076. дои : 10.1214/aoms/1177704472 . JSTOR 2237880 .
^ Хасти, Тревор ; Тибширани, Роберт ; Фридман, Джером Х. (2001). Элементы статистического обучения: интеллектуальный анализ данных, логические выводы и прогнозирование: с 200 полноцветными иллюстрациями . Нью-Йорк: Спрингер. ISBN 0-387-95284-5 . OCLC 46809224 .

Источники

Брайан Д. Рипли (1996). Распознавание образов и нейронные сети . Кембридж: Издательство Кембриджского университета. ISBN 978-0521460866 .
Тревор Хэсти , Роберт Тибширани и Джером Фридман. Элементы статистического обучения . Нью-Йорк: Спрингер, 2001. ISBN 0-387-95284-5 . (См. главу 6.)
Ци Ли и Джеффри С. Расин. Непараметрическая эконометрика: теория и практика . Издательство Принстонского университета, 2007 г., ISBN 0-691-12161-3 . (См. главу 1.)
Д.В. Скотт. Многомерная оценка плотности. Теория, практика и визуализация . Нью-Йорк: Уайли, 1992.
Б. В. Сильверман . Оценка плотности . Лондон: Чепмен и Холл, 1986. ISBN 978-0-412-24620-3

Внешние ссылки

CREEM: Центр исследований в области экологического и экологического моделирования. Загрузка бесплатных пакетов программного обеспечения для оценки плотности Distance 4 (от исследовательского подразделения по оценке популяций дикой природы «RUWPA») и WiSP .
Сводка содержимого репозитория машинного обучения UCI (исходный набор данных из 732 записей и дополнительные примечания см. в «Базе данных по диабету индейцев пима»).
Код MATLAB для одномерной и двумерной оценки плотности
Программное обеспечение libAGF C++ для оценки переменной плотности ядра .

[1] Альберто Бернаккья, Симоне Пиголотти, Самосогласованный метод оценки плотности, Журнал Королевского статистического общества, серия B: Статистическая методология, том 73, выпуск 3, июнь 2011 г., страницы 407–422, https://doi.org/10.1111 /j.1467-9868.2011.00772.x

[2] «Диабет у индийских женщин Пима - документация R» .

[3] Смит, Дж.В., Эверхарт, Дж.Э., Диксон, В.К., Ноулер, В.К. и Йоханнес, Р.С. (1988). Р. А. Гринс (ред.). «Использование алгоритма обучения ADAP для прогнозирования возникновения сахарного диабета» . Материалы симпозиума по компьютерным приложениям в медицинской помощи (Вашингтон, 1988) . Лос-Аламитос, Калифорния: 261–265. ПМК 2245318 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )

[4] «Функции поддержки и наборы данных для Венейблса и МАССЫ Рипли» .

[5] Сильверман, BW (1986). Оценка плотности для статистики и анализа данных . Чепмен и Холл. ISBN 978-0412246203 .

[6] Калькулятор распределений вероятностей и функций плотности.

[7] Джефф Х., Гивенс (2013). Вычислительная статистика. Уайли. п. 330. ISBN 978-0-470-53331-4 .

[8] Пиментел, Марко А.Ф.; Клифтон, Дэвид А.; Клифтон, Лей; Тарасенко, Лионель (2 января 2014 г.). «Обзор обнаружения новизны». Обработка сигналов . 99 (июнь 2014 г.): 215–249. дои : 10.1016/j.sigpro.2013.12.026 .

[9] Иллюстрация гистограмм и функций плотности вероятности.

[Kernel_density_estimation_Ros1956-10] Розенблатт, М. (1956). «Замечания о некоторых непараметрических оценках функции плотности» . Анналы математической статистики . 27 (3): 832–837. дои : 10.1214/aoms/1177728190 .

[Kernel_density_estimation_Par1962-11] Парзен, Э. (1962). «Об оценивании функции плотности вероятности и режима» . Анналы математической статистики . 33 (3): 1065–1076. дои : 10.1214/aoms/1177704472 . JSTOR 2237880 .

[Kernel_density_estimation_:0-12] Хасти, Тревор ; Тибширани, Роберт ; Фридман, Джером Х. (2001). Элементы статистического обучения: интеллектуальный анализ данных, логические выводы и прогнозирование: с 200 полноцветными иллюстрациями . Нью-Йорк: Спрингер. ISBN 0-387-95284-5 . OCLC 46809224 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]