Октакуб (скульптура)

Октакуб , — большая из нержавеющей стали скульптура выставленная на математическом факультете Университета штата Пенсильвания в Государственном колледже, штат Пенсильвания . Скульптура представляет собой математический объект, называемый 24-клеточным или «октакубом». Поскольку настоящая 24-ячеечная камера четырехмерна , произведение искусства на самом деле является проекцией в трехмерный мир.

Октакуб обладает очень высокой внутренней симметрией , которая соответствует особенностям химии ( молекулярная симметрия ) и физики ( квантовая теория поля ).

Скульптура была разработана Адрианом Окняну [ де ] , профессором математики в Университете штата Пенсильвания . Механический цех университета потратил больше года на выполнение сложной металлообработки. Octacube была профинансирована выпускницей в память о ее муже Кермите Андерсоне, погибшем во время терактов 11 сентября .

произведение искусства

имеет Металлический скелет Octacube размеры около 6 футов (1,8 метра) во всех трех измерениях. Это сложная конструкция из неокрашенных трехугольных фланцев. Основание представляет собой гранитный блок высотой 3 фута (0,91 метра) с гравировкой. ^[1]

Автором изображения выступил Адриан Окняну, профессор математики штата Пенсильвания. Он предоставил спецификации для 96 треугольных частей скульптуры из нержавеющей стали и для их сборки. Изготовление производилось в механическом цехе Пенсильванского университета под руководством Джерри Андерсона. Работа заняла больше года и включала в себя гибку, сварку и резку. Обсуждая строительство, Окняну сказал: ^[1]

Очень сложно заставить 12 стальных листов идеально соприкоснуться друг с другом (и конформно) в каждой из 23 вершин, не оставив следов сварки. Люди, построившие его, действительно являются экспертами мирового уровня и перфекционистами, художниками по стали.

Из-за отражающего света металла под разными углами внешний вид выглядит приятно странно. В некоторых случаях зеркальные поверхности создают иллюзию прозрачности, показывая отражения с неожиданных сторон конструкции. Создатель скульптуры-математик прокомментировал: ^[1]

Когда я увидел настоящую скульптуру, я был в шоке. Я никогда не представлял себе игру света на поверхностях. Существуют тонкие оптические эффекты, которые вы можете почувствовать, но не можете уловить.

Вид на Октакуб с разных точек зрения

Интерпретация

Правильные формы

Платоновы тела представляют собой трехмерные формы, обладающие особой высокой симметрией . Это следующий шаг вперед по размеру по сравнению с двумерными правильными многоугольниками (квадратами, равносторонними треугольниками и т. д.). Пять платоновых тел — это тетраэдр (4 грани), куб (6 граней), октаэдр (8 граней), додекаэдр (12 граней) и икосаэдр (20 граней). Они известны со времен древних греков и ценятся за эстетическую привлекательность и философское, даже мистическое значение. (См. также «Тимей» , диалог Платона .)

Платоновы тела

Тетраэдр	Куб	Октаэдр	Додекаэдр	Икосаэдр

В более высоких измерениях аналогами Платоновых тел являются правильные многогранники . Эти формы были впервые описаны в середине 19 века швейцарским математиком Людвигом Шлефли . В четырех измерениях их шесть : пентахорон ( 5-ячеечный ), тессеракт ( 8-ячеечный ), гексадекахорон ( 16-ячеечный ), октакуб ( 24-ячеечный ), гекатоникосахорон ( 120-ячеечный ) и гексакосихорон ( 600 ячеек ).

24-ячейка состоит из 24 октаэдров , соединенных в 4-мерном пространстве. из 24 ячеек Вершинная фигура (трехмерная фигура, образующаяся при срезании четырехмерного угла) представляет собой куб. Несмотря на свое многозначительное название, октакуб не является четырехмерным аналогом ни октаэдра, ни куба. Фактически, это единственный из шести правильных четырехмерных многогранников, у которого отсутствует соответствующее платоново тело. ^{[примечание 1]}

Попытки представить себе 24-клеточную систему

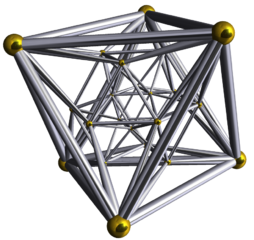Диаграмма Шлегеля	4-мерное вращение

Прогнозы

Окняну объясняет концептуальную проблему работы в четвертом измерении: ^[1] «Хотя математики могут абстрактно работать с четвертым измерением, добавляя четвертую координату к трем, которые мы используем для описания точки в пространстве, четвертое пространственное измерение трудно визуализировать».

Хотя невозможно увидеть или создать четырехмерные объекты, их можно перенести в более низкие измерения, чтобы получить о них некоторое представление. Аналогией преобразования 4-мерной 24-клеточной ячейки в ее трехмерную скульптуру является картографическая проекция , где поверхность трехмерной Земли (или глобуса) сводится к плоской двухмерной плоскости (переносимой карте). Это делается либо с помощью света, «отбрасывающего тень» от глобуса на карту, либо с помощью какого-либо математического преобразования. Существует множество различных типов картографических проекций: всем известная прямоугольная Меркатора (используется для навигации), круговая гномоническая (первая изобретенная проекция) и некоторые другие. Все они имеют ограничения, заключающиеся в том, что они показывают некоторые особенности в искаженном виде («нельзя сплющить апельсиновую корку, не повредив ее»), но они являются полезными наглядными пособиями и удобными справочными материалами.

Точно так же, как внешняя часть Земли представляет собой двумерную кожу (согнутую в третье измерение), внешняя часть четырехмерной фигуры представляет собой трехмерное пространство (но свернутое через гиперпространство, четвертое измерение). Однако, как поверхность земного шара не может быть отображена на плоскость без некоторых искажений, так и внешняя трехмерная форма 24-клеточной четырехмерной гиперформы не может быть отображена. На изображении справа показано, как 24 ячейки проецируются в пространство как трехмерный объект (а затем изображение представляет собой его двухмерную визуализацию с перспективой для помощи глазу). Некоторые искажения:

Изогнутые линии краев: они прямые в четырех измерениях, но при проекции в более низкое измерение они кажутся изогнутыми (аналогичные эффекты возникают при картографировании Земли).
Из-за сложности объекта необходимо использовать полупрозрачные грани, чтобы было видно множество «коробочек» (октаэдрических ячеек).
Отчетливо видны только 23 клетки. 24-я ячейка — это «снаружи внутри», все внешнее пространство вокруг объекта, как оно видно в трех измерениях.

Чтобы нанести на карту 24 ячейки, Окнеану использует родственную проекцию, которую он называет оконной радиальной стереографической проекцией . Как и в стереографической проекции, в трехмерном пространстве показаны изогнутые линии. Вместо использования полупрозрачных поверхностей в гранях ячеек вырезаются «окна», чтобы можно было видеть внутренние ячейки. Кроме того, физически присутствуют только 23 вершины. 24-я вершина «находится в бесконечности» из-за проекции; мы видим восемь ног и рук скульптуры, расходящихся наружу от центра трехмерной скульптуры. ^[1]

Симметрия

Скульптура Октакуб обладает очень высокой симметрией. Структура из нержавеющей стали имеет такую же симметрию, как куб или октаэдр. Произведение искусства можно представить в виде куба: руки и ноги конструкции доходят до углов. Вообразить октаэдр сложнее; оно предполагает размышление о гранях визуализируемого куба, образующих углы октаэдра. Куб и октаэдр имеют одинаковое количество и тип симметрии: октаэдрическая симметрия , называемая Oh ₍ порядок 48) в математической записи. Некоторые, но не все элементы симметрии

3 различные четыре оси вращения (по одной через каждую пару противоположных граней визуализируемого куба): вверх/вниз, внутрь/наружу и влево/вправо, как показано на фотографии.
4 разные оси тройного вращения (по одной через каждую пару противоположных углов куба [вдоль каждой из противоположных пар рук и ног])
6 различных осей двойного вращения (по одной через середину каждого противоположного края визуализируемого куба)
9 зеркальных плоскостей, которые делят визуализируемый куб пополам.
- 3, которые разрезают его сверху/снизу, слева/справа и спереди/сзади. Эти зеркала представляют собой отражающую двугранную субсимметрию D _2h порядка 8 (подчиненную симметрию любого объекта с октаэдрической симметрией).
- 6, которые идут по диагоналям противоположных граней визуализируемого куба (они проходят по двойным наборам пар рук-ног). Эти зеркала представляют его отражающую тетраэдрическую субсимметрию T _d порядка 24 (подчиненную симметрию любого объекта с октаэдрической симметрией).

Используя точки середины комнаты, скульптура представляет корневые системы типа D4, B4=C4 и F4, то есть все 4d, кроме A4. Он может визуализировать проекцию D4 на B3 и D4 на G2.

Научные аллюзии

Многие молекулы имеют ту же симметрию, что и скульптура Октакуба . Органическая молекула кубан (C ₈ H ₈ ) является одним из примеров. Руки и ноги скульптуры подобны выступающим наружу атомам водорода. Гексафторид серы (или любая молекула с точной октаэдрической молекулярной геометрией ) также имеет ту же симметрию, хотя сходство не такое уж большое.

Молекулы одинаковой симметрии

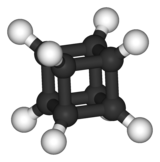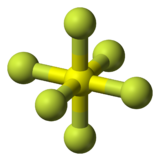Кубинский	Гексафторид серы

Octacube также показывает параллели с концепциями теоретической физики. Создатель Окняну исследует математические аспекты квантовой теории поля (КТП). назвал эту тему медали Филдса Обладатель Эд Виттен самой сложной областью физики. ^[2] Часть работы Окнеану заключается в построении теоретических и даже физических моделей особенностей симметрии в КТП. Окнеану приводит взаимосвязь внутренней и внешней половин структуры, аналогичную взаимосвязи частиц со спином 1/2 (например, электронов ) и частиц со спином 1 (например, фотонов ). ^[1]

Мемориал

Octacube был заказан и профинансирован Джилл Андерсон, выпускницей математического факультета ПГУ 1965 года, в память о ее муже Кермите, еще одном выпускнике математического факультета 1965 года, погибшем в результате террористических атак 11 сентября . ^[1] Подводя итог мемориала, Андерсон сказал: ^[1]

Я надеюсь, что скульптура побудит студентов, преподавателей, администраторов, выпускников и друзей задуматься и оценить удивительный мир математики. Я также надеюсь, что все, кто увидит скульптуру, начнут осознавать тот отрезвляющий факт, что каждый уязвим перед чем-то ужасным, происходящим с ним, и что мы все должны научиться жить одним днем, извлекая самое лучшее из того, что дано нам. нас. Было бы здорово, если бы каждый, кто посмотрит « Октакуб», уходил с ощущением, что быть добрым к другим — это хороший образ жизни.

Андерсон также профинансировал математическую стипендию на имя Кермита, в то же время проект скульптуры продолжался. ^[1]

Прием

Более полное объяснение скульптуры, включая то, как она была создана, как финансировалось ее строительство и ее роль в математике и физике , было предоставлено Пенсильванским университетом. ^[1] Кроме того, Окняну предоставил собственный комментарий. ^[3]

См. также

Художники:

Сальвадор Дали , художник, изображающий аллюзии четвертого измерения.
Дэвид Смит , скульптор абстрактной геометрической нержавеющей стали.
Тони Смит , еще один создатель больших абстрактных геометрических скульптур.

Математика:

Теория групп , математическая дисциплина, которая исторически включала в себя множество исследований симметрии.
Операторная алгебра и теория представлений , области математических исследований Окняну

Ссылки

Примечания

^ Четырехмерный аналог куба — 8-клеточный тессеракт . (Аналогично, трехмерным аналогом квадрата является куб.) Четырехмерным аналогом октаэдра является 16-клеточный гексадекахорон . Не существует правильного многогранника ( Платонового тела ), 4-мерным аналогом которого является октакуб (24 ячейки), но 4-D аналогом квазиправильного кубооктаэдра ( Архимедово тело ) является октакуб ( 24 ячейки ).

Цитаты

^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж Информационный бюллетень об Octacube , факультет математики Пенсильванского государственного университета, 13 октября 2005 г. (по состоянию на 6 мая 2013 г.)
^ «Прекрасные умы, Том 20: Эд Виттен» . ла Република . 2010 . Проверено 22 июня 2012 г. Здесь .
^ Математика 24-клеток , веб-сайт, поддерживаемый Адрианом Окнеану. Архивировано 1 сентября 2006 г. в Wayback Machine.

Внешние ссылки

Видео из штата Пенсильвания об Octacube
Пользователь создал видео о воображении четырехмерного объекта (но тессеракта). Обратите внимание на обсуждение прогнозов примерно через 22 минуты и обсуждение ячеек модели примерно через 35 минут.

40 ° 47'51,5 "с.ш. 77 ° 51'43,7" з.д. / 40,797639 ° с.ш. 77,862139 ° з.д. / 40,797639; -77,862139

[2] Четырехмерный аналог куба — 8-клеточный тессеракт . (Аналогично, трехмерным аналогом квадрата является куб.) Четырехмерным аналогом октаэдра является 16-клеточный гексадекахорон . Не существует правильного многогранника ( Платонового тела ), 4-мерным аналогом которого является октакуб (24 ячейки), но 4-D аналогом квазиправильного кубооктаэдра ( Архимедово тело ) является октакуб ( 24 ячейки ).

[PS1-1] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж Информационный бюллетень об Octacube , факультет математики Пенсильванского государственного университета, 13 октября 2005 г. (по состоянию на 6 мая 2013 г.)

[3] «Прекрасные умы, Том 20: Эд Виттен» . ла Република . 2010 . Проверено 22 июня 2012 г. Здесь .

[4] Математика 24-клеток , веб-сайт, поддерживаемый Адрианом Окнеану. Архивировано 1 сентября 2006 г. в Wayback Machine.

[1]

[примечание 1]

[2]

[3]