Lotka–Volterra equations

Эта статья об уравнениях хищник-жертва. Чтобы узнать об уравнениях конкуренции, см. Конкурентные уравнения Лотки – Вольтерра .

Уравнения Лотки-Вольтерра , также известные как модель хищник-жертва Лотки-Вольтерра , представляют собой пару нелинейных дифференциальных уравнений первого порядка , часто используемых для описания динамики биологических систем , в которых взаимодействуют два вида: один в качестве хищника , а другой в качестве хищника. другой как добыча. Популяции меняются со временем в соответствии с парой уравнений: $${\begin{aligned}{\frac {dx}{dt}}&=\alpha x-\beta xy,\\{\frac {dy}{dt}}&=-\gamma y+\delta xy,\end{aligned}}$$

где

• переменная добычи ( x — плотность популяции например, количество кроликов на квадратный километр);
• переменная y — плотность популяции какого-либо хищника (например, количество лисиц на квадратный километр);
• ${\tfrac {dy}{dt}}$ и ${\tfrac {dx}{dt}}$ представляют мгновенные темпы роста двух популяций;
• т представляет время;
• добычи Параметры , α и β , описывают, соответственно, максимальную скорость роста добычи на душу населения и влияние присутствия хищников на уровень смертности жертв.
• Параметры хищника, γ , δ , соответственно описывают уровень смертности хищника на душу населения и влияние присутствия добычи на скорость роста хищника.
• Все параметры положительные и реальные.

Решение дифференциальных уравнений является детерминированным и непрерывным . Это, в свою очередь, означает, что поколения хищника и жертвы постоянно перекрываются.

Система уравнений Лотки–Вольтерра является примером модели Колмогорова , Это более общая структура, которая может моделировать динамику экологических систем с взаимодействием хищник-жертва, конкуренцией , болезнями и мутуализмом .

Биологическая интерпретация и модельные предположения

Предполагается, что жертва имеет неограниченный запас пищи и размножается в геометрической прогрессии, если только она не подвергается нападению хищников; этот экспоненциальный рост представлен в приведенном выше уравнении термином αx . Предполагается, что скорость нападения хищников на жертву пропорциональна скорости встречи хищников и жертвы; выше это представлено как βxy . Если хотя бы x или y равны нулю, хищничества быть не может. С помощью этих двух членов приведенное выше уравнение добычи можно интерпретировать следующим образом: скорость изменения популяции добычи определяется ее собственным темпом роста минус скорость, с которой на нее охотятся.

Термин δxy представляет собой рост популяции хищников. (Обратите внимание на сходство со скоростью хищничества; однако используется другая константа, поскольку скорость роста популяции хищников не обязательно равна скорости, с которой они поедают добычу). Термин γy представляет собой уровень потерь хищников из-за естественной смерти или эмиграции; это приводит к экспоненциальному затуханию в отсутствие добычи. Следовательно, уравнение выражает, что скорость изменения популяции хищника зависит от скорости, с которой он поедает добычу, за вычетом его собственного уровня смертности.

Модель «хищник-жертва» Лотки-Вольтерры делает ряд предположений об окружающей среде и биологии популяций хищников и жертв:

1. Популяция добычи всегда находит достаточно еды.
2. Кормовая база популяции хищников полностью зависит от численности популяции жертв.
3. Скорость изменения численности населения пропорциональна ее численности.
4. В ходе этого процесса окружающая среда не меняется в пользу одного вида, и генетическая адаптация несущественна.
5. Хищники имеют безграничный аппетит.
6. Обе популяции могут быть описаны одной переменной. Это равнозначно предположению, что популяции не имеют пространственного или возрастного распределения, которое способствует динамике.

Биологическая значимость модели

Некоторое количество мехов зайца-беляка (желтый, на заднем плане) и канадской рыси (черная линия, на переднем плане), проданных компании Гудзонова залива . Канадские рыси едят зайцев-снегоступов.

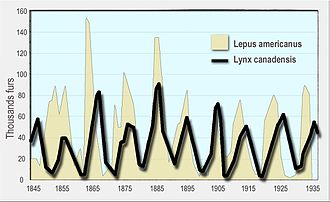
Ни одно из приведенных выше предположений вряд ли справедливо для естественных популяций. Тем не менее, модель Лотки-Вольтерра демонстрирует два важных свойства популяций хищников и жертв, и эти свойства часто распространяются на варианты модели, в которых эти предположения смягчены:

Во-первых, динамика популяций хищников и жертв имеет тенденцию к колебаниям. В естественных популяциях наблюдались колебания численности хищников и жертв, например, о рыси и зайце-снегоступе. данные компании Гудзонова залива а также популяции лосей и волков в национальном парке Айл-Рояль .

Во-вторых, популяционное равновесие этой модели обладает тем свойством, что равновесная плотность добычи (задаваемая выражением $x=\gamma /\delta$) зависит от параметров хищника и равновесной плотности хищника (задаваемой выражением $y=\alpha /\beta$) от параметров жертвы. Следствием этого является то, что увеличение, например, скорости роста добычи, $\alpha$, приводит к увеличению равновесной плотности хищников, но не равновесной плотности жертв. Улучшение окружающей среды для добычи приносит пользу хищнику, а не добыче (это связано с парадоксом пестицидов и парадоксом обогащения ). Проявлением этого явления служит возросший процент вылова хищных рыб, увеличившийся в годы 1-й мировой войны (1914–18), когда скорость роста добычи увеличилась за счет сокращения промыслового усилия.

Еще одним примером является экспериментальное удобрение океана железом. В нескольких экспериментах в океане было растворено большое количество солей железа. Ожидалось, что железо, которое является лимитирующим питательным веществом для фитопланктона, будет стимулировать рост фитопланктона и изолировать углекислый газ из атмосферы. Добавление железа обычно приводит к кратковременному цветению фиопланктона, который быстро потребляется другими организмами (например, мелкой рыбой или зоопланктоном ) и ограничивает эффект обогащения главным образом увеличением плотности хищников, что, в свою очередь, ограничивает секвестрацию углерода. Это предсказано равновесной плотностью населения в модели «хищник-жертва» Лотки-Вольтерры и является особенностью, которая переносится на более сложные модели, в которых ограничительные предположения простой модели смягчены.

Приложения к экономике и маркетингу

Модель Лотки – Вольтерры имеет дополнительные приложения в таких областях, как экономика. и маркетинг. Его можно использовать для описания динамики рынка с несколькими конкурентами, взаимодополняющими платформами и продуктами, экономикой совместного использования и многим другим. Существуют ситуации, в которых один из конкурентов вытесняет других конкурентов с рынка, и другие ситуации, в которых рынок достигает равновесия, при котором каждая фирма стабилизирует свою долю рынка. Также можно описать ситуации, в которых происходят циклические изменения в отрасли или хаотичные ситуации, в которых нет равновесия, а изменения часты и непредсказуемы.

История

«хищник-жертва» Лотки-Вольтерра Модель была первоначально предложена Альфредом Дж. Лоткой в ​​теории автокаталитических химических реакций в 1910 году. По сути, это было логистическое уравнение : первоначально выведен Пьером Франсуа Верхюльстом . расширил модель В 1920 году Лотка через Андрея Колмогорова до «органических систем», используя в качестве примера виды растений и виды травоядных животных. а в 1925 году он использовал эти уравнения для анализа взаимодействия хищник-жертва в своей книге по биоматематике . Тот же набор уравнений был опубликован в 1926 году Вито Вольтеррой , математиком и физиком, который заинтересовался математической биологией . Расследование Вольтерры было вдохновлено его общением с морским биологом Умберто Д'Анкона , который в то время ухаживал за его дочерью, а позже должен был стать его зятем. Д'Анкона изучал уловы рыбы в Адриатическом море и заметил, что в годы 1-й мировой войны (1914–18) процент выловленной хищной рыбы увеличился. Это озадачило его, поскольку за годы войны усилия рыболовства значительно сократились, а поскольку предпочтительным уловом является добыча рыбы, интуитивно можно было бы ожидать, что это приведет к увеличению процента добычи рыбы. Вольтерра разработал свою модель для объяснения наблюдения Д'Анконы и сделал это независимо от Альфреда Лотки. В своей публикации он упомянул более раннюю работу Лотки, после чего модель стала известна как «модель Лотки-Вольтерры».

Позже модель была расширена, включив в нее зависящий от плотности рост добычи и функциональную реакцию формы, разработанной К.С. Холлингом ; модель, которая стала известна как модель Розенцвейга – Макартура. Модели Лотки-Вольтерры и Розенцвейга-Макартура использовались для объяснения динамики естественных популяций хищников и жертв.

В конце 1980-х годов появилась альтернатива модели Лотки-Вольтерры «хищник-жертва» (и ее обобщения, зависящие от общей жертвы) - модель, зависящая от соотношения, или модель Ардити-Гинзбурга . Обоснованность моделей, зависящих от добычи или соотношения, широко обсуждается.

Уравнения Лотки-Вольтерра имеют долгую историю использования в экономической теории ; их первоначальную заявку обычно приписывают Ричарду Гудвину в 1965 году. или 1967 год.

Решения уравнений

Уравнения имеют периодические решения. Эти решения не имеют простого выражения в терминах обычных тригонометрических функций , хотя они вполне сносны.

Если ни один из неотрицательных параметров α , β , γ , δ не обращается в нуль, три можно включить в нормализацию переменных, чтобы оставить только один параметр: поскольку первое уравнение однородно по x , а второе по y , параметры β / α и δ / γ поглощаются при нормализации y и x соответственно, а γ — при нормализации t , так что только α / γ остается произвольным. Это единственный параметр, влияющий на характер решений.

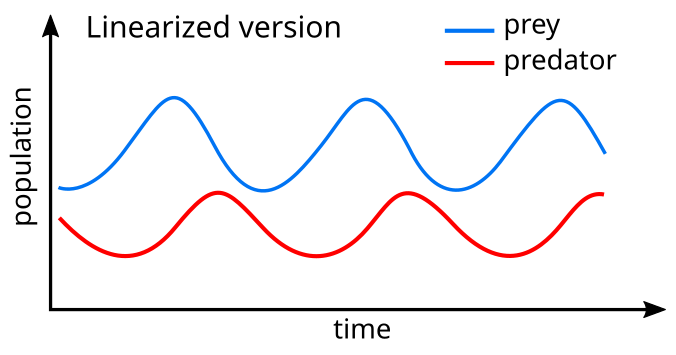
Линеаризация простому уравнений дает решение, подобное гармоническому движению. при этом популяция хищников отстает от популяции добычи на 90° в цикле.

Дополнительная информация: Предельный цикл.

Простой пример

Популяционная динамика проблемы кроликов и лисиц упомянута в стороне.

График в фазовом пространстве задачи «хищник-жертва» для различных начальных условий популяции хищников.

Предположим, есть два вида животных: кролик (добыча) и лиса (хищник). Если первоначальная плотность составляет 10 кроликов и 10 лисиц на квадратный километр, можно построить график развития этих двух видов с течением времени; с учетом параметров темпы роста и смертности кроликов составляют 1,1 и 0,4, а у лисиц - 0,1 и 0,4 соответственно. Выбор временного интервала произволен.

Можно также построить решения параметрически в виде орбит в фазовом пространстве без представления времени, но с одной осью, представляющей количество добычи, а другой осью, представляющей плотность хищников за все время.

Это соответствует исключению времени из двух приведенных выше дифференциальных уравнений для получения одного дифференциального уравнения.

${\frac {dy}{dx}}=-{\frac {y}{x}}{\frac {\delta x-\gamma }{\beta y-\alpha }}$

связывая переменные x (хищник) и y (добыча). Решениями этого уравнения являются замкнутые кривые. Он поддается разделению переменных : интегрированию

${\frac {\beta y-\alpha }{y}}\,dy+{\frac {\delta x-\gamma }{x}}\,dx=0$

дает неявное отношение

$V=\delta x-\gamma \ln(x)+\beta y-\alpha \ln(y),$

где V — постоянная величина, зависящая от начальных условий и сохраняющаяся на каждой кривой.

Отступление: эти графики иллюстрируют серьезное потенциальное ограничение в применении в качестве биологической модели: при таком конкретном выборе параметров в каждом цикле популяция кроликов сокращается до чрезвычайно низкой численности, но восстанавливается (в то время как популяция лисиц остается значительной на уровне самая низкая плотность кроликов). Однако в реальных ситуациях случайные колебания дискретного числа особей могут привести к фактическому вымиранию кроликов, а, как следствие, и лисиц. Эту задачу моделирования назвали «проблемой атто-лисы», причем атто -лиса является условным 10 ⁻¹⁸ лисы. Плотность 10 ⁻¹⁸ лисиц на квадратный километр соответствует в среднем примерно 5×10 ⁻¹⁰ лисиц на поверхности земли, что в практическом плане означает, что лисы вымерли.

Гамильтонова структура системы

Поскольку количество $V(x,y)$ сохраняется во времени, она играет роль гамильтоновой функции системы. Чтобы убедиться в этом, мы можем определить скобку Пуассона следующим образом: $\{f,g\}=-xy\left({\frac {\partial f}{\partial x}}{\frac {\partial g}{\partial y}}-{\frac {\partial f}{\partial y}}{\frac {\partial g}{\partial x}}\right)$. Тогда уравнения Гамильтона будут иметь вид $${\begin{cases}{\dot {x}}=\{x,V\}=\alpha x-\beta xy,\\{\dot {y}}=\{y,V\}=\delta xy-\gamma y.\end{cases}}$$Переменные $x$ и $y$ не являются каноническими, поскольку $\{x,y\}=-xy\neq 1$. Однако, используя преобразования $p=\ln(x)$ и $q=\ln(y)$ мы пришли к канонической форме уравнений Гамильтона с гамильтонианом $H(q,p)=V(x(q,p),y(q,p))=\delta e^{p}-\gamma p+\beta e^{q}-\alpha q$: $${\begin{cases}{\dot {q}}={\frac {\partial H}{\partial p}}=\delta e^{p}-\gamma ,\\{\dot {p}}=-{\frac {\partial H}{\partial q}}=\alpha -\beta e^{q}.\end{cases}}$$

График в фазовом пространстве еще одного примера

Менее крайний пример охватывает:

α знак равно 2/3 , β знак равно 4/3 , γ знак равно 1 знак равно δ . Предположим, что x и y измеряют тысячи каждый. Круги обозначают начальные условия добычи и хищника от x = y = 0,9 до 1,8 с шагом 0,1. Фиксированная точка находится в (1, 1/2).

Динамика системы

В модельной системе хищники процветают, когда добыча многочисленна, но в конечном итоге превосходят запасы пищи и сокращаются. Поскольку популяция хищников невелика, популяция жертв снова увеличится. Эта динамика продолжается в численности населения цикле роста и сокращения .

Равновесие населения

Равновесие численности населения возникает в модели, когда ни один из уровней численности населения не меняется, т.е. когда обе производные равны 0: $$x(\alpha -\beta y)=0,$$$$-y(\gamma -\delta x)=0.$$

Приведенная выше система уравнений дает два решения: $$\{y=0,\ \ x=0\}$$и $$\left\{y={\frac {\alpha }{\beta }},\ \ x={\frac {\gamma }{\delta }}\right\}.$$

Следовательно, существует два равновесия.

Первое решение фактически представляет собой вымирание обоих видов. Если обе популяции равны 0, то они будут оставаться такими до бесконечности. Второе решение представляет собой фиксированную точку, в которой обе популяции поддерживают свою текущую, ненулевую численность, и в упрощенной модели делают это бесконечно. Уровни численности населения, при которых достигается это равновесие, зависят от выбранных значений параметров α , β , γ и δ .

Стабильность фиксированных точек

Стабильность фиксированной точки в начале координат можно определить, выполнив линеаризацию с использованием частных производных .

Матрица Якоби модели хищник-жертва: $$J(x,y)={\begin{bmatrix}\alpha -\beta y&-\beta x\\\delta y&\delta x-\gamma \end{bmatrix}}.$$и известна как матрица сообщества .

Первая фиксированная точка (затухание)

При оценке в установившемся состоянии (0, 0) матрица Якоби J становится $$J(0,0)={\begin{bmatrix}\alpha &0\\0&-\gamma \end{bmatrix}}.$$

Собственные значения этой матрицы равны $$\lambda _{1}=\alpha ,\quad \lambda _{2}=-\gamma .$$

В модели α и γ всегда больше нуля, и поэтому знаки приведенных выше собственных значений всегда будут различаться. Следовательно, фиксированная точка в начале координат является седловой точкой .

Нестабильность этой неподвижной точки имеет значение. Если бы она была стабильной, к ней могли бы быть привлечены ненулевые популяции, и поэтому динамика системы могла бы привести к исчезновению обоих видов во многих случаях начального уровня популяции. Однако, поскольку фиксированная точка происхождения является седловой и, следовательно, нестабильной, из этого следует, что вымирание обоих видов в модели затруднено. (На самом деле, это могло произойти только в том случае, если бы жертва была искусственно полностью уничтожена, в результате чего хищники умерли от голода. Если бы хищники были уничтожены, популяция жертв в этой простой модели росла бы без ограничений.) Популяции жертв и хищников могут приблизиться к нулю и все равно восстановиться.

Вторая фиксированная точка (колебания)

Оценка J во второй фиксированной точке приводит к $$J\left({\frac {\gamma }{\delta }},{\frac {\alpha }{\beta }}\right)={\begin{bmatrix}0&-{\frac {\beta \gamma }{\delta }}\\{\frac {\alpha \delta }{\beta }}&0\end{bmatrix}}.$$

Собственные значения этой матрицы равны $$\lambda _{1}=i{\sqrt {\alpha \gamma }},\quad \lambda _{2}=-i{\sqrt {\alpha \gamma }}.$$

Поскольку собственные значения являются чисто мнимыми и сопряжены друг с другом, эта неподвижная точка должна быть либо центром замкнутых орбит в локальной окрестности, либо спиралью притяжения или отталкивания. В консервативных системах должны существовать замкнутые орбиты в локальной окрестности неподвижных точек, существующих в минимумах и максимумах сохраняющейся величины. Сохраняющаяся величина получена выше как $V=\delta x-\gamma \ln(x)+\beta y-\alpha \ln(y)$ на орбитах. Таким образом, орбиты вокруг фиксированной точки замкнуты и эллиптические , поэтому решения являются периодическими, колеблющимися по небольшому эллипсу вокруг фиксированной точки с частотой $\omega ={\sqrt {\lambda _{1}\lambda _{2}}}={\sqrt {\alpha \gamma }}$ и период $T=2{\pi }/({\sqrt {\lambda _{1}\lambda _{2}}})$.

Как показано на циркуляционных колебаниях на рисунке выше, кривые уровня представляют собой замкнутые орбиты, окружающие фиксированную точку: уровни популяций хищника и жертв циклически колеблются и колеблются без затухания вокруг фиксированной точки с частотой. $\omega ={\sqrt {\alpha \gamma }}$.

Значение константы движения V или, что то же самое, K = exp(− V ) , $K=y^{\alpha }e^{-\beta y}x^{\gamma }e^{-\delta x}$, можно найти для замкнутых орбит вблизи неподвижной точки.

Увеличение K приближает замкнутую орбиту к фиксированной точке. Наибольшее значение константы K получается при решении оптимизационной задачи $$y^{\alpha }e^{-\beta y}x^{\gamma }e^{-\delta x}={\frac {y^{\alpha }x^{\gamma }}{e^{\delta x+\beta y}}}\longrightarrow \max _{x,y>0}.$$ Таким образом, максимальное значение K достигается в стационарной (неподвижной) точке. $\left({\frac {\gamma }{\delta }},{\frac {\alpha }{\beta }}\right)$ и составляет $$K^{*}=\left({\frac {\alpha }{\beta e}}\right)^{\alpha }\left({\frac {\gamma }{\delta e}}\right)^{\gamma },$$где е — число Эйлера .

См. также

• Конкурентные уравнения Лотки – Вольтерра
• Обобщенное уравнение Лотки – Вольтерра.
• Мутуализм и уравнение Лотки – Вольтерра
• Матрица сообщества
• Динамика населения
• Динамика численности рыбного хозяйства
• Модель Николсона – Бейли
• Реакционно-диффузионная система
• Парадокс обогащения
• Законы Ланчестера , аналогичная система дифференциальных уравнений для военных сил.
• Random generalized Lotka–Volterra model
• Модель потребительских ресурсов

Дальнейшее чтение

• Хофбауэр, Йозеф; Зигмунд, Карл (1998). «Динамические системы и уравнения Лотки – Вольтерра». Эволюционные игры и демографическая динамика . Нью-Йорк: Издательство Кембриджского университета. стр. 1–54. ISBN  0-521-62570-Х .
• Каплан, Дэниел; Гласс, Леон (1995). Понимание нелинейной динамики . Нью-Йорк: Спрингер. ISBN  978-0-387-94440-1 .
• Ли, скорая помощь (1968). «Экологическая роль уравнений Вольтерра». Некоторые математические проблемы биологии . - современная дискуссия с использованием данных компании Гудзонова залива о рыси и зайцах в Канаде с 1847 по 1903 год.
• Мюррей, доктор юридических наук (2003). Математическая биология I: Введение . Нью-Йорк: Спрингер. ISBN  978-0-387-95223-9 . '
• Конспект лекций курса Стефано Аллесины по экологии сообщества: https://stefanoallesina.github.io/Theoretical_Community_Ecology/

Внешние ссылки

• Из демонстрационного проекта Wolfram — требуется проигрыватель CDF (бесплатно) :
  • Уравнения хищник-жертва
  • Модель «Хищник-жертва»
  • Динамика хищник-жертва с функциональной реакцией второго типа
  • Экосистема «Хищник-жертва»: агентное моделирование в реальном времени
• Алгоритмическое моделирование Лотки-Вольтерра (Веб-моделирование).