Кривизна

Эта статья о математике и связанных с ней понятиях геометрии. Чтобы узнать о других значениях, см. Кривизна (значения) .

Продолжительность: 23 секунды. 0:23

дикого типа Мигрирующая клетка Dictyostelium discoideum , граница которой окрашена кривизной. Масштабная линейка: 5 мкм.

В математике геометрии кривизна – это любое из нескольких тесно связанных понятий в , которые интуитивно измеряют величину, на которую кривая отклоняется от прямой линии или на которую поверхность отклоняется от плоскости . Если кривая или поверхность содержится в большем пространстве, кривизну можно определить внешне относительно окружающего пространства. Кривизну римановых многообразий размерности не менее двух можно определить внутренне, без привязки к большему пространству.

Для кривых каноническим примером является круг , кривизна которого равна обратной величине его радиуса . Меньшие круги изгибаются резче и, следовательно, имеют большую кривизну. Кривизна в точке дифференцируемой кривой — это кривизна соприкасающейся с ней окружности , то есть окружности, которая лучше всего аппроксимирует кривую вблизи этой точки. Кривизна прямой равна нулю. В отличие от тангенса , который является векторной величиной, кривизна в точке обычно является скалярной величиной, то есть выражается одним действительным числом .

более высокой размерности Для поверхностей (и, в более общем плане, для многообразий ), вложенных в евклидово пространство , понятие кривизны более сложное, поскольку оно зависит от выбора направления на поверхности или многообразии. Это приводит к понятиям максимальной кривизны , минимальной кривизны и средней кривизны .

История

В «Трактате о конфигурациях качеств и движений» философ и математик XIV века Николь Орем вводит понятие кривизны как меры отклонения от прямолинейности; для кругов кривизна обратно пропорциональна радиусу; и он пытается распространить эту идею на другие кривые как на непрерывно меняющуюся величину.

Кривизна дифференцируемой кривой первоначально определялась через соприкасающиеся окружности . В этом случае Огюстен-Луи Коши показал, что центр кривизны является точкой пересечения двух бесконечно близких нормалей к кривой.

Плоские кривые

Интуитивно понятно, что кривизна описывает для любой части кривой, насколько сильно меняется направление кривой на небольшом пройденном расстоянии (например, угол в рад/м ), поэтому это мера мгновенной скорости изменения направления . точки, которая движется кривая: чем больше кривизна, тем больше скорость изменения. Другими словами, кривизна измеряет, насколько быстро вращается единичный касательный вектор к кривой в точке p. когда точка p движется с единичной скоростью по кривой. Фактически, можно доказать, что эта мгновенная скорость изменения и есть кривизна. Точнее, предположим, что точка движется по кривой с постоянной скоростью в одну единицу, то есть положение точки P ( s ) является функцией параметра s , который можно рассматривать как время или как длина дуги от заданного начала. Пусть T ( s ) — единичный касательный вектор кривой в точке ( s ) , который также является производной P P ( s ) по s . Тогда производная T ( s ) по s представляет собой вектор, нормальный к кривой и длина которого равна кривизне.

Чтобы иметь смысл, определение кривизны и ее различные характеристики требуют, чтобы кривая была непрерывно дифференцируемой вблизи P , чтобы иметь касательную, которая непрерывно меняется; требуется также, чтобы кривая была дважды дифференцируемой в точке P для обеспечения существования задействованных пределов и производной T ( s ) .

Характеристика кривизны через производную единичного касательного вектора, вероятно, менее интуитивна, чем определение через соприкасающуюся окружность, но формулы для вычисления кривизны вывести легче. Поэтому, а также из-за ее использования в кинематике , эту характеристику часто дают как определение кривизны.

Соприкасающийся круг

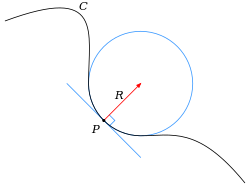
Исторически кривизна дифференцируемой кривой определялась через соприкасающуюся окружность , которая наилучшим образом аппроксимирует кривую в определенной точке. Точнее, для данной точки P на кривой каждая другая точка Q кривой определяет окружность (или иногда линию), проходящую через Q и касающуюся кривой в точке P . Соприкасающийся круг — это предел , если он существует, этого круга, когда стремится к P. Q Тогда центр и радиус кривизны кривой в точке P являются центром и радиусом соприкасающейся окружности. Кривизна обратна радиусу кривизны. То есть кривизна

$\kappa ={\frac {1}{R}},$

где R — радиус кривизны (весь круг имеет такую ​​кривизну, ее можно прочитать как поворот на 2π на длине 2π R ).

Этим определением трудно манипулировать и выразить его в формулах. Поэтому были введены другие эквивалентные определения.

С точки зрения параметризации длины дуги

Любая дифференцируемая кривая может быть параметризована по длине дуги . В случае плоской кривой это означает существование параметризации γ ( s ) = ( x ( s ), y ( s )) , где x и y — вещественнозначные дифференцируемые функции, производные которых удовлетворяют условию

$\|{\boldsymbol {\gamma }}'\|={\sqrt {x'(s)^{2}+y'(s)^{2}}}=1.$

Это означает, что касательный вектор

$\mathbf {T} (s)={\bigl (}x'(s),y'(s){\bigr )}$

имеет длину, равную единице, и, таким образом, является единичным касательным вектором .

Если кривая дважды дифференцируема, то есть если существуют вторые производные x и y , то существует производная T ( s ) . Этот вектор нормален к кривой, его длина равна кривизне κ ( s ) и ориентирован к центру кривизны. То есть,

${\begin{aligned}\mathbf {T} (s)&={\boldsymbol {\gamma }}'(s),\\[8mu]\|\mathbf {T} (s)\|^{2}&=1\ {\text{(constant)}}\implies \mathbf {T} '(s)\cdot \mathbf {T} (s)=0,\\[5mu]\kappa (s)&=\|\mathbf {T} '(s)\|=\|{\boldsymbol {\gamma }}''(s)\|={\sqrt {x''(s)^{2}+y''(s)^{2}}}\end{aligned}}$

Более того, поскольку радиус кривизны (при условии 𝜿 ( s ) ≠ 0)

$R(s)={\frac {1}{\kappa (s)}},$

а центр кривизны находится на нормали к кривой, то центром кривизны является точка

$\mathbf {C} (s)={\boldsymbol {\gamma }}(s)+{\frac {1}{\kappa (s)^{2}}}\mathbf {T} '(s).$

(В случае, если кривизна равна нулю, центр кривизны не находится нигде на плоскости R ² и часто говорят, что он расположен «на бесконечности».)

Если N ( s ) — единичный вектор нормали, полученный из T ( s ) вращением против часовой стрелки ⁠ π / 2 ⁠ , тогда

$\mathbf {T} '(s)=k(s)\mathbf {N} (s),$

с k ( s ) знак равно ± κ ( s ) . Действительное число k ( s ) называется ориентированной кривизной или знаковой кривизной . Это зависит как от ориентации плоскости (определение против часовой стрелки), так и от ориентации кривой, предусмотренной параметризацией. Фактически, замена переменной s → – s обеспечивает другую параметризацию длины дуги и меняет знак k ( s ) .

С точки зрения общей параметризации

Пусть γ ( t ) = ( x ( t ), y ( t )) — собственное параметрическое представление дважды дифференцируемой плоской кривой. Здесь собственно означает, что в области определения параметризации производная ⁠ d γ / dt ⁠ определен, дифференцируем и нигде не равен нулевому вектору.

При такой параметризации знаковая кривизна равна

$k={\frac {x'y''-y'x''}{{\bigl (}{x'}^{2}+{y'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}},$

где штрихи относятся к производным по t . Таким образом, кривизна κ равна

$\kappa ={\frac {\left|x'y''-y'x''\right|}{{\bigl (}{x'}^{2}+{y'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}}.$

Их можно выразить в бескоординатном виде как

$k={\frac {\det \left({\boldsymbol {\gamma }}',{\boldsymbol {\gamma }}''\right)}{\|{\boldsymbol {\gamma }}'\|^{3}}},\qquad \kappa ={\frac {\left|\det \left({\boldsymbol {\gamma }}',{\boldsymbol {\gamma }}''\right)\right|}{\|{\boldsymbol {\gamma }}'\|^{3}}}.$

Эти формулы можно вывести из частного случая параметризации длины дуги следующим образом. Из приведенных выше условий параметризации следует, что длина дуги s является дифференцируемой монотонной функцией параметра t и, наоборот, что t является монотонной функцией от s . Более того, заменив при необходимости s на – s , можно предположить, что эти функции возрастают и имеют положительную производную. Используя обозначения предыдущего раздела и правило цепочки , имеем

${\frac {d{\boldsymbol {\gamma }}}{dt}}={\frac {ds}{dt}}\mathbf {T} ,$

и, таким образом, взяв норму обеих сторон

${\frac {dt}{ds}}={\frac {1}{\|{\boldsymbol {\gamma }}'\|}},$

где штрих обозначает дифференцирование по t .

Кривизна — это норма производной T по s . Используя приведенную выше формулу и цепное правило, эту производную и ее норму можно выразить только через γ ′ и γ ″ , при этом параметр длины дуги s полностью исключается, что дает приведенные выше формулы для кривизны.

График функции

График функции y = f ( x ) является частным случаем параметризованной кривой вида

${\begin{aligned}x&=t\\y&=f(t).\end{aligned}}$

Поскольку первая и вторая производные x равны 1 и 0, предыдущие формулы упрощаются до

$\kappa ={\frac {\left|y''\right|}{{\bigl (}1+{y'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}},$

для кривизны и для

$k={\frac {y''}{{\bigl (}1+{y'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}},$

для знаковой кривизны.

В общем случае кривой знак знаковой кривизны несколько произволен, так как зависит от ориентации кривой. В случае графика функции существует естественная ориентация по возрастанию значения x . Это делает существенным знак знаковой кривизны.

Знак знаковой кривизны тот же, что и знак второй производной f . Если оно положительное, то график имеет вогнутость вверх, а если отрицательное, то график имеет вогнутость вниз. Если оно равно нулю, то имеется точка перегиба или точка волнистости .

Когда наклон графика (то есть производной функции) мал, знаковая кривизна хорошо аппроксимируется второй производной. Точнее, используя обозначение большого О , имеем

$k(x)=y''{\Bigl (}1+O{\bigl (}{\textstyle y'}^{2}{\bigr )}{\Bigr )}.$

принято В физике и технике аппроксимировать кривизну второй производной, например, в теории балок или для вывода волнового уравнения натянутой струны, а также в других приложениях, где задействованы небольшие наклоны. Это часто позволяет системы, которые в остальном являются нелинейными, рассматривать примерно как линейные.

Полярные координаты

Если кривая определяется в полярных координатах радиусом, выраженным как функция полярного угла, то есть r является функцией θ , то ее кривизна равна

$\kappa (\theta )={\frac {\left|r^{2}+2{r'}^{2}-r\,r''\right|}{{\bigl (}r^{2}+{r'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}}$

где штрих относится к дифференцированию по θ .

Это следует из формулы для общей параметризации при рассмотрении параметризации

${\begin{aligned}x&=r(\theta )\cos \theta \\y&=r(\theta )\sin \theta \end{aligned}}$

Неявная кривая

Для кривой, определяемой неявным уравнением F ( x , y ) = 0 с частными производными, обозначенными F _x , F _y , F _xx , F _xy , F _yy ,кривизна определяется выражением

$\kappa ={\frac {\left|F_{y}^{2}F_{xx}-2F_{x}F_{y}F_{xy}+F_{x}^{2}F_{yy}\right|}{{\bigl (}F_{x}^{2}+F_{y}^{2}{\bigr )}{\vphantom {'}}^{3/2}}}.$

Знаковая кривизна не определена, поскольку она зависит от ориентации кривой, не предусмотренной неявным уравнением. Обратите внимание, что изменение F на – F не изменит кривую, определяемую F ( x , y ) = 0 , но изменит знак числителя, если абсолютное значение было опущено в предыдущей формуле.

Точка кривой, где F _x = F _y = 0, является особой точкой , а это означает, что кривая не дифференцируема в этой точке, а значит, и кривизна не определена (чаще всего точка является либо точкой пересечения, либо точкой пересечения). острие ) .

Приведенную выше формулу для кривизны можно вывести из выражения кривизны графика функции, используя теорему о неявной функции и тот факт, что на такой кривой имеем

${\frac {dy}{dx}}=-{\frac {F_{x}}{F_{y}}}.$

Примеры

Может быть полезно на простых примерах убедиться, что различные формулы, приведенные в предыдущих разделах, дают один и тот же результат.

Круг

Обычная параметризация круга радиуса r : γ ( t ) = ( r cos t , r sin t ) . Формула кривизны дает

$k(t)={\frac {r^{2}\sin ^{2}t+r^{2}\cos ^{2}t}{{\bigl (}r^{2}\cos ^{2}t+r^{2}\sin ^{2}t{\bigr )}{\vphantom {'}}^{3/2}}}={\frac {1}{r}}.$

Отсюда, как и ожидалось, следует, что радиус кривизны — это радиус круга, а центр кривизны — это центр круга.

Круг — это редкий случай, когда параметризацию длины дуги легко вычислить, поскольку она

${\boldsymbol {\gamma }}(s)=\left(r\cos {\frac {s}{r}},\,r\sin {\frac {s}{r}}\right).$

Это параметризация длины дуги, поскольку норма

${\boldsymbol {\gamma }}'(s)=\left(-\sin {\frac {s}{r}},\,\cos {\frac {s}{r}}\right)$

равен единице. Эта параметризация дает то же значение кривизны, поскольку она представляет собой деление на r ³ как в числителе, так и в знаменателе предыдущей формулы.

Тот же круг также можно определить неявным уравнением F ( x , y ) = 0 с F ( x , y ) = x ² + и ² – р ² . Тогда формула кривизны в этом случае дает

${\begin{aligned}\kappa &={\frac {\left|F_{y}^{2}F_{xx}-2F_{x}F_{y}F_{xy}+F_{x}^{2}F_{yy}\right|}{{\bigl (}F_{x}^{2}+F_{y}^{2}{\bigr )}{\vphantom {'}}^{3/2}}}\\&={\frac {8y^{2}+8x^{2}}{{\bigl (}4x^{2}+4y^{2}{\bigr )}{\vphantom {'}}^{3/2}}}\\&={\frac {8r^{2}}{{\bigl (}4r^{2}{\bigr )}{\vphantom {'}}^{3/2}}}={\frac {1}{r}}.\end{aligned}}$

Парабола

Рассмотрим параболу y = ax ² + бх + с .

Это график функции с производной 2 ax + b и второй производной 2 a . Итак, знаковая кривизна равна

$k(x)={\frac {2a}{{\bigl (}1+\left(2ax+b\right)^{2}{\bigr )}{\vphantom {)}}^{3/2}}}.$

Он имеет знак a для всех значений x . Это означает, что если а > 0 , то вогнутость всюду направлена ​​вверх; если a < 0 , вогнутость направлена ​​вниз; для a = 0 кривизна всюду равна нулю, что подтверждает, что в этом случае парабола вырождается в прямую.

(Беззнаковая) кривизна максимальна при x = – ⁠ b / 2 a ⁠ , то есть в точке покоя (нулевой производной) функции, являющейся вершиной параболы.

Рассмотрим параметризацию γ ( t ) = ( t , at ² + bt + c ) знак равно ( Икс , y ) . Первая производная x равна 1 , а вторая производная равна нулю. Подстановка в формулу для общей параметризации дает точно такой же результат, как указано выше, с x заменой на t . Если мы используем простые числа для производных по параметру t .

Та же парабола также может быть определена неявным уравнением F ( x , y ) = 0 с F ( x , y ) = ax ² + bx + c – y . Поскольку F _y = –1 и F _yy = F _xy = 0 , можно получить точно такое же значение для (беззнаковой) кривизны. Однако кривизна со знаком здесь бессмысленна, поскольку – F ( x , y ) = 0 является действительным неявным уравнением для той же параболы, которое дает противоположный знак кривизны.

Формулы Френе – Серре для плоских кривых

Векторы T и N в двух точках плоской кривой — транслированная версия второго кадра (пунктир) и δ T — изменение T . Здесь δs — расстояние между точками. В пределе ⁠ d T / ds ⁠ будет в N. направлении Кривизна описывает скорость вращения рамы.

Выражение кривизны. С точки зрения параметризации длины дуги , по сути, это первая формула Френе – Серре.

$\mathbf {T} '(s)=\kappa (s)\mathbf {N} (s),$

где штрихи относятся к производным по длине дуги s , а N ( s ) — единичный вектор нормали в направлении T ′(s) .

Поскольку плоские кривые имеют нулевое кручение , вторая формула Френе – Серре дает соотношение

${\begin{aligned}{\frac {d\mathbf {N} }{ds}}&=-\kappa \mathbf {T} ,\\&=-\kappa {\frac {d{\boldsymbol {\gamma }}}{ds}}.\end{aligned}}$

Для общей параметризации параметром t нужны выражения, включающие производные по t . Поскольку они получаются умножением на ⁠ ds / dt ⁠ производные по s , которые есть для любой правильной параметризации

$\mathbf {N} '(t)=-\kappa (t){\boldsymbol {\gamma }}'(t).$

Гребень кривизны

Гребень кривизны

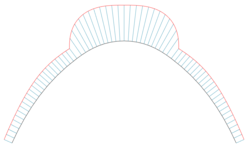
Гребень кривизны может использоваться для графического представления кривизны каждой точки кривой. Если $t\mapsto x(t)$ является параметризованной кривой, ее гребенка определяется как параметризованная кривая

$t\mapsto x(t)+d\kappa (t)n(t)$

где $\kappa ,n$ – вектор кривизны и нормали, $d$ — коэффициент масштабирования (выбирается для улучшения графического представления).

Пространственные кривые

Анимация кривизны и вектора ускорения T ′( s )

Как и в случае с кривыми в двух измерениях, кривизна регулярной пространственной кривой C в трех измерениях (и выше) представляет собой величину ускорения частицы, движущейся с единичной скоростью по кривой. Таким образом, если γ ( s ) является параметризацией длины дуги C , то единичный касательный вектор T ( s ) определяется выражением

$\mathbf {T} (s)={\boldsymbol {\gamma }}'(s)$

а кривизна - это величина ускорения:

$\kappa (s)=\|\mathbf {T} '(s)\|=\|{\boldsymbol {\gamma }}''(s)\|.$

Направление ускорения — это единичный вектор нормали N ( s ) , который определяется формулой

$\mathbf {N} (s)={\frac {\mathbf {T} '(s)}{\|\mathbf {T} '(s)\|}}.$

Плоскость, содержащая два вектора T ( s ) и N ( s ), является плоскостью, соприкасающейся с кривой в точке γ ( s ) . Кривизна имеет следующую геометрическую интерпретацию. существует окружность, В соприкасающейся плоскости, касающейся γ ( s ), которой ряд Тейлора в точке контакта второго порядка совпадает с рядом Тейлора γ ( s ) . Это соприкасающийся круг с кривой. Радиус окружности R ( s ) называется радиусом кривизны , а кривизна обратна радиусу кривизны:

$\kappa (s)={\frac {1}{R(s)}}.$

Касательная, кривизна и вектор нормали вместе описывают поведение кривой второго порядка вблизи точки. В трех измерениях поведение кривой третьего порядка описывается родственным понятием кручения , которое измеряет степень, в которой кривая имеет тенденцию двигаться по винтовой траектории в пространстве. Кручение и кривизна связаны формулами Френе – Серре (в трех измерениях) и их обобщением (в более высоких измерениях).

Общие выражения

Для параметрически определенной пространственной кривой в трех измерениях, заданной в декартовых координатах как γ ( t ) = ( x ( t ), y ( t ), z ( t )) , кривизна равна

$\kappa ={\frac {\sqrt {{\bigl (}z''y'-y''z'{\bigr )}{\vphantom {'}}^{2}+{\bigl (}x''z'-z''x'{\bigr )}{\vphantom {'}}^{2}+{\bigl (}y''x'-x''y'{\bigr )}{\vphantom {'}}^{2}}}{{\bigl (}{x'}^{2}+{y'}^{2}+{z'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}},$

где штрих означает дифференцирование по параметру t . Независимо от системы координат это можно выразить формулой

$\kappa ={\frac {{\bigl \|}{\boldsymbol {\gamma }}'\times {\boldsymbol {\gamma }}''{\bigr \|}}{{\bigl \|}{\boldsymbol {\gamma }}'{\bigr \|}{\vphantom {'}}^{3}}}$

где × обозначает векторное векторное произведение . Следующая формула действительна для кривизны кривых в евклидовом пространстве любой размерности:

$\kappa ={\frac {\sqrt {{\bigl \|}{\boldsymbol {\gamma }}'{\bigr \|}{\vphantom {'}}^{2}{\bigl \|}{\boldsymbol {\gamma }}''{\bigr \|}{\vphantom {'}}^{2}-{\bigl (}{\boldsymbol {\gamma }}'\cdot {\boldsymbol {\gamma }}''{\bigr )}{\vphantom {'}}^{2}}}{{\bigl \|}{\boldsymbol {\gamma }}'{\bigr \|}{\vphantom {'}}^{3}}}.$

Кривизна от дуги и длины хорды

Учитывая две точки P и Q на C , пусть s ( P , Q ) будет длиной дуги части кривой между P и Q и пусть d ( P , Q ) обозначает длину отрезка прямой от P до Q. , Кривизна C в точке P определяется пределом

$\kappa (P)=\lim _{Q\to P}{\sqrt {\frac {24{\bigl (}s(P,Q)-d(P,Q){\bigr )}}{s(P,Q){\vphantom {Q}}^{3}}}}$

где предел берется, когда точка Q приближается к P на C . Знаменатель с тем же успехом можно принять равным d ( P , Q ) ³ . Формула справедлива в любом измерении. Более того, если рассматривать предел независимо по обе стороны от P , это определение кривизны иногда может учитывать особенность в P. точке Формула следует путем проверки ее для соприкасающегося круга.

Поверхности

Более широкий охват этой темы см. в разделе «Дифференциальная геометрия поверхностей» .

Кривизна кривых, нарисованных на поверхности, является основным инструментом определения и изучения кривизны поверхности.

Кривые на поверхностях

Для кривой, нарисованной на поверхности (встроенной в трехмерное евклидово пространство ), определяются несколько кривизн, которые связывают направление кривизны с единичным вектором нормали поверхности , включая:

• нормальная кривизна
• геодезическая кривизна
• геодезическое кручение

У любой неособой кривой на гладкой поверхности касательный вектор T содержится в касательной плоскости поверхности. Нормальная кривизна — kn _и это кривизна кривой, проецируемой на плоскость, содержащую касательную T кривой нормаль к поверхности u ; геодезическая кривизна g k _— это кривизна кривой, проецируемой на касательную плоскость поверхности; а геодезическое кручение (или относительное кручение ), τ _r , измеряет скорость изменения нормали к поверхности вокруг касательной кривой.

Пусть кривая параметризована по длине дуги , и пусть t = u × T так, что T , t , u образуют ортонормированный базис , называемый рамкой Дарбу . Вышеуказанные количества связаны соотношением:

${\begin{pmatrix}\mathbf {T} '\\\mathbf {t} '\\\mathbf {u} '\end{pmatrix}}={\begin{pmatrix}0&\kappa _{\mathrm {g} }&\kappa _{\mathrm {n} }\\-\kappa _{\mathrm {g} }&0&\tau _{\mathrm {r} }\\-\kappa _{\mathrm {n} }&-\tau _{\mathrm {r} }&0\end{pmatrix}}{\begin{pmatrix}\mathbf {T} \\\mathbf {t} \\\mathbf {u} \end{pmatrix}}$

Основная кривизна

Седловая поверхность с нормальными плоскостями в направлениях главных кривизн.

Основная статья: Главная кривизна

Все кривые на поверхности с одинаковым касательным вектором в данной точке будут иметь одинаковую нормальную кривизну, которая совпадает с кривизной кривой, полученной при пересечении поверхности с плоскостью, содержащей T и u . Если взять все возможные касательные векторы, то максимальные и минимальные значения нормальной кривизны в точке называются главными кривизнами , k ₁ и k ₂ , а направления соответствующих касательных векторов называются главными нормальными направлениями .

Обычные разделы

Кривизну можно оценить по нормальным сечениям поверхности , аналогично § Кривым на поверхностях выше (см., например, радиус кривизны Земли ).

Развертывающиеся поверхности

Некоторые изогнутые поверхности, например, сделанные из гладкого листа бумаги, можно сгладить до плоскости, никоим образом не исказив их внутренние характеристики. Такие развертывающиеся поверхности имеют нулевую гауссову кривизну (см. ниже).

Гауссова кривизна

Основная статья: Гауссова кривизна

В отличие от кривых, которые не имеют внутренней кривизны, но имеют внешнюю кривизну (они имеют кривизну только при условии вложения), поверхности могут иметь внутреннюю кривизну, независимую от вложения. Гауссова кривизна , названная в честь Карла Фридриха Гаусса , равна произведению главных кривизн k ₁ k ₂ . Имеет размерность длины ⁻² и положителен для сфер , отрицателен для однополостных гиперболоидов и равен нулю для плоскостей и цилиндров . Он определяет, является ли поверхность локально выпуклой (когда она положительная) или локально седловидной (когда она отрицательная).

Гауссова кривизна является внутренним свойством поверхности, то есть она не зависит от конкретного вложения поверхности; интуитивно это означает, что муравьи, живущие на поверхности, могли определить гауссову кривизну. Например, муравей, живущий на сфере, мог измерить сумму внутренних углов треугольника и определить, что он больше 180 градусов, а это означает, что пространство, в котором он обитает, имеет положительную кривизну. С другой стороны, муравей, живущий на цилиндре, не заметил бы такого отклонения от евклидовой геометрии ; в частности, муравей не смог обнаружить, что две поверхности имеют разную среднюю кривизну (см. ниже), что является чисто внешним типом кривизны.

Формально гауссова кривизна зависит только от римановой метрики поверхности. Это Гаусса знаменитая «Теорема Эгрегиум» , которую он нашел, занимаясь географическими исследованиями и картографированием.

Внутреннее определение гауссовой кривизны в точке P следующее: представьте себе муравья, привязанного к P короткой нитью длины r . Он обходит P, нить полностью натянута, и измеряет длину C ( r ) одного полного обхода P. пока Если бы поверхность была плоской, муравей нашел бы C ( r ) = 2π r . На искривленных поверхностях формула для C ( r ) будет другой, а гауссова кривизна K в точке P может быть вычислена по теореме Бертрана – Диге – Пюизо как

$K=\lim _{r\to 0^{+}}3\left({\frac {2\pi r-C(r)}{\pi r^{3}}}\right).$

Интеграл гауссовой кривизны по поверхности всей поверхности тесно связан с эйлеровой характеристикой ; см . теорему Гаусса–Бонне .

Дискретным аналогом кривизны, соответствующим концентрации кривизны в точке и особенно полезным для многогранников , является (угловой) дефект ; аналогом теоремы Гаусса – Бонне является теорема Декарта о полном угловом дефекте .

Поскольку (гауссова) кривизна может быть определена без ссылки на пространство вложения, нет необходимости, чтобы поверхность была встроена в пространство более высокой размерности, чтобы быть искривленной. Такая внутренне искривленная двумерная поверхность является простым примером риманова многообразия .

Средняя кривизна

Основная статья: Средняя кривизна

Средняя кривизна — это внешняя мера кривизны, равная половине суммы главных кривизн . ⁠ k ₁ + k ₂ / 2 ⁠ . Имеет размерность длины ⁻¹ . Средняя кривизна тесно связана с первым изменением площади поверхности . В частности, минимальная поверхность, такая как мыльная пленка, имеет нулевую среднюю кривизну, а мыльный пузырь имеет постоянную среднюю кривизну. В отличие от кривизны Гаусса, средняя кривизна является внешней и зависит от вложения, например, цилиндр и плоскость локально изометричны, но средняя кривизна плоскости равна нулю, а средняя кривизна цилиндра не равна нулю.

Вторая фундаментальная форма

Основная статья: Вторая фундаментальная форма

Внутреннюю и внешнюю кривизну поверхности можно объединить во второй фундаментальной форме. Это квадратичная форма в касательной плоскости к поверхности в точке, значение которой в конкретном касательном векторе X к поверхности является нормальной составляющей ускорения кривой вдоль касательной к поверхности X поверхности ; то есть это нормальная кривизна кривой, касательной к X (см. Выше ). Символически,

$\operatorname {I\!I} (\mathbf {X} ,\mathbf {X} )=\mathbf {N} \cdot (\nabla _{\mathbf {X} }\mathbf {X} )$

где N — единица измерения нормали к поверхности. Для единичных касательных векторов X вторая фундаментальная форма принимает максимальное значение k ₁ и минимальное значение k ₂ , которые встречаются в главных направлениях u ₁ и u ₂ соответственно. Таким образом, по теореме о главной оси вторая фундаментальная форма равна

$\operatorname {I\!I} (\mathbf {X} ,\mathbf {X} )=k_{1}\left(\mathbf {X} \cdot \mathbf {u} _{1}\right)^{2}+k_{2}\left(\mathbf {X} \cdot \mathbf {u} _{2}\right)^{2}.$

Таким образом, вторая фундаментальная форма кодирует как внутреннюю, так и внешнюю кривизну.

Оператор формы

Дополнительная информация: Оператор формы.

Инкапсуляцию кривизны поверхности можно найти в операторе формы S , который представляет собой самосопряженный линейный оператор от касательной плоскости к себе (в частности, дифференциал отображения Гаусса ).

Для поверхности с касательными векторами X и нормалью N оператор формы можно компактно выразить в обозначениях суммирования индексов как

$\partial _{a}\mathbf {N} =-S_{ba}\mathbf {X} _{b}.$

(Сравните альтернативное выражение кривизны плоской кривой.)

Уравнения Вайнгартена дают значение S через коэффициенты первой и второй фундаментальных форм как

$S=\left(EG-F^{2}\right)^{-1}{\begin{pmatrix}eG-fF&fG-gF\\fE-eF&gE-fF\end{pmatrix}}.$

Главные кривизны — это собственные значения оператора формы, главные направления кривизны — его собственные векторы , кривизна Гаусса — его определитель , а средняя кривизна — половина его следа .

Искривление пространства

Дополнительная информация: Кривизна римановых многообразий и искривленное пространство.

«Кривизна пространства» перенаправляется сюда. Не путать с искривлением пространства-времени .

В рамках первого аргумента пространство трех или более измерений может быть искривлено по своей природе. Кривизна является внутренней в том смысле, что это свойство, определенное в каждой точке пространства, а не свойство, определенное по отношению к большему пространству, которое ее содержит. В общем, искривленное пространство может быть задумано, а может и не быть задумано как встроенное в окружающее пространство более высокого измерения ; если нет, то его кривизну можно определить только внутренне.

После открытия внутреннего определения кривизны, которое тесно связано с неевклидовой геометрией , многие математики и ученые задавались вопросом, может ли обычное физическое пространство быть искривленным, хотя успех евклидовой геометрии до того времени означал, что радиус кривизны должен быть астрономически большим. В общей теории относительности , описывающей гравитацию и космологию , идея слегка обобщается на «искривление пространства-времени »; В теории относительности пространство-время представляет собой псевдориманово многообразие . После определения временной координаты трехмерное пространство, соответствующее конкретному времени, обычно представляет собой искривленное риманово многообразие; но поскольку выбор временной координаты в значительной степени произволен, физически значимой является лежащая в основе кривизна пространства-времени.

пространства Хотя произвольно искривленное пространство очень сложно описать, кривизна локально изотропного и однородного описывается одной гауссовой кривизной, как и для поверхности; математически это сильные условия, но они соответствуют разумным физическим предположениям (все точки и все направления неразличимы). Положительная кривизна соответствует обратному квадратному радиусу кривизны; примером является сфера или гиперсфера . Примером отрицательно искривленного пространства является гиперболическая геометрия (см. также: неположительная кривизна ). Пространство или пространство-время с нулевой кривизной называется плоским . Например, евклидово пространство является примером плоского пространства, а пространство Минковского — примером плоского пространства-времени. Однако в обоих случаях есть и другие примеры плоской геометрии. , И тору и цилиндру могут быть присвоены плоские метрики, но они различаются топологией . Для искривленного пространства возможны и другие топологии. (см. также: Форма Вселенной ) .

Обобщения

Перемещение вектора по кривой от A → N → B → A дает другой вектор. Невозможность вернуться к исходному вектору измеряется голономностью поверхности. В пространстве без кривизны угол α равен 0 градусов, а в пространстве с кривизной угол α больше 0 градусов. Чем больше пространство искривлено, тем больше величина угла α.

Математическое понятие кривизны также определяется в гораздо более общем контексте. Многие из этих обобщений подчеркивают различные аспекты кривизны, как она понимается в более низких измерениях.

Одним из таких обобщений является кинематическое. Кривизну кривой, естественно, можно рассматривать как кинематическую величину, представляющую силу, которую ощущает определенный наблюдатель, движущийся по кривой; аналогично, кривизну в более высоких измерениях можно рассматривать как своего рода приливную силу (это один из способов представления о кривизне сечения ). Это обобщение кривизны зависит от того, как близлежащие пробные частицы расходятся или сходятся, когда им разрешено свободно перемещаться в пространстве; см. поле Якоби .

Другое широкое обобщение кривизны связано с изучением параллельного переноса на поверхности. Например, если вектор перемещается по петле на поверхности сферы, сохраняя параллельность на протяжении всего движения, то конечное положение вектора может не совпадать с начальным положением вектора. Это явление известно как голономия . Различные обобщения в абстрактной форме отражают эту идею кривизны как меры голономии; см. форма кривизны . Тесно связанное понятие кривизны исходит из калибровочной теории в физике, где кривизна представляет собой поле, а векторный потенциал поля — это величина, которая, как правило, зависит от пути: она может измениться, если наблюдатель движется по петле.

Еще два обобщения кривизны — это скалярная кривизна и кривизна Риччи . В искривленной поверхности, такой как сфера, площадь диска на поверхности отличается от площади диска того же радиуса в плоском пространстве. Эта разница (в подходящем пределе) измеряется скалярной кривизной. Разница в площади сектора диска измеряется кривизной Риччи. Скалярная кривизна и кривизна Риччи определяются аналогичным образом в трех и более высоких измерениях. Они особенно важны в теории относительности, где они оба появляются на стороне уравнений поля Эйнштейна , которые представляют геометрию пространства-времени (другая сторона которого представляет наличие материи и энергии). Эти обобщения кривизны лежат, например, в основе представления о том, что кривизна может быть свойством меры ; см . кривизну меры .

Другое обобщение кривизны основано на способности сравнивать искривленное пространство с другим пространством, имеющим постоянную кривизну. Часто это делается с помощью треугольников в пробелах. Понятие треугольника имеет смысл в метрических пространствах , и это приводит к появлению CAT( k ) пространств .

См. также

• Форма кривизны соответствующего понятия кривизны для векторных расслоений и главных расслоений со связностью
• Кривизна меры для понятия кривизны в теории меры
• Кривизна параметрических поверхностей
• Кривизна римановых многообразий для обобщений кривизны Гаусса на римановы многообразия более высокой размерности
• Вектор кривизны и геодезическая кривизна для соответствующих понятий кривизны кривых в римановых многообразиях любой размерности
• Степень кривизны
• Дифференциальная геометрия кривых для полного рассмотрения кривых, вложенных в евклидово пространство произвольной размерности.
• Диоптрия — мера кривизны, используемая в оптике.
• Эволюта , местоположение центров кривизны данной кривой.
• Основная теорема о кривых
• Теорема Гаусса – Бонне для элементарного применения кривизны.
• Карта Гаусса для получения дополнительных геометрических свойств кривизны Гаусса.
• Принцип наименьшего ограничения Гаусса , выражение принципа наименьшего действия.
• Средняя кривизна в одной точке поверхности
• Минимальный радиус поворота железной дороги
• Радиус кривизны
• Вторая фундаментальная форма внешней кривизны гиперповерхностей вообще.
• Извилистость
• Кручение кривой

Ссылки

• Кулидж, Джулиан Л. (июнь 1952 г.). «Неудовлетворительная история кривизны». Американский математический ежемесячник . 59 (6): 375–379. дои : 10.2307/2306807 . JSTOR   2306807 .
• Соколов, Дмитрий Дмитриевич (2001) [1994], «Кривизна» , Энциклопедия Математики , EMS Press
• Клайн, Моррис (1998). Исчисление: интуитивный и физический подход . Дувр. стр. 457–461. ISBN  978-0-486-40453-0 . ( ограниченная онлайн-копия , стр. 457, в Google Книгах )
• Клаф, А. Альберт (1956). Курс повышения квалификации по исчислению . Дувр. стр. 151–168 . ISBN  978-0-486-20370-6 . ( ограниченная онлайн-копия , стр. 151, в Google Книгах )
• Кейси, Джеймс (1996). Исследование кривизны . Вьюег+Тойбнер. ISBN  978-3-528-06475-4 .

Внешние ссылки

• Фейнмановские лекции по физике Vol. II гл. 42: Искривленное пространство
• История кривизны
• Кривизна, внутренняя и внешняя на MathPages