Теорема о разделении гиперплоскостей

Теорема о разделении гиперплоскостей

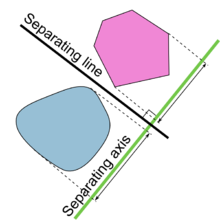Иллюстрация теоремы об отделении гиперплоскостей.
Тип	Теорема
Поле	Выпуклая геометрия Топологические векторные пространства Обнаружение столкновений
Предполагается	Герман Минковский
Открытая проблема	Нет
Обобщения	Теорема Хана – Банаха о разделении

В геометрии — теорема об отделении гиперплоскости это теорема о непересекающихся выпуклых множествах в n -мерном евклидовом пространстве . Есть несколько довольно похожих версий. В одной из версий теоремы, если оба этих множества замкнуты и хотя бы одно из них компактно , то между ними существует гиперплоскость и даже две параллельные гиперплоскости между ними, разделенные промежутком. В другой версии, если оба непересекающихся выпуклых множества открыты, между ними есть гиперплоскость, но не обязательно какой-либо разрыв. Ось, ортогональная разделяющей гиперплоскости, является разделяющей осью , поскольку ортогональные проекции выпуклых тел на ось не пересекаются.

Теорема о разделении гиперплоскостей принадлежит Герману Минковскому . Теорема Хана-Банаха о разделении обобщает результат на топологические векторные пространства .

Родственным результатом является теорема о опорной гиперплоскости .

В контексте машин опорных векторов оптимально разделяющая гиперплоскость или гиперплоскость с максимальным запасом — это гиперплоскость , которая разделяет две выпуклые оболочки точек и равноудалена от них.

Заявления и доказательства

Теорема о разделении гиперплоскостей - Позволять $A$ и $B$ — два непересекающихся непустых выпуклых подмножества $\mathbb {R} ^{n}$. Тогда существует ненулевой вектор $v$ и реальное число $c$ такой, что

$\langle x,v\rangle \geq c\,{\text{ and }}\langle y,v\rangle \leq c$

для всех $x$ в $A$ и $y$ в $B$; то есть гиперплоскость $\langle \cdot ,v\rangle =c$, $v$ нормальный вектор отделяет $A$ и $B$.

Если оба множества замкнуты и хотя бы одно из них компактно, то разделение может быть строгим, т. е. $\langle x,v\rangle >c_{1}\,{\text{ and }}\langle y,v\rangle <c_{2}$ для некоторых $c_{1}>c_{2}$

Во всех случаях предполагайте $A,B$ быть непересекающимися, непустыми и выпуклыми подмножествами $\mathbb {R} ^{n}$. Краткое изложение результатов следующее:

сводная таблица

$A$	$B$	$\langle x,v\rangle$	$\langle y,v\rangle$
		$\geq c$	$\leq c$
закрытый компактный	закрыто	$>c_{1}$	$<c_{2}$ с $c_{2}<c_{1}$
закрыто	закрытый компактный	$>c_{1}$	$<c_{2}$ с $c_{2}<c_{1}$
открыть		$>c$	$\leq c$
открыть	открыть	$>c$	$<c$

Число измерений должно быть конечным. В бесконечномерных пространствах есть примеры двух замкнутых, выпуклых, непересекающихся множеств, которые не могут быть разделены замкнутой гиперплоскостью (гиперплоскостью, в которой непрерывный линейный функционал равен некоторой константе) даже в слабом смысле, когда неравенства не являются строгими.

Здесь компактность гипотезы ослабить нельзя; см. пример в разделе Контрпримеры и уникальность . Эта версия теоремы разделения действительно обобщается на бесконечномерные области; это обобщение более широко известно как теорема разделения Хана – Банаха .

Доказательство основано на следующей лемме:

Лемма — Пусть $A$ и $B$ быть двумя непересекающимися замкнутыми подмножествами $\mathbb {R} ^{n}$и предположим $A$ компактен. Тогда существуют точки $a_{0}\in A$ и $b_{0}\in B$ минимизация расстояния $\|a-b\|$ над $a\in A$ и $b\in B$.

Доказательство леммы

Позволять $a\in A$ и $b\in B$ — любая пара точек, и пусть $r_{1}=\|b-a\|$. С $A$ компактен, он содержится в некотором шаре с центром $a$; пусть радиус этого шара будет $r_{2}$. Позволять $S=B\cap {\overline {B_{r_{1}+r_{2}}(a)}}$ быть пересечением $B$ с закрытым шаром радиуса $r_{1}+r_{2}$ вокруг $a$. Затем $S$ компактен и непуст, поскольку содержит $b$. Поскольку функция расстояния непрерывна, существуют точки $a_{0}$ и $b_{0}$ чье расстояние $\|a_{0}-b_{0}\|$ является минимумом по всем парам точек в $A\times S$. Осталось показать, что $a_{0}$ и $b_{0}$ фактически имеют минимальное расстояние по всем парам точек в $A\times B$. Предположим от противного, что существуют точки $a'$ и $b'$ такой, что $\|a'-b'\|<\|a_{0}-b_{0}\|$. Тогда, в частности, $\|a'-b'\|<r_{1}$, и по неравенству треугольника $\|a-b'\|\leq \|a'-b'\|+\|a-a'\|<r_{1}+r_{2}$. Поэтому $b'$ содержится в $S$, что противоречит тому факту, что $a_{0}$ и $b_{0}$ имел минимальное расстояние $A\times S$. $\square$

Доказательство иллюстрации.

Доказательство теоремы

Сначала докажем второй случай. (Смотрите схему.)

блог, $A$ компактен. По лемме существуют точки $a_{0}\in A$ и $b_{0}\in B$ минимального расстояния друг от друга.С $A$ и $B$ непересекающиеся, мы имеем $a_{0}\neq b_{0}$. Теперь построим две гиперплоскости $L_{A},L_{B}$ перпендикулярно отрезку $[a_{0},b_{0}]$, с $L_{A}$ через $a_{0}$ и $L_{B}$ через $b_{0}$. Мы утверждаем, что ни $A$ ни $B$ входит в пространство между $L_{A},L_{B}$, и, следовательно, перпендикулярные гиперплоскости к $(a_{0},b_{0})$ удовлетворяют требованию теоремы.

Алгебраически гиперплоскости $L_{A},L_{B}$ определяются вектором $v:=b_{0}-a_{0}$и две константы $c_{A}:=\langle v,a_{0}\rangle <c_{B}:=\langle v,b_{0}\rangle$, такой, что $L_{A}=\{x:\langle v,x\rangle =c_{A}\},L_{B}=\{x:\langle v,x\rangle =c_{B}\}$. Наше утверждение состоит в том, что $\forall a\in A,\langle v,a\rangle \leq c_{A}$ и $\forall b\in B,\langle v,b\rangle \geq c_{B}$.

Предположим, есть какой-то $a\in A$ такой, что $\langle v,a\rangle >c_{A}$, тогда пусть $a'$ быть основанием перпендикуляра из $b_{0}$ к отрезку прямой $[a_{0},a]$. С $A$ является выпуклым, $a'$ находится внутри $A$, и по планарной геометрии, $a'$ ближе к $b_{0}$ чем $a_{0}$, противоречие. Аналогичный аргумент применим и к $B$.

Теперь о первом случае.

Подход к обоим $A,B$ изнутри через $A_{1}\subseteq A_{2}\subseteq \cdots \subseteq A$ и $B_{1}\subseteq B_{2}\subseteq \cdots \subseteq B$, такой, что каждый $A_{k},B_{k}$ замкнуто и компактно, а объединения являются относительными внутренностями $\mathrm {relint} (A),\mathrm {relint} (B)$. (Подробную информацию см . на соответствующей внутренней странице.)

Теперь во втором случае для каждой пары $A_{k},B_{k}$ существует некоторый единичный вектор $v_{k}$ и реальное число $c_{k}$, такой, что $\langle v_{k},A_{k}\rangle <c_{k}<\langle v_{k},B_{k}\rangle$.

Поскольку единичная сфера компактна, мы можем взять сходящую подпоследовательность, так что $v_{k}\to v$. Позволять $c_{A}:=\sup _{a\in A}\langle v,a\rangle ,c_{B}:=\inf _{b\in B}\langle v,b\rangle$. Мы утверждаем, что $c_{A}\leq c_{B}$, таким образом отделяя $A,B$.

Предположим, что нет, тогда существует некоторое $a\in A,b\in B$ такой, что $\langle v,a\rangle >\langle v,b\rangle$, то поскольку $v_{k}\to v$, для достаточно большого $k$, у нас есть $\langle v_{k},a\rangle >\langle v_{k},b\rangle$, противоречие.

Поскольку разделяющая гиперплоскость не может пересекать внутренности открытых выпуклых множеств, имеем следствие:

Теорема разделения I. Пусть $A$ и $B$ — два непересекающихся непустых выпуклых множества. Если $A$ открыт, то существует ненулевой вектор $v$ и реальное число $c$ такой, что

$\langle x,v\rangle >c\,{\text{ and }}\langle y,v\rangle \leq c$

для всех $x$ в $A$ и $y$ в $B$. Если оба множества открыты, то существует ненулевой вектор $v$ и реальное число $c$ такой, что

$\langle x,v\rangle >c\,{\text{ and }}\langle y,v\rangle <c$

для всех $x$ в $A$ и $y$ в $B$.

Случай с возможными пересечениями

Если наборы $A,B$ имеют возможные пересечения, но их относительные внутренности не пересекаются, то доказательство первого случая по-прежнему применимо без изменений, что дает:

Теорема разделения II . Пусть $A$ и $B$ — два непустых выпуклых подмножества $\mathbb {R} ^{n}$ с непересекающимися относительными интерьерами. Тогда существует ненулевой вектор $v$ и реальное число $c$ такой, что

$\langle x,v\rangle \geq c\,{\text{ and }}\langle y,v\rangle \leq c$

в частности, у нас есть теорема об опорной гиперплоскости .

Поддержка теоремы о гиперплоскости - если $A$ является выпуклым множеством в $\mathbb {R} ^{n},$ и $a_{0}$ точка на границе это $A$, то существует опорная гиперплоскость $A$ содержащий $a_{0}$.

Доказательство

Если аффинный интервал $A$ это еще не все $\mathbb {R} ^{n}$, затем расширите аффинный пролет до опорной гиперплоскости. Еще, $\mathrm {relint} (A)=\mathrm {int} (A)$ не пересекается с $\mathrm {relint} (\{a_{0}\})=\{a_{0}\}$, поэтому применим приведенную выше теорему.

Обратная теорема

Обратите внимание, что существование гиперплоскости, которая «разделяет» два выпуклых множества только в слабом смысле нестрогих обоих неравенств, очевидно, не означает, что эти два множества не пересекаются. Оба множества могут иметь точки, расположенные на гиперплоскости.

Контрпримеры и уникальность

Теорема неприменима, если одно из тел не выпукло.

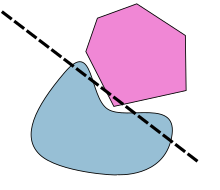
Если один из A или B не выпуклый, то существует множество возможных контрпримеров. Например, A и B могут быть концентрическими кругами. Более тонкий контрпример — это тот, в котором A и B оба замкнуты, но ни один из них не компактен. Например, если A — замкнутая полуплоскость и B ограничена одним плечом гиперболы, то строго разделяющей гиперплоскости не существует:

$A=\{(x,y):x\leq 0\}$

$B=\{(x,y):x>0,y\geq 1/x\}.\$

(Хотя, согласно второй теореме, существует гиперплоскость, разделяющая их внутренности.) Другой тип контрпримера имеет A компактный и B открытый. Например, A может быть закрытым квадратом, а B может быть открытым квадратом, A. касающимся

В первом варианте теоремы, очевидно, разделяющая гиперплоскость никогда не бывает единственной. Во второй версии он может быть уникальным, а может и не быть. Технически разделяющая ось никогда не бывает уникальной, поскольку ее можно перемещать; во втором варианте теоремы разделяющая ось может быть единственной с точностью до переноса.

Угол рога является хорошим контрпримером для многих случаев разделения гиперплоскостей. Например, в $\mathbb {R} ^{2}$, единичный круг не пересекается с открытым интервалом $((1,0),(1,1))$, но единственная линия, разделяющая их, содержит все $((1,0),(1,1))$. Это показывает, что если $A$ закрыт и $B$ относительно открыт, то не обязательно существует строгое для $B$. Однако, если $A$ является замкнутым многогранником , то такое разделение существует.

Больше вариантов

Лемму Фаркаша и связанные с ней результаты можно понимать как теоремы разделения гиперплоскостей, когда выпуклые тела определяются конечным числом линейных неравенств.

Можно найти больше результатов.

Использование при обнаружении столкновений

При обнаружении столкновений теорема разделения гиперплоскостей обычно используется в следующей форме:

Теорема о разделяющей оси . Два замкнутых выпуклых объекта не пересекаются, если существует линия («разделяющая ось»), на которую проекции двух объектов не пересекаются.

Независимо от размерности разделяющая ось всегда представляет собой линию.Например, в 3D пространство разделено плоскостями, но разделяющая ось перпендикулярна разделяющей плоскости.

Теорему о разделяющей оси можно применить для быстрого обнаружения столкновений между полигональными сетками. каждой грани Нормаль или направление другого элемента используется в качестве разделительной оси. Обратите внимание, что это дает возможное разделение осей, а не разделение линий/плоскостей.

В 3D использование только нормалей граней не позволит разделить некоторые непересекающиеся случаи, связанные с ребром. Требуются дополнительные оси, состоящие из векторных произведений пар ребер, взятых по одному от каждого объекта.

Для повышения эффективности параллельные оси могут рассчитываться как одна ось.

См. также

• Двойной конус
• Лемма Фаркаса
• Теорема Кирхбергера
• Оптимальное управление

Ссылки

• Бойд, Стивен П.; Ванденберге, Ливен (2004). Выпуклая оптимизация (PDF) . Издательство Кембриджского университета. ISBN  978-0-521-83378-3 .
• Гольштейн Е.Г.; Третьяков, Н.В. (1996). Модифицированные лагранжианы и монотонные отображения в оптимизации . Нью-Йорк: Уайли. п. 6. ISBN  0-471-54821-9 .
• Симидзу, Киётака; Ишизука, Йо; Бард, Джонатан Ф. (1997). Недифференцируемое и двухуровневое математическое программирование . Бостон: Академическое издательство Kluwer. п. 19. ISBN  0-7923-9821-1 .

• Солтан, В. (2021). Носители и свойства отделимости выпуклых множеств конечной размерности . Экстракт математики. Том. 36, нет. 2, 241–278.

Внешние ссылки

• Обнаружение столкновений и реагирование на них