Разбиение Аммана – Бинкера

Часть мозаики из апериодического набора плиток A5 Аммана, украшенная конечными локальными правилами соответствия, которые создают бесконечную глобальную структуру, такую как мозаика Аммана – Бинкера.

В геометрии мозаика Аммана -Бинкера — это непериодическая мозаика , которая может быть создана либо с помощью апериодического набора прототипов , как это сделал Роберт Амманн в 1970-х годах, либо с помощью метода вырезания и проецирования, как это независимо сделал Ф.П.М. Бинкер . Это один из пяти наборов мозаик, открытых Амманном и описанных в книге « Мозаики и шаблоны» . ^{[ 1 ]}

Разбиения Аммана – Бинкера обладают многими свойствами, похожими на более известные разбиения Пенроуза :

Они непериодичны, что означает отсутствие трансляционной симметрии .
Их непериодичность подразумевается их иерархической структурой: мозаики представляют собой мозаики замещения, возникающие из правил замены для выращивания все больших и больших участков. Эта структура замещения также подразумевает, что:
Любая конечная область (участок) в тайлинге появляется бесконечно много раз в этом тайлинге и, по сути, в любом другом тайлинге. Таким образом, все бесконечные мозаики выглядят похожими друг на друга, если рассматривать только конечные участки.
Они квазикристаллические : реализованные как физическая структура, мозаика Аммана – Бинкера будет вызывать дифракцию Брэгга ; дифрактограмма обнаруживает как лежащую в основе восьмикратную симметрию, так и дальний порядок. Этот порядок отражает тот факт, что мозаики организованы не посредством трансляционной симметрии, а скорее посредством процесса, который иногда называют «дефляцией» или «инфляцией».
Вся эта бесконечная глобальная структура создается посредством локальных правил сопоставления для пары плиток, среди самых простых когда-либо найденных апериодических наборов плиток, набора Аммана A5. ^{[ 1 ]}

Были предложены различные методы описания замощений: правила сопоставления, замены, схемы разреза и проекта. ^{[ 2 ]} и покрытия. ^{[ 3 ]}^{[ 4 ]} В 1987 году Ван, Чен и Куо объявили об открытии квазикристалла восьмиугольной симметрии. ^{[ 5 ]}

Описание плитки

Пара плиток A5 A и B Аммана, украшенная соответствующими правилами; любое замощение этими замощениями обязательно непериодично, и поэтому плитки апериодичны.

Правила замены Аммана A5, используемые для доказательства того, что плитки A5 могут образовывать только непериодические иерархические мозаики и, следовательно, являются апериодическими плитками.

Плитки A и B Аммана в его паре A5 - ромб с углами 45-135 градусов и треугольник с углами 45-45-90 градусов, украшенные правилами соответствия, которые допускали только определенное расположение в каждом регионе, что приводит к непериодическим, иерархическим и квазипериодическим структурам. каждого из бесконечного числа отдельных разбиений Аммана–Бинкера.

Альтернативный набор плиток, также обнаруженный Амманном и помеченный как «Амманн 4» в Грюнбауме и Шепарде. ^{[ 1 ]} состоит из двух невыпуклых частей с прямыми краями. Один состоит из двух квадратов, накладывающихся на меньший квадрат, а другой состоит из большого квадрата, прикрепленного к меньшему квадрату. На рисунках ниже показаны фрагменты и части мозаики.

Это правило замены альтернативного набора плиток.

Отношения между двумя наборами плиток.

В дополнение к стрелкам по краям в обычном наборе плиток правила сопоставления для обоих наборов плиток могут быть выражены путем рисования частей больших стрелок в вершинах и требования их объединения в полные стрелки.

Кац ^{[ 6 ]} изучил дополнительные мозаики, которые можно получить, отбросив ограничения вершин и наложив только требование совпадения стрелок ребер. Поскольку это требование само по себе сохраняется правилами замены, любое новое замощение имеет бесконечную последовательность «увеличенных» копий, полученных последовательным применением правила замены. Каждая мозаика в последовательности неотличима от истинной мозаики Аммана – Бинкера в последовательно большем масштабе. Поскольку некоторые из этих мозаик являются периодическими, из этого следует, что никакое украшение плиток, которое действительно вызывает апериодичность, не может быть определено путем рассмотрения любого конечного участка мозаики. Таким образом, ориентацию вершинных стрелок, вызывающих апериодичность, можно определить только на основе всей бесконечной мозаики.

Разбиение обладает также экстремальным свойством: среди разбиений, ромбы которых чередуются (т. е. всякий раз, когда два ромба соседствуют или разделены рядом квадратов, они появляются в разных ориентациях), доля квадратов оказывается минимальной в разбиении Аммана. – мозаика Бинкера. ^{[ 7 ]}

Особенности соотношения Пелла и серебра

Разбиения Аммана – Бинкера тесно связаны с отношением серебра ( $1+{\sqrt {2}}$ ) и числа Пелла .

схема замещения $R\to RrR;r\to R$ вводит соотношение как коэффициент масштабирования: его матрица представляет собой матрицу замены Пелла, а серия слов, полученная в результате замены, обладает тем свойством, что число $r$ песок $R$ s равны последовательным числам Пелля.
собственные значения матрицы замены равны $1+{\sqrt {2}}$ и $1-{\sqrt {2}}$ .
В альтернативном наборе плиток длинные края имеют $1+{\sqrt {2}}$ стороны в раз длиннее, чем короткие края.
Один набор червей Конвея , образованный короткой и длинной диагоналями ромбов, образует вышеуказанные струны, где r — короткая диагональ, а R — длинная диагональ. Следовательно, стержни Аммана также образуют упорядоченные сетки Пелла. ^{[ 8 ]}

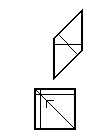Бары Ammann для обычного тайлсета. Если считать, что жирные внешние линии имеют длину $2{\sqrt {2}}$ , стержни разбивают ребра на отрезки длиной $1+{\sqrt {2}}$ и ${\sqrt {2}}-1$ . Эта плитка называется плиткой Ammann A5 .

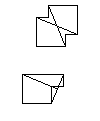Бары Амманна для альтернативного набора локаций. Обратите внимание, что полосы асимметричной плитки частично выходят за ее пределы. Эта плитка называется плиткой Ammann A4 .

Проектно-разрезное строительство

Тессерактические соты имеют восьмикратную вращательную симметрию, что соответствует восьмикратной вращательной симметрии тессеракта . Матрица вращения, представляющая эту симметрию:

A={\begin{bmatrix}0&0&0&-1\\1&0&0&0\\0&-1&0&0\\0&0&-1&0\end{bmatrix}}.

Преобразование этой матрицы в новые координаты, заданные формулой

B={\begin{bmatrix}-1/2&0&-1/2&{\sqrt {2}}/2\\1/2&{\sqrt {2}}/2&-1/2&0\\-1/2&0&-1/2&-{\sqrt {2}}/2\\-1/2&{\sqrt {2}}/2&1/2&0\end{bmatrix}}

будет производить:

BAB^{-1}={\begin{bmatrix}{\sqrt {2}}/2&{\sqrt {2}}/2&0&0\\-{\sqrt {2}}/2&{\sqrt {2}}/2&0&0\\0&0&-{\sqrt {2}}/2&{\sqrt {2}}/2\\0&0&-{\sqrt {2}}/2&-{\sqrt {2}}/2\end{bmatrix}}.

Эта третья матрица соответствует повороту как на 45° (в первых двух измерениях), так и на 135° (в последних двух измерениях). Затем мы можем получить мозаику Аммана–Бенкера, спроектировав пластину гиперкубов либо по первым двум, либо по двум последним новым координатам.

В качестве альтернативы, мозаику Аммана-Бенкера можно получить, нарисовав ромбы и квадраты вокруг точек пересечения пары квадратных решеток одинакового масштаба, наложенных под углом 45 градусов. Эти два метода были разработаны Бинкером в его статье.

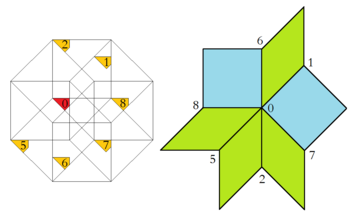
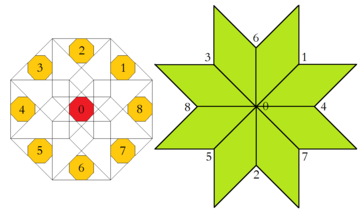
Сходным многомерным вложением в тессерактические соты является конструкция Клотца, подробно описанная в ее применении здесь, в статье Бааке и Джозефа. ^{[ 9 ]} Таким образом, восьмиугольную область принятия можно дополнительно разделить на части, каждая из которых затем дает начало ровно одной конфигурации вершин. Более того, относительная площадь любой из этих областей равна частоте соответствующей конфигурации вершин внутри бесконечной мозаики.

Область приемлемой области и соответствующая конфигурация вершин

Ссылки и примечания

^ Перейти обратно: ^а ^б ^с Грюнбаум, Б .; Шепард, GC (1986). Плитки и узоры . Нью-Йорк: Фриман. ISBN 0-7167-1193-1 .
^ Beenker FPM, Алгебраическая теория непериодических мозаик плоскости двумя простыми строительными блоками: квадратом и ромбом, Отчет TH 82-WSK-04 (1982), Technische Hogeschool, Эйндховен
^ Ф. Гелер, в материалах 6-й Международной конференции по квазикристаллам под редакцией С. Такеучи и Т. Фудзивара, World Научный, Сингапур, 1998, с. 95.
^ Бен-Авраам, С.И.; Гелер, Ф. (1999). «Описание покрывающего кластера восьмиугольных квазикристаллов MnSiAl» (PDF) . Физический обзор B . 60 (2): 860–864. дои : 10.1103/PhysRevB.60.860 . Архивировано из оригинала (PDF) 17 июня 2007 г.
^ Ван, Н.; Чен, Х.; Куо, К.Х. (1987). «Двумерный квазикристалл с восьмикратной вращательной симметрией» (PDF) . Письма о физических отзывах . 59 (9): 1010–1013. Бибкод : 1987PhRvL..59.1010W . дои : 10.1103/PhysRevLett.59.1010 . ПМИД 10035936 .
^ Кац, А (1995). «Правила соответствия и квазипериодичность: восьмиугольные мозаики». В Акселе, Ф.; Гратиас, Д. (ред.). За пределами квазикристаллов . Спрингер. стр. 141–189. дои : 10.1007/978-3-662-03130-8_6 . ISBN 978-3-540-59251-8 .
^ Бедарид, Н.; Ферник, Т. (2013). «Возвращение к плиткам Аммана-Бенкера». В Шмиде, С.; Уизерс, Р.; Лифшиц Р. (ред.). Апериодические кристаллы . Спрингер. стр. 59–65. arXiv : 1208.3545v1 . дои : 10.1007/978-94-007-6431-6_8 . ISBN 978-94-007-6430-9 . S2CID 8483564 .
^ Соколар, JES (1989). «Простые восьмиугольные и додекагональные квазикристаллы». Физический обзор B . 39 (15): 10519–10551. Бибкод : 1989PhRvB..3910519S . дои : 10.1103/PhysRevB.39.10519 . ПМИД 9947860 . МР0998533.
^ Бааке, М; Джозеф, Д. (1990). «Идеальные и дефектные конфигурации вершин в плоской восьмиугольной квазирешетке». Физический обзор B . 42 (13): 8091–8102. Бибкод : 1990PhRvB..42.8091B . дои : 10.1103/physrevb.42.8091 . ПМИД 9994979 .

Внешние ссылки

[ReferenceA-1] Перейти обратно: ^а ^б ^с Грюнбаум, Б .; Шепард, GC (1986). Плитки и узоры . Нью-Йорк: Фриман. ISBN 0-7167-1193-1 .

[2] Beenker FPM, Алгебраическая теория непериодических мозаик плоскости двумя простыми строительными блоками: квадратом и ромбом, Отчет TH 82-WSK-04 (1982), Technische Hogeschool, Эйндховен

[3] Ф. Гелер, в материалах 6-й Международной конференции по квазикристаллам под редакцией С. Такеучи и Т. Фудзивара, World Научный, Сингапур, 1998, с. 95.

[4] Бен-Авраам, С.И.; Гелер, Ф. (1999). «Описание покрывающего кластера восьмиугольных квазикристаллов MnSiAl» (PDF) . Физический обзор B . 60 (2): 860–864. дои : 10.1103/PhysRevB.60.860 . Архивировано из оригинала (PDF) 17 июня 2007 г.

[5] Ван, Н.; Чен, Х.; Куо, К.Х. (1987). «Двумерный квазикристалл с восьмикратной вращательной симметрией» (PDF) . Письма о физических отзывах . 59 (9): 1010–1013. Бибкод : 1987PhRvL..59.1010W . дои : 10.1103/PhysRevLett.59.1010 . ПМИД 10035936 .

[6] Кац, А (1995). «Правила соответствия и квазипериодичность: восьмиугольные мозаики». В Акселе, Ф.; Гратиас, Д. (ред.). За пределами квазикристаллов . Спрингер. стр. 141–189. дои : 10.1007/978-3-662-03130-8_6 . ISBN 978-3-540-59251-8 .

[7] Бедарид, Н.; Ферник, Т. (2013). «Возвращение к плиткам Аммана-Бенкера». В Шмиде, С.; Уизерс, Р.; Лифшиц Р. (ред.). Апериодические кристаллы . Спрингер. стр. 59–65. arXiv : 1208.3545v1 . дои : 10.1007/978-94-007-6431-6_8 . ISBN 978-94-007-6430-9 . S2CID 8483564 .

[8] Соколар, JES (1989). «Простые восьмиугольные и додекагональные квазикристаллы». Физический обзор B . 39 (15): 10519–10551. Бибкод : 1989PhRvB..3910519S . дои : 10.1103/PhysRevB.39.10519 . ПМИД 9947860 . МР0998533.

[9] Бааке, М; Джозеф, Д. (1990). «Идеальные и дефектные конфигурации вершин в плоской восьмиугольной квазирешетке». Физический обзор B . 42 (13): 8091–8102. Бибкод : 1990PhRvB..42.8091B . дои : 10.1103/physrevb.42.8091 . ПМИД 9994979 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]