Выпуклый набор

Иллюстрация выпуклого множества в форме деформированного круга. Отрезок линии, соединяющий точки x и y, полностью лежит внутри множества, показанного зеленым цветом. Поскольку это верно для любых потенциальных расположений двух точек внутри множества, множество является выпуклым.

Иллюстрация невыпуклого множества. Отрезок линии, соединяющий точки x и y, частично выходит за пределы набора, показанного красным, а пересечение набора с линией происходит в двух местах, показанных черным.

В геометрии подмножество евклидова пространства или, в более общем смысле, аффинное пространство над действительными числами , является выпуклым , если для любых двух точек в подмножестве подмножество содержит весь отрезок прямой соединяющий их . Эквивалентно, выпуклое множество или выпуклая область — это подмножество, которое пересекает каждую линию в один сегмент линии (возможно, пустой). Например, сплошной куб — ​​это выпуклое множество, но все, что полое или имеет углубление, например, в форме полумесяца , не является выпуклым.

Граница выпуклого множества на плоскости всегда является выпуклой кривой . Пересечение всех выпуклых множеств, содержащих данное подмножество евклидова пространства, называется выпуклой оболочкой A A . Это наименьшее выпуклое множество, A. содержащее

Выпуклая функция — это вещественная функция, определенная на интервале, обладающая тем свойством, что ее надграфик (множество точек на графике функции или над ним) является выпуклым множеством. Выпуклая минимизация — это область оптимизации , которая изучает проблему минимизации выпуклых функций над выпуклыми множествами. Раздел математики, посвященный изучению свойств выпуклых множеств и выпуклых функций, называется выпуклым анализом .

Понятие выпуклого множества можно обобщить, как описано ниже.

Определения

Функция эпиграф является выпуклой тогда и только тогда, когда ее , область (зеленый цвет) над ее графиком (синий цвет), представляет собой выпуклое множество.

Пусть S — векторное пространство или аффинное пространство над действительными числами или, в более общем смысле, над некоторым упорядоченным полем (сюда входят евклидовы пространства, которые являются аффинными пространствами). Подмножество соединяющий C из S является выпуклым , если для всех x и y в C отрезок, включен x и y , в C .

Это означает, что аффинная комбинация (1 − t ) x + ty принадлежит C для всех x, y в C и t в интервале [0, 1] . Отсюда следует, что выпуклость инвариантна относительно аффинных преобразований . Кроме того, это означает, что выпуклое множество в вещественном или комплексном топологическом векторном пространстве линейно связно (и, следовательно, также связно ).

Множество C есть строго выпуклый , если каждая точка отрезка, соединяющего x и y кроме конечных точек, находится внутри топологической внутренности C , . Замкнутое выпуклое подмножество является строго выпуклым тогда и только тогда, когда каждая его граничная точка является крайней точкой .

Множество C если абсолютно выпукло, оно выпукло и уравновешено .

Примеры

Выпуклые подмножества R (множество действительных чисел) — это интервалы и точки R . Некоторыми примерами выпуклых подмножеств евклидовой плоскости являются сплошные правильные многоугольники , сплошные треугольники и пересечения сплошных треугольников. Некоторыми примерами выпуклых подмножеств евклидова трехмерного пространства являются архимедовы тела и платоновые тела . Многогранники Кеплера -Пуансо являются примерами невыпуклых множеств.

Невыпуклый набор

Множество, которое не является выпуклым, называется невыпуклым множеством . Многоугольник , не являющийся выпуклым, иногда называют вогнутым многоугольником . а в некоторых источниках в более общем смысле термин « вогнутое множество» используется для обозначения невыпуклого множества, но большинство властей запрещают такое использование.

Дополнение иногда выпуклого множества, такое как надграфик , вогнутой функции называют обратно-выпуклым множеством , особенно в контексте математической оптимизации .

Свойства

Учитывая r точек u ₁ , ..., ur _λ в выпуклом множестве S и r неотрицательных чисел λ ₁ , ..., λ _r таких, что 1 ₊ ... + λ _r = 1 , аффинная комбинация

$$\sum _{k=1}^{r}\lambda _{k}u_{k}$$

принадлежит С. ​Поскольку определение выпуклого множества соответствует случаю r = 2 , это свойство характеризует выпуклые множества.

Такая аффинная комбинация называется выпуклой комбинацией u 1 _, , ur _... .

Пересечения и союзы

Коллекция выпуклых подмножеств векторного пространства, аффинного пространства или евклидова пространства обладает следующими свойствами:

1. Пустое множество и все пространство выпуклые.
2. Пересечение любого набора выпуклых множеств является выпуклым.
3. Объединение по включению последовательности выпуклых множеств называется выпуклым, если они образуют неубывающую цепочку . Для этого свойства важно ограничение на цепи, поскольку объединение двух выпуклых множеств не обязательно должно быть выпуклым.

Замкнутые выпуклые множества

Замкнутые выпуклые множества — это выпуклые множества, содержащие все свои предельные точки . Их можно охарактеризовать как пересечения замкнутых полупространств (множеств точек в пространстве, лежащих на гиперплоскости и по одну ее сторону ).

Из только что сказанного ясно, что такие пересечения выпуклы и тоже будут замкнутыми множествами. Чтобы доказать обратное, т. е. любое замкнутое выпуклое множество можно представить как такое пересечение, нужна опорная теорема о гиперплоскости в виде того, что для данного замкнутого выпуклого множества C и точки P вне его существует замкнутое полупространство H , которое содержит C а не P. , Теорема о опорной гиперплоскости является частным случаем теоремы Хана–Банаха функционального анализа .

Выпуклые множества и прямоугольники

Пусть C — выпуклое тело на плоскости (выпуклое множество, внутренность которого непуста). Мы можем вписать прямоугольник r в C так, что гомотетическая копия R прямоугольника r описана вокруг C . Положительный коэффициент гомотетии не превышает 2 и:

$${\tfrac {1}{2}}\cdot \operatorname {Area} (R)\leq \operatorname {Area} (C)\leq 2\cdot \operatorname {Area} (r)$$

Бляшке-Сантало

Набор ${\mathcal {K}}^{2}$ всех плоских выпуклых тел можно параметризовать через диаметр выпуклого тела D , его внутренний радиус r (самый большой круг, содержащийся в выпуклом теле) и его радиус описанной окружности R (наименьший круг, содержащий выпуклое тело). Фактически это множество можно описать набором неравенств, заданных формулами

$$2r\leq D\leq 2R$$

$$R\leq {\frac {\sqrt {3}}{3}}D$$

$$r+R\leq D$$

$$D^{2}{\sqrt {4R^{2}-D^{2}}}\leq 2R(2R+{\sqrt {4R^{2}-D^{2}}})$$

и может быть представлен как образ функции g , отображающей выпуклое тело в R ² точка, заданная формулой ( r / R , D /2 R ). Образ этой функции известен как ( r , D , R ) диаграмма Блачке-Сантало.

Диаграмма Бляшке-Сантало ( r , D , R ) для плоских выпуклых тел. $\mathbb {L}$ обозначает отрезок прямой, $\mathbb {I} _{\frac {\pi }{3}}$ равносторонний треугольник, $\mathbb {RT}$ треугольник Рело и $\mathbb {B} _{2}$ единичный круг.

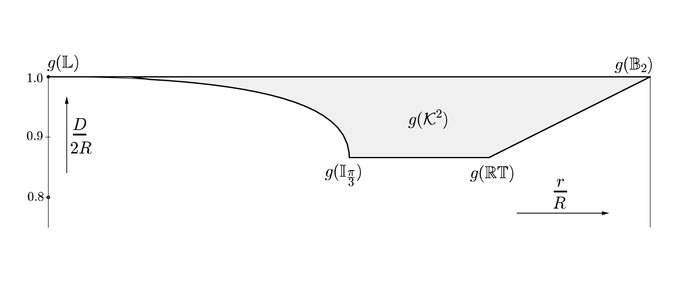
Альтернативно, набор ${\mathcal {K}}^{2}$ также может быть параметризован по ширине (наименьшему расстоянию между любыми двумя различными параллельными опорными гиперплоскостями), периметру и площади.

Другая недвижимость

Пусть X — топологическое векторное пространство и $C\subseteq X$ быть выпуклым.

• $\operatorname {Cl} C$ и $\operatorname {Int} C$ оба выпуклы (т. е. замыкание и внутренность выпуклых множеств выпуклы).
• Если $a\in \operatorname {Int} C$ и $b\in \operatorname {Cl} C$ затем $[a,b[\,\subseteq \operatorname {Int} C$ (где $[a,b[\,:=\left\{(1-r)a+rb:0\leq r<1\right\}$).
• Если $\operatorname {Int} C\neq \emptyset$ затем:
  • $\operatorname {cl} \left(\operatorname {Int} C\right)=\operatorname {Cl} C$, и
  • $\operatorname {Int} C=\operatorname {Int} \left(\operatorname {Cl} C\right)=C^{i}$, где $C^{i}$ является внутренностью C . алгебраической

оболочки и

Выпуклые оболочки

Основная статья: выпуклая оболочка

Каждое подмножество A векторного пространства содержится в наименьшем выпуклом множестве (называемом выпуклой оболочкой A ) , а именно в пересечении всех выпуклых множеств, A. содержащих Оператор выпуклой оболочки Conv() обладает характерными свойствами оператора выпуклой оболочки :

• обширный : S ⊆ Conv( S ) ,
• неубывающее : S ⊆ T означает, что Conv( S ) ⊆ Conv( T ) и
• идемпотент : Conv(Conv( S )) = Conv( S ) .

Операция выпуклой оболочки необходима для того, чтобы набор выпуклых множеств образовал решетку , в которой операция « соединения » представляет собой выпуклую оболочку объединения двух выпуклых множеств.

$$\operatorname {Conv} (S)\vee \operatorname {Conv} (T)=\operatorname {Conv} (S\cup T)=\operatorname {Conv} {\bigl (}\operatorname {Conv} (S)\cup \operatorname {Conv} (T){\bigr )}.$$

Пересечение любого набора выпуклых множеств само по себе является выпуклым, поэтому выпуклые подмножества векторного пространства (вещественного или комплексного) образуют полную решетку .

Дополнение Минковского

Основная статья: дополнение Минковского

Минковский сложение множеств. Сумма = квадратов Q ₁ [0,1] ² и Q ₂ =[1,2] ² это квадрат Q ₁ +Q ₂ =[1,3] ² .

В реальном векторном пространстве сумма Минковского двух (непустых) множеств, S ₁ и S ₂ , определяется как набор S ₁ + S _2, образованный путем поэлементного сложения векторов из наборов слагаемых.

$$S_{1}+S_{2}=\{x_{1}+x_{2}:x_{1}\in S_{1},x_{2}\in S_{2}\}.$$

В более общем смысле, сумма Минковского конечного семейства (непустых) множеств Sn _{- это набор ,} образованный поэлементным сложением векторов

$$\sum _{n}S_{n}=\left\{\sum _{n}x_{n}:x_{n}\in S_{n}\right\}.$$

Для сложения Минковского нулевое множество   {0} , содержащее только нулевой вектор   0, имеет особое значение : для каждого непустого подмножества S векторного пространства

$$S+\{0\}=S;$$

в алгебраической терминологии {0} — это единичный элемент сложения Минковского (на наборе непустых множеств).

сумм

Сложение Минковского хорошо себя ведет по отношению к операции взятия выпуклых оболочек, как показывает следующее предложение:

Пусть S1 _{их суммы} , S2 _. — подмножества вещественного векторного пространства, выпуклая оболочка Минковского — это сумма Минковского их выпуклых оболочек

$$\operatorname {Conv} (S_{1}+S_{2})=\operatorname {Conv} (S_{1})+\operatorname {Conv} (S_{2}).$$

Этот результат справедлив в более общем смысле для каждого конечного набора непустых множеств:

$${\text{Conv}}\left(\sum _{n}S_{n}\right)=\sum _{n}{\text{Conv}}\left(S_{n}\right).$$

В математической терминологии операции суммирования Минковского и формирования выпуклых оболочек являются коммутирующими операциями.

Суммы

Сумма Минковского двух компактных выпуклых множеств компактна. Сумма выпуклого компакта и выпуклого замкнутого множества замкнута.

Следующая знаменитая теорема, доказанная Дьедонне в 1966 году, дает достаточное условие замкнутости разности двух замкнутых выпуклых подмножеств. Он использует концепцию конуса рецессии непустого выпуклого подмножества S , определяемого как:

$$\operatorname {rec} S=\left\{x\in X\,:\,x+S\subseteq S\right\},$$

где это множество представляет собой выпуклый конус, содержащий $0\in X$ и удовлетворение $S+\operatorname {rec} S=S$. Заметим, что если S замкнуто и выпукло, то $\operatorname {rec} S$ закрыто и для всех $s_{0}\in S$,

$$\operatorname {rec} S=\bigcap _{t>0}t(S-s_{0}).$$

Теорема (Дьедонне). Пусть A и B — непустые, замкнутые и выпуклые подмножества локально выпуклого топологического векторного пространства такие, что $\operatorname {rec} A\cap \operatorname {rec} B$ является линейным подпространством. Если A или B , локально компактны то A − B замкнуто.

выпуклости

Понятие выпуклости в евклидовом пространстве можно обобщить, изменив определение в тех или иных аспектах. Используется общее название «обобщенная выпуклость», поскольку полученные объекты сохраняют определенные свойства выпуклых множеств.

Звездо-выпуклые (звездообразные) множества

Основная статья: Звездный домен

Пусть C — множество в вещественном или комплексном векторном пространстве. C является выпуклой звездой (звездообразной), если существует x ₀ в C такой, что отрезок прямой от x ₀ до любой точки y в C содержится в C . Следовательно, непустое выпуклое множество всегда звездно-выпуклое, но звездчатое множество не всегда выпуклое.

Ортогональная выпуклость

Основная статья: Ортогональная выпуклая оболочка

Примером обобщенной выпуклости является ортогональная выпуклость .

Множество S в евклидовом пространстве называется ортогонально-выпуклым или орто-выпуклым , если любой отрезок, параллельный любой из координатных осей, соединяющих две точки S полностью лежит внутри S. , Легко доказать, что пересечение любого набора ортовыпуклых множеств является ортовыпуклым. Справедливы и некоторые другие свойства выпуклых множеств.

Неевклидова геометрия

Определение выпуклого множества и выпуклой оболочки естественным образом распространяется на неевклидову геометрию, определяя геодезически выпуклое множество как такое, которое содержит геодезические, соединяющие любые две точки множества.

Заказать топологию

Выпуклость может быть распространена на полностью упорядоченное множество X, наделенное порядковой топологией .

Пусть Y ⊆ X. ​Подпространство Y является выпуклым множеством, если для каждой пары точек a , b в Y такой, что a ⩽ b , интервал [ a , b ] = { x ∈ X | a ≤ x ≤ b } содержится в Y . То есть Y является выпуклым тогда и только тогда, когда для всех a , b в Y , a ⩽ b влечет [ a , b ⊆ Y. ]

Выпуклое множество вообще не связно: контрпример дается подпространством {1,2,3} в Z , которое одновременно выпукло и несвязно.

Выпуклые пространства

Понятие выпуклости можно обобщить и на другие объекты, если в качестве аксиом выбрать определенные свойства выпуклости .

Для данного множества X выпуклость : над X — это совокупность 𝒞 подмножеств X, удовлетворяющая следующим аксиомам

1. Пустое множество и X находятся в 𝒞
2. Пересечение любой коллекции из 𝒞 находится в 𝒞 .
3. Объединение цепи (по отношению включения ) элементов из 𝒞 находится в 𝒞 .

Элементы 𝒞 называются выпуклыми множествами, а пара ( X , 𝒞 ) называется выпуклым пространством . Для обычной выпуклости справедливы первые две аксиомы, а третья тривиальна.

Альтернативное определение абстрактной выпуклости, более подходящее для дискретной геометрии , см. в разделе « Выпуклая геометрия, связанная с антиматроидами» .

Выпуклые пространства

Основная статья: Выпуклое пространство

Выпуклость можно обобщить как абстрактную алгебраическую структуру: пространство является выпуклым, если можно взять выпуклые комбинации точек.

См. также

• Поглощающий набор
• Алгоритмические задачи на выпуклых множествах
• Ограниченное множество (топологическое векторное пространство)
• Теорема Брауэра о неподвижной точке
• Сложная выпуклость
• Выпуклая оболочка
• Выпуклая серия
• Выпуклое метрическое пространство
• Теорема Каратеодори (выпуклая оболочка)
• Теория Шоке
• Теорема Хелли
• Голоморфно выпуклая оболочка
• Цело-выпуклое множество
• Джон эллипсоид
• Псевдовыпуклость
• Теорема Радона
• Лемма Шепли – Фолкмана.
• Симметричный набор

Внешние ссылки

• «Выпуклое подмножество» . Энциклопедия математики . ЭМС Пресс . 2001 [1994].
• Лекции по выпуклым множествам , заметки Нильса Лауритцена, в Орхусском университете , март 2010 г.