Область

Эта статья о геометрической величине. Чтобы узнать о других значениях, см. Площадь (значения) .

Область
Площади этого квадрата и этого диска одинаковы.
Общие символы	А или С
единица СИ	Квадратный метр [м 2 ]
В базовых единицах СИ	1 м 2
Измерение	${\mathsf {L}}^{2}$

Площадь – это мера региона размера на поверхности . Площадь плоской области или плоская область относится к площади формы или плоской пластинки , а площадь поверхности относится к площади открытой поверхности или границе трехмерного объекта . Под площадью можно понимать количество материала заданной толщины, которое потребуется для изготовления модели определенной формы, или количество краски, необходимое для покрытия поверхности одним слоем. Это двумерный аналог длины кривой ( твердого тела ( одномерное понятие) или объема трехмерное понятие).Две разные области могут иметь одинаковую площадь (как при квадратуре круга ); в синекдохе слово «площадь» иногда используется для обозначения региона, например, « многоугольная область ».

Площадь фигуры можно измерить, сравнив ее с квадратами фиксированного размера. В Международной системе единиц (СИ) стандартной единицей площади является квадратный метр (записывается как м). ² ), то есть площадь квадрата со стороной один метр . Фигура площадью три квадратных метра будет иметь такую ​​же площадь, как три таких квадрата. В математике площадь единичного квадрата определяется как единица, а площадь любой другой формы или поверхности представляет собой безразмерное действительное число .

Существует несколько известных формул для площадей простых фигур, таких как треугольники , прямоугольники и круги . Используя эти формулы, площадь любого многоугольника можно найти, разделив многоугольник на треугольники . Для фигур с изогнутой границей обычно требуется расчет площади. Действительно, проблема определения площади плоских фигур была основным мотивом исторического развития исчисления .

Для твердой формы, такой как сфера , конус или цилиндр, площадь ее граничной поверхности называется площадью поверхности . Формулы для площади поверхности простых фигур были вычислены еще древними греками , но вычисление площади поверхности более сложной формы обычно требует многомерного исчисления .

Площадь играет важную роль в современной математике. Помимо своей очевидной важности в геометрии и исчислении, площадь связана с определением определителей в линейной алгебре и является основным свойством поверхностей в дифференциальной геометрии . При анализе площадь подмножества плоскости определяется с помощью меры Лебега : хотя не каждое подмножество измеримо, если предположить аксиому выбора. В целом площадь в высшей математике рассматривается как частный случай объема двумерных областей.

Площадь можно определить с помощью аксиом, определяя ее как функцию набора определенных плоских фигур в набор действительных чисел. Можно доказать, что такая функция существует.

Формальное определение

Смотрите также: мера Иордании

Подход к определению того, что подразумевается под «площадью», основан на аксиомах . «Площадь» можно определить как функцию набора M особых видов плоских фигур (называемых измеримыми множествами) до набора действительных чисел, которая удовлетворяет следующим свойствам:

• Для всех S в M 0 a ( S ) ≥ .
• Если S и T находятся в M, то также S ∪ T и S ∩ T , а также а ( S ∪ T ) знак равно а ( S ) + а ( Т ) - а ( S ∩ Т ) .
• Если S и T находятся в M, причем S ⊆ T , то T - S находится в M и a ( T - S ) = a ( T ) - a ( S ) .
• Если множество S находится в M и S конгруэнтно T, то T также находится в M и a ( S ) = a ( T ) .
• Каждый прямоугольник R в M. находится Если прямоугольник имеет длину h и ширину k , то a ( R ) = hk .
• Пусть Q — множество, заключенное между двумя ступенчатыми S и T. областями Ступенчатая область образуется из конечного объединения соседних прямоугольников, опирающихся на общее основание, т.е. S ⊆ Q ⊆ T . Если существует уникальный номер c такой, что a ( S ) ⩽ c ⩽ a ( T ) для всех таких ступенчатых областей S и T , то a ( Q ) = c .

Можно доказать, что такая функция площади действительно существует.

Единицы

квадратного метра Квадрат из трубы ПВХ

Каждой единице длины соответствует единица площади, а именно площадь квадрата с данной длиной стороны. Таким образом, площади можно измерять в квадратных метрах (м ² ), квадратные сантиметры (см ² ), квадратные миллиметры (мм ² ), квадратные километры (км ² ), квадратные футы (футы ² ), квадратных ярдов (ярдов ² ), квадратные мили (ми ² ) и так далее. Алгебраически эти единицы можно рассматривать как квадраты соответствующих единиц длины.

Единицей площади в системе СИ является квадратный метр, который считается производной единицей системы СИ .

Конверсии

Хотя в 1 см 10 мм, но есть 100 мм. ² в 1 см ² .

Расчет площади квадрата, длина и ширина которого равны 1 метру, будет выглядеть следующим образом:

1 метр × 1 метр = 1 м ²

Итак, прямоугольник с разными сторонами (скажем, длина 3 метра и ширина 2 метра) будет иметь площадь в квадратных единицах, которую можно рассчитать как:

3 метра × 2 метра = 6 м ² . Это эквивалентно 6 миллионам квадратных миллиметров. Другие полезные преобразования:

• 1 квадратный километр = 1 000 000 квадратных метров
• 1 квадратный метр = 10 000 квадратных сантиметров = 1 000 000 квадратных миллиметров.
• 1 квадратный сантиметр = 100 квадратных миллиметров.

Неметрические единицы

В неметрических единицах преобразование между двумя квадратными единицами представляет собой квадрат преобразования между соответствующими единицами длины.

1 фут = 12 дюймов ,

соотношение между квадратными футами и квадратными дюймами

1 квадратный фут = 144 квадратных дюйма,

где 144 = 12 ² = 12 × 12. Аналогично:

• 1 квадратный ярд = 9 квадратных футов
• 1 квадратная миля = 3 097 600 квадратных ярдов = 27 878 ​​400 квадратных футов.

Кроме того, коэффициенты пересчета включают в себя:

• 1 квадратный дюйм = 6,4516 квадратных сантиметров.
• 1 квадратный фут = 0,092  903  04 квадратных метра.
• 1 квадратный ярд = 0,836  127  36 квадратных метров.
• 1 квадратная миля = 2,589 988 110 336 квадратных километров.

Другие единицы, включая исторические

См. Также: Категория: Единицы площади.

Есть несколько других общих единиц площади. Это была первоначальная единица площади в метрической системе :

• 1 соток = 100 квадратных метров

Хотя площадь вышла из употребления, гектар по-прежнему широко используется для измерения земли:

• 1 гектар = 100 соток = 10 000 квадратных метров = 0,01 квадратных километров.

Другие необычные метрические единицы площади включают тетраду , гектаду и мириаду .

Акр также обычно используется для измерения земельных площадей, где

• 1 акр = 4840 квадратных ярдов = 43560 квадратных футов.

Акр составляет примерно 40% гектара.

В атомном масштабе площадь измеряется в амбарах , так что:

• 1 сарай = 10 ⁻²⁸ квадратные метры.

Сарай обычно используется при описании площади поперечного сечения взаимодействия в ядерной физике .

В Южной Азии (в основном в Индии), хотя страны используют единицы СИ в качестве официальных, многие жители Южной Азии по-прежнему используют традиционные единицы. Каждое административное деление имеет свою единицу площади, некоторые из них имеют одинаковые названия, но разные значения. Официального консенсуса относительно значений традиционных единиц измерения нет. Таким образом, преобразования между единицами СИ и традиционными единицами могут иметь разные результаты в зависимости от того, какая ссылка использовалась.

Некоторые традиционные единицы Южной Азии, имеющие фиксированную стоимость:

• 1 килла = 1 акр
• 1 Гумаон = 1 акр
• 1 канал = 0,125 акра (1 акр = 8 каналов)
• 1 десятичный знак = 48,4 квадратных ярда
• 1 Чатак = 180 квадратных футов

История

Площадь круга

Основная статья: Площадь круга § История

В V веке до нашей эры Гиппократ Хиосский был первым, кто показал, что площадь диска (область, заключенная в круг) пропорциональна квадрату его диаметра, как часть его квадратуры луны Гиппократа . но не определил константу пропорциональности . Евдокс Книдский , также живший в V веке до нашей эры, также обнаружил, что площадь диска пропорциональна квадрату его радиуса.

Впоследствии в книге I Евклида «Начал» речь шла о равенстве площадей двумерных фигур. Математик Архимед использовал инструменты евклидовой геометрии , чтобы показать, что площадь внутри круга равна площади прямоугольного треугольника , основание которого имеет длину окружности круга, а высота равна радиусу круга в своей книге «Измерение круга» . (Окружность равна 2 π r , а площадь треугольника равна половине произведения основания на высоту, что дает площадь π r ² для диска.) Архимед аппроксимировал значение π (и, следовательно, площадь круга единичного радиуса) с помощью своего метода удвоения , в котором он вписал правильный треугольник в круг и записал его площадь, а затем удвоил число сторон до дайте правильный шестиугольник , а затем многократно удваивайте количество сторон по мере того, как площадь многоугольника становилась все ближе и ближе к площади круга (и делал то же самое с описанными многоугольниками ).

Площадь треугольника

Этот раздел представляет собой отрывок из книги «Площадь треугольника § История» . [ редактировать ]

Герон Александрийский нашел так называемую формулу Герона для площади треугольника через его стороны, и доказательство можно найти в его книге «Метрика» , написанной около 60 г. н.э. Было высказано предположение, что Архимед знал эту формулу более двух столетий назад. и поскольку Метрика представляет собой собрание математических знаний, доступных в древнем мире, возможно, что формула предшествует ссылке, приведенной в этой работе. В 300 году до нашей эры греческий математик Евклид доказал, что площадь треугольника вдвое меньше площади параллелограмма с тем же основанием и высотой в своей книге «Начала геометрии» .

В 499 году Арьябхата , великий математик - астроном классической эпохи индийской математики и индийской астрономии , выразил площадь треугольника как половину произведения основания на высоту в Арьябхатье (раздел 2.6).

Формула, эквивалентная формуле Герона, была открыта китайцами независимо от греков. Оно было опубликовано в 1247 году в «Шушу Цзючжан» (« Математический трактат в девяти разделах »), написанном Цинь Цзюшао .

Четырехсторонняя площадь

В VII веке нашей эры Брахмагупта разработал формулу, теперь известную как формула Брахмагупты , для определения площади вписанного четырехугольника ( четырехугольника, вписанного в круг) через его стороны. В 1842 году немецкие математики Карл Антон Бретшнайдер и Карл Георг Кристиан фон Штаудт независимо друг от друга нашли формулу, известную как формула Бретшнайдера , для площади любого четырехугольника.

Общая площадь полигона

Разработка декартовых координат Рене Декартом разработать формулу геодезиста для площади любого многоугольника с известным вершин расположением в 17 веке позволила Гауссу в 19 веке .

Области, определенные с помощью расчетов

Развитие интегрального исчисления в конце 17 века предоставило инструменты, которые впоследствии можно было использовать для вычисления более сложных областей, таких как площадь эллипса и площади поверхности различных изогнутых трехмерных объектов.

Формулы площади

Формулы многоугольников

Основная статья: Многоугольник § Площадь

Для несамопересекающегося ( простого ) многоугольника декартовы координаты $(x_{i},y_{i})$ ( i =0, 1, ..., n которого -1), n ​​вершин известны, площадь определяется по формуле геодезиста :

$A={\frac {1}{2}}{\Biggl \vert }\sum _{i=0}^{n-1}(x_{i}y_{i+1}-x_{i+1}y_{i}){\Biggr \vert }$

где когда i = n -1, то i +1 выражается как модуль n и поэтому относится к 0.

Прямоугольники

Площадь этого прямоугольника равна lw .

Самая простая формула площади — это формула площади прямоугольника . Учитывая прямоугольник длиной l и шириной w , формула площади:

А = lw (прямоугольник).

То есть площадь прямоугольника равна произведению длины на ширину. В частном случае, поскольку l = w в случае квадрата, площадь квадрата с длиной стороны s определяется по формуле:

А = с ² (квадрат).

Формула площади прямоугольника вытекает непосредственно из основных свойств площади и иногда принимается как определение или аксиома . С другой стороны, если геометрия разрабатывается раньше арифметики , эту формулу можно использовать для определения умножения действительных чисел .

Диссекция, параллелограммы и треугольники

Основные статьи: Площадь треугольника и Параллелограмм § Формула площади

Параллелограмм можно разрезать и перестроить так, чтобы получился прямоугольник.

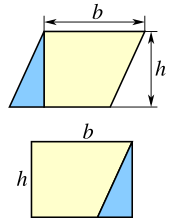
Большинство других простых формул площади следуют из метода рассечения .Это предполагает разрезание фигуры на части, площади которых должны быть равны площади исходной фигуры.Например, любой параллелограмм можно разделить на трапецию и прямоугольный треугольник , как показано на рисунке слева. Если треугольник переместить на другую сторону трапеции, то полученная фигура будет прямоугольником. Отсюда следует, что площадь параллелограмма равна площади прямоугольника:

A = bh (параллелограмм).

Параллелограмм, разделенный на два равных треугольника

Однако тот же параллелограмм можно разрезать и по диагонали на два равных треугольника, как показано на рисунке справа. Отсюда следует, что площадь каждого треугольника равна половине площади параллелограмма:

$A={\frac {1}{2}}bh$ (треугольник).

Аналогичные аргументы можно использовать для нахождения формул площади трапеции. а также более сложные многоугольники .

Область изогнутых форм

Круги

Круг можно разделить на сектора , которые перестраиваются, образуя приблизительный параллелограмм .

Основная статья: Площадь круга

Формула площади круга ( более правильно называемого площадью, заключенной в круг или площадь диска ) основана на аналогичном методе. Учитывая круг радиуса r , его можно разделить на сектора , как показано на рисунке справа. Каждый сектор имеет примерно треугольную форму, и сектора можно переставлять, образуя приблизительный параллелограмм. Высота этого параллелограмма равна r , а ширина равна половине длины окружности, или π r . Таким образом, общая площадь круга равна π r ² :

А = π р ² (круг).

Хотя разделение, используемое в этой формуле, является лишь приблизительным, ошибка становится все меньше и меньше по мере того, как круг разбивается на все больше и больше секторов. Предел ровно площадей приближенных параллелограммов равен π r ² , что является площадью круга.

Этот аргумент на самом деле представляет собой простое применение идей исчисления . В древние времена метод исчерпания использовался аналогичным образом для нахождения площади круга, и теперь этот метод признан предшественником интегрального исчисления . Используя современные методы, площадь круга можно вычислить с помощью определенного интеграла :

$A\;=\;2\int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx\;=\;\pi r^{2}.$

Эллипсы

Основная статья: Эллипс § Площадь

Формула площади, заключенной в эллипс, связана с формулой круга; для эллипса с большой и малой полуосями x и y формула:

$A=\pi xy.$

Неплоская поверхность

Основная статья: Площадь поверхности

Архимед показал, что площадь поверхности сферы ровно в четыре раза превышает площадь плоского диска того же радиуса, а объем, заключенный сферой, составляет ровно 2/3 объема цилиндра той же высоты и радиуса.

Большинство основных формул площади поверхности можно получить, разрезав поверхности и выровняв их (см.: Развертывающиеся поверхности ). Например, если боковую поверхность цилиндра (или любой призмы ) разрезать вдоль, поверхность можно расплющить в прямоугольник. Аналогично, если сделать разрез вдоль стороны конуса , боковую поверхность можно сгладить до сектора круга и вычислить полученную площадь.

Формулу площади поверхности сферы вывести сложнее: поскольку сфера имеет ненулевую гауссову кривизну , ее нельзя сплющить. Формула площади поверхности сферы впервые была получена Архимедом в его работе «О сфере и цилиндре» . Формула:

А = 4 πр ² (сфера),

где r — радиус сферы. Как и в случае с формулой площади круга, любой вывод этой формулы по своей сути использует методы, аналогичные исчислению .

Общие формулы

Площади двумерных фигур

Площадь треугольника $A={\tfrac {b\cdot h}{2}}$

• Треугольник ​ : ${\tfrac {1}{2}}Bh$ (где B — любая сторона, а h — расстояние от прямой, на которой лежит B , до другой вершины треугольника). высота h Эту формулу можно использовать, если известна . Если известны длины трех сторон, формулу Герона : можно использовать ${\sqrt {s(s-a)(s-b)(s-c)}}$ где a , b , c — стороны треугольника, а $s={\tfrac {1}{2}}(a+b+c)$ составляет половину его периметра. Если задан угол и две входящие в него стороны, то площадь равна ${\tfrac {1}{2}}ab\sin(C)$ где C — заданный угол, a и b — его стороны. Если треугольник изображен на координатной плоскости, можно использовать матрицу, которая упрощается до абсолютного значения ${\tfrac {1}{2}}(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3})$. Эта формула также известна как формула шнурков и представляет собой простой способ определения площади координатного треугольника путем замены трех точек (x ₁ ,y ₁ ) , (x ₂ ,y ₂ ) и (x ₃ ,y ₃ ) . Формулу шнурков также можно использовать для определения площадей других многоугольников, если известны их вершины. Другой подход к координатному треугольнику — использовать математический анализ для определения площади.
• Простой многоугольник , построенный на сетке точек на равном расстоянии (т. е. точек с целочисленными координатами), такой, что все вершины многоугольника являются точками сетки: $i+{\frac {b}{2}}-1$, где i — количество точек сетки внутри многоугольника, а b — количество граничных точек. Этот результат известен как теорема Пика .

Площадь в исчислении

Интегрирование можно рассматривать как измерение площади под кривой, определяемой f ( x ), между двумя точками (здесь a и b ).

Площадь между двумя графиками можно оценить, вычислив разницу между интегралами двух функций.

• Площадь между кривой с положительным значением и горизонтальной осью, измеренная между двумя значениями a и b (b определяется как большее из двух значений) на горизонтальной оси, определяется интегралом от a до b функции, которая представляет собой кривую:

$A=\int _{a}^{b}f(x)\,dx.$

• Площадь между двух функций равна интегралу одной функции ( x f ( g ) минус интеграл другой функции x ) графиками :

$A=\int _{a}^{b}(f(x)-g(x))\,dx,$ где $f(x)$ это кривая с большим значением y.

• Область, ограниченная функцией $r=r(\theta )$ выраженный в полярных координатах :

$A={1 \over 2}\int r^{2}\,d\theta .$

• Площадь, ограниченная параметрической кривой ${\vec {u}}(t)=(x(t),y(t))$ с конечными точками ${\vec {u}}(t_{0})={\vec {u}}(t_{1})$ задается линейными интегралами :

$\oint _{t_{0}}^{t_{1}}x{\dot {y}}\,dt=-\oint _{t_{0}}^{t_{1}}y{\dot {x}}\,dt={1 \over 2}\oint _{t_{0}}^{t_{1}}(x{\dot {y}}-y{\dot {x}})\,dt$

или z -компонент

${1 \over 2}\oint _{t_{0}}^{t_{1}}{\vec {u}}\times {\dot {\vec {u}}}\,dt.$

(Подробнее см. теорему Грина § Вычисление площади .) Таков принцип работы механического устройства планиметра .

Ограниченная область между двумя квадратичными функциями

Чтобы найти ограниченную площадь между двумя квадратичными функциями , мы сначала вычитаем одну из другой, записывая разницу как $$f(x)-g(x)=ax^{2}+bx+c=a(x-\alpha )(x-\beta )$$где f ( x ) — квадратичная верхняя граница, а g ( x ) — квадратичная нижняя граница. Используя приведенные выше формулы интеграла площади и формулу Виеты , мы можем получить, что $$A={\frac {(b^{2}-4ac)^{3/2}}{6a^{2}}}={\frac {a}{6}}(\beta -\alpha )^{3},\qquad a\neq 0.$$Вышесказанное остается в силе, если одна из ограничивающих функций линейна, а не квадратична.

Площадь поверхности трехмерных фигур

• Конус : $\pi r\left(r+{\sqrt {r^{2}+h^{2}}}\right)$, где r — радиус круглого основания, а h — высота. Это также можно переписать как $\pi r^{2}+\pi rl$ или $\pi r(r+l)\,\!$ где r — радиус, а l — наклонная высота конуса. $\pi r^{2}$ это базовая площадь, а $\pi rl$ – площадь боковой поверхности конуса.
• Куб : $6s^{2}$, где s — длина ребра.
• Цилиндр : $2\pi r(r+h)$, где r — радиус основания, а h — высота. $2\pi r$ также можно переписать как $\pi d$, где d — диаметр.
• Призма : $2B+Ph$, где B — площадь основания, P — периметр основания, а h — высота призмы.
• пирамида : $B+{\frac {PL}{2}}$, где B — площадь основания, P — периметр основания, а L — длина наклона.
• Прямоугольная призма : $2(\ell w+\ell h+wh)$, где $\ell$ — длина, w — ширина, h — высота.

Общая формула площади поверхности

Общая формула площади поверхности графика непрерывно дифференцируемой функции $z=f(x,y),$ где $(x,y)\in D\subset \mathbb {R} ^{2}$ и $D$ представляет собой область в плоскости xy с гладкой границей:

$A=\iint _{D}{\sqrt {\left({\frac {\partial f}{\partial x}}\right)^{2}+\left({\frac {\partial f}{\partial y}}\right)^{2}+1}}\,dx\,dy.$

Еще более общая формула площади графика параметрической поверхности в векторной форме $\mathbf {r} =\mathbf {r} (u,v),$ где $\mathbf {r}$ является непрерывно дифференцируемой векторной функцией $(u,v)\in D\subset \mathbb {R} ^{2}$ является:

$A=\iint _{D}\left|{\frac {\partial \mathbf {r} }{\partial u}}\times {\frac {\partial \mathbf {r} }{\partial v}}\right|\,du\,dv.$

Список формул

Дополнительные общие формулы площади:

Форма	Формула	Переменные
Квадрат	$A=s^{2}$
Прямоугольник	$A=ab$
Треугольник	$A={\frac {1}{2}}bh\,\!$
Треугольник	$A={\frac {1}{2}}ab\sin(\gamma )\,\!$
Треугольник ( формула Герона )	$A={\sqrt {s(s-a)(s-b)(s-c)}}\,\!$	$s={\tfrac {1}{2}}(a+b+c)$
Равнобедренный треугольник	$A={\frac {c}{4}}{\sqrt {4a^{2}-c^{2}}}$
Правильный треугольник ( равносторонний треугольник )	$A={\frac {\sqrt {3}}{4}}a^{2}\,\!$
Ромб / Воздушный змей	$A={\frac {1}{2}}de$
Параллелограмм	$A=ah_{a}\,\!$
Трапеция	$A={\frac {(a+c)h}{2}}\,\!$
Правильный шестиугольник	$A={\frac {3}{2}}{\sqrt {3}}a^{2}\,\!$
Правильный восьмиугольник	$A=2(1+{\sqrt {2}})a^{2}\,\!$
Правильный многоугольник ( $n$ стороны)	$A=n{\frac {ar}{2}}={\frac {pr}{2}}$ $\quad ={\tfrac {1}{4}}na^{2}\cot({\tfrac {\pi }{n}})$ $\quad =nr^{2}\tan({\tfrac {\pi }{n}})$ $\quad ={\tfrac {1}{4n}}p^{2}\cot({\tfrac {\pi }{n}})$ $\quad ={\tfrac {1}{2}}nR^{2}\sin({\tfrac {2\pi }{n}})\,\!$	$p=na\$ ( периметр ) $r={\tfrac {a}{2}}\cot({\tfrac {\pi }{n}}),$ ${\tfrac {a}{2}}=r\tan({\tfrac {\pi }{n}})=R\sin({\tfrac {\pi }{n}})$ $r:$ окружности радиус $R:$ описанной окружности радиус
Круг	$A=\pi r^{2}={\frac {\pi d^{2}}{4}}$ ( $d=2r:$ диаметр )
Круговой сектор	$A={\frac {\theta }{2}}r^{2}={\frac {L\cdot r}{2}}\,\!$
Эллипс	$A=\pi ab\,\!$
Интеграл	$A=\int _{a}^{b}f(x)\mathrm {d} x,\ f(x)\geq 0$
	Площадь поверхности
Сфера	$A=4\pi r^{2}=\pi d^{2}$
Кубовидный	$A=2(ab+ac+bc)$
Цилиндр (включая низ и верх)	$A=2\pi r(r+h)$
Конус (включая низ)	$A=\pi r(r+{\sqrt {r^{2}+h^{2}}})$
Тор	$A=4\pi ^{2}\cdot R\cdot r$
Поверхность революции	$A=2\pi \int _{a}^{b}\!f(x){\sqrt {1+\left[f'(x)\right]^{2}}}\mathrm {d} x$ (вращение вокруг оси X)

Приведенные выше расчеты показывают, как найти площади многих распространенных фигур .

Площади неправильных (и, следовательно, произвольных) многоугольников можно вычислить с помощью « формулы геодезиста » (формулы шнурков).

Отношение площади к периметру

Изопериметрическое неравенство гласит, что для замкнутой кривой длины L (поэтому область, которую она охватывает, имеет периметр L ) и для площади A области, которую она ограничивает,

$4\pi A\leq L^{2},$

и равенство имеет место тогда и только тогда, когда кривая представляет собой круг . Таким образом, круг имеет наибольшую площадь среди всех замкнутых фигур с данным периметром.

С другой стороны, фигура с заданным периметром L может иметь сколь угодно малую площадь, как показано на ромбе , который «опрокинут» на сколь угодно далеко так, что два его угла сколь угодно близки к 0°, а два других сколь угодно близки. до 180°.

Для круга отношение площади к окружности (термин, обозначающий периметр круга) равно половине радиуса r . Это видно из формулы площади πr ² и формула окружности 2 πr .

Площадь правильного многоугольника равна половине его периметра, умноженного на апофему (где апофема — это расстояние от центра до ближайшей точки на любой стороне).

Фракталы

Удвоение длины ребра многоугольника умножает его площадь на четыре, что составляет два (отношение длины новой стороны к старой), возведенное в степень двойки (размер пространства, в котором находится многоугольник). Но если все одномерные длины фрактала, нарисованного в двух измерениях, удваиваются, пространственное содержание фрактала масштабируется в степени двойки, которая не обязательно является целым числом. Эта мощность называется фрактальной размерностью фрактала.

Биссектрисы площади

Основная статья: Биссектриса § Биссектрисы площади и биссектрисы периметра

Существует бесконечное количество линий, делящих площадь треугольника пополам. Три из них являются медианами треугольника (которые соединяют середины сторон с противоположными вершинами), и они совпадают треугольника в центроиде ; действительно, это единственные биссектрисы площади, проходящие через центр тяжести. Любая линия, проходящая через треугольник, которая делит площадь треугольника и его периметр пополам, проходит через центр треугольника (центр вписанной окружности ) . В любом треугольнике их может быть один, два или три.

Любая линия, проходящая через середину параллелограмма, делит площадь пополам.

Все биссектрисы круга или другого эллипса проходят через центр, а любые хорды, проходящие через центр, делят площадь пополам. В случае круга это диаметры круга.

Оптимизация

Учитывая контур провода, поверхность наименьшей площади, охватывающая («заполняющая») его, является минимальной поверхностью . Знакомые примеры включают мыльные пузыри .

Вопрос о площади заполнения римановой окружности остается открытым.

Круг имеет наибольшую площадь среди всех двумерных объектов с таким же периметром.

Циклический многоугольник (вписанный в окружность) имеет наибольшую площадь среди всех многоугольников с заданным количеством сторон одинаковой длины.

Версия изопериметрического неравенства для треугольников гласит, что треугольник наибольшей площади среди всех треугольников с данным периметром является равносторонним .

Треугольник наибольшей площади из всех вписанных в данный круг является равносторонним; и треугольник наименьшей площади из всех описанных вокруг данной окружности является равносторонним.

Отношение площади вписанной окружности к площади равностороннего треугольника. ${\frac {\pi }{3{\sqrt {3}}}}$, больше, чем у любого неравностороннего треугольника.

Отношение площади к квадрату периметра равностороннего треугольника, ${\frac {1}{12{\sqrt {3}}}},$ больше, чем для любого другого треугольника.

См. также

• Четырехугольник Брахмагупты , вписанный четырехугольник с целыми сторонами, целыми диагоналями и целой площадью.
• Равноугольная карта
• Геронов треугольник — треугольник с целыми сторонами и целой площадью.
• Список неравенств треугольника
• Треугольник с площадью одной седьмой — внутренний треугольник, площадь которого составляет одну седьмую площади эталонного треугольника.

• Теорема Рауса , обобщение треугольника площади одной седьмой.

• Порядки величины — список областей по размеру.
• Вывод формулы пятиугольника
• Планиметр — инструмент для измерения небольших территорий, например на картах.
• Площадь выпуклого четырехугольника
• Пятиугольник Роббинса — вписанный пятиугольник, длины сторон и площадь которого являются рациональными числами.