✖


Jump to content

Эффект бабочки

Чтобы узнать о других значениях, см. Эффект бабочки (значения) .
График странного аттрактора Лоренца для значений ρ=28, σ = 10, β = 8/3. Эффект бабочки или чувствительная зависимость от начальных условий — это свойство динамической системы , что, начиная с любого из различных сколь угодно близких альтернативных начальных условий на аттракторе, повторяющиеся точки будут произвольно разнесены друг от друга.
Продолжительность: 3 минуты 40 секунд.
Экспериментальная демонстрация эффекта бабочки с шестью записями одного и того же двойного маятника . В каждой записи маятник начинается практически с одного и того же начального состояния. Со временем различия в динамике вырастают от почти незаметных до резких.

В теории хаоса эффект бабочки — это чувствительная зависимость от начальных условий , при которой небольшое изменение в одном состоянии детерминированной нелинейной системы может привести к большим различиям в более позднем состоянии.

Термин тесно связан с работами математика и метеоролога Эдварда Нортона Лоренца . Он отметил, что эффект бабочки основан на метафорическом примере, когда детали торнадо ( точное время формирования, точный путь) находятся под влиянием незначительных возмущений, таких как далекая бабочка, взмахивающая крыльями несколькими неделями ранее. Первоначально Лоренц использовал чайку, вызывающую шторм, но к 1972 году его убедили сделать это более поэтично, используя бабочку и торнадо. [1] [2] Он обнаружил этот эффект, когда наблюдал за выполнением своей модели погоды с исходными данными о состоянии, которые были округлены, казалось бы, несущественным образом. Он отметил, что погодная модель не сможет воспроизвести результаты прогонов с неокругленными данными о начальных условиях. Очень небольшое изменение начальных условий привело к совершенно иному результату. [3]

Идея о том, что малые причины могут иметь большие последствия в погоде, ранее была признана французским математиком и физиком Анри Пуанкаре . Американский математик и философ Норберт Винер также внес свой вклад в эту теорию. Работа Лоренца поместила понятие неустойчивости земной атмосферы на количественную основу и связала понятие неустойчивости со свойствами больших классов динамических систем, которые испытывают нелинейную динамику и детерминированный хаос . [4]

Концепция эффекта бабочки с тех пор используется вне контекста науки о погоде как широкий термин для любой ситуации, когда небольшое изменение должно стать причиной более серьезных последствий.

История [ править ]

См. Также: Теория хаоса § Популярная, но неточная аналогия хаоса.

В «Призвании человека» (1800) Иоганн Готлиб Фихте говорит: «Нельзя было убрать с места ни единой песчинки, не изменив тем самым… что-то во всех частях неизмеримого целого».

Теория хаоса и чувствительная зависимость от начальных условий были описаны во многих источниках литературы. Об этом свидетельствует случай задачи трех тел Пуанкаре в 1890 году. [5] Позже он предположил, что подобные явления могут быть распространены, например, в метеорологии. [6]

В 1898 году Жак Адамар отметил общую расходимость траекторий в пространствах отрицательной кривизны. Пьер Дюэм обсуждал возможное общее значение этого в 1908 году. [5]

В 1950 году Алан Тьюринг заметил: «Смещение одного электрона на миллиардную долю сантиметра в один момент может сыграть решающую роль в том, погибнет ли человек год спустя в лавине или сбежит». [7]

Идея о том, что смерть одной бабочки может в конечном итоге оказать далеко идущее волновое воздействие на последующие исторические события, впервые появилась в « Звук грома рассказе Рэя Брэдбери » 1952 года . «Звук грома» рассказывает о путешествиях во времени. [8]

Точнее, однако, почти точная идея и точная формулировка — о крыле крошечного насекомого, влияющем на ветры всей атмосферы — были опубликованы в детской книге, которая стала чрезвычайно успешной и известной во всем мире в 1962 году, за год до публикации Лоренца:

«...что бы мы ни делали, это влияет на все и всех остальных, хотя бы в малейшей степени. Почему, когда комнатная муха взмахивает крыльями, ветерок облетает мир».

-- Принцесса чистого разума

— Нортон Джастер, «Призрачная платная будка»

В 1961 году Лоренц использовал численную компьютерную модель, чтобы в качестве ярлыка повторить прогноз погоды, полученный в середине предыдущего прогона. Он ввел начальное условие 0,506 из распечатки вместо ввода значения полной точности 0,506127. В результате получился совершенно другой погодный сценарий. [9]

Лоренц писал:

В какой-то момент я решил повторить некоторые вычисления, чтобы подробнее изучить происходящее. Я остановил компьютер, набрал строку цифр, которую он распечатал некоторое время назад, и снова включил его. Я пошел в коридор выпить чашечку кофе и вернулся примерно через час, за это время компьютер смоделировал погоду примерно за два месяца. Напечатанные цифры не были похожи на старые. Я сразу заподозрил слабую вакуумную лампу или какую-то другую неисправность компьютера, что не было редкостью, но прежде чем обращаться в сервис, я решил посмотреть, где именно произошла ошибка, зная, что это может ускорить процесс обслуживания. Вместо внезапного разрыва я обнаружил, что новые значения сначала повторяли старые, но вскоре после этого отличались на одну, а затем и на несколько единиц в последнем [десятичном] знаке, а затем стали различаться в предпоследнем месте и затем на месте перед этим. Фактически, различия более или менее стабильно удваивались каждые четыре дня или около того, пока все сходство с исходным результатом не исчезло где-то на втором месяце. Этого было достаточно, чтобы понять, что произошло: числа, которые я ввел, были не точными исходными числами, а округленными значениями, которые фигурировали в исходной распечатке. Виновниками были первоначальные ошибки округления; они постоянно усиливались, пока не стали доминировать в решении.

- Э. Н. Лоренц, Сущность хаоса , U. Washington Press, Сиэтл (1993), стр. 134. [10]

В 1963 году Лоренц опубликовал теоретическое исследование этого эффекта в широко цитируемой плодотворной статье под названием «Детерминированный непериодический поток» . [3] [11] (расчеты выполнены на компьютере Royal McBee LGP-30 ). [12] [13] В другом месте он заявил:

Один метеоролог заметил, что, если бы теория была верна, одного взмаха крыльев чайки было бы достаточно, чтобы навсегда изменить ход погоды. Споры еще не разрешены, но самые последние данные, похоже, говорят в пользу чаек. [13]

Следуя предложениям коллег, в более поздних выступлениях и статьях Лоренц использовал более поэтичную бабочку . По словам Лоренца, когда он не смог придумать название для доклада, который он должен был выступить на 139-м собрании Американской ассоциации содействия развитию науки в 1972 году, Филип Мерилис придумал: « Вызывает ли взмах крыльев бабочки в Бразилии торнадо?» в Техасе? как титул. [1] Хотя бабочка, взмахивающая крыльями, осталась неизменной в выражении этой концепции, местоположение бабочки, последствия и расположение последствий сильно различались. [14]

Эта фраза относится к идее о том, что крылья бабочки могут создавать крошечные изменения в атмосфере , которые в конечном итоге могут изменить путь торнадо или задержать, ускорить или даже предотвратить появление торнадо в другом месте. Бабочка не приводит в действие торнадо и не создает его напрямую, но этот термин подразумевает, что взмах крыльев бабочки может вызвать торнадо: в том смысле, что взмах крыльев является частью начальных условий взаимосвязанного комплекса. сеть; один набор условий приводит к торнадо, а другой — нет. Взмах крыла представляет собой небольшое изменение начального состояния системы, которое приводит к крупномасштабным изменениям событий (сравните: эффект домино ). Если бы бабочка не махала крыльями, траектория системы могла бы быть совершенно иной, но в равной степени возможно, что набор условий без взмахов крыльями бабочки является набором, который приводит к торнадо.

Эффект бабочки представляет собой очевидную проблему для прогнозирования, поскольку начальные условия такой системы, как погода, никогда не могут быть известны с полной точностью. Эта проблема мотивировала развитие ансамблевого прогнозирования , при котором ряд прогнозов делается на основе возмущенных начальных условий. [15]

Некоторые ученые с тех пор утверждают, что погодная система не так чувствительна к начальным условиям, как считалось ранее. [16] Дэвид Оррелл утверждает, что основной причиной ошибки прогноза погоды является ошибка модели, при этом чувствительность к начальным условиям играет относительно небольшую роль. [17] [18] Стивен Вольфрам также отмечает, что уравнения Лоренца сильно упрощены и не содержат членов, отражающих эффекты вязкости; он считает, что эти условия будут иметь тенденцию гасить небольшие возмущения. [19] Недавние исследования с использованием обобщенных моделей Лоренца , которые включали дополнительные диссипативные члены и нелинейность, показали, что для возникновения хаоса требуется больший параметр нагрева. [20]

Хотя «эффект бабочки» часто объясняют как синоним чувствительной зависимости от начальных условий, описанной Лоренцем в его статье 1963 года (и ранее наблюдавшейся Пуанкаре), первоначально применялась метафора бабочки. [1] к работе он опубликовал в 1969 году [21] что продвинуло идею на шаг дальше. Лоренц предложил математическую модель того, как крошечные движения в атмосфере масштабируются и влияют на более крупные системы. Он обнаружил, что системы в этой модели можно предсказать только до определенного момента в будущем, и кроме этого уменьшение ошибки в начальных условиях не повысит предсказуемость (пока ошибка не равна нулю). Это продемонстрировало, что детерминированная система может быть «неотличима с точки зрения наблюдения» от недетерминированной с точки зрения предсказуемости. Недавнее повторное рассмотрение этой статьи позволяет предположить, что она бросила серьезный вызов идее о детерминированности нашей Вселенной, сравнимый с проблемами, которые ставит квантовая физика. [22] [23]

В книге «Сущность хаоса» , опубликованной в 1993 году, [24] Лоренц определил эффект бабочки как: «Явление, при котором небольшое изменение состояния динамической системы приводит к тому, что последующие состояния сильно отличаются от состояний, которые последовали бы без изменений». Эта особенность аналогична чувствительной зависимости решений от начальных условий (SDIC) в . [3] В той же книге Лоренц применил катание на лыжах и разработал идеализированную модель катания на лыжах для выявления чувствительности изменяющихся во времени траекторий к исходным положениям. Горизонт предсказуемости определяется до начала SDIC. [25]

Иллюстрации [ править ]

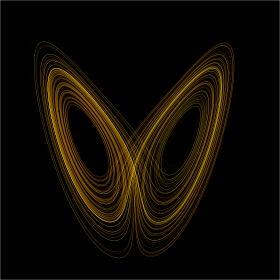
Эффект бабочки в аттракторе Лоренца.
время 0 ≤ t ≤ 30 (больше) z координата (большая)
На этих рисунках показаны два участка трехмерной эволюции двух траекторий (одна синего цвета, другая желтого цвета) за один и тот же период времени в аттракторе Лоренца, начиная с двух начальных точек, отличающихся всего на 10 −5 в координате х . Первоначально две траектории кажутся совпадающими, на что указывает небольшая разница между координатой z синей и желтой траекторий, но при t > 23 разница столь же велика, как и значение траектории. Окончательное положение конусов указывает на то, что две траектории больше не совпадают при t = 30.
Анимация аттрактора Лоренца показывает непрерывную эволюцию.

Теория математическое определение и

Смотрите также: Теория хаоса § Новаторский вклад Лоренца в хаотическое моделирование

Возвратность , приближенное возвращение системы к исходным условиям, вместе с чувствительной зависимостью от начальных условий, являются двумя основными ингредиентами хаотического движения. Их практические последствия заключаются в том, что сложные системы , такие как погода , трудно предсказать в течение определенного периода времени (примерно неделю в случае погоды), поскольку невозможно полностью точно измерить начальные атмосферные условия.

Динамическая система демонстрирует чувствительную зависимость от начальных условий, если точки, сколь угодно близкие друг к другу, со временем расходятся с экспоненциальной скоростью. Определение не топологическое, а по существу метрическое. Лоренц [24] определил чувствительную зависимость следующим образом:

Свойство, характеризующее орбиту (т. е. решение), если большинство других орбит, проходящих близко к ней в какой-то момент, не остаются близкими к ней с течением времени.

Если M — пространство состояний карты , затем отображает чувствительную зависимость от начальных условий, если для любого x в M и любого δ > 0 существуют y в M с расстоянием d (. , .) такие, что и такое, что

для некоторого положительного параметра a . Определение не требует, чтобы все точки окрестности отделялись от базовой точки x , но требует одного положительного показателя Ляпунова . Помимо положительного показателя Ляпунова, еще одной важной особенностью хаотических систем является ограниченность. [26]

Простейшая математическая основа, демонстрирующая чувствительную зависимость от начальных условий, обеспечивается конкретной параметризацией логистической карты :

которая, в отличие от большинства хаотических карт, имеет решение в замкнутой форме :

где начального состояния параметр дается . Для рационального , после конечного числа итераций отображается в периодическую последовательность . Но почти все иррациональны, а поскольку иррациональны , никогда не повторяется – оно непериодично. Это уравнение решения ясно демонстрирует две ключевые особенности хаоса – растяжение и складывание: фактор 2. н показывает экспоненциальный рост растяжения, что приводит к чувствительной зависимости от начальных условий (эффект бабочки), в то время как функция синуса в квадрате сохраняет свернуто в диапазоне [0, 1].

В физических системах [ править ]

В погоде [ править ]

Обзор [ править ]

Эффект бабочки наиболее известен с точки зрения погоды; это можно легко продемонстрировать, например, в стандартных моделях прогнозирования погоды. Климатологи Джеймс Аннан и Уильям Коннолли объясняют, что хаос важен в разработке методов прогнозирования погоды; модели чувствительны к начальным условиям. Они добавляют предостережение: «Конечно, существование неизвестной бабочки, взмахивающей крыльями, не имеет прямого отношения к прогнозам погоды, поскольку потребуется слишком много времени, чтобы такое маленькое возмущение выросло до значительных размеров, и у нас есть еще много неотложных задач. неопределенности, о которых стоит беспокоиться. Поэтому прямое влияние этого явления на прогноз погоды часто бывает несколько ошибочным». [27]

типов Дифференциация эффектов бабочки

Концепция эффекта бабочки включает в себя несколько явлений. Два вида эффектов бабочки, включая чувствительную зависимость от начальных условий, [3] и способность малейшего возмущения создавать организованную циркуляцию на больших расстояниях, [1] не совсем одинаковы. [28] Сравнение двух видов эффектов бабочки [1] [3] и третий вид эффекта бабочки [21] [22] [23] было задокументировано. [29] В недавних исследованиях [25] [30] Сообщалось, что как метеорологические, так и неметеорологические линейные модели показали, что нестабильность играет роль в возникновении эффекта бабочки, который характеризуется кратким, но значительным экспоненциальным ростом в результате небольшого возмущения.

об эффекте Недавние дебаты бабочки

Первый вид эффекта бабочки, известный как SDIC (чувствительная зависимость от начальных условий), широко известен и демонстрируется с помощью идеализированных хаотических моделей. Однако мнения расходятся относительно второго типа эффекта бабочки, а именно влияния взмахов крыльев бабочки на образование торнадо, как указано в двух статьях 2024 года. [31] [32] Для третьего типа эффекта бабочки ограниченная предсказуемость в модели Лоренца 1969 года объясняется масштабными взаимодействиями в одной статье. [22] и из-за плохой подготовки системы в другом более позднем исследовании. [25]

в хаотических системах предсказуемость Конечная

По словам Лайтхилла (1986), [33] наличие SDIC (широко известного как эффект бабочки) подразумевает, что хаотические системы имеют конечный предел предсказуемости. В обзоре литературы, [34] Было обнаружено, что точку зрения Лоренца на предел предсказуемости можно свести к следующему утверждению:

  • (А). Модель Лоренца 1963 года качественно раскрыла суть конечной предсказуемости в такой хаотической системе, как атмосфера. Однако он не определил точный предел предсказуемости атмосферы.
  • (Б). В 1960-х годах двухнедельный предел предсказуемости первоначально оценивался на основе удвоения времени в пять дней в реальных моделях. С тех пор это открытие было задокументировано Charney et al. (1966) [35] [36] и стал консенсусом.

Недавно был создан короткий видеоролик, в котором представлен взгляд Лоренца на предел предсказуемости. [37]

нехаотические системы Пересмотренные на хаотические и взгляды

Выявив сосуществование хаотических и нехаотических аттракторов в моделях Лоренца, Шен и его коллеги предложили пересмотренную точку зрения, согласно которой «погода обладает хаосом и порядком», в отличие от традиционного взгляда на то, что «погода хаотична». [38] [39] [40] В результате не всегда проявляется чувствительная зависимость от начальных условий (SDIC). А именно, SDIC появляется, когда две орбиты (т. е. решения) становятся хаотическим аттрактором; он не появляется, когда две орбиты движутся к одному и тому же точечному аттрактору. Приведенная выше анимация движения двойного маятника дает аналогию. При больших углах качания движение маятника часто бывает хаотичным. [41] [42] Для сравнения, при малых углах поворота движения нехаотичны.Мультистабильность определяется, когда система (например, система двойного маятника ) содержит более одного ограниченного аттрактора, зависящего только от начальных условий. Мультистабильность была проиллюстрирована с помощью каякинга на рисунке справа (т. е. рисунок 1 [43] ), где появление сильных течений и застойной области свидетельствует о неустойчивости и локальной устойчивости соответственно. В результате, когда два каяка движутся по сильному течению, на их траекториях отображается SDIC. С другой стороны, когда два каяка попадают в застойную зону, они оказываются в ловушке, не проявляя типичного SDIC (хотя может произойти хаотический переходный процесс). Такие особенности SDIC или отсутствие SDIC предполагают два типа решений и иллюстрируют природу мультистабильности.

Принимая во внимание изменяющуюся во времени мультистабильность, которая связана с модуляцией крупномасштабных процессов (например, сезонным воздействием) и совокупной обратной связью мелкомасштабных процессов (например, конвекции), приведенная выше пересмотренная точка зрения уточняется следующим образом:

«Атмосфера обладает хаосом и порядком; она включает в себя, например, возникающие организованные системы (такие как торнадо) и изменяющиеся во времени воздействия повторяющихся сезонов». [43] [44]

В квантовой механике [ править ]

Возможность чувствительной зависимости от начальных условий (эффект бабочки) изучалась в ряде случаев в квазиклассической и квантовой физике, включая атомы в сильных полях и анизотропную задачу Кеплера . [45] [46] Некоторые авторы утверждали, что экстремальная (экспоненциальная) зависимость от начальных условий не ожидается при чисто квантовых методах лечения; [47] [48] однако чувствительная зависимость от начальных условий, продемонстрированная в классическом движении, включена в полуклассические трактовки, разработанные Мартином Гуцвиллером. [49] и Джон Б. Делос и его коллеги. [50] Теория случайных матриц и моделирование с помощью квантовых компьютеров доказывают, что некоторые версии эффекта бабочки в квантовой механике не существуют. [51]

Другие авторы предполагают, что эффект бабочки можно наблюдать в квантовых системах. Збышек П. Каркушевский и др. рассмотрим эволюцию во времени квантовых систем, имеющих несколько разные гамильтонианы . Они исследуют уровень чувствительности квантовых систем к небольшим изменениям в их данных гамильтонианах. [52] Дэвид Пулин и др. представил квантовый алгоритм для измерения снижения точности, который «измеряет скорость, с которой идентичные начальные состояния расходятся, когда они подвергаются несколько разной динамике». Они считают снижение точности «ближайшим квантовым аналогом (чисто классического) эффекта бабочки». [53] В то время как классический эффект бабочки учитывает эффект небольшого изменения положения и/или скорости объекта в данной гамильтоновой системе , квантовый эффект бабочки учитывает эффект небольшого изменения в гамильтоновой системе с заданным начальным положением и скоростью. . [54] [55] Эффект квантовой бабочки был продемонстрирован экспериментально. [56] Квантовая и квазиклассическая трактовки чувствительности системы к начальным условиям известны как квантовый хаос . [47] [54]

В популярной культуре [ править ]

Основная статья: Эффект бабочки в популярной культуре

В названной статье представлены примеры или сравнения эффекта бабочки в различных средах, таких как литература (например, «Звук грома»), фильмы, телевидение (например, «Симпсоны»), видеоигры (например, «Жизнь странна»), экспансивные проекты, основанные на искусственном интеллекте. языковые модели и многое другое.

См. также [ править ]

Ссылки [ править ]

  1. ↑ Перейти обратно: Перейти обратно: а б с д и «Предсказуемость: взмах крыльев бабочки в Бразилии вызвал торнадо в Техасе?» (PDF) . Архивировано (PDF) из оригинала 9 октября 2022 г. Проверено 23 декабря 2021 г.
  2. ^ «Когда Лоренц открыл эффект бабочки» . 22 мая 2015 года . Проверено 23 декабря 2021 г.
  3. ↑ Перейти обратно: Перейти обратно: а б с д и Лоренц, Эдвард Н. (март 1963 г.). «Детерминированный непериодический поток» . Журнал атмосферных наук . 20 (2): 130–141. Бибкод : 1963JAtS...20..130L . doi : 10.1175/1520-0469(1963)020<0130:dnf>2.0.co;2 .
  4. ^ Рувас-Николис, Екатерина; Николис, Грегуар (4 мая 2009 г.). «Эффект бабочки» . Схоларпедия . Том. 4. с. 1720. Бибкод : 2009SchpJ...4.1720R . doi : 10.4249/scholarpedia.1720 . Архивировано из оригинала 02 января 2016 г. Проверено 2 января 2016 г.
  5. ↑ Перейти обратно: Перейти обратно: а б Некоторые исторические заметки: История теории хаоса. Архивировано 19 июля 2006 г. в Wayback Machine.
  6. ^ Стивс, Бонни; Мациевский, AJ (сентябрь 2001 г.). Беспокойная Вселенная. Применение гравитационной динамики N-тел к планетарным звездным и галактическим системам . США: CRC Press. ISBN  0750308222 . Проверено 6 января 2014 г.
  7. ^ Вычислительная техника и интеллект
  8. ^ Флам, Фэй (15 июня 2012 г.). «Физика «Звука грома» Рэя Брэдбери » . Филадельфийский исследователь . Архивировано из оригинала 24 сентября 2015 г. Проверено 2 сентября 2015 г.
  9. ^ Глейк, Джеймс (1987). Хаос: создание новой науки . Викинг. п. 16. ISBN  0-8133-4085-3 .
  10. ^ Моттер, Адилсон Э.; Кэмпбелл, Дэвид К. (2013). «Хаос в пятьдесят». Физика сегодня . 66 (5): 27–33. arXiv : 1306.5777 . Бибкод : 2013ФТ....66е..27М . дои : 10.1063/PT.3.1977 . S2CID   54005470 .
  11. ^ Запись цитирования в Академии Google
  12. ^ «Часть 19» . Cs.ualberta.ca. 1960-11-22. Архивировано из оригинала 17 июля 2009 г. Проверено 8 июня 2014 г.
  13. ↑ Перейти обратно: Перейти обратно: а б Лоренц, Эдвард Н. (1963). «Предсказуемость гидродинамического потока» (PDF) . Труды Нью-Йоркской академии наук . 25 (4): 409–432. дои : 10.1111/j.2164-0947.1963.tb01464.x . Архивировано (PDF) из оригинала 10 октября 2014 г. Проверено 1 сентября 2014 г.
  14. ^ «Эффект бабочки: вариации на тему мема» . AP42... и всё . Архивировано из оригинала 11 ноября 2011 года . Проверено 3 августа 2011 г.
  15. ^ Вудс, Остин (2005). Среднесрочный прогноз погоды: европейский подход; История Европейского центра среднесрочных прогнозов погоды . Нью-Йорк: Спрингер. п. 118 . ISBN  978-0387269283 .
  16. ^ Оррелл, Дэвид; Смит, Леонард; Баркмейер, Ян; Палмер, Тим (2001). «Ошибка модели в прогнозе погоды» . Нелинейные процессы в геофизике . 9 (6): 357–371. Бибкод : 2001NPGeo...8..357O . дои : 10.5194/npg-8-357-2001 .
  17. ^ Оррелл, Дэвид (2002). «Роль показателя в росте ошибок прогноза: насколько хаотична погода?» . Теллус . 54А (4): 350–362. Бибкод : 2002TellA..54..350O . дои : 10.3402/tellusa.v54i4.12159 .
  18. ^ Оррелл, Дэвид (2012). Истина или красота: наука и поиск порядка . Нью-Хейвен: Издательство Йельского университета. п. 208. ИСБН  978-0300186611 .
  19. ^ Вольфрам, Стивен (2002). Новый вид науки . Вольфрам Медиа. п. 998 . ISBN  978-1579550080 .
  20. ^ Шен, Бо-Вэнь (2019). «Агрегированная отрицательная обратная связь в обобщенной модели Лоренца» . Международный журнал бифуркации и хаоса . 29 (3): 1950037–1950091. Бибкод : 2019IJBC...2950037S . дои : 10.1142/S0218127419500378 . S2CID   132494234 .
  21. ↑ Перейти обратно: Перейти обратно: а б Лоренц, Эдвард Н. (июнь 1969 г.). «Предсказуемость потока, обладающего многими масштабами движения». Теллус . XXI (3): 289–297. Бибкод : 1969Tell...21..289L . дои : 10.1111/j.2153-3490.1969.tb00444.x .
  22. ↑ Перейти обратно: Перейти обратно: а б с Тим, Палмер (19 мая 2017 г.). «Эффект бабочки – что это на самом деле означает?» . Канал факультета математики Оксфордского университета на YouTube . Архивировано из оригинала 31 октября 2021 г. Проверено 13 февраля 2019 г.
  23. ↑ Перейти обратно: Перейти обратно: а б Эмануэль, Керри (26 марта 2018 г.). «Эдвард Н. Лоренц и конец картезианской Вселенной» . Канал Департамента наук о Земле, атмосфере и планетах Массачусетского технологического института на Youtube . Архивировано из оригинала 31 октября 2021 г. Проверено 13 февраля 2019 г.
  24. ↑ Перейти обратно: Перейти обратно: а б Лоренц, Эдвард Н. (1993). Сущность хаоса . Лондон: UCL Press. ISBN  0-203-21458-7 . OCLC   56620850 .
  25. ↑ Перейти обратно: Перейти обратно: а б с Шен, Бо-Вэнь; Пилке, Роджер А.; Цзэн, Сюбинь (07 мая 2022 г.). «Одна седловая точка и два типа чувствительности в моделях Лоренца 1963 и 1969 годов» . Атмосфера . 13 (5): 753. Бибкод : 2022Атм..13..753С . дои : 10.3390/atmos13050753 . ISSN   2073-4433 .
  26. ^ В., Джордан, Доминик (2011). Нелинейные обыкновенные дифференциальные уравнения: введение для ученых и инженеров . Оксфордский университет. Нажимать. ISBN  978-0-19-920825-8 . OCLC   772641393 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
  27. ^ «Хаос и климат» . RealClimate. 4 ноября 2005 г. Архивировано из оригинала 02 июля 2014 г. Проверено 8 июня 2014 г.
  28. ^ Шен, Бо-Вэнь (01 мая 2014 г.). «Нелинейная обратная связь в пятимерной модели Лоренца» . Журнал атмосферных наук . 71 (5): 1701–1723. Бибкод : 2014JAtS...71.1701S . doi : 10.1175/JAS-D-13-0223.1 . ISSN   0022-4928 . S2CID   123683839 .
  29. ^ Шен, Бо-Вэнь; Пилке, Роджер А.; Цзэн, Сюбин; Цуй, Цзялин; Фаги-Наини, Сара; Паксон, Вэй; Атлас, Роберт (04 июля 2022 г.). «Три вида эффектов бабочки в моделях Лоренца» . Энциклопедия . 2 (3): 1250–1259. дои : 10.3390/энциклопедия2030084 . ISSN   2673-8392 .
  30. ^ Сайки, Ёситака; Йорк, Джеймс А. (2 мая 2023 г.). «Может ли взмах крыльев бабочки перенести торнадо в Техас без хаоса?» . Атмосфера . 14 (5): 821. Бибкод : 2023Атмос..14..821С . дои : 10.3390/atmos14050821 . ISSN   2073-4433 .
  31. ^ Пилке-старший, Роджер; Шен, Бо-Вэнь; Цзэн, Сюбинь (01 мая 2024 г.). «Эффект бабочки: может ли бабочка в Бразилии вызвать торнадо в Техасе?» . По погоде . 77 (3): 14–18.
  32. ^ Палмер, Тим (01 мая 2024 г.). «Настоящий эффект бабочки и червивые яблоки» . Физика сегодня . 77 (5): 30–35. doi : 10.1063/pt.eike.hsbz . ISSN   0031-9228 .
  33. ^ Лайтхилл, Джеймс (08 сентября 1986 г.). «Недавно признанная неспособность предсказуемости в ньютоновской динамике» . Труды Лондонского королевского общества. А. Математические и физические науки . 407 (1832): 35–50. Бибкод : 1986РСПСА.407...35Л . дои : 10.1098/rspa.1986.0082 . ISSN   0080-4630 . S2CID   86552243 .
  34. ^ Шен, Бо-Вэнь; Пилке, Роджер А.; Цзэн, Сюбин; Цзэн, Сипин (22 июля 2023 г.). «Взгляд Лоренца на предел предсказуемости атмосферы» . Энциклопедия . 3 (3): 887–899. дои : 10.3390/энциклопедия3030063 . ISSN   2673-8392 . В эту статью включен текст из этого источника, доступного по лицензии CC BY 4.0 .
  35. ^ Осуществимость глобального эксперимента по наблюдению и анализу . 1 января 1966 г. дои : 10.17226/21272 . ISBN  978-0-309-35922-1 .
  36. ^ ГАРП (01.03.1969). «Руководство по ГАРП» . Бык. амер. Метеор. Соц . 50 (3): 136–141. Бибкод : 1969BAMS...50..136. . дои : 10.1175/1520-0477-50.3.136 .
  37. ^ Шен, Бо-Вэнь; Пилке-старший, Роджер; Цзэн, Сюбин; Цзэн, Сипин (13 сентября 2023 г.). «Взгляд Лоренца на предел предсказуемости» . Энциклопедия паб . Проверено 13 сентября 2023 г.
  38. ^ Шен, Бо-Вэнь; Пилке, Роджер А.; Цзэн, Сюбин; Байк, Чон-Джин; Фаги-Наини, Сара; Цуй, Цзялин; Атлас, Роберт (01 января 2021 г.). «Хаотична ли погода?: Сосуществование хаоса и порядка в обобщенной модели Лоренца» . Бюллетень Американского метеорологического общества . 102 (1): Е148–Е158. Бибкод : 2021BAMS..102E.148S . дои : 10.1175/BAMS-D-19-0165.1 . ISSN   0003-0007 . S2CID   208369617 .
  39. ^ Шен, Бо-Вэнь; Пилке, Р.А. старший; Цзэн, X.; Байк, Ж.-Ж.; Фагих-Наини, С.; Кюи, Дж.; Атлас, Р.; Рейес, ТАЛ (2021). «Хаотична ли погода? Сосуществуют хаотические и нехаотические аттракторы в моделях Лоренца» . В Скиадасе, Христос Х.; Димотикалис, Яннис (ред.). 13-я Международная конференция по хаотическому моделированию и симуляции . Спрингерские слушания в сложности. Чам: Международное издательство Springer. стр. 805–825. дои : 10.1007/978-3-030-70795-8_57 . ISBN  978-3-030-70795-8 . S2CID   245197840 .
  40. ^ Антес, Ричард А. (14 августа 2022 г.). «Предсказуемость и предсказания» . Атмосфера . 13 (8): 1292. Бибкод : 2022Атмос..13.1292А . дои : 10.3390/atmos13081292 . ISSN   2073-4433 .
  41. ^ Рихтер, PH; Шольц, Х.-Й. (1984), «Хаос в классической механике: двойной маятник» , «Стохастические явления и хаотическое поведение в сложных системах» , серия Спрингера по синергетике, том. 21, Берлин, Гейдельберг: Springer Berlin Heidelberg, стр. 86–97, doi : 10.1007/978-3-642-69591-9_9 , ISBN  978-3-642-69593-3 , получено 11 июля 2022 г.
  42. ^ Шинброт, Трой, Селсо А. Гребоги, Джек Уиздом, Джеймс А. Йорк (1992). «Хаос в двойном маятнике» . Американский журнал физики . 60 (6): 491–499. Бибкод : 1992AmJPh..60..491S . дои : 10.1119/1.16860 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
  43. ↑ Перейти обратно: Перейти обратно: а б Шен, Бо-Вэнь; Пилке-старший, Роджер Пилке; Цзэн, Сюбин; Цуй, Цзялин; Фаги-Наини, Сара; Паксон, Вэй; Кесаркар, Амит; Цзэн, Сипин; Атлас, Роберт (12 ноября 2022 г.). «Двойная природа хаоса и порядка в атмосфере» . Атмосфера . 13 (11): 1892. Бибкод : 2022Атм..13.1892С . дои : 10.3390/atmos13111892 . ISSN   2073-4433 . Текст был скопирован из этого источника, который доступен по международной лицензии Creative Commons Attribution 4.0 .
  44. ^ Шен, Бо-Вэнь (21 февраля 2023 г.). «Изучение теории хаоса на предмет моностабильности и мультистабильности» . Ютуб .
  45. ^ Хеллер, Э.Дж.; Томсович, С. (июль 1993 г.). «Постмодернистская квантовая механика». Физика сегодня . 46 (7): 38–46. Бибкод : 1993PhT....46g..38H . дои : 10.1063/1.881358 .
  46. ^ Гуцвиллер, Мартин К. (1990). Хаос в классической и квантовой механике . Нью-Йорк: Springer-Verlag. ISBN  0-387-97173-4 .
  47. ↑ Перейти обратно: Перейти обратно: а б Рудник, Зеев (январь 2008 г.). «Что такое... квантовый хаос?» (PDF) . Уведомления Американского математического общества . Архивировано (PDF) из оригинала 02 октября 2009 г.
  48. ^ Берри, Майкл (1989). «Квантовая хаология, а не квантовый хаос». Физика Скрипта . 40 (3): 335–336. Бибкод : 1989PhyS...40..335B . дои : 10.1088/0031-8949/40/3/013 . S2CID   250776260 .
  49. ^ Гуцвиллер, Мартин К. (1971). «Периодические орбиты и классические условия квантования». Журнал математической физики . 12 (3): 343. Бибкод : 1971JMP....12..343G . дои : 10.1063/1.1665596 .
  50. ^ Гао Дж. И Делос Дж. Б. (1992). "Замкнутоорбитальная теория колебаний сечений фотопоглощения атомов в сильном электрическом поле. II. Вывод формул" . Физический обзор А. 46 (3): 1455–1467. Бибкод : 1992PhRvA..46.1455G . дои : 10.1103/PhysRevA.46.1455 . ПМИД   9908268 . S2CID   7877923 .
  51. ^ Ян, Бин; Синицын, Николай А. (2020). «Восстановление поврежденной информации и вневременно упорядоченные корреляторы». Письма о физических отзывах . 125 (4): 040605. arXiv : 2003.07267 . Бибкод : 2020PhRvL.125d0605Y . doi : 10.1103/PhysRevLett.125.040605 . ПМИД   32794812 . S2CID   212725801 .
  52. ^ Каркушевский, Збышек П.; Яржински, Кристофер; Журек, Войцех Х. (2002). «Квантовая хаотическая среда, эффект бабочки и декогеренция». Письма о физических отзывах . 89 (17): 170405. arXiv : quant-ph/0111002 . Бибкод : 2002PhRvL..89q0405K . doi : 10.1103/PhysRevLett.89.170405 . ПМИД   12398653 . S2CID   33363344 .
  53. ^ Пулен, Дэвид; Блюм-Когоут, Робин; Лафламм, Раймонд и Оливье, Гарольд (2004). «Экспоненциальное ускорение с использованием одного бита квантовой информации: измерение среднего снижения точности». Письма о физических отзывах . 92 (17): 177906. arXiv : quant-ph/0310038 . Бибкод : 2004PhRvL..92q7906P . doi : 10.1103/PhysRevLett.92.177906 . ПМИД   15169196 . S2CID   6218604 .
  54. ↑ Перейти обратно: Перейти обратно: а б Пулен, Дэвид. «Приблизительное руководство по квантовому хаосу» (PDF) . Архивировано из оригинала (PDF) 4 ноября 2010 г.
  55. ^ Перес, А. (1995). Квантовая теория: концепции и методы . Дордрехт: Клювер Академик.
  56. ^ Ли, Джэ Сын и Хитрин, АК (2004). «Квантовый усилитель: измерение с запутанными спинами» . Журнал химической физики . 121 (9): 3949–51. Бибкод : 2004JChPh.121.3949L . дои : 10.1063/1.1788661 . ПМИД   15332940 .

Дальнейшее чтение [ править ]

Внешние ссылки [ править ]

Найдите эффект бабочки в Викисловаре, бесплатном словаре.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Butterfly_effect&oldid=1226015505"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: b03ff27f70069e215933657c7f414701__1716853140
URL1:https://arc.ask3.ru/arc/aa/b0/01/b03ff27f70069e215933657c7f414701.html
Заголовок, (Title) документа по адресу, URL1:
Butterfly effect - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)