Волатильность (финансы)

Индекс волатильности CBOE (VIX) с декабря 1985 г. по май 2012 г. (дневное закрытие)

В финансах волатильность (обычно обозначаемая «σ») — это степень изменения ряда торговых цен во времени, обычно измеряемая стандартным отклонением логарифмической доходности .

Историческая волатильность измеряет временной ряд прошлых рыночных цен. Подразумеваемая волатильность рассчитана на будущее и рассчитывается на основе рыночной цены торгуемого на рынке производного инструмента (в частности, опциона).

Терминология волатильности

Описанная здесь волатильность относится к фактической волатильности , а точнее:

фактическая текущая волатильность финансового инструмента за определенный период (например, 30 дней или 90 дней), основанная на исторических ценах за указанный период, при этом последнее наблюдение соответствует самой последней цене.
фактическая историческая волатильность , которая относится к волатильности финансового инструмента в течение определенного периода, но с последним наблюдением на дату в прошлом.
- Почти синонимом является реализованная волатильность , квадратный корень реализованной дисперсии , который, в свою очередь, рассчитывается с использованием суммы квадратов доходности, деленной на количество наблюдений.
фактическая будущая волатильность , которая относится к волатильности финансового инструмента в течение определенного периода, начиная с текущего момента и заканчивая будущей датой (обычно датой истечения срока действия опциона ) .

Теперь обратившись к подразумеваемой волатильности , мы имеем:

историческая подразумеваемая волатильность , которая относится к подразумеваемой волатильности, наблюдаемой на основе исторических цен финансового инструмента (обычно опционов)
текущая подразумеваемая волатильность , которая относится к подразумеваемой волатильности, наблюдаемой из текущих цен финансового инструмента.
будущая подразумеваемая волатильность , которая относится к подразумеваемой волатильности, наблюдаемой из будущих цен финансового инструмента.

Для финансового инструмента, цена которого следует гауссовскому случайному блужданию или винеровскому процессу , ширина распределения увеличивается с увеличением времени. Это связано с тем, что с увеличением времени возрастает вероятность того, что цена инструмента будет все дальше отходить от первоначальной цены. Однако вместо того, чтобы увеличиваться линейно, волатильность увеличивается пропорционально квадратному корню из времени по мере увеличения времени, поскольку ожидается, что некоторые колебания будут компенсировать друг друга, поэтому наиболее вероятное отклонение после удвоенного времени не будет в два раза больше расстояния от нуля.

Поскольку наблюдаемые изменения цен не соответствуют распределениям Гаусса, другие распределения, такие как распределение Леви . часто используются ^[1] Они могут захватывать такие атрибуты, как « толстые хвосты ».Волатильность — это статистическая мера отклонения от среднего значения любой случайной величины, такой как параметры рынка и т. д.

Математическое определение

Для любого фонда, который развивается случайным образом со временем, волатильность определяется как стандартное отклонение последовательности случайных величин, каждая из которых представляет собой доходность фонда за некоторую соответствующую последовательность (одинаковых) периодов времени.

Таким образом, «годовая» волатильность σ _{в год} инструмента представляет собой стандартное отклонение годовой логарифмической доходности . ^[2]

Обобщенная волатильность σ _T для временного горизонта T в годах выражается как:

\sigma _{\text{T}}=\sigma _{\text{annually}}{\sqrt {T}}.

Следовательно, если дневная логарифмическая доходность акций имеет стандартное отклонение σ _{в день} , а период доходности равен P в торговых днях, годовая волатильность равна

\sigma _{\text{annually}}=\sigma _{\text{daily}}{\sqrt {P}}.

так

\sigma _{\text{T}}=\sigma _{\text{daily}}{\sqrt {PT}}.

Распространено предположение, что P = 252 торговых дня в любом году. Тогда, если σ _daily = 0,01, годовая волатильность равна

\sigma _{\text{annually}}=0.01{\sqrt {252}}=0.1587.

Ежемесячная волатильность (т. $T={\tfrac {1}{12}}$ года) это

\sigma _{\text{monthly}}=0.01{\sqrt {\tfrac {252}{12}}}=0.0458.

Формулы, использованные выше для преобразования показателей доходности или волатильности из одного периода времени в другой, предполагают использование конкретной базовой модели или процесса. Эти формулы являются точной экстраполяцией случайного блуждания или винеровского процесса, шаги которого имеют конечную дисперсию. Однако в более общем плане для естественных случайных процессов точная взаимосвязь между показателями волатильности для разных периодов времени более сложна. Некоторые используют показатель устойчивости Леви α для экстраполяции естественных процессов:

\sigma _{T}=T^{1/\alpha }\sigma .\,

Если α = 2, процесса Винера получается соотношение масштабирования , но некоторые люди полагают, что α < 2 для финансовой деятельности, такой как акции, индексы и т. д. Это было обнаружено Бенуа Мандельбротом , который изучил цены на хлопок и обнаружил, что они соответствуют альфа-стабильному распределению Леви с α = 1,7. (См. New Scientist, 19 апреля 1997 г.)

Происхождение волатильности

Много исследований было посвящено моделированию и прогнозированию волатильности финансовых доходов, но лишь немногие теоретические модели объясняют, как вообще возникает волатильность.

Ролл (1984) показывает, что на волатильность влияет микроструктура рынка . ^[3] Глостен и Милгром (1985) показывают, что по крайней мере один источник волатильности можно объяснить процессом предоставления ликвидности. Когда маркет-мейкеры предполагают возможность неблагоприятного отбора , они корректируют свои торговые диапазоны, что, в свою очередь, увеличивает диапазон ценовых колебаний. ^[4]

В сентябре 2019 года JPMorgan Chase определил эффект президента США Дональда Трампа и твитов назвал его индексом Вольфефе, сочетающим волатильность и «ковфефе» мем .

Волатильность для инвесторов

Волатильность важна для инвесторов как минимум по восьми причинам: ^{[ нужна ссылка ]} некоторые из которых являются альтернативными утверждениями одного и того же признака или непосредственно следуют друг за другом:

Чем шире колебания цен на инвестиции, тем труднее в эмоциональном плане не волноваться;
Волатильность цен торгового инструмента может помочь определить размер позиции в портфеле;
Когда денежные потоки от продажи ценных бумаг необходимы в определенную дату в будущем для погашения известного фиксированного обязательства, более высокая волатильность означает большую вероятность дефицита;
Более высокая волатильность доходов при накоплении пенсионных накоплений приводит к более широкому распределению возможных окончательных значений портфеля;
Более высокая волатильность доходности после выхода на пенсию может привести к тому, что вывод средств окажет более сильное постоянное влияние на стоимость портфеля;
Волатильность цен дает возможность любому, кто обладает инсайдерской информацией, покупать активы дешево и продавать их по завышенной цене;
Волатильность влияет на цену опционов , являясь параметром модели Блэка-Шоулза .

Волатильность в зависимости от направления

Волатильность не измеряет направление изменений цен, а лишь их дисперсию. Это связано с тем, что при расчете стандартного отклонения (или дисперсии ) все различия возводятся в квадрат, так что отрицательные и положительные различия объединяются в одну величину. Два инструмента с разной волатильностью могут иметь одинаковую ожидаемую доходность, но инструмент с более высокой волатильностью будет иметь большие колебания стоимости за определенный период времени.

Например, акции с более низкой волатильностью могут иметь ожидаемую (среднюю) доходность 7% при годовой волатильности 5%. Игнорируя совокупный эффект, это будет указывать на доходность от примерно отрицательных 3% до положительных 17% в большинстве случаев (19 раз из 20, или 95% по правилу двух стандартных отклонений). Акции с более высокой волатильностью и той же ожидаемой доходностью 7%, но с годовой волатильностью 20%, в большинстве случаев будут указывать доходность от примерно отрицательных 33% до положительных 47% (19 раз из 20, или 95%). Эти оценки предполагают нормальное распределение ; на самом деле движение цен на акции оказывается лептокуртотическим (с толстым хвостом).

Волатильность с течением времени

Хотя уравнение Блэка-Шоулза предполагает предсказуемую постоянную волатильность, на реальных рынках этого не наблюдается. Среди более реалистичных моделей — модели Эмануэля Дермана и Иража Кани . ^[5] и Бруно Дюпире , локальная волатильность процесс Пуассона , при котором волатильность переходит на новые уровни с предсказуемой частотой, и все более популярная модель стохастической волатильности Хестона . ^[6][ссылка не работает]

Общеизвестно, что многие типы активов испытывают периоды высокой и низкой волатильности. То есть в некоторые периоды цены быстро растут и падают, а в другие периоды вообще почти не движутся. ^[7] На валютном рынке изменения цен носят сезонный гетероскедастичный характер с периодами в один день и одну неделю. ^[8]^[9]

Периоды, когда цены быстро падают ( крах ), часто сопровождаются еще большим падением цен или необычным ростом цен. Кроме того, за моментом, когда цены быстро растут (возможный пузырь ), часто может последовать еще больший рост цен или их падение на необычную величину.

Чаще всего экстремальные движения не возникают «из ниоткуда»; их предвещают более крупные движения, чем обычно, или известная неопределенность в отношении конкретных будущих событий. Это называется авторегрессионной условной гетероскедастичностью . Труднее сказать, имеют ли такие крупные движения одно и то же направление или противоположное. И рост волатильности не всегда предвещает дальнейшее повышение – волатильность может просто снова пойти вниз.

Показатели волатильности зависят не только от периода, в течение которого она измеряется, но и от выбранного временного разрешения, поскольку поток информации между краткосрочными и долгосрочными трейдерами асимметричен. ^{[ нужны разъяснения ]} В результате волатильность, измеренная с высоким разрешением, содержит информацию, которая не покрывается волатильностью с низким разрешением, и наоборот. ^[10]

По паритету рисков взвешена волатильность трех активов: золота, казначейских облигаций и Nasdaq, выступающих в качестве прокси для рыночного портфеля. ^{[ нужны разъяснения ]} похоже, имеет низкую точку на уровне 4% после того, как летом 2014 года он поднялся вверх в восьмой раз с 1974 года. ^{[ нужны разъяснения ]}^{[ нужна ссылка ]}

Альтернативные меры волатильности

Некоторые авторы отмечают, что реализованная и подразумеваемая волатильность являются мерами, ориентированными на прошлое и будущее, и не отражают текущую волатильность. Для решения этой проблемы была предложена альтернатива — ансамблевые меры волатильности. Одна из мер определяется как стандартное отклонение доходности ансамбля, а не временного ряда доходности. ^[11] Другой рассматривает регулярную последовательность изменений направлений как показатель мгновенной волатильности. ^[12]

Волатильность в отношении торговли опционами

Один из методов измерения волатильности, часто используемый фирмами, занимающимися количественной торговлей опционами, делит волатильность на два компонента. Чистая волатильность — величина волатильности, вызванная стандартными событиями, такими как ежедневные транзакции и общий шум, — и грязная волатильность, величина, вызванная конкретными событиями, такими как прибыль или объявления политики. ^[13] Например, в такой компании, как Microsoft, будет чистая волатильность, вызванная тем, что люди покупают и продают ежедневно, но грязные (или события) события, такие как квартальная прибыль или, возможно, антимонопольное объявление.

Разбивка волатильности на два компонента полезна для точного определения стоимости опциона, особенно при определении того, какие события могут способствовать колебанию. Работа фундаментальных аналитиков в маркет-мейкерах и специализированных фирмах по торговле опционами обычно связана с попытками присвоить этим числам числовые значения.

Параметризация подразумеваемой волатильности

Существует несколько известных параметризаций поверхности подразумеваемой волатильности: Шенбухера, SVI и gSVI. ^[14]

Оценка сырой волатильности

Используя упрощение приведенной выше формулы, можно оценить годовую волатильность, основываясь исключительно на приблизительных наблюдениях. Предположим, вы заметили, что индекс рыночных цен, который имеет текущее значение около 10 000, в течение многих дней перемещался в среднем примерно на 100 пунктов в день. Это будет означать дневное движение на 1%, вверх или вниз.

Чтобы перевести это в годовое исчисление, вы можете использовать «правило 16», то есть умножить на 16, чтобы получить 16% годовой волатильности. Обоснованием этого является то, что 16 — это квадратный корень из 256, что примерно соответствует количеству торговых дней в году (252). При этом также используется тот факт, что стандартное отклонение суммы n независимых переменных (с равными стандартными отклонениями) в √n раз превышает стандартное отклонение отдельных переменных.

Однако важно то, что это не учитывает (а в некоторых случаях может придавать чрезмерный вес) случайные крупные изменения рыночных цен, которые происходят реже, чем раз в год.

Средняя величина наблюдений представляет собой просто аппроксимацию стандартного отклонения рыночного индекса. Предполагая, что ежедневные изменения рыночного индекса обычно распределяются со средним нулем и стандартным отклонением σ , ожидаемое значение величины наблюдений составляет √(2/ $π$ ) σ = 0,798 σ . Конечным результатом является то, что этот грубый подход занижает истинную волатильность примерно на 20%.

Оценка совокупного годового темпа роста (CAGR)

Рассмотрим ряд Тейлора :

\log(1+y)=y-{\tfrac {1}{2}}y^{2}+{\tfrac {1}{3}}y^{3}-{\tfrac {1}{4}}y^{4}+\cdots

Взяв только первые два члена, получим:

\mathrm {CAGR} \approx \mathrm {AR} -{\tfrac {1}{2}}\sigma ^{2}

Таким образом, волатильность математически представляет собой тормоз для среднегодового темпа роста (формализованного как « налог на волатильность »). На самом деле, большинство финансовых активов имеют отрицательную асимметрию и лептокуртозис, поэтому эта формула имеет тенденцию быть чрезмерно оптимистичной. Некоторые используют формулу:

\mathrm {CAGR} \approx \mathrm {AR} -{\tfrac {1}{2}}k\sigma ^{2}

для грубой оценки, где k — эмпирический коэффициент (обычно от пяти до десяти). ^{[ нужна ссылка ]}

Критика моделей прогнозирования волатильности

Показатели VIX (слева) по сравнению с прошлой волатильностью (справа) в качестве 30-дневных предсказателей волатильности за период с января 1990 г. по сентябрь 2009 г. Волатильность измеряется как стандартное отклонение однодневной доходности S&P500 за месячный период. Синие линии обозначают линейные регрессии , в результате чего показаны коэффициенты корреляции r . Обратите внимание, что VIX имеет практически такую же предсказательную силу, как и прошлая волатильность, поскольку показанные коэффициенты корреляции почти идентичны.

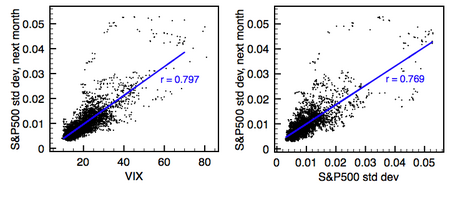
Несмотря на сложную структуру большинства моделей прогнозирования волатильности, критики утверждают, что их предсказательная сила аналогична прогностической силе простых показателей, таких как простая прошлая волатильность. ^[15]^[16] особенно вне выборки, когда для оценки моделей и их проверки используются разные данные. ^[17] Другие работы согласились, но критики утверждают, что не смогли правильно реализовать более сложные модели. ^[18] Некоторые практики и портфельные менеджеры , похоже, полностью игнорируют или отвергают модели прогнозирования волатильности. Например, Нассим Талеб » знаменитым названием назвал одну из своих статей в журнале «Управление портфелем «Мы не совсем понимаем, о чем говорим, когда говорим о волатильности». ^[19] В аналогичной заметке Эмануэль Дерман выразил разочарование огромным количеством эмпирических моделей, не подкрепленных теорией. ^[20] Он утверждает, что, хотя «теории — это попытки раскрыть скрытые принципы, лежащие в основе окружающего нас мира, как это сделал Альберт Эйнштейн со своей теорией относительности», мы должны помнить, что «модели — это метафоры — аналогии, которые описывают одну вещь относительно другой».

См. также

Бета (финансы) – финансовый показатель
Дисперсия – статистическое свойство, позволяющее количественно определить, насколько распределен набор данных.
Финансовая экономика - академическая дисциплина, связанная с обменом денег.
IVX – внутридневной индекс волатильности, подобный VIX, для ценных бумаг США и биржевых инструментов.
Жюль Реньо - французский экономист.
Риск – вероятность того, что произойдет что-то плохое.
VIX – Индекс волатильности
Улыбка волатильности – модели подразумеваемой волатильности, возникающие при ценообразовании финансовых опционов.
Налог на волатильность – математический финансовый термин
Риск волатильности
Бета волатильности

Ссылки

^ «Распределение сборов» . wilmottwiki.com .
^ «Расчет исторической волатильности: пошаговый пример» (PDF) . Архивировано из оригинала 30 марта 2012 года . Проверено 18 августа 2011 г. {{cite web}}: CS1 maint: bot: исходный статус URL неизвестен ( ссылка )
^ Ролл, Р. (1984): «Простая неявная мера эффективного спреда спроса и предложения на эффективном рынке», Journal of Finance 39 (4), 1127–1139.
^ Глостен, Л. Р. и П. Р. Милгром (1985): «Цены спроса, предложения и сделок на специализированном рынке с неоднородно информированными трейдерами», Journal of Financial Economics 14 (1), 71–100.
^ Дерман Э., Ирадж Кани (1994). « Езда на улыбке». РИСК, 7 (2) февраля 1994 г., стр. 139–145, стр. 32–39» (PDF) . Риск. Архивировано из оригинала (PDF) 10 июля 2011 года . Проверено 1 июня 2007 г. {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь ) CS1 maint: несколько имен: список авторов ( ссылка )
^ «Волатильность» . wilmottwiki.com .
^ «Использование скачков волатильности с помощью кредитных спредов» .
^ Мюллер, Ульрих А.; Дакоронья, Мишель М.; Олсен, Ричард Б.; Пикте, Оливье В.; Шварц, Матиас; Моргенегг, Клод (1 декабря 1990 г.). «Статистическое исследование курсов иностранных валют, эмпирические доказательства закона масштабирования изменения цен и внутридневной анализ». Журнал банковского дела и финансов . 14 (6): 1189–1208. дои : 10.1016/0378-4266(90)90009-Q . ISSN 0378-4266 .
^ Петров Владимир; Голуб, Антон; Олсен, Ричард (июнь 2019 г.). «Мгновенная сезонность волатильности высокочастотных рынков во время внутреннего изменения направления» . Журнал риска и финансового менеджмента . 12 (2): 54. doi : 10.3390/jrfm12020054 . hdl : 10419/239003 .
^ Мюллер, Ульрих А.; Дакоронья, Мишель; Дэйв, Рахал Д.; Олсен, Ричард; Пикте, Оливье В.; фон Вайцзекер, Якоб (1997). "Волатильность различного временного разрешения - Анализ динамики компонентов рынка" . Журнал эмпирических финансов . 4 (2–3): 213–239. дои : 10.1016/S0927-5398(97)00007-8 . ISSN 0927-5398 .
^ Саркисян, Джек (2016). «Экспресс-измерение волатильности рынка с использованием концепции эргодичности». дои : 10.2139/ssrn.2812353 . S2CID 168496910 . ССНР 2812353 . {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )
^ Петров Владимир; Голуб, Антон; Олсен, Ричард (июнь 2019 г.). «Мгновенная сезонность волатильности высокочастотных рынков во время внутреннего изменения направления» . Журнал риска и финансового менеджмента . 12 (2): 54. doi : 10.3390/jrfm12020054 . hdl : 10419/239003 .
^ «Очистка подразумеваемых объемов» . Лунная башнямета . Проверено 26 июня 2024 г.
^ Бабак Махдави Дамгани и Эндрю Кос (2013). «Деарбитраж со слабой улыбкой». Уилмотт. {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь ) http://www.readcube.com/articles/10.1002/wilm.10201?locale=en
^ Камби, Р.; Фиглевски, С.; Хасбрук, Дж. (1993). «Прогнозирование волатильности и корреляций с помощью моделей EGARCH». Журнал деривативов . 1 (2): 51–63. дои : 10.3905/jod.1993.407877 . S2CID 154028452 .
^ Джорион, П. (1995). «Прогнозирование волатильности на валютном рынке». Журнал финансов . 50 (2): 507–528. дои : 10.1111/j.1540-6261.1995.tb04793.x . JSTOR 2329417 .
^ Брукс, Крис ; Персанд, Гита (2003). «Прогнозирование волатильности для управления рисками». Журнал прогнозирования . 22 (1): 1–22. CiteSeerX 10.1.1.595.9113 . дои : 10.1002/для.841 . ISSN 1099-131X . S2CID 154615850 .
^ Андерсен, Торбен Г.; Боллерслев, Тим (1998). «Ответ скептикам: да, стандартные модели волатильности действительно дают точные прогнозы». Международное экономическое обозрение . 39 (4): 885–905. CiteSeerX 10.1.1.28.454 . дои : 10.2307/2527343 . JSTOR 2527343 .
^ Гольдштейн, Дэниел и Талеб, Нассим, (28 марта 2007 г.) «Мы не совсем понимаем, о чем говорим, когда говорим о волатильности» . Журнал управления портфелем 33 (4), 2007 г.
^ Дерман, Эмануэль (2011): Models.Behaving.Badly: почему путаница иллюзий с реальностью может привести к катастрофе на Уолл-стрит и в жизни», под ред. Свободная пресса.

Внешние ссылки

Графическое сравнение подразумеваемой и исторической волатильности ^{[ постоянная мертвая ссылка ]}, видео
Диболд, Фрэнсис X.; Хикман, Эндрю; Иноуэ, Ацуши и Шуерманн, Тил (1996) «Преобразование 1-дневной волатильности в h-дневную волатильность: масштабирование с помощью sqrt(h) хуже, чем вы думаете»
Краткое введение в альтернативные математические концепции волатильности.
Оценка волатильности на основе прогнозируемой плотности доходности. Пример основан на ежедневном распределении доходности Google с использованием стандартной функции плотности.
Исследовательский документ, включающий выдержку из отчета под названием «Определение богатой и дешевой волатильности с помощью расширенной перезаписи вызовов», отчета Райана Реникера и Деваприи Маллик из Lehman Brothers (2005).

Дальнейшее чтение

Бартрам, Зёнке М.; Браун, Грегори В.; Штульц, Рене М. (август 2012 г.). «Почему акции США более волатильны?» (PDF) . Журнал финансов . 67 (4): 1329–1370. дои : 10.1111/j.1540-6261.2012.01749.x . S2CID 18587238 . ССНН 2257549 .
Натенберг, Шелдон (2015). Волатильность опционов и цены: передовые торговые стратегии и методы (второе изд.). Нью-Йорк. ISBN 978-0071818773 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )

[1] «Распределение сборов» . wilmottwiki.com .

[2] «Расчет исторической волатильности: пошаговый пример» (PDF) . Архивировано из оригинала 30 марта 2012 года . Проверено 18 августа 2011 г. {{cite web}}: CS1 maint: bot: исходный статус URL неизвестен ( ссылка )

[3] Ролл, Р. (1984): «Простая неявная мера эффективного спреда спроса и предложения на эффективном рынке», Journal of Finance 39 (4), 1127–1139.

[4] Глостен, Л. Р. и П. Р. Милгром (1985): «Цены спроса, предложения и сделок на специализированном рынке с неоднородно информированными трейдерами», Journal of Financial Economics 14 (1), 71–100.

[derman-5] Дерман Э., Ирадж Кани (1994). « Езда на улыбке». РИСК, 7 (2) февраля 1994 г., стр. 139–145, стр. 32–39» (PDF) . Риск. Архивировано из оригинала (PDF) 10 июля 2011 года . Проверено 1 июня 2007 г. {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь ) CS1 maint: несколько имен: список авторов ( ссылка )

[6] «Волатильность» . wilmottwiki.com .

[7] «Использование скачков волатильности с помощью кредитных спредов» .

[8] Мюллер, Ульрих А.; Дакоронья, Мишель М.; Олсен, Ричард Б.; Пикте, Оливье В.; Шварц, Матиас; Моргенегг, Клод (1 декабря 1990 г.). «Статистическое исследование курсов иностранных валют, эмпирические доказательства закона масштабирования изменения цен и внутридневной анализ». Журнал банковского дела и финансов . 14 (6): 1189–1208. дои : 10.1016/0378-4266(90)90009-Q . ISSN 0378-4266 .

[9] Петров Владимир; Голуб, Антон; Олсен, Ричард (июнь 2019 г.). «Мгновенная сезонность волатильности высокочастотных рынков во время внутреннего изменения направления» . Журнал риска и финансового менеджмента . 12 (2): 54. doi : 10.3390/jrfm12020054 . hdl : 10419/239003 .

[10] Мюллер, Ульрих А.; Дакоронья, Мишель; Дэйв, Рахал Д.; Олсен, Ричард; Пикте, Оливье В.; фон Вайцзекер, Якоб (1997). "Волатильность различного временного разрешения - Анализ динамики компонентов рынка" . Журнал эмпирических финансов . 4 (2–3): 213–239. дои : 10.1016/S0927-5398(97)00007-8 . ISSN 0927-5398 .

[11] Саркисян, Джек (2016). «Экспресс-измерение волатильности рынка с использованием концепции эргодичности». дои : 10.2139/ssrn.2812353 . S2CID 168496910 . ССНР 2812353 . {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )

[12] Петров Владимир; Голуб, Антон; Олсен, Ричард (июнь 2019 г.). «Мгновенная сезонность волатильности высокочастотных рынков во время внутреннего изменения направления» . Журнал риска и финансового менеджмента . 12 (2): 54. doi : 10.3390/jrfm12020054 . hdl : 10419/239003 .

[13] «Очистка подразумеваемых объемов» . Лунная башнямета . Проверено 26 июня 2024 г.

[damghani-14] Бабак Махдави Дамгани и Эндрю Кос (2013). «Деарбитраж со слабой улыбкой». Уилмотт. {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь ) http://www.readcube.com/articles/10.1002/wilm.10201?locale=en

[15] Камби, Р.; Фиглевски, С.; Хасбрук, Дж. (1993). «Прогнозирование волатильности и корреляций с помощью моделей EGARCH». Журнал деривативов . 1 (2): 51–63. дои : 10.3905/jod.1993.407877 . S2CID 154028452 .

[16] Джорион, П. (1995). «Прогнозирование волатильности на валютном рынке». Журнал финансов . 50 (2): 507–528. дои : 10.1111/j.1540-6261.1995.tb04793.x . JSTOR 2329417 .

[17] Брукс, Крис ; Персанд, Гита (2003). «Прогнозирование волатильности для управления рисками». Журнал прогнозирования . 22 (1): 1–22. CiteSeerX 10.1.1.595.9113 . дои : 10.1002/для.841 . ISSN 1099-131X . S2CID 154615850 .

[18] Андерсен, Торбен Г.; Боллерслев, Тим (1998). «Ответ скептикам: да, стандартные модели волатильности действительно дают точные прогнозы». Международное экономическое обозрение . 39 (4): 885–905. CiteSeerX 10.1.1.28.454 . дои : 10.2307/2527343 . JSTOR 2527343 .

[19] Гольдштейн, Дэниел и Талеб, Нассим, (28 марта 2007 г.) «Мы не совсем понимаем, о чем говорим, когда говорим о волатильности» . Журнал управления портфелем 33 (4), 2007 г.

[20] Дерман, Эмануэль (2011): Models.Behaving.Badly: почему путаница иллюзий с реальностью может привести к катастрофе на Уолл-стрит и в жизни», под ред. Свободная пресса.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

v т и Волатильность
Modelling volatility	Implied volatility Volatility smile Volatility clustering Local volatility Stochastic volatility Jump-diffusion models ARCH and GARCH
Trading volatility	Volatility arbitrage Straddle Volatility swap IVX VIX

v т и Финансовые рынки
Types of markets	Primary market Secondary market Third market Fourth market
Types of stocks	Common stock Golden share Preferred stock Restricted stock Tracking stock
Share capital	Authorised capital Issued shares Shares outstanding Treasury stock
Participants	Broker Floor broker Inter-dealer broker Broker-dealer Market maker Trader Floor trader Proprietary trader Quantitative analyst Investor Hedger Speculator Arbitrager Scalper Regulator
Trading venues	Exchange List of stock exchanges Trading hours Over-the-counter (off-exchange) Alternative Trading System (ATS) Multilateral trading facility (MTF) Electronic communication network (ECN) Direct market access (DMA) Straight-through processing (STP) Dark pool (private exchange) Crossing network Liquidity aggregator
Stock valuation	Alpha Arbitrage pricing theory (APT) Beta Buffett indicator (Cap-to-GDP) Book value (BV) Capital asset pricing model (CAPM) Capital market line (CML) Dividend discount model (DDM) Dividend yield Earnings yield EV/EBITDA Fed model Net asset value (NAV) Security characteristic line Security market line (SML) T-model
Trading theories and strategies	Algorithmic trading Buy and hold Contrarian investing Dollar cost averaging Efficient-market hypothesis (EMH) Fundamental analysis Growth stock Market timing Modern portfolio theory (MPT) Momentum investing Mosaic theory Pairs trade Post-modern portfolio theory (PMPT) Random walk hypothesis (RMH) Sector rotation Style investing Swing trading Technical analysis Trend following Value averaging Value investing
Related terms	Bid–ask spread Block trade Cross listing Dividend Dual-listed company DuPont analysis Efficient frontier Financial law Flight-to-quality Government bond Greenspan put Haircut Initial public offering (IPO) Long Mandatory offer Margin Market anomaly Market capitalization Market depth Market manipulation Market trend Mean reversion Momentum Open outcry Order book Position Public float Public offering Rally Returns-based style analysis Reverse stock split Share repurchase Short selling Slippage Speculation Squeeze-out Stock dilution Stock exchange Stock market index Stock split Stock swap Trade Tender offer Uptick rule Volatility Voting interest Yield