✖


Jump to content

Борромео кольца

Это хорошая статья. Нажмите здесь для получения дополнительной информации.
(Перенаправлено с кольца Борромео )

Борромео кольца
Л6а4
Пересечение нет. 6
Гиперболический объем 7.327724753
Палка нет. 9
Обозначение Конвея .1
Обозначение A – B 6 3
2
Тистлтуэйт Л6а4
Другой
чередующийся , гиперболический

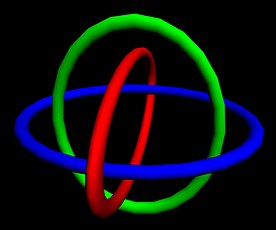
В математике . кольца Борромео [а] Это три простые замкнутые кривые в трехмерном пространстве, которые топологически связаны и не могут быть отделены друг от друга, но распадаются на две незавязанные и несвязанные петли, когда любая из трех разрезается или удаляется. Чаще всего эти кольца изображаются в виде трех кругов на плоскости по образцу диаграммы Венна , попеременно пересекающихся друг над другом и под друг другом в точках пересечения. Говорят, что другие тройки кривых образуют кольца Борромео, если они топологически эквивалентны кривым, изображенным на этом рисунке.

Кольца Борромео названы в честь итальянского Дома Борромео , который использовал круглую форму этих колец как элемент своего герба , но конструкции, основанные на кольцах Борромео, использовались во многих культурах, в том числе у скандинавов и в Японии. . Они использовались в христианской символике как знак Троицы , а в современной торговле как логотип пива Ballantine , что дало им альтернативное название «кольца Ballantine» . Физические экземпляры колец Борромео были созданы из связанных ДНК или других молекул, и у них есть аналоги в состоянии Ефимова и ядрах Борромео , оба из которых имеют три компонента, связанных друг с другом, хотя никакие два из них не связаны.

Геометрически кольца Борромео могут быть реализованы посредством связанных эллипсов или (используя вершины правильного икосаэдра ) связанных золотых прямоугольников . Их невозможно реализовать с помощью окружностей в трехмерном пространстве, но высказано предположение, что их можно реализовать с помощью копий любой некруговой простой замкнутой кривой в пространстве. В теории узлов можно доказать, что кольца Борромео зацеплены, подсчитав их Фокса n -раскраски . В качестве связей они бывают брунновскими , знакопеременными , алгебраическими и гиперболическими . В арифметической топологии некоторые тройки простых чисел обладают свойствами зацепления, аналогичными кольцам Борромео.

Определение и обозначения

[ редактировать ]

В математических публикациях кольца Борромео часто определяются как диаграмма связей , рисунок кривых на плоскости с отмеченными пересечениями, указывающими, какая кривая или часть кривой проходит выше или ниже при каждом пересечении. Такой рисунок можно преобразовать в систему кривых в трехмерном пространстве, вложив плоскость в пространство и деформировав нарисованные на нем кривые выше или ниже вложенной плоскости при каждом пересечении, как указано на схеме. Обычно используемая диаграмма колец Борромео состоит из трех равных кругов с центрами в точках равностороннего треугольника , достаточно близко друг к другу, чтобы их внутренние части имели общее пересечение (например, на диаграмме Венна или трех кругов, используемых для определения треугольника Рело). ). Его пересечения чередуются сверху и снизу, если рассматривать их последовательно вокруг каждого круга; [2] [3] [4] Другой эквивалентный способ описать отношение «больше-меньше» между тремя кругами состоит в том, что каждый круг проходит над вторым кругом в обоих их пересечениях и под третьим кругом в обоих их пересечениях. [5] Два звена называются эквивалентными, если существует непрерывная деформация пространства ( объемлющая изотопия ), переводящая одно в другое, и кольца Борромео могут относиться к любому звену, эквивалентному в этом смысле стандартной диаграмме для этого звена. [4]

В «Атласе узлов» кольца Борромео обозначены кодом «L6a4»; обозначение означает, что это ссылка с шестью пересечениями и чередующейся диаграммой, четвертая из пяти чередующихся звеньев с 6 пересечениями, определенных Морвен Тистлтуэйт в списке всех простых ссылок, содержащих до 13 пересечений. [6] В таблицах узлов и звеньев в книге Дейла Рольфсена « Узлы и звенья» 1976 года , расширяющей более ранние списки Александра и Бриггса, сделанные в 1920-х годах, кольцам Борромео были присвоены обозначения Александра-Бриггса «6». 3
2 », что означает, что это второе из трех перечисленных в списке 6-пересекающихся 3-компонентных звеньев. [6] [7] Обозначение Конвея для колец Борромео, «.1», представляет собой сокращенное описание стандартной диаграммы связей для этой ссылки. [8]

История и символика

[ редактировать ]
Валькнут на камне Стора Хаммарс I
Символ христианской Троицы , адаптированный из рукописи XIII века.
Связанные треугольники в храме Марундисварар

Название «кольца Борромео» происходит от использования этих колец в форме трех связанных кругов на семьи Борромео гербе аристократической в Северной Италии . [9] [10] Само звено намного древнее и появилось в форме валкнута , трех соединенных равносторонних треугольников с параллельными сторонами, на скандинавских камнях с изображениями, датируемыми 7 веком. [11] Храм Омива в Японии также украшен мотивом колец Борромео в их традиционной круглой форме. [2] VI века Каменный столб в храме Марундисварар в Индии изображает три равносторонних треугольника, повернутых друг относительно друга, образуя правильную эннеаграмму ; подобно кольцам Борромео, эти три треугольника связаны, а не попарно, [12] но эта схема пересечения описывает другое звено, чем кольца Борромео. [13]

Поверхность Зейферта колец Борромео.

Кольца Борромео использовались в разных контекстах для обозначения силы единства. [14] В частности, некоторые использовали этот дизайн как символ Троицы . [3] Французская рукопись XIII века, изображающая кольца Борромео, помеченные как единство в троице, была потеряна во время пожара в 1940-х годах, но воспроизведена в книге 1843 года Адольфом Наполеоном Дидроном . Дидрон и другие предположили, что описание Троицы как трех равных кругов в песне 33 « Данте » Рая было вдохновлено похожими изображениями, хотя Данте не детализирует геометрическое расположение этих кругов. [15] [16] Психоаналитик Жак Лакан нашел вдохновение в кольцах Борромео как модели для своей топологии человеческой субъективности, где каждое кольцо представляет собой фундаментальный лакановский компонент реальности («реальный», «воображаемый» и «символический»). [17]

Кольца использовались в качестве логотипа пива Ballantine и до сих пор используются в пиве марки Ballantine, которое сейчас распространяется нынешним владельцем бренда, Pabst Brewing Company . [18] [19] По этой причине их иногда называют «кольцами Баллантайна». [3] [18]

Первой работой по теории узлов, включавшей кольца Борромео, был каталог узлов и связей, составленный в 1876 году Питером Тейтом . [3] В развлекательной математике кольца Борромео были популяризированы Мартином Гарднером , который представил поверхности Зейферта для колец Борромео в своей колонке « Математические игры » в сентябре 1961 года в журнале Scientific American . [19] В 2006 году Международный математический союз на 25-м Международном конгрессе математиков в Мадриде, Испания, решил использовать новый логотип, основанный на кольцах Борромео. [2]

Частичные и множественные кольца

[ редактировать ]

В средневековой и ренессансной Европе ряд визуальных знаков состоит из трех элементов, переплетенных между собой так же, как кольца Борромео показаны переплетенными (в их обычном двумерном изображении), но с отдельными элементами, не представляющими собой замкнутые петли. Примерами таких символов являются Снолделева. каменные рога [20] и полумесяцы Дианы Пуатье . [3]

Некоторые связи теории узлов содержат несколько конфигураций колец Борромео; одно пятипетлевое звено этого типа используется в качестве символа в дискордианстве , основанном на изображении в Principia Discordia . [21]

Математические свойства

[ редактировать ]

Связанность

[ редактировать ]
Алгебраическая диаграмма зацеплений колец Борромео. Вертикальная пунктирная черная средняя линия представляет собой сферу Конвея, разделяющую диаграмму на два клубка .

В теории узлов кольца Борромео являются простым примером брунновской связи , связи, которую невозможно разделить, но которая распадается на отдельные незавязанные петли, как только удаляется какой-либо из ее компонентов. Существует бесконечно много брунновских звеньев и бесконечно много брунновских звеньев с тремя кривыми, из которых простейшими являются кольца Борромео. [13] [22]

Есть несколько способов увидеть, что кольца Борромео связаны. Один из них — использовать Фокса n -раскраски , раскраски дуг диаграммы связей с целыми числами по модулю n, так что при каждом пересечении два цвета на нижнем пересечении имеют то же среднее значение (по модулю n ), что и цвет пересекающей дуги, и чтобы использовалось как минимум два цвета. Число раскрасок, удовлетворяющих этим условиям, является инвариантом узла и не зависит от выбранной для связи диаграммы. Тривиальная связь с тремя компонентами имеет раскраски, полученные из его стандартной диаграммы путем выбора цвета независимо для каждого компонента и отбрасывания раскраски, в которых используется только один цвет. С другой стороны, для стандартной диаграммы колец Борромео одни и те же пары дуг встречаются в двух точках пересечения, в результате чего пересекающие их дуги имеют одинаковый цвет друг с другом, из чего следует, что единственные раскраски, которые соответствуют условия пересечения нарушают условие использования более чем одного цвета. Поскольку тривиальное звено имеет множество допустимых раскрасок, а кольца Борромео — ни одной, они не могут быть эквивалентными. [4] [23]

Кольца Борромео представляют собой чередующееся звено , поскольку их обычная диаграмма звеньев имеет пересечения, которые поочередно проходят над и под каждой кривой, по порядку вдоль кривой. Они также являются алгебраической связью , связью, которую можно разложить сферами Конвея на 2-клубки . Они представляют собой простейшее попеременное алгебраическое звено, не имеющее диаграммы, являющейся одновременно попеременно и алгебраической. [24] следует Из гипотез Тейта , что число пересечений колец Борромео (наименьшее количество пересечений в любой из их диаграмм зацепления) равно 6, числу пересечений в их знакопеременной диаграмме. [4]

Форма кольца

[ редактировать ]
Реализация колец Борромео с помощью эллипсов
Три соединенных золотых прямоугольника в правильном икосаэдре.

Кольца Борромео обычно рисуются так, что их кольца проецируются на круги в плоскости рисунка, но трехмерные круговые кольца Борромео являются невозможным объектом : невозможно сформировать кольца Борромео из кругов в трехмерном пространстве. [4] В более общем плане Майкл Х. Фридман и Ричард Скора ( 1987 ) с помощью четырехмерной гиперболической геометрии доказали , что ни одна брунновская связь не может быть точно круговой. [25] Для трех колец в их обычном расположении Борромео это можно увидеть из рассмотрения диаграммы связей . Если предположить, что две окружности соприкасаются в двух точках пересечения, то они лежат либо на плоскости, либо на сфере. В любом случае третий круг должен пройти через эту плоскость или сферу четыре раза, не лежа в ней, что невозможно. [26] Другой аргумент в пользу невозможности круговых реализаций, предложенный Хельге Твербергом , использует инверсную геометрию для преобразования любых трех кругов так, чтобы один из них стал линией, что упрощает утверждение, что два других круга не соединяются с ним, образуя кольца Борромео. . [27]

Однако кольца Борромео можно реализовать с помощью эллипсов. [2] Их можно считать имеющими сколь угодно малый эксцентриситет : независимо от того, насколько близкой к круглой может быть их форма, пока они не являются идеально круглыми, они могут образовывать борромеевские связи, если расположены соответствующим образом. Реализацию колец Борромео тремя взаимно перпендикулярными золотыми прямоугольниками можно найти внутри правильного икосаэдра, соединив три противоположные пары его ребер. [2] Каждые три незавязанных многоугольника в евклидовом пространстве можно объединить после подходящего масштабного преобразования в кольца Борромео. Если все три полигона плоские, то масштабирование не требуется. [28] В частности, поскольку кольца Борромео могут быть реализованы тремя треугольниками, минимальное количество сторон, возможное для каждой из его петель, число палочек колец Борромео равно девяти. [29]

Нерешенная задача по математике :
Существуют ли три незавязанные кривые, а не все окружности, которые не могут образовывать кольца Борромео?
(еще нерешенные задачи по математике)

В более общем плане Мэтью Кук предположил , что любые три незавязанные простые замкнутые кривые в пространстве, а не все круги, можно объединить без масштабирования, чтобы сформировать кольца Борромео. После того, как Джейсон Кантарелла предложил возможный контрпример, Хью Нельсон Ховардс ослабил гипотезу и стал применять ее к любым трем плоским кривым, которые не являются кругами. С другой стороны, хотя брунновских звеньев с тремя звеньями бесконечно много, кольца Борромео — единственные, которые можно составить из трёх выпуклых кривых. [28]

Длина каната

[ редактировать ]
Логотип Международного математического союза

В теории узлов длина веревки узла или звена — это наименьшая длина гибкой веревки (радиуса один), которая может ее реализовать. Математически такую ​​реализацию можно описать гладкой кривой, трубчатая окрестность которой радиусом один избегает самопересечений. Минимальная длина веревки колец Борромео не доказана, но наименьшее достигнутое значение реализуется тремя копиями двухлепестковой плоской кривой. [2] [30] Хотя он напоминает более раннего кандидата на минимальную длину каната, построенного из четырех дуг окружностей радиуса два, [31] она немного отличается от этой формы и состоит из 42 гладких частей, определяемых эллиптическими интегралами , что делает ее на доли процента короче, чем кусочно-круговая реализация. Именно эта реализация, призванная минимизировать длину веревки, была использована для логотипа Международного математического союза . Его длина составляет , а наилучшая доказанная нижняя граница длины равна . [2] [30]

Для дискретного аналога длины веревки, кратчайшего представления, использующего только ребра целочисленной решетки , минимальная длина колец Борромео равна точно . Это длина представления с использованием трех целочисленные прямоугольники, вписанные в икосаэдр Джессена так же, как представление золотыми прямоугольниками вписано в правильный икосаэдр. [32]

Гиперболическая геометрия

[ редактировать ]
Дополнение к кольцам Борромео, гиперболическое многообразие, образованное из двух идеальных октаэдров, неоднократно наблюдаемое с этой точки зрения. Кольца находятся бесконечно далеко, в вершинах октаэдра.

Кольца Борромео являются гиперболическими зацеплениями : пространство, окружающее кольца Борромео (их дополнение зацепления ), допускает полную гиперболическую метрику конечного объема. Хотя гиперболические связи сейчас считаются многочисленными, кольца Борромео были одним из первых примеров, гиперболические связи которых были доказаны в 1970-х годах. [33] [34] и это дополнение ссылки было центральным примером в видео Not Knot , выпущенном в 1991 году Центром геометрии . [35]

Гиперболические многообразия каноническим образом можно разложить на склейки гиперболических многогранников (разложение Эпштейна–Пеннера), а для дополнения Борромео это разложение состоит из двух идеальных правильных октаэдров . [34] [36] Объем равен борромео дополнения где – функция Лобачевского и константа каталонская . [36] Дополнение к кольцам Борромео универсально в том смысле, что каждое замкнутое 3- многообразие является разветвленным накрытием над этим пространством. [37]

Теория чисел

[ редактировать ]

В арифметической топологии существует аналогия между узлами и простыми числами , в которой рассматриваются связи между простыми числами. Тройка простых чисел (13, 61, 937) связаны по модулю 2 ( символ Редеи равен -1), но попарно несвязаны по модулю 2 ( все символы Лежандра равны 1). Поэтому эти простые числа были названы «собственной тройкой Борромео по модулю 2». [38] или «модуль 2 простых чисел Борромео». [39]

Физические реализации

[ редактировать ]

по Узел «кулак обезьяны» сути представляет собой трехмерное представление колец Борромео, хотя в большинстве случаев и трехслойное. [40] Скульптор Джон Робинсон создал произведения искусства из трех равносторонних треугольников , сделанных из листового металла , соединенных в кольца Борромео и напоминающих трехмерную версию валькнута. [13] [29] Обычная конструкция складного деревянного штатива состоит из трех частей, вырезанных из цельного куска дерева, причем каждая часть состоит из двух отрезков дерева, ножек и верхних сторон треноги, соединенных двумя сегментами дерева, окружающими удлиненную центральную часть. дырка в детали. Еще одна из трех частей проходит через каждое из этих отверстий, соединяя три части вместе в виде колец Борромео. Штативы этой формы были описаны как результат ручных ремесел Индии или Африки. [41] [42]

В химии молекулярные кольца Борромео являются молекулярными аналогами колец Борромео, которые представляют собой механически взаимосвязанные молекулярные конструкции . В 1997 году биолог Чэндэ Мао и его коллеги из Нью-Йоркского университета сумели сконструировать набор колец из ДНК . [43] В 2003 году химик Фрейзер Стоддарт и его коллеги из Калифорнийского университета в Лос-Анджелесе использовали координационную химию , чтобы за один этап построить набор колец из 18 компонентов. [44] Кольцевые структуры Борромео использовались для описания кластеров благородных металлов, экранированных поверхностным слоем тиолатных лигандов. [45] Библиотека сетей Борромео была синтезирована Джузеппе Реснати и его коллегами посредством галогенными связями управляемой самосборки, . [46] Чтобы получить доступ к молекулярному кольцу Борромео, состоящему из трех неравных циклов, Джей С. Сигел и его коллеги предложили пошаговый синтез. [47]

В физике квантово-механический аналог колец Борромео называется состоянием гало или состоянием Ефимова и состоит из трёх связанных частиц, не связанных попарно. Существование таких состояний было предсказано физиком Виталием Ефимовым в 1970 году и подтверждено многочисленными экспериментами, начавшимися в 2006 году. [48] [49] Это явление тесно связано с ядром Борромео — стабильным атомным ядром, состоящим из трёх групп частиц, которые попарно нестабильны. [50] Другой аналог колец Борромео в квантовой теории информации предполагает запутанность трёх кубитов в состоянии Гринбергера-Хорна-Цайлингера . [14]

Примечания

[ редактировать ]
  1. ^ Произносится / b ɒ r oʊ ˈ m iː ə n / [1]

Ссылки

[ редактировать ]
  1. ^ Макки и Маккей, 1922 г. Произношение 10 000 имен собственных
  2. ^ Jump up to: а б с д и ж г Ганн, Чарльз; Салливан, Джон М. (2008), «Кольца Борромео: видео о новом логотипе ИДУ» , в Сарханги, Реза; Секин, Карло Х. (ред.), Бриджес Леуварден: математика, музыка, искусство, архитектура, культура , Лондон: Tarquin Publications, стр. 63–70, ISBN  978-0-9665201-9-4 ; см. само видео в разделе « Кольца Борромео: новый логотип IMU. Архивировано 8 марта 2021 г. в Wayback Machine » [с видео], Международный математический союз.
  3. ^ Jump up to: а б с д и Кромвель, Питер; Бельтрами, Элизабетта; Рампичини, Марта (март 1998 г.), «Кольца Борромео», Математический турист, The Mathematical Intelligencer , 20 (1): 53–62, doi : 10.1007/bf03024401 , S2CID   189888135
  4. ^ Jump up to: а б с д и Айгнер, Мартин ; Циглер, Гюнтер М. (2018), «Глава 15: Кольца Борромео не существуют», Доказательства из КНИГИ (6-е изд.), Springer, стр. 99–106, doi : 10.1007/978-3-662- 57265-8_15 , ISBN  978-3-662-57265-8
  5. ^ Чемберленд, Марк; Герман, Юджин А. (2015), «Камень-ножницы-бумага и кольца Борромео», The Mathematical Intelligencer , 37 (2): 20–25, doi : 10.1007/s00283-014-9499-4 , MR   3356112 , S2CID   558993
  6. ^ Jump up to: а б « Кольца Борромео », Атлас узлов .
  7. ^ Рольфсен, Дейл (1990), Узлы и связи , Серия лекций по математике, том. 7 (2-е изд.), Publish or Perish, Inc., Хьюстон, Техас, стр. 7 (2-е изд.), Publish or Perish, Inc., Хьюстон, Техас, с. 425, ISBN  0-914098-16-0 , МР   1277811
  8. ^ Конвей, Дж. Х. (1970), «Перечисление узлов и связей, а также некоторые из их алгебраических свойств», Вычислительные проблемы в абстрактной алгебре (Proc. Conf., Oxford, 1967) , Oxford: Pergamon, стр. 329–358, MR   0258014 ; см. описание обозначений, с. 332–333, и вторую строку таблицы, с. 348.
  9. ^ Крам Браун, Александр (декабрь 1885 г.), «О случае переплетения поверхностей» , Труды Королевского общества Эдинбурга , 13 : 382–386.
  10. ^ Шёк, Ричард Дж. (весна 1968 г.), «Математика и языки литературной критики», Журнал эстетики и художественной критики , 26 (3): 367–376, doi : 10.2307/429121 , JSTOR   429121
  11. ^ Брунс, Карсон Дж.; Стоддарт, Дж. Фрейзер (2011), «Механическая связь: произведение искусства», в Фаббрицци, Л. (редактор), « Красота в химии» , «Темы современной химии», том. 323, Springer, стр. 19–72, номер документа : 10.1007/128_2011_296 , PMID   22183145.
  12. ^ Лакшминараян, Арул (май 2007 г.), «Треугольники Борромео и простые узлы в древнем храме», Resonance , 12 (5): 41–47, doi : 10.1007/s12045-007-0049-7 , S2CID   120259064
  13. ^ Jump up to: а б с Джаблан, Славик В. (1999), «Так ли редки борромеевские связи?» , Материалы 2-го Международного симпозиума по симметрии Катачи U, Часть 1 (Цукуба, 1999), Форма , 14 (4): 269–277, MR   1770213
  14. ^ Jump up to: а б Аравинд, ПК (1997), «Борромеевская запутанность состояния GHZ» (PDF) , в Коэне, RS; Хорн, М.; Стейчел, Дж. (ред.), Потенциал, запутанность и страсть на расстоянии , Бостонские исследования в области философии науки, Springer, стр. 53–59, doi : 10.1007/978-94-017-2732-7_4 , МР   1739812
  15. ^ Дидрон, Адольф Наполеон (1843), Iconographie Chrétienne (на французском языке), Париж: Imprimerie Royale, стр. 568–569
  16. ^ Сайбер, Ариэль; Мбирика, аБа (2013), «Три гири райских 237–272 33» (PDF) , Исследования Данте (131): JSTOR   ,
  17. ^ Рэгланд-Салливан, Элли; Милованович, Драган (2004), «Введение: топологически говоря» , Лакан: топологически говоря , Другая пресса, ISBN  978-1-892746-76-4
  18. ^ Jump up to: а б Глик, Нед (сентябрь 1999 г.), «Символ пива Ballantine с тремя кольцами», Математический турист, The Mathematical Intelligencer , 21 (4): 15–16, doi : 10.1007/bf03025332 , S2CID   123311380
  19. ^ Jump up to: а б Гарднер, Мартин (сентябрь 1961 г.), «Поверхности с краями, соединенными таким же образом, как три кольца известной конструкции» , Mathematical Games , Scientific American , переиздано как Гарднер, Мартин (1991), «Узлы и кольца Борромео», «Неожиданное зависание и другие математические развлечения» , University of Chicago Press, стр. 24–33 ; см. также Гарднер, Мартин (сентябрь 1978 г.), «Тороиды доктора Клонфейка», Научная фантастика Азимова , том. 2, нет. 5, с. 29
  20. ^ Бэрд, Джозеф Л. (1970), «Unferth the þyle », Medium Ævum , 39 (1): 1–12, doi : 10.2307/43631234 , JSTOR   43631234 , на камне также есть изображения трех переплетенных рогов.
  21. ^ «Мандала» , Principia Discordia (4-е изд.), март 1970 г., стр. 43
  22. ^ Бай, Шэн; Ван, Вейбиао (2020), «Новые критерии и конструкции брунновских связей», Журнал теории узлов и ее разветвлений , 29 (13): 2043008, 27, arXiv : 2006.10290 , doi : 10.1142/S0218216520430087 , MR   4213076 , S2   Идентификатор клиента 219792382
  23. ^ Наньес, Олли (октябрь 1993 г.), «Элементарное доказательство того, что кольца Борромео неразрывны», American Mathematical Monthly , 100 (8): 786–789, doi : 10.2307/2324788 , JSTOR   2324788
  24. ^ Тистлтуэйт, Морвен Б. (1991), «Об алгебраической части переменного звена» , Pacific Journal of Mathematics , 151 (2): 317–333, doi : 10.2140/pjm.1991.151.317 , MR   1132393
  25. ^ Фридман, Майкл Х .; Скора, Ричард (1987), «Странные действия групп на сферах», Журнал дифференциальной геометрии , 25 : 75–98, doi : 10.4310/jdg/1214440725 ; см., в частности, лемму 3.2, с. 89
  26. ^ Линдстрем, Бернт; Зеттерстрем, Ханс-Олов (1991), «Круги Борромео невозможны», American Mathematical Monthly , 98 (4): 340–341, doi : 10.2307/2323803 , JSTOR   2323803 . Однако обратите внимание, что Ганн и Салливан (2008) пишут, что эта ссылка «кажется, неправильно относится только к случаю, когда трехмерная конфигурация имеет проекцию, гомеоморфную» обычному трехокружному изображению звена.
  27. ^ Тверберг, Хельге (2010), «О кольцах Борромео» (PDF) , The Mathematical Scientist , 35 (1): 57–60, MR   2668444
  28. ^ Jump up to: а б Ховардс, Хью Нельсон (2013), «Формирование колец Борромео из произвольных многоугольных узлов», Журнал теории узлов и ее разветвлений , 22 (14): 1350083, 15, arXiv : 1406.3370 , doi : 10.1142/S0218216513500831 , MR   3190 121 , S2CID   119674622
  29. ^ Jump up to: а б Бургель, Х.; Францблау, Д.С.; Гучера, КР (1996), «Тайна связанных треугольников», Mathematics Magazine , 69 (2): 94–102, doi : 10.1080/0025570x.1996.11996399 , JSTOR   2690662 , MR   1394792
  30. ^ Jump up to: а б Кантарелла, Джейсон; Фу, Джозеф Х.Г.; Куснер, Роб; Салливан, Джон М .; Ринкл, Нэнси К. (2006), «Критичность проблемы связи Геринга» (PDF) , Geometry & Topology , 10 (4): 2055–2116, arXiv : math/0402212 , doi : 10.2140/gt.2006.10.2055 , МР   2284052
  31. ^ Кантарелла, Джейсон; Куснер, Роберт Б.; Салливан, Джон М. (2002), «О минимальной длине узлов и звеньев» (PDF) , Inventiones Mathematicae , 150 (2): 257–286, arXiv : math/0103224 , Bibcode : 2002InMat.150..257C , doi : 10.1007/s00222-002-0234-y , MR   1933586 , S2CID   730891
  32. ^ Уберти, Р.; Янсе ван Ренсбург, EJ; Орландини, Э.; Теси, MC; Уиттингтон, С.Г. (1998), «Минимальные звенья в кубической решетке», Уиттингтон, Стюарт Г.; Самнерс, Витт Де; Лодж, Тимоти (ред.), Топология и геометрия в науке о полимерах , Тома IMA по математике и ее приложениям, том. 103, Нью-Йорк: Springer, стр. 89–100, doi : 10.1007/978-1-4612-1712-1_9 , MR   1655039 ; см. таблицу 2, с. 97
  33. ^ Райли, Роберт (1979), «Эллиптический путь от параболических представлений к гиперболическим структурам», в Фенн, Роджер (редактор), Топология низкомерных многообразий: материалы Второй Сассексской конференции, 1977 , Конспекты лекций по математике, том . 722, Springer, стр. 99–133, doi : 10.1007/BFb0063194 , ISBN.  978-3-540-09506-4 , МР   0547459
  34. ^ Jump up to: а б Рэтклифф, Джон Г. (2006), «Дополняющие кольца Борромео» , «Основы гиперболических многообразий » , «Тексты для аспирантов по математике», том. 149 (2-е изд.), Springer, стр. 459–461, ISBN.  978-0-387-33197-3 , МР   2249478
  35. ^ Эбботт, Стив (июль 1997 г.), «Обзор Not Knot и дополнение к Not Knot », The Mathematical Gazette , 81 (491): 340–342, doi : 10.2307/3619248 , JSTOR   3619248 , S2CID   64589738
  36. ^ Jump up to: а б Уильям Терстон (март 2002 г.), «7. Вычисление объема» , Геометрия и топология трехмерных многообразий , с. 165, заархивировано из оригинала (PDF) 27 июля 2020 г. , получено 17 января 2012 г.
  37. ^ Хилден, Хью М.; Лосано, Мария Тереза ; Монтесинос, Хосе Мария (1983), «Звено Уайтхеда, кольца Борромео и узел 9 46 универсальны», Seminario Matemático de Barcelona , ​​34 (1): 19–28, MR   0747855
  38. ^ Фогель, Денис (2005), Произведения Масси в когомологиях Галуа числовых полей [ Произведения Масси в когомологиях Галуа числовых полей ], Математический институт, Университет Георга-Августа, Геттинген: Семинары, зимний семестр 2004/2005, Геттинген: Universitätsdrucke Göttingen, стр. 93–98, номер документа : 10.11588/heidok.00004418 , MR   2206880.
  39. ^ Моришита, Масанори (2010), «Аналогии между узлами и простыми числами, трехмерными многообразиями и числовыми кольцами», Sugaku Expositions , 23 (1): 1–30, arXiv : 0904.3399 , MR   2605747
  40. ^ Эшли, Клиффорд Уоррен (1993) [1944], Книга узлов Эшли , Doubleday, стр. 354, ISBN  978-0-385-04025-9
  41. ^ Фриман, Джим (2015), «Собираем подсказки по необычным объектам Марго» , Бюллетень Исторического общества Тьюксбери , 24
  42. ^ «Африканские кольца Борромео» , Математика и узлы , Центр популяризации математики, Уэльский университет, 2002 г. , получено 12 февраля 2021 г.
  43. ^ Мао, К.; Сан, В.; Симан, Северная Каролина (1997), «Сборка колец Борромео из ДНК», Nature , 386 (6621): 137–138, Bibcode : 1997Natur.386..137M , doi : 10.1038/386137b0 , PMID   9062186 , S2CID   4321733
  44. ^ Jump up to: а б Чичак, Келли С.; Кантрилл, Стюарт Дж.; Пиз, Энтони Р.; Чиу, Шэн-Сянь; Кейв, Гарет, Западная Вирджиния; Этвуд, Джерри Л.; Стоддарт, Дж. Фрейзер (28 мая 2004 г.), «Молекулярные кольца Борромео» (PDF) , Science , 304 (5675): 1308–1312, Бибкод : 2004Sci...304.1308C , doi : 10.1126/science.1096914 , PMID   15166376 , S2CID   45191675
  45. ^ Натараджан, Ганапати; Мэтью, Амму; Негиси, Юичи; Уеттен, Роберт Л.; Прадип, Талаппил (02 декабря 2015 г.), «Единая основа для понимания структуры и модификаций атомарно точных монослойных защищенных кластеров золота», The Journal of Physical Chemistry C , 119 (49): 27768–27785, doi : 10.1021/ acs.jpcc.5b08193 , ISSN   1932-7447
  46. ^ Кумар, Виджит; Пилати, Туллио; Терранео, Джанкарло; Мейер, Франк; Метранголо, Пьеранджело; Реснати, Джузеппе (2017), «Сети Борромео с галогенными связями по дизайну: топологическая инвариантность и метрическая настройка в библиотеке многокомпонентных систем», Chemical Science , 8 (3): 1801–1810, doi : 10.1039/C6SC04478F , PMC   5477818 , PMID   28694953
  47. ^ Великс, Янис; Зайферт, Хелен М.; Франц, Дерик К.; Клостерман, Джереми К.; Ценг, Джуй-Чанг; Линден, Энтони; Сигел, Джей С. (2016), «К молекулярной связи Борромео с тремя неравными кольцами: двухцепочные комплексы рутения (ii) кольцо в кольце», Organic Chemistry Frontiers , 3 (6): 667–672, doi : 10.1039/c6qo00025h
  48. ^ Кремер, Т.; Марк, М.; Вальдбургер, П.; Данзл, Дж.Г.; Чин, К.; Энгезер, Б.; Ланге, AD; Пилч, К.; Яаккола, А.; Нэгерль, Х.-К.; Гримм, Р. (2006), «Доказательства существования ефимовских квантовых состояний в ультрахолодном газе атомов цезия», Nature , 440 (7082): 315–318, arXiv : cond-mat/0512394 , Bibcode : 2006Natur.440..315K , doi : 10.1038/nature04626 , PMID   16541068 , S2CID   4379828
  49. ^ Московиц, Клара (16 декабря 2009 г.), «Странная физическая теория доказана спустя почти 40 лет» , Live Science
  50. ^ Танака, К. (2010), «Наблюдение большого сечения реакции в ядре капельной линии». 22 C", Physical Review Letters , 104 (6): 062701, Bibcode : 2010PhRvL.104f2701T , doi : 10.1103/PhysRevLett.104.062701 , PMID   20366816 , S2CID   7951719
[ редактировать ]
Викискладе есть медиафайлы по теме колец Борромео .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Borromean_rings&oldid=1205916452"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: 5f926078498b0e59e14468a22ccafb5d__1707581880
URL1:https://arc.ask3.ru/arc/aa/5f/5d/5f926078498b0e59e14468a22ccafb5d.html
Заголовок, (Title) документа по адресу, URL1:
Borromean rings - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)