Пропозициональная формула

В логике высказываний — пропозициональная формула это тип синтаксической формулы , которая правильно сформирована . Если значения всех переменных в формуле высказывания заданы, это определяет уникальное значение истинности . Пропозициональную формулу можно также назвать пропозициональным выражением , предложением или пропозициональной формулой .

Пропозициональная формула строится из простых предложений , таких как «пять больше трех», или пропозициональных переменных, таких как p и q , с использованием связок или логических операторов, таких как НЕ, И, ИЛИ или ПОДРАЗУМЕВАЕТСЯ; например:

( p AND NOT q ) ПОДРАЗУМЕВАЕТ ( p OR q ).

В математике формулу высказывания часто кратко называют « предложением », но, точнее, формула высказывания — это не предложение, а формальное выражение , обозначающее предложение , формальный объект обсуждения, точно так же, как выражение, подобное поскольку « x + y » не является значением, а обозначает значение. В некоторых контекстах сохранение этого различия может иметь важное значение.

Предложения

Для целей исчисления высказываний предложения ( высказывания, предложения, утверждения) считаются простыми или сложными. Сложные предложения считаются связанными сентенциальными связками, наиболее распространенными из которых являются «И», «ИЛИ», «ЕСЛИ... ТО...», «НИ... НИ...»,» ... ЭКВИВАЛЕНТНО..." . Связывающая точка с запятой «;» и связка «НО» считаются выражениями «И». Считается, что последовательность дискретных предложений связана операторами «И», а формальный анализ применяет рекурсивное «правило скобок» по отношению к последовательностям простых предложений (подробнее см. ниже о правильно построенных формулах ).

Например: Утверждение: «Эта корова синяя. Эта лошадь оранжевая, а вот эта лошадь фиолетовая». на самом деле представляет собой сложное предложение, связанное с помощью «И»: («Эта корова синяя» И «Эта лошадь оранжевая») И «Эта лошадь фиолетового цвета»).

Простые предложения носят декларативный характер, то есть они высказывают утверждения о состоянии или природе конкретного объекта ощущения, например: «Эта корова синяя», «Это койот!» («Этот койот ЕСТЬ там , за камнями»). Таким образом, простые «примитивные» утверждения должны относиться к конкретным объектам или конкретным состояниям ума. Каждый из них должен иметь как минимум субъект (непосредственный объект мысли или наблюдения), глагол (предпочтительно в активном залоге и настоящем времени) и, возможно, прилагательное или наречие. "Собака!" вероятно, подразумевает «Я вижу собаку», но его следует отвергнуть как слишком двусмысленное.

Пример: «Эта фиолетовая собака бежит», «Эта корова синяя», «Выключатель М31 замкнут», «Эта кепка снята», «Завтра пятница».

Для целей исчисления высказываний сложное предложение обычно можно переформулировать в серию простых предложений, хотя результат, вероятно, будет звучать неестественно.

Связь между формулами высказываний и предикатов

Исчисление предикатов идет на шаг дальше, чем исчисление высказываний, в «анализе внутренней структуры высказываний». Он разбивает простое предложение на две части (i) его субъект (объект ( единственное или множественное число) дискурса) и (ii) предикат (глагол или, возможно, глагольное предложение, которое утверждает качество или атрибут объекта(ов) )). Затем исчисление предикатов обобщает форму «субъект|предикат» (где | символизирует конкатенацию (связывание) символов) в форму со следующей структурой пустого субъекта «___|предикат», а предикат, в свою очередь, обобщается на все вещи с это имущество.

превращается в два предложения Пример: «У этой синей свиньи есть крылья» в исчислении высказываний : «У этой свиньи есть крылья» И «Эта свинья синяя», внутренняя структура которых не учитывается. Напротив, в исчислении предикатов первое предложение разбивается на «эта свинья» в качестве подлежащего и «имеет крылья» в качестве предиката. Таким образом он утверждает, что объект «эта свинья» является членом класса (набора, коллекции) «крылатых вещей». Второе предложение утверждает, что объект «эта свинья» имеет атрибут «синий» и, следовательно, является членом класса «синие вещи». Можно было бы записать два предложения, связанных с AND, как:

p|W И p|B

Обобщение «этой свиньи» на (потенциального) члена двух классов «крылатые существа» и «синие существа» означает, что она имеет истинностное отношение с обоими этими классами. Другими словами, в данной области дискурса «крылатые вещи» p либо оказывается членом этой области, либо нет. Таким образом, существует связь W (крылатость) между p (свинья) и { T, F }, W(p) оценивается как { T, F }, где { T, F } — это набор логических значений «истина» и « ЛОЖЬ". Аналогично для B (голубизна), p (свинья) и { T, F }: B(p) оценивается как { T, F }. Итак, теперь можно проанализировать связанные утверждения «B(p) И W(p)» на предмет их общей истинностной ценности, т.е.:

( B(p) AND W(p) ) оценивается как { T, F }

В частности, простые предложения, в которых используются понятия «все», «некоторые», «некоторые», «один из» и т. д., называемые логическими кванторами, обрабатываются исчислением предикатов. Наряду с новым символизмом функции «F(x)» введены два новых символа: ∀ (Для всех) и ∃ (Существует ..., По крайней мере один из ... существует и т. д.). Исчисление предикатов, но не исчисление высказываний, может установить формальную достоверность следующего утверждения:

«У всех синих свиней есть крылья, но у некоторых свиней крыльев нет, поэтому некоторые свиньи не синие».

Личность

Тарский утверждает, что понятие ИДЕНТИЧНОСТИ (в отличие от ЛОГИЧЕСКОЙ ЭКВИВАЛЕНТНОСТИ) лежит вне исчисления высказываний; однако он отмечает, что если логика должна быть полезна для математики и других наук, она должна содержать «теорию» ИДЕНТИЧНОСТИ. Некоторые авторы ссылаются на «логику предикатов с тождеством», чтобы подчеркнуть это расширение. Подробнее об этом смотрите ниже.

Алгебра высказываний, исчисление высказываний

Алгебра (а их много разных), в широком смысле, представляет собой метод, с помощью которого набор символов, называемых переменными, вместе с некоторыми другими символами, такими как круглые скобки (, ), и некоторым подмножеством символов, таких как *, +, ~ , &, ∨, =, ≡, ∧, ￢ управляются в рамках системы правил. Говорят, что эти символы и их правильно сформированные цепочки представляют объекты, но в конкретной алгебраической системе эти объекты не имеют значения. алгебры Таким образом, работа внутри алгебры становится упражнением в соблюдении определенных законов (правил) синтаксиса (образование символов), а не в семантике (значении) символов. Смыслы следует искать вне алгебры.

Чтобы правильно сформированная последовательность символов в алгебре (формула) имела некоторую полезность вне алгебры, символам присваиваются значения, а в конечном итоге переменным присваиваются значения; затем по ряду правил вычисляется формула.

Когда значения ограничиваются двумя и применяются к понятию простых предложений (например, устных высказываний или письменных утверждений), связанных пропозициональными связками, вся эта алгебраическая система символов, правил и методов оценки обычно называется исчислением высказываний или исчислением предложений. .

Хотя некоторые из знакомых правил арифметической алгебры продолжают соблюдаться в алгебре высказываний (например, коммутативные и ассоциативные законы для И и ИЛИ), некоторые — нет (например, законы распределения для И, ИЛИ и НЕ).

Полезность пропозициональных формул

Анализ: В дедуктивном рассуждении философы, риторы и математики сводят аргументы к формулам, а затем изучают их (обычно с помощью таблиц истинности ) на предмет правильности (обоснованности). Например: является ли следующий аргумент обоснованным?

«Учитывая, что сознания достаточно для искусственного интеллекта и только сознательные существа могут пройти тест Тьюринга , прежде чем мы сможем прийти к выводу, что робот является искусственным интеллектом, робот должен пройти тест Тьюринга».

Инженеры анализируют логические схемы созданные ими , используя методы синтеза, а затем применяют различные методы сокращения и минимизации для упрощения своих проектов.

Синтез: инженеры, в частности, синтезируют пропозициональные формулы (которые в конечном итоге превращаются в схемы символов) из таблиц истинности . Например, можно записать таблицу истинности того, как должно вести себя двоичное сложение с учетом сложения переменных «b» и «a» и «carry_in» «ci» и результатов «carry_out» «co» и «sum» Σ. :

• Пример: в строке 5 ( (b+a) + ci) = ( (1+0) + 1 ) = число «2». записанное в виде двоичного числа, это 10 ₂ , где «co»=1 и Σ=0, как показано в крайних правых столбцах.

ряд	б	а	Там		(б+а)+ци	со	С
0	0	0	0		0	0	0
1	0	0	1		1	0	1
2	0	1	0		1	0	1
3	0	1	1		2	1	0
4	1	0	0		1	0	1
5	1	0	1		2	1	0
6	1	1	0		2	1	0
7	1	1	1		3	1	1

Пропозициональные переменные

Простейшим типом пропозициональной формулы является пропозициональная переменная . Простые ( атомарные ) символические выражения часто обозначаются переменными с именами p , q или P , Q и т. д. Пропозициональная переменная предназначена для представления атомарного предложения (утверждения), например «Сейчас суббота» = p (здесь символ = означает «... присвоена переменная с именем ...») или «Я хожу в кино только в понедельник» = q .

Присвоение истинностного значения, оценка формулы

Оценка пропозициональной формулы начинается с присвоения значения истинности каждой переменной. Поскольку каждая переменная представляет собой простое предложение, значения истинности применяются к «истине» или «ложности» этих простых предложений.

Ценности истины в риторике, философии и математике

Значений истинности всего два: {ИСТИНА "Т", ЛОЖЬ "F" }. Эмпирик ) разделяет все предложения на два широких класса: аналитические — истинные, несмотря ни на что (например, тавтология , и синтетические — выведенные из опыта и, следовательно, поддающиеся подтверждению третьими лицами ( теория проверки значения). Эмпирики считают, что, как правило, чтобы прийти к истинностному значению синтетического предложения , значения (шаблоны сопоставления с образцом) должны сначала быть применены к словам, а затем эти шаблоны значений должны быть сопоставлены с тем, что это такое. утверждал. Например, мое высказывание «Эта корова синяя !» Является ли это утверждение ПРАВДОЙ? Я правда это сказал. И, может быть, я вижу синюю корову — если я не лгу, мое утверждение является ПРАВДОЙ относительно объекта моего (возможно, ошибочного) восприятия. Но действительно ли синяя корова существует? Что вы видите, когда смотрите в то же окно? Чтобы приступить к проверке, вам понадобится предварительное представление (шаблон) как о «корове», так и о « синем », а также способность сопоставить эти шаблоны с объектом ощущения (если он действительно существует).

Истинные ценности в инженерии

Инженеры стараются избегать представлений об истине и ложности, которые сбивают с толку философов, но в конечном итоге инженеры должны доверять своим измерительным приборам. В поисках надежности инженеры предпочитают извлекать известные объекты из небольшой библиотеки — объекты, которые имеют четко определенное и предсказуемое поведение даже в больших комбинациях (отсюда и название исчисления высказываний: «комбинаторная логика»). Наименьшее количество вариантов поведения одного объекта — два (например, { ВЫКЛ, ВКЛ }, { открытие, закрытие }, { ВВЕРХ, ВНИЗ } и т. д.), и они ставятся в соответствие с { 0, 1 }. Такие элементы называются цифровыми ; те, у кого непрерывный диапазон поведения, называются аналоговыми . Всякий раз, когда решения должны быть приняты в аналоговой системе, инженер часто преобразует аналоговое поведение (дверь 45,32146% ВВЕРХ) в цифровое (например, ВНИЗ=0) с помощью компаратора .

Таким образом, присвоение значения переменным и двум символам-значениям { 0, 1 } происходит «извне» формулы, которая представляет поведение (обычно) составного объекта. Примером может служить дверь гаража с двумя «конечными выключателями»: один для ВВЕРХ, обозначенный SW_U, другой для ВНИЗ, обозначенный SW_D, и все остальное, что находится в электрической схеме двери. Проверка схемы (либо схемы, либо самих объектов — двери, выключателей, проводов, печатной платы и т. д.) может обнаружить, что на плате «узел 22» переходит в +0 В, когда контакты переключателя «SW_D " находятся в механическом контакте ("закрыты") и дверь находится в положении "вниз" (95 % вниз), а "узел 29" переходит в +0 В, когда дверь находится в положении "ВВЕРХ" на 95 % и контакты переключателя SW_U находятся в положении "ВВЕРХ" при механическом контакте («закрыто»). Инженер должен определить значения этих напряжений и всех возможных комбинаций (всех 4), включая «плохие» (например, оба узла 22 и 29 на 0 вольт, что означает, что дверь открыта и закрыта одновременно) . Схема бездумно реагирует на любое напряжение, которое она испытывает, не осознавая ПРАВДЫ или ЛОЖИ, ПРАВИЛЬНОСТИ или НЕПРАВИЛЬНОСТИ, БЕЗОПАСНОСТИ или ОПАСНОСТИ.

Пропозициональные связки

Произвольные пропозициональные формулы строятся из пропозициональных переменных и других пропозициональных формул с помощью пропозициональных связок . Примеры связок включают в себя:

• Унарная связка отрицания. Если $\alpha$ это формула, то $\lnot \alpha$ это формула.
• Классические бинарные связки $\land ,\lor ,\to ,\leftrightarrow$. Так, например, если $\alpha$ и $\beta$ являются формулами, так что $(\alpha \to \beta )$.
• Другие двоичные связки, такие как NAND, NOR и XOR.
• Троичная связка ЕСЛИ... ТО... ИНАЧЕ...
• Постоянные 0-арные связки ⊤ и ⊥ (попеременно константы { T, F }, { 1, 0 } и т. д.)
• Связка «теория-расширение» РАВНО (альтернативно ИДЕНТИЧНОСТЬ или знак «=" в отличие от «логической связки» $\leftrightarrow$)

Соединения риторики, философии и математики

Ниже приведены связи, общие для риторики, философии и математики, вместе с их таблицами истинности . Используемые символы будут различаться от автора к автору и в зависимости от области деятельности. В общем, аббревиатуры «T» и «F» обозначают оценки ИСТИНА и ЛОЖЬ, применяемые к переменным в формуле высказывания (например, утверждение: «Эта корова синяя» будет иметь истинностное значение «Т» для Истины или «Т». F» означает Ложь, в зависимости от обстоятельств.).

Связки имеют несколько различных словоупотреблений, например, «а ПОДРАЗУМЕВАЕТ Б» также говорится «ЕСЛИ а, ТО б». Некоторые из них показаны в таблице.

						б только если а
						b ДОСТАТОЧНО ДЛЯ	б ИМЕННО КОГДА
						а НЕОБХОДИМО ДЛЯ б	б ЕСЛИ И ТОЛЬКО ЕСЛИ а; б МКФ а
					включительно ИЛИ	ЕСЛИ б ТО а	b НЕОБХОДИМО И ДОСТАТОЧНО ДЛЯ
		отрицание	отрицание	соединение	дизъюнкция	импликация	двуусловный
переменные		НЕ б	НЕ	б И а	б ИЛИ а	б ПОДРАЗУМЕВАЕТ а	b ЯВЛЯЕТСЯ логически эквивалентным a ***	f IS тавтология	НИ а НИ б	б штрих а	исключительный ИЛИ
б	а	¬(б)	¬(а)	(б ∧ а)	(б ∨ а)	(б → а)	(б ↔ а)	(f = формула)	(а НО б)	(б|а)	различный
Ф	Ф	Т	Т	Ф	Ф	Т	Т	Т	Т	Т	Ф
Ф	Т	Т	Ф	Ф	Т	Т	Ф	Т	Ф	Т	Т
Т	Ф	Ф	Т	Ф	Т	Ф	Ф	Т	Ф	Т	Т
Т	Т	Ф	Ф	Т	Т	Т	Т	Т	Ф	Ф	Ф

Инженерные соединения

Инженерные символы менялись с годами, но они являются обычным явлением. Иногда они выглядят просто как коробки с символами внутри. «a» и «b» называются «входами», а «c» называется «выходом».

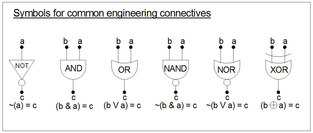
В общем, инженерные связки ничем не отличаются от математических связок, за исключением того, что они обычно оцениваются как «1» = «T» и «0» = «F». Это делается для целей анализа/минимизации и синтеза формул с использованием понятия минтермов и карт Карно (см. ниже). Инженеры также используют слова «логическое произведение» из « понятия Буля (a*a = a) и логическая сумма» из Джевонса (a+a = a). понятия

					логический продукт	логическая сумма			полусумматор (без переноса)
									исключительный ИЛИ
номер строки	переменные		НЕТ	НЕТ	И	ИЛИ	NAND	НИ	БЕСПЛАТНО
б*2 1 +а*2 0	б	а	~(б)	~(а)	(б и а)	(б ∨ а)	~(б и а)	~(б ∨ а)	⊕
0	0	0	1	1	0	0	1	1	0
1	0	1	1	0	0	1	1	0	1
2	1	0	0	1	0	1	1	0	1
3	1	1	0	0	1	1	0	0	0

СЛУЧАЙНАЯ связка: ЕСЛИ... ТО... ИНАЧЕ...

Связка IF... THEN... ELSE... появляется как простейшая форма оператора CASE теории рекурсии и теории вычислений и является связкой, отвечающей за условные переходы (переходы, переходы). Из этой связки могут быть построены все остальные связки (подробнее см. ниже). Хотя «IF c THEN b ELSE a» звучит как импликация, в своей наиболее сокращенной форме это переключатель, который принимает решение и предлагает в качестве результата только одну из двух альтернатив «a» или «b» (отсюда и название оператора переключения) . на языке программирования C ).

Следующие три предложения эквивалентны (на что указывает знак логической эквивалентности ≡):

1. (ЕСЛИ 'счетчик равен нулю' ТО 'перейти к инструкции b ' ELSE 'перейти к инструкции a ') ≡
2. ( (c → b) & (~c → a) ) ≡ ( ( ЕСЛИ 'счетчик равен нулю' ТО 'перейти к инструкции b ' ) И ( ЕСЛИ 'Это НЕ тот случай, когда счетчик равен нулю' ТОГДА 'перейти к инструкции а ) " ≡
3. ( (c & b) ∨ (~c & a)) ≡ " ( 'Счетчик равен нулю' И 'перейти к инструкции b ) ИЛИ ('Это НЕ тот случай, когда 'счетчик равен нулю' И 'перейти к инструкции a ) "

Таким образом, ЕСЛИ... ТО... ИНАЧЕ - в отличие от импликации - не дает неоднозначного результата «ИСТИНА», когда первое предложение ложно, т.е. c = F в (c → b). Например, большинство людей отвергнут следующее сложное предложение как бессмысленное, не имеющее смысла, потому что второе предложение не связано по смыслу с первым.

Пример: Предложение «ЕСЛИ «Уинстон Черчилль был китайцем» ТО «Солнце всходит на востоке» оценивается как ИСТИНА, учитывая, что утверждение «Уинстон Черчилль был китайцем» является ЛОЖЬЮ, а предложение «Солнце восходит на востоке» оценивается как ИСТИНА. .

Признавая эту проблему, знак → формальной импликации в исчислении высказываний называется материальной импликацией, чтобы отличить его от повседневной, интуитивной импликации.

Использование конструкции IF... THEN... ELSE позволяет избежать противоречий, поскольку предлагает полностью детерминированный выбор между двумя заявленными альтернативами; он предлагает два «объекта» (две альтернативы b и a) и выбирает между ними исчерпывающе и однозначно. В приведенной ниже таблице истинности d1 представляет собой формулу: ( (ЕСЛИ c, ТОГДА b) И (ЕСЛИ НЕ-c, ТОГДА a)). Его полностью сокращенная форма d2 представляет собой формулу: ( (c И b) ИЛИ (НЕ-c И a). Эти две формулы эквивалентны, как показано в столбцах «=d1» и «=d2». Инженеры-электрики называют полностью сокращенную форму d2. формула оператора AND-OR-SELECT. Оператор CASE (или SWITCH) представляет собой расширение одной и той же идеи до n возможных, но взаимоисключающих результатов. Инженеры-электрики называют оператор CASE мультиплексором .

											d1																		d2
ряд	с	б	а		(	(	с	→	б	)	&	(	~	(	с	)	→	а	)	)	=d1		(	(	с	&	б	)	∨	(	~	(	с	)	&	а	)	)	=d2
0	0	0	0				0	1	0		0		1		0		0	0			0				0	0	0		0		1		0		0	0			0
1	0	0	1				0	1	0		1		1		0		1	1			1				0	0	0		1		1		0		1	1			1
2	0	1	0				0	1	1		0		1		0		0	0			0				0	0	1		0		1		0		0	0			0
3	0	1	1				0	1	1		1		1		0		1	1			1				0	0	1		1		1		0		1	1			1
4	1	0	0				1	0	0		0		0		1		1	0			0				1	0	0		0		0		1		0	0			0
5	1	0	1				1	0	0		0		0		1		1	1			0				1	0	0		0		0		1		0	1			0
6	1	1	0				1	1	1		1		0		1		1	0			1				1	1	1		1		0		1		0	0			1
7	1	1	1				1	1	1		1		0		1		1	1			1				1	1	1		1		0		1		0	1			1

ИДЕНТИЧНОСТЬ и оценка

В первой таблице этого раздела отмечена *** запись «логическая эквивалентность», чтобы отметить тот факт, что « логическая эквивалентность » — это не то же самое, что «идентичность». Например, большинство согласится, что утверждение «Эта корова синяя» идентично утверждению «Эта корова синяя». С другой стороны, в речи иногда появляется логическая эквивалентность, как в этом примере: «'Солнце светит' означает 'Я еду на велосипеде'». В переводе в пропозициональную формулу слова становятся: «ЕСЛИ 'Солнце светит' ТО' Я езжу на велосипеде», И ЕСЛИ «Я езжу на велосипеде», ТО «светит солнце»»:

«IF's' THEN 'b' AND IF 'b' THEN 's'» пишется как ((s → b) & (b → s)) или сокращенно как (s ↔ b). Поскольку самая правая строка символов представляет собой определение нового символа в терминах символов слева, использование знака IDENTITY = уместно:

((s → b) & (b → s)) = (s ↔ b)

Разные авторы используют разные знаки логической эквивалентности: ↔ (например, Суппес, Гудштейн, Гамильтон), ≡ (например, Роббин), ⇔ (например, Бендер и Уильямсон). Обычно тождество записывается как знак равенства =. Единственное исключение из этого правила можно найти в Principia Mathematica . Подробнее о философии понятия ИДЕНТИЧНОСТИ см. в законе Лейбница .

Как отмечалось выше, Тарский считает, что ИДЕНТИЧНОСТЬ находится за пределами исчисления высказываний, но он утверждает, что без понятия «логика» недостаточна для математики и дедуктивных наук. Фактически, знак входит в исчисление высказываний, когда необходимо вычислить формулу.

В некоторых системах нет таблиц истинности, а есть только формальные аксиомы (например, строки символов из набора { ~, →, (, ), переменные p ₁ , p ₂ , p ₃ , ... } и правила формирования формул. (правила о том, как создать больше строк символов из предыдущих строк, используя, например, замену и modus ponens ), результатом такого расчета будет другая формула (т.е., однако, в конечном итоге, если кто-то захочет). Чтобы использовать исчисление для изучения понятий достоверности и истинности, необходимо добавить аксиомы, которые определяют поведение символов, называемых «значениями истинности» {T, F} (или {1, 0} и т. д.) относительно других символов.

Например, Гамильтон использует два символа = и ≠, когда он определяет понятие оценки v любых правильно построенных формул (wffs) A и B в своем «исчислении формальных утверждений» L. Оценка v является функцией от wffs его систему L в диапазон (выход) {T, F}, при условии, что каждой переменной p1 _, p2 _, p3 _в wff присвоено произвольное значение истинности {T, F}.

v ( A ) ≠ v (~ A ) ( я )

v ( A → B ) = F тогда и только тогда, когда v ( A ) = T и v ( B ) = F ( ii )

Два определения ( i ) и ( ii ) определяют эквивалент таблиц истинности для связок ~ (НЕ) и → (ИМПЛИКАЦИЯ) его системы. Первый выводит F ≠ T и T ≠ F, другими словами, « v ( A ) не означает v (~ A )». Определение ( ii ) задает третью строку в таблице истинности, а остальные три строки получаются в результате применения определения ( i ). В частности ( ii ) присваивает значение F (или значение «F») всему выражению. Определения также служат правилами формирования, которые позволяют подставлять в формулу ранее полученное значение:

		v(A→B)
(	v(A)	→	v(B)	)
	Ф	Т	Ф
	Ф	Т	Т
	Т	Ф	Ф
	Т	Т	Т

Некоторые формальные системы с самого начала определяют эти аксиомы оценки в форме определенных формул, таких как закон противоречия или законы тождества и ничтожности. Выбор того, какие из них использовать, а также таких законов, как коммутация и распределение, остается за разработчиком системы, если набор аксиом является полным (т.е. достаточным для формирования и оценки любой правильно сформированной формулы, созданной в системе). .

Более сложные формулы

Как показано выше, связка CASE (IF c THEN b ELSE a ) строится либо из связок с двумя аргументами IF ... THEN ... и AND, либо из связок OR и AND и NOT с одним аргументом. Такие связки, как n-аргумент AND (a & b & c & ... & n), OR (a ∨ b ∨ c ∨ ... ∨ n), создаются из строк AND и OR с двумя аргументами и записываются в сокращенная форма без скобок. Эти, а также другие связи можно затем использовать в качестве строительных блоков для дальнейших связей. Риторы, философы и математики используют таблицы истинности и различные теоремы для анализа и упрощения своих формул.

Электротехника использует нарисованные символы и соединяет их линиями, которые обозначают математический акт замещения и замены. Затем они проверяют свои рисунки с помощью таблиц истинности и упрощают выражения, как показано ниже, используя карты Карно или теоремы. Таким образом, инженеры создали множество «комбинаторной логики» (то есть соединений без обратной связи), таких как «декодеры», «кодеры», «многофункциональные вентили», «мажоритарная логика», «двоичные сумматоры», «арифметико-логические блоки». и т. д.

Определения

Определение создает новый символ и его поведение, часто в целях сокращения. После представления определения можно использовать любую форму эквивалентного символа или формулу. Следующий символизм = _Df соответствует соглашению Райхенбаха. Несколько примеров удобных определений, взятых из набора символов { ~, &, (, ) } и переменных. Каждое определение представляет собой логически эквивалентную формулу, которую можно использовать для замены или замены.

• определение новой переменной: (c & d) = _Df s
• ИЛИ: ~(~a & ~b) = _Df (a ∨ b)
• ВЫВОД: (~a ∨ b) = _Df (a → b)
• XOR: (~a & b) ∨ (a & ~b) = _Df (a ⊕ b)
• ЛОГИЧЕСКАЯ ЭКВИВАЛЕНТНОСТЬ: ( (a → b) & (b → a)) = _Df ( a ≡ b )

Аксиомы и схемы определений

Приведенные выше определения для ИЛИ, ИМПЛИКАЦИИ, исключающего ИЛИ и логической эквивалентности на самом деле являются схемами (или «схемами»), то есть моделями ( демонстрациями, примерами) для общего формата формулы , но показаны (в иллюстративных целях) конкретными буквами a. , b, c для переменных, тогда как любые буквы переменных могут стоять на своих местах, если замена букв соответствует приведенному ниже правилу замены.

Пример: В определении (~a ∨ b) = _Df (a → b) могут использоваться другие символы переменных, такие как «SW2» и «CON1», т.е. формально:

a = _Df SW2, b = _Df мы будем иметь CON1, поэтому в качестве примера схемы определения _{(~SW2 ∨ CON1) = Df} (SW2 → CON1)

Замена против замены

Замена : переменная или подформула, подлежащая замене другой переменной, константой или подформулой, должна быть заменена во всех случаях во всей формуле.

Пример: (c & d) ∨ (p & ~(c & ~d)), но (q1 & ~q2) ≡ d. Теперь везде, где встречается переменная «d», замените (q ₁ & ~q ₂ ):

(c & (q ₁ & ~q ₂ )) ∨ (p & ~(c & ~(q ₁ & ~q ₂ )))

Замена : (i) заменяемая формула должна быть в пределах тавтологии, т.е. логически эквивалентна (связана ≡ или ↔) с формулой, которая ее заменяет, и (ii) в отличие от замены допустимо, чтобы замена происходила только в одном месте. (т.е. для одной формулы).

Пример. Используйте этот набор схем/эквивалентов формул:

1. ( (а ∨ 0) ≡ а ).
2. ( (а и ~а) ≡ 0).
3. ( (~a ∨ b) знак равно _Df (a → b)).
6. ( ~(~а) ≡ а)

1. начните с «а»: а
2. Используйте 1, чтобы заменить «a» на (a ∨ 0): (a ∨ 0)
3. Используйте понятие «схема», чтобы заменить b на a в 2: ( (a & ~a) ≡ 0 )
4. Используйте 2, чтобы заменить 0 на (b & ~b): ( a ∨ (b & ~b) )
5. (см. ниже, как распределить «a ∨» по (b и ~b) и т. д.)

Индуктивное определение

Классическое представление логики высказываний (см. Enderton 2002) использует связки $\lnot ,\land ,\lor ,\to ,\leftrightarrow$. Набор формул для данного набора пропозициональных переменных индуктивно определяется как наименьший набор выражений, такой что:

• Каждая пропозициональная переменная в наборе представляет собой формулу,
• $(\lnot \alpha )$ это формула всякий раз, когда $\alpha$ есть, и
• $(\alpha \,\Box \,\beta )$ это формула всякий раз, когда $\alpha$ и $\beta$ представляют собой формулы и $\Box$ это одна из бинарных связок $\land ,\lor ,\to ,\leftrightarrow$.

Это индуктивное определение можно легко расширить, чтобы охватить дополнительные связи.

Индуктивное определение можно также перефразировать в терминах операции замыкания (Эндертон 2002). Пусть V обозначает набор пропозициональных переменных, а X _V обозначает набор всех строк алфавита, включая символы в V , левые и правые круглые скобки и все рассматриваемые логические связки. Каждая логическая связка соответствует операции построения формулы, функции от XX _V до XX _V :

• Учитывая строку z , операция ${\mathcal {E}}_{\lnot }(z)$ возвращает $(\lnot z)$.
• Учитывая строки y и z , операция ${\mathcal {E}}_{\land }(y,z)$ возвращает $(y\land z)$. Есть подобные операции ${\mathcal {E}}_{\lor }$, ${\mathcal {E}}_{\to }$, и ${\mathcal {E}}_{\leftrightarrow }$ соответствующие остальным бинарным связкам.

Множество формул над V определяется как наименьшее подмножество XX _V, содержащее V и замкнутое относительно всех операций построения формул.

Разбор формул

Следующие «законы» исчисления высказываний используются для «редукции» сложных формул. «Законы» можно легко проверить с помощью таблиц истинности. Для каждого закона главная (самая внешняя) связка связана с логической эквивалентностью ≡ или тождеством =. Полный анализ всех 2 ^н комбинации значений истинности для n различных переменных приведут к появлению столбца из единиц (T) под этой связкой. Этот вывод делает каждый закон по определению тавтологией. А для данного закона, поскольку его формулы слева и справа эквивалентны (или идентичны), их можно заменять друг другом.

• Пример: Следующая таблица истинности представляет собой закон Де Моргана для поведения НЕ над ИЛИ: ~(a ∨ b) ≡ (~a & ~b). Слева от главной связки ≡ (желтый столбец с надписью «натянутый») формула ~(b ∨ a) имеет значение (1, 0, 0, 0) под меткой «P». Справа от «натянутой» формула (~(b) ∨ ~(a)) также имеет значение (1, 0, 0, 0) под меткой «Q». Поскольку два столбца имеют эквивалентные оценки, логическая эквивалентность ≡ при «натянутом» значении равна (1, 1, 1, 1), т. е. P ≡ Q. Таким образом, любую формулу можно заменить другой, если она появляется в более крупной формуле.

				П						тугой						вопрос
б	а		(	~	(	б	V	а	)	≡	(	~	(	б	)	&	~	(	а	)	)	)
0	0			1		0	0	0		1		1		0		1	1		0
0	1			0		0	1	1		1		1		0		0	0		1
1	0			0		1	1	0		1		0		1		0	1		0
1	1			0		1	1	1		1		0		1		0	0		1

Предприимчивые читатели могут поставить перед собой задачу изобрести «аксиоматическую систему», которая использует символы { ∨, &, ~, (, ), переменные a, b, c }, правила формирования, указанные выше, и как можно меньшее количество перечисленных законов. ниже, а затем выведите в виде теорем остальные, а также оценки таблицы истинности для ∨, & и ~. В одном наборе, приписываемом Хантингтону (1904) (Suppes:204), используются восемь законов, определенных ниже.

При использовании в аксиоматической системе символы 1 и 0 (или T и F) считаются правильно составленными формулами и, таким образом, подчиняются тем же правилам, что и переменные. Таким образом, перечисленные ниже законы на самом деле являются схемами аксиом , то есть они заменяют бесконечное число примеров. Таким образом, ( x ∨ y ) ≡ ( y ∨ x ) может использоваться в одном случае, ( p ∨ 0 ) ≡ ( 0 ∨ p ), а в другом случае ( 1 ∨ q ) ≡ ( q ∨ 1 ) и т. д.

Соединительный стаж (символ ранга)

В общем, чтобы избежать путаницы при анализе и оценке пропозициональных формул, можно широко использовать круглые скобки. Однако довольно часто авторы их опускают. Чтобы проанализировать сложную формулу, сначала необходимо знать старшинство или ранг каждой связки (кроме *) над другими связками. Чтобы «правильно сформировать» формулу, начните с связки с самым высоким рангом и добавьте круглые скобки вокруг ее компонентов, затем переместите ее вниз по рангу (обращая пристальное внимание на область действия связки, в которой она работает). От самого старшего к младшему, со знаками предикатов ∀x и ∃x, IDENTITY = и арифметическими знаками, добавленными для полноты:

≡

(ЛОГИЧЕСКАЯ ЭКВИВАЛЕНТНОСТЬ)

→

(ИМПЛИКАЦИЯ)

&

(И)

∨

(ИЛИ)

~

(НЕТ)

∀x

(ДЛЯ ВСЕХ х)

∃x

(СУЩЕСТВУЕТ х)

=

(ЛИЧНОСТЬ)

+

(арифметическая сумма)

*

(арифметическое умножение)

'

(s, арифметический преемник).

Таким образом, формулу можно разобрать, но поскольку NOT не подчиняется закону распределения, круглые скобки вокруг внутренней формулы (~c и ~d) обязательны:

Пример: «d & c ∨ w» переписано как ( (d & c) ∨ w )

Пример: «a & a → b ≡ a & ~a ∨ b», переписанный (строго) таков:

• ≡ имеет старшинство: ( ( a & a → b ) ≡ ( a & ~a ∨ b ) )
• → имеет старшинство: ( ( a & (a → b) ) ≡ ( a & ~a ∨ b ) )
• & имеет старшинство с обеих сторон: ( ( ( (a) & (a → b) ) ) ≡ ( ( (a) & (~a ∨ b) ) )
• ~ имеет старшинство: ( ( ( (a) & (a → b) ) ) ≡ ( ( (a) & (~(a) ∨ b) ) )
• проверьте 9 (-круглая скобка и 9)-круглая скобка: ( ( ( (a) & (a → b) ) ) ≡ ( ( (a) & (~(a) ∨ b) ) )

Пример:

d & c ∨ p & ~(c & ~d) ≡ c & d ∨ p & c ∨ p & ~d переписано как ( ( ​​(d & c) ∨ ( p & ~((c & ~(d)) ) ) ) ≡ ( (c & d) ∨ (p & c) ∨ (p & ~(d)) ) )

Коммутативные и ассоциативные законы

И И, и ИЛИ подчиняются коммутативному закону и ассоциативному закону :

• Коммутативный закон для OR: ( a ∨ b ) ≡ ( b ∨ a )
• Коммутативный закон для AND: (a и b) ≡ (b и a)
• Ассоциативный закон для ОР: (( a ∨ b ) ∨ c ) ≡ ( a ∨ (b ∨ c) )
• Ассоциативный закон для AND: (( a & b ) & c ) ≡ ( a & (b & c) )

Опуск круглых скобок в строках И и ИЛИ : Связки считаются унарными (с одной переменной, например НЕ) и бинарными (т. е. с двумя переменными И, ИЛИ, ПОДРАЗУМЕВАЮТСЯ). Например:

( (c & d) ∨ (p & c) ∨ (p & ~d)) выше должно быть записано ( ((c & d) ∨ (p & c)) ∨ (p & ~(d) ) ) или, возможно, ( (c & d) ∨ ( (p & c) ∨ (p & ~(d)) ) )

Однако демонстрация таблицы истинности показывает, что форма без лишних скобок вполне адекватна.

Опуск круглых скобок в отношении NOT с одной переменной : хотя ~(a), где a — одна переменная, совершенно ясно, ~a является адекватным и представляет собой обычный способ этого литерала появления . Если НЕ находится над формулой, содержащей более одного символа, круглые скобки обязательны, например ~(a ∨ b).

Распределительные законы

OR распределяет по AND, а AND распределяет по OR. NOT не распределяется по AND или OR. См. ниже закон де Моргана:

• Дистрибутивный закон для OR: ( c ∨ ( a & b) ) ≡ ( (c ∨ a) & (c ∨ b) )
• Распределительный закон для AND: ( c & ( a ∨ b) ) ≡ ( (c & a) ∨ (c & b) )

Законы де Моргана

НЕ при распределении по ИЛИ или И делает что-то необычное (опять же, это можно проверить с помощью таблицы истинности):

• Закон де Моргана для ОР: ¬(a ∨ b) ≡ (¬a ^ ¬b)
• Закон де Моргана для И: ¬(a ^ b) ≡ (¬a ∨ ¬b)

Законы поглощения

Поглощение, в частности первое, приводит к отличию «законов» логики от «законов» арифметики:

• Поглощение (идемпотентность) для ОР: (a ∨ a) ≡ a
• Поглощение (идемпотентность) для И: (a и a) ≡ a

Законы оценки: тождество, ничтожность и дополнение.

Знак «=» (в отличие от логической эквивалентности ≡, попеременно ↔ или ⇔) символизирует присвоение значения или значения. Таким образом, строка (a & ~(a)) символизирует «0», т.е. она означает то же самое, что и символ «0». В некоторых «системах» это будет аксиома (определение), возможно, отображаемая как ( (a & ~ (a)) = _Df 0 ); в других системах его можно получить из таблицы истинности, приведенной ниже:

					с						тугой	с
а		(	(	а	&	~	(	а	)	)	≡	0	)
0				0	0	1		0			1	0
1				1	0	0		1			1	0

• Коммутация равенства: (a = b) ≡ (b = a)
• Тождество для OR: (a ∨ 0) = a или (a ∨ F) = a
• Идентичность для AND: (a & 1) = a или (a & T) = a
• Недействительность для OR: (a ∨ 1) = 1 или (a ∨ T) = T
• Недействительность для AND: (a & 0) = 0 или (a & F) = F
• Дополнение для OR: (a ∨ ~a) = 1 или (a ∨ ~a) = T, закон исключенного третьего
• Дополнение для AND: (a & ~a) = 0 или (a & ~a) = F, закон противоречия

Двойной негатив (инволюция)

• ¬(¬а) ≡ а

Правильно составленные формулы (wffs)

Ключевым свойством формул является то, что их можно однозначно проанализировать, чтобы определить структуру формулы с точки зрения ее пропозициональных переменных и логических связок. Когда формулы записаны в инфиксной записи , как указано выше, уникальная читабельность обеспечивается за счет соответствующего использования круглых скобок в определении формул. Кроме того, формулы могут быть записаны в польской или обратной польской нотации , что полностью исключает необходимость использования круглых скобок.

Индуктивное определение инфиксных формул в предыдущем разделе можно преобразовать в формальную грамматику в форме Бэкуса-Наура :

<formula> ::= <propositional variable>
| ( ¬ <formula> )
| ( <formula> ∧ <formula>)
| ( <formula> ∨ <formula> )
| ( <formula> → <formula> )
| ( <formula> ↔ <formula> )

Можно показать, что любое выражение, сопоставленное с грамматикой, имеет сбалансированное количество левых и правых скобок, а любой непустой начальный сегмент формулы имеет больше левых, чем правых скобок. Этот факт можно использовать для создания алгоритма разбора формул. Например, предположим, что выражение x начинается с $(\lnot$. Начиная со второго символа, найдите самое короткое подвыражение y из x , в котором есть сбалансированные круглые скобки. Если x — формула, то после этого выражения остается ровно один символ, этот символ — закрывающая скобка, а сам y — формула. Эту идею можно использовать для создания анализатора рекурсивного спуска для формул.

Пример подсчета скобок :

Этот метод определяет как «1» главную связку — связку, под которой происходит общая оценка формулы для крайних круглых скобок (которые часто опускаются). Он также определяет самую внутреннюю связку, с которой можно было бы начать вычисление формулы без использования таблицы истинности, например, на «уровне 6».

	начинать	(	(	(	с	&	д	)	V	(	п	&	~	(	(	с	&	~	(	д	)	)	)	)	)	=	(	(	(	с	&	д	)	V	(	п	&	д	)	)	V	(	п	&	~	(	с	)	)	)	)
считать	0	1	2	3	3	3	3	2	2	3	3	3	3	4	5	5	5	5	6	6	5	4	3	3	1	1	2	3	4	4	4	4	3	3	4	4	4	4	3	2	2	3	3	3	3	3	3	3	2	1	0

Правильно составленные формулы и действительные формулы в выводах

Понятие валидного аргумента обычно применяется к выводам в аргументах, но аргументы сводятся к пропозициональным формулам и могут оцениваться так же, как и любая другая пропозициональная формула. Здесь действительный вывод означает: «Формула, которая представляет вывод, оценивается как «истина» под своей основной связкой, независимо от того, какие истинностные значения присвоены ее переменным», т.е. формула является тавтологией. Вполне возможно, что формула будет корректной, но недействительной. Другими словами, «правильная формулировка необходима для того, чтобы формула была действительной, но этого недостаточно » . Единственный способ узнать, является ли он корректным действительным , и — это подвергнуть его проверке с помощью таблицы истинности или с помощью «законов»:

• Пример 1. Что можно сделать со следующим трудным для понимания утверждением? Это действительно? «Если солнечно, но если лягушка квакает, то это не солнечно, тогда это то же самое, что сказать, что лягушка не квакает». Преобразуйте это в пропозициональную формулу следующим образом:

  «IF (a AND (IF b THEN NOT-a) THEN NOT-a», где «a» означает «солнечно», а «b» означает «лягушка квакает»:

  ( ( (а) & ( (б) → ~(а) ) ≡ ~(б) )

  Это правильно сформулировано, но действительно ли это ? Другими словами, при вычислении это приведет к тавтологии (все T) под символом логической эквивалентности ≡ ? Ответ НЕТ, это недействительно. Однако, если реконструировать его как импликацию , этот аргумент действителен .

  «Сказать, что солнечно, но если лягушка квакает, то это не солнечно, подразумевается , что лягушка не квакает».

  Кваканью лягушки могли помешать и другие обстоятельства: возможно, ее съел журавль.

• Пример 2 (из Райхенбаха через Бертрана Рассела):

  «Если у свиней есть крылья, то некоторых крылатых животных можно есть. Некоторые крылатые животные вкусны, поэтому у свиней есть крылья».

  ( ((a) → (b)) & (b) → (a) ) правильно сформирован, но недопустимый аргумент, как показано красной оценкой основного импликации:

В	Г												аргумент
а	б		(	(	(	а	->	б	)	&	б	)	->	а	)
0	0					0	1	0		0	0		1	0
0	1					0	1	1		1	1		0	0
1	0					1	0	0		0	0		1	1
1	1					1	1	1		1	1		1	1

Уменьшенные наборы соединительных элементов

Инженерный символ связки И-НЕ («штрих») можно использовать для построения любой пропозициональной формулы. Идея о том, что истинность (1) и ложность (0) могут быть определены в терминах этой связки, показана в последовательности И-НЕ слева, а выводы четырех оценок И-НЕ b показаны внизу. Более распространенный метод — использовать определение NAND из таблицы истинности.

Набор логических связок называется полным, если каждая пропозициональная формула тавтологически эквивалентна формуле, содержащей только связки из этого набора. Существует множество комплектов соединительных элементов, в том числе $\{\land ,\lnot \}$, $\{\lor ,\lnot \}$, и $\{\to ,\lnot \}$. Есть две двоичные связки, которые являются самостоятельными и соответствуют NAND и NOR соответственно. Некоторые пары не являются полными, например $\{\land ,\lor \}$.

Инсульт (NAND)

Двоичная связка, соответствующая И-НЕ, называется штрихом Шеффера и пишется с помощью вертикальной черты | или вертикальная стрелка ↑. Полнота этой связи была отмечена в Principia Mathematica (1927: xvii). Поскольку он сам по себе завершен, все остальные связки можно выразить только с помощью штриха. Например, где символ «≡» обозначает логическую эквивалентность :

~ р ≡ р|р

р → q ≡ p|~q

п ∨ q ≡ ~p|~q

р и q ≡ ~(p|q)

В частности, нулевые связки $\top$ (представляющий истину) и $\bot$ (представляющее ложность) можно выразить с помощью штриха:

$\top \equiv (a|(a|a))$

$\bot \equiv (\top |\top )$

ЕСЛИ... ТО... ДРУГОЕ

Эта связка вместе с {0, 1}, (или {F, T} или { $\bot$, $\top$ } ) образует полный набор. Далее соотношение IF...THEN...ELSE ( c, b, a) = d представляет ( (c → b) ∨ (~c → a) ) ≡ ( (c & b) ∨ (~c & а) ) = d

(в, б, а):

(с, 0, 1) ≡ ~ с

(в, б, 1) ≡ (в → б)

(с, с, а) ≡ (с ∨ а)

(в, б, в) ≡ (в и б)

Пример: Ниже показано, как будет проходить основанное на теоремах доказательство «(c, b, 1) ≡ (c → b)», ниже доказательства приводится его проверка с помощью таблицы истинности. (Примечание: (c → b) определяется как (~c ∨ b)):

• Начните с сокращенной формы: ( (c & b) ∨ (~c & a))
• Замените a на «1»: ( (c & b) ∨ (~c & 1) )
• Тождество (~c & 1) = ~c: ( (c & b) ∨ (~c) )
• Закон коммутации для V: ( (~c) ∨ (c & b))
• Распределите "~c V" по (c и b): (((~c) ∨ c) & ((~c) ∨ b)
• Закон исключенного третьего (((~c) ∨ c ) = 1 ): ( (1) & ((~c) ∨ b ) )
• Распределите "(1) &" по ((~c) ∨ b): ( ((1) & (~c)) ∨ ((1) & b )) )
• Коммутативность и идентичность (( 1 & ~c) = (~c & 1) = ~c и (( 1 & b) ≡ (b & 1) ≡ b: ( ~c ∨ b )
• ( ~c ∨ b ) определяется как c → b КЭД

В следующей таблице истинности столбец, помеченный как «натянутый» для тавтологии, оценивает логическую эквивалентность (обозначенную здесь ≡) между двумя столбцами, помеченными d. Поскольку все четыре строки под словом «натянуты» имеют единицы, эквивалентность действительно представляет собой тавтологию.

												д										тугой						д
ряды	с	б	а		(	(	(	с	&	б	)	V	(	~	(	с	)	&	а	)	)	≡	(	~	(	с	)	V	б	)	)
0,1	0	0	1					0	0	0		1		1		0		1	1			1		1		0		1	0
2,3	0	1	1					0	0	1		1		1		0		1	1			1		1		0		1	1
4,5	1	0	1					1	0	0		0		0		1		0	1			1		0		1		0	0
6,7	1	1	1					1	1	1		1		0		1		0	1			1		0		1		1	1

Нормальные формы

Произвольная пропозициональная формула может иметь очень сложную структуру. Часто удобно работать с формулами, имеющими более простые формы, известные как нормальные формы . Некоторые распространенные нормальные формы включают конъюнктивную нормальную форму и дизъюнктивную нормальную форму . Любую пропозициональную формулу можно привести к конъюнктивной или дизъюнктивной нормальной форме.

Приведение к нормальной форме

Таблица истинности будет содержать 2 ^н строк, где n — количество переменных (например, три переменные «p», «d», «c» дают 2 ³ ряды). Каждая строка представляет минтерм. Каждый минтерм можно найти на диаграмме Хассе, диаграмме Вейча и карте Карно. (Оценки «p», показанные в таблице истинности, не показаны на диаграммах Хассе, Вейча и Карно; они показаны на карте Карно в следующем разделе.)

Приведение к нормальной форме относительно просто, если подготовлена ​​таблица истинности формулы. Но дальнейшие попытки минимизировать количество литералов (см. ниже) требуют некоторых инструментов: сокращение по законам Де Моргана и таблицам истинности может быть громоздким, но карты Карно очень подходят для небольшого числа переменных (5 или меньше). Существуют некоторые сложные табличные методы для более сложных схем с несколькими выходами, но они выходят за рамки этой статьи; подробнее см. Алгоритм Куайна – МакКласки .

Буквальный, термин и альтернативный

В электротехнике переменная x или ее отрицание ~(x) может называться литералом . Строка литералов, соединенных операторами AND, называется термином. Строка литералов, соединенных оператором OR, называется альтермом. Обычно литерал ~(x) сокращается до ~x. Иногда символ & вообще опускается, как при алгебраическом умножении.

• Примеры
  1. a, b, c, d — переменные. ((( a & ~(b)) & ~(c)) & d) — это термин. Это можно сократить как (a & ~b & ~c & d) или a~b~cd.
  2. p, q, r, s — переменные. (((p ∨ ~(q)) ∨ r) ∨ ~(s) ) является альтермом. Это можно сократить как (p ∨ ~q ∨ r ∨ ~s).

Минтермс

Точно так же, как 2 ^н Таблица истинности строк отображает оценку пропозициональной формулы для всех 2 ^н возможных значений его переменных, n переменных дает 2 ^н -квадратная карта Карно (хотя мы не можем нарисовать ее в полномерной реализации). Например, 3 переменные дают 2 ³ = 8 рядов и 8 квадратов Карно; Четыре переменные дают 16 строк таблицы истинности и 16 квадратов и, следовательно, 16 минтермов . Каждый квадрат карты Карно и соответствующая ему оценка таблицы истинности представляют один минтерм.

Любую пропозициональную формулу можно свести к «логической сумме» (ИЛИ) активных (т.е. со значением «1» или «Т») минтермов. В такой форме формула называется дизъюнктивной нормальной формой . Но даже несмотря на то, что он находится в такой форме, он не обязательно минимизируется ни по количеству терминов, ни по количеству литералов.

В следующей таблице обратите внимание на своеобразную нумерацию строк: (0, 1, 3, 2, 6, 7, 5, 4, 0). Первый столбец представляет собой десятичный эквивалент двоичного эквивалента цифр «cba», другими словами:

• Пример

  сба ₂ = с*2 ² + б*2 ¹ + а*2 ⁰ :

  cba = (c=1, b=0, a=1) = 101 ₂ = 1*2 ² + 0*2 ¹ + 1*2 ⁰ = 5 ₁₀

Такая нумерация возникает потому, что при перемещении вниз по таблице от строки к строке только одна переменная одновременно меняет свое значение. Код Грея выведен из этого понятия. Это понятие можно распространить на трех- и четырехмерные гиперкубы, называемые диаграммами Хассе , где переменные в каждом углу изменяются только по одной при движении по краям куба. Диаграммы Хассе (гиперкубы), сплюснутые в двух измерениях, представляют собой либо диаграммы Вейча , либо карты Карно (это практически одно и то же).

При работе с картами Карно всегда нужно иметь в виду, что верхний край «обтекает» нижний край, а левый край обтекает правый край — диаграмма Карно на самом деле представляет собой трех-, четырех- или n-мерную диаграмму. сплющенный предмет.

десятичный эквивалент (c, b, a)	с	б	а	минтерм
0	0	0	0	(~c, ~b и ~a)
1	0	0	1	(~в и ~б и а)
3	0	1	1	(~ в, б и а)
2	0	1	0	(~в, б и ~а)
6	1	1	0	(в, б и ~а)
7	1	1	1	(в, б и а)
5	1	0	1	(в и ~б и а)
4	1	0	0	(в, ~б и ~а)
0	0	0	0	(~а и ~б и ~в)

Редукция методом карт (Вейтч, Карно)

Вейтч усовершенствовал понятие диаграмм Венна , преобразовав круги в примыкающие друг к другу квадраты, а Карно упростил диаграмму Вейча, преобразовав минтермы, записанные в их буквальной форме (например, ~abc~d), в числа. Метод протекает следующим образом:

Создайте таблицу истинности формулы

Составьте таблицу истинности формулы. Пронумеруйте его строки, используя двоичные эквиваленты переменных (обычно последовательно от 0 до n-1) для n переменных.

Технически, пропозициональная функция была сведена к ее (неминимизированной) конъюнктивной нормальной форме: каждая строка имеет свое минимальное выражение, и к ним можно применить операцию ИЛИ, чтобы получить формулу в ее (неминимизированной) конъюнктивной нормальной форме.

Пример: ((c & d) ∨ (p & ~(c & (~d)))) = q в конъюнктивной нормальной форме:

( (~p & d & c) ∨ (p & d & c) ∨ (p & d & ~c) ∨ (p & ~d & ~c) ) = q

Однако эту формулу можно сократить как по количеству членов (с 4 до 3), так и по общему количеству ее литералов (с 12 до 6).

ряд	Минтермс	п	д	с	(	(	с	&	д	)	∨	(	п	&	~	(	(	с	&	~	(	д	)	)	)	)	)	Активные минтермы	Формула в конъюнктивной нормальной форме
0	( ~p & ~d & ~c )	0	0	0			0	0	0		0		0	0	1			0	0	1		0
1	( ~p & ~d & c)	0	0	1			1	0	0		0		0	0	0			1	1	1		0
2	( ~p & d & ~c )	0	1	0			0	0	1		0		0	0	1			0	0	0		1
3	( ~p & d & c )	0	1	1			1	1	1		1		0	0	1			1	0	0		1						(~p, d и c)
4	( p & ~d & ~c )	1	0	0			0	0	0		1		1	1	1			0	0	1		0						(~p, d и c)
5	(p & ~d & c)	1	0	1			1	0	0		0		1	0	0			1	1	1		0
6	( p & d & ~ c )	1	1	0			0	0	1		1		1	1	1			0	0	0		1						(п, д и ~ с)
7	( п и д и с )	1	1	1			0	1	1		1		1	1	1			1	0	0		1						( п и д и с )
											д																		= (~p&d&c) ∨ (~p&d&c) ∨ (p&d&~c ) ∨ (p&d&c )

Создайте карту Карно формулы.

Этапы редукции с использованием карты Карно. Конечным результатом является ИЛИ (логическая «сумма») трех сокращенных членов.

Используйте значения формулы (например, «p»), найденные с помощью метода таблицы истинности, и поместите их в соответствующие (связанные) квадраты Карно (они пронумерованы в соответствии с соглашением о коде Грея). Если в таблице появляются значения «d» для «неважно», это добавляет гибкости на этапе сокращения.

Уменьшите минтермы

Минтермы соседних (примыкающих) 1-квадратов (Т-квадратов) можно сократить по числу их литералов , при этом число термов также уменьшится. Два примыкающих квадрата (2 х 1 по горизонтали или 1 х 2 по вертикали, даже края представляют собой примыкающие квадраты) теряют один литерал, четыре квадрата в прямоугольнике 4 х 1 (горизонтальном или вертикальном) или квадрате 2 х 2 (даже четыре угла представляют примыкающие квадраты) квадраты) теряют два литерала, восемь квадратов в прямоугольнике теряют 3 литерала и т. д. (Один ищет самый большой квадрат или прямоугольники и игнорирует меньшие квадраты или прямоугольники, полностью содержащиеся в нем.) Этот процесс продолжается до тех пор, пока не будут учтены все примыкающие квадраты, в этот момент пропозициональная формула минимизируется.

Например, квадраты №3 и №7 соприкасаются. Эти два смежных квадрата могут потерять один литерал (например, «p» из квадратов №3 и №7), четыре квадрата в прямоугольнике или квадрате теряют два литерала, восемь квадратов в прямоугольнике теряют 3 литерала и т. д. (Ищется наибольший квадрат или прямоугольник.) Этот процесс продолжается до тех пор, пока не будут учтены все примыкающие квадраты, после чего говорят, что формула высказывания минимизируется.

Пример: Метод карты обычно выполняется путем проверки. Следующий пример расширяет алгебраический метод, чтобы показать «хитрость» объединения термов на карте Карно:

Минтермы №3 и №7 упираются, №7 и №6 упираются, а №4 и №6 упираются (поскольку края стола загибаются). Значит, каждую из этих пар можно сократить.

Обратите внимание, что по закону идемпотентности (A ∨ A) = A мы можем создать больше термов. Тогда по законам ассоциации и распределения исчезающие переменные могут быть объединены в пары, а затем «исчезнут» по Закону противоречия (x & ~x)=0. В следующем примере скобки [ и ] используются только для отслеживания терминов; они не имеют особого значения:

• Приведите формулу к конъюнктивной нормальной форме с сокращаемой формулой:

q = ( (~p & d & c) ∨ (p & d & c) ∨ (p & d & ~c) ∨ (p & ~d & ~c) ) = ( #3 ∨ #7 ∨ #6 ∨ #4 )

• Идемпотентность (поглощение) [ А ∨ А) = А:

( #3 ∨ [ #7 ∨ #7 ] ∨ [ #6 ∨ #6 ] ∨ #4 )

• Ассоциативный закон (x ∨ (y ∨ z)) = ( (x ∨ y) ∨ z )

( [ #3 ∨ #7 ] ∨ [ #7 ∨ #6 ] ∨ [ #6 ∨ #4] )

[ (~p & d & c) ∨ (p & d & c) ] ∨ [ (p & d & c) ∨ (p & d & ~c) ] ∨ [ (p & d & ~c) ∨ (p & ~d & ~c) ] .

• Распределительный закон ( x & (y ∨ z)) = ( (x & y) ∨ (x & z)):

( [ (d & c) ∨ (~p & p) ] ∨ [ (p & d) ∨ (~c & c) ] ∨ [ (p & ~c) ∨ (c & ~c) ] )

• Коммутативный закон и закон противоречия (x & ~x) = (~x & x) = 0:

( [ (d & c) ∨ (0) ] ∨ [ (p & d) ∨ (0) ] ∨ [ (p & ~c) ∨ (0) ] )

• Закон тождества ( x ∨ 0 ) = x, приводящий к сокращенной форме формулы:

q знак равно ( (d & c) ∨ (p & d) ∨ (p & ~c) )

Проверьте сокращение с помощью таблицы истинности.

ряд	Минтермс	п	д	с	(	(	д	&	с	)	∨	(	п	&	д	)	∨	(	п	&	~	(	с	)	)
0	( ~p & ~d & ~c )	0	0	0			0	0	0		0		0	0	0		0		0	0	1		0
1	( ~p & ~d & c)	0	0	1			0	0	1		0		0	0	0		0		0	0	0		1
2	( ~p & d & ~c )	0	1	0			1	0	0		0		0	0	1		0		0	0	1		0
3	( ~p & d & c )	0	1	1			1	1	1		1		0	0	1		1		0	0	0		1
4	( p & ~d & ~c )	1	0	0			0	0	0		0		1	0	0		1		1	1	1		0
5	(p & ~d & c)	1	0	1			0	0	1		0		1	0	0		0		1	0	0		1
6	( p & d & ~ c )	1	1	0			1	0	0		1		1	1	1		1		1	1	1		0
7	( п и д и с )	1	1	1			1	1	1		1		1	1	1		1		1	0	0		1
																	д

Импредикативные предложения

Учитывая следующие примеры-определения, что можно сделать из последующих рассуждений:

(1) «Это предложение простое». (2) «Это сложное предложение, и оно соединяется с помощью AND».

Затем присвойте переменную «s» самому левому предложению «Это простое предложение». Определите «составное» c = «не простое» ~s и присвойте c = ~s «Это сложное предложение»; присвойте «j» значению «Оно [это предложение] соединено оператором AND». Второе предложение можно выразить так:

(НЕ(ы) И j)

Если значения истинности должны быть помещены в предложения c = ~s и j, то все они явно являются ЛОЖЬЮ: например, «Это сложное предложение» является ЛОЖЬЮ (оно простое по определению). Поэтому их союз (И) — ложь. Но если взять это предложение в собранном виде, это ПРАВДА.

Это пример парадоксов, возникающих в результате непредикативного определения , то есть когда объект m имеет свойство P, но объект m определен в терминах свойства P. Лучший совет для ритора или человека, занимающегося дедуктивным анализом, — избегать неопределенных определений, но в то же время внимательно следить за ними, поскольку они действительно могут создавать парадоксы. С другой стороны, инженеры заставляют их работать в форме пропозициональных формул с обратной связью.

Пропозициональная формула с «обратной связью»

Понятие пропозициональной формулы, появляющейся как одна из своих собственных переменных, требует правила формирования, которое позволяет присваивать формулу переменной. В общем, не существует никаких условий (ни аксиоматических, ни истинностных систем объектов и отношений), которые запрещали бы это.

Самый простой случай возникает, когда формула ИЛИ становится одним из ее собственных входных данных, например, p = q. Начнем с (p ∨ s) = q, затем пусть p = q. Заметьте, что «определение» q зависит от самого «q», а также от «s» и связки ИЛИ; таким образом, это определение q является непредикативным. Любое из двух условий может привести к: колебания или память.

Полезно представить формулу как черный ящик . Без знания того, что происходит «внутри» формулы-«коробки», снаружи может показаться, что результат больше не является функцией только входных данных. То есть иногда кто-то смотрит на q и видит 0, а иногда 1. Чтобы избежать этой проблемы, нужно знать состояние (условие) «скрытой» переменной p внутри блока (т. е. значение q, возвращенное и присвоенное п). Когда это становится известно, кажущееся несоответствие исчезает.

Чтобы понять [предсказать] поведение формул с обратной связью, требуется более сложный анализ последовательных цепей . Пропозициональные формулы с обратной связью в своей простейшей форме приводят к конечным автоматам; они также приводят к воспоминаниям в форме лент Тьюринга и противомашинных счетчиков. Из комбинаций этих элементов можно построить любую ограниченную вычислительную модель (например, машины Тьюринга , счетчиковые машины , регистровые машины , компьютеры Macintosh и т. д.).

Колебания

В абстрактном (идеальном) случае простейшая осциллирующая формула — это НЕ, возвращаемая самому себе: ~(~(p=q)) = q. Анализ абстрактной (идеальной) пропозициональной формулы в таблице истинности обнаруживает несоответствие как для случаев p=1, так и для случаев p=0: когда p=1, q=0, этого не может быть, потому что p=q; то же самое для случаев p=0 и q=1.

		д
п		~	(	п	)	= q
0		1		0		1	вопросы и ответы противоречивы
1		0		1		0	вопросы и ответы противоречивы

Колебания с задержкой : Если задержка (идеальный или неидеальный) вставляется в абстрактную формулу между p и q, тогда p будет колебаться между 1 и 0: 101010...101... до бесконечности . Если задержка и NOT не являются абстрактными (т.е. не идеальными), тип используемого анализа будет зависеть от точной природы объектов, составляющих генератор; такие вещи выходят за рамки математики и относятся к инженерному делу.

Анализ требует вставки задержки, а затем разрыва цикла между задержкой и входом «p». Задержку следует рассматривать как своего рода предложение, в котором «qd» (q-задержка) является выходом, а «q» — входом. Это новое предложение добавляет еще один столбец в таблицу истинности. Теперь несоответствие возникает между «qd» и «p», как показано красным; два устойчивых состояния в результате:

			д
qd	п	(	~	(	п	)	= q
0	0		1		0		1	состояние 1
0	1		0		1		0	qd и p несовместимы
1	0		1		0		1	qd и p несовместимы
1	1		0		1		0	состояние 0

Память

Простейшие результаты памяти возникают, когда выход ИЛИ возвращается к одному из его входов, в данном случае выход «q» возвращается обратно в «p». Следующий простейший вариант — это «триггер», показанный под однократным флипом. Анализ формул такого типа можно выполнить либо путем сокращения пути обратной связи, либо путем добавления (идеальной) задержки в путь. Разрезанный путь и предположение о том, что нигде в «схеме» не происходит никакой задержки, приводят к несогласованности для некоторых общих состояний (комбинация входов и выходов, например (p=0, s=1, r=1), приводит к несогласованности ). При наличии задержки эти несоответствия являются лишь временными и исчезают по истечении срока задержки. Рисунки справа называются диаграммами состояний .

Память с тактовым триггером («c» — это «часы», а «d» — «данные»). Данные могут измениться в любой момент, когда тактовый сигнал c=0; когда тактовый сигнал c=1, выход q «отслеживает» значение данных d. Когда c меняется от 1 до 0, оно «захватывает» значение d = q, и оно продолжает появляться в q, независимо от того, что делает d (пока c остается 0).

Незамедлительно необходимо устранить несоответствия из анализа таблицы истинности. С учетом понятия «задержка» это условие представляет собой мгновенное несоответствие между возвращаемой выходной переменной q и p = q _Delayed .

Таблица истинности показывает строки, в которых возникают несоответствия между p = q, _{задержанным} на входе, и q на выходе. После «разрыва» обратной связи, построение таблицы истинности происходит обычным способом. Но впоследствии в каждой строке выходной сигнал q сравнивается с теперь уже независимым входным сигналом p и отмечаются любые несоответствия между p и q (т. е. p=0 вместе с q=1 или p=1 и q=0); когда «линия» «переделывается», то и то, и другое становится невозможным по Закону противоречия ~(p & ~p)). Строки, обнаруживающие несоответствия, либо считаются переходными состояниями , либо просто исключаются как несогласованные и, следовательно, «невозможные».

Одноразовая память

Что касается простейших результатов памяти, когда выход ИЛИ возвращается к одному из его входов, в этом случае выход «q» возвращается в «p». Учитывая, что формула сначала оценивается (инициализируется) с p=0 и q=0, она «перевернется» один раз, когда «установлена» на s=1. После этого выход «q» будет поддерживать «q» в «перевернутом» состоянии (состояние q=1). Это поведение, теперь зависящее от времени, показано диаграммой состояний справа от однократного переворота.

				д
п	с	(	с	∨	п	)	= q
0	0		0	0	0		0	состояние 0, с=0
0	1		1	1	0			вопросы и ответы противоречивы
1	0		0	1	1		1	состояние 1 с s = 0
1	1		1	1	1		1	состояние 1 с s = 1

Триггерная память

Следующий простейший случай — это триггер «установка-сброс», показанный под однократным триггером. Учитывая, что r=0, s=0 и q=0 вначале, он «устанавливается» (s=1) аналогично однократному перевороту. Однако имеется возможность «сбросить» q=0, когда «r»=1. Дополнительные сложности возникают, если и set=1, и reset=1. В этой формуле set=1 приводит к тому, что выходной сигнал q=1, поэтому, когда и если (s=0 и r=1) триггер будет сброшен. Или, если (s=1 и r=0), триггер будет установлен. В абстрактном (идеальном) случае, когда s=1 ⇒ s=0 и r=1 ⇒ r=0 одновременно, формула q будет неопределенной (неразрешимой). Из-за задержек в «реальном» ИЛИ, И и НЕ результат вначале будет неизвестен, но впоследствии будет предсказуем.

					д
п	с	р	(	с	∨	(	п	&	~	(	р	)	)	)	= q
0	0	0		0	0		0	0	1		0				0	состояние 0 с (s=0 & r=0)
0	0	1		0	0		0	0	0		1				0	состояние 0 с (s=0 и r=1)
0	1	0		1	1		0	0	1		0					вопросы и ответы противоречивы
0	1	1		1	1		0	0	0		1					вопросы и ответы противоречивы
1	0	0		0	1		1	1	1		0				1	состояние 1 с ( s=0 & r=0 )
1	0	1		0	0		1	0	0		1					вопросы и ответы противоречивы
1	1	0		1	1		1	1	1		0				1	состояние 1 с ( s=1 & r=0 )
1	1	1		1	1		1	0	0		1				1	состояние 1 с одновременным включением и отключением 1

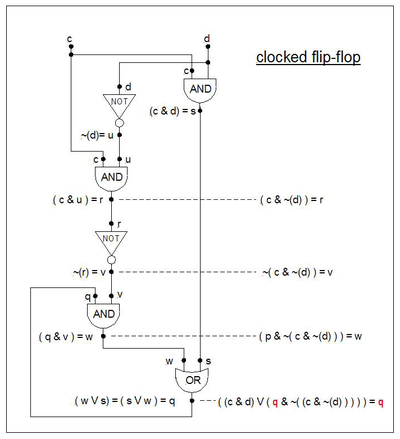
Тактируемая триггерная память

Формула, известная как «тактируемая триггерная» память («c» — это «такты», а «d» — «данные»), приведена ниже. Это работает следующим образом: когда c = 0, данные d (либо 0, либо 1) не могут «пройти», чтобы повлиять на выход q. Когда c = 1, данные d «проходят», а вывод q «следует» за значением d. Когда c изменяется от 1 до 0, последнее значение данных остается «захваченным» на выходе «q». Пока c=0, d может изменять значение, не вызывая изменения q.

• Примеры
  1. ( ( c & d ) ∨ ( p & ( ~( c & ~( d ) ) ) ) = q , но теперь пусть p = q:
  2. ( ( c & d ) ∨ ( q & ( ~( c & ~( d ) ) ) ) знак равно q

Диаграмма состояний по форме похожа на диаграмму состояний триггера, но с другой маркировкой переходов.

							с			д			В	v				р	в
ряд	д	д	с	(	(	с	&	д	)	∨	(	д	&	~	(	(	с	&	~	(	д	)	)	)	)	)	=q	Описание
0	0	0	0			0	0	0		0		0	0	1			0	0	1		0						0	состояние 0 с (s=0 и r=0), 0 захвачен
1	0	0	1			1	0	0		0		0	0	0			1	1	1		0						0	состояние 0 с (d=0 & c=1): q=0 следует за d=0
2	0	1	0			0	0	1		0		0	0	1			0	0	0		1						0	состояние 0 с (d=1 и r=0), 0 захвачен
3	0	1	1			1	1	1		1		0	0	1			1	0	0		1							вопросы и ответы противоречивы
4	1	0	0			0	0	0		1		1	1	1			0	0	1		0						1	состояние 1 с (d =0 и c=0), 1 захвачено
5	1	0	1			1	0	0		0		1	0	0			1	1	1		0							вопросы и ответы противоречивы
6	1	1	0			0	0	1		1		1	1	1			0	0	0		1						1	состояние 1 с (d =1 и c=0), 1 захвачено
7	1	1	1			1	1	1		1		1	1	1			1	0	0		1						1	состояние 1 с (d=1 & c=1): q=1 следует за d=1

Историческое развитие

Бертран Рассел (1912:74) перечисляет три закона мышления, вытекающие из Аристотеля : (1) Закон тождества : «Все, что есть, есть», (2) Закон непротиворечия : «Ничто не может одновременно быть и не быть». и (3) Закон исключенного третьего : «Все должно быть или не быть».

• Пример: Здесь O — выражение о БЫТИИ или КАЧЕСТВЕ объекта:
  1. Закон тождества: O = O
  2. Закон противоречия: ~(O & ~(O))
  3. Закон исключенного третьего: (O ∨ ~(O))

Использование слова «все» в законе исключенного третьего делает формулировку этого закона Расселом открытой для дискуссий. Если ограничиться выражением о БЫТИИ или КАЧЕСТВЕ со ссылкой на конечный набор объектов (конечную «вселенную дискурса»), члены которой могут быть исследованы один за другим на наличие или отсутствие утверждения, тогда закон считается интуиционистски подходящим. Таким образом, утверждение типа: «Этот объект должен либо БЫТЬ, либо НЕ БЫТЬ (в коллекции)» или «Этот объект должен либо иметь это КАЧЕСТВО, либо НЕ иметь этого КАЧЕСТВА (относительно объектов в коллекции)» является приемлемым. Подробнее смотрите на диаграмме Венна .

Хотя исчисление высказываний возникло у Аристотеля, понятие алгебры , применимое к высказываниям, пришлось отложить до начала XIX века. В качестве (неблагоприятной) реакции на 2000-летнюю традицию силлогизмов Аристотеля Джона Локка ( в «Очерке о человеческом понимании» 1690 г.) использовалось слово «семиотика» (теория использования символов). К 1826 году Ричард Уэйтли критически проанализировал силлогистическую логику, сочувствуя семиотике Локка. Работа Джорджа Бентама (1827 г.) привела к появлению понятия «количественной оценки предиката» (1827 г.) (сегодня символизируемого как ∀ ≡ «для всех»). «Ссора», спровоцированная Уильямом Гамильтоном по поводу спора о приоритете с Огастесом Де Морганом , «вдохновила Джорджа Буля изложить свои идеи по логике и опубликовать их как MAL [Математический анализ логики] в 1847 году» (Grattin-Guinness and Bornet 1997). :xxviii).

О его вкладе Грэттин-Гиннесс и Борнет комментируют:

«Главным единственным нововведением Буля был закон [x ^н = x ] для логики: он утверждал, что умственные действия по выбору свойства x и выбору x снова и снова - это то же самое, что выбор x один раз... В результате этого он сформировал уравнения x•(1-x)=0 и x+(1-x)=1, что для него выражало соответственно закон противоречия и закон исключенного третьего» (стр. xxviiff). Для Буля «1» было вселенной дискурса , а «0» было ничем.

Масштабное начинание Готтлоба Фреге (1879 г.) привело к формальному исчислению суждений, но его символика настолько устрашающа, что оказала небольшое влияние, за исключением одного человека: Бертрана Рассела . Сначала, будучи учеником Альфреда Норта Уайтхеда, он изучил работу Фреге и предложил (известную и печально известную) поправку к ней (1904 г.), касающуюся проблемы антиномии , которую он обнаружил в трактовке Фреге (см. парадокс Рассела ). Работа Рассела привела к сотрудничеству с Уайтхедом, в результате которого в 1912 году был выпущен первый том Principia Mathematica (PM). Именно здесь впервые появилось то, что мы считаем «современной» логикой высказываний. В частности, PM вводит НЕ, ИЛИ и символ утверждения ⊦ в качестве примитивов. В терминах этих понятий они определяют ИМПЛИКАЦИЯ → (по определению *1.01: ~p ∨ q), затем И (по определению *3.01: ~(~p ∨ ~q)), затем ЭКВИВАЛЕНТНОСТЬ p ←→ q (*4.01: ( п → q) & ( q → п ) ).

• Генри М. Шеффер (1921) и Жан Никод демонстрируют, что только одна связка - «штрих» | достаточно для выражения всех формул высказываний.
• Эмиль Пост (1921) развивает метод анализа на основе таблицы истинности в своем «Введении в общую теорию элементарных предложений». Он отмечает инсульт Никода | .
• Уайтхед и Рассел добавляют введение к своей переизданию «ПМ» 1927 года, частично добавляя благоприятное отношение к «инсульту».

Логика вычислений и переключения :

• Уильям Экклс и Ф.В. Джордан (1919) описывают «пусковое реле», сделанное из вакуумной лампы.
• Джордж Стибиц (1937) изобретает двоичный сумматор с использованием механических реле. Он строит это на своем кухонном столе.

Пример: Учитывая двоичные биты a _i и b _i и перенос ( c_in _i ), их сумма Σ _i и перенос (c_out _i ) равна:

• ( ( а _я XOR b _я ) XOR c_in _i )= Σ _i
• ( а _я & б _я ) ∨ c_in _я ) знак равно c_out _я ;

• Алан Тьюринг строит множитель с помощью реле (1937–1938). Для этого ему приходится вручную наматывать катушки реле.
• Учебники по «схемам переключения» появляются в начале 1950-х годов.
• Уиллард Куайн (1952 и 1955), Э. Вейтч (1952) и М. Карно (1953) разрабатывают методы карт для упрощения пропозициональных функций.
• Джордж Х. Мили (1955) и Эдвард Ф. Мур (1956) обращаются к теории последовательных (т.е. переключающих схем) «машин».
• Э. Дж. МакКласки и Х. Шорр разрабатывают метод упрощения пропозициональных (переключающих) схем (1962).

Ссылки

• Розенблум, Пол (1950). Элементы математической логики . Минеола, Нью-Йорк: ISBN Dover Publications, Inc.  0-486-44617-4 .
• Клини, Стивен (1952). Введение в метаматематику . Амстердам: Издательство Северной Голландии.
• Бендер, Эдвард А. и Уильямсон, С. Гилл , 2005, Краткий курс дискретной математики , Dover Publications, Минеола, штат Нью-Йорк, ISBN   0-486-43946-1 . Этот текст используется в «двухчетвертном курсе [информатики] для младших классов» в Калифорнийском университете в Сан-Диего.
• Эндертон, Х.Б. , 2002, Математическое введение в логику. Харкорт/Академическая пресса. ISBN   0-12-238452-0
• Гудстейн, Р.Л. , (Pergamon Press, 1963), 1966, (Дуврское издание, 2007 г.), Булева алгебра , Dover Publications, Inc. Минола, Нью-Йорк, ISBN   0-486-45894-6 . Акцент на понятии «алгебра классов» с теоретико-множественными символами, такими как ∩, ∪, ' (НЕ), ⊂ (ПОДРАЗУЕТСЯ). Позже Гольдштейн заменяет их на &, ∨, ￢, → (соответственно) в своей трактовке «Логики предложений», стр. 76–93.
• Айвор Граттан-Гиннесс и Жерар Борне 1997, Джордж Буль: Избранные рукописи по логике и ее философии , Биркхойзер Верлаг, Бэзил, ISBN   978-0-8176-5456-6 (Бостон).
• А.Г. Гамильтон, 1978, Логика для математиков , Издательство Кембриджского университета, Кембридж, Великобритания, ISBN   0-521-21838-1 .
• Э. Дж. МакКласки , 1965, «Введение в теорию коммутационных цепей» , издательство McGraw-Hill Book Company, Нью-Йорк. Нет ISBN. Номер карточки каталога Библиотеки Конгресса 65-17394. Маккласки был учеником Уилларда Куайна и разработал несколько известных теорем вместе с Куайном и самостоятельно. Для тех, кто интересуется историей, книга содержит множество ссылок.
• Марвин Л. Мински, 1967, Вычисления: конечные и бесконечные машины , Prentice-Hall, Inc, Энглвуд Клиффс, Нью-Джерси. Нет ISBN. Номер карточки каталога Библиотеки Конгресса 67-12342. Полезно, особенно для вычислимости, плюс хорошие источники.
• Джоэл В. Роббин , 1969, 1997, Математическая логика: первый курс , Dover Publications, Inc., Минеола, Нью-Йорк, ISBN   0-486-45018-X (пбк.).
• Патрик Суппес 1957 (Дуврское издание 1999 г.), Введение в логику , Dover Publications, Inc., Минеола, Нью-Йорк. ISBN   0-486-40687-3 (пбк.). Эта книга издана и легко доступна.
• На своей странице 204 в сноске он ссылается на свой набор аксиом на EV Huntington , «Sets of Independent Postulats for the Algebra of Logic», Transactions of the American Mathematical Society , Vol. 5 91904) стр. 288-309.
• Альфред Тарский , 1941 (издание в Дувре, 1995 г.), «Введение в логику и методологию дедуктивных наук» , Dover Publications, Inc., Минеола, Нью-Йорк. ISBN   0-486-28462-X (пбк.). Эта книга издана и легко доступна.
• Жан ван Хейеноорт, 1967, 3-е издание с поправками 1976 г., От Фреге до Гёделя: справочник по математической логике, 1879–1931 , издательство Гарвардского университета, Кембридж, Массачусетс. ISBN   0-674-32449-8 (pbk.) Перевод/перепечатки Фреге (1879 г.), письма Рассела Фреге (1902 г.) и письма Фреге Расселу (1902 г.), Парадокса Ричарда (1905 г.), Поста (1921 г.) можно найти. здесь.
• Альфред Норт Уайтхед и Бертран Рассел, 1927 г., 2-е издание, издание в мягкой обложке до * 53, 1962 г., Principia Mathematica , Cambridge University Press, без ISBN. В период между первым изданием 1912 года и вторым изданием 1927 года Его Величество Шеффер ( 1921) и Жан Никод (год не указан) обратили внимание Рассела и Уайтхеда на то, что то, что они считали своими примитивными пропозициями (связками), можно свести к одиночный |, ныне известный как «штрих» или И-НЕ (НЕ-И, НИ… НИ…). Рассел-Уайтхед обсуждает это в своем «Введении ко второму изданию» и дает определения, обсуждавшиеся выше.
• Уильям Э. Уикс 1968, Логическое проектирование с помощью интегральных микросхем , John Wiley & Sons, Inc., Нью-Йорк. Нет ISBN. Номер карточки каталога Библиотеки Конгресса: 68-21185. Подробное изложение методов инженерного анализа и синтеза, см. МакКласки, 1965. В отличие от Суппеса, изложение «булевой алгебры» Уиккса начинается с набора постулатов, имеющих характер таблицы истинности, а затем выводит из них обычные теоремы (стр. 18 и далее).

Внешние ссылки

• СМИ, связанные с пропозициональной формулой, на Викискладе?