Теория Янга – Миллса

Нерешенная задача по физике :

Теория Янга – Миллса и разрыв масс. Квантовые частицы, описываемые теорией, имеют массу, но классические волны поля движутся со скоростью света. ^[1]

(еще нерешенные задачи по физике)

Теория Янга-Миллса — это квантовая теория поля ядерной связи, разработанная Чэнь Нин Яном и Робертом Миллсом в 1953 году, а также общий термин для класса подобных теорий. Теория Янга-Миллса — это калибровочная теория, основанная на специальной унитарной группе $SU(n)$ или, в более общем смысле, на любой компактной группе Ли . Теория Янга-Миллса стремится описать поведение элементарных частиц с использованием этих неабелевых групп Ли и лежит в основе объединения электромагнитного взаимодействия и слабых взаимодействий (т.е. $U(1) \times SU(2)$ ), а также квантовая хромодинамика , теория сильного взаимодействия (на основе $SU(3)$ ). Таким образом, это составляет основу понимания Стандартной модели физики элементарных частиц.

История и качественное описание

Калибровочная теория в электродинамике

Все известные фундаментальные взаимодействия можно описать с помощью калибровочных теорий, но на их разработку ушли десятилетия. ^[2] Новаторская работа Германа Вейля над этим проектом началась в 1915 году, когда его коллега Эмми Нётер доказала, что каждая сохраняющаяся физическая величина имеет соответствующую симметрию, и завершилась в 1928 году, когда он опубликовал свою книгу, применяющую геометрическую теорию симметрии ( теорию групп ) к квантовой механике. . ^[3]^: 194 Вейль назвал соответствующую симметрию в теореме Нётер «калибровочной симметрией» по аналогии со стандартизацией расстояний в железнодорожных колеях .

Эрвин Шредингер в 1922 году, за три года до работы над своим уравнением, связал концепцию группы Вейля с зарядом электрона. Шрёдингер показал, что группа $U(1)$ произвел фазовый сдвиг $e^{i\theta }$ в электромагнитных полях, соответствующих закону сохранения электрического заряда. ^[3]^: 198 По мере развития теории квантовой электродинамики в 1930-х и 1940-х годах $U(1)$ групповые трансформации играли центральную роль. Многие физики считали, что должен быть аналог динамики нуклонов. Чэнь Нин Ян особенно был одержим этой возможностью.

Ян и Миллс открывают калибровочную теорию ядерной силы

Основная идея Янга заключалась в том, чтобы найти в ядерной физике сохраняющуюся величину, сравнимую с электрическим зарядом, и использовать ее для разработки соответствующей калибровочной теории, сравнимой с электродинамикой. Он остановился на сохранении изоспина — квантового числа, которое отличает нейтрон от протона, но не добился прогресса в теории. ^[3]^: 200 Летом 1953 года, отдыхая от Принстона, Ян встретил сотрудника, который мог помочь: Роберта Миллса . Как описывает сам Миллс:

«В течение 1953–1954 учебного года Ян был посетителем Брукхейвенской национальной лаборатории ... Я тоже был в Брукхейвене... и был назначен в тот же офис, что и Ян. Ян, который неоднократно демонстрировал свою щедрость. физикам, начинающим свою карьеру, рассказал мне о своей идее обобщения калибровочной инвариантности, и мы довольно подробно обсудили ее ... Я смог внести кое-что в дискуссии, особенно в отношении процедур квантования, и в небольшой степени в работе однако, несмотря на формализм, ключевые идеи принадлежали Яну». ^[4]

Летом 1953 года Ян и Миллс расширили концепцию калибровочной теории для абелевых групп , например квантовой электродинамики , на неабелевы группы, выбрав группу $SU(2)$ дать объяснение сохранению изоспина при столкновениях с сильными взаимодействиями. Презентация работы Янга в Принстоне в феврале 1954 года была подвергнута сомнению Паули, задав вопрос о массе в поле, разработанной с помощью идеи калибровочной инвариантности. ^[3]^: 202 Паули знал, что это может быть проблемой, поскольку он работал над применением калибровочной инвариантности, но решил не публиковать ее, рассматривая безмассовые возбуждения теории как «нефизические «теневые частицы»». ^[2]^: 13 Ян и Миллс опубликованы в октябре 1954 года; ближе к концу статьи они признаются:

Далее мы подошли к вопросу о массе $b$ квант, на который у нас нет удовлетворительного ответа. ^[5]

Эта проблема нефизического безмассового возбуждения блокировала дальнейший прогресс. ^[3]

концепция частиц, приобретающих массу посредством нарушения симметрии Идея была отложена до 1960 года, когда была выдвинута в безмассовых теориях, первоначально Джеффри Голдстоуном , Йоитиро Намбу и Джованни Йона-Лазинио . Это побудило к значительному возобновлению исследований теории Янга-Миллса, которые оказались успешными в формулировке как электрослабого объединения , так и квантовой хромодинамики (КХД). Электрослабое взаимодействие описывается калибровочной группой $SU(2) \times U(1)$ , а КХД представляет собой $SU(3)$ -теорию Янга – Миллса. Безмассовые калибровочные бозоны электрослабого $SU(2) \times U(1)$ после спонтанного нарушения симметрии смешиваются с образованием трех массивных слабых бозонов ( $В +$ , $В -$ , и $С 0$ ), а также еще безмассовое фотонное поле. Динамика поля фотонов и его взаимодействие с веществом, в свою очередь, определяются $калибровочной теорией U(1)$ квантовой электродинамики. Стандартная модель объединяет сильное взаимодействие с единым электрослабым взаимодействием (объединяющим слабое и электромагнитное взаимодействие ) через группу симметрии $SU(3) \times SU(2) \times U(1)$ . В современную эпоху сильное взаимодействие не объединяется с электрослабым взаимодействием, но на основании наблюдаемого хода констант связи считается, что ^{[ нужна ссылка ]} все они сходятся к одному значению при очень высоких энергиях.

Феноменология при более низких энергиях в квантовой хромодинамике до конца не изучена из-за трудностей управления такой теорией с сильной связью. Это может быть причиной того, что удержание не было теоретически доказано, хотя это последовательное экспериментальное наблюдение. Это показывает, почему удержание КХД при низких энергиях является очень актуальной математической проблемой и почему проблема существования Янга-Миллса и проблема запрещения масс является проблемой Премии тысячелетия .

Параллельная работа над неабелевыми калибровочными теориями.

В 1953 году в частной переписке Вольфганг Паули сформулировал шестимерную теорию уравнений поля Эйнштейна общей теории относительности , распространив пятимерную теорию Калуцы, Клейна , Фока и других на многомерное внутреннее пространство. ^[6] Однако нет никаких свидетельств того, что Паули разработал лагранжиан калибровочного поля или его квантование. Поскольку Паули обнаружил, что его теория «приводит к некоторым довольно нефизическим теневым частицам», он воздержался от официальной публикации своих результатов. ^[6] Хотя Паули не опубликовал свою шестимерную теорию, он прочитал по ней две лекции на семинаре в Цюрихе в ноябре 1953 года. ^[6]

В январе 1954 года Рональд Шоу, аспирант Кембриджского университета, также разработал неабелеву калибровочную теорию ядерных сил. ^[7]Однако для сохранения калибровочной инвариантности теории нужны были безмассовые частицы . Поскольку в то время такие безмассовые частицы не были известны, Шоу и его руководитель Абдус Салам решили не публиковать свою работу. ^[7]Вскоре после того, как Ян и Миллс опубликовали свою статью в октябре 1954 года, Салам призвал Шоу опубликовать свою работу, чтобы отметить его вклад. Шоу отказался, и вместо этого это лишь глава его докторской диссертации, опубликованной в 1956 году. ^[8]^[9]

Математический обзор

Д

​ х 1 \otimes σ 3

коэффициент BPST-инстантона на

(x 1, х 2)

-кусочек

ℝ 4

где

σ 3

— третья матрица Паули (вверху слева). Д

​ х 2 \otimes коэффициент σ 3

(вверху справа). Эти коэффициенты определяют ограничение инстантона

A

BPST с

g =2, ρ =1, z =0

на этот срез. Соответствующая напряженность поля сосредоточена вокруг

z = 0

(внизу слева). Визуальное представление напряженности поля BPST-инстантона с центром

z

на компактификации

S 4

из

ℝ 4

(внизу справа). Инстантон BPST представляет собой классическое инстантонное решение уравнений Янга – Миллса на

ℝ 4

.

Теории Янга – Миллса являются особыми примерами калибровочных теорий с неабелевой группой симметрии, заданной лагранжианом

\ {\mathcal {L}}_{\mathrm {gf} }=-{\tfrac {1}{2}}\operatorname {tr} (F^{2})=-{\tfrac {1}{4}}F^{a\mu \nu }F_{\mu \nu }^{a}\

с генераторами $\ T^{a}\$ алгебры Ли с индексом $a$ , соответствующей $F$ -величинам ( форме кривизны или напряженности поля), удовлетворяющим

\ \operatorname {tr} \left(T^{a}\ T^{b}\right)={\tfrac {1}{2}}\delta ^{ab}\ ,\qquad \left[T^{a},\ T^{b}\right]=i\ f^{abc}\ T^{c}~.

Здесь $ф абв$ являются структурными константами алгебры Ли (полностью антисимметричны, если генераторы алгебры Ли нормализованы так, что $\ \operatorname {tr} (T^{a}\ T^{b})\$ пропорционально $\ \delta ^{ab}\$ ), ковариантная производная определяется как

\ D_{\mu }=I\ \partial _{\mu }-i\ g\ T^{a}\ A_{\mu }^{a}\ ,

$I$ — единичная матрица (соответствующая размеру генераторов), $\ A_{\mu }^{a}\$ — векторный потенциал, а $g$ — константа связи . В четырех измерениях константа связи $g$ представляет собой чистое число, а для $группы SU(n)$ она имеет $\ a,b,c=1\ldots n^{2}-1~.$

Отношение

\ F_{\mu \nu }^{a}=\partial _{\mu }A_{\nu }^{a}-\partial _{\nu }A_{\mu }^{a}+g\ f^{abc}\ A_{\mu }^{b}\ A_{\nu }^{c}\

можно получить с помощью коммутатора

\ \left[D_{\mu },D_{\nu }\right]=-i\ g\ T^{a}\ F_{\mu \nu }^{a}~.

Поле обладает свойством самодействия, и получаемые уравнения движения называются полулинейными, поскольку нелинейности бывают как с производными, так и без них. Это означает, что управлять этой теорией можно только с помощью теории возмущений с малыми нелинейностями. ^{[ нужна ссылка ]}

Обратите внимание, что переход между «верхними» («контравариантными») и «нижними» («ковариантными») компонентами вектора или тензора тривиален для индексов (например, $\ f^{abc}=f_{abc}\$ ), тогда как для µ и ν оно нетривиально и соответствует, например, обычной сигнатуре Лоренца, $\ \eta _{\mu \nu }={\rm {diag}}(+---)~.$

Из данного лагранжиана можно вывести уравнения движения, заданные формулой

\ \partial ^{\mu }F_{\mu \nu }^{a}+g\ f^{abc}\ A^{\mu b}\ F_{\mu \nu }^{c}=0~.

положить $\ F_{\mu \nu }=T^{a}F_{\mu \nu }^{a}\ ,$ их можно переписать как

\ \left(D^{\mu }F_{\mu \nu }\right)^{a}=0~.

Тождество Бьянки сохраняется

\ \left(D_{\mu }\ F_{\nu \kappa }\right)^{a}+\left(D_{\kappa }\ F_{\mu \nu }\right)^{a}+\left(D_{\nu }\ F_{\kappa \mu }\right)^{a}=0\

что эквивалентно тождеству Якоби

\ \left[D_{\mu },\left[D_{\nu },D_{\kappa }\right]\right]+\left[D_{\kappa },\left[D_{\mu },D_{\nu }\right]\right]+\left[D_{\nu },\left[D_{\kappa },D_{\mu }\right]\right]=0\

с $\ \left[D_{\mu },F_{\nu \kappa }^{a}\right]=D_{\mu }\ F_{\nu \kappa }^{a}~.$ Определите тензор двойной силы $\ {\tilde {F}}^{\mu \nu }={\tfrac {1}{2}}\varepsilon ^{\mu \nu \rho \sigma }F_{\rho \sigma }\ ,$ то тождество Бьянки можно переписать как

\ D_{\mu }{\tilde {F}}^{\mu \nu }=0~.

Источник $\ J_{\mu }^{a}\$ входит в уравнения движения как

\ \partial ^{\mu }F_{\mu \nu }^{a}+g\ f^{abc}\ A^{b\mu }\ F_{\mu \nu }^{c}=-J_{\nu }^{a}~.

Обратите внимание, что токи должны правильно меняться при преобразованиях калибровочной группы.

Приведем некоторые комментарии о физических размерах муфты. В $измерениях D$ поле масштабируется как $\ \left[A\right]=\left[L^{\left({\tfrac {2-D}{2}}\right)}\right]\$ и поэтому связь должна масштабироваться как $\ \left[g^{2}\right]=\left[L^{\left(D-4\right)}\right]~.$ Это означает, что теория Янга – Миллса не перенормируема для размерностей больше четырех. Кроме того, при $D = 4$ связь безразмерна, и как поле, так и площадь связи имеют одинаковые размерности поля и связи безмассовой квартической скалярной теории поля . Итак, эти теории разделяют масштабную инвариантность на классическом уровне.

Квантование

Метод квантования теории Янга – Миллса заключается в использовании функциональных методов, то есть интегралов по путям . вводится $Производящий функционал для n$ -точечных функций как

\ Z[j]=\int [\mathrm {d} A]\ \exp \left[-{\tfrac {i}{2}}\int \mathrm {d} ^{4}x\ \operatorname {tr} \left(F^{\mu \nu }\ F_{\mu \nu }\right)+i\ \int \mathrm {d} ^{4}x\ j_{\mu }^{a}(x)\ A^{a\mu }(x)\right]\ ,

но этот интеграл не имеет никакого смысла, поскольку потенциальный вектор может быть выбран произвольно из-за калибровочной свободы . Эта проблема уже была известна в квантовой электродинамике, но здесь становится более серьезной из-за неабелевых свойств калибровочной группы. Выход был дан Людвигом Фаддеевым и Виктором Поповым с введением призрачного поля (см. призрак Фаддеева–Попова ), обладающего свойством нефизичности, поскольку оно хотя и согласуется со статистикой Ферми–Дирака , но представляет собой комплексное скалярное поле. , что нарушает теорему о спин-статистике . Итак, мы можем записать производящий функционал как

{\begin{aligned}Z[j,{\bar {\varepsilon }},\varepsilon ]&=\int [\mathrm {d} \ A][\mathrm {d} \ {\bar {c}}][\mathrm {d} \ c]\ \exp {\Bigl \{}i\ S_{F}\ \left[\partial A,A\right]+i\ S_{gf}\left[\partial A\right]+i\ S_{g}\left[\partial c,\partial {\bar {c}},c,{\bar {c}},A\right]{\Bigr \}}\\&\exp \left\{i\int \mathrm {d} ^{4}x\ j_{\mu }^{a}(x)A^{a\mu }(x)+i\int \mathrm {d} ^{4}x\ \left[{\bar {c}}^{a}(x)\ \varepsilon ^{a}(x)+{\bar {\varepsilon }}^{a}(x)\ c^{a}(x)\right]\right\}\end{aligned}}

существование

S_{F}=-{\tfrac {1}{2}}\int \mathrm {d} ^{4}x\ \operatorname {tr} \left(F^{\mu \nu }\ F_{\mu \nu }\right)\

для поля,

S_{gf}=-{\frac {1}{2\xi }}\int \mathrm {d} ^{4}x\ (\partial \cdot A)^{2}\

для крепления манометра и

\ S_{g}=-\int \mathrm {d} ^{4}x\ \left({\bar {c}}^{a}\ \partial _{\mu }\partial ^{\mu }c^{a}+g\ {\bar {c}}^{a}\ f^{abc}\ \partial _{\mu }\ A^{b\mu }\ c^{c}\right)\

для призрака. Это выражение обычно используется для вывода правил Фейнмана (см. диаграмму Фейнмана ). Здесь у нас есть $c а$ для призрачного поля, а $ξ$ фиксирует выбор калибровки для квантования. Правила Фейнмана, полученные из этого функционала, следующие:

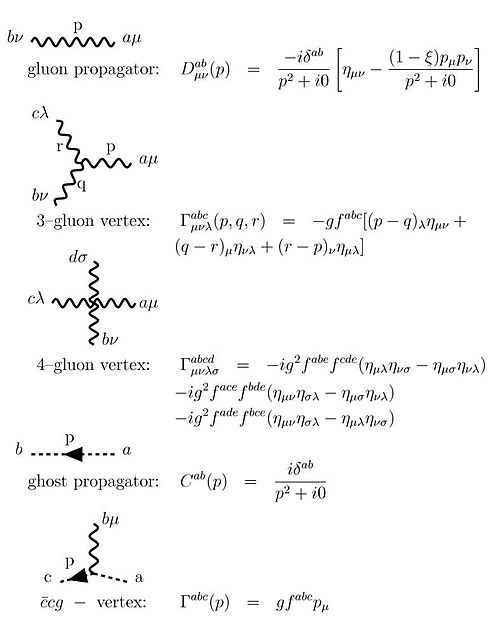
Эти правила для диаграмм Фейнмана можно получить, если переписать приведенный выше производящий функционал в виде

{\begin{aligned}Z[j,{\bar {\varepsilon }},\varepsilon ]&=\exp \left(-i\ g\int \mathrm {d} ^{4}x\ {\frac {\delta }{i\ \delta \ {\bar {\varepsilon }}^{a}(x)}}\ f^{abc}\partial _{\mu }\ {\frac {i\ \delta }{\delta \ j_{\mu }^{b}(x)}}\ {\frac {i\ \delta }{\delta \ \varepsilon ^{c}(x)}}\right)\\&\qquad \times \exp \left(-i\ g\int \mathrm {d} ^{4}x\ f^{abc}\partial _{\mu }{\frac {i\ \delta }{\delta \ j_{\nu }^{a}(x)}}{\frac {i\ \delta }{\delta \ j_{\mu }^{b}(x)}}\ {\frac {i\ \delta }{\delta \ j^{c\nu }(x)}}\right)\\&\qquad \qquad \times \exp \left(-i\ {\frac {g^{2}}{4}}\int \mathrm {d} ^{4}x\ f^{abc}\ f^{ars}{\frac {i\ \delta }{\delta \ j_{\mu }^{b}(x)}}\ {\frac {i\ \delta }{\delta \ j_{\nu }^{c}(x)}}\ {\frac {\ i\delta }{\delta \ j^{r\mu }(x)}}{\frac {i\ \delta }{\delta \ j^{s\nu }(x)}}\right)\\&\qquad \qquad \qquad \times Z_{0}[j,{\bar {\varepsilon }},\varepsilon ]\end{aligned}}

с

Z_{0}[j,{\bar {\varepsilon }},\varepsilon ]=\exp \left(-\int \mathrm {d} ^{4}x\ \mathrm {d} ^{4}y\ {\bar {\varepsilon }}^{a}(x)\ C^{ab}(x-y)\ \varepsilon ^{b}(y)\right)\exp \left({\tfrac {1}{2}}\int \mathrm {d} ^{4}x\ \mathrm {d} ^{4}y\ j_{\mu }^{a}(x)\ D^{ab\mu \nu }(x-y)\ j_{\nu }^{b}(y)\right)\

являющийся производящим функционалом свободной теории. Разлагая по $g$ и вычисляя функциональные производные , мы можем получить все $n$ -точечные функции с помощью теории возмущений. Используя формулу сокращения LSZ, мы получаем из $n$ -точечных функций соответствующие амплитуды процесса, сечения и скорости затухания . Теория перенормируема, а поправки конечны при любом порядке теории возмущений.

Для квантовой электродинамики призрачное поле отделяется, поскольку калибровочная группа абелева. Это можно видеть из связи между калибровочным полем и призрачным полем, которое $\ {\bar {c}}^{a}\ f^{abc}\ \partial _{\mu }A^{b\mu }\ c^{c}~.$ В абелевом случае все структурные константы $\ f^{abc}\$ равны нулю, поэтому связи нет. В неабелевом случае призрачное поле оказывается полезным способом переписать квантовую теорию поля без физических последствий для наблюдаемых теории, таких как сечения или скорости распада.

Одним из наиболее важных результатов, полученных в теории Янга–Миллса, является асимптотическая свобода . Этот результат можно получить, если предположить, что константа связи $g$ мала (так малы нелинейности), как и для высоких энергий, и применить теорию возмущений . Актуальность этого результата обусловлена тем, что теория Янга-Миллса, описывающая сильное взаимодействие и асимптотическую свободу, позволяет правильно трактовать экспериментальные результаты, полученные в результате глубоконеупругого рассеяния .

Чтобы получить поведение теории Янга–Миллса при высоких энергиях и, таким образом, доказать асимптотическую свободу, применяется теория возмущений, предполагающая малую связь. Это проверено апостериорно в ультрафиолетовом пределе . В противоположном пределе, инфракрасном пределе, ситуация противоположная, поскольку связь слишком велика, чтобы теория возмущений была надежной. Большинство трудностей, с которыми сталкиваются исследования, связаны с управлением теорией при низких энергиях. Это интересный случай, присущий описанию адронной материи и, в более общем плане, всем наблюдаемым связанным состояниям глюонов и кварков и их удержанию (см. Адроны ). Наиболее используемый метод изучения теории в этом пределе — попытаться решить ее на компьютерах (см. Теорию калибровочной решетки ). В этом случае необходимы большие вычислительные ресурсы, чтобы быть уверенным в получении правильного предела бесконечного объема (меньшего шага решетки). Это предел, с которым необходимо сравнивать результаты. Меньшее расстояние и большая связь не являются независимыми друг от друга, и для каждого из них необходимы более крупные вычислительные ресурсы. На сегодняшний день ситуация выглядит несколько удовлетворительной для адронного спектра и расчета глюонных и духовых пропагаторов, но Спектры глюбола и гибридов пока остаются под вопросом ввиду экспериментального наблюдения таких экзотических состояний. Действительно, $σ-$ резонанс ^[10]^[11]не наблюдается ни в одном из таких расчетов решетки, и были выдвинуты противоположные интерпретации. Это горячо обсуждаемый вопрос.

Открытые проблемы

Теории Янга-Миллса получили общее признание в физическом сообществе после того, как Джерард 'т Хофт в 1972 году разработал их перенормировку, опираясь на формулировку проблемы, разработанную его советником Мартинусом Вельтманом . ^[12]Перенормируемость получается, даже если калибровочные бозоны, описываемые этой теорией, являются массивными, как в электрослабой теории, при условии, что масса является лишь «приобретенной» массой, порожденной механизмом Хиггса .

были найдены инварианты дифференцируемых структур на четырехмерных многообразиях Математика теории Янга-Миллса является очень активной областью исследований, в которой, например, благодаря работам Саймона Дональдсона . Кроме того, область теорий Янга-Миллса была включена в » Института математики Клея список « Задачи премии тысячелетия . Здесь задача-приз состоит, в частности, в доказательстве гипотезы о том, что низшие возбуждения чистой теории Янга–Миллса (т. е. без полей материи) имеют конечную разницу масс по отношению к вакуумному состоянию. Другая открытая проблема, связанная с этой гипотезой, — доказательство свойства конфайнмента в присутствии дополнительных фермионов.

В физике обзор теорий Янга – Миллса обычно начинается не с анализа возмущений или аналитических методов, а в последнее время с систематического применения численных методов к калибровочным теориям решетки .

См. также

Ссылки

^ «Янг-Миллс и разрыв в массах» . Математический институт Клея . Проверено 9 апреля 2024 г.
^ Jump up to: Перейти обратно: ^а ^б О'Рейфертай, Лохлайнн; Штрауманн, Норберт (1 января 2000 г.). «Калибровочная теория: историческое происхождение и некоторые современные разработки» . Обзоры современной физики . 72 (1): 1–23. дои : 10.1103/RevModPhys.72.1 . ISSN 0034-6861 .
^ Jump up to: Перейти обратно: ^а ^б ^с ^д ^и Бэгготт, Дж. Э. (2013). Квантовая история: история за 40 мгновений (Впечатление: 3-е изд.). Оксфорд: Оксфордский университет. Нажимать. ISBN 978-0-19-956684-6 .
^ Грей, Джереми; Уилсон, Робин (6 декабря 2012 г.). Математические беседы: выборки из журнала Mathematical Intelligencer . Springer Science & Business Media. п. 63. ИСБН 9781461301950 – через Google Книги.
^ Ян, Китай ; Миллс, Р. (1954). «Сохранение изотопического спина и изотопической калибровочной инвариантности» . Физический обзор . 96 (1): 191–195. Бибкод : 1954PhRv...96..191Y . дои : 10.1103/PhysRev.96.191 .
^ Jump up to: Перейти обратно: ^а ^б ^с Штрауманн, Н. (2000). «Об изобретении Паули неабелевой теории Калуцы-Клейна в 1953 году». arXiv : gr-qc/0012054 .
^ Jump up to: Перейти обратно: ^а ^б Атья, М. (2017). «Рональд Шоу 1929–2016 Майкла Атьи (1954)» . Годовой отчет Тринити-колледжа (памятник). 2017 : 137–146.
^ Шоу, Рональд (сентябрь 1956 г.). Проблема типов частиц и другие вклады в теорию элементарных частиц (кандидатская диссертация). Кембриджский университет . гл. 3, стр. 34–46.
^ Фрейзер, Гордон (2008). Космический гнев: Абдус Салам – первый учёный-мусульманин, получивший Нобелевскую премию . Оксфорд, Великобритания: Издательство Оксфордского университета. п. 117. ИСБН 978-0199208463 .
^ Каприни, И.; Коланджело, Дж.; Лейтвайлер, Х. (2006). «Масса и ширина низшего резонанса в КХД». Письма о физических отзывах . 96 (13): 132001. arXiv : hep-ph/0512364 . Бибкод : 2006PhRvL..96m2001C . doi : 10.1103/PhysRevLett.96.132001 . ПМИД 16711979 . S2CID 42504317 .
^ Индурайн, Ф.Дж.; Гарсиа-Мартин, Р.; Пелаес, младший (2007). «Экспериментальный статус изоскалярной S-волны ππ при низкой энергии: $полюс f$ ₀ (600) и длина рассеяния». Физический обзор D . 76 (7): 074034. arXiv : hep-ph/0701025 . Бибкод : 2007PhRvD..76g4034G . дои : 10.1103/PhysRevD.76.074034 . S2CID 119434312 .
^ 'т Хоофт, Г .; Вельтман, М. (1972). «Регуляризация и перенормировка калибровочных полей» . Ядерная физика Б . 44 (1): 189–213. Бибкод : 1972НуФБ..44..189Т . дои : 10.1016/0550-3213(72)90279-9 . hdl : 1874/4845 .

Дальнейшее чтение

Книги

Фрэмптон, П. (2008). Теории калибровочного поля (3-е изд.). Вайли-ВЧ . ISBN 978-3-527-40835-1 .
Ченг, Т.-П.; Ли, Л.-Ф. (1983). Калибровочная теория физики элементарных частиц . Издательство Оксфордского университета . ISBN 0-19-851961-3 .
'т Хоофт, Г. , изд. (2005). 50 лет теории Янга-Миллса . Сингапур: World Scientific . ISBN 981-238-934-2 .

Статьи

Светличный, Георгий (1999). «Подготовка к калибровочной теории». arXiv : math-ph/9902027 .
Гросс, Д. (1992). «Теория калибровки – прошлое, настоящее и будущее» . Проверено 5 мая 2015 г.

Внешние ссылки

«Поле Янга-Миллса» , Математическая энциклопедия , EMS Press , 2001 [1994]
«Теория Янга – Миллса» . Дисперсионная Вики . Архивировано из оригинала 3 июня 2021 г. Проверено 30 августа 2018 г.
«Проблемы премии тысячелетия» . Клея Математический институт . Архивировано из оригинала 16 января 2009 г. Проверено 24 ноября 2008 г.

[1] «Янг-Миллс и разрыв в массах» . Математический институт Клея . Проверено 9 апреля 2024 г.

[oraifearthagh-2] Jump up to: Перейти обратно: ^а ^б О'Рейфертай, Лохлайнн; Штрауманн, Норберт (1 января 2000 г.). «Калибровочная теория: историческое происхождение и некоторые современные разработки» . Обзоры современной физики . 72 (1): 1–23. дои : 10.1103/RevModPhys.72.1 . ISSN 0034-6861 .

[Baggott40-3] Jump up to: Перейти обратно: ^а ^б ^с ^д ^и Бэгготт, Дж. Э. (2013). Квантовая история: история за 40 мгновений (Впечатление: 3-е изд.). Оксфорд: Оксфордский университет. Нажимать. ISBN 978-0-19-956684-6 .

[4] Грей, Джереми; Уилсон, Робин (6 декабря 2012 г.). Математические беседы: выборки из журнала Mathematical Intelligencer . Springer Science & Business Media. п. 63. ИСБН 9781461301950 – через Google Книги.

[YM-5] Ян, Китай ; Миллс, Р. (1954). «Сохранение изотопического спина и изотопической калибровочной инвариантности» . Физический обзор . 96 (1): 191–195. Бибкод : 1954PhRv...96..191Y . дои : 10.1103/PhysRev.96.191 .

[Straumann-6] Jump up to: Перейти обратно: ^а ^б ^с Штрауманн, Н. (2000). «Об изобретении Паули неабелевой теории Калуцы-Клейна в 1953 году». arXiv : gr-qc/0012054 .

[shaw-7] Jump up to: Перейти обратно: ^а ^б Атья, М. (2017). «Рональд Шоу 1929–2016 Майкла Атьи (1954)» . Годовой отчет Тринити-колледжа (памятник). 2017 : 137–146.

[8] Шоу, Рональд (сентябрь 1956 г.). Проблема типов частиц и другие вклады в теорию элементарных частиц (кандидатская диссертация). Кембриджский университет . гл. 3, стр. 34–46.

[9] Фрейзер, Гордон (2008). Космический гнев: Абдус Салам – первый учёный-мусульманин, получивший Нобелевскую премию . Оксфорд, Великобритания: Издательство Оксфордского университета. п. 117. ИСБН 978-0199208463 .

[ccl-10] Каприни, И.; Коланджело, Дж.; Лейтвайлер, Х. (2006). «Масса и ширина низшего резонанса в КХД». Письма о физических отзывах . 96 (13): 132001. arXiv : hep-ph/0512364 . Бибкод : 2006PhRvL..96m2001C . doi : 10.1103/PhysRevLett.96.132001 . ПМИД 16711979 . S2CID 42504317 .

[ygp-11] Индурайн, Ф.Дж.; Гарсиа-Мартин, Р.; Пелаес, младший (2007). «Экспериментальный статус изоскалярной S-волны ππ при низкой энергии: $полюс f$ ₀ (600) и длина рассеяния». Физический обзор D . 76 (7): 074034. arXiv : hep-ph/0701025 . Бибкод : 2007PhRvD..76g4034G . дои : 10.1103/PhysRevD.76.074034 . S2CID 119434312 .

[12] 'т Хоофт, Г .; Вельтман, М. (1972). «Регуляризация и перенормировка калибровочных полей» . Ядерная физика Б . 44 (1): 189–213. Бибкод : 1972НуФБ..44..189Т . дои : 10.1016/0550-3213(72)90279-9 . hdl : 1874/4845 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]