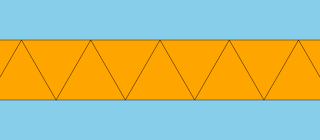
Апейрогональная призма

Апейрогональная призма
Тип	Полурегулярная черепица
Конфигурация вершин	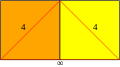4.4.∞
Символ Шлефли	т{2,∞}
Символ Витхоффа	2 ∞ | 2
Диаграмма Кокстера
Симметрия	[∞,2], (*∞22)
Симметрия вращения	[∞,2] + , (∞22)
Аббревиатура Бауэрса	Азип
Двойной	Апейрогональная бипирамида
Характеристики	Вершинно-транзитивный

В геометрии апейрогональная призма или бесконечная призма — арифметический предел семейства призм ; его можно рассматривать как бесконечный многогранник или замощение плоскости.

Торольд Госсет назвал это двумерной полупроверкой , похожей на одну строку шахматной доски .

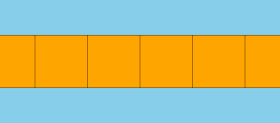
Если стороны квадратные , это равномерная мозаика . Если раскрасить два набора чередующихся квадратов, он все равно будет однородным.

• 
  Вариант униформы с квадратными гранями чередующихся цветов.
• 
  Его двойная мозаика представляет собой апейрогональную бипирамиду .

Связанные мозаики и многогранники

Апейрогональное замощение является арифметическим пределом семейства призм t{2, p } или p .4.4, поскольку p стремится к бесконечности , тем самым превращая призму в евклидово замощение.

Операция чередования может создать апейрогональную антипризму, состоящую из трех треугольников и одного апейрогона в каждой вершине.

Подобно однородным многогранникам и однородным мозаикам , восемь однородных мозаик могут быть основаны на правильной аперогональной мозаике . Выпрямленные усеченная и согнутые формы дублируются, а так как дважды бесконечность также является бесконечностью, то и всеусеченная формы также дублируются, поэтому количество уникальных форм сокращается до четырех: апейрогональная мозаика, апейрогональный осоэдр, апейрогональная призма и апейрогональная антипризма .

Правильные или равномерные апейрогональные мозаики порядка 2.

(∞ 2 2)	Витхофф символ	Шлефли символ	Коксетер диаграмма	Вертекс конфиг.	Мозаичное изображение	Название плитки
Родитель	2 | ∞ 2	{∞,2}		∞.∞		Апейрогональный двугранник
Усечено	2 2 | ∞	т{∞,2}
Исправленный	2 | ∞ 2	г{∞,2}
биректифицированный (двойной)	∞ | 2 2	{2,∞}		2 ∞		Апейрогональный осоэдр
Битусеченный	2 ∞ | 2	т{2,∞}		4.4.∞		Апейрогональный призма
Отмененный	∞ 2 | 2	рр{∞,2}
Всеусеченный ( Количественно усечено )	∞ 2 2 |	tr{∞,2}		4.4.∞
пренебрежительный	| ∞ 2 2	ср{∞,2}		3.3.3.∞		Апейрогональный антипризма

Ссылки

• Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики, Макмиллан, 1900 г.
• Грюнбаум, Бранко ; Шепард, GC (1987). Плитки и узоры . WH Фриман и компания. ISBN  0-7167-1193-1 .
• Конвей, Джон Х.; Хайди Бургель; Хаим Гудман-Штраус (2008). Симметрии вещей . ISBN  978-1-56881-220-5 .