Линейный дискриминантный анализ

Линейный дискриминантный анализ ( LDA ), нормальный дискриминантный анализ ( NDA ) или анализ дискриминантной функции — это обобщение линейного дискриминанта Фишера , метода, используемого в статистике и других областях для поиска линейной комбинации признаков, которая характеризует или разделяет два или более классов. предметов или событий. Полученную комбинацию можно использовать в качестве линейного классификатора или, что чаще, для уменьшения размерности перед последующей классификацией .
LDA тесно связан с дисперсионным анализом (ANOVA) и регрессионным анализом , которые также пытаются выразить одну зависимую переменную как линейную комбинацию других характеристик или измерений. [2] [3] Однако ANOVA использует категориальные независимые переменные и непрерывную зависимую переменную , тогда как дискриминантный анализ имеет непрерывные независимые переменные и категориальную зависимую переменную ( т. е. метку класса). [4] Логистическая регрессия и пробит-регрессия больше похожи на LDA, чем на ANOVA, поскольку они также объясняют категориальную переменную значениями непрерывных независимых переменных. Эти другие методы предпочтительнее в приложениях, где неразумно предполагать, что независимые переменные имеют нормальное распределение, что является фундаментальным предположением метода LDA.
LDA также тесно связан с анализом главных компонентов (PCA) и факторным анализом , поскольку они оба ищут линейные комбинации переменных, которые лучше всего объясняют данные. [5] LDA явно пытается смоделировать разницу между классами данных. PCA, напротив, не учитывает никаких различий в классе, а факторный анализ строит комбинации признаков на основе различий, а не сходства. Дискриминантный анализ также отличается от факторного анализа тем, что он не является методом взаимозависимости: необходимо проводить различие между независимыми переменными и зависимыми переменными (также называемыми критериальными переменными).
LDA работает, когда измерения независимых переменных для каждого наблюдения являются непрерывными величинами. При работе с категориальными независимыми переменными эквивалентным методом является дискриминантный анализ соответствия. [6] [7]
Дискриминантный анализ используется, когда группы известны априори (в отличие от кластерного анализа ). Каждый случай должен иметь оценку по одному или нескольким количественным предикторным показателям, а также оценку по групповому показателю. [8] Проще говоря, дискриминантный функциональный анализ — это классификация — действие по распределению вещей на группы, классы или категории одного и того же типа.
История
[ редактировать ]Оригинальный дихотомический дискриминантный анализ был разработан сэром Рональдом Фишером в 1936 году. [9] Он отличается от ANOVA или MANOVA , которые используются для прогнозирования одной (ANOVA) или нескольких (MANOVA) непрерывных зависимых переменных с помощью одной или нескольких независимых категориальных переменных. Анализ дискриминантной функции полезен для определения того, эффективен ли набор переменных для прогнозирования принадлежности к категории. [10]
ЛДА для двух классов
[ редактировать ]Рассмотрим набор наблюдений (также называемые признаками, атрибутами, переменными или измерениями) для каждого образца объекта или события известного класса. . Этот набор образцов называется обучающим набором в контексте контролируемого обучения . Тогда задача классификации состоит в том, чтобы найти хороший предиктор для класса. любой выборки того же распределения (не обязательно из обучающего набора), учитывая только наблюдение . [11] : 338
LDA подходит к проблеме, предполагая, что условные функции плотности вероятности и оба являются нормальным распределением со средним и ковариационным параметрами и , соответственно. При этом предположении оптимальным по Байесу решением является прогнозирование точек как принадлежащих ко второму классу, если логарифм отношений правдоподобия больше некоторого порога T, так что:
Без каких-либо дополнительных предположений полученный классификатор называется квадратичным дискриминантным анализом (QDA).
Вместо этого LDA делает дополнительное упрощающее гомоскедастичности предположение ( т. е . что ковариации классов идентичны, поэтому ) и что ковариации имеют полный ранг.В этом случае отменяются несколько условий:
- потому что является эрмитовым
и вышеуказанный критерий принятия решениястановится порогом скалярного произведения
для некоторой пороговой константы c , где
Это означает, что критерий входа быть в классе является чисто функцией этой линейной комбинации известных наблюдений.
Часто бывает полезно рассматривать этот вывод в геометрических терминах: критерий входа быть в классе является чисто функцией проекции точки многомерного пространства на вектор (таким образом, мы рассматриваем только его направление). Другими словами, наблюдение принадлежит если соответствует находится на некоторой стороне гиперплоскости, перпендикулярной . Местоположение плоскости определяется порогом .
Предположения
[ редактировать ]Допущения дискриминантного анализа такие же, как и для MANOVA. Анализ весьма чувствителен к выбросам, и размер наименьшей группы должен быть больше, чем количество переменных-предикторов. [8]
- Многомерная нормальность : независимые переменные являются нормальными для каждого уровня группирующей переменной. [10] [8]
- Гомогенность дисперсии/ковариации ( гомоскедастичность ): дисперсия групповых переменных одинакова на всех уровнях предикторов. Можно проверить с помощью Бокса M. статистики [10] Однако было предложено использовать линейный дискриминантный анализ, когда ковариации равны, и что квадратичный дискриминантный анализ может использоваться, когда ковариации не равны. [8]
- Независимость : предполагается, что участники выбраны случайным образом, и оценка участника по одной переменной считается независимой от оценок по этой переменной для всех других участников. [10] [8]
Было высказано предположение, что дискриминантный анализ относительно устойчив к небольшим нарушениям этих предположений. [12] а также было показано, что дискриминантный анализ может быть надежным при использовании дихотомических переменных (где многомерная нормальность часто нарушается). [13]
Дискриминантные функции
[ редактировать ]Дискриминантный анализ работает путем создания одной или нескольких линейных комбинаций предикторов, создавая новую скрытую переменную для каждой функции. Эти функции называются дискриминантными функциями. Возможное количество функций равно либо где = количество групп, или (количество предикторов), в зависимости от того, какое из них меньше. Первая созданная функция максимизирует различия между группами по этой функции. Вторая функция максимизирует различия в этой функции, но также не должна коррелировать с предыдущей функцией. Это продолжается и с последующими функциями с требованием, чтобы новая функция не коррелировала ни с одной из предыдущих функций.
Данная группа , с наборов выборочного пространства, существует дискриминантное правило, такое, что если , затем . Дискриминантный анализ находит «хорошие» области чтобы минимизировать ошибку классификации, что приводит к высокому проценту правильной классификации в таблице классификации. [14]
Каждой функции присваивается дискриминантный балл. [ нужны разъяснения ] чтобы определить, насколько хорошо он предсказывает размещение группы.
- Коэффициенты структурной корреляции: корреляция между каждым предиктором и дискриминантной оценкой каждой функции. Это корреляция нулевого порядка (т. е. без поправки на другие предикторы). [15]
- Стандартизированные коэффициенты: вес каждого предиктора в линейной комбинации, которая является дискриминантной функцией. Как и в уравнении регрессии, эти коэффициенты являются частичными (т. е. скорректированы с учетом других предикторов). Указывает уникальный вклад каждого предиктора в прогнозирование группового назначения.
- Функции в центроидах групп: для каждой функции указаны средние дискриминантные оценки для каждой группирующей переменной. Чем дальше друг от друга находятся средства, тем меньше ошибок будет в классификации.
Правила дискриминации
[ редактировать ]- Максимальная вероятность : Назначает к группе, которая максимизирует плотность населения (группы). [16]
- Дискриминантное правило Байеса: присваивает группе, которая максимизирует , где π i представляет априорную вероятность этой классификации, и представляет плотность населения. [16]
- Линейное дискриминантное правило Фишера : максимизирует соотношение между SS между и SS внутри и находит линейную комбинацию предикторов для прогнозирования группы. [16]
Собственные значения
[ редактировать ]Собственное значение в дискриминантном анализе является характеристическим корнем каждой функции. [ нужны разъяснения ] Это показатель того, насколько хорошо эта функция дифференцирует группы: чем больше собственное значение, тем лучше дифференцируется функция. [8] Однако к этому следует относиться с осторожностью, поскольку собственные значения не имеют верхнего предела. [10] [8] Собственное значение можно рассматривать как отношение SS между и SS внутри, как в ANOVA, когда зависимой переменной является дискриминантная функция, а группы — уровни IV. [ нужны разъяснения ] . [10] Это означает, что наибольшее собственное значение связано с первой функцией, второе по величине — со второй и т. д.
Размер эффекта
[ редактировать ]Некоторые предлагают использовать собственные значения в качестве меры величины эффекта , однако это обычно не поддерживается. [10] Вместо этого каноническая корреляция является предпочтительной мерой размера эффекта. Оно похоже на собственное значение, но представляет собой квадратный корень из отношения SS между и SS total . Это корреляция между группами и функцией. [10] Другой популярной мерой размера эффекта является процент дисперсии. [ нужны разъяснения ] для каждой функции. Это рассчитывается по формуле: ( λ x /Σλ i ) X 100, где λ x — собственное значение функции, а Σ λ i — сумма всех собственных значений. Это говорит нам, насколько сильным является прогноз для этой конкретной функции по сравнению с другими. [10] Правильно классифицированный процент также можно проанализировать как величину эффекта. Значение каппа может описать это с поправкой на случайное согласие. [10] Каппа нормализует все категории, а не предвзято относится к классам со значительно хорошими или плохими показателями. [ нужны разъяснения ] [17]
Канонический дискриминантный анализ для k классов
[ редактировать ]Канонический дискриминантный анализ (CDA) находит оси ( k - 1 канонических координат , k — количество классов), которые лучше всего разделяют категории. Эти линейные функции некоррелированы и, по сути, определяют оптимальное пространство k - 1 через n -мерное облако данных, которое лучше всего разделяет (проекции в этом пространстве) k групп. см. в разделе « Мультиклассовый LDA Подробности ».
Линейный дискриминант Фишера
[ редактировать ]Термины «линейный дискриминант Фишера» и «LDA» часто используются как синонимы, хотя Фишера оригинальная статья [2] на самом деле описывает немного другой дискриминант, который не учитывает некоторые предположения LDA, такие как нормально распределенные классы или равные ковариации классов .
Предположим, что два класса наблюдений имеют средства и ковариации . Тогда линейная комбинация признаков будут иметь средства и отклонения для . Фишер определил разделение между этими двумя распределениями как отношение дисперсии между классами к дисперсии внутри классов:
Эта мера в некотором смысле является мерой отношения сигнал/шум для маркировки классов. Можно показать, что максимальное разделение происходит, когда
Когда предположения LDA удовлетворены, приведенное выше уравнение эквивалентно LDA.
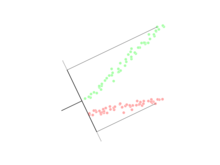
Обязательно обратите внимание, что вектор – нормаль к дискриминантной гиперплоскости . Например, в двумерной задаче линия, которая лучше всего разделяет две группы, перпендикулярна .
Как правило, точки данных, подлежащие различению, проецируются на ; затем порог, который лучше всего разделяет данные, выбирается на основе анализа одномерного распределения. Общего правила для порога не существует. Однако если проекции точек обоих классов имеют примерно одинаковое распределение, хорошим выбором будет гиперплоскость между проекциями двух средних: и . В этом случае параметр c в пороговом состоянии можно найти явно:
- .
Метод Оцу связан с линейным дискриминантом Фишера и был создан для бинаризации гистограммы пикселей в изображении в оттенках серого путем оптимального выбора порога черного/белого, который минимизирует внутриклассовую дисперсию и максимизирует межклассовую дисперсию внутри или между оттенками серого, назначенными черному и белому. классы белых пикселей.
Мультиклассовый LDA
[ редактировать ]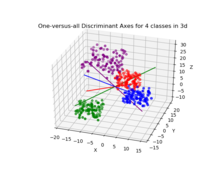

В случае, когда существует более двух классов, анализ, используемый при выводе дискриминанта Фишера, может быть расширен, чтобы найти подпространство , которое, по-видимому, содержит всю изменчивость классов. [18] Это обобщение принадлежит Ч.Р. Рао . [19] Предположим, что каждый из классов C имеет среднее значение и та же ковариация . Тогда разброс между изменчивостью классов может быть определен выборочной ковариацией средних значений класса.
где является средним значением класса. Классовое разделение в направлении в этом случае будет дано
Это означает, что когда является собственным вектором расстояние будет равно соответствующему собственному значению .
Если диагонализуема, изменчивость между объектами будет содержаться в подпространстве, охватываемом собственными векторами, соответствующими C - 1 наибольшим собственным значениям (поскольку имеет ранг C − 1 не более). Эти собственные векторы в основном используются при уменьшении признаков, как в PCA. Собственные векторы, соответствующие меньшим собственным значениям, будут иметь тенденцию быть очень чувствительными к точному выбору обучающих данных, и часто необходимо использовать регуляризацию, как описано в следующем разделе.
требуется классификация Если вместо уменьшения размерности , существует ряд альтернативных методов. Например, классы могут быть разделены, и для классификации каждого раздела может использоваться стандартный дискриминант Фишера или LDA. Типичным примером этого является принцип «один против остальных», когда баллы одного класса помещаются в одну группу, а все остальное — в другую, а затем применяется LDA. В результате появятся классификаторы C, результаты которых объединяются. Еще один распространенныйМетод представляет собой парную классификацию, при которой для каждой пары классов создается новый классификатор ( давая C ( C всего - 1)/2 классификаторов), при этом отдельные классификаторы объединяются для получения окончательной классификации.
Инкрементный LDA
[ редактировать ]Типичная реализация метода LDA требует, чтобы все образцы были доступны заранее. Однако бывают ситуации, когда весь набор данных недоступен и входные данные наблюдаются в виде потока. В этом случае желательно, чтобы при извлечении признаков LDA была возможность обновлять вычисленные признаки LDA путем наблюдения за новыми выборками без запуска алгоритма на всем наборе данных. Например, во многих приложениях реального времени, таких как мобильная робототехника или онлайн-распознавание лиц, важно обновлять извлеченные функции LDA, как только становятся доступны новые наблюдения. Методика извлечения признаков LDA, которая позволяет обновлять функции LDA путем простого наблюдения за новыми образцами, представляет собой инкрементный алгоритм LDA , и эта идея широко изучалась в течение последних двух десятилетий. [20] Чаттерджи и Ройчоудхури предложили инкрементальный самоорганизующийся алгоритм LDA для обновления функций LDA. [21] В другой работе Демир и Озмехмет предложили алгоритмы локального онлайн-обучения для постепенного обновления функций LDA с использованием исправления ошибок и правил обучения Хебба. [22] Позже Алияри и др. разработал быстрые инкрементные алгоритмы для обновления функций LDA путем наблюдения за новыми образцами. [20]
Практическое использование
[ редактировать ]На практике средние значения класса и ковариации неизвестны. Однако их можно оценить по обучающему набору. либо оценку максимального правдоподобия , либо максимальную апостериорную Вместо точного значения в приведенных выше уравнениях можно использовать оценку. Хотя оценки ковариации можно считать в некотором смысле оптимальными, это не означает, что результирующий дискриминант, полученный заменой этих значений, является оптимальным в каком-либо смысле, даже если предположение о нормально распределенных классах верно.
Другая сложность в применении LDA и дискриминанта Фишера к реальным данным возникает, когда количество измерений каждой выборки (т. е. размерность каждого вектора данных) превышает количество выборок в каждом классе. [5] В этом случае оценки ковариации не имеют полного ранга и поэтому не могут быть инвертированы. Есть несколько способов справиться с этим. Один из них — использовать псевдообратную матрицу вместо обычной обратной матрицы в приведенных выше формулах. Однако лучшей числовой стабильности можно добиться, сначала спроецировав задачу на подпространство, охватываемое . [23] Другая стратегия борьбы с небольшим размером выборки — использовать оценку сжатия ковариационной матрицы, котораяможет быть выражено математически как
где - единичная матрица, и – интенсивность усадки или параметр регуляризации .Это приводит к структуре регуляризованного дискриминантного анализа. [24] или дискриминантный анализ усадки. [25]
Кроме того, во многих практических случаях линейные дискриминанты не подходят. LDA и дискриминант Фишера можно расширить для использования в нелинейной классификации с помощью трюка с ядром . Здесь исходные наблюдения эффективно отображаются в нелинейное пространство более высокого измерения. Линейная классификация в этом нелинейном пространстве эквивалентна нелинейной классификации в исходном пространстве. Наиболее часто используемым примером этого является ядро дискриминанта Фишера .
LDA можно обобщить до множественного дискриминантного анализа , где c становится категориальной переменной с N возможными состояниями вместо двух. Аналогично, если классовые условные плотности являются нормальными с общими ковариациями, то это достаточная статистика для являются значениями N проекций, которые представляют собой подпространство , охватываемое N средними значениями, аффинно проецируемыми обратной ковариационной матрицей. Эти проекции можно найти, решив обобщенную проблему собственных значений , где числитель — это ковариационная матрица, сформированная путем обработки средних значений как выборок, а знаменатель — это общая ковариационная матрица. см. в разделе « Мультиклассовый LDA Подробности » выше.
Приложения
[ редактировать ]Помимо приведенных ниже примеров, LDA применяется в позиционировании и управлении продуктами .
Прогноз банкротства
[ редактировать ]При прогнозировании банкротства на основе коэффициентов бухгалтерского учета и других финансовых переменных линейный дискриминантный анализ был первым статистическим методом, применяемым для систематического объяснения того, какие фирмы вступили в банкротство, а какие выжили. Несмотря на ограничения, в том числе известное несоответствие учетных коэффициентов предположениям о нормальном распределении LDA, Эдварда Альтмана 1968 года модель [26] по-прежнему является ведущей моделью в практическом применении. [27] [28] [29]
Распознавание лиц
[ редактировать ]При компьютеризированном распознавании лиц каждое лицо представлено большим количеством значений пикселей. Линейный дискриминантный анализ в основном используется здесь для уменьшения количества признаков до более управляемого числа перед классификацией. Каждое из новых измерений представляет собой линейную комбинацию значений пикселей, образующих шаблон. Линейные комбинации, полученные с помощью линейного дискриминанта Фишера, называются гранями Фишера , а те, которые получены с помощью соответствующего анализа главных компонент, называются собственными гранями .
Маркетинг
[ редактировать ]В маркетинге дискриминантный анализ когда-то часто использовался для определения факторов, которые отличают различные типы клиентов и/или продуктов, на основе опросов или других форм сбора данных. логистическая регрессия Сейчас более широко используются или другие методы. Использование дискриминантного анализа в маркетинге можно описать следующими этапами:
- Сформулируйте проблему и соберите данные. Определите основные атрибуты, которые потребители используют для оценки продуктов в этой категории. Используйте методы количественного маркетингового исследования (например, опросы ), чтобы собрать данные из выборки потенциальных клиентов, касающиеся их оценок всех атрибутов продукта. Этап сбора данных обычно выполняется специалистами по маркетинговым исследованиям. В вопросах опроса респонденту предлагается оценить продукт от одного до пяти (или от 1 до 7, или от 1 до 10) по ряду характеристик, выбранных исследователем. Выбирается от пяти до двадцати атрибутов. Они могут включать такие вещи, как простота использования, вес, точность, долговечность, красочность, цена или размер. Выбранные атрибуты будут различаться в зависимости от изучаемого продукта. Тот же вопрос задается обо всех продуктах в исследовании. Данные по нескольким продуктам кодифицируются и вводятся в статистические программы, такие как R , SPSS или SAS . (Этот шаг аналогичен факторному анализу).
- Оцените коэффициенты дискриминантной функции и определите статистическую значимость и достоверность. Выберите соответствующий метод дискриминантного анализа. Прямой метод предполагает оценку дискриминантной функции так, чтобы все предикторы оценивались одновременно. Пошаговый метод вводит предикторы последовательно. Метод двух групп следует использовать, когда зависимая переменная имеет две категории или состояния. Множественный дискриминантный метод используется, когда зависимая переменная имеет три или более категориальных состояния. Используйте лямбду Уилкса для проверки значимости в SPSS или F stat в SAS. Наиболее распространенный метод, используемый для проверки достоверности, — это разделение выборки на оценочную или аналитическую выборку, а также проверочную или контрольную выборку. Оценочная выборка используется при построении дискриминантной функции. Проверочная выборка используется для построения матрицы классификации, которая содержит количество правильно классифицированных и неправильно классифицированных случаев. Процент правильно классифицированных случаев называется коэффициент попадания .
- Нанесите результаты на двухмерную карту, определите размеры и интерпретируйте результаты. Статистическая программа (или связанный с ней модуль) отобразит результаты. На карте будет отображен каждый продукт (обычно в двухмерном пространстве). Расстояние продуктов друг от друга указывает на то, насколько они различаются. Размеры должны быть отмечены исследователем. Это требует субъективного суждения и часто является очень сложной задачей. См. картирование восприятия .
Биомедицинские исследования
[ редактировать ]Основным применением дискриминантного анализа в медицине является оценка тяжести состояния больного и прогноз исхода заболевания. Например, при ретроспективном анализе больных делят на группы по тяжести заболевания – легкая, среднетяжелая и тяжелая форма. Затем изучаются результаты клинических и лабораторных анализов, чтобы выявить статистически разные переменные в этих группах. Используя эти переменные, строятся дискриминантные функции для классификации тяжести заболевания у будущих пациентов. Кроме того, линейный дискриминантный анализ (LDA) может помочь выбрать более дискриминантные образцы для увеличения данных, улучшая производительность классификации. [30]
В биологии аналогичные принципы используются для классификации и определения групп различных биологических объектов, например, для определения типов фагов Salmonella enteritidis на основе инфракрасных спектров Фурье-преобразования. [31] обнаружить животное происхождение кишечной палочки, изучая факторы ее вирулентности [32] и т. д.
Науки о Земле
[ редактировать ]Этот метод можно использовать для разделения зон изменения. [ нужны разъяснения ] . Например, когда доступны разные данные из разных зон, дискриминантный анализ может найти закономерность в данных и эффективно их классифицировать. [33]
Сравнение с логистической регрессией
[ редактировать ]Дискриминантный функциональный анализ очень похож на логистическую регрессию , и оба могут использоваться для ответа на одни и те же исследовательские вопросы. [10] Логистическая регрессия не имеет такого количества предположений и ограничений, как дискриминантный анализ. Однако, когда предположения дискриминантного анализа выполняются, он оказывается более эффективным, чем логистическая регрессия. [34] В отличие от логистической регрессии, дискриминантный анализ можно использовать при небольших размерах выборки. Было показано, что когда размеры выборки равны и сохраняется однородность дисперсии/ковариации, дискриминантный анализ является более точным. [8] Несмотря на все эти преимущества, логистическая регрессия, тем не менее, стала распространенным выбором, поскольку предположения дискриминантного анализа редко выполняются. [9] [8]
Линейный дискриминант в больших размерностях
[ редактировать ]Геометрические аномалии в высших измерениях приводят к известному проклятию размерности . Тем не менее, правильное использование явления концентрации меры может облегчить вычисления. [35] Важный случай благословения феномена размерности был подчеркнут Донохо и Таннером: если выборка по существу многомерна, то каждая точка может быть отделена от остальной части выборки с помощью линейного неравенства с высокой вероятностью даже для экспоненциально больших выборок. [36] Эти линейные неравенства можно выбрать в стандартной (фишеровской) форме линейного дискриминанта для богатого семейства вероятностных распределений. [37] В частности, такие теоремы доказываются для лог-вогнутых распределений, включая многомерное нормальное распределение (доказательство основано на неравенствах концентрации для лог-вогнутых мер [38] ) и для мер произведения на многомерном кубе (это доказывается с помощью неравенства концентрации Талагранда для пространств вероятностей произведения). Разделение данных с помощью классических линейных дискриминантов упрощает задачу исправления ошибок для систем искусственного интеллекта в большой размерности. [39]
См. также
[ редактировать ]- Интеллектуальный анализ данных
- Обучение дереву решений
- Факторный анализ
- Дискриминантный анализ Кернела Фишера
- Логит (для логистической регрессии )
- Линейная регрессия
- Множественный дискриминантный анализ
- Многомерное масштабирование
- Распознавание образов
- Регрессия предпочтений
- Квадратичный классификатор
- Статистическая классификация
Ссылки
[ редактировать ]- ^ Холтел, Фредерик (20 февраля 2023 г.). «Линейный дискриминантный анализ (LDA) может быть таким простым» . Середина . Проверено 18 мая 2024 г.
- ^ Jump up to: а б Фишер, Р.А. (1936). «Использование множественных измерений в таксономических задачах» (PDF) . Анналы евгеники . 7 (2): 179–188. дои : 10.1111/j.1469-1809.1936.tb02137.x . hdl : 2440/15227 .
- ^ Маклахлан, Дж.Дж. (2004). Дискриминантный анализ и статистическое распознавание образов . Уайли Интерсайенс. ISBN 978-0-471-69115-0 . МР 1190469 .
- ^ Анализ количественных данных: введение для социальных исследователей, Дебра Ветчер-Хендрикс, стр.288
- ^ Jump up to: а б Мартинес, AM; Как, AC (2001). «PCA против LDA» (PDF) . Транзакции IEEE по анализу шаблонов и машинному интеллекту . 23 (2): 228–233. дои : 10.1109/34.908974 . Архивировано из оригинала (PDF) 11 октября 2008 г. Проверено 30 июня 2010 г.
- ^ Абди, Х. (2007) «Дискриминантный анализ соответствия». В: Нью-Джерси Салкинд (ред.): Энциклопедия измерений и статистики . Таузенд-Оукс (Калифорния): Сейдж. стр. 270–275.
- ^ Перьер, Г.; Тиулуза, Дж. (2003). «Использование дискриминантного анализа соответствия для прогнозирования субклеточного расположения бактериальных белков». Компьютерные методы и программы в биомедицине . 70 (2): 99–105. дои : 10.1016/s0169-2607(02)00011-1 . ПМИД 12507786 .
- ^ Jump up to: а б с д и ж г час я Бююкозтюрк, Ш. & Чоклук-Бёкеоглу, О. (2008). Дискриминантный функциональный анализ: Понятие и применение . Исследования в области образования – Евразийский журнал исследований в области образования, 33, 73-92.
- ^ Jump up to: а б Коэн и др. Прикладной множественный регрессионный/корреляционный анализ для поведенческих наук 3-е изд. (2003). Группа Тейлор и Фрэнсис.
- ^ Jump up to: а б с д и ж г час я дж к Хансен, Джон (2005). «Использование SPSS для Windows и Macintosh: анализ и понимание данных» . Американский статистик . 59 : 113. дои : 10.1198/tas.2005.s139 .
- ^ Венейблс, Западная Нью-Йорк; Рипли, Б.Д. (2002). Современная прикладная статистика с S (4-е изд.). Спрингер Верлаг. ISBN 978-0-387-95457-8 .
- ^ Лахенбрух, Пенсильвания (1975). Дискриминантный анализ . Нью-Йорк: Хафнер
- ^ Клека, Уильям Р. (1980). Дискриминантный анализ . Количественные приложения в серии социальных наук, № 19. Таузенд-Оукс, Калифорния: Sage Publications.
- ^ Хардл, В., Симар, Л. (2007). Прикладной многомерный статистический анализ . Шпрингер Берлин Гейдельберг. стр. 289–303.
- ^ Гарсон, Джорджия (2008). Дискриминантный функциональный анализ. https://web.archive.org/web/20080312065328/http://www2.chass.ncsu.edu/garson/pA765/discrim.htm .
- ^ Jump up to: а б с Хардл В., Симар Л. (2007). Прикладной многомерный статистический анализ . Шпрингер Берлин Гейдельберг. стр. 289-303.
- ^ Израиль, Стивен А. (июнь 2006 г.). «Показатели производительности: как и когда». Геокарто Интернэшнл . 21 (2): 23–32. Бибкод : 2006GeoIn..21...23I . дои : 10.1080/10106040608542380 . ISSN 1010-6049 . S2CID 122376081 .
- ^ Гарсон, Джорджия (2008). Дискриминантный функциональный анализ. «PA 765: Дискриминантный функциональный анализ» . Архивировано из оригинала 12 марта 2008 г. Проверено 4 марта 2008 г. .
- ^ Рао, RC (1948). «Использование множественных измерений в задачах биологической классификации». Журнал Королевского статистического общества, серия B. 10 (2): 159–203. дои : 10.1111/j.2517-6161.1948.tb00008.x . JSTOR 2983775 .
- ^ Jump up to: а б Алияр Гассабе, Юнесс; Руджич, Франк; Могаддам, Хамид Абришами (1 июня 2015 г.). «Быстрое постепенное извлечение функций LDA». Распознавание образов . 48 (6): 1999–2012. Бибкод : 2015PatRe..48.1999A дои : 10.1016/j.patcog.2014.12.012 .
- ^ Чаттерджи, К.; Ройчоудхури, вице-президент (1 мая 1997 г.). «О самоорганизующихся алгоритмах и сетях для признаков разделимости классов». Транзакции IEEE в нейронных сетях . 8 (3): 663–678. дои : 10.1109/72.572105 . ISSN 1045-9227 . ПМИД 18255669 .
- ^ Демир, ГК; Озмехмет, К. (01 марта 2005 г.). «Алгоритмы локального онлайн-обучения для линейного дискриминантного анализа». Распознавание образов. Летт . 26 (4): 421–431. Бибкод : 2005PaReL..26..421D . дои : 10.1016/j.patrec.2004.08.005 . ISSN 0167-8655 .
- ^ Ю, Х.; Ян, Дж. (2001). «Прямой алгоритм LDA для многомерных данных — с применением для распознавания лиц». Распознавание образов . 34 (10): 2067–2069. Бибкод : 2001PatRe..34.2067Y . CiteSeerX 10.1.1.70.3507 . дои : 10.1016/s0031-3203(00)00162-x .
- ^ Фридман, Дж. Х. (1989). «Регуляризованный дискриминантный анализ» (PDF) . Журнал Американской статистической ассоциации . 84 (405): 165–175. CiteSeerX 10.1.1.382.2682 . дои : 10.2307/2289860 . JSTOR 2289860 . МР 0999675 .
- ^ Ахдесмяки, М.; Стриммер, К. (2010). «Выбор функций в задачах прогнозирования омики с использованием кошачьих оценок и контроля уровня ложного необнаружения». Анналы прикладной статистики . 4 (1): 503–519. arXiv : 0903.2003 . дои : 10.1214/09-aoas277 . S2CID 2508935 .
- ^ Альтман, Эдвард И. (1968). «Финансовые коэффициенты, дискриминантный анализ и прогнозирование корпоративного банкротства». Журнал финансов . 23 (4): 589–609. дои : 10.2307/2978933 . JSTOR 2978933 .
- ^ Агарвал, Винет; Таффлер, Ричард (2005). «Двадцать пять лет z-показателей в Великобритании: действительно ли они работают?» (PDF) .
- ^ Агарвал, Винет; Таффлер, Ричард (2007). «Двадцать пять лет модели Z-Score Таффлера: действительно ли она обладает прогнозирующей способностью?». Бухгалтерский учет и бизнес-исследования . 37 (4): 285–300. дои : 10.1080/00014788.2007.9663313 .
- ^ Бимпонг, Патрик; и др. (2020). «Оценка прогнозной силы и манипуляций с прибылью. Прикладное исследование зарегистрированных на бирже компаний потребительских товаров и услуг в Гане с использованием 3 моделей Z-Score» . Экспертный журнал финансов . 8 (1): 1–26.
- ^ Моради, М; Демирель, Х (2024). «Классификация болезни Альцгеймера с использованием трехмерной условно-прогрессивной выборки данных на основе GAN и LDA». Обработка сигналов, изображений и видео . 18 (2): 1847–1861.
- ^ Прейснер, О; Гиомар, Р; Мачадо, Дж; Менезес, Дж. К.; Лопес, Дж. А. (2010). «Применение инфракрасной спектроскопии с преобразованием Фурье и хемометрики для дифференциации типов фагов серовара Salmonella enterica Enteritidis» . Appl Environ Microbiol . 76 (11): 3538–3544. Бибкод : 2010ApEnM..76.3538P . дои : 10.1128/aem.01589-09 . ПМЦ 2876429 . ПМИД 20363777 .
- ^ Дэвид, Делавэр; Линн, AM; Хан, Дж; Фоли, СЛ (2010). «Оценка профиля факторов вирулентности при характеристике ветеринарных изолятов Escherichia coli» . Appl Environ Microbiol . 76 (22): 7509–7513. Бибкод : 2010ApEnM..76.7509D . дои : 10.1128/aem.00726-10 . ПМК 2976202 . ПМИД 20889790 .
- ^ Тахмасеби, П.; Хезархани, А.; Мортазави, М. (2010). «Применение дискриминантного анализа для разделения изменений; медное месторождение Сунгун, Восточный Азербайджан, Иран. Австралия» (PDF) . Журнал фундаментальных и прикладных наук . 6 (4): 564–576.
- ^ Тревор Хэсти; Роберт Тибширани; Джером Фридман. Элементы статистического обучения. Интеллектуальный анализ данных, вывод и прогнозирование (второе изд.). Спрингер. п. 128.
- ^ Kainen PC (1997) Использование геометрических аномалий большой размерности: когда сложность упрощает вычисления . В: Карни М., Уорвик К. (ред.) Интенсивные компьютерные методы управления и обработки сигналов: проклятие размерности, Springer, 1997, стр. 282–294.
- ^ Донохо, Д., Таннер, Дж. (2009) Наблюдаемая универсальность фазовых переходов в многомерной геометрии, что имеет значение для современного анализа данных и обработки сигналов , Phil. Пер. Р. Сок. А 367, 4273–4293.
- ^ Горбань, Александр Н.; Голубков, Александр; Гречук, Богдан; Миркес, Евгений М.; Тюкин, Иван Юрьевич (2018). «Коррекция систем искусственного интеллекта линейными дискриминантами: вероятностные основы». Информационные науки . 466 : 303–322. arXiv : 1811.05321 . дои : 10.1016/j.ins.2018.07.040 . S2CID 52876539 .
- ^ Гедон, О., Милман, Э. (2011) Интерполяция оценок тонкой оболочки и резких больших отклонений для изотропных логарифмически вогнутых мер , Geom. Функц. Анальный. 21 (5), 1043–1068.
- ^ Горбань, Александр Н.; Макаров Валерий А.; Тюкин, Иван Юрьевич (июль 2019 г.). «Необоснованная эффективность небольших нейронных ансамблей в многомерном мозге» . Обзоры физики жизни . 29 : 55–88. arXiv : 1809.07656 . Бибкод : 2019PhLRv..29...55G . дои : 10.1016/j.plrev.2018.09.005 . ПМИД 30366739 .
Дальнейшее чтение
[ редактировать ]- Дуда, Р.О.; Харт, ЧП; Аист, Д.Х. (2000). Классификация шаблонов (2-е изд.). Уайли Интерсайенс. ISBN 978-0-471-05669-0 . МР 1802993 .
- Хильбе, Дж. М. (2009). Модели логистической регрессии . Чепмен и Холл/CRC Press. ISBN 978-1-4200-7575-5 .
- Мика, С.; и др. (1999). «Дискриминантный анализ Фишера с ядрами». Нейронные сети для обработки сигналов IX: Материалы семинара Общества обработки сигналов IEEE 1999 г. (кат. № 98TH8468) . стр. 41–48. CiteSeerX 10.1.1.35.9904 . дои : 10.1109/NNSP.1999.788121 . ISBN 978-0-7803-5673-3 . S2CID 8473401 .
{{cite book}}: CS1 maint: дата и год ( ссылка ) - Макфарланд, Х. Ричард; Дональд, Сент-Пи Ричардс (2001). «Точные вероятности ошибочной классификации для подключаемых нормальных квадратичных дискриминантных функций. I. Случай равных средних» . Журнал многомерного анализа . 77 (1): 21–53. дои : 10.1006/jmva.2000.1924 .
- Макфарланд, Х. Ричард; Дональд, Сент-Пи Ричардс (2002). «Точные вероятности ошибочной классификации для подключаемых нормальных квадратичных дискриминантных функций. II. Гетерогенный случай» . Журнал многомерного анализа . 82 (2): 299–330. дои : 10.1006/jmva.2001.2034 .
- Хагигат, М.; Абдель-Мотталеб, М.; Алхалаби, В. (2016). «Дискриминантный корреляционный анализ: объединение уровней признаков в реальном времени для мультимодального биометрического распознавания» . Транзакции IEEE по информационной криминалистике и безопасности . 11 (9): 1984–1996. дои : 10.1109/TIFS.2016.2569061 . S2CID 15624506 .
Внешние ссылки
[ редактировать ]- Дискриминантный корреляционный анализ (DCA) статьи Хагигат (см. выше)
- ALGLIB содержит реализацию LDA с открытым исходным кодом на C#/C++/Pascal/VBA.
- LDA в Python — реализация LDA в Python
- Учебное пособие по LDA с использованием MS Excel
- Биомедицинская статистика. Дискриминантный анализ
- StatQuest: линейный дискриминантный анализ (LDA), подробно объясненный на YouTube
- Конспекты курса: Анализ дискриминантных функций, Дж. Дэвид Гарсон, Университет штата Северная Каролина.
- Учебник по дискриминантному анализу в Microsoft Excel от Карди Текномо
- Конспекты курса, Анализ дискриминантных функций, Дэвид В. Стокбургер, Университет штата Миссури. Архивировано 3 марта 2016 г. в Wayback Machine.
- Дискриминантный функциональный анализ (DA), Джон Поулсен и Аарон Френч, Государственный университет Сан-Франциско.

















































