Бинарный номер

Двоичное число -это число , выраженное в базовых -2 системе численных или бинарной цифровой системы , метод представления чисел , в котором используются только два символа для натуральных чисел : обычно «0» ( ноль ) и «1» ( один ). Двоичное число может также относиться к рациональному числу , которое имеет конечное представление в бинарной системе цифр, то есть коэффициент целого числа с силой двух.

Система цифр базы 2 представляет собой нотацию с Radix 2 позиционную . Каждая цифра упоминается как немного или бинарная цифра. Из-за своей прямой реализации в цифровой электронной схеме с использованием логических ворот бинарная система используется почти всеми современными компьютерами и компьютерными устройствами , в качестве предпочтительной системы использования, по различным другим человеческим методам связи, из-за простоты Язык и шумовой иммунитет в физической реализации. ^{[ 1 ]}

История

Современная бинарная система была изучена в Европе в 16 -м и 17 -м веках Томасом Харриотом , Хуан Карамуэлем Й Лобковиц и Готфридом Лейбнизом . Тем не менее, системы, связанные с бинарными числами, появились ранее во многих культурах, включая Древний Египет, Китай и Индию.

Египет

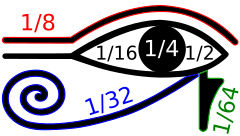
Кребцы древнего Египта использовали две разные системы для своих фракций: египетские фракции (не связанные с системой бинарных чисел) и фракции Horus-Eye (так называемые, потому что многие историки математики считают, что символы, используемые для этой системы, могут быть организованы для формирования Глаз Гора , хотя это было оспорено). ^{[ 2 ]} Фракции Horus-Eye-это бинарная система нумерации для дробного количества зерна, жидкостей или других мер, в которых доля Hekat выражается в виде суммы бинарных фракций 1/2, 1/4, 1/8, 1 /16, 1/32 и 1/64. Ранние формы этой системы можно найти в документах Пятой династии Египта , приблизительно 2400 г. до н.э., и ее полностью развитая иероглифическая форма датируется девятнадцатой династией Египта , приблизительно 1200 г. до н.э. ^{[ 3 ]}

Метод, используемый для древнего египетского умножения, также тесно связан с бинарными числами. В этом методе умножение одного числа на секунду выполняется последовательности шагов, в которых значение (первоначально первое из двух чисел) либо удвоится, либо добавлено первое число обратно в него; Порядок, в котором эти шаги должны выполняться, определяется бинарным представлением второго числа. Этот метод можно увидеть в использовании, например, в математическом папирусе Rhind , который датируется около 1650 г. до н.э. ^{[ 4 ]}

Китай

I Ching датируется 9 -м веком до нашей эры в Китае. ^{[ 5 ]} Бинарная нотация в I Ching используется для интерпретации техники его четвертичного гадания . ^{[ 6 ]}

Он основан на даосской двойственности Инь и Ян . ^{[ 7 ]} Восемь триграмм (багуа) и набор из 64 гексаграмм («шестьдесят четыре» Gua) , аналогичные трехбитными и шестибитными бинарными цифрами, использовались, по крайней мере, еще в династии Древнего Китая. ^{[ 5 ]}

Ученый династия Сун (1011–1077) переставил гексаграммы в формате , Шао Йонг который напоминает современные бинарные цифры, хотя он не намеревал математически использовать свою аранжировку. ^{[ 6 ]} Просмотр наименее значительного бита на вершине одиночных гексаграмм на площади Шао Йонга ^{[ 8 ]} и чтение вдоль рядов либо снизу вправо влево с твердыми линиями, как 0, и разбитыми линиями как 1 или сверху слева вниз с правыми сплошными линиями как 1, а разбитые линии, как 0 гексаграммы можно интерпретировать как последовательность от 0 до 63. ^{[ 9 ]}

Классическая древность

Этруски разделили внешний край газничной печени на шестнадцать частей, каждая из которых была написана с именем божественности и ее области неба. Каждый регион печени создавал бинарное чтение, которое было объединено в окончательный бинар для гадания. ^{[ 10 ]}

Гадания в древнегреческой Додоне Оракул работал, рисуя из отдельных банок, вопросов планшетов и «да» и «нет» гранул. Результат был затем объединен, чтобы сделать окончательное пророчество. ^{[ 11 ]}

Индия

Индийский ученый Пингала (ок. 2 -го века до нашей эры) разработала бинарную систему для описания просодии . ^{[ 12 ]}^{[ 13 ]} Он описал счетчики в виде коротких и длинных слогов (последние равны по длине до двух коротких слогов). ^{[ 14 ]} Они были известны как лагху (свет) и гуру (тяжелые) слоги.

Индуистская классика Пингалы под названием Chandaḥāstra (8.23) описывает формирование матрицы, чтобы придать уникальную ценность для каждого метра. «Чандашшастра» буквально переводится на науку метров на санскрите. Бинарные представления в системе Пингалы увеличиваются вправо, а не влево, как в бинарных числах современной позиционной нотации . ^{[ 15 ]} В системе Пингалы числа начинаются с номера один, а не нулевой. Четыре коротких слога «0000» - это первый шаблон и соответствует значению One. Числовое значение получается путем добавления одного к сумме значений места . ^{[ 16 ]}

Африка

ИФА - это африканская система гадания . Похоже на I Ching , но имеет до 256 бинарных знаков, ^{[ 17 ]} В отличие от I Ching , который имеет 64. Ифа возник в Западной Африке 15 -го века среди людей йоруба . В 2008 году ЮНЕСКО добавила IFá в свой список « шедевров орального и нематериального наследия человечества ». ^{[ 18 ]}^{[ 19 ]}

Другие культуры

Жители острова Мангарева во французской полинезии использовали гибридную бинарную десятичную систему до 1450 года. ^{[ 20 ]} Разрезные барабаны с двоичными тонами используются для кодирования сообщений по всей Африке и Азии. ^{[ 7 ]} Наборы бинарных комбинаций, аналогичные I Ching, также использовались в традиционных африканских системах гадания, таких как Ifá , а также в средневековой западной геомантии . Большинство коренных австралийских языков используют систему базы-2. ^{[ 21 ]}

Западные предшественники Лейбниза

В конце 13 -го века Рамон Ллалл имел стремление объяснить всю мудрость во всех ветвях человеческих знаний того времени. Для этой цели он разработал общий метод или «ARS Generalis», основанный на бинарных комбинациях ряда простых основных принципов или категорий, для которых он считался предшественником компьютерной науки и искусственного интеллекта. ^{[ 22 ]}

В 1605 году Фрэнсис Бэкон обсудил систему, посредством которой буквы алфавита могут быть сведены к последовательностям бинарных цифр, которые затем могут быть закодированы как едва видимые изменения в шрифте в любом случайном тексте. ^{[ 23 ]} Важно отметить, что для общей теории бинарной кодирования он добавил, что этот метод может использоваться с любыми объектами вообще: «При условии, что эти объекты могут только на двойную разницу; как колокольчиками, трубами, огнями и факелами, от отчета мушкетов и любых инструментов подобной природы ». ^{[ 23 ]} (См. Шифр бекона .)

В 1617 году Джон Нейпир описал систему, которую он назвал арифметикой, для выполнения бинарных вычислений с использованием непозиционного представления буквами. Томас Харриот исследовал несколько систем нумерации позиционной нумерации, включая бинарную, но не опубликовал свои результаты; Они были найдены позже среди его документов. ^{[ 24 ]} Возможно, первая публикация системы в Европе была Хуан Карамуэль и Лобковиц в 1700 году. ^{[ 25 ]}

Лейбник

Лейбниц писал более сотен рукописей на бинарном бинарии, большинство из которых остаются неопубликованными. ^{[ 26 ]} Перед своей первой выделенной работой в 1679 году многочисленные рукописи представляют ранние попытки изучить бинарные концепции, включая таблицы чисел и основные расчеты, часто набрасываемые на полях работ, не связанных с математикой. ^{[ 26 ]}

Его первая известная работа над бинарной, «о бинарной прогрессии» , в 1679 году Лейбниц ввел преобразование между десятичным и бинарным, а также алгоритмы для выполнения основных арифметических операций, таких как добавление, вычитание, умножение и разделение с использованием бинарных чисел. Он также разработал. форма бинарной алгебры для расчета квадрата шестизначного числа и извлечения квадратных корней. ^{[ 26 ]}

Его самая известная работа появляется в его статье объяснения De L'Arithmétique Binaire (опубликовано в 1703 году). Полное название статьи Лейбниза переводится на английский как «объяснение бинарной арифметики, в котором используются только символы 1 и 0, с некоторыми замечаниями о его полезности и на свете, который он бросает на древние китайские фигуры футо » . ^{[ 27 ]} Система Лейбниза использует 0 и 1, как современная бинарная система цифр. Пример бинарной системы цифр Лейбниза заключается в следующем: ^{[ 27 ]}

0 0 0 1 Числовое значение 2 ⁰

0 0 1 0 Числовое значение 2 ¹

0 1 0 0 Числовое значение 2 ²

1 0 0 0 Числовое значение 2 ³

В соответствии с священником -иезуитом Йоахимом Буветом в 1700 году, который сделал себя экспертом в I Ching, в то время как миссионер в Китае, Лейбниц объяснил свою бинарную нотацию, и Буве продемонстрировал в своих письмах 1701 года, что я был независимым, параллельным изобретением бинарной нотации. Leibniz & Bouvet пришел к выводу, что это картирование было доказательством крупных достижений Китая в той философской математике, которой он восхищался. ^{[ 28 ]} Из этого параллельного изобретения Либниц написал в своем «объяснении бинарной арифметики», что «это реституция их значения после такого большого интервала времени будет казаться тем более любопытным». ^{[ 29 ]}

Отношение было центральной идеей для его универсальной концепции языка или характеристики Universalis , популярной идеи, за которой будут следить его преемники, такие как Готтлоб Фреге и Джордж Бул, в формировании современной символической логики . ^{[ 30 ]} Лейбниц был впервые познакомился с I Ching через его контакт с французским иезуитом Йоахимом Буве , который посетил Китай в 1685 году в качестве миссионера. Лейбниц рассматривал гексаграммы I как утверждение универсальности своих собственных религиозных убеждений как христианина. ^{[ 31 ]} Бинарные цифры были центральными для богословия Лейбниза. Он полагал, что бинарные числа были символом христианской идеи Creatio ex nihilo или творения из ничего. ^{[ 32 ]}

[Концепция, которая] нелегко передать язычникам, - это творение бывшего Нихило через Всемогущую силу Бога. Теперь можно сказать, что ничто в мире не может лучше представить и продемонстрировать эту силу, чем происхождение чисел, так как она представлена здесь с помощью простой и неукрашенной презентации одного и нуля или ничего.
- Письмо Лейбниза к герцогу Брансуику, прикрепленное с I Ching гексаграммами ^{[ 31 ]}

Более поздние события

В 1854 году британский математик Джордж Бул опубликовал знаковую бумагу с подробной информацией о алгебраической системе логики , которая станет известной как логическая алгебра . Его логическое исчисление должно было стать важным в разработке цифровых электронных схем. ^{[ 33 ]}

В 1937 году Клод Шеннон произвел диссертацию своего хозяина в MIT , которая внедрила логическую алгебру и бинарную арифметику, используя электронные реле и переключатели впервые в истории. Под названием символический анализ ретрансляционных цепей и коммутации , тезис Шеннона по существу основал практическую цифровую конструкцию. ^{[ 34 ]}

В ноябре 1937 года Джордж Стибиц , затем работал в Bell Labs , завершил компьютер на основе реле, он назвал «Модель K» (для « K Itchen», где он его собрал), который рассчитывал с использованием бинарного дополнения. ^{[ 35 ]} Bell Labs уполномочил полную исследовательскую программу в конце 1938 года со Стибицем у руля. Их комплексный номер компьютера, завершенный 8 января 1940 года, смог рассчитать комплексные числа . В демонстрации конференции Американского математического общества в Дартмутском колледже смог отправить удаленные команды калькулятора комплекса по телефонам 11 сентября 1940 года Стибиц . Это была первая вычислительная машина, когда -либо использовавшаяся удаленно через телефонную линию. Некоторые участники конференции, которые стали свидетелями демонстрации, были Джон фон Нейманн , Джон Мохли и Норберт Винер , которые написали об этом в своих мемуарах. ^{[ 36 ]}^{[ 37 ]}^{[ 38 ]}

Компьютер Z1 , который был спроектирован и построен Konrad Zuse между 1935 и 1938 годами, использовал логику логики и бинарные номера с плавающей запятой . ^{[ 39 ]}

Представительство

Любое число может быть представлено последовательности битов (двоичные цифры), которая, в свою очередь, может быть представлен любым механизмом, способным быть в двух взаимоисключающих состояниях. Любой из следующих рядов символов может быть истолкован как бинарное числовое значение 667:

1	0	1	0	0	1	1	0	1	1
\|	―	\|	―	―	\|	\|	―	\|	\|
☒	☐	☒	☐	☐	☒	☒	☐	☒	☒
и	не	и	не	не	и	и	не	и	и

Числовое значение, представленное в каждом случае, зависит от значения, назначенного каждому символу. В более ранние дни вычислений, переключателей, перфорированных отверстий и перфорированных бумажных лент использовались для представления двоичных значений. ^{[ 40 ]} В современном компьютере числовые значения могут быть представлены двумя разными напряжениями ; На магнитном диске . магнитные полярности можно использовать «Положительное», « да » или «на» состояние не обязательно эквивалентно численному значению одного; Это зависит от архитектуры в использовании.

В соответствии с обычным представлением цифр с использованием арабских цифр , двоичные числа обычно записываются с использованием символов 0 и 1 . При написании двоичные цифры часто подписываются, префикс или суффикс, чтобы указать их основание или radix . Следующие обозначения эквивалентны:

100101 Бинарный (явное утверждение формата)
100101b (суффикс, указывающий бинарный формат; также известный как конвенция Intel ^{[ 41 ]}^{[ 42 ]})
100101b (суффикс, указывающий бинарный формат)
Bin 100101 (префикс, указывающий бинарный формат)
100101 ₂ (подписка, указывающий на базовую 2 (бинарную) нотацию)
%100101 (префикс, указывающий бинарный формат; также известный как конвенция Motorola ^{[ 41 ]}^{[ 42 ]})
0B100101 (префикс, указывающий бинарный формат, распространен в языках программирования)
6B100101 (префикс, указывающий количество бит в двоичном формате, распространенный на языках программирования)
#B100101 (префикс, указывающий бинарный формат, распространенный на языках программирования LISP)

При говорят, что бинарные цифры обычно читаются по цифровой цифре, чтобы отличить их от десятичных цифр. Например, бинарное число 100 произносится на одну ноль нуля , а не сто , чтобы сделать свою бинарную природу явной и для целей правильности. Поскольку бинарное число 100 представляет значение четырех, было бы смущено называть цифру как сотню (слово, которое представляет совершенно другое значение или количество). В качестве альтернативы, бинарное число 100 может быть рассмотрено как «четыре» (правильное значение ), но это не делает его бинарной природы явной.

Считая в бинарном

Десятичный число	Бинарный число
0	0
1	1
2	10
3	11
4	100
5	101
6	110
7	111
8	1000
9	1001
10	1010
11	1011
12	1100
13	1101
14	1110
15	1111

Подсчет в двоичном языке аналогичен подсчету в любой другой системе чисел. Начиная с одной цифры, подсчет проходит через каждый символ, в растущем порядке. Перед изучением бинарного подсчета полезно кратко обсудить более знакомую систему десятичного подсчета в качестве ориентира.

Десятичное подсчет

Десятичное подсчет использует десять символов от 0 до 9 . Подсчет начинается с постепенной замены наименее значимой цифры (самой правой цифры), которая часто называется первой цифрой . Когда доступные символы для этой позиции исчерпаны, наименее значимая цифра сбросится до 0 , а следующая цифра более высокой значимости (одна позиция слева) увеличивается ( переполнение ) и постепенное замену резюме цифр низкого порядка. Этот метод сброса и переполнения повторяется для каждой цифры значимости. Подсчет прогрессирует следующим образом:

000, 001, 002, ... 007, 008, 009 (самая правая цифра сбросится до нуля, а цифра слева увеличивается)

0 1 0, 011, 012, ...

...

090, 091, 092, ... 097, 098, 099 (самые правые две цифры сброшены на нули, а следующая цифра увеличена)

1 00, 101, 102, ...

Бинарный счет

Бинарный подсчет следует той же процедуре, и опять же, постепенная замена начинается с наименее значимой бинарной цифры или бита (самая правая, также называемая первым битом только два символа 0 и 1 ), за исключением того, что доступны . Таким образом, после того, как немного достигает 1 в двоичном языке, приращение сбрасывает его до 0, но также вызывает увеличение следующего бита влево:

0000,

000 1 , (самый правый бит начинается, и следующий бит увеличивается)

00 1 0, 0011 (самые правые два бита начинаются заново, а следующий бит увеличивается)

0 1 00, 0101, 0110, 0111, (самые правые три бита запускаются, и следующий бит увеличен)

1 000, 1001, 1010, 1011, 1100, 1101, 1110, 1111 ...

В бинарной системе каждый бит представляет собой растущую мощность 2, причем самый правый бит представляет 2 ⁰, следующий, представляющий 2 ¹, затем 2 ², и так далее. Значение бинарного числа - это сумма полномочий 2, представленных каждым битом «1». Например, двоичное число 100101 преобразуется в десятичную форму следующим образом:

100101 ₂ = [ ( 1 ) × 2 ⁵ ] + [ ( 0 ) × 2 ⁴ ] + [ ( 0 ) × 2 ³ ] + [ ( 1 ) × 2 ² ] + [ ( 0 ) × 2 ¹ ] + [ ( 1 ) × 2 ⁰ ]

100101 ₂ = [ 1 × 32 ] + [ 0 × 16 ] + [ 0 × 8 ] + [ 1 × 4 ] + [ 0 × 2 ] + [ 1 × 1 ]

100101 ₂ = 37 ₁₀

Фракции

Фракции в бинарной арифметике прекращаются только в том случае, если знаменатель является силой 2 . В результате 1/10 не имеет конечного бинарного представления ( 10 имеет основные факторы 2 и 5 ). Это приводит к тому, что 10 × 1/10 не будет точно равным 1 в бинарной арифметике с плавающей точкой . В качестве примера, чтобы интерпретировать бинарное выражение для 1/3 = .010101 ..., это означает: 1/3 = 0 × 2 ⁻¹ + 1 × 2 ⁻² + 0 × 2 ⁻³ + 1 × 2 ⁻⁴ + ... = 0,3125 + ... точное значение не может быть найдено с суммой конечного числа обратных мощностей двух, нулей и одних в двоичном представлении 1/3 альтернативных навсегда.

Фракция	Десятичный	Бинарный	Дробное приближение
1/1	1 или 0,999 ...	1 или 0. 1	1/2 + 1/4 + 1/8...
1/2	0,5 или 0,4999 ...	0,1 или 0,0 1	1/4 + 1/8 + 1/16 . . .
1/3	0.333...	0. 01	1/4 + 1/16 + 1/64 . . .
1/4	0,25 или 0,29996 ...	0,01 или 0,00 1	1/8 + 1/16 + 1/32 . . .
1/5	0,2 или 0,1990 ...	0. 0011	1/8 + 1/16 + 1/128 . . .
1/6	0.1666...	0.001 01	1/8 + 1/32 + 1/128 . . .
1/7	0.142857142857...	0. 001	1/8 + 1/64 + 1/512 . . .
1/8	0,125 или 0,124999 ...	0,001 или 0,000 1	1/16 + 1/32 + 1/64 . . .
1/9	0.111...	0. 000111	1/16 + 1/32 + 1/64 . . .
1/10	0,1 или 0,0999 ...	0.0 0011	1/16 + 1/32 + 1/256 . . .
1/11	0.090909...	0. 0001011101	1/16 + 1/64 + 1/128 . . .
1/12	0.08333...	0.0001 01	1/16 + 1/64 + 1/256 . . .
1/13	0.076923076923...	0. 000100111011	1/16 + 1/128 + 1/256 . . .
1/14	0.0714285714285...	0.0 001	1/16 + 1/128 + 1/1024 . . .
1/15	0.0666...	0. 0001	1/16 + 1/256 . . .
1/16	0,0625 или 0,0624999 ...	0,0001 или 0,0000 1	1/32 + 1/64 + 1/128 . . .

Бинарная арифметика

Арифметика в бинарном языке очень похожа на арифметику в других позиционных обозначений системах цифр . Добавление, вычитание, умножение и деление могут быть выполнены на бинарных цифрах.

Добавление

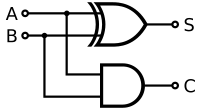
Самая простая арифметическая операция в бинарной форме - дополнение. Добавление двух однозначных двоичных чисел относительно просто, используя форму переноса:

0 + 0 → 0

0 + 1 → 1

1 + 0 → 1

1 + 1 → 0, переносить 1 (так как 1 + 1 = 2 = 0 + (1 × 2 ¹) )

Добавление двух цифр «1» дает цифру «0», а 1 необходимо будет добавить в следующий столбец. Это похоже на то, что происходит в десятичном виде, когда определенные однозначные числа объединяются вместе; Если результат равен или превышает значение Radix (10), цифра слева увеличивается:

5 + 5 → 0, переносить 1 (так как 5 + 5 = 10 = 0 + (1 × 10 ¹) )

7 + 9 → 6, переносить 1 (с 7 + 9 = 16 = 6 + (1 × 10 ¹) )

Это известно как ношение . Когда результат добавления превышает значение цифры, процедура состоит в том, чтобы «переносить» избыточное количество, деленное на Radix (то есть 10/10) слева, добавив его к следующему позиционному значению. Это правильно, так как следующая позиция имеет вес, который выше фактором, равным Radix. Ношение работы одинаково в бинарном виде:

  1 1 1 1 1    (carried digits)
    0 1 1 0 1
+   1 0 1 1 1
-------------
= 1 0 0 1 0 0 = 36

В этом примере добавляются два цифры: 01101 ₂ (13 ₁₀ ) и 10111 ₂ (23 ₁₀ ). Верхний ряд показывает используемые биты переноса. Начиная с самого правого столбца, 1 + 1 = 10 ₂ . 1 переносится слева, а 0 записывается в нижней части правого столбца. Второй столбец с правого добавляется: 1 + 0 + 1 = 10 ₂ снова; 1 переносится, а 0 записано внизу. Третий столбец: 1 + 1 + 1 = 11 ₂ . На этот раз 1 переносится, а 1 написан в нижнем ряду. Такое разбирательство дает окончательный ответ 100100 ₂ (36 ₁₀ ).

Когда компьютеры должны добавлять два числа, правило, которое: x xor y = (x + y) mod 2 Для любых двух битов x и y также позволяют очень быстро расчет.

Метод длительного переноса

Упрощением для многих бинарных проблем с добавлением является «метод долгого переноса» или «Брукхаус метод бинарного добавления». Этот метод особенно полезен, когда одно из чисел содержит длинный участок. Он основан на простой предпосылке, которая при бинарной системе, когда ему дают участок цифр, полностью составленные исключительно из n Ones (где n - любая целочисленная длина), добавление 1 приведет к номеру 1, за которой следует строка из n Zeros. Эта концепция следует, логически, как в десятичной системе, где добавление 1 к строке n 9s приведет к номеру 1, за которым следует строка из n 0s:

     Binary                        Decimal
    1 1 1 1 1     likewise        9 9 9 9 9
 +          1                  +          1
  ———————————                   ———————————
  1 0 0 0 0 0                   1 0 0 0 0 0

Такие длинные струны довольно распространены в бинарной системе. Из этого можно обнаружить, что большие бинарные числа могут быть добавлены с использованием двух простых шагов, без чрезмерных операций переноса. В следующем примере добавляются два цифры: 1 1 1 1 0 1 1 1 1 1 0 ₂ (958 ₁₀ ) и 1 0 1 0 1 1 0 0 1 1 ₂ (691 ₁₀ ), используя метод традиционного переноса. слева и метод длинного переноса справа:

Traditional Carry Method                       Long Carry Method
                                vs.
  1 1 1   1 1 1 1 1      (carried digits)   1 ←     1 ←            carry the 1 until it is one digit past the "string" below
    1 1 1 0 1 1 1 1 1 0                       1 1 1 0 1 1 1 1 1 0  cross out the "string",
+   1 0 1 0 1 1 0 0 1 1                   +   1 0 1 0 1 1 0 0 1 1  and cross out the digit that was added to it
———————————————————————                    ——————————————————————
= 1 1 0 0 1 1 1 0 0 0 1                     1 1 0 0 1 1 1 0 0 0 1

Верхний ряд показывает используемые биты переноса. Вместо стандартного переноса от одного столбца в другой, можно добавить «1» с самым низким порядком с «1» в соответствующем значении места под ним, и «1» может быть перенесен на одну цифру после конца конца ряд. «Используемые» числа должны быть скрещены, так как они уже добавлены. Другие длинные строки также могут быть отменены с использованием той же техники. Затем просто объедините все оставшиеся цифры обычно. Работа таким образом дает окончательный ответ 1 1 0 0 1 1 1 0 0 0 1 ₂ (1649 ₁₀ ). В нашем простом примере с использованием небольших чисел метод традиционного переноса требовал восемь операций переноса, однако метод длительного переноса требовал только двух, что представляет существенное сокращение усилий.

Дополнительная таблица

	0	1
0	0	1
1	1	10

Таблица бинарной добавления аналогична, но не такая же, как таблица истинности логической дизъюнкции операции $\lor$ Полем Разница в том, что $1\lor 1=1$ , пока $1+1=10$ .

Вычитание

Вычитание работает почти так же:

0 − 0 → 0

0 - 1 → 1, займи 1

1 − 0 → 1

1 − 1 → 0

Вычитание «1» цифры из цифры «0» дает цифру «1», в то время как 1 должна быть вычтена из следующего столбца. Это известно как заимствование . Принцип такой же, как и для переноски. Когда результат вычитания составляет меньше 0, наименьшее возможное значение цифры, процедура состоит в том, чтобы «позаимствовать» дефицит, разделенный на Radix (то есть 10/10) слева, вычитая его из следующего позиции ценить.

    *   * * *   (starred columns are borrowed from)
  1 1 0 1 1 1 0
−     1 0 1 1 1
----------------
= 1 0 1 0 1 1 1

  *             (starred columns are borrowed from)
  1 0 1 1 1 1 1
–   1 0 1 0 1 1
----------------
= 0 1 1 0 1 0 0

Вычитание положительного числа эквивалентно добавлению равного отрицательного числа абсолютного значения . Компьютеры используют подписанные репрезентации для обработки отрицательных чисел - чаще всего обозначения двух комплемента . Такие представления устраняют необходимость в отдельной операции «вычитания». Используя нотацию двух комплемента, вычитание может быть обобщено следующей формулой:

A - b = a + не b + 1

Умножение

Умножение в двоичном языке аналогично его десятичному аналому. Два числа А и B может быть умножен на частичные продукты: для каждой цифры в Б , продукт этой цифры в A рассчитывается и записывается на новой линии, сдвинутой влево так, чтобы его самая правая цифра выступила с цифрой в Б, который использовался. Сумма всех этих частичных продуктов дает конечный результат.

Поскольку в двоичном биназе есть только две цифры, есть только два возможных результата каждого частичного умножения:

Если цифра в B равен 0, частичный продукт также 0
Если цифра в B равен 1, частичный продукт равен А

Например, двоичные номера 1011 и 1010 умножаются следующим образом:

           1 0 1 1   (A)
         × 1 0 1 0   (B)
         ---------
           0 0 0 0   ← Corresponds to the rightmost 'zero' in B
   +     1 0 1 1     ← Corresponds to the next 'one' in B
   +   0 0 0 0
   + 1 0 1 1
   ---------------
   = 1 1 0 1 1 1 0

Бинарные числа также могут быть умножены на биты после двоичной точки :

               1 0 1 . 1 0 1     A (5.625 in decimal)
             × 1 1 0 . 0 1       B (6.25 in decimal)
             -------------------
                   1 . 0 1 1 0 1   ← Corresponds to a 'one' in B
     +           0 0 . 0 0 0 0     ← Corresponds to a 'zero' in B
     +         0 0 0 . 0 0 0
     +       1 0 1 1 . 0 1
     +     1 0 1 1 0 . 1
     ---------------------------
     =   1 0 0 0 1 1 . 0 0 1 0 1 (35.15625 in decimal)

См. Также алгоритм умножения Бута .

Таблица умножения

	0	1
0	0	0
1	0	1

Таблица бинарного умножения такая же, как и истина, логического соединения таблица $\land$ .

Разделение

Длительное разделение в бинарном виде снова похоже на его десятичный аналог.

В приведенном ниже примере делитель составляет 101 ₂ , или 5 в десятичном виде, а дивиденд - 11011 ₂ , или 27 в десятичном. Процедура такая же, как и у десятичного длинного деления ; Здесь Divisor 101 ₂ входит в первые три цифры 110 ₂ дивидендов один раз, поэтому на верхней строке написан «1». Этот результат умножается на делитель и вычитается из первых трех цифр дивидендов; Следующая цифра (A «1») включена для получения новой трехзначной последовательности:

              1
        ___________
1 0 1   ) 1 1 0 1 1
        − 1 0 1
          -----
          0 0 1

Затем процедура повторяется с новой последовательности, продолжая до тех пор, пока цифры в дивиденде не будут исчерпаны:

             1 0 1
       ___________
1 0 1  ) 1 1 0 1 1
       − 1 0 1
         -----
             1 1 1
         −   1 0 1
             -----
             0 1 0

Таким образом, коэффициент 11011 _2, деленная на 101 ₂ , составляет 101 ₂ , как показано на верхней линии, в то время как оставшаяся часть, показанная на нижней линии, составляет 10 ₂ . В десятичном режиме это соответствует тому факту, что 27, разделенные на 5, составляет 5, с оставшейся частью 2.

Помимо длинного деления, можно также разработать процедуру, чтобы обеспечить чрезмерную отгрузку от частичного оставшегося на каждой итерации, что приводит к альтернативным методам, которые являются менее систематическими, но в результате более гибких.

Квадратный корень

Процесс принятия бинарной квадратной корневой цифры с помощью цифр такой же, как и для десятичного квадратного корня и объясняется здесь . Примером:

             1 0 0 1
            ---------
           √ 1010001
             1
            ---------
      101     01 
               0
             --------
      1001     100
                 0
             --------
      10001    10001
               10001
              -------
                   0

Побитовые операции

Хотя это и не связано прямо с численной интерпретацией бинарных символов, последовательности битов могут манипулировать с использованием логических операторов . Когда таким образом манипулируется строкой бинарных символов, она называется кусочкой ; Логические операторы и , или и XOR могут выполняться на соответствующих битах в двух двоичных цифрах, предоставленных в качестве входных данных. Операция Logical Not может выполняться на отдельных битах в одном двоичном цифре, предоставленном в качестве входных данных. Иногда такие операции могут использоваться в качестве арифметических коротких вырубков, а также могут иметь и другие вычислительные преимущества. Например, арифметический сдвиг, слева от бинарного числа, является эквивалентом умножения на (положительную, интегральную) силу 2.

Преобразование в другие системы чисел и из них

Десятичный до бинарного

Преобразование (357) ₁₀ в бинарную обозначения приводит к (101100101)

базовых 10 Чтобы преобразовать из целого числа в эквивалент базы-2 (бинарный), число делится на два . Остальная часть является наименее знаменитым битом . Коэффициент снова разделен на два; Его остаток становится следующим наименее значительным битом. Этот процесс повторяется до тех пор, пока не будет достигнут коэффициент одного из них. Последовательность остатков (включая окончательный коэффициент одного) образует двоичное значение, так как каждый остаток должен быть либо нулевым, либо один при разделении на два. Например, (357) ₁₀ выражается как (1011001011111) _2.^{[ 43 ]}

Бинарный до десятичного десятичного

Преобразование из базы-2 в базу-10 просто инвертирует предыдущий алгоритм. Биты бинарного числа используются один за другим, начиная с наиболее значимого (наиболее левого) бита. Начиная со значения 0, предварительное значение удваивается, а затем добавляется следующий бит, чтобы получить следующее значение. Это может быть организовано в многоцелевой столе. Например, чтобы преобразовать 10010101101 ₂ в десятичное значение:

Предварительное значение	× 2 +	Следующий бит	= Следующее значение
0	× 2 +	1	= 1
1	× 2 +	0	= 2
2	× 2 +	0	= 4
4	× 2 +	1	= 9
9	× 2 +	0	= 18
18	× 2 +	1	= 37
37	× 2 +	0	= 74
74	× 2 +	1	= 149
149	× 2 +	1	= 299
299	× 2 +	0	= 598
598	× 2 +	1	= 1197

Результат 1197 ₁₀ . Первое предварительное значение 0 является просто начальным десятичным значением. Этот метод является применением схемы Хорнера .

Бинарный	1	0	0	1	0	1	0	1	1	0	1
Десятичный	1×2 ¹⁰ +	0×2 ⁹ +	0×2 ⁸ +	1×2 ⁷ +	0×2 ⁶ +	1×2 ⁵ +	0×2 ⁴ +	1×2 ³ +	1×2 ² +	0×2 ¹ +	1×2 ⁰ =	1197

Дробные части числа преобразуются с помощью аналогичных методов. Они снова основаны на эквивалентности смещения с удвоением или вдвое.

В дробном двоичном числе, таком как 0,110101101011 ₂ , первая цифра ${\textstyle {\frac {1}{2}}}$ , второй ${\textstyle ({\frac {1}{2}})^{2}={\frac {1}{4}}}$ и т. д. Итак, если есть 1, в первую очередь после десятичного десятичного ${\textstyle {\frac {1}{2}}}$ и наоборот. Вдвое это число - по крайней мере 1. Это предполагает алгоритм: неоднократно удваивает число, которое нужно преобразовать, запишите, если результат составляет не менее 1, а затем выбросьте целочисленную часть.

Например, ${\textstyle ({\frac {1}{3}})_{10}}$ , в бинарном, есть:

Конвертирование	Результат
${\textstyle {\frac {1}{3}}}$	0.
${\textstyle {\frac {1}{3}}\times 2={\frac {2}{3}}<1}$	0.0
${\textstyle {\frac {2}{3}}\times 2=1{\frac {1}{3}}\geq 1}$	0.01
${\textstyle {\frac {1}{3}}\times 2={\frac {2}{3}}<1}$	0.010
${\textstyle {\frac {2}{3}}\times 2=1{\frac {1}{3}}\geq 1}$	0.0101

Таким образом, повторяющаяся десятичная доля 0. 3 ... эквивалентна повторной бинарной фракции 0. 01 ....

Или, например, 0,1 ₁₀ в двоичном

Конвертирование	Результат
0.1	0.
0,1 × 2 = 0,2 <1	0.0
0,2 × 2 = 0,4 <1	0.00
0,4 × 2 = 0,8 <1	0.000
0.8 × 2 = 1.6 ≥ 1	0.0001
0.6 × 2 = 1.2 ≥ 1	0.00011
0,2 × 2 = 0,4 <1	0.000110
0,4 × 2 = 0,8 <1	0.0001100
0.8 × 2 = 1.6 ≥ 1	0.00011001
0.6 × 2 = 1.2 ≥ 1	0.000110011
0,2 × 2 = 0,4 <1	0.0001100110

Это также повторяющаяся бинарная фракция 0,0 0011 ... Может быть удивительным, что завершение десятичных дробей может иметь повторяющиеся расширения в бинарном. Именно по этой причине многие удивляются, обнаружив, что 1/10 + ... + 1/10 (добавление 10 чисел) отличается от 1 в бинарной арифметике с плавающей запятой . Фактически, единственные бинарные фракции с прекращающими расширениями имеют форму целого числа, деленных на силу 2, которой нет 1/10.

Окончательное преобразование - от двоичных до десятичных дробей. Единственная трудность возникает с повторными фракциями, но в остальном метод состоит в том, чтобы сдвинуть фракцию на целое число, преобразовать ее, как указано выше, а затем делить на соответствующую силу двух в десятичной основе. Например:

${\begin{aligned}x&=&1100&.1{\overline {01110}}\ldots \\x\times 2^{6}&=&1100101110&.{\overline {01110}}\ldots \\x\times 2&=&11001&.{\overline {01110}}\ldots \\x\times (2^{6}-2)&=&1100010101\\x&=&1100010101/111110\\x&=&(789/62)_{10}\end{aligned}}$

Еще один способ превращения из бинарного в десятичный, часто быстрее для человека, знакомного с шестнадцатеричным , - это сделать это косвенно - первое конвертирование ( $x$ в бинарном) в ( $x$ в шестнадцатеричной), а затем преобразование ( $x$ в шестнадцатеричном) в ( $x$ в десятичном).

Для очень больших чисел эти простые методы неэффективны, поскольку они выполняют большое количество умножений или подразделений, где один операнд очень большой. Простой алгоритм разделения и подтверждает более эффективен асимптотически: учитывая бинарное число, он разделен на 10 ^k, где k выбирается так, чтобы коэффициент примерно равнялся оставшимся; Затем каждая из этих произведений преобразуется в десятичное значение, и они объединяются . Учитывая десятичное число, его можно разделить на два части примерно одного размера, каждый из которых преобразуется в двоичный файл, после чего первая преобразованная часть умножается на 10 ^k и добавлено ко второй преобразованной части, где k -это количество десятичных цифр во второй, наименее значительной части перед преобразованием.

Шестнадцатеричный

0 _гекс	=	0 _{декабря}	=	0 _{октября}	0	0	0	0
1 _гекс	=	1 _{декабря}	=	1 _{октября}	0	0	0	1
2 _гекс	=	2 _{декабря}	=	2 _{октября}	0	0	1	0
3 _гекс	=	3 _{декабря}	=	3 _{октября}	0	0	1	1

4 _гекс	=	4 _{декабря}	=	4 _{октября}	0	1	0	0
5 _HEX	=	5 _{декабря}	=	5 _{октября}	0	1	0	1
6 _гекс	=	6 _{декабря}	=	6 _{октября}	0	1	1	0
7 _гекс	=	7₇	=	7 _{октября}	0	1	1	1

8 _гекс	=	8 _{декабря}	=	10 _{октября}	1	0	0	0
9 _Гекс	=	9 _{декабря}	=	11 _{октября}	1	0	0	1
Гекс	=	10 _{декабря}	=	12 _{октября}	1	0	1	0
B _HEX	=	11 _{декабря}	=	13 _{октября}	1	0	1	1

C _HEX	=	12 _{декабря}	=	14 _{октября}	1	1	0	0
D _Hex	=	13 _{декабря}	=	15 _{октября}	1	1	0	1
E _Hex	=	14 _{декабря}	=	16 _{октября}	1	1	1	0
F _Hex	=	15 _{декабря}	=	17 _{октября}	1	1	1	1

Бинарник может быть более легко преобразован в и из шестнадцатеричного. Это связано с тем, что Radix шестнадцатеричной системы (16) является мощностью Radix бинарной системы (2). Более конкретно, 16 = 2 ⁴Таким образом, для представления одной цифры шестнадцатеричной, как показано в соседней таблице, требуется четыре цифры бинарных знаков.

Чтобы преобразовать шестнадцатеричное число в его бинарный эквивалент, просто замените соответствующие бинарные цифры:

3a ₁₆ = 0011 1010 ₂

E7 ₁₆ = 1110 0111 ₂

Чтобы преобразовать бинарное число в его шестнадцатеричный эквивалент, разделите его на группы по четырем битам. Если количество битов не множество из четырех, просто вставьте дополнительные 0 битов влево (называемой накладной ). Например:

1010010 ₂ = 0101 0010 сгруппирован с прокладкой = 52 ₁₆

11011101 ₂ = 1101 1101 Группирован = DD ₁₆

Чтобы преобразовать шестнадцатеричное число в его десятичный эквивалент, умножьте десятичный эквивалент каждой шестнадцатеричной цифры на соответствующую мощность 16 и добавьте полученные значения:

C0E7 ₁₆ = (12 × 16 ³) + (0 × 16 ²) + (14 × 16 ¹) + (7 × 16 ⁰) = (12 × 4096) + (0 × 256) + (14 × 16) + (7 × 1) = 49,383 ₁₀

Восьми

Бинарник также легко преобразуется в восьмимерную систему цифр, поскольку воськал использует Radix 8, который является силой двух (а именно 2 ³, поэтому для представления восьми цифр) требуется ровно три двоичных цифр). Переписка между восьмисенцами и бинарными цифрами такая же, как и для первых восьми цифр шестнадцатеричных в таблице выше. Бинарный 000 эквивалентен восьмиуровне 0, бинарный 111 эквивалентен октальному 7 и т. Д.

Восьми	Бинарный
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

Конвертирование из восьми в двоичную доходу так же, как и для шестнадцатеричной :

65 ₈ = 110 101 ₂

17 ₈ = 001 111 ₂

И от бинарного до восьмиугольника:

101100 ₂ = 101 100 ₂ Группирован = 54 ₈

10011 ₂ = 010 011 ₂ сгруппировано с прокладкой = 23 ₈

И от октального до десятичного десятичного:

65 ₈ = (6 × 8 ¹) + (5 × 8 ⁰) = (6 × 8) + (5 × 1) = 53 ₁₀

127 ₈ = (1 × 8 ²) + (2 × 8 ¹) + (7 × 8 ⁰) = (1 × 64) + (2 × 8) + (7 × 1) = 87 ₁₀

Представляя реальные числа

Неинтегеры могут быть представлены с использованием отрицательных мощностей, которые изложены из других цифр с помощью точки Radix (называемой десятичной точкой в десятичной системе). Например, двоичное число 11.01 ₂ означает:

1 × 2 ¹	(1 × 2 = 2 )	плюс
1 × 2 ⁰	(1 × 1 = 1 )	плюс
0 × 2 ⁻¹	(0 × 1 ⁄ 2 = 0 )	плюс
1 × 2 ⁻²	(1 × 1 ⁄ 4 = 0.25 )

В общей сложности 3,25 десятичных знаков.

Все диадические рациональные числа ${\frac {p}{2^{a}}}$ Иметь прекращение бинарного цифра - двоичное представление имеет конечное количество терминов после точки Радикса. Другие рациональные числа имеют бинарное представление, но вместо того, чтобы заканчивать, они повторяются , с конечной последовательности цифр, повторяющихся на неопределенный срок. Например

${\frac {1_{10}}{3_{10}}}={\frac {1_{2}}{11_{2}}}=0.01010101{\overline {01}}\ldots \,_{2}$ ${\frac {12_{10}}{17_{10}}}={\frac {1100_{2}}{10001_{2}}}=0.1011010010110100{\overline {10110100}}\ldots \,_{2}$

Феномен того, что бинарное представление любого рационального заканчивается, либо повторяется, также происходит в других системах численности на основе Radix. Смотрите, например, объяснение в десятичном . Другое сходство - это существование альтернативных представлений для любого прекращающего представления, полагаясь на тот факт, что 0,111111 ... является суммой геометрической серии 2 ⁻¹ + 2 ⁻² + 2 ⁻³ + ... что 1.

Бинарные цифры, которые не заканчивают, и не представляют иррациональные цифры . Например,

0.10100100010000100000100 ... имеет шаблон, но это не повторяющаяся схема фиксированной длины, поэтому число иррационально
1.01101010000010011110011111111111110 ... это двоичное представление ${\sqrt {2}}$ , квадратный корень 2 , еще один иррациональный. У него нет заметного рисунка.

Смотрите также

Ссылки

^ «3.3. Бинарный и его преимущества - CS160 Reader» . Computerscience.chemeketa.edu . Получено 22 мая 2022 года .
^ Робсон, Элеонора ; Стедолл, Жаклин , ред. (2009), «Миф № 2: Фракции глаз Хора», Оксфордский справочник по истории математики , Oxford University Press, p. 790, ISBN 9780199213122
^ Chrisomalis, Stephen (2010), Численная нотация: сравнительная история , издательство Кембриджского университета, с. 42–43, ISBN 9780521878180 .
^ Rudman, Peter Strom (2007), Как произошла математика: первые 50 000 лет , Prometheus Books, с. 135–136, ISBN 9781615921768 .
^ Jump up to: ^а ^{беременный} Эдвард Хакер; Стив Мур; Лоррейн Патско (2002). I Ching: аннотированная библиография . Routledge. п. 13. ISBN 978-0-415-93969-0 .
^ Jump up to: ^а ^{беременный} Редмонд, Джеффри; Hon, Tze-Ki (2014). Учите I Ching . Издательство Оксфордского университета. п. 227. ISBN 978-0-19-976681-9 .
^ Jump up to: ^а ^{беременный} Джонатан Шектман (2003). Новаторские научные эксперименты, изобретения и открытия 18 -го века . Greenwood Publishing. п. 29. ISBN 978-0-313-32015-6 .
^ Маршалл, Стив. «Последовательности гексаграммы Yijing: квадрат Шао Юн (последовательность fuxi)» . Получено 15 сентября 2022 года . Вы могли бы сказать, что [бинарная последовательность Fuxi] - это более разумный способ отмены гексаграммы как двоичные цифры ... рассуждения, если таковые имеются, которые сообщают [Королев WEN] последовательность неизвестна.
^ Чжунляйан, Ши; Венжао, Ли; Power, Hans (2000). GW Leibnisim Syna 1697: Берлин 4. Бис 7. Баттобер Франц Штайнер Верлаг. стр. 165–170. ISBN 3515074481 .
^ Коллинз, Дерек (2008). «Сопоставление внутренностей: практика греческой гепатоскопии» . Американский журнал филологии . 129 (3): 319–345. ISSN 0002-9475 .
^ Джонстон, Сара Илс (2008). Древнегреческий гадания . Блэквелл Древние религии (1. Малден, Массачусетс: Wiley-Blackwell. ISBN 978-1-4051-1573-5 .
^ Санчес, Хулио; Кантон, Мария П. (2007). Программирование микроконтроллера: Microchip Pic . Бока Ратон, Флорида: CRC Press. п. 37. ISBN 978-0-8493-7189-9 .
^ WS Anglin и J. Lambek, The Heritage of Thales , Springer, 1995, ISBN 0-387-945444-X
^ Математика для поэтов и барабанщиков архивировала 16 июня 2012 года на машине Wayback (PDF, 145 КБ)
^ Стахов, Алексей ; Олсен, Скотт Энтони (2009). Математика гармонии: от Евклида до современной математики и информатики . Мировой научный. ISBN 978-981-277-582-5 .
^ Б. Ван Нутен, «Бинарные числа в индийской древности», Журнал индийских исследований, том 21, 1993, с. 31–50
^ Ландри, Тимоти Р. (2019). Vodún: секретность и поиск божественной силы . Современная этнография (1 -е изд.). Филадельфия: Университет Пенсильвании Пресс. п. 25. ISBN 978-0-8122-5074-9 .
^ Ландри 2019 , с. 154
^ «Система гадания IFA» . Получено 5 июля 2017 года .
^ Бендер, Андреа; Беллер, Зигард (16 декабря 2013 г.). «Мангареван изобретение бинарных шагов для облегчения расчета» . Труды Национальной академии наук . 111 (4): 1322–1327. doi : 10.1073/pnas.1309160110 . PMC 3910603 . PMID 24344278 .
^ Бауэрн, Клэр; Zentz, Джейсон (2012). «Разнообразие в системах цифр австралийских языков» . Антропологическая лингвистика . 54 (2): 133–160. ISSN 0003-5483 . JSTOR 23621076 .
^ (См. Bonner 2007 [1] Архивировано 3 апреля 2014 года в The Wayback Machine , Fidora et al. 2011 [2] Архивировано 8 апреля 2019 года на машине Wayback )
^ Jump up to: ^а ^{беременный} Бэкон, Фрэнсис (1605). «Содействие обучению» . Лондон с. Глава 1.
^ Ширли, Джон У. (1951). «Бинарная нумерация перед Лейбнизом». Американский журнал физики . 19 (8): 452–454. Bibcode : 1951amjph..19..452s . doi : 10.1119/1.1933042 .
^ Ineichen, R. (2008). «Лейбник, Карамуил, Харро и двойная система» (PDF) . Сообщения от немецкой математической ассоциации (на немецком языке). 16 (1): 12–15. Doi : 10.1515/dmvm-2008-0009 . S2CID 179000299 .
^ Jump up to: ^а ^{беременный} ^в Стрикленд, Ллойд (2020), Шрираман, Бхарат (ред.), «Лейбниц по системам номеров» , Справочник по истории и философии математической практики , Cham: Springer International Publishing, стр. 1–31, DOI : 10.1007/978- 3-030-19071-2_90-1 , ISBN 978-3-030-19071-2 , Получено 20 августа 2024 г.
^ Jump up to: ^а ^{беременный} Лейбниц Г., Объяснение бинарной арифметики, Die Mathematische Schriften, ed. C. Gerhardt, Berlin 1879, Vol. Энтузиазм перевод [3]
^ "Bouvet и Leibniz: научная переписка" , Swiderski 1980
^ Лейбниц : «Китайцы потеряли значение ковы или линий Фуси, возможно, более тысячи лет назад, и они написали комментарии по предмету, в котором они искали, я не знаю, что далеко не знает, так что их истина Объяснение теперь должно прийти от европейцев. ³ знаменитый французский иезуит, который живет в Пекине, мой метод подсчета на 0 и 1, и больше ничего не требовалось, чтобы заставить его признать, что это был ключом к фигурам Фуси. Пишу мне 14 ноября 1701 года, он прислал мне великую фигуру философского принца, которая достигает 64 и не оставляет никакого места, чтобы сомневаться в правде о нашем интерпретации, так что можно сказать, что этот отец расшифровал загадку Фуси, с помощью того, что я сообщил ему. И поскольку эти фигуры, пожалуй, самый древний памятник [GM VII, P227], которая существует в мире, это реституция их значения, после такого большого интервала времени, будет казаться тем более любопытным ».
^ Эйтон, Эрик Дж. (1985). Лейбниц: биография Тейлор и Фрэнсис. Стр. 245–8 ISBN 0-85274-470-6 .
^ Jump up to: ^а ^{беременный} Джех Смит (2008). Лейбниц: Какой рационалист?: Какой рационалист? Полем Спрингер. п. 415. ISBN 978-1-4020-8668-7 .
^ Юен-Тин Лай (1998). Лейбник, Мистика и религия . Спрингер. С. 149–150. ISBN 978-0-7923-5223-5 .
^ Бул, Джордж (2009) [1854]. Исследование законов мышления, на которых основаны математические теории логики и вероятностей (Macmillan, публикации Dover, перепечатаны с исправлениями [1958] из.). Нью -Йорк: издательство Кембриджского университета. ISBN 978-1-108-00153-3 .
^ Шеннон, Клод Элвуд (1940). Символический анализ ретрансляционных цепей (тезис). Кембридж: Массачусетский технологический институт. HDL : 1721.1/11173 .
^ «Зал славы национальных изобретателей - Джордж Р. Стибиц» . 20 августа 2008 года. Архивировано с оригинала 9 июля 2010 года . Получено 5 июля 2010 года .
^ "Джордж Стибиц: Био" . Департамент математики и компьютерных наук, Университет Денисона. 30 апреля 2004 года . Получено 5 июля 2010 года .
^ «Пионеры - люди и идеи, которые имели значение - Джордж Стибиц (1904–1995)» . Керри Редшоу. 20 февраля 2006 г. Получено 5 июля 2010 года .
^ «Джордж Роберт Стибиц - некролог» . Компьютерная история Ассоциации Калифорнии. 6 февраля 1995 г. Получено 5 июля 2010 года .
^ Рохас, Рауль (апрель -июнь 1997). «Наследие Конрада Зуса: архитектура Z1 и Z3» (PDF) . IEEE ANNALS ИСТОРИЯ ИСКУССТВА . 19 (2): 5–16. doi : 10.1109/85.586067 . Архивировано (PDF) из оригинала 3 июля 2022 года . Получено 3 июля 2022 года . (12 страниц)
^ «Представление бинарного - ревизия 1 - компьютерная наука GCSE» . Би -би -си . Получено 26 июня 2019 года .
^ Jump up to: ^а ^{беременный} Кювелер, Герд; Schwoch, Дитрих (2013) [1996]. Рабочая книга по информатике - практика - ориентированное на введение в обработку данных с задачей проекта (на немецком языке). Vieweg-Verlag, переиздание: Springer-Verlag. Doi : 10.1007/978-3-322-92907-5 . ISBN 978-3-528-04952-2 . 9783322929075.
^ Jump up to: ^а ^{беременный} Кювелер, Герд; Шух, Дитрих (4 октября 2007 г.). Компьютерная наука для инженеров и натуральных ученых: технология ПК и микрокомпьютера, компьютерные сети (на немецком языке). Том 2 (5 изд.). Vieweg, переиздание: Springer-Verlag. ISBN 978-3834891914 . 9783834891914.
^ «Базовая система» . Архивировано с оригинала 23 октября 2017 года . Получено 31 августа 2016 года .

Внешние ссылки

Бинарная система в кусочке
Преобразование фракций в узле
Билайлеральная система цифр сэра Фрэнсиса Бэкона архивировала 23 сентября 2016 года на машине Wayback , предшествует системе бинарных чисел.

[1] «3.3. Бинарный и его преимущества - CS160 Reader» . Computerscience.chemeketa.edu . Получено 22 мая 2022 года .

[2] Робсон, Элеонора ; Стедолл, Жаклин , ред. (2009), «Миф № 2: Фракции глаз Хора», Оксфордский справочник по истории математики , Oxford University Press, p. 790, ISBN 9780199213122

[3] Chrisomalis, Stephen (2010), Численная нотация: сравнительная история , издательство Кембриджского университета, с. 42–43, ISBN 9780521878180 .

[4] Rudman, Peter Strom (2007), Как произошла математика: первые 50 000 лет , Prometheus Books, с. 135–136, ISBN 9781615921768 .

[HackerMoore2002-5] Jump up to: ^а ^{беременный} Эдвард Хакер; Стив Мур; Лоррейн Патско (2002). I Ching: аннотированная библиография . Routledge. п. 13. ISBN 978-0-415-93969-0 .

[redmond-hon-6] Jump up to: ^а ^{беременный} Редмонд, Джеффри; Hon, Tze-Ki (2014). Учите I Ching . Издательство Оксфордского университета. п. 227. ISBN 978-0-19-976681-9 .

[scientific-7] Jump up to: ^а ^{беременный} Джонатан Шектман (2003). Новаторские научные эксперименты, изобретения и открытия 18 -го века . Greenwood Publishing. п. 29. ISBN 978-0-313-32015-6 .

[Marshall-8] Маршалл, Стив. «Последовательности гексаграммы Yijing: квадрат Шао Юн (последовательность fuxi)» . Получено 15 сентября 2022 года . Вы могли бы сказать, что [бинарная последовательность Fuxi] - это более разумный способ отмены гексаграммы как двоичные цифры ... рассуждения, если таковые имеются, которые сообщают [Королев WEN] последовательность неизвестна.

[Shao_Yong’s_”Xiantian_Tu'‘-9] Чжунляйан, Ши; Венжао, Ли; Power, Hans (2000). GW Leibnisim Syna 1697: Берлин 4. Бис 7. Баттобер Франц Штайнер Верлаг. стр. 165–170. ISBN 3515074481 .

[10] Коллинз, Дерек (2008). «Сопоставление внутренностей: практика греческой гепатоскопии» . Американский журнал филологии . 129 (3): 319–345. ISSN 0002-9475 .

[11] Джонстон, Сара Илс (2008). Древнегреческий гадания . Блэквелл Древние религии (1. Малден, Массачусетс: Wiley-Blackwell. ISBN 978-1-4051-1573-5 .

[12] Санчес, Хулио; Кантон, Мария П. (2007). Программирование микроконтроллера: Microchip Pic . Бока Ратон, Флорида: CRC Press. п. 37. ISBN 978-0-8493-7189-9 .

[13] WS Anglin и J. Lambek, The Heritage of Thales , Springer, 1995, ISBN 0-387-945444-X

[14] Математика для поэтов и барабанщиков архивировала 16 июня 2012 года на машине Wayback (PDF, 145 КБ)

[15] Стахов, Алексей ; Олсен, Скотт Энтони (2009). Математика гармонии: от Евклида до современной математики и информатики . Мировой научный. ISBN 978-981-277-582-5 .

[16] Б. Ван Нутен, «Бинарные числа в индийской древности», Журнал индийских исследований, том 21, 1993, с. 31–50

[17] Ландри, Тимоти Р. (2019). Vodún: секретность и поиск божественной силы . Современная этнография (1 -е изд.). Филадельфия: Университет Пенсильвании Пресс. п. 25. ISBN 978-0-8122-5074-9 .

[FOOTNOTELandry2019154-18] Ландри 2019 , с. 154

[19] «Система гадания IFA» . Получено 5 июля 2017 года .

[20] Бендер, Андреа; Беллер, Зигард (16 декабря 2013 г.). «Мангареван изобретение бинарных шагов для облегчения расчета» . Труды Национальной академии наук . 111 (4): 1322–1327. doi : 10.1073/pnas.1309160110 . PMC 3910603 . PMID 24344278 .

[21] Бауэрн, Клэр; Zentz, Джейсон (2012). «Разнообразие в системах цифр австралийских языков» . Антропологическая лингвистика . 54 (2): 133–160. ISSN 0003-5483 . JSTOR 23621076 .

[22] (См. Bonner 2007 [1] Архивировано 3 апреля 2014 года в The Wayback Machine , Fidora et al. 2011 [2] Архивировано 8 апреля 2019 года на машине Wayback )

[Bacon1605-23] Jump up to: ^а ^{беременный} Бэкон, Фрэнсис (1605). «Содействие обучению» . Лондон с. Глава 1.

[24] Ширли, Джон У. (1951). «Бинарная нумерация перед Лейбнизом». Американский журнал физики . 19 (8): 452–454. Bibcode : 1951amjph..19..452s . doi : 10.1119/1.1933042 .

[25] Ineichen, R. (2008). «Лейбник, Карамуил, Харро и двойная система» (PDF) . Сообщения от немецкой математической ассоциации (на немецком языке). 16 (1): 12–15. Doi : 10.1515/dmvm-2008-0009 . S2CID 179000299 .

[:0-26] Jump up to: ^а ^{беременный} ^в Стрикленд, Ллойд (2020), Шрираман, Бхарат (ред.), «Лейбниц по системам номеров» , Справочник по истории и философии математической практики , Cham: Springer International Publishing, стр. 1–31, DOI : 10.1007/978- 3-030-19071-2_90-1 , ISBN 978-3-030-19071-2 , Получено 20 августа 2024 г.

[lnz-27] Jump up to: ^а ^{беременный} Лейбниц Г., Объяснение бинарной арифметики, Die Mathematische Schriften, ed. C. Gerhardt, Berlin 1879, Vol. Энтузиазм перевод [3]

[28] "Bouvet и Leibniz: научная переписка" , Swiderski 1980

[29] Лейбниц : «Китайцы потеряли значение ковы или линий Фуси, возможно, более тысячи лет назад, и они написали комментарии по предмету, в котором они искали, я не знаю, что далеко не знает, так что их истина Объяснение теперь должно прийти от европейцев. ³ знаменитый французский иезуит, который живет в Пекине, мой метод подсчета на 0 и 1, и больше ничего не требовалось, чтобы заставить его признать, что это был ключом к фигурам Фуси. Пишу мне 14 ноября 1701 года, он прислал мне великую фигуру философского принца, которая достигает 64 и не оставляет никакого места, чтобы сомневаться в правде о нашем интерпретации, так что можно сказать, что этот отец расшифровал загадку Фуси, с помощью того, что я сообщил ему. И поскольку эти фигуры, пожалуй, самый древний памятник [GM VII, P227], которая существует в мире, это реституция их значения, после такого большого интервала времени, будет казаться тем более любопытным ».

[30] Эйтон, Эрик Дж. (1985). Лейбниц: биография Тейлор и Фрэнсис. Стр. 245–8 ISBN 0-85274-470-6 .

[smith-31] Jump up to: ^а ^{беременный} Джех Смит (2008). Лейбниц: Какой рационалист?: Какой рационалист? Полем Спрингер. п. 415. ISBN 978-1-4020-8668-7 .

[lniz-32] Юен-Тин Лай (1998). Лейбник, Мистика и религия . Спрингер. С. 149–150. ISBN 978-0-7923-5223-5 .

[33] Бул, Джордж (2009) [1854]. Исследование законов мышления, на которых основаны математические теории логики и вероятностей (Macmillan, публикации Dover, перепечатаны с исправлениями [1958] из.). Нью -Йорк: издательство Кембриджского университета. ISBN 978-1-108-00153-3 .

[34] Шеннон, Клод Элвуд (1940). Символический анализ ретрансляционных цепей (тезис). Кембридж: Массачусетский технологический институт. HDL : 1721.1/11173 .

[35] «Зал славы национальных изобретателей - Джордж Р. Стибиц» . 20 августа 2008 года. Архивировано с оригинала 9 июля 2010 года . Получено 5 июля 2010 года .

[36] "Джордж Стибиц: Био" . Департамент математики и компьютерных наук, Университет Денисона. 30 апреля 2004 года . Получено 5 июля 2010 года .

[37] «Пионеры - люди и идеи, которые имели значение - Джордж Стибиц (1904–1995)» . Керри Редшоу. 20 февраля 2006 г. Получено 5 июля 2010 года .

[38] «Джордж Роберт Стибиц - некролог» . Компьютерная история Ассоциации Калифорнии. 6 февраля 1995 г. Получено 5 июля 2010 года .

[zuse-39] Рохас, Рауль (апрель -июнь 1997). «Наследие Конрада Зуса: архитектура Z1 и Z3» (PDF) . IEEE ANNALS ИСТОРИЯ ИСКУССТВА . 19 (2): 5–16. doi : 10.1109/85.586067 . Архивировано (PDF) из оригинала 3 июля 2022 года . Получено 3 июля 2022 года . (12 страниц)

[40] «Представление бинарного - ревизия 1 - компьютерная наука GCSE» . Би -би -си . Получено 26 июня 2019 года .

[Kueveler-Schwoch_1996-41] Jump up to: ^а ^{беременный} Кювелер, Герд; Schwoch, Дитрих (2013) [1996]. Рабочая книга по информатике - практика - ориентированное на введение в обработку данных с задачей проекта (на немецком языке). Vieweg-Verlag, переиздание: Springer-Verlag. Doi : 10.1007/978-3-322-92907-5 . ISBN 978-3-528-04952-2 . 9783322929075.

[Kueveler-Schwoch_2007-42] Jump up to: ^а ^{беременный} Кювелер, Герд; Шух, Дитрих (4 октября 2007 г.). Компьютерная наука для инженеров и натуральных ученых: технология ПК и микрокомпьютера, компьютерные сети (на немецком языке). Том 2 (5 изд.). Vieweg, переиздание: Springer-Verlag. ISBN 978-3834891914 . 9783834891914.

[43] «Базовая система» . Архивировано с оригинала 23 октября 2017 года . Получено 31 августа 2016 года .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

[ 26 ]

[ 27 ]

[ 28 ]

[ 29 ]

[ 30 ]

[ 31 ]

[ 32 ]

[ 33 ]

[ 34 ]

[ 35 ]

[ 36 ]

[ 37 ]

[ 38 ]

[ 39 ]

[ 40 ]

[ 41 ]

[ 42 ]

[ 43 ]