Квантовый логический вентиль

В квантовых вычислениях и, в частности, с квантовыми схемами в модели вычислений , квантовый логический вентиль (или просто квантовый вентиль ) представляет собой базовую квантовую схему, работающую на небольшом количестве кубитов . Квантовые логические вентили являются строительными блоками квантовых схем, как и классические логические вентили для обычных цифровых схем.
В отличие от многих классических логических элементов, квантовые логические элементы обратимы . Классические вычисления можно выполнять, используя только обратимые вентили. Например, обратимый вентиль Тоффоли может реализовать все логические функции , часто за счет необходимости использования вспомогательных битов . У вентиля Тоффоли есть прямой квантовый эквивалент, показывающий, что квантовые схемы могут выполнять все операции, выполняемые классическими схемами.
Квантовые вентили являются унитарными операторами и описываются как унитарные матрицы относительно некоторого ортонормированного базиса . Обычно вычислительная основа используется , которая, если не сравнивать ее с чем-то, просто означает, что для квантовой системы d -уровня (такой как кубит , квантовый регистр или кутриты и кудиты ) [1] : 22–23 ортонормированные базисные векторы обозначены или используйте двоичную запись .
История
[ редактировать ]Текущие обозначения квантовых вентилей были разработаны многими основателями квантовой информатики, включая Адриано Баренко, Чарльза Беннета , Ричарда Клива , Дэвида П. ДиВинченцо , Нормана Марголуса , Питера Шора , Тихо Слиатора, Джона А. Смолина и Харальда Вайнфуртера. [2] основываясь на обозначениях, введенных Ричардом Фейнманом в 1986 году. [3]
Представительство
[ редактировать ]
Вращения вокруг осей x, y, z сферы Блоха представлены воротами оператора вращения .
Квантовые логические элементы представлены унитарными матрицами . Ворота, которые действуют на кубиты представлены унитарная матрица и набор всех таких элементов с групповой операцией умножения матриц [а] – унитарная группа U(2 н ). [2] Квантовые состояния , на которые действуют ворота, представляют собой единичные векторы в комплексные измерения с комплексной евклидовой нормой ( 2-норма ). [4] : 66 [5] : 56, 65 Базисные векторы (иногда называемые собственными состояниями ) — это возможные результаты, если состояние кубитов измеряется , а квантовое состояние — это линейная комбинация этих результатов. Наиболее распространенные квантовые вентили работают с векторными пространствами из одного или двух кубитов, точно так же, как обычные классические логические вентили работают с одним или двумя битами .
Несмотря на то, что квантовые логические элементы принадлежат к непрерывным группам симметрии , реальное оборудование неточно и, следовательно, ограничено в точности. Применение вентилей обычно приводит к ошибкам, и точность квантовых состояний со временем снижается. Если используется коррекция ошибок , используемые элементы дополнительно ограничиваются конечным набором. [4] : гл. 10 [1] : гл. 14 Далее в этой статье это игнорируется, поскольку основное внимание уделяется свойствам идеальных квантовых вентилей.
Квантовые состояния обычно обозначаются «кетами» из обозначения, известного как bra–ket .
Векторное представление одного кубита :
Здесь, и — комплексные амплитуды вероятности кубита. Эти значения определяют вероятность измерения 0 или 1 при измерении состояния кубита. см . в разделе измерений Подробности ниже.
Нулевое значение представлено кетом , а значение единицы представлено кетом .
Тензорное произведение (или произведение Кронекера ) используется для объединения квантовых состояний. Комбинированное состояние регистра кубитов представляет собой тензорное произведение составляющих его кубитов. Тензорное произведение обозначается символом .
Векторное представление двух кубитов: [6]
Действие вентиля на конкретное квантовое состояние находится путем умножения вектора , который представляет состояние матрицей представляющий ворота. Результатом является новое квантовое состояние. :
Яркие примеры
[ редактировать ]Существует несчетное количество ворот. Некоторые из них были названы разными авторами. [2] [1] [4] [5] [7] [8] [9] Ниже приведены некоторые из наиболее часто используемых в литературе.
Идентификационные ворота
[ редактировать ]Идентификационный вентиль — это единичная матрица , обычно записываемая как I , и определяемая для одного кубита как
где I не зависит от базиса и не изменяет квантовое состояние. Идентификационный вентиль наиболее полезен при математическом описании результатов различных операций вентиля или при обсуждении многокубитных схем.
Ворота Паули ( X , Y , Z )
[ редактировать ]Ворота Паули три матрицы Паули и действовать на один кубит. Паули X , Y и Z соответствуют, соответственно, вращению вокруг x , y и z осей сферы Блоха на радианы. [б]
Гейт Паули- X является квантовым эквивалентом вентиля НЕ для классических компьютеров относительно стандартного базиса. , , который выделяет ось z на сфере Блоха . Иногда его называют переворотом битов, поскольку он отображает к и к . Аналогично, Паули- Y отображения к и к . Паули З покидает базовое состояние без изменений и карты к . Из-за этой природы Паули Z иногда называют фазовым переворотом.
Эти матрицы обычно представляются в виде
Матрицы Паули являются инволютивными , что означает, что квадрат матрицы Паули является единичной матрицей .
Матрицы Паули также антикоммутируют , например
Матричная экспонента матрицы Паули — оператор вращения , часто записываемый как
Управляемые ворота
[ редактировать ]
Управляемые вентили действуют на 2 или более кубитов, причем один или несколько кубитов выполняют функцию управления некоторой операцией. [2] Например, управляемый вентиль НЕ (или CNOT или CX) действует на 2 кубита и выполняет операцию НЕ на втором кубите только тогда, когда первый кубит , а в противном случае оставляет его без изменений. Что касается основы , , , , он представлен эрмитовой унитарной матрицей:
Вентиль CNOT (или управляемый Паули- Х ) можно описать как вентиль, который отображает базисные состояния. , где это XOR .
CNOT можно выразить в базисе Паули как:
Будучи эрмитовым унитарным оператором, CNOT обладает тем свойством , что и , и является инволютивным .
В более общем смысле, если U — это вентиль, который работает с одним кубитом с матричным представлением.
тогда вентиль с контролируемым U — это вентиль, который работает с двумя кубитами таким образом, что первый кубит служит управляющим. Он отображает базовые состояния следующим образом.
Матрица, представляющая управляемый U, равна
Когда U является одним из операторов Паули, X , Y , Z соответствующие термины «контролируемый- X », «контролируемый- Y » или «контролируемый- Z ». , иногда используются [4] : 177–185 Иногда это сокращается до C X , CY и C Z .
В общем, любой унитарный вентиль с одним кубитом можно выразить как , где H — эрмитова матрица , и тогда управляемый U —
Управление может быть распространено на гейты с произвольным количеством кубитов. [2] и функции в языках программирования. [10] Функции могут быть обусловлены состояниями суперпозиции. [11] [12]
Классический контроль
[ редактировать ]
На принципиальных схемах одинарные линии — это кубиты , а двойные линии — биты .
Воротами также можно управлять с помощью классической логики. Квантовый компьютер управляется классическим компьютером и ведет себя как сопроцессор , который получает инструкции от классического компьютера о том, какие вентили на каких кубитах выполнять. [13] : 42–43 [14] Классический контроль — это просто включение или исключение вентилей в последовательность команд квантового компьютера. [4] : 26–28 [1] : 87–88
Ворота фазового сдвига
[ редактировать ]Фазовый сдвиг — это семейство однокубитных вентилей, которые отображают базовые состояния. и . Вероятность измерения или не изменяется после применения этого вентиля, однако он изменяет фазу квантового состояния. Это эквивалентно отслеживанию горизонтального круга (линии постоянной широты) или вращению вокруг оси z на сфере Блоха с помощью радианы. Вентиль фазового сдвига представлен матрицей:
где – фазовый сдвиг с периодом 2π . Некоторыми распространенными примерами являются Т- ворота, где (исторически известный как вентиль), фазовый вентиль (также известный как вентиль S, пишется как S , хотя S иногда используется для вентилей SWAP), где и Паули- Z, ворота где
Вентиляторы фазового сдвига связаны друг с другом следующим образом:
Обратите внимание, что фазовый вентиль не является эрмитовым (за исключением всех ). Эти ворота отличаются от своих эрмитовых сопряженных: . Два сопряженных (или сопряженных транспонированных ) вентиля и иногда включаются в наборы команд. [15] [16]
Ворота Адамара
[ редактировать ]Ворота Адамара или Уолш-Адамара, названные в честь Жака Адамара ( Французский: [adamaʁ] ) и Джозефа Л. Уолша , действует на один кубит. Он отображает базовые состояния и (он создает равное состояние суперпозиции, если задано состояние вычислительного базиса). Два государства и иногда пишут и соответственно. Ворота Адамара совершают поворот относительно оси в сфере Блоха и поэтому является инволютивным . Она представлена матрицей Адамара :
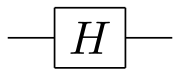
Если эрмитиан (так ) Вентиль Адамара используется для изменения базиса , он переворачивает и . Например, и
Обмен воротами
[ редактировать ]
Ворота подкачки меняют местами два кубита. Что касается основы , , , , оно представлено матрицей
Своп-вентиль можно разложить в форму суммирования:
Ворота Тоффоли (CCNOT)
[ редактировать ]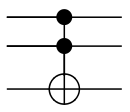
Ворота Тоффоли, названные в честь Томмазо Тоффоли и также называемые воротами CCNOT или Немецкими воротами. , представляет собой 3-битный вентиль, универсальный для классических вычислений, но не для квантовых. Квантовый вентиль Тоффоли — это тот же вентиль, определенный для 3 кубитов. Если мы ограничимся приемом только входных кубитов, которые и , то если первые два бита находятся в состоянии он применяет Pauli- X (или NOT) к третьему биту, иначе он ничего не делает. Это пример ворот CC-U (унитарный с управляемым управлением). Поскольку это квантовый аналог классического вентиля, он полностью определяется таблицей истинности. Ворота Тоффоли универсальны в сочетании с однокубитными воротами Адамара. [17]
| Таблица истинности | Матричная форма | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ворота Тоффоли связаны с классическим оператором И ( ) и исключающее ИЛИ ( ) операции, поскольку он выполняет отображение о состояниях в вычислительном базисе.
Ворота Тоффоли можно выразить с помощью матриц Паули как
Универсальные квантовые ворота
[ редактировать ]
Набор универсальных квантовых гейтов — это любой набор гейтов, к которому может быть сведена любая возможная операция на квантовом компьютере, то есть любая другая унитарная операция может быть выражена как конечная последовательность гейтов из этого набора. Технически это невозможно с чем-то меньшим, чем несчетный набор гейтов, поскольку количество возможных квантовых гейтов несчетно, тогда как количество конечных последовательностей из конечного набора счетно . Чтобы решить эту проблему, нам нужно лишь, чтобы любая квантовая операция могла быть аппроксимирована последовательностью элементов из этого конечного множества. Более того, для унитаров с постоянным числом кубитов теорема Соловея–Китаева гарантирует, что это можно сделать эффективно. Проверить универсальность набора квантовых вентилей можно с помощью теории групп . методов [18] и/или отношение к (приблизительным) унитарным Т-образным конструкциям [19]
Некоторые универсальные наборы квантовых вентилей включают:
- Операторы вращения R x ( θ ) , R y ( θ ) , R z ( θ ) , вентиль фазового сдвига P ( φ ) [с] и CNOT обычно используются для формирования универсального набора квантовых вентилей. [20] [д]
- Множество Клиффорда {CNOT, H , S } + T вентиль. Набор Клиффорда сам по себе не является универсальным набором квантовых вентилей, поскольку его можно эффективно смоделировать классически в соответствии с теоремой Готтсмана-Нилла .
- Ворота Тоффоли + ворота Адамара. [17] Один только вентиль Тоффоли образует набор универсальных вентилей для обратимых схем булевой алгебраической логики, которые охватывают все классические вычисления.
Немецкие ворота
[ редактировать ]Однозатворный набор универсальных квантовых вентилей также можно сформулировать с использованием параметризованного трехкубитного вентиля Дойча. , [21] назван в честь физика Дэвида Дойча . Это общий случай CC-U , или унитарного вентиля «управляемый-управляемый» , и он определяется как
К сожалению, работающие ворота Дойча остались недоступными из-за отсутствия протокола. Есть предложения реализовать вентиль Дойча с диполь-дипольным взаимодействием в нейтральных атомах. [22]
Универсальный логический вентиль для обратимых классических вычислений, вентиль Тоффоли, сводится к вентилю Дойча. , тем самым показывая, что все обратимые классические логические операции могут быть выполнены на универсальном квантовом компьютере.
Также существуют одиночные двухкубитные вентили, достаточные для универсальности. В 1996 году Адриано Баренко показал, что гейт Дойча можно разложить, используя только один двухкубитный гейт ( гейт Баренко ), но это трудно реализовать экспериментально. [1] : 93 Эта функция является эксклюзивной для квантовых схем, поскольку не существует классического двухбитного вентиля, который был бы одновременно обратимым и универсальным. [1] : 93 Универсальные двухкубитные вентили могут быть реализованы для улучшения классических обратимых схем в быстрых микропроцессорах с низким энергопотреблением. [1] : 93
Состав схемы
[ редактировать ]Ворота с последовательной проводкой
[ редактировать ]
Предположим, что у нас есть двое ворот A и B, которые оба действуют на кубиты. Когда B помещается после A тогда эффект двух вентилей можно описать как один вентиль C. в последовательной схеме ,
где это умножение матриц . Полученные ворота C будут иметь те же размеры, что A и B. и Порядок, в котором элементы будут появляться на принципиальной схеме, меняется на обратный при их умножении. [4] : 17–18,22–23,62–64 [5] : 147–169
Например, размещение вентиля Паули X после вентиля Паули Y , оба из которых действуют на один кубит, можно описать как один комбинированный вентиль C :
Символ продукта ( ) часто опускается.
Экспоненты квантовых ворот
[ редактировать ]Все действительные показатели унитарных матриц также являются унитарными матрицами, и все квантовые вентили являются унитарными матрицами.
Положительные целочисленные показатели эквивалентны последовательностям последовательно соединенных вентилей (например, ), а действительные показатели степени являются обобщением последовательной схемы. Например, и оба являются действительными квантовыми воротами.
для любой унитарной матрицы . Единичная матрица ( ) ведет себя как NOP [23] [24] и может быть представлен в виде оголенного провода в квантовых схемах или вообще не показан.
Все элементы являются унитарными матрицами, так что и , где это сопряженное транспонирование . Это означает, что отрицательные показатели вентилей являются унитарными инверсиями своих положительно возведенных в степень аналогов: . Например, некоторые отрицательные показатели фазовых вентилей равны и .
Заметим, что для эрмитовой матрицы и из-за унитарности, так для всех эрмитовых ворот. Они инволютивны . Примерами эрмитовых ворот являются ворота Паули , Адамара , CNOT , SWAP и Тоффоли . Каждая эрмитова унитарная матрица имеет свойство , которое где
Параллельные ворота
[ редактировать ]
Тензорное произведение (или произведение Кронекера ) двух квантовых вентилей — это вентиль, равный двум параллельным вентилям. [4] : 71–75 [5] : 148
Если мы, как на картинке, объединим вентиль Паули- Y с вентилем Паули- X параллельно, то это можно записать так:
И ворота Паули- X , и ворота Паули- Y действуют на один кубит. Получившиеся ворота действовать на два кубита.
Иногда символ тензорного произведения опускается, и вместо него для операторов используются индексы. [25]
Преобразование Адамара
[ редактировать ]Ворота это ворота Адамара ( ) применяется параллельно к 2 кубитам. Это можно записать как:
Этот «двухкубитный параллельный вентиль Адамара» будет применяться, например, к двухкубитному нулевому вектору ( ), создать квантовое состояние, которое имеет равную вероятность наблюдаться в любом из четырех возможных результатов; , , , и . Эту операцию мы можем записать так:
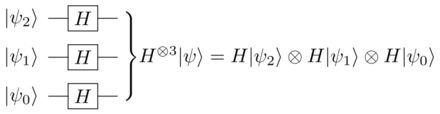
Здесь амплитуда для каждого измеримого состояния равна 1 ⁄ 2 . Вероятность наблюдения любого состояния равна квадрату абсолютного значения амплитуды измеримых состояний, что в приведенном выше примере означает, что в одном из четырех случаев мы наблюдаем какой-либо из отдельных четырех случаев. смотрите в измерении Подробности .
выполняет преобразование Адамара для двух кубитов. Аналогично ворота выполняет преобразование Адамара регистре в кубиты.
При обращении в реестр все кубиты инициализированы преобразование Адамара помещает квантовый регистр в суперпозицию с равной вероятностью измерения в любом из его возможные состояния:
Это состояние представляет собой равномерную суперпозицию и генерируется на первом этапе в некоторых алгоритмах поиска, например, при усилении амплитуды и оценке фазы .
Измерение этого состояния приводит к получению случайного числа между и . [и] Насколько случайное число зависит от точности логических элементов. Если его не измерить, это квантовое состояние с равной амплитудой вероятности. для каждого из его возможных состояний.
Преобразование Адамара действует на регистр. с кубиты такие, что следующее:
Приложение к запутанным состояниям
[ редактировать ]Если два или более кубитов рассматриваются как одно квантовое состояние, это объединенное состояние равно тензорному произведению составляющих его кубитов. Любое состояние, которое можно записать как тензорное произведение составляющих его подсистем, называется разделимыми состояниями . С другой стороны, запутанное состояние — это любое состояние, которое не может быть тензорно факторизовано, или, другими словами: запутанное состояние не может быть записано как тензорное произведение составляющих его состояний кубитов. Особую осторожность следует проявлять при применении вентилей к составляющим кубитам, образующим запутанные состояния.
Если у нас есть набор из N кубитов, которые запутаны, и мы хотим применить квантовый вентиль к M < N кубитам в наборе, нам придется расширить вентиль, чтобы он мог занять N кубитов. Это приложение можно реализовать, объединив вентиль с единичной матрицей так, чтобы их тензорное произведение стало вентилем, действующим на N кубитов. Единичная матрица ( ) — это представление вентиля, который отображает каждое состояние на себя (т. е. вообще ничего не делает). На принципиальной схеме идентификационный вентиль или матрица часто выглядят как оголенный провод.

Например, ворота Адамара ( ) действует на один кубит, но если мы скормим ему первый из двух кубитов, составляющих запутанное состояние Белла , мы не можем легко написать эту операцию. Нам нужно расширить ворота Адамара с идентификационными воротами так что мы можем воздействовать на квантовые состояния, охватывающие два кубита:
Ворота теперь можно применить к любому двухкубитному состоянию, запутанному или другому. Ворота оставит второй кубит нетронутым и применит преобразование Адамара к первому кубиту. Если применить это к состоянию Белла в нашем примере, мы можем записать это как:
Вычислительная сложность и тензорное произведение
[ редактировать ]Временная сложность умножения двух -матрицы не менее , [26] если использовать классическую машину. Поскольку размер ворот, которые работают на кубиты это это означает, что время моделирования шага в квантовой схеме (посредством перемножения вентилей), работающей с общими запутанными состояниями, равно . По этой причине считается невозможным моделировать большие запутанные квантовые системы с помощью классических компьютеров. Однако подмножества вентилей, такие как вентили Клиффорда или тривиальный случай схем, которые реализуют только классические булевы функции (например, комбинации X , CNOT , Тоффоли ), можно эффективно моделировать на классических компьютерах.
Вектор состояния квантового регистра с кубиты это сложные записи. Хранение амплитуд вероятности в виде списка значений с плавающей запятой нецелесообразно для больших значений. .
Унитарная инверсия ворот
[ редактировать ]
Поскольку все квантовые логические элементы обратимы , любая композиция из нескольких элементов также обратима. Все произведения и тензорные произведения (т.е. последовательные и параллельные комбинации) унитарных матриц также являются унитарными матрицами. Это означает, что можно построить инверсию всех алгоритмов и функций, если они содержат только вентили.
Инициализация, измерение, ввод-вывод и спонтанная декогеренция — это побочные эффекты квантовых компьютеров. Однако ворота являются чисто функциональными и биективными .
Если является унитарной матрицей , то и . Кинжал ( ) обозначает сопряженное транспонирование . Его еще называют эрмитовым сопряженным .
Если функция является продуктом ворота, , унитарная обратная функция можно построить:
Потому что имеем, после неоднократного применения на себе
Аналогично, если функция состоит из двух ворот и параллельно, тогда и .
Ворота, являющиеся своими унитарными обратными, называются эрмитовыми или самосопряженными операторами . Некоторые элементарные элементы, такие как ворота Адамара ( H ) и Паули ( I , X , Y , Z ), являются эрмитовыми операторами, тогда как другие, такие как элементы фазового сдвига ( S , T , P , CPhase ), обычно таковыми не являются.
Например, алгоритм сложения можно использовать для вычитания, если он выполняется «в обратном порядке», как его унитарный обратный алгоритм. Обратное квантовое преобразование Фурье является унитарным обратным. Унитарные инверсии также можно использовать для невычисления . Языки программирования для квантовых компьютеров, такие как Microsoft Q # , [10] Бернхарда Омера QCL , [13] : 61 и IBM от Qiskit , [27] содержат инверсию функций как концепции программирования.
Измерение
[ редактировать ]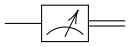
Измерение (иногда называемое наблюдением ) необратимо и, следовательно, не является квантовым вентилем, поскольку оно присваивает наблюдаемому квантовому состоянию одно значение. Измерение берет квантовое состояние и проецирует его на один из базисных векторов с вероятностью, равной квадрату длины вектора (в 2-нормальном [4] : 66 [5] : 56, 65 ) вдоль этого базисного вектора. [1] : 15–17 [28] [29] [30] Это известно как правило Борна и появляется [и] как стохастическая необратимая операция, поскольку она вероятностно устанавливает квантовое состояние равным базисному вектору, который представляет измеренное состояние. Говорят, что в момент измерения состояние « схлопывается » до определенного единственного значения, которое было измерено. Почему и как, или даже если [31] [32] квантовое состояние коллапсирует при измерении, называется проблемой измерения .
Вероятность измерения значения с амплитудой вероятности является , где это модуль .
Измерение одного кубита, квантовое состояние которого представлено вектором , приведет к с вероятностью и в с вероятностью .
Например, измерение кубита с квантовым состоянием даст с равной вероятностью либо или .
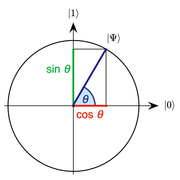
Примечание: вероятность измерения и вероятность измерения .
Квантовое состояние который охватывает n кубитов, можно записать в виде вектора в сложные размеры: . Это связано с тем, что тензорное произведение n кубитов является вектором в размеры. Таким образом, регистр из n кубитов можно измерить до регистр из n классических битов. отдельные состояния, подобно тому, как может храниться отдельные государства. В отличие от битов классических компьютеров, квантовые состояния могут иметь ненулевые амплитуды вероятности одновременно в нескольких измеримых значениях. Это называется суперпозицией .
Сумма всех вероятностей для всех исходов всегда должна быть равна 1 . [ф] По-другому можно сказать, что теорема Пифагора, обобщенная на имеет, что все квантовые состояния с n кубитами должно удовлетворять [г] где - амплитуда вероятности для измеримого состояния . Геометрическая интерпретация этого состоит в том, что возможное пространство значений квантового состояния с n кубитами — это поверхность единичной сферы в и что примененные к нему унитарные преобразования (то есть квантовые логические элементы) представляют собой вращения сферы. Вращения, которые совершают ворота, образуют группу симметрии U(2 н ) . В таком случае измерение представляет собой вероятностную проекцию точек на поверхности этой сложной сферы на базисные векторы , охватывающие пространство (и маркирующие результаты).
Во многих случаях пространство представляется как гильбертово пространство. а не какой-то конкретный -мерное комплексное пространство. Количество измерений (определяемых базисными векторами и, следовательно, также возможными результатами измерения) часто подразумевается операндами, например, как необходимое пространство состояний для решения проблемы . В Гровера алгоритме Гровер назвал этот общий набор базисных векторов «база данных» .
Выбор базисных векторов для измерения квантового состояния повлияет на результат измерения. [1] : 30–35 [4] : 22, 84–85, 185–188 [33] см . в разделе «Изменение базиса» и «Энтропия фон Неймана» Подробности . В этой статье мы всегда используем вычислительную основу , а это значит, что мы обозначили базисные векторы регистра - кубитов n или используйте двоичное представление .
В квантовой механике базисные векторы составляют ортонормированный базис .
Примером использования альтернативной основы измерения является шифр BB84 .
Влияние измерения на запутанные состояния
[ редактировать ]
Если два квантовых состояния (т. е. кубиты или регистры ) запутаны (это означает, что их объединенное состояние не может быть выражено как тензорное произведение ), измерение одного регистра влияет или раскрывает состояние другого регистра, частично или полностью разрушая его состояние. Этот эффект можно использовать для вычислений, и он используется во многих алгоритмах.
Комбинация Адамара-CNOT действует на нулевое состояние следующим образом:

Это результирующее состояние является состоянием Белла. . Его нельзя описать как тензорное произведение двух кубитов. Нет решения для
потому что, например, w должно быть одновременно ненулевым и нулевым в случае xw и yw .
Квантовое состояние охватывает два кубита. Это называется запутанностью . Измерение одного из двух кубитов, составляющих это состояние Белла, приведет к тому, что другой кубит логически должен иметь то же значение, оба должны быть одинаковыми: либо он будет найден в состоянии или в штате . Если мы измерим один из кубитов, например, , то другой кубит также должен быть , потому что их объединенное состояние стало . Измерение одного из кубитов разрушает все квантовое состояние, охватывающее два кубита.
Состояние GHZ — это похожее запутанное квантовое состояние, охватывающее три или более кубитов.
Этот тип присвоения значений происходит мгновенно на любом расстоянии , и по состоянию на 2018 год это было экспериментально проверено QUESS на расстояниях до 1200 километров. [34] [35] [36] То, что явления происходят мгновенно, а не за время, необходимое для прохождения расстояния, разделяющего кубиты, со скоростью света, называется парадоксом ЭПР , и в физике остается открытым вопрос, как его разрешить. Первоначально она была решена путем отказа от предположения о локальном реализме , но другие интерпретации появились и . Дополнительную информацию см. в тестовых экспериментах Белла . Теорема об отсутствии связи доказывает, что это явление нельзя использовать для передачи классической информации со скоростью, превышающей скорость света .
Измерение на регистрах с попарно запутанными кубитами
[ редактировать ]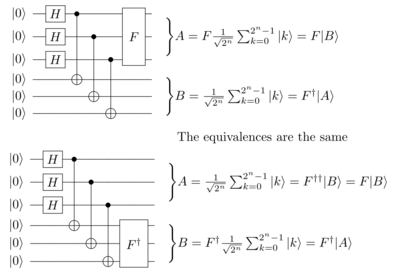
Возьмите регистр A с n кубитами, инициализированными и пропустите его через параллельный вентиль Адамара . Регистр A затем перейдет в состояние которые имеют равную вероятность при измерении оказаться в любом из своих возможные состояния; к . Возьмем второй регистр B, также с n кубитами, инициализированными и попарно CNOT его кубиты с кубитами в регистре A, так что для каждого p кубиты и образует государство .
Если мы теперь измерим кубиты в регистре A, то обнаружится, что регистр B содержит то же значение, что и A. Однако если вместо этого мы применим квантовый логический элемент F к A и затем измерим, тогда , где является обратным F . унитарным
Из-за того, как действуют унитарные инверсии ворот , . Например, скажем , затем .
Равенство будет соблюдаться независимо от того, в каком порядке выполняются измерения (в регистрах A или B), предполагая, что F завершился до завершения. Измерение может даже осуществляться случайным и одновременным чередованием кубит за кубитом, поскольку назначение измерений одного кубита будет ограничивать возможное пространство значений других запутанных кубитов.
Несмотря на то, что равенства выполняются, вероятности измерения возможных результатов могут измениться в результате применения F , что может быть и целью алгоритма квантового поиска.
Этот эффект разделения значений посредством запутанности используется в алгоритме Шора , оценке фазы и в квантовом подсчёте . Использование преобразования Фурье для усиления амплитуд вероятностей состояний решения некоторой задачи — это общий метод, известный как « ловля Фурье ». [37]
Синтез логических функций
[ редактировать ]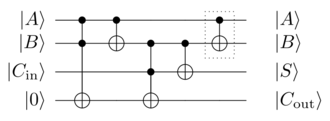
Функции и процедуры, использующие только вентили, сами по себе могут быть описаны как матрицы, как и меньшие вентили. Матрица, представляющая квантовую функцию, действующую на кубиты имеют размер . Например, функция, действующая на «кубайт» ( регистр из 8 кубитов), будет представлена матрицей с элементы.
Унитарные преобразования, которых нет в наборе вентилей, изначально доступных на квантовом компьютере (примитивные вентили), можно синтезировать или аппроксимировать путем объединения доступных примитивных вентилей в схеме . Один из способов сделать это — факторизовать матрицу, которая кодирует унитарное преобразование, в произведение тензорных произведений (т.е. последовательных и параллельных схем) доступных примитивных элементов. Группа 2 U( д ) — группа симметрии вентилей, действующих на кубиты. [2] Тогда факторизация — это проблема поиска пути в U(2 д ) из порождающего набора примитивных элементов. Теорема Соловея-Китаева показывает, что при достаточном наборе примитивных элементов существует эффективное приближение для любого элемента. Для общего случая с большим количеством кубитов такой прямой подход к синтезу схем трудноразрешим . [38] [39] Это накладывает ограничения на то, насколько большие функции могут быть грубо разложены на примитивные квантовые вентили. Обычно квантовые программы вместо этого строятся с использованием относительно небольших и простых квантовых функций, аналогичных обычному классическому программированию.
природы вентилей Из-за унитарной все функции должны быть обратимыми и всегда быть биективными отображениями входа на выход. Всегда должна существовать функция такой, что . Функции, которые не являются обратимыми, можно сделать обратимыми, добавив вспомогательные кубиты ко входу или выходу, или к тому и другому. После завершения функции вспомогательные кубиты можно либо не вычислять , либо оставить нетронутыми. Измерение или иное сжатие квантового состояния вспомогательного кубита (например, путем повторной инициализации его значения или его спонтанной декогеренции ), которое не было невычислено, может привести к ошибкам. [40] [41] поскольку их состояние может быть связано с кубитами, которые все еще используются в вычислениях.
Логически необратимые операции, например сложение по модулю. из двух -кубитные регистры a и b , , [час] можно сделать логически обратимым, добавив информацию к выходным данным, так что входные данные можно вычислить на основе выходных данных (т. е. существует функция ). В нашем примере это можно сделать, передав один из входных регистров на выход: . Затем выходные данные можно использовать для вычисления входных данных (т. е. учитывая выходные данные и , мы можем легко найти входные данные; дано и ) и функция становится биективной.
Все логические алгебраические выражения могут быть закодированы как унитарные преобразования (квантовые логические элементы), например, с использованием комбинаций элементов Паули-X , CNOT и Тоффоли . Эти вентили функционально завершены в области булевой логики.
В библиотеках Q# , QCL , Qiskit и других языках квантового программирования доступно множество унитарных преобразований . Оно также встречается в литературе. [42] [43]
Например, , где это количество кубитов, составляющих регистр , реализовано в QCL следующим образом: [44] [13] [12]
cond qufunct inc(qureg x) { // increment register
int i;
for i = #x-1 to 0 step -1 {
CNot(x[i], x[0::i]); // apply controlled-not from
} // MSB to LSB
}

В QCL уменьшение осуществляется путем «отмены» приращения. Префикс ! вместо этого используется для запуска унитарной обратной функции. !inc(x) является обратным inc(x) и вместо этого выполняет операцию . The cond Ключевое слово означает, что функция может быть условной . [11]
В модели вычислений, используемой в этой статье ( модель квантовой схемы ), классический компьютер генерирует композицию вентилей для квантового компьютера, а квантовый компьютер ведет себя как сопроцессор , который получает инструкции от классического компьютера о том, к каким примитивным вентилям следует обращаться. какие кубиты. [13] : 36–43 [14] Измерение квантовых регистров приводит к получению двоичных значений, которые классический компьютер может использовать в своих вычислениях. Квантовые алгоритмы часто содержат как классическую, так и квантовую часть. Неизмеренный ввод-вывод (отправка кубитов на удаленные компьютеры без разрушения их квантовых состояний) можно использовать для создания сетей квантовых компьютеров . Затем замену запутанности можно использовать для реализации распределенных алгоритмов с помощью квантовых компьютеров, которые не связаны напрямую. Примерами распределенных алгоритмов, которые требуют использования лишь нескольких квантовых логических вентилей, являются сверхплотное кодирование , квантовое византийское соглашение и BB84 протокол обмена ключами шифрования .
См. также
[ редактировать ]- Адиабатические квантовые вычисления
- Министерство национальной обороны
- Клеточный автомат
- Облачные квантовые вычисления
- Контрфактическая определенность
- Контрфактические квантовые вычисления
- Принцип Ландауэра
- Логическая связка
- Односторонний квантовый компьютер
- Квантовый алгоритм
- Квантовый клеточный автомат
- Квантовый канал
- Квантовый конечный автомат
- Квантовая логика
- Квантовая память
- Квантовая сеть
- Так же, как Зенон
- Реверсивные вычисления
- Унитарное преобразование (квантовая механика)
Примечания
[ редактировать ]- ^ Матричное умножение квантовых вентилей определяется как последовательные схемы .
- ^ Обратите внимание, здесь полное вращение вокруг сферы Блоха. радиан, в отличие от ворот оператора вращения , где полный оборот
- ^ либо P-, либо Ph- вентиль, как Можно использовать [2] : 11 [1] : 76–83
- ^ Этот набор точно генерирует все возможные унитарные ворота. Однако, поскольку глобальная фаза не имеет значения для результатов измерения, можно построить универсальные квантовые подмножества, например, набор, содержащий R y ( θ ) , R z ( θ ) и CNOT, охватывает только все унитарные единицы с определителем ±1, но этого достаточно для квантовых вычислений. .
- ^ Перейти обратно: а б Является ли это на самом деле стохастическим эффектом, зависит от того, какая интерпретация квантовой механики правильна (и может ли какая-либо интерпретация быть правильной). Например, теория Де Бройля-Бома и многомировая интерпретация утверждают детерминизм . (В многомировой интерпретации квантовый компьютер — это машина, запускающая программы ( квантовые схемы ), которая выбирает реальность, в которой вероятность наличия состояний решения проблемы велика . То есть машина чаще всего заканчивается в реальности, где она дает правильный ответ. Поскольку все результаты реализуются в отдельных вселенных в соответствии с интерпретацией многих миров, общий результат является детерминированным, однако эта интерпретация не меняет механику работы машины.)
- ^ См. Аксиомы вероятности § Вторая аксиома.
- ^ Гипотенуза имеет длину 1 , потому что сумма вероятностей равна 1, поэтому вектор квантового состояния является единичным вектором .
- ^ Ввод кубиты, но результат просто кубиты. Удаление информации не является обратимой (или унитарной ) операцией и поэтому не допускается. См. также принцип Ландауэра .
Ссылки
[ редактировать ]- ^ Перейти обратно: а б с д и ж г час я дж Колин П. Уильямс (2011). Исследования в области квантовых вычислений . Спрингер . ISBN 978-1-84628-887-6 .
- ^ Перейти обратно: а б с д и ж г Баренко, Адриано; Беннетт, Чарльз Х.; Клив, Ричард; ДиВинченцо, Дэвид П.; Марголус, Норман; Шор, Питер; Слитор, Тихо; Смолин, Джон А.; Вайнфуртер, Харальд (1 ноября 1995 г.). «Элементарные вентили для квантовых вычислений». Физический обзор А. 52 (5). Американское физическое общество (APS): 3457–3467. arXiv : Quant-ph/9503016 . Бибкод : 1995PhRvA..52.3457B . дои : 10.1103/physreva.52.3457 . ISSN 1050-2947 . ПМИД 9912645 . S2CID 8764584 .
- ^ Перейти обратно: а б Фейнман, Ричард П. (1986). «Квантово-механические компьютеры». Основы физики . 16 (6). Springer Science and Business Media LLC: 507–531. Бибкод : 1986FoPh...16..507F . дои : 10.1007/bf01886518 . ISSN 0015-9018 . S2CID 122076550 .
- ^ Перейти обратно: а б с д и ж г час я Нильсен, Майкл А .; Чуанг, Исаак (2010). Квантовые вычисления и квантовая информация . Кембридж: Издательство Кембриджского университета . ISBN 978-1-10700-217-3 . OCLC 43641333 .
- ^ Перейти обратно: а б с д и Янофски, Носон С.; Маннуччи, Мирко (2013). Квантовые вычисления для компьютерщиков . Издательство Кембриджского университета . ISBN 978-0-521-87996-5 .
- ^ Прескилл, Джон (6 июня 2021 г.). «Квантовые вычисления 40 лет спустя». стр. 10–15. arXiv : 2106.10522 [ квант-ph ].
- ^ «Электронная библиотека» . IBM ( Кискит ).
- ^ «cQASM: Операции с кубитными воротами» . КуТех.
- ^ «Microsoft.Quantum.Intrinsic пространство имен» . Майкрософт ( Q# ). 28 июля 2023 г.
- ^ Перейти обратно: а б Операции и функции (документация Q#)
- ^ Перейти обратно: а б Омер, Бернхард (2 сентября 2009 г.). «Структурированное квантовое программирование» (PDF) . Институт теоретической физики Венского технического университета. стр. 72, 92–107. Архивировано из оригинала (PDF) 27 марта 2022 г.
- ^ Перейти обратно: а б Омер, Бернхард (29 апреля 2003 г.). «Классические концепции квантового программирования». Международный журнал теоретической физики . 44 (7): 943–955. arXiv : Quant-ph/0211100 . дои : 10.1007/s10773-005-7071-x . S2CID 119373370 .
- ^ Перейти обратно: а б с д Омер, Бернхард (20 января 2000 г.). Квантовое программирование в QCL (PDF) (Диссертация). Институт теоретической физики Венского технического университета. Архивировано из оригинала (PDF) 1 июня 2022 года . Проверено 24 мая 2021 г.
- ^ Перейти обратно: а б Паука С.Дж., Дас В., Калра Р., Мойни А., Ян Й., Тренер М., Буске А., Канталюб С., Дик Н., Гарднер Г.К., Манфра М.Дж., Рейли DJ (2021). «Криогенный КМОП-чип для генерации управляющих сигналов для нескольких кубитов». Природная электроника . 4 (4): 64–70. arXiv : 1912.01299 . дои : 10.1038/s41928-020-00528-y . S2CID 231715555 .
- ^ «ТдгГейт» . Онлайн-документация Qiskit .
- ^ «Т-кинжалные ворота» . Онлайн-документация cQASM.
- ^ Перейти обратно: а б Ааронов, Дорит (9 января 2003 г.). «Простое доказательство того, что Тоффоли и Адамар квантово универсальны». arXiv : Quant-ph/0301040 .
- ^ Савицкий, Адам; Карнас, Катажина (01 ноября 2017 г.). «Универсальность однокудитных вентилей» . Анналы Анри Пуанкаре . 18 (11): 3515–3552. arXiv : 1609.05780 . Бибкод : 2017AnHP...18.3515S . дои : 10.1007/s00023-017-0604-z . ISSN 1424-0661 . S2CID 253594045 .
- ^ Савицкий, Адам; Маттиоли, Лоренцо; Зимборас, Золтан (12 мая 2022 г.). «Проверка универсальности набора квантовых вентилей» . Физический обзор А. 105 (5): 052602. arXiv : 2111.03862 . Бибкод : 2022PhRvA.105e2602S . doi : 10.1103/PhysRevA.105.052602 . S2CID 248761038 .
- ^ Уильямс, Колин П. (2011), Уильямс, Колин П. (редактор), «Квантовые ворота» , Исследования в области квантовых вычислений , Тексты по информатике, Лондон: Springer, стр. 51–122, doi : 10.1007/978- 1-84628-887-6_2 , ISBN 978-1-84628-887-6 , получено 14 мая 2021 г.
- ^ Дойч, Дэвид (8 сентября 1989 г.), «Квантовые вычислительные сети», Proc. Р. Сок. Лонд. A , 425 (1989): 73–90, Bibcode : 1989RSPSA.425...73D , doi : 10.1098/rspa.1989.0099 , S2CID 123073680
- ^ Ши, Сяо-Фэн (22 мая 2018 г.). «Дойч, Тоффоли и Кнот Гейтс через ридберговскую блокаду нейтральных атомов» . Применена физическая проверка . 9 (5): 051001. arXiv : 1710.01859 . Бибкод : 2018PhRvP...9e1001S . doi : 10.1103/PhysRevApplied.9.051001 . ISSN 2331-7019 . S2CID 118909059 .
- ^ «Я операция» . docs.microsoft.com . 28 июля 2023 г.
- ^ "ИГейт" . qiskit.org . Онлайн-документация Qiskit .
- ^ Потеря, Дэниел; ДиВинченцо, Дэвид П. (1 января 1998 г.). «Квантовые вычисления с квантовыми точками» . Физический обзор А. 57 (1): 120–126. arXiv : cond-mat/9701055 . Бибкод : 1998PhRvA..57..120L . дои : 10.1103/physreva.57.120 . ISSN 1050-2947 . Пример в уравнении 2.
- ^ Раз, Ран (2002). «О сложности матричного произведения». Материалы тридцать четвертого ежегодного симпозиума ACM по теории вычислений . стр. 144–151. дои : 10.1145/509907.509932 . ISBN 1581134959 . S2CID 9582328 .
{{cite book}}: CS1 maint: дата и год ( ссылка ) - ^ «UnitaryGate § UnitaryGate adjoint()» . docs.quantum.ibm.com .
- ^ Гриффитс, диджей (2008). Введение в элементарные частицы (2-е изд.) . Джон Уайли и сыновья . стр. 115–121, 126. ISBN. 978-3-527-40601-2 .
- ^ Дэвид Альберт (1994). Квантовая механика и опыт . Издательство Гарвардского университета . п. 35. ISBN 0-674-74113-7 .
- ^ Шон М. Кэрролл (2019). Пространство-время и геометрия: Введение в общую теорию относительности . Издательство Кембриджского университета . стр. 376–394. ISBN 978-1-108-48839-6 .
- ^ Дэвид Уоллес (2012). Возникающая мультивселенная: квантовая теория согласно интерпретации Эверетта . Издательство Оксфордского университета . ISBN 9780199546961 .
- ^ Шон М. Кэрролл (2019). Что-то глубоко скрытое: квантовые миры и возникновение пространства-времени . Случайный дом пингвинов . ISBN 9781524743017 .
- ^ Q# Онлайн-руководство: Измерение
- ^ Хуан Юань Цао; Шэн-Кай Ляо; Лян Цзи-Цай; Вэй-Юэ Лю; Хуэй Дай; Юнь-Хун Ли; Фэн-Чжи Ли; Цзы-Цин Цзя; Цзянь-Цзюнь Цзя; И-Линь Чжоу; Чжан На Ван; Чжэнь-Цай Чжу; Ю-Ао Чен; Чэн-Чжи Пэн; Цзянь -Вэй Пань » Распределение запутанности по данным спутников на расстояние более 1200 километров». Quantum Optics . 356 (6343): 1140–1144. : 1707.01339 . doi : 10.1126 /science.aan3211 . PMID 28619937. arXiv S2CID 5206894 .
- ^ Биллингс, Ли (23 апреля 2020 г.). «Китай побил рекорд «жутких действий на расстоянии», готовясь к квантовому Интернету» . Научный американец .
- ^ Попкин, Габриэль (15 июня 2017 г.). «Китайский квантовый спутник совершает «жуткие действия» на рекордном расстоянии» . Наука – АААС .
- ^ Ааронсон, Скотт (2009). «BQP и полиномиальная иерархия». arXiv : 0910.4698 [ квант-ph ].
- ^ Доусон, Кристофер М.; Нильсен, Майкл (1 января 2006 г.). «Алгоритм Соловая-Китаева» . Квантовая информация и вычисления . 6 (1). Раздел 5.1, уравнение 23. arXiv : quant-ph/0505030 . дои : 10.26421/QIC6.1-6 .
- ^ Маттео, Оливия Ди (2016). «Распараллеленный синтез квантовых схем» . Квантовая наука и технология . 1 (1): 015003. arXiv : 1606.07413 . Бибкод : 2016QS&T....1a5003D . дои : 10.1088/2058-9565/1/1/015003 . S2CID 62819073 .
- ^ Ааронсон, Скотт (2002). «Нижняя квантовая граница для рекурсивной выборки Фурье». Квантовая информация и вычисления . 3 (2): 165–174. arXiv : Quant-ph/0209060 . Бибкод : 2002quant.ph..9060A . дои : 10.26421/QIC3.2-7 .
- ^ Онлайн-руководство Q#: Управление квантовой памятью
- ^ Ре, Асака; Казумицу, Сакаи; Рёко, Яхаги (2020). «Квантовая схема быстрого преобразования Фурье» . Квантовая обработка информации . 19 (277): 277. arXiv : 1911.03055 . Бибкод : 2020QuIP...19..277A . дои : 10.1007/s11128-020-02776-5 . S2CID 207847474 .
- ^ Монтасер, Раша (2019). «Новая конструкция обратимого полного сумматора/вычитателя с использованием R-вентиля». Международный журнал теоретической физики . 58 (1): 167–183. arXiv : 1708.00306 . Бибкод : 2019IJTP...58..167M . дои : 10.1007/s10773-018-3921-1 . S2CID 24590164 .
- ^ Исходный код QCL 0.6.4, файл "lib/examples.qcl"
Источники
[ редактировать ]- Нильсен, Майкл А .; Чуанг, Исаак (2000). Квантовые вычисления и квантовая информация . Кембридж: Издательство Кембриджского университета . ISBN 0521632358 . OCLC 43641333 .
- Уильямс, Колин П. (2011). Исследования в области квантовых вычислений . Спрингер . ISBN 978-1-84628-887-6 .
- Янофски, Носон С.; Маннуччи, Мирко (2013). Квантовые вычисления для компьютерщиков . Издательство Кембриджского университета . ISBN 978-0-521-87996-5 .
































































![{\displaystyle T={\begin{bmatrix}1&0\\0&e^{i{\frac {\pi }{4}}}\end{bmatrix}}=P\left({\frac {\pi }{4 }}\right)={\sqrt {S}}={\sqrt[{4}]{Z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c88bbaf48f6f443648d8e67637a140138ef2cd)













































































































































