Доска жирный шрифт

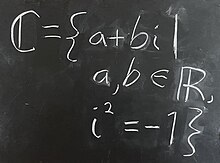
Blackboard полужирный — это стиль написания жирных символов на доске путем удвоения определенных штрихов, обычно используемый в математических лекциях , а также производный стиль шрифта , используемый в печатных математических текстах. Стиль чаще всего используется для представления наборов чисел. $\mathbb {N}$ ( натуральные числа ), $\mathbb {Z}$ ( целые числа ), $\mathbb {Q}$ ( рациональное число ), $\mathbb {R}$ ( действительные числа ) и $\mathbb {C}$ ( комплексные числа ).

Чтобы имитировать жирный шрифт на пишущей машинке , символ можно напечатать поверх самого себя (так называемое двойное зачеркивание ); ^[1] Создаваемые таким образом символы называются двойными штрихами , и это название иногда используется для жирных символов на доске. ^[2] например, в Юникода именах глифов .

В типографике шрифт с не сплошными символами называется встроенным , ручным или открытым . ^[3]

История [ править ]

Традиционно различные символы в печати обозначались жирным шрифтом , а на досках и в рукописях «волнистым подчеркиванием, или заключением в круг, или даже волнистым зачеркиванием». ^[6]

Большинство пишущих машинок вообще не имеют выделенных жирных символов. Чтобы придать пишущей машинке эффект жирности, символ можно нанести двойным ударом с небольшим смещением или без него. К середине 1960-х годов аксессуары для пишущих машинок, такие как Doublebold, могли автоматически наносить двойной удар по каждому символу во время работы. ^[7] Хотя этот метод делает символ более смелым и может эффективно подчеркнуть слова или отрывки, изолированный символ с двойным ударом не всегда явно отличается от своего аналога с одинарным ударом. ^[8]^[9]

Жирный шрифт Blackboard возник в результате попытки написать на пишущих машинках и классных досках жирные символы, которые были разборчивыми, но отчетливыми, возможно, начиная с конца 1950-х годов во Франции, а затем в начале 1960-х годов он прижился на математическом факультете Принстонского университета . ^[8]^[10]Авторы-математики начали печатать буквы, набранные полужирным шрифтом, дважды зачеркивая их со значительным смещением или перечеркивая буквой I , создавая новые символы, такие как ИК , В , СС , или ЗЗ ; у доски преподаватели начали писать жирные символы определенными двойными штрихами. ^[8]^[10] Эти обозначения прижились: жирный шрифт на доске распространился из класса в класс и теперь используется во всем мире. ^[8]

Этот стиль начал появляться в печати с середины 1960-х годов. Ранние примеры включают Роберта Ганнинга и Хьюго Росси « Аналитические функции нескольких комплексных переменных» (1965). ^[12]^[10] и » Линн Лумис и Шломо Штернберга ( «Продвинутое исчисление 1968). ^[11]Но первоначальное внедрение носило спорадический характер, и большинство издателей продолжали использовать жирный шрифт. В 1979 году Уайли рекомендовал своим авторам избегать «теневых или контурных букв с двойной подложкой, иногда называемых жирным шрифтом на доске», потому что их не всегда можно было напечатать; ^[13] в 1982 году Уайли отказался включать жирные буквы, выделенные на доске, в математические книги, потому что получить этот шрифт было сложно и дорого. ^[14]

Дональд Кнут предпочитал жирный шрифт, а не жирный шрифт на доске, и поэтому не включил жирный шрифт на доске в шрифт Computer Modern , который он создал для системы математического набора текста TeX , которую он впервые выпустил в 1978 году. ^[14] Когда Кнуту The TeXbook 1984 года понадобился пример жирного шрифта на доске для указателя, он создал $\mathrm {I\!R}$ использование букв I и R с отрицательным пробелом между ними; ^[15] в 1988 году Роберт Мессер расширил это до полного набора макросов «жирной доски для бедняков», перепечатывая каждую заглавную букву тщательно расположенными символами I или вертикальными линиями. ^[16]

Не все авторы-математики были удовлетворены такими обходными путями. В 1985 году Американское математическое общество создало простой жирный шрифт в виде мела для доски для использования с пакетом AMS-TeX , созданным Майклом Спиваком , доступ к которому осуществляется с помощью \Bbbкоманда (для «жирного шрифта на доске»); Несколько лет спустя, в 1990 году, AMS выпустила обновление с новым жирным шрифтом в стиле доски, предназначенным для лучшего соответствия Times . ^[17] С тех пор было создано множество других жирных шрифтов для классной доски, некоторые из которых соответствуют стилю традиционных встроенных шрифтов, а другие по форме ближе к буквам, нарисованным мелом. ^[18]

Юникод включил наиболее распространенные буквы, выделенные на доске жирным шрифтом, среди « буквоподобных символов » в версии 1.0 (1991 г.), унаследованных от стандарта кодировки символов Xerox . Более поздние версии Unicode расширили этот набор до всех прописных и строчных латинских букв, а также множества других символов, включая « Математические буквенно-цифровые символы ». ^[19]

В профессионально набранных книгах издатели и авторы постепенно стали использовать жирный шрифт, и его использование теперь стало обычным явлением. ^[14]но некоторые до сих пор используют обычные жирные символы. Некоторые авторы используют жирные буквы на доске или в рукописях, но в печати предпочитают обычный жирный шрифт; например, Жан-Пьер Серр использовал жирный шрифт на доске в лекциях, но постоянно использовал обычный жирный шрифт для тех же символов в своих опубликованных работах. ^[20] со Рекомендации Чикагского руководства по стилю временем менялись: в 1993 году, в 14-м издании, оно рекомендовало, чтобы «жирный шрифт на доске использовался только в классе» (13.14); В 2003 году в 15-м издании говорилось, что «открытые символы (на доске) зарезервированы для знакомых систем чисел» (14.12). В международном стандарте ISO 80000-2 :2019 $R$ указан как символ действительных чисел, но отмечены «символы $IR$ и $\mathbb {R}$ также используются», и аналогично для $N$ , $Z$ , $Q$ , $C$ и $P$ ( простые числа ). ^[21]

Кодировка [ править ]

TeX , стандартная система набора математических текстов, не содержит прямой поддержки жирных символов на доске, но Американское математическое общество распространяет популярную коллекцию AMSFonts , загружаемую из amssymb пакет, который включает в себя жирный шрифт для заглавных латинских букв, доступ к которому осуществляется с помощью \mathbb (например \mathbb{R} производит $\mathbb {R}$ ). ^[23]

В Юникоде некоторые из наиболее распространенных символов, выделенных на доске жирным шрифтом (ℂ, ℍ, ℕ, ℙ, ℚ, ℝ и ℤ), закодированы в базовой многоязычной плоскости (BMP) в области буквоподобных символов (2100–214F) , называемой ДВОЙНАЯ ЗАГЛАВНАЯ C и т. д. Остальные, однако, закодированы вне BMP, в математических буквенно-цифровых символах (1D400–1D7FF) , а именно из U+1D538 к U+1D550 (заглавные буквы, за исключением закодированных в BMP), U+1D552 к U+1D56B (строчная) и U+1D7D8 к U+1D7E1 (цифры).

Использование [ править ]

В следующей таблице показаны все доступные жирные символы Юникода. ^[24]

В первом столбце показана буква, обычно отображаемая системой разметки LaTeX . Во втором столбце показан код Unicode. В третьем столбце показан сам символ Юникода (который будет корректно отображаться только в браузерах, поддерживающих Юникод и имеющих доступ к подходящему шрифту). В четвертом столбце описаны некоторые типичные варианты использования в математических текстах. ^[25] Некоторые символы (особенно $\mathbb {C} ,\mathbb {Q} ,\mathbb {R}$ и $\mathbb {Z}$ ) почти универсальны в своей интерпретации, ^[14] в то время как другие более разнообразны в использовании.

Латекс	Кодовая точка Юникода (шестнадцатеричный)	Символ Юникода	Использование математики
$\mathbb {A}$	`U+1D538`	𝔸	Представляет аффинное пространство , $\mathbb {A} ^{n}$ , или кольцо Аделей . Иногда представляет алгебраические числа , ^[26] алгебраическое замыкание $\mathbb {Q}$ (чаще пишут ${\overline {\mathbb {Q} }}$ или Q ), или целые алгебраические числа , важное подкольцо алгебраических чисел.
	`U+1D552`	𝕒
$\mathbb {B}$	`U+1D539`	𝔹	Иногда представляет шар , логическую область или Брауэра группу поля .
	`U+1D553`	𝕓
$\mathbb {C}$	`U+2102`	ℂ	Представляет набор комплексных чисел . ^[14]
	`U+1D554`	𝕔
$\mathbb {D}$	`U+1D53B`	𝔻	Представляет единичный диск на комплексной плоскости , например, как модель конформного диска гиперболической плоскости . По обобщению $\mathbb {D} ^{n}$ может означать n -мерный шар . Изредка $\mathbb {D}$ может означать десятичные дроби (см. число ), комплексные числа или область обсуждения .
	`U+1D555`	𝕕
	`U+2145`	ⅅ
	`U+2146`	ⅆ	Может представлять собой дифференциальный символ.
$\mathbb {E}$	`U+1D53C`	𝔼	Представляет ожидаемое значение , случайной величины или евклидово пространство , или поле в башне полей , или действительные числа Евдокса .
	`U+1D556`	𝕖
	`U+2147`	ⅇ	Иногда используется для математической константы $e$ .
$\mathbb {F}$	`U+1D53D`	𝔽	Представляет поле . ^[26] Часто используется для конечных полей с индексом, указывающим порядок. ^[26] Также представляет поверхность Хирцебруха или свободную группу с индексом, указывающим количество генераторов (или набора генераторов, если он бесконечен).
	`U+1D557`	𝕗
$\mathbb {G}$	`U+1D53E`	𝔾	Представляет грассманиан или группу , особенно алгебраическую группу .
	`U+1D558`	𝕘
$\mathbb {H}$	`U+210D`	ℍ	Представляет кватернионы (H означает Гамильтон ), ^[26] или верхняя полуплоскость , или гиперболическое пространство , ^[26] или гипергомологии комплекса.
	`U+1D559`	𝕙
$\mathbb {I}$	`U+1D540`	𝕀	Замкнутый единичный интервал или идеал полиномов , исчезающих на подмножестве . Иногда тождественное отображение алгебраической структуры или индикаторной функции . Набор мнимых чисел (т.е. набор всех действительных кратных мнимой единицы).
	`U+1D55A`	𝕚
	`U+2148`	ⅈ	Иногда используется для обозначения мнимой единицы .
$\mathbb {J}$	`U+1D541`	𝕁	Иногда представляет собой иррациональные числа , $\mathbb {R} \smallsetminus \mathbb {Q}$ .
	`U+1D55B`	𝕛
	`U+2149`	ⅉ
$\mathbb {K}$	`U+1D542`	𝕂	Представляет поле . ^[26]Это слово происходит от немецкого слова Körper , которое по-немецки означает «поле» (буквально «тело»; по-французски этот термин — « корпус» ). Может также использоваться для обозначения компактного пространства .
$\mathbb {k}$	`U+1D55C`	𝕜	Представляет поле .
$\mathbb {L}$	`U+1D543`	𝕃	Представляет мотив Лефшеца. См. Мотив (алгебраическая геометрия) .
	`U+1D55D`	𝕝
$\mathbb {M}$	`U+1D544`	𝕄	Иногда представляет группу монстров . Набор всех размером m на n матриц иногда обозначается $\mathbb {M} (m,n)$ . В геометрической алгебре представляет моторную группу жестких движений. В функциональном программировании и формальной семантике обозначает конструктор типа монады .
	`U+1D55E`	𝕞
$\mathbb {N}$	`U+2115`	ℕ	Представляет набор натуральных чисел . ^[21] Может включать или не включать ноль .
	`U+1D55F`	𝕟
$\mathbb {O}$	`U+1D546`	𝕆	Представляет октонионы . ^[26]
	`U+1D560`	𝕠
$\mathbb {P}$	`U+2119`	ℙ	Представляет проективное пространство , вероятность события, ^[26] простые числа , ^[21] набор степеней , положительные действительные числа, иррациональные числа или частичное множество вынуждающий .
	`U+1D561`	𝕡
$\mathbb {Q}$	`U+211A`	ℚ	Представляет набор рациональных чисел . ^[14] (Q означает частное .)
	`U+1D562`	𝕢
$\mathbb {R}$	`U+211D`	ℝ	Представляет набор действительных чисел . ^[14]
	`U+1D563`	𝕣
$\mathbb {S}$	`U+1D54A`	𝕊	Представляет сферу или спектр сфер , а иногда и седенионы .
	`U+1D564`	𝕤
$\mathbb {T}$	`U+1D54B`	𝕋	Представляет группу окружностей , в частности единичную окружность в комплексной плоскости (и $\mathbb {T} ^{n}$ n - мерный тор ) или Гекке (Гекке обозначал свои операторы как Tn _или алгебру $\mathbb {T} _{n}$ ), или тропическое полукольцо , или твисторное пространство .
	`U+1D565`	𝕥
$\mathbb {U}$	`U+1D54C`	𝕌
	`U+1D566`	...
$\mathbb {V}$	`U+1D54D`	𝕍	Представляет векторное пространство или аффинное многообразие , созданное набором полиномов, или в теории вероятностей и статистике дисперсию .
	`U+1D567`	𝕧
$\mathbb {W}$	`U+1D54E`	𝕎	Представляет целые числа (здесь в смысле неотрицательных целых чисел), которые также представлены выражением $\mathbb {N} _{0}$ .
	`U+1D568`	𝕨
$\mathbb {X}$	`U+1D54F`	𝕏	Иногда используется для обозначения произвольного метрического пространства .
	`U+1D569`	𝕩
$\mathbb {Y}$	`U+1D550`	𝕐
	`U+1D56A`	𝕪
$\mathbb {Z}$	`U+2124`	ℤ	Представляет набор целых чисел . ^[14] (Z означает Zahlen , что по-немецки означает «числа», и zählen , что по-немецки означает «считать».) Когда у него есть положительный целочисленный индекс, это может означать конечную циклическую группу такого размера.
	`U+1D56B`	𝕫

	`U+213E`	ℾ
	`U+213D`	ℽ
	`U+213F`	ℿ
	`U+213C`	ℼ
	`U+2140`	⅀

	`U+1D7D8`	𝟘	В алгебре логических высказываний это представляет противоречие или ложность.
	`U+1D7D9`	𝟙	В теории множеств - верхний элемент принудительного частичного множества или иногда единичная матрица в кольце матриц . Также используется для индикаторной функции и функции единичного шага , а также для тождественного оператора или тождественной матрицы . В геометрической алгебре представляет собой единичный антискаляр, единичный элемент под геометрическим антипроизведением. В алгебре логических высказываний это представляет собой тавтологию.
	`U+1D7DA`	𝟚	В теории категорий — интервальная категория.
	`U+1D7DB`	𝟛
	`U+1D7DC`	𝟜
	`U+1D7DD`	𝟝
	`U+1D7DE`	𝟞
	`U+1D7DF`	𝟟
	`U+1D7E0`	𝟠
	`U+1D7E1`	𝟡

Кроме того, жирный шрифт μ _n (не встречается в Юникоде или amsmath LaTeX) иногда используется теоретиками чисел и алгебраическими геометрами для обозначения групповой схемы степени корней n -й из единицы . ^[27]

Примечание. В LaTeX отображаются только заглавные латинские буквы, поскольку в реализации Википедии используется жирный шрифт AMSFonts для доски, который не поддерживает другие символы.

См. также [ править ]

Ссылки [ править ]

^ Гилрит, Чарльз Т. (1993). «Графическая окраска текста: типографские и диаграфические измерения» . Видимый язык . 27 (3): 336–361.
^ Розендорф, Теодор (2009). Справочник по типографскому столу . Дубовый холм Пресс. стр. 89–90.
^ Брингхерст, Роберт (1992). «Словарь типографских терминов» . Элементы типографского стиля . Хартли и Маркс. п. 234. ИСБН 0-88179-033-8 . Строчный : буква, в которой внутренние части основных штрихов вырезаны, оставив края более или менее неповрежденными. Встроенные грани осветляют цвет, сохраняя при этом формы и пропорции исходного лица.
Хатчингс, Р.С. (1965). «Встроенные и контурные» . Руководство по декоративным шрифтам . Гастингс Хаус. стр. 10–11.

Консуэгра, Дэвид (2004). Американский тип: дизайн и дизайнеры . Олворт Пресс. «Шрифты ручной работы» , с. 280; «Встроенные шрифты» , с. 282; «Открытые шрифты» , с. 286–287.
^ Ганнинг, Роберт К. (1966). Лекции по римановым поверхностям . Математические заметки. Издательство Принстонского университета. п. 1.
^ Нарасимхан, Рагхаван (1966). Введение в теорию аналитических пространств . Конспект лекций по математике. Том. 25. Спрингер. п. 9. дои : 10.1007/bfb0077071 . ISBN 978-3-540-03608-1 .
^ Ходжман, Чарльз Д.; Селби, Сэмюэл М.; Уэст, Роберт С., ред. (1959). Стандартные математические таблицы CRC (12-е изд.). Издательство «Химическая резина». п. 494.
Чаунди, Теодор В.; Барретт, PR; Бэти, Чарльз (1954). Печать математики . Издательство Оксфордского университета. п. 52. Знаком жирного шрифта является волнистая линия под соответствующими словами или символами; в целях безопасности на полях можно добавить слово «жирный».
^ Карч, Р. Рэндольф (1970). Процедуры графического искусства . Американское техническое общество. п. 199.
^ Перейти обратно: ^а ^б ^с ^д Уэбб, Стивен (2018). «Набор натуральных чисел ℕ» . Столкновение символов: путешествие по богатству глифов . Спрингер. стр. 198–199, 233.
^ Пример двухстрочного шрифта, произведенного ударным принтером начала 1980-х годов, можно найти в:
Уэйт, Митчелл; Арка, Джули (1982). Учебник по текстовому процессору . БАЙТ/МакГроу-Хилл. стр. 76–77.
^ Перейти обратно: ^а ^б ^с Рудольф, Ли (6 октября 2003 г.). "Re: История жирного шрифта на доске?" . Группа новостей : compt.text.tex . Архивировано из оригинала 23 сентября 2021 г. Проверено 25 июля 2023 г.
Этот пост в Usenet ( отраженный The Math Forum ), похоже, был одним из источников для Webb 2018 ; см . стр. 233
^ Перейти обратно: ^а ^б Лумис, Линн Гарольд ; Штернберг, Шломо (1968). Продвинутое исчисление . Эддисон Уэсли. п. 241. Более позднее пересмотренное издание доступно на веб-сайте Штернберга .
^ Ганнинг, Роберт С .; Росси, Хьюго (1965). Аналитические функции нескольких комплексных переменных . Прентис-Холл.
^ Руководство для авторов Wiley-Interscience и Ronald Press по подготовке и производству рукописей и иллюстраций (2-е изд.). Джон Уайли и сыновья. 1979.
^ Перейти обратно: ^а ^б ^с ^д ^Это ^ж ^г ^час Кранц, С. (2001). «2.8 Технические вопросы». Справочник по типографии для математических наук . Чепмен и Холл/CRC. п. 35. ISBN 9781584881490 .
^ Knuth, Donald (1984). The TeXbook. Addison-Wesley. p. 460.
^ Мессер, Роберт (1988). «Доска жирным шрифтом» (PDF) . БУКСИР . 9 (1): 19–20.
^ Битон, Барбара (1985). «Математические символы и кириллические шрифты, готовые к распространению» (PDF) . БУКСИР . 6 (2): 59–63.
Спивак, Михаил (1986). Радость TeX: Руководство для гурманов по набору текста с помощью пакета макросов AMS-TeX . Американское математическое общество. п. 260.
«Поступление в январе от Американского математического общества» (PDF) . БУКСИР . 10 (3): 365–366. 1989.
Битон, Барбара (05 сентября 2020 г.). «Re: Кто разработал жирные буквы AMS на математической доске и когда?» . Обмен стеками TeX–LaTeX . Проверено 27 июля 2023 г. Начерченные жирным шрифтом буквы [1985] [...] имеют блочный вид, чем-то похожи на жирные буквы на доске Monotype, но гораздо более низкого качества. (Неудивительно, что Кнуту они не понравились.)
^ Вит, Ульрик (2012). «Разработка математических шрифтов OpenType: прогресс и проблемы» (PDF) . БУКСИР . 33 (3): 302–308. Варианты дизайна алфавитов Blackboard Bold снова делятся на несколько групп. Одна группа предпочитает дизайн с засечками, который является производным от основного шрифта с засечками: [...] Другая группа предпочитает дизайн без засечек, который может быть не связан с основным шрифтом без засечек: [...] Наконец, дизайн отдельные буквы могут значительно различаться в разных математических шрифтах, и это дополнительный фактор при выборе шрифта. Например, у некоторых пользователей могут быть довольно сильные предпочтения относительно таких деталей, как двойное ударение по основе или диагонали буквы «N».
^ Алипранд, Джоан; Аллен, Джули; и др., ред. (2003). «Математические буквенно-цифровые символы: U + 1D400 – U + 1D7FF» . Стандарт Юникод, версия 4.0 . Аддисон-Уэсли. стр. 354–357.
^ Пример лекции Серра: видеодоклад «Плохо пишу математику» (часть 3/3) , начало в 7’08″
Пример форзаца: Серр, Жан-Пьер (1994). Когомологии Галуа . Спрингер.
^ Перейти обратно: ^а ^б ^с «7. Стандартные наборы чисел и интервалы». ISO 80000-2 Величины и единицы: математика (2-е изд.). Международная Организация Стандартизации . Август 2019. Таблица 3, №2-7.4.
^ Куммер, Олаф (2006). «двойной штрих — набор математических символов двойным штрихом» . Комплексная сеть архивов TeX . Проверено 27 июля 2023 г.
^ Пакин, Скотт (25 июня 2020 г.). Полный список символов LATEX (PDF) . Архивировано (PDF) из оригинала 9 октября 2022 г.
^ Карлайл, Дэвид; Ион, Патрик (2023). «Двойной удар (открытое лицо, жирный шрифт на доске)» . Определения объектов XML для символов (Технический отчет) (3-е изд.). Консорциум Всемирной паутины . Проверено 27 июля 2023 г. Примечание. Символы, выделенные [желтым цветом], находятся в плоскости 0 [базовая многоязычная плоскость], а не в блоке математических буквенно-цифровых символов в плоскости 1.
^ Вайсштейн, Эрик В. «Двойной удар» . mathworld.wolfram.com . Проверено 21 декабря 2022 г.
^ Перейти обратно: ^а ^б ^с ^д ^Это ^ж ^г ^час Севрюк, Михаил Б. (2 декабря 1998 г.). «Письмо на компьютере: некоторые обескураживающие переживания» . Математический семинар Арнольда .
^ Милн, Джеймс С. (1980). Этальные когомологии . Издательство Принстонского университета. стр. XIII, 66.

[gilreath-1] Гилрит, Чарльз Т. (1993). «Графическая окраска текста: типографские и диаграфические измерения» . Видимый язык . 27 (3): 336–361.

[rosendorf-2] Розендорф, Теодор (2009). Справочник по типографскому столу . Дубовый холм Пресс. стр. 89–90.

[typography-3] Брингхерст, Роберт (1992). «Словарь типографских терминов» . Элементы типографского стиля . Хартли и Маркс. п. 234. ИСБН 0-88179-033-8 . Строчный : буква, в которой внутренние части основных штрихов вырезаны, оставив края более или менее неповрежденными. Встроенные грани осветляют цвет, сохраняя при этом формы и пропорции исходного лица.
Хатчингс, Р.С. (1965). «Встроенные и контурные» . Руководство по декоративным шрифтам . Гастингс Хаус. стр. 10–11.

Консуэгра, Дэвид (2004). Американский тип: дизайн и дизайнеры . Олворт Пресс. «Шрифты ручной работы» , с. 280; «Встроенные шрифты» , с. 282; «Открытые шрифты» , с. 286–287.

[gunning-4] Ганнинг, Роберт К. (1966). Лекции по римановым поверхностям . Математические заметки. Издательство Принстонского университета. п. 1.

[narasimhan-5] Нарасимхан, Рагхаван (1966). Введение в теорию аналитических пространств . Конспект лекций по математике. Том. 25. Спрингер. п. 9. дои : 10.1007/bfb0077071 . ISBN 978-3-540-03608-1 .

[manuscripts-6] Ходжман, Чарльз Д.; Селби, Сэмюэл М.; Уэст, Роберт С., ред. (1959). Стандартные математические таблицы CRC (12-е изд.). Издательство «Химическая резина». п. 494.
Чаунди, Теодор В.; Барретт, PR; Бэти, Чарльз (1954). Печать математики . Издательство Оксфордского университета. п. 52. Знаком жирного шрифта является волнистая линия под соответствующими словами или символами; в целях безопасности на полях можно добавить слово «жирный».

[karch-7] Карч, Р. Рэндольф (1970). Процедуры графического искусства . Американское техническое общество. п. 199.

[webb-8] Перейти обратно: ^а ^б ^с ^д Уэбб, Стивен (2018). «Набор натуральных чисел ℕ» . Столкновение символов: путешествие по богатству глифов . Спрингер. стр. 198–199, 233.

[waite-arca-9] Пример двухстрочного шрифта, произведенного ударным принтером начала 1980-х годов, можно найти в:
Уэйт, Митчелл; Арка, Джули (1982). Учебник по текстовому процессору . БАЙТ/МакГроу-Хилл. стр. 76–77.

[rudolph-10] Перейти обратно: ^а ^б ^с Рудольф, Ли (6 октября 2003 г.). "Re: История жирного шрифта на доске?" . Группа новостей : compt.text.tex . Архивировано из оригинала 23 сентября 2021 г. Проверено 25 июля 2023 г.
Этот пост в Usenet ( отраженный The Math Forum ), похоже, был одним из источников для Webb 2018 ; см . стр. 233

[loomis-sternberg-11] Перейти обратно: ^а ^б Лумис, Линн Гарольд ; Штернберг, Шломо (1968). Продвинутое исчисление . Эддисон Уэсли. п. 241. Более позднее пересмотренное издание доступно на веб-сайте Штернберга .

[gunning-rossi-12] Ганнинг, Роберт С .; Росси, Хьюго (1965). Аналитические функции нескольких комплексных переменных . Прентис-Холл.

[wiley-13] Руководство для авторов Wiley-Interscience и Ronald Press по подготовке и производству рукописей и иллюстраций (2-е изд.). Джон Уайли и сыновья. 1979.

[krantz-14] Перейти обратно: ^а ^б ^с ^д ^Это ^ж ^г ^час Кранц, С. (2001). «2.8 Технические вопросы». Справочник по типографии для математических наук . Чепмен и Холл/CRC. п. 35. ISBN 9781584881490 .

[knuth-15] Knuth, Donald (1984). The TeXbook. Addison-Wesley. p. 460.

[messer-16] Мессер, Роберт (1988). «Доска жирным шрифтом» (PDF) . БУКСИР . 9 (1): 19–20.

[amstex-17] Битон, Барбара (1985). «Математические символы и кириллические шрифты, готовые к распространению» (PDF) . БУКСИР . 6 (2): 59–63.
Спивак, Михаил (1986). Радость TeX: Руководство для гурманов по набору текста с помощью пакета макросов AMS-TeX . Американское математическое общество. п. 260.
«Поступление в январе от Американского математического общества» (PDF) . БУКСИР . 10 (3): 365–366. 1989.
Битон, Барбара (05 сентября 2020 г.). «Re: Кто разработал жирные буквы AMS на математической доске и когда?» . Обмен стеками TeX–LaTeX . Проверено 27 июля 2023 г. Начерченные жирным шрифтом буквы [1985] [...] имеют блочный вид, чем-то похожи на жирные буквы на доске Monotype, но гораздо более низкого качества. (Неудивительно, что Кнуту они не понравились.)

[vieth-18] Вит, Ульрик (2012). «Разработка математических шрифтов OpenType: прогресс и проблемы» (PDF) . БУКСИР . 33 (3): 302–308. Варианты дизайна алфавитов Blackboard Bold снова делятся на несколько групп. Одна группа предпочитает дизайн с засечками, который является производным от основного шрифта с засечками: [...] Другая группа предпочитает дизайн без засечек, который может быть не связан с основным шрифтом без засечек: [...] Наконец, дизайн отдельные буквы могут значительно различаться в разных математических шрифтах, и это дополнительный фактор при выборе шрифта. Например, у некоторых пользователей могут быть довольно сильные предпочтения относительно таких деталей, как двойное ударение по основе или диагонали буквы «N».

[unicode-19] Алипранд, Джоан; Аллен, Джули; и др., ред. (2003). «Математические буквенно-цифровые символы: U + 1D400 – U + 1D7FF» . Стандарт Юникод, версия 4.0 . Аддисон-Уэсли. стр. 354–357.

[serre-20] Пример лекции Серра: видеодоклад «Плохо пишу математику» (часть 3/3) , начало в 7’08″
Пример форзаца: Серр, Жан-Пьер (1994). Когомологии Галуа . Спрингер.

[iso-21] Перейти обратно: ^а ^б ^с «7. Стандартные наборы чисел и интервалы». ISO 80000-2 Величины и единицы: математика (2-е изд.). Международная Организация Стандартизации . Август 2019. Таблица 3, №2-7.4.

[doublestroke-22] Куммер, Олаф (2006). «двойной штрих — набор математических символов двойным штрихом» . Комплексная сеть архивов TeX . Проверено 27 июля 2023 г.

[pakin-23] Пакин, Скотт (25 июня 2020 г.). Полный список символов LATEX (PDF) . Архивировано (PDF) из оригинала 9 октября 2022 г.

[w3c-24] Карлайл, Дэвид; Ион, Патрик (2023). «Двойной удар (открытое лицо, жирный шрифт на доске)» . Определения объектов XML для символов (Технический отчет) (3-е изд.). Консорциум Всемирной паутины . Проверено 27 июля 2023 г. Примечание. Символы, выделенные [желтым цветом], находятся в плоскости 0 [базовая многоязычная плоскость], а не в блоке математических буквенно-цифровых символов в плоскости 1.

[weisstein-25] Вайсштейн, Эрик В. «Двойной удар» . mathworld.wolfram.com . Проверено 21 декабря 2022 г.

[sevryuk-26] Перейти обратно: ^а ^б ^с ^д ^Это ^ж ^г ^час Севрюк, Михаил Б. (2 декабря 1998 г.). «Письмо на компьютере: некоторые обескураживающие переживания» . Математический семинар Арнольда .

[milne-27] Милн, Джеймс С. (1980). Этальные когомологии . Издательство Принстонского университета. стр. XIII, 66.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]