3-7 кисромбиллей
| 3-7 кисромбиллей | |
|---|---|
 | |
| Тип | Двойная полуправильная гиперболическая мозаика |
| Лица | Прямоугольный треугольник |
| Края | бесконечный |
| Вершины | бесконечный |
| Диаграмма Кокстера | |
| Группа симметрии | [7,3], (*732) |
| Группа вращения | [7,3] + , (732) |
| Двойной многогранник | Усеченная трехгептагональная мозаика |
| Конфигурация лица | Версия 4.6.14 |
| Характеристики | лице-переходный |
В геометрии 3—7 -ромбилловое замощение представляет собой полуправильное двойственное замощение гиперболической плоскости . Он состоит из конгруэнтных прямоугольных треугольников , в каждой вершине которых сходятся 4, 6 и 14 треугольников.
На изображении показана проекция модели диска Пуанкаре на гиперболическую плоскость.
Он помечен как V4.6.14, потому что каждая грань прямоугольного треугольника имеет три типа вершин: одна с 4 треугольниками, одна с 6 треугольниками и одна с 14 треугольниками. Это двойная мозаика усеченной трехгептагональной мозаики , в каждой вершине которой есть один квадрат, один семиугольник и один тетракаидекагон.
Именование [ править ]
Название 3-7 киромбилль дано Конвеем , рассматривая его как ромбическую мозаику 3-7, разделенную оператором kis , добавляющую центральную точку к каждому ромбу и разделяющую на четыре треугольника.
Симметрия [ править ]
В [7,3] нет подгрупп удаления зеркал. Единственная небольшая индексная подгруппа - это чередование, [7,3] + , (732).
| Тип | рефлексивный | Вращательный |
|---|---|---|
| индекс | 1 | 2 |
| Диаграмма |  |  |
| Коксетер ( орбифолд ) | [7,3] = (*732) | [7,3] + = (732) |
Связанные многогранники и мозаики [ править ]
Из этого мозаики путем объединения треугольников можно построить три равноэдральных (правильных или квазиправильных) мозаики:
| Пуанкаре диск модель |  |  |  |
|---|---|---|---|
| Центр | Семиугольник | Треугольник | ромбический |
| Кляйн диск модель |  |  |  |
| Связанный плитка |  |  | 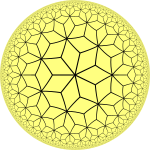 |
| Семиугольная плитка | Треугольная плитка | Ромбическая плитка |
| Однородные семиугольные/треугольные мозаики |
|---|
Топологически он связан с последовательностью многогранников; смотри обсуждение . Эта группа особенна тем, что имеет все четное количество ребер на вершину и образует биссектрисы через многогранники и бесконечные линии на плоскости, а также является областями отражения для (2,3, n ) групп треугольников – для семиугольной мозаики, важная (2,3,7) группа треугольников .
См. также равномерные мозаики гиперболической плоскости с симметрией (2,3,7) .
Кисромбильные мозаики можно рассматривать как последовательность ромбических мозаик, начиная с куба, с гранями, разделенными или зацелованными в углах центральной точкой грани.
| * n 32 мутация симметрии всеусеченных мозаик: 4.6.2n |
|---|

Так же, как группа треугольников (2,3,7) является фактором модульной группы (2,3,∞), связанная с ней мозаика является фактором модульной мозаики, как показано на видео справа.
Ссылки [ править ]
- Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)






































