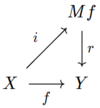Кофибрация

В математике , в частности в теории гомотопий , — непрерывное отображение между топологическими пространствами.

$i:A\to X$,

является корасслоением , если оно обладает свойством гомотопического расширения относительно всех топологических пространств. $S$. То есть, $i$ является корасслоением, если для каждого топологического пространства $S$, и для любых непрерывных отображений $f,f':A\to S$ и $g:X\to S$ с $g\circ i=f$, для любой гомотопии $h:A\times I\to S$ от $f$ к $f'$, существует непрерывное отображение $g':X\to S$ и гомотопия $h':X\times I\to S$ от $g$ к $g'$ такой, что $h'(i(a),t)=h(a,t)$ для всех $a\in A$ и $t\in I$. (Здесь, $I$ обозначает единичный интервал $[0,1]$.)

Это определение формально двойственно определению расслоения , которое должно удовлетворять свойству гомотопического подъема относительно всех пространств; это один из примеров более широкой двойственности Экмана – Хилтона в топологии.

Корасслоения являются фундаментальной концепцией теории гомотопий. Квиллен предложил понятие модельной категории как формальную основу для построения теории гомотопий в более общих категориях; Модельная категория наделена тремя выделенными классами морфизмов, называемых расслоениями , корасслоениями и слабыми эквивалентностями, удовлетворяющими определенным аксиомам подъема и факторизации.

Определение

Гомотопическая теория

В дальнейшем пусть $I=[0,1]$ обозначают единичный интервал.

Карта $i\colon A\to X$ топологических пространств называется корасслоением ^{стр. 51} если для любой карты $f:A\to S$ такое, что существует расширение $X$, то есть есть карта $f':X\to S$ такой, что $f'\circ i=f$, мы можем расширить гомотопию отображений $H:A\times I\to S$ к гомотопии отображений $H':X\times I\to S$, где

${\begin{aligned}H(a,0)&=f(a)\\H'(x,0)&=f'(x)\end{aligned}}$

Мы можем закодировать это условие в следующей коммутативной диаграмме

где $S^{I}$ это путей пространство $S$ оснащен топологией компактно-открытый.

Понятие кофибрации в категории модели см. в категории модели .

Примеры

В топологии

Топологи уже давно изучают понятия «хорошего вложения в подпространство», многие из которых подразумевают, что отображение является корасслоением или наоборот, или имеет аналогичные формальные свойства в отношении гомологии. В 1937 году Борсук доказал, что если $X$ является бинормальным пространством ( $X$ нормально, а его произведение с единичным интервалом $X\times I$ нормально), то каждое замкнутое подпространство $X$ обладает свойством гомотопического продолжения относительно любого абсолютного ретракта окрестностей. Аналогично, если $A$ является замкнутым подпространством $X$ и включение подпространства $A\times I\cup X\times {1}\subset X\times I$ является абсолютным ретрактом окрестности, то включение $A$ в $X$ является кофибрацией. Во вводном учебнике Хэтчера «Алгебраическая топология» используется техническое понятие хорошей пары , которая имеет ту же длинную точную последовательность в сингулярных гомологиях, связанных с корасслоением, но не эквивалентна. Понятие корасслоения отличается от них тем, что его гомотопическое определение более поддается формальному анализу и обобщению.

Если $f:X\to Y$ является непрерывным отображением топологических пространств, существует связанное с ним топологическое пространство $Mf$ называется отображения цилиндром $f$. Существует каноническое вложение подпространства $i:X\to Mf$ и карта проекции $r:Mf\to Y$ такой, что $r\circ i=f$ как показано на коммутативной диаграмме ниже. Более того, $i$ является кофибрацией и $r$ является гомотопической эквивалентностью. Этот результат можно резюмировать, сказав, что «всякое отображение эквивалентно в гомотопической категории корасслоению».

Арне Стрём доказал усиление этого результата: каждая карта $f:X\to Y$ факторы как композиция корасслоения и гомотопической эквивалентности, которая также является расслоением .

Топологическое пространство $X$ с выделенной базовой точкой $x$ называется корректным, если отображение включения ${x}\to X$ является кофибрацией.

Карта включения $S^{n-1}\to D^{n}$ граничной сферы твердого диска является корасслоением для любого $n$.

Часто используется тот факт, что клеточное включение является кофибрацией (так, например, если $(X,A)$ является парой CW , тогда $A\to X$ является кофибрацией). Это следует из предыдущего факта и того факта, что корасслоения устойчивы при выталкивании, поскольку выталкивания представляют собой отображения склейки с $n-1$ скелет.

В сетевых комплексах

Позволять ${\mathcal {A}}$ быть абелевой категорией с достаточным количеством проективов.

Если мы позволим $C_{+}({\mathcal {A}})$ – категория цепных комплексов, которые $0$ в градусах $q<<0$, то существует структура категории модели ^{стр. 1.2} где слабые эквивалентности — это квазиизоморфизмы , расслоения — это эпиморфизмы, а корасслоения — это отображения

$i:C_{\bullet }\to D_{\bullet }$

которые являются по степени моническими и комплексом коядра ${\text{Coker}}(i)_{\bullet }$ представляет собой комплекс проективных объектов в ${\mathcal {A}}$. Отсюда следует, что кофибрантные объекты — это комплексы, все объекты которых проективны.

Симплициальные множества

Категория ${\textbf {SSet}}$ симплициальных множеств ^{стр. 1.3} существует модельная структура категорий, в которой расслоения являются в точности расслоениями Кана, все корасслоения представляют собой инъективные отображения, а слабые эквивалентности представляют собой симплициальные отображения, которые становятся гомотопическими эквивалентностями после применения функтора геометрической реализации.

Свойства

• Для хаусдорфовых пространств каждое корасслоение является замкнутым включением (инъективным с замкнутым образом); результат также обобщается на слабые хаусдорфовые пространства .
• Выталкивание . кофибрации является кофибрацией То есть, если $g\colon A\to B$ — любое (непрерывное) отображение (между компактно порожденными пространствами) и $i\colon A\to X$ является корасслоением, то индуцированное отображение $B\to B\cup _{g}X$ является кофибрацией.
• Картографический цилиндр можно понимать как выталкивание $i\colon A\to X$ и вложение (на одном конце единичного интервала) $i_{0}\colon A\to A\times I$. То есть отображающий цилиндр можно определить как $Mi=X\cup _{i}(A\times I)$. По универсальному свойству выталкивания $i$ является корасслоением именно тогда, когда цилиндр отображения можно построить для любого пространства X .
• Корасслоение ( A , X ) существует тогда и только тогда, когда существует ретракция от $X\times I$ к $(A\times I)\cup (X\times \{0\})$, поскольку это выталкивание и, таким образом, вызывает отображение каждого разумного пространства на диаграмме.
• Аналогичные эквивалентности можно установить для пар деформация-ретракт и для пар деформация-ретракт окрестности.

Конструкции с корасслоениями

Замена

Обратите внимание, что в категории модели ${\mathcal {M}}$ если $i:*\to X$ не является корасслоением, то отображающий цилиндр $Mi$ образует кофибрантную замену . Фактически, если мы работаем только с категорией топологических пространств, замена кофибранта для любого отображения точки в пространство образует замену кофибранта.

Кофибер

Для кофибрации $A\to X$ мы определяем кослой как индуцированное фактор-пространство $X/A$. В общем, для $f:X\to Y$, коволокно ^{стр. 59} определяется как фактор-пространство

$C_{f}=M_{f}/(A\times \{0\})$

который является конусом отображения $f$. Гомотопически кослой действует как гомотопическое коядро отображения. $f:X\to Y$. Фактически, для точечных топологических пространств копредел гомотопический

${\underset {\to }{\text{hocolim}}}\left({\begin{matrix}X&\xrightarrow {f} &Y\\\downarrow &&\\\end{matrix}}\right)=C_{f}$

На самом деле последовательность карт $X\to Y\to C_{f}$ поставляется с последовательностью коволокон , которая действует как выделенный треугольник в триангулированных категориях.

См. также

• Расслоение
• Гомотопический копредел
• Гомотопическое волокно

Ссылки

• Питер Мэй, «Краткий курс алгебраической топологии» : в главе 6 определяются и обсуждаются корасслоения, и они используются повсюду.
• Браун, Рональд . «7. Кофибрации». Топология и группоиды . ISBN  978-1-4196-2722-4 . Глава 7 содержит множество результатов, которых нет в других местах.