Факторный эксперимент
В статистике полный факторный эксперимент — это эксперимент, план которого состоит из двух или более факторов, каждый из которых имеет дискретные возможные значения или «уровни», и экспериментальные единицы которого учитывают все возможные комбинации этих уровней для всех таких факторов. Полный факторный план можно также назвать полностью скрещенным планом . Такой эксперимент позволяет исследователю изучить влияние каждого фактора на переменную ответа , а также влияние взаимодействия между факторами на переменную ответа.
Для подавляющего большинства факторных экспериментов каждый фактор имеет только два уровня. Например, если каждый из двух факторов занимает два уровня, факторный эксперимент будет включать в общей сложности четыре комбинации лечения и обычно называется факторным планом 2×2 . В такой схеме взаимодействие между переменными часто является наиболее важным. Это применимо даже к сценариям, в которых присутствует основной эффект и взаимодействие.
Если количество комбинаций в полном факторном плане слишком велико, чтобы его можно было реализовать с точки зрения логистики, можно использовать дробный факторный план , в котором некоторые из возможных комбинаций (обычно не менее половины) опускаются.
Часто используются другие термины для «комбинаций лечения», такие как серии (эксперимента), точки (комбинации рассматриваются как вершины графика и ячейки (возникающие как пересечения строк и столбцов).
История
[ редактировать ]Факторные планы использовались в 19 веке Джоном Беннетом Лоузом и Джозефом Генри Гилбертом из Ротамстедской экспериментальной станции . [1]
Рональд Фишер утверждал в 1926 году, что «сложные» планы (например, факторные планы) более эффективны, чем изучение одного фактора за раз. [2] Фишер писал:
«Ни один афоризм не повторяется чаще в связи с полевыми испытаниями, чем то, что мы должны задавать Природе несколько вопросов или, в идеале, один вопрос за раз. Писатель убежден, что эта точка зрения совершенно ошибочна. Природа, полагает он, будет лучше всего ответить на логичную и тщательно продуманную анкету; действительно, если мы зададим ей один-единственный вопрос, она часто откажется отвечать, пока не будет обсуждена другая тема».
Факторный план позволяет определить влияние нескольких факторов и даже взаимодействие между ними с помощью такого же количества испытаний, которое необходимо для определения любого из эффектов в отдельности с той же степенью точности.
Фрэнк Йейтс внес значительный вклад, особенно в анализ дизайна, с помощью анализа Йейтса .
Термин «факториал», возможно, не использовался в печати до 1935 года, когда Фишер использовал его в своей книге «План экспериментов» . [3]
Преимущества и недостатки факторных экспериментов.
[ редактировать ]Многие люди изучают влияние только одного фактора или переменной. По сравнению с такими однофакторными экспериментами (OFAT) факторные эксперименты имеют ряд преимуществ. [4] [5]
- Факторные планы более эффективны, чем эксперименты OFAT. Они предоставляют больше информации по той же или меньшей цене. Они могут найти оптимальные условия быстрее, чем эксперименты OFAT.
- Когда эффект одного фактора различен для разных уровней другого фактора, его нельзя обнаружить с помощью плана эксперимента OFAT. необходимы факторные планы Для обнаружения таких взаимодействий . Использование OFAT при наличии взаимодействия может привести к серьезному непониманию того, как реакция меняется в зависимости от факторов.
- Факторные планы позволяют оценить влияние одного фактора на нескольких уровнях других факторов, что дает выводы, которые справедливы в ряде экспериментальных условий.
Основным недостатком полного факторного плана является требование к размеру выборки, который растет экспоненциально с увеличением количества рассматриваемых факторов или входных данных. [6] Альтернативные стратегии с повышенной вычислительной эффективностью включают дробные факторные планы , выборку латинского гиперкуба и методы квазислучайной выборки .
Пример преимуществ факторных экспериментов
[ редактировать ]В своей книге «Улучшение почти всего: идеи и эссе» статистик Джордж Бокс приводит множество примеров преимуществ факторных экспериментов. Вот один из них. [7] Инженеры производителя подшипников SKF хотели знать, повлияет ли переход на менее дорогую конструкцию «сепаратора» на срок службы подшипников. Инженеры обратились к статистику Кристеру Хеллстранду за помощью в разработке эксперимента. [8]
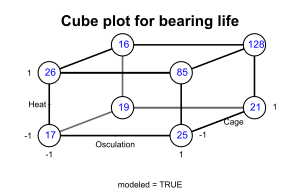
Бокс сообщает следующее. «Результаты были оценены с помощью ускоренного испытания на долговечность… Прогоны были дорогими, поскольку их нужно было проводить на реальной производственной линии, и экспериментаторы планировали провести четыре прогона со стандартной сепаратором и четыре с модифицированной сепаратором. Кристер спросил, есть ли были и другие факторы, которые они хотели бы проверить. Они сказали, что они есть, но дополнительные прогоны превысят их бюджет. Кристер показал им, как можно протестировать два дополнительных фактора «бесплатно» – без увеличения количества прогонов и без сокращения. точность оценки эффекта клетки. вершины куба..."«В каждом случае стандартное состояние обозначается знаком минус, а измененное состояние — знаком плюс. Измененными факторами были термообработка, соприкосновение наружного кольца и конструкция сепаратора. Цифры показывают относительную продолжительность срока службы подшипников. Если вы посмотрите на [кубический график], то увидите, что выбор конструкции клетки не имел большого значения… Но если усреднить пары чисел для конструкции клетки, вы получите [таблицу ниже], которая выглядит так: показывает, что сделали два других фактора… Это привело к удивительному открытию, что в этом конкретном случае срок службы подшипника может быть увеличен в пять раз, если два фактора: соприкосновение наружного кольца и термическая обработка внутреннего кольца будут увеличены вместе. "
| Соприкосновение — | Оскуляция + | |
|---|---|---|
| Тепло — | 18 | 23 |
| Тепло + | 21 | 106 |
«Помня о том, что подобные подшипники изготавливались на протяжении десятилетий, поначалу удивительно, что открытие столь важного усовершенствования могло занять так много времени. Вероятное объяснение состоит в том, что большинство инженеров до недавнего времени использовали только один фактор при экспериментирование со временем, эффекты взаимодействия были упущены».
Пример
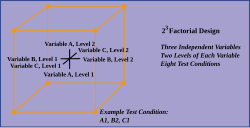
[ редактировать ]Простейший факторный эксперимент содержит два уровня для каждого из двух факторов. Предположим, инженер желает изучить общую мощность, потребляемую каждым из двух разных двигателей A и B, работающих на каждой из двух разных скоростей: 2000 или 3000 об/мин. Факторный эксперимент будет состоять из четырех экспериментальных блоков: двигатель A со скоростью 2000 об/мин, двигатель B со скоростью 2000 об/мин, двигатель A со скоростью 3000 об/мин и двигатель B со скоростью 3000 об/мин. Каждая комбинация одного уровня, выбранного из каждого фактора, присутствует один раз.
Этот эксперимент является примером 2 2 Факторный эксперимент (или 2×2), названный так потому, что он рассматривает два уровня (базовые) для каждого из двух факторов (степень или верхний индекс), или #levels #факторы , производя 2 2 = 4 факториала.
Проекты могут включать множество независимых переменных. В качестве еще одного примера: влияние трех входных переменных можно оценить в восьми экспериментальных условиях, показанных в виде углов куба.
Это может проводиться с репликацией или без нее, в зависимости от ее предполагаемой цели и имеющихся ресурсов. Он покажет влияние трех независимых переменных на зависимую переменную и возможные взаимодействия.
Обозначения
[ редактировать ]Факторные эксперименты описываются двумя вещами: количеством факторов и количеством уровней каждого фактора. Например, факторный эксперимент 2×3 имеет два фактора: первый на двух уровнях, а второй на трех уровнях. В таком эксперименте имеется 2×3=6 лечебных комбинаций или ячеек. Аналогичным образом, эксперимент 2×2×3 включает три фактора: два на 2 уровнях и один на 3, всего 12 комбинаций лечения. Если каждый фактор имеет s уровней (так называемый фиксированный уровень или симметричный план), эксперимент обычно обозначается s. к , где k — количество факторов. Таким образом, 2 5 Эксперимент имеет 5 факторов, каждый на 2 уровнях. Эксперименты, которые не имеют фиксированного уровня, называются смешанными или асимметричными .
Существуют различные традиции обозначения уровней каждого фактора. Если у фактора уже есть натуральные единицы, то используются именно они. Например, эксперимент по аквакультуре креветок. [9] могут иметь такие коэффициенты, как температура 25°C и 35°C, плотность 80 или 160 креветок на 40 литров и соленость 10%, 25% и 40%. Однако во многих случаях уровни факторов представляют собой просто категории, а кодирование уровней несколько произвольно. Например, уровни фактора 6-го уровня могут обозначаться просто 1, 2,..., 6.
Б А | 1 | 2 | 3 |
| 1 | 11 | 12 | 13 |
| 2 | 21 | 22 | 23 |
Комбинации лечения обозначаются упорядоченными парами или, в более общем смысле, упорядоченными кортежами . В эксперименте по аквакультуре упорядоченная тройка (25, 80, 10) представляет собой комбинацию обработки, имеющую самый низкий уровень каждого фактора. В обычном эксперименте 2×3 упорядоченная пара (2, 1) будет указывать ячейку, в которой фактор A находится на уровне 2, а фактор B — на уровне 1. Круглые скобки часто опускаются, как показано в прилагаемой таблице.
| Оба низкие | 00 | −− | (1) |
| Низкий | 01 | −+ | а |
| Дуть | 10 | +− | б |
| Оба высокие | 11 | ++ | аб |
Для обозначения уровней факторов в 2 к экспериментов, в литературе фигурируют три конкретные системы:
- Значения 1 и 0;
- значения 1 и -1, часто сокращенно + и -;
- Строчная буква с показателем степени 0 или 1.
Если эти значения представляют «низкие» и «высокие» настройки лечения, то естественно, чтобы 1 представляла «высокие» независимо от того, используются ли 0 и 1 или -1 и 1. Это показано в прилагаемой таблице для 2× 2 эксперимент. Если уровни факторов являются просто категориями, соответствие может быть иным; например, естественно представлять «контрольные» и «экспериментальные» условия, кодируя «контроль» как 0, если используются 0 и 1, и как 1, если используются 1 и -1. [примечание 1] Пример последнего приведен ниже . Этот пример иллюстрирует другое использование кодирования +1 и -1.
Для других фиксированных уровней ( s к ) экспериментов значения 0, 1, ..., с -1 часто используются для обозначения уровней факторов. Это значения целых чисел по модулю s, когда s простое. [примечание 2]
Контрасты, основные эффекты и взаимодействия
[ редактировать ]Б А | 1 | 2 | 3 |
| 1 | м 11 | м 12 | м 13 |
| 2 | м 21 | м 22 | м 23 |
Ожидаемый ответ на данную комбинацию лечения называется средним значением ячейки . [12] обычно обозначается греческой буквой μ. (Термин «ячейка» заимствован из его использования в таблицах данных .) Здесь эти обозначения проиллюстрированы для эксперимента 2 × 3.
Контраст средних значений ячеек представляет собой линейную комбинацию средних значений ячеек, в которой сумма коэффициентов равна 0. Контрасты представляют интерес сами по себе и являются строительными блоками, с помощью которых определяются основные эффекты и взаимодействия.
В проиллюстрированном здесь эксперименте 2 × 3 выражение
представляет собой контраст, который сравнивает средние ответы комбинаций лечения 11 и 12. (Коэффициенты здесь равны 1 и –1.) Контраст
Говорят, что он относится к основному эффекту фактора А , поскольку он контрастирует с ответами на уровень «1» фактора. с таковыми для уровня «2». основной эффект А Говорят, что отсутствует , если это выражение равно 0.
Взаимодействие в факторном эксперименте представляет собой отсутствие аддитивности между факторами, а также выражается контрастами. В эксперименте 2×3 контрасты
и
принадлежат взаимодействию A×B ; взаимодействие отсутствует (аддитивность присутствует ), если эти выражения равны 0. [13] [14] Аддитивность можно рассматривать как своего рода параллелизм между факторами, как показано в разделе «Анализ» ниже .
Поскольку именно коэффициенты этих контрастов несут существенную информацию, их часто отображают в виде векторов-столбцов . Для примера выше такая таблица может выглядеть так: [15]
| клетка | |||||
|---|---|---|---|---|---|
| 11 | 1 | 1 | 0 | 1 | 1 |
| 12 | 1 | −1 | 1 | -1 | 0 |
| 13 | 1 | 0 | −1 | 0 | −1 |
| 21 | −1 | 1 | 0 | −1 | -1 |
| 22 | −1 | −1 | 1 | 1 | 0 |
| 23 | −1 | 0 | −1 | 0 | 1 |
Столбцы такой таблицы называются векторами контраста : их компоненты в сумме дают 0. Каждый эффект определяется как расположением компонентов в ее столбцах, так и количеством столбцов .
Структура компонентов этих столбцов отражает общие определения, данные Бозе : [16]
- Вектор контраста относится к основному действию конкретного фактора, если значения его компонентов зависят только от уровня этого фактора.
- Вектор контраста принадлежит взаимодействию двух факторов , скажем A и B , если (i) значения его компонентов зависят только от уровней A и B , и (ii) он ортогонален (перпендикулярен) векторам контраста, представляющим Основные А и Б. эффекты [примечание 3]
Аналогичные определения справедливы для взаимодействия более чем двух факторов. Например, в примере 2 × 3 шаблон столбца A соответствует шаблону уровней фактора A , обозначенному первым компонентом каждой ячейки.
Количество столбцов, необходимых для указания каждого эффекта, представляет собой степени свободы эффекта. [примечание 4] и является важной величиной при дисперсионном анализе . Формула выглядит следующим образом: [18] [19]
- Главный эффект для фактора с s уровнями имеет s −1 степеней свободы.
- Взаимодействие двух факторов с уровнями s 1 и s 2 соответственно имеет ( s 1 −1)( s 2 −1) степеней свободы.
Формула для более чем двух факторов следует этой схеме. В приведенном выше примере 2 × 3 степени свободы для двух основных эффектов и взаимодействия (количество столбцов для каждого) равны 1, 2 и 2 соответственно.
Примеры
[ редактировать ]В таблицах в следующих примерах записи в столбце «Ячейка» представляют собой комбинации лечения: первый компонент каждой комбинации — это уровень фактора A , второй — фактора B , а третий (в 2 × 2 × 2 уровень фактора С. пример ) Сумма записей в каждом из остальных столбцов равна 0, так что каждый столбец представляет собой вектор контраста.
| клетка | ||||||||
|---|---|---|---|---|---|---|---|---|
| 00 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 01 | 1 | 1 | -1 | 0 | -1 | 0 | -1 | 0 |
| 02 | 1 | 1 | 0 | -1 | 0 | -1 | 0 | -1 |
| 10 | -1 | 0 | 1 | 1 | -1 | -1 | 0 | 0 |
| 11 | -1 | 0 | -1 | 0 | 1 | 0 | 0 | 0 |
| 12 | -1 | 0 | 0 | -1 | 0 | 1 | 0 | 0 |
| 20 | 0 | -1 | 1 | 1 | 0 | 0 | -1 | -1 |
| 21 | 0 | -1 | -1 | 0 | 0 | 0 | 1 | 0 |
| 22 | 0 | -1 | 0 | -1 | 0 | 0 | 0 | 1 |
Эксперимент 3 × 3: Здесь мы ожидаем 3-1 = 2 степени свободы для каждого из основных эффектов факторов A и B и (3-1)(3-1) = 4 степени свободы для A × B. взаимодействия . Это учитывает количество столбцов для каждого эффекта в прилагаемой таблице.
Два вектора контраста для A от уровня фактора A. зависят только В этом можно убедиться, заметив, что шаблон записей в каждом столбце A такой же, как шаблон первого компонента «ячейки». (При необходимости это покажет сортировка таблицы по A. эти два вектора принадлежат основному эффекту A. ) Таким образом , Аналогично, два вектора контраста для B зависят только от уровня фактора B именно второго компонента «клетки», поэтому они относятся к основному эффекту B. , а
Последние четыре вектора-столбца принадлежат взаимодействию A × B , поскольку их записи зависят от значений обоих факторов и поскольку все четыре столбца ортогональны столбцам для A и B . Последнее можно проверить, взяв скалярное произведение .
Эксперимент 2 × 2 × 2: он будет иметь 1 степень свободы для каждого основного эффекта и взаимодействия. Например, двухфакторное взаимодействие будет иметь (2-1)(2-1) = 1 степень свободы. Таким образом, для указания каждого из семи эффектов требуется всего один столбец.
| клетка | |||||||
|---|---|---|---|---|---|---|---|
| 000 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 001 | 1 | 1 | −1 | 1 | −1 | −1 | −1 |
| 010 | 1 | −1 | 1 | −1 | 1 | −1 | −1 |
| 011 | 1 | −1 | −1 | −1 | −1 | 1 | 1 |
| 100 | −1 | 1 | 1 | −1 | −1 | 1 | −1 |
| 101 | −1 | 1 | −1 | −1 | 1 | −1 | 1 |
| 110 | −1 | −1 | 1 | 1 | −1 | −1 | 1 |
| 111 | −1 | −1 | −1 | 1 | 1 | 1 | −1 |
Столбцы A , B и C представляют соответствующие основные эффекты, поскольку записи в каждом столбце зависят только от уровня соответствующего фактора. Например, записи в столбце B что и средний компонент «ячейки», как можно увидеть при сортировке по B. следуют тому же шаблону ,
Столбцы для AB , AC и BC представляют соответствующие двухфакторные взаимодействия. Например, (i) записи в столбце BC зависят от второго и третьего ( B и C ) компонентов ячейки и не зависят от первого ( A ) компонента, как можно увидеть при сортировке по BC ; и (ii) столбец BC ортогонален столбцам B и C , что можно проверить путем вычисления скалярного произведения.
Наконец, столбец ABC представляет трехфакторное взаимодействие: его записи зависят от уровней всех трех факторов и ортогональны остальным шести векторам контраста.
Объединенные и прочитанные построчно, столбцы A, B, C дают альтернативное обозначение, упомянутое выше, для комбинаций лечения (ячейок) в этом эксперименте: ячейка 000 соответствует +++, 001 - ++- и т. д.
В столбцах от A до ABC число 1 можно заменить любой константой, поскольку полученные столбцы по-прежнему будут векторами контраста. Например, в экспериментах 2×2×2 принято использовать число 1/4. [примечание 5] определить каждый основной эффект или взаимодействие и объявить, например, что контраст
является «основным» эффектом фактора A , числовой величиной, которую можно оценить. [20]
Выполнение
[ редактировать ]При более чем двух факторах 2 к Факторный эксперимент обычно можно рекурсивно спланировать, начиная с 2 к -1 факторный эксперимент путем повторения 2 к -1 эксперимента, относя первый повтор к первому (или низкому) уровню нового фактора, а второй повтор - ко второму (или высокому) уровню. Эту структуру можно обобщить, например , для разработки трех повторов для трех факторов уровня и т. д .
Факторный эксперимент позволяет оценить погрешность эксперимента двумя способами. Эксперимент можно повторить или принцип разреженности эффектов часто использовать . Повторение чаще встречается для небольших экспериментов и является очень надежным способом оценки экспериментальной ошибки. Когда количество факторов велико (обычно более 5 факторов, но это зависит от приложения), копирование проекта может стать трудным с операционной точки зрения. В этих случаях принято запускать только одну копию плана и предполагать, что взаимодействия факторов более определенного порядка (скажем, между тремя или более факторами) незначительны. При этом предположении оценки таких взаимодействий высокого порядка являются оценками точного нуля, то есть на самом деле оценкой экспериментальной ошибки.
Когда имеется много факторов, потребуется множество экспериментальных запусков, даже без повторения. Например, экспериментируя с 10 факторами на двух уровнях, каждый дает 2 10 =1024 комбинации. В какой-то момент это становится невозможным из-за высокой стоимости или недостаточности ресурсов. В этом случае дробный факторный план можно использовать .
Как и в любом статистическом эксперименте, экспериментальные серии в факторном эксперименте должны быть рандомизированы, чтобы уменьшить влияние систематической ошибки на результаты эксперимента. На практике это может стать серьезной эксплуатационной проблемой.
Факторные эксперименты можно использовать, когда имеется более двух уровней каждого фактора. Однако количество экспериментальных прогонов, необходимых для трехуровневых (или более) факторных планов, будет значительно больше, чем для их двухуровневых аналогов. Таким образом, факторные планы менее привлекательны, если исследователь желает рассмотреть более двух уровней.
Анализ
[ редактировать ]Факторный эксперимент можно проанализировать с помощью ANOVA или регрессионного анализа . [21] Чтобы вычислить основной эффект фактора «А» в двухуровневом эксперименте, вычтите среднюю реакцию всех экспериментальных серий, для которых А находился на низком (или первом) уровне, из средней реакции всех экспериментальных серий, для которых А был на своем высоком (или втором) уровне.
Другие полезные инструменты исследовательского анализа для факторных экспериментов включают графики основных эффектов , графики взаимодействия , графики Парето и график нормальной вероятности предполагаемых эффектов.
Когда факторы непрерывны, двухуровневые факторные планы предполагают, что эффекты линейны . Если квадратичный для фактора ожидается эффект, следует использовать более сложный эксперимент, например, центральный составной план . Оптимизация факторов, которые могут иметь квадратичные эффекты, является основной целью методологии поверхности отклика .
Пример анализа
[ редактировать ]Монтгомери [4] приводит следующий пример анализа факторного эксперимента:
Инженер хотел бы увеличить скорость фильтрации (производительность) процесса производства химического вещества и уменьшить количество формальдегида, используемого в этом процессе. Предыдущие попытки снизить содержание формальдегида привели к снижению скорости фильтрации. Текущая скорость фильтрации составляет 75 галлонов в час. Учитываются четыре фактора: температура (А), давление (В), концентрация формальдегида (С) и скорость перемешивания (D). Каждый из четырех факторов будет проверен на двух уровнях.
Далее знаки минус (-) и плюс (+) будут указывать, находится ли фактор на низком или высоком уровне соответственно.
| А | Б | С | Д | Скорость фильтрации |
|---|---|---|---|---|
| − | − | − | − | 45 |
| + | − | − | − | 71 |
| − | + | − | − | 48 |
| + | + | − | − | 65 |
| − | − | + | − | 68 |
| + | − | + | − | 60 |
| − | + | + | − | 80 |
| + | + | + | − | 65 |
| − | − | − | + | 43 |
| + | − | − | + | 100 |
| − | + | − | + | 45 |
| + | + | − | + | 104 |
| − | − | + | + | 75 |
| + | − | + | + | 86 |
| − | + | + | + | 70 |
| + | + | + | + | 96 |
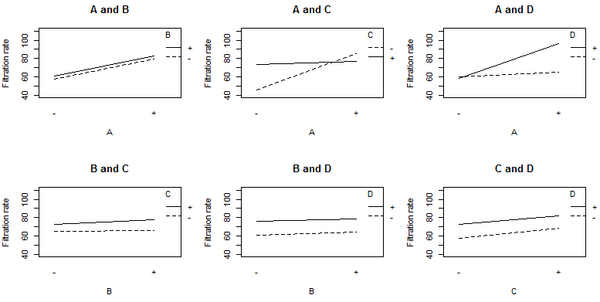
- График основных эффектов, показывающий скорости фильтрации для низких (-) и высоких (+) настроек для каждого фактора.
- График эффектов взаимодействия, показывающий среднюю скорость фильтрации на каждой из четырех возможных комбинаций уровней для данной пары факторов.
Непараллельные линии на графике взаимодействия A:C указывают на то, что эффект фактора A зависит от уровня фактора C. Аналогичные результаты справедливы и для взаимодействия A:D. Графики показывают, что фактор B мало влияет на скорость фильтрации. ( Дисперсионный анализ ANOVA), включающий все 4 фактора и все возможные условия взаимодействия между ними, дает оценки коэффициентов, показанные в таблице ниже.
| Коэффициенты | Оценивать |
|---|---|
| Перехват | 70.063 |
| А | 10.813 |
| Б | 1.563 |
| С | 4.938 |
| Д | 7.313 |
| А: Б | 0.063 |
| А:С | −9.063 |
| Б:С | 1.188 |
| ОБЪЯВЛЕНИЕ | 8.313 |
| Б:Д | −0.188 |
| К:Д | −0.563 |
| А:Б:С | 0.938 |
| А:Б:Д | 2.063 |
| А:С:Д | −0.813 |
| Б:С:Д | −1.313 |
| А:Б:С:Д | 0.688 |
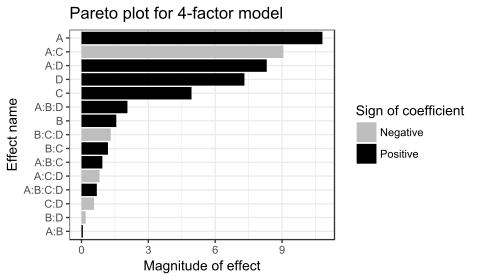
Поскольку имеется 16 наблюдений и 16 коэффициентов (перехват, основные эффекты и взаимодействия), значения p для этой модели невозможно рассчитать. Значения коэффициентов и графики показывают, что важными факторами являются A, C и D, а также условия взаимодействия A:C и A:D.
Все коэффициенты для A, C и D в ANOVA положительны, что предполагает запуск процесса со всеми тремя переменными, установленными на высокое значение. Однако основным эффектом каждой переменной является среднее значение по уровням других переменных. Приведенный выше график взаимодействия A:C показывает, что эффект фактора A зависит от уровня фактора C, и наоборот. Фактор А (температура) очень мало влияет на скорость фильтрации, когда фактор С находится на уровне +. Но фактор А оказывает большое влияние на скорость фильтрации, когда фактор С (формальдегид) находится на уровне –. Комбинация A на уровне + и C на уровне − дает самую высокую скорость фильтрации. Это наблюдение показывает, как пофакторный анализ может упустить важные взаимодействия. Только изменяя одновременно оба фактора А и С, инженер мог обнаружить, что эффект фактора А зависит от уровня фактора С.

Наилучшая скорость фильтрации наблюдается, когда A и D находятся на высоком уровне, а C — на низком уровне. Этот результат также удовлетворяет цели снижения содержания формальдегида (фактор С). Поскольку B не кажется важным, его можно исключить из модели. Выполнение ANOVA с использованием факторов A, C и D, а также условий взаимодействия A:C и A:D дает результат, показанный в следующей таблице, в которой все условия значимы (значение p <0,05).
| Коэффициент | Оценивать | Стандартная ошибка | значение t | p-значение |
|---|---|---|---|---|
| Перехват | 70.062 | 1.104 | 63.444 | 2.3 × 10 −14 |
| А | 10.812 | 1.104 | 9.791 | 1.9 × 10 −6 |
| С | 4.938 | 1.104 | 4.471 | 1.2 × 10 −3 |
| Д | 7.313 | 1.104 | 6.622 | 5.9 × 10 −5 |
| А:С | −9.063 | 1.104 | −8.206 | 9.4 × 10 −6 |
| ОБЪЯВЛЕНИЕ | 8.312 | 1.104 | 7.527 | 2 × 10 −5 |
См. также
[ редактировать ]- Комбинаторный дизайн
- Планирование экспериментов
- Ортогональный массив
- Дизайн Плакетта-Бермана
- Методы Тагучи
- t-критерий Уэлча
Пояснительные сноски
[ редактировать ]- ^ Этот выбор дает соответствие 01 ←→ +−, противоположное приведенному в таблице. Для этого есть и алгебраические причины. [10] Выбор кодирования с помощью + и – не важен, «пока маркировка единообразна». [11]
- ^ Такой выбор уровней факторов облегчает использование алгебры для решения определенных проблем планирования эксперимента. Если s уровни можно обозначать элементами конечного поля GF(s) . — степень простого числа, то по той же причине
- ^ Ортогональность определяется путем вычисления скалярного произведения векторов.
- ^ Степени свободы эффекта на самом деле представляют собой размерность векторного пространства , а именно пространства всех векторов контрастности, принадлежащих этому эффекту. [17]
- ^ И 1/2 к-1 через 2 к эксперименты.
Примечания
[ редактировать ]- ^ Йейтс, Фрэнк ; Мазер, Кеннет (1963). «Рональд Эйлмер Фишер» . Биографические мемуары членов Королевского общества . 9 . Лондон, Англия: Королевское общество : 91–120. дои : 10.1098/rsbm.1963.0006 .
- ^ Фишер, Рональд (1926). «План полевых экспериментов» (PDF) . Журнал Министерства сельского хозяйства Великобритании . 33 . Лондон, Англия: Министерство сельского хозяйства и рыболовства: 503–513.
- ^ «Самые ранние известные варианты использования некоторых математических слов (F)» . jeff560.tripod.com .
- ^ Перейти обратно: а б Монтгомери, Дуглас К. (2013). Планирование и анализ экспериментов (8-е изд.). Хобокен, Нью-Джерси: Уайли . ISBN 978-1-119-32093-7 .
- ^ Олерт, Гэри (2000). Первый курс планирования и анализа экспериментов (пересмотренная ред.). Нью-Йорк: WH Freeman and Company . ISBN 978-0-7167-3510-6 .
- ^ Тонг, К. (2006). «Стратегии совершенствования методов стратифицированной выборки». Проектирование надежности и системная безопасность . 91 (10–11): 1257–1265. дои : 10.1016/j.ress.2005.11.027 .
- ^ Джордж EP, Box (2006). Улучшение почти всего: идеи и эссе (пересмотренная ред.). Хобокен, Нью-Джерси: Уайли . АСИН B01FKSM9VY .
- ^ Хеллстранд, К.; Остерхорн, AD; Шервин, диджей; Герсон, М. (24 февраля 1989 г.). «Необходимость современного повышения качества и некоторый опыт его внедрения при производстве подшипников качения [и обсуждение]». Философские труды Королевского общества . 327 (1596): 529–537. дои : 10.1098/rsta.1989.0008 . S2CID 122252479 .
- ^ Кюль (2000 , стр. 200–205)
- ^ Ченг (2019 , Замечание 8.1)
- ^ Бокс, Охотник и Охотник (1978 , стр. 307)
- ^ Хокинг (1985 , стр. 73). Хокинг и другие используют термин «среднее значение совокупности» для обозначения ожидаемого значения.
- ^ Грейбилл (1976 , стр. 559-560)
- ^ Бедер (2022 , стр. 29–30)
- ^ Молитва (2022 , пример 5.21)
- ^ Бозе (1947 , стр. 110–111)
- ^ Ченг (2019 , стр. 77)
- ^ Кюль (2000 , стр. 202)
- ^ Ченг (2019 , стр. 78)
- ^ Коробка, Hunter & Hunter (2005 , стр. 180)
- ^ Коэн, Дж (1968). «Множественная регрессия как общая система анализа данных». Психологический вестник . 70 (6): 426–443. CiteSeerX 10.1.1.476.6180 . дои : 10.1037/h0026714 .
Ссылки
[ редактировать ]- Бедер, Джей Х. (2022). Линейные модели и проектирование . Чам, Швейцария: Springer . дои : 10.1007/978-3-031-08176-7 . ISBN 978-3-031-08175-0 . S2CID 253542415 .
- Бозе , RC (1947). «Математическая теория симметричного факторного плана». Санкхья . 8 : 107–166.
- Коробка, GE ; Хантер, В.Г.; Хантер, Дж. С. (1978). Статистика для экспериментаторов: введение в проектирование, анализ данных и построение моделей . Уайли. ISBN 978-0-471-09315-2 .
- Коробка, GE ; Хантер, В.Г.; Хантер, Дж. С. (2005). Статистика для экспериментаторов: дизайн, инновации и открытия (2-е изд.). Уайли. ISBN 978-0-471-71813-0 .
- Ченг, Цзин-Шуй (2019). Теория факторного планирования: одно- и многоуровневые эксперименты . Бока-Ратон, Флорида: CRC Press. ISBN 978-0-367-37898-1 .
- Дин, Анджела; Восс, Дэниел; Драгулич, Данель (2017). Планирование и анализ экспериментов (2-е изд.). Чам, Швейцария: Springer . ISBN 978-3-319-52250-0 .
- Грейбилл, Франклин А. (1976). Фундаментальные концепции планирования экспериментов (3-е изд.). Нью-Йорк: Холт, Райнхарт и Уинстон. ISBN 0-03-061706-5 .
- Хикс, Чарльз Р. (1982). Теория и применение линейной модели . Пасифик Гроув, Калифорния: Уодсворт и Брукс/Коул. ISBN 0-87872-108-8 .
- Хокинг, Рональд Р. (1985). Анализ линейных моделей . Пасифик Гроув, Калифорния: Брукс/Коул . ISBN 978-0534036188 .
- Кюль, Роберт О. (2000). Планирование экспериментов: статистические принципы планирования и анализа исследований (2-е изд.). Пасифик Гроув, Калифорния: Брукс/Коул. ISBN 978-0534368340 .
- Ву, К.Ф. Джефф; Хамада, Майкл С. (30 марта 2021 г.). Эксперименты: планирование, анализ и оптимизация . Джон Уайли и сыновья. ISBN 978-1-119-47010-6 .