Треугольная бипирамида
| Треугольная бипирамида | |
|---|---|
 | |
| Тип | Бипирамида Дельтаэдры Джонсон Я 11 – Я 12 – Я 13 |
| Лица | 6 треугольников |
| Края | 9 |
| Вершины | 5 |
| Конфигурация вершин | |
| Группа симметрии | |
| Двойной многогранник | треугольная призма |
| Характеристики | выпуклый |
| Сеть | |
 | |
В геометрии треугольная бипирамида — это шестигранник с шестью треугольными гранями, построенный путем соединения двух тетраэдров, расположенных лицом к лицу. Эту же форму еще называют треугольной дипирамидой. [1] [2] или тригональная бипирамида . [3] Если эти тетраэдры правильные, то все грани треугольной бипирамиды равносторонние . Это пример дельтаэдра и тела Джонсона .
Многие многогранники связаны с треугольной бипирамидой, например, новые подобные формы, полученные с помощью разных подходов, а также треугольная призма как ее двойственный многогранник . Многие применения треугольной бипирамиды включают молекулярную геометрию тригональной бипирамиды , которая описывает ее кластер атомов , решение проблемы Томсона и представление систем цветового порядка к восемнадцатому веку.
Строительство и недвижимость
[ редактировать ]Как и другие бипирамиды , треугольную бипирамиду можно построить, соединив два тетраэдра лицом к лицу. [2] Эти тетраэдры покрывают свое треугольное основание, так что полученный многогранник имеет шесть треугольников, пять вершин и девять ребер. [3] Треугольная бипирамида называется прямой, если тетраэдры симметрично правильные и обе их вершины лежат на линии, проходящей через центр основания; в противном случае он наклонен . [4] [5]

Согласно теореме Стейница , граф можно представить как скелет многогранника, если он является плоским и 3-связным графом . Другими словами, ребра этого графа не пересекаются, а только пересекаются в точке, и одна из любых двух вершин при удалении покидает связный подграф. Треугольная бипирамида представлена графом с девятью ребрами, построенным путем добавления одной вершины, соединяющейся с вершинами графа -колеса, представляющего тетраэдры . [6] [7]
Как и другие правые бипирамиды, треугольная бипирамида обладает симметрией трехмерной точечной группы , группы диэдра. двенадцатого порядка: внешний вид треугольной бипирамиды не меняется при повороте ее на одну, две трети и полный угол вокруг оси симметрии (линия, проходящая через две вершины и центр основания по вертикали), и она обладает зеркальной симметрией относительно к любой биссектрисе основания; он также симметричен, поскольку отражается в горизонтальной плоскости. [8]
Как твердое тело Джонсона
[ редактировать ]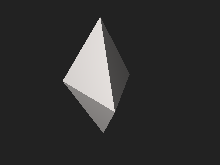
Если тетраэдры правильные, то все ребра треугольной бипирамиды равны по длине, образуя равносторонние треугольные грани. Многогранник, гранями которого являются только равносторонние треугольники, называется дельтаэдром . Существует всего восемь различных выпуклых дельтаэдров, один из которых представляет собой треугольную бипирамиду с правильными многоугольными гранями. [1] В более общем смысле, выпуклый многогранник, в котором все грани являются правильными многоугольниками, является телом Джонсона , а каждый выпуклый дельтаэдр — телом Джонсона. Треугольная бипирамида с правильными гранями входит в число тел Джонсона как двенадцатое тело Джонсона. . [9]
Площадь поверхности треугольной бипирамиды в шесть раз больше, чем у каждого треугольника. Его объем можно вычислить, разрезав его на два тетраэдра и сложив их объемы. В случае длины ребра , Это: [10]
Двугранный угол треугольной бипирамиды можно получить сложением двугранного угла двух правильных тетраэдров. Двугранный угол треугольной бипирамиды между соседними треугольными гранями равен углу правильного тетраэдра и составляет 70,5°. В случае ребра, к которому прикреплены два тетраэдра, двугранный угол соседних треугольников вдвое больше - 141,1 °. [11]
Связанные многогранники
[ редактировать ]
Некоторые типы треугольных бипирамид могут быть получены разными способами. Например, Клитопа многогранников — это конструкция, предполагающая соединение пирамид; в случае треугольной бипирамиды ее Клитоп можно построить из треугольной бипирамиды, прикрепив тетраэдры к каждой из ее граней, накрыв и заменив их тремя другими треугольниками; скелет полученного многогранника представляет собой граф Гольднера – Харари . [12] [13] Другой тип треугольной бипирамиды — это отсечение всех ее вершин; этот процесс известен как усечение . [14]
Бипирамиды — двойственный многогранник призм ; , у которого вершины бипирамид соответствуют граням призмы, а ребра между парами вершин одной соответствуют ребрам между парами граней другой двойной он снова дает сам исходный многогранник. Следовательно, треугольная бипирамида является двойственным многогранником треугольной призме , и наоборот. [15] [3] Треугольная призма имеет пять граней, девять ребер и шесть вершин и обладает той же симметрией, что и треугольная бипирамида. [3]
Приложения
[ редактировать ]
Проблема Томсона касается конфигурации заряженных частиц на сфере с минимальной энергией. Один из них — треугольная бипирамида, представляющая собой известное решение для случая пяти электронов путем размещения вершин треугольной бипирамиды, вписанной в сферу . [16] Этому решению помогает математически строгий компьютер. [17]
В геометрии химического соединения тригонально -бипирамидальная молекулярная геометрия может быть описана как кластер атомов треугольной бипирамиды. Эта молекула имеет элемент основной группы без активной неподеленной пары , как описано в модели, предсказывающей геометрию молекул, известной как теория VSEPR . [18] Некоторыми примерами этой структуры являются пентафторид фосфора и пентахлорид фосфора в газовой фазе. [19]
При изучении теории цвета треугольная бипирамида использовалась для представления трехмерной системы порядка цветов в основном цвете . Немецкий астроном Тобиас Майер в 1758 году представил, что каждая из его вершин представляет цвет: белый и черный — это верхняя и нижняя осевые вершины соответственно, тогда как остальные вершины — красный, синий и желтый. [20] [21]
Ссылки
[ редактировать ]- ^ Перейти обратно: а б Тригг, Чарльз В. (1978). «Бесконечный класс дельтаэдров». Журнал «Математика» . 51 (1): 55–57. дои : 10.1080/0025570X.1978.11976675 . JSTOR 2689647 . МР 1572246 .
- ^ Перейти обратно: а б Раджваде, Арканзас (2001). Выпуклые многогранники с условиями регулярности и третья проблема Гильберта . Тексты и чтения по математике. Книжное агентство Индостан. п. 84. дои : 10.1007/978-93-86279-06-4 . ISBN 978-93-86279-06-4 .
- ^ Перейти обратно: а б с д Кинг, Роберт Б. (1994). «Многогранная динамика» . В Бончеве Данаил Д.; Мекенян О.Г. (ред.). Теоретико-графовые подходы к химической реакционной способности . Спрингер. дои : 10.1007/978-94-011-1202-4 . ISBN 978-94-011-1202-4 .
- ^ Ню, Вэньсинь; Сюй, Гобао (2011). «Кристаллографический контроль нанокристаллов благородных металлов». Нано сегодня . 6 (3): 265–285. дои : 10.1016/j.nantod.2011.04.006 .
- ^ Александров, Виктор (2017). «Во сколько раз можно увеличить объем выпуклого многогранника за счет изометрических деформаций?». Beiträge zur Algebra und Geometry . 58 (3): 549–554. arXiv : 1607.06604 . дои : 10.1007/s13366-017-0336-8 .
- ^ Тутте, WT (2001). Теория графов . Издательство Кембриджского университета. п. 113. ИСБН 978-0-521-79489-3 .
- ^ Саджад, Вассид; Сардар, Мухаммад С.; Пан, Сян-Фэн (2024). «Расчет расстояния сопротивления и индекса Кирхгофа цепочки треугольной бипирамиды-гексаэдра». Прикладная математика и вычислительная техника . 461 : 1–12. дои : 10.1016/j.amc.2023.128313 . S2CID 261797042 .
- ^ Александр, Дэниел С.; Кеберлин, Джералин М. (2014). Элементарная геометрия для студентов (6-е изд.). Cengage Обучение. п. 403. ИСБН 978-1-285-19569-8 .
- ^ Уэхара, Рюхей (2020). Введение в вычислительное оригами: мир новой вычислительной геометрии . Спрингер. дои : 10.1007/978-981-15-4470-5 . ISBN 978-981-15-4470-5 . S2CID 220150682 .
- ^ Берман, Мартин (1971). «Выпуклые многогранники с правильными гранями». Журнал Института Франклина . 291 (5): 329–352. дои : 10.1016/0016-0032(71)90071-8 . МР 0290245 .
- ^ Джонсон, Норман В. (1966). «Выпуклые многогранники с правильными гранями» . Канадский математический журнал . 18 : 169–200. дои : 10.4153/cjm-1966-021-8 . МР 0185507 . S2CID 122006114 . Збл 0132.14603 .
- ^ Грюнбаум, Бранко (1967). Выпуклые многогранники . Уайли Интерсайенс. п. 357. . Та же страница, 2-е изд., Тексты для выпускников по математике 221, Springer-Verlag, 2003, ISBN 978-0-387-40409-7 .
- ^ Эвальд, Гюнтер (1973). «Гамильтоновы схемы в симплициальных комплексах». Геометрии посвященные . 2 (1): 115–125. дои : 10.1007/BF00149287 . S2CID 122755203 .
- ^ Хаджи-Акбари, Амир; Чен, Элизабет Р.; Энгель, Майкл; Глотцер, Шэрон К. (2013). «Упаковка и самостоятельная сборка усеченных треугольных бипирамид». Физ. Преподобный Е. 88 (1): 012127. arXiv : 1304.3147 . Бибкод : 2013PhRvE..88a2127H . дои : 10.1103/physreve.88.012127 . ПМИД 23944434 . S2CID 8184675 . .
- ^ Сибли, Томас К. (2015). Мыслить геометрически: обзор геометрии . Математическая ассоциация Америки. п. 53. ИСБН 978-1-939512-08-6 .
- ^ Слоан, Нью-Джерси ; Хардин, Р.Х.; Дафф, TDS; Конвей, Дж. Х. (1995), «Кластеры твердых сфер с минимальной энергией», Дискретная и вычислительная геометрия , 14 (3): 237–259, doi : 10.1007/BF02570704 , MR 1344734 , S2CID 26955765
- ^ Шварц, Ричард Эван (2013). «Пятиэлектронный случай проблемы Томсона». Экспериментальная математика . 22 (2): 157–186. дои : 10.1080/10586458.2013.766570 . S2CID 38679186 .
- ^ Петруччи, Р.Х.; WS, Харвуд; ФГ, Сельдь (2002). Общая химия: принципы и современные приложения (8-е изд.). Прентис-Холл. стр. 413–414. ISBN 978-0-13-014329-7 . См. таблицу 11.1.
- ^ Хаускрофт, CE; Шарп, AG (2004). Неорганическая химия (2-е изд.). Прентис Холл. п. 407. ИСБН 978-0-13-039913-7 .
- ^ Куени, Рольф Г. (2003). Цветовое пространство и его подразделения: порядок цветов от древности до наших дней . Джон и сыновья Уайли. п. 53. ИСБН 978-0-471-46146-3 .
- ^ Куени, Рольф Г. (2013). Цвет: введение в практику и принципы . Джон и сыновья Уайли. п. 198. ИСБН 978-1-118-17384-8 .






