Коэффициент корреляции Пирсона

Не путать с коэффициентом детерминации .

Примеры диаграмм рассеяния с разными значениями коэффициента корреляции ( ρ )

Несколько наборов точек ( x , y ) с коэффициентом корреляции x и y для каждого набора. Корреляция отражает силу и направление линейной зависимости (верхний ряд), но не наклон этой зависимости (средний) и многие аспекты нелинейных связей (нижний). Примечание: фигура в центре имеет наклон 0, но в этом случае коэффициент корреляции не определен, поскольку дисперсия Y равна нулю.

В статистике коэффициент корреляции Пирсона ( ПКК ) — это коэффициент корреляции , который измеряет линейную корреляцию между двумя наборами данных. Это отношение между ковариацией двух переменных и произведением их стандартных отклонений ; таким образом, это, по сути, нормализованное измерение ковариации, так что результат всегда имеет значение от -1 до 1. Как и сама ковариация, эта мера может отражать только линейную корреляцию переменных и игнорировать многие другие типы отношений или корреляции. В качестве простого примера можно было бы ожидать, что возраст и рост выборки детей из начальной школы будут иметь коэффициент корреляции Пирсона значительно больше 0, но меньше 1 (поскольку 1 будет представлять собой нереально идеальную корреляцию).

Именование и история

Она была разработана Карлом Пирсоном на основе схожей идеи, выдвинутой Фрэнсисом Гальтоном в 1880-х годах, математическая формула для которой была выведена и опубликована Огюстом Браве в 1844 году. Таким образом, наименование коэффициента является примером закона Стиглера .

Определение

Коэффициент корреляции Пирсона представляет собой ковариацию двух переменных, деленную на произведение их стандартных отклонений. Форма определения включает в себя «момент продукта», то есть среднее значение (первый момент начала координат) произведения случайных величин с поправкой на среднее значение; отсюда и модификатор product-moment в названии.

Для населения

Коэффициент корреляции Пирсона, применительно к популяции , обычно обозначается греческой буквой ρ (rho) и может называться коэффициентом корреляции популяции или коэффициентом корреляции Пирсона популяции . Учитывая пару случайных величин $(X,Y)$ (например, Рост и Вес), формула для ρ является

$$\rho _{X,Y}={\frac {\operatorname {cov} (X,Y)}{\sigma _{X}\sigma _{Y}}}$$

где

• $\operatorname {cov}$ это ковариация
• $\sigma _{X}$ стандартное отклонение ​ $X$
• $\sigma _{Y}$ стандартное отклонение $Y$.

Формула для $\operatorname {cov} (X,Y)$ может быть выражено через среднее значение и ожидание . С

$\operatorname {cov} (X,Y)=\operatorname {\mathbb {E} } [(X-\mu _{X})(Y-\mu _{Y})],$

формула для $\rho$ также можно записать как

$$\rho _{X,Y}={\frac {\operatorname {\mathbb {E} } [(X-\mu _{X})(Y-\mu _{Y})]}{\sigma _{X}\sigma _{Y}}}$$

где

• $\sigma _{Y}$ и $\sigma _{X}$ определены как указано выше
• $\mu _{X}$ это среднее значение $X$
• $\mu _{Y}$ это среднее значение $Y$
• $\operatorname {\mathbb {E} }$ это ожидание.

Формула для $\rho$ можно выразить через нецентрированные моменты. С

${\begin{aligned}\mu _{X}={}&\operatorname {\mathbb {E} } [\,X\,]\\\mu _{Y}={}&\operatorname {\mathbb {E} } [\,Y\,]\\\sigma _{X}^{2}={}&\operatorname {\mathbb {E} } \left[\,\left(X-\operatorname {\mathbb {E} } [X]\right)^{2}\,\right]=\operatorname {\mathbb {E} } \left[\,X^{2}\,\right]-\left(\operatorname {\mathbb {E} } [\,X\,]\right)^{2}\\\sigma _{Y}^{2}={}&\operatorname {\mathbb {E} } \left[\,\left(Y-\operatorname {\mathbb {E} } [Y]\right)^{2}\,\right]=\operatorname {\mathbb {E} } \left[\,Y^{2}\,\right]-\left(\,\operatorname {\mathbb {E} } [\,Y\,]\right)^{2}\\&\operatorname {\mathbb {E} } [\,\left(X-\mu _{X}\right)\left(Y-\mu _{Y}\right)\,]=\operatorname {\mathbb {E} } [\,\left(X-\operatorname {\mathbb {E} } [\,X\,]\right)\left(Y-\operatorname {\mathbb {E} } [\,Y\,]\right)\,]=\operatorname {\mathbb {E} } [\,X\,Y\,]-\operatorname {\mathbb {E} } [\,X\,]\operatorname {\mathbb {E} } [\,Y\,]\,,\end{aligned}}$

формула для $\rho$ также можно записать как $$\rho _{X,Y}={\frac {\operatorname {\mathbb {E} } [\,X\,Y\,]-\operatorname {\mathbb {E} } [\,X\,]\operatorname {\mathbb {E} } [\,Y\,]}{{\sqrt {\operatorname {\mathbb {E} } \left[\,X^{2}\,\right]-\left(\operatorname {\mathbb {E} } [\,X\,]\right)^{2}}}~{\sqrt {\operatorname {\mathbb {E} } \left[\,Y^{2}\,\right]-\left(\operatorname {\mathbb {E} } [\,Y\,]\right)^{2}}}}}.$$

Для образца

Коэффициент корреляции Пирсона, примененный к выборке , обычно выражается формулой $r_{xy}$ и может называться выборочным коэффициентом корреляции или выборочным коэффициентом корреляции Пирсона . Мы можем получить формулу для $r_{xy}$ путем подстановки оценок ковариаций и дисперсий на основе выборки в приведенную выше формулу. Учитывая парные данные $\left\{(x_{1},y_{1}),\ldots ,(x_{n},y_{n})\right\}$ состоящий из $n$ пары, $r_{xy}$ определяется как

$$r_{xy}={\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{{\sqrt {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}{\sqrt {\sum _{i=1}^{n}(y_{i}-{\bar {y}})^{2}}}}}$$

где

• $n$ размер выборки
• $x_{i},y_{i}$ отдельные точки выборки, индексированные i
• ${\textstyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$ (выборочное среднее); и аналогично для ${\bar {y}}$.

Перестановка дает нам это формула для $r_{xy}$:

$r_{xy}={\frac {\sum _{i}x_{i}y_{i}-n{\bar {x}}{\bar {y}}}{{\sqrt {\sum _{i}x_{i}^{2}-n{\bar {x}}^{2}}}~{\sqrt {\sum _{i}y_{i}^{2}-n{\bar {y}}^{2}}}}},$

где $n,x_{i},y_{i},{\bar {x}},{\bar {y}}$ определяются, как указано выше.

Повторная перестановка дает нам формулу для $r_{xy}$:

$r_{xy}={\frac {n\sum x_{i}y_{i}-\sum x_{i}\sum y_{i}}{{\sqrt {n\sum x_{i}^{2}-\left(\sum x_{i}\right)^{2}}}~{\sqrt {n\sum y_{i}^{2}-\left(\sum y_{i}\right)^{2}}}}},$

где $n,x_{i},y_{i}$ определяются, как указано выше.

Эта формула предлагает удобный однопроходный алгоритм расчета выборочных корреляций, хотя в зависимости от задействованных чисел он иногда может быть численно нестабильным .

Эквивалентное выражение дает формулу для $r_{xy}$ как среднее произведений стандартных оценок следующим образом:

$r_{xy}={\frac {1}{n-1}}\sum _{i=1}^{n}\left({\frac {x_{i}-{\bar {x}}}{s_{x}}}\right)\left({\frac {y_{i}-{\bar {y}}}{s_{y}}}\right)$

где

• $n,x_{i},y_{i},{\bar {x}},{\bar {y}}$ определены, как указано выше, и $s_{x},s_{y}$ определены ниже
• ${\textstyle \left({\frac {x_{i}-{\bar {x}}}{s_{x}}}\right)}$ — стандартный балл (аналогично для стандартного балла $y$).

Альтернативные формулы для $r_{xy}$ также доступны. Например, можно использовать следующую формулу для $r_{xy}$:

$r_{xy}={\frac {\sum x_{i}y_{i}-n{\bar {x}}{\bar {y}}}{(n-1)s_{x}s_{y}}}$

где

• $n,x_{i},y_{i},{\bar {x}},{\bar {y}}$ определяются, как указано выше, и:
• ${\textstyle s_{x}={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}}$ ( выборочное стандартное отклонение ); и аналогично для $s_{y}$.

Для совместно гауссовских распределений

Если $(X,Y)$ является совместно гауссовским , со средним нулем и дисперсией $\Sigma$, затем $\Sigma ={\begin{bmatrix}\sigma _{X}^{2}&\rho _{X,Y}\sigma _{X}\sigma _{Y}\\\rho _{X,Y}\sigma _{X}\sigma _{Y}&\sigma _{Y}^{2}\\\end{bmatrix}}$.

Практические вопросы

В условиях сильного шума извлечение коэффициента корреляции между двумя наборами стохастических переменных является нетривиальной задачей, в частности, когда канонический корреляционный анализ сообщает об ухудшении значений корреляции из-за сильного шума. Обобщение подхода дано в другом месте.

В случае отсутствия данных Гаррен вывел оценку максимального правдоподобия .

Некоторые распределения (например, стабильные распределения, отличные от нормального распределения ) не имеют определенной дисперсии.

Математические свойства

Значения коэффициентов корреляции Пирсона как для выборки, так и для совокупности находятся в диапазоне от -1 до 1 или между ними. Корреляции, равные +1 или -1, соответствуют точкам данных, лежащим точно на прямой (в случае выборочной корреляции), или двумерное распределение, полностью поддерживаемое линией (в случае корреляции населения). Коэффициент корреляции Пирсона симметричен: corr( X , Y ) = corr( Y , X ).

Ключевым математическим свойством коэффициента корреляции Пирсона является то, что он инвариантен при отдельных изменениях местоположения и масштаба двух переменных. То есть мы можем преобразовать X в a + bX и преобразовать Y в c + dY , где a , b , c и d — константы с b , d > 0 , без изменения коэффициента корреляции. (Это справедливо как для генеральных, так и для выборочных коэффициентов корреляции Пирсона.) Более общие линейные преобразования действительно меняют корреляцию: см. § Декорреляция n случайных величин, чтобы узнать об этом.

Интерпретация

Коэффициент корреляции находится в диапазоне от -1 до 1. Абсолютное значение, равное ровно 1, означает, что линейное уравнение идеально описывает взаимосвязь между X и Y , причем все точки данных лежат на прямой . Знак корреляции определяется наклоном регрессии : значение +1 подразумевает, что все точки данных лежат на линии, для которой Y увеличивается по мере увеличения X , тогда как значение -1 подразумевает линию, на которой Y увеличивается, а X уменьшается. Значение 0 означает, что между переменными нет линейной зависимости.

В более общем смысле, ( X _i - X )( Y _i - Y ) положительно тогда и только тогда, когда X _i и Y _i лежат по одну сторону от своих соответствующих средних значений. Таким образом, коэффициент корреляции является положительным, если X _i и Y _i имеют тенденцию быть одновременно больше или одновременно меньше своих соответствующих средних значений. Коэффициент корреляции является отрицательным ( антикорреляция ), если X _i и Y _i имеют тенденцию лежать на противоположных сторонах своих соответствующих средних значений. При этом чем сильнее та или иная тенденция, тем больше абсолютное значение коэффициента корреляции.

Роджерс и Найсвандер каталогизировал тринадцать способов интерпретации корреляции или простых ее функций:

• Функция необработанных оценок и средних значений
• Стандартизованная ковариация
• Стандартизованный наклон линии регрессии
• Среднее геометрическое двух наклонов регрессии
• Квадратный корень из отношения двух дисперсий
• Среднее перекрестное произведение стандартизированных переменных
• Функция угла между двумя стандартизированными линиями регрессии
• Функция угла между двумя переменными векторами
• Изменена дисперсия разницы между стандартизированными оценками.
• Оценка по правилу воздушного шара
• Относится к двумерным эллипсам изоконцентрации.
• Функция статистики испытаний из запланированных экспериментов
• Соотношение двух средств

Геометрическая интерпретация

Линии регрессии для y = g _X ( x ) [ красный ] и Икс знак равно г _Y ( y ) [ синий ]

Для нецентрированных данных существует связь между коэффициентом корреляции и углом φ между двумя линиями регрессии, y = g _X ( x ) и x = g _Y ( y ) , полученными путем регрессии y по x и x по y соответственно. (Здесь φ измеряется против часовой стрелки в пределах первого квадранта, образованного вокруг точки пересечения линий, если r > 0 , или против часовой стрелки от четвертого до второго квадранта, если r < 0. ) Можно показать что если стандартные отклонения равны, то r = sec φ − tan φ , где sec и tan — тригонометрические функции .

Для центрированных данных (т. е. данных, которые были сдвинуты выборочными средними их соответствующих переменных так, чтобы среднее значение каждой переменной было равно нулю), коэффициент корреляции также можно рассматривать как косинус угла θ . между двумя наблюдаемыми значениями векторы в N -мерном пространстве (для N наблюдений каждой переменной).

Для набора данных можно определить как нецентрированные (не соответствующие Пирсону), так и центрированные коэффициенты корреляции. В качестве примера предположим, что валовой национальный продукт пяти стран составляет 1, 2, 3, 5 и 8 миллиардов долларов соответственно. Предположим, что в этих же пяти странах (в том же порядке) уровень бедности составляет 11%, 12%, 13%, 15% и 18%. Тогда пусть x и y — упорядоченные 5-элементные векторы, содержащие приведенные выше данные: x = (1, 2, 3, 5, 8) и y = (0,11, 0,12, 0,13, 0,15, 0,18) .

С помощью обычной процедуры нахождения угла θ между двумя векторами (см. скалярное произведение ) нецентрированный коэффициент корреляции равен

$\cos \theta ={\frac {\mathbf {x} \cdot \mathbf {y} }{\left\|\mathbf {x} \right\|\left\|\mathbf {y} \right\|}}={\frac {2.93}{{\sqrt {103}}{\sqrt {0.0983}}}}=0.920814711.$

Этот нецентрированный коэффициент корреляции идентичен косинусному подобию . Приведенные выше данные были намеренно выбраны так, чтобы они идеально коррелировали: y = 0,10 + 0,01 x . Следовательно, коэффициент корреляции Пирсона должен быть ровно единицей. Центрирование данных (сдвиг x на ℰ( x ) = 3,8 и y на ℰ( y ) = 0,138 ) дает x = (-2,8, -1,8, -0,8, 1,2, 4,2) и y = (-0,028, -0,018, −0,008, 0,012, 0,042) , откуда

$\cos \theta ={\frac {\mathbf {x} \cdot \mathbf {y} }{\left\|\mathbf {x} \right\|\left\|\mathbf {y} \right\|}}={\frac {0.308}{{\sqrt {30.8}}{\sqrt {0.00308}}}}=1=\rho _{xy},$

как и ожидалось.

Интерпретация размера корреляции

Этот рисунок дает представление о том, как полезность корреляции Пирсона для прогнозирования значений зависит от ее величины. Учитывая совместно нормальные X , Y с корреляцией ρ , $1-{\sqrt {1-\rho ^{2}}}$ (показано здесь как функция от ρ ) — это коэффициент, на который данный прогнозирования для Y может быть уменьшен при соответствующем значении X. интервал Например, если ρ = 0,5, то 95%-ный интервал прогнозирования Y | X будет примерно на 13% меньше 95%-го интервала прогнозирования Y .

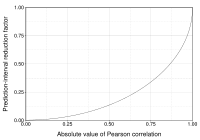
Некоторые авторы предложили рекомендации по интерпретации коэффициента корреляции. Однако все подобные критерии в некоторой степени произвольны. Интерпретация коэффициента корреляции зависит от контекста и целей. Корреляция 0,8 может быть очень низкой, если проверять физический закон с использованием высококачественных инструментов, но может считаться очень высокой в ​​социальных науках, где может быть больший вклад усложняющих факторов.

Вывод

Статистический вывод, основанный на коэффициенте корреляции Пирсона, часто фокусируется на одной из следующих двух целей:

• Одна из целей состоит в том, чтобы проверить нулевую гипотезу о том, что истинный коэффициент корреляции ρ равен 0, на основе значения выборочного коэффициента корреляции r .
• Другая цель — получить доверительный интервал , который при повторной выборке с заданной вероятностью будет содержать ρ .

Методы достижения одной или обеих этих целей обсуждаются ниже.

Использование теста перестановки

Тесты перестановок обеспечивают прямой подход к проверке гипотез и построению доверительных интервалов. Перестановочный тест коэффициента корреляции Пирсона включает следующие два этапа:

1. Используя исходные парные данные ( x _i , y _i ), случайным образом переопределите пары, чтобы создать новый набор данных ( x _i , y _{i '} ), где i ' являются перестановкой набора {1,..., n }. Перестановка i выбирается случайным образом с равными вероятностями, размещенными на всех n ! возможные перестановки. Это эквивалентно рисованию i' случайным образом без замены из набора {1, ..., n }. При начальной загрузке , тесно связанном подходе, i и i' равны и рисуются с заменой из {1, ..., n };
2. Постройте коэффициент корреляции r из рандомизированных данных.

Чтобы выполнить тест на перестановку, повторите шаги (1) и (2) большое количество раз. Значение p для теста перестановки — это доля значений r , полученных на этапе (2), которые превышают коэффициент корреляции Пирсона, рассчитанный на основе исходных данных. Здесь «больше» может означать либо то, что значение больше по величине, либо больше по знаку, в зависимости от того, ли двусторонний или односторонний требуется тест.

Использование бутстрапа

Бутстрап можно использовать для построения доверительных интервалов для коэффициента корреляции Пирсона. В «непараметрическом» бутстрапе n пар ( x _i , y _i ) повторно выбираются «с заменой» из наблюдаемого набора из n пар, а коэффициент корреляции r вычисляется на основе повторно дискретизированных данных. Этот процесс повторяется большое количество раз, и эмпирическое распределение повторно выбранных значений r используется для аппроксимации выборочного распределения статистики. 95% доверительный интервал для ρ можно определить как интервал, охватывающий от 2,5 до 97,5 процентиля повторно выбранных значений r .

Стандартная ошибка

Если $x$ и $y$ являются случайными величинами с простой линейной связью между ними с аддитивным нормальным шумом (т. е. y= a + bx + e), то стандартная ошибка, связанная с корреляцией, равна

$\sigma _{r}={\sqrt {\frac {1-r^{2}}{n-2}}}$

где $r$ это корреляция и $n$ размер выборки.

Стьюдента Тестирование с использованием t -распределения

Критические значения коэффициента корреляции Пирсона, которые необходимо превысить, чтобы считаться значимо отличным от нуля на уровне 0,05.

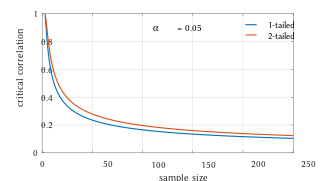
Для пар из некоррелированного двумерного нормального распределения выборочное распределение стьюдентизированного коэффициента корреляции Пирсона следует Стьюдента t -распределению со степенями свободы n - 2. В частности, если базовые переменные имеют двумерное нормальное распределение, переменная

$t={\frac {r}{\sigma _{r}}}=r{\sqrt {\frac {n-2}{1-r^{2}}}}$

-распределение Стьюдента имеет t в нулевом случае (нулевая корреляция). Это приблизительно справедливо в случае ненормальных наблюдаемых значений, если размеры выборки достаточно велики. Для определения критических значений r необходима обратная функция:

$r={\frac {t}{\sqrt {n-2+t^{2}}}}.$

В качестве альтернативы можно использовать асимптотические подходы на большой выборке.

Еще одна ранняя статья предоставляет графики и таблицы для общих значений ρ для небольших размеров выборки и обсуждает вычислительные подходы.

-распределению Стьюдента В случае, когда основные переменные не являются нормальными, выборочное распределение коэффициента корреляции Пирсона следует t , но степени свободы уменьшаются.

Использование точного распределения

Для данных, которые следуют двумерному нормальному распределению , точная функция плотности f ( r ) для выборочного коэффициента корреляции r нормального двумерного распределения равна

$f(r)={\frac {(n-2)\,\mathrm {\Gamma } (n-1)\left(1-\rho ^{2}\right)^{\frac {n-1}{2}}\left(1-r^{2}\right)^{\frac {n-4}{2}}}{{\sqrt {2\pi }}\,\operatorname {\Gamma } {\mathord {\left(n-{\tfrac {1}{2}}\right)}}(1-\rho r)^{n-{\frac {3}{2}}}}}{}_{2}\mathrm {F} _{1}{\mathord {\left({\tfrac {1}{2}},{\tfrac {1}{2}};{\tfrac {1}{2}}(2n-1);{\tfrac {1}{2}}(\rho r+1)\right)}}$

где $\Gamma$ и функция гамма - ${}_{2}\mathrm {F} _{1}(a,b;c;z)$ — гипергеометрическая функция Гаусса .

В частном случае, когда $\rho =0$ (нулевая корреляция населения), точную функцию плотности f ( r ) можно записать как

$f(r)={\frac {\left(1-r^{2}\right)^{\frac {n-1}{2}}}{\operatorname {\mathrm {B} } {\mathord {\left({\tfrac {1}{2}},{\tfrac {n+1}{2}}\right)}}}},$

где $\mathrm {B}$ — это бета-функция , которая является одним из способов записи плотности t-распределения Стьюдента для коэффициента корреляции стьюдентизированной выборки, как указано выше.

Использование точного доверительного распределения

Доверительные интервалы и тесты можно рассчитать на основе доверительного распределения . Точная доверительная плотность для ρ равна

$$\pi (\rho \mid r)={\frac {\nu (\nu -1)\Gamma (\nu -1)}{{\sqrt {2\pi }}\Gamma \left(\nu +{\frac {1}{2}}\right)}}\left(1-r^{2}\right)^{\frac {\nu -1}{2}}\cdot \left(1-\rho ^{2}\right)^{\frac {\nu -2}{2}}\cdot \left(1-r\rho \right)^{\frac {1-2\nu }{2}}\operatorname {F} \left({\tfrac {3}{2}},-{\tfrac {1}{2}};\nu +{\tfrac {1}{2}};{\tfrac {1+r\rho }{2}}\right)$$

где $\operatorname {F}$ — гипергеометрическая функция Гаусса и $\nu =n-1>1$.

Использование преобразования Фишера

Основная статья: Преобразование Фишера

На практике доверительные интервалы и проверка гипотез, касающихся ρ, обычно выполняются с использованием преобразования, стабилизирующего дисперсию , преобразования Фишера , $F$:

$F(r)\equiv {\tfrac {1}{2}}\,\ln \left({\frac {1+r}{1-r}}\right)=\operatorname {artanh} (r)$

F ( r ) приблизительно соответствует нормальному распределению с

${\text{mean}}=F(\rho )=\operatorname {artanh} (\rho )$    и стандартная ошибка $={\text{SE}}={\frac {1}{\sqrt {n-3}}},$

где n — размер выборки. Ошибка аппроксимации минимальна при большом объеме выборки. $n$ и маленький $r$ и $\rho _{0}$ и увеличивается в противном случае.

Используя аппроксимацию, z-показатель равен

$z={\frac {x-{\text{mean}}}{\text{SE}}}=[F(r)-F(\rho _{0})]{\sqrt {n-3}}$

при нулевой гипотезе , что $\rho =\rho _{0}$, при условии, что пары выборок независимы, одинаково распределены и подчиняются двумерному нормальному распределению . Таким образом, приблизительное значение p можно получить из таблицы нормальной вероятности. Например, если наблюдается z = 2,2 и требуется двустороннее значение p для проверки нулевой гипотезы, согласно которой $\rho =0$, значение p равно 2 Φ(−2,2) = 0,028 , где Φ — стандартная нормальная кумулятивная функция распределения .

Чтобы получить доверительный интервал для ρ, мы сначала вычисляем доверительный интервал для F ( $\rho$):

$100(1-\alpha )\%{\text{CI}}:\operatorname {artanh} (\rho )\in [\operatorname {artanh} (r)\pm z_{\alpha /2}{\text{SE}}]$

Обратное преобразование Фишера возвращает интервал в шкалу корреляции.

$100(1-\alpha )\%{\text{CI}}:\rho \in [\tanh(\operatorname {artanh} (r)-z_{\alpha /2}{\text{SE}}),\tanh(\operatorname {artanh} (r)+z_{\alpha /2}{\text{SE}})]$

Например, предположим, что мы наблюдаем r = 0,7 при размере выборки n = 50 и хотим получить 95% доверительный интервал для ρ . Преобразованное значение ${\textstyle \operatorname {arctanh} \left(r\right)=0.8673}$, поэтому доверительный интервал преобразованной шкалы равен $0.8673\pm {\frac {1.96}{\sqrt {47}}}$, или (0,5814, 1,1532). Преобразование обратно в шкалу корреляции дает (0,5237, 0,8188).

Регрессионный анализ по методу наименьших квадратов

Более общую нелинейную зависимость см. в разделе « Коэффициент детерминации § В множественной линейной модели» .

Квадрат выборочного коэффициента корреляции обычно обозначается r ² и является частным случаем коэффициента детерминации . В этом случае он оценивает долю дисперсии Y , которая объясняется X в простой линейной регрессии . Итак, если у нас есть наблюдаемый набор данных $Y_{1},\dots ,Y_{n}$ и подобранный набор данных ${\hat {Y}}_{1},\dots ,{\hat {Y}}_{n}$ тогда в качестве отправной точки общее изменение Y _i вокруг их среднего значения можно разложить следующим образом:

$\sum _{i}(Y_{i}-{\bar {Y}})^{2}=\sum _{i}(Y_{i}-{\hat {Y}}_{i})^{2}+\sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2},$

где ${\hat {Y}}_{i}$ представляют собой подобранные значения из регрессионного анализа. Это можно переставить, чтобы дать

$1={\frac {\sum _{i}(Y_{i}-{\hat {Y}}_{i})^{2}}{\sum _{i}(Y_{i}-{\bar {Y}})^{2}}}+{\frac {\sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}{\sum _{i}(Y_{i}-{\bar {Y}})^{2}}}.$

Два слагаемых выше представляют собой долю дисперсии Y , которая объясняется X (справа) и необъясняется X (слева).

Далее мы применяем свойство модели регрессии наименьших квадратов , заключающееся в том, что выборочная ковариация между ${\hat {Y}}_{i}$ и $Y_{i}-{\hat {Y}}_{i}$ равен нулю. Таким образом, можно записать выборочный коэффициент корреляции между наблюдаемыми и подобранными значениями ответа в регрессии (расчеты ожидаются, предполагается статистика Гаусса).

${\begin{aligned}r(Y,{\hat {Y}})&={\frac {\sum _{i}(Y_{i}-{\bar {Y}})({\hat {Y}}_{i}-{\bar {Y}})}{\sqrt {\sum _{i}(Y_{i}-{\bar {Y}})^{2}\cdot \sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}}}\\[6pt]&={\frac {\sum _{i}(Y_{i}-{\hat {Y}}_{i}+{\hat {Y}}_{i}-{\bar {Y}})({\hat {Y}}_{i}-{\bar {Y}})}{\sqrt {\sum _{i}(Y_{i}-{\bar {Y}})^{2}\cdot \sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}}}\\[6pt]&={\frac {\sum _{i}[(Y_{i}-{\hat {Y}}_{i})({\hat {Y}}_{i}-{\bar {Y}})+({\hat {Y}}_{i}-{\bar {Y}})^{2}]}{\sqrt {\sum _{i}(Y_{i}-{\bar {Y}})^{2}\cdot \sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}}}\\[6pt]&={\frac {\sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}{\sqrt {\sum _{i}(Y_{i}-{\bar {Y}})^{2}\cdot \sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}}}\\[6pt]&={\sqrt {\frac {\sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}{\sum _{i}(Y_{i}-{\bar {Y}})^{2}}}}.\end{aligned}}$

Таким образом

$r(Y,{\hat {Y}})^{2}={\frac {\sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}{\sum _{i}(Y_{i}-{\bar {Y}})^{2}}}$

где $r(Y,{\hat {Y}})^{2}$ — это доля дисперсии Y, линейной функцией X. объясняемая

В приведенном выше выводе тот факт, что

$\sum _{i}(Y_{i}-{\hat {Y}}_{i})({\hat {Y}}_{i}-{\bar {Y}})=0$

можно доказать, заметив, что частные производные остаточной суммы квадратов ( RSS ) по β ₀ и β ₁ равны 0 в модели наименьших квадратов, где

${\text{RSS}}=\sum _{i}(Y_{i}-{\hat {Y}}_{i})^{2}$.

В конечном итоге уравнение можно записать в виде

$r(Y,{\hat {Y}})^{2}={\frac {{\text{SS}}_{\text{reg}}}{{\text{SS}}_{\text{tot}}}}$

где

• ${\text{SS}}_{\text{reg}}=\sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}$
• ${\text{SS}}_{\text{tot}}=\sum _{i}(Y_{i}-{\bar {Y}})^{2}$.

Символ ${\text{SS}}_{\text{reg}}$ называется регрессионной суммой квадратов, также называемой объясненной суммой квадратов , и ${\text{SS}}_{\text{tot}}$ — общая сумма квадратов (пропорциональная дисперсии данных).

Чувствительность к распределению данных

Дополнительная информация: Корреляция и зависимость § Чувствительность к распределению данных.

Существование

Коэффициент корреляции Пирсона для населения определяется в терминах моментов и, следовательно, существует для любого двумерного распределения вероятностей , для которого генеральной совокупности ковариация определена предельные дисперсии генеральной совокупности и определены , которые не равны нулю. Некоторые распределения вероятностей, такие как распределение Коши , имеют неопределенную дисперсию и, следовательно, ρ не определен, если X или Y следует такому распределению. В некоторых практических приложениях, например, когда данные предположительно имеют распределение с тяжелым хвостом , это является важным фактором. Однако существование коэффициента корреляции обычно не вызывает беспокойства; например, если диапазон распределения ограничен, ρ всегда определен.

Размер выборки

• Если размер выборки умеренный или большой, а популяция нормальная, то в случае двумерного нормального распределения коэффициент корреляции выборки представляет собой оценку максимального правдоподобия коэффициента корреляции популяции и является асимптотически несмещенным и эффективным , что примерно означает что невозможно построить более точную оценку, чем выборочный коэффициент корреляции.
• Если размер выборки велик, а совокупность не является нормальной, то коэффициент корреляции выборки остается примерно несмещенным, но может быть неэффективным.
• Если размер выборки велик, то коэффициент корреляции выборки является последовательной оценкой коэффициента корреляции генеральной совокупности, пока выборочные средние, дисперсии и ковариация последовательны (что гарантируется при закона больших чисел ). применении
• Если размер выборки невелик, то выборочный коэффициент корреляции r не является несмещенной оценкой ρ . Вместо этого необходимо использовать скорректированный коэффициент корреляции: определение см. в других разделах этой статьи.
• Корреляции могут быть разными для несбалансированных дихотомических данных, когда в выборке есть ошибка дисперсии.

Надежность

Как и многие широко используемые статистические данные, выборочная статистика r не является устойчивой . поэтому его значение может ввести в заблуждение, если выбросы . присутствуют В частности, PMCC не является ни надежным с точки зрения распределения, ни и не устойчив к выбросам (см. Робастную статистику § Определение ). Проверка диаграммы рассеяния между X и Y обычно выявляет ситуацию, когда отсутствие устойчивости может быть проблемой, и в таких случаях может быть целесообразно использовать надежную меру связи. Однако обратите внимание, что, хотя большинство надежных оценок ассоциации каким-то образом измеряют статистическую зависимость , их, как правило, нельзя интерпретировать в той же шкале, что и коэффициент корреляции Пирсона.

Статистический вывод для коэффициента корреляции Пирсона чувствителен к распределению данных. Точные тесты и асимптотические тесты, основанные на преобразовании Фишера, могут применяться, если данные примерно нормально распределены, но в противном случае могут вводить в заблуждение. В некоторых ситуациях бутстреп можно применять для построения доверительных интервалов, а тесты перестановок можно применять для проверки гипотез. Эти непараметрические подходы могут дать более значимые результаты в некоторых ситуациях, когда двумерная нормальность не соблюдается. Однако стандартные версии этих подходов полагаются на возможность обмена данными, что означает отсутствие упорядочения или группировки анализируемых пар данных, которые могли бы повлиять на поведение оценки корреляции.

Стратифицированный анализ — это один из способов либо компенсировать отсутствие двумерной нормальности, либо изолировать корреляцию, возникающую в результате одного фактора, при этом контролируя другой. Если W представляет членство в кластере или другой фактор, который желательно контролировать, мы можем стратифицировать данные на основе значения W , а затем рассчитать коэффициент корреляции внутри каждого слоя. Затем оценки на уровне страты можно объединить для оценки общей корреляции с учетом W .

Варианты

См. Также: Корреляция и зависимость § Другие меры зависимости между случайными величинами.

Вариации коэффициента корреляции можно рассчитывать для разных целей. Вот несколько примеров.

Скорректированный коэффициент корреляции

Выборочный коэффициент корреляции r не является несмещенной оценкой ρ . Для данных, которые следуют двумерному нормальному распределению , математическое ожидание E[ r ] для выборочного коэффициента корреляции r нормального двумерного распределения равно

$\operatorname {\mathbb {E} } \left[r\right]=\rho -{\frac {\rho \left(1-\rho ^{2}\right)}{2n}}+\cdots ,\quad$ поэтому r является смещенной оценкой $\rho .$

Уникальная несмещенная оценка минимальной дисперсии r _adj определяется выражением

$r_{\text{adj}}=r\,\mathbf {_{2}F_{1}} \left({\frac {1}{2}},{\frac {1}{2}};{\frac {n-1}{2}};1-r^{2}\right),$ ( 1 )

где:

• $r,n$ определяются, как указано выше,
• $\mathbf {_{2}F_{1}} (a,b;c;z)$ — гипергеометрическая функция Гаусса .

Приближенно несмещенную оценку r _adj можно получить усекая E[ r ] и решая это усеченное уравнение:

$r=\operatorname {\mathbb {E} } [r]\approx r_{\text{adj}}-{\frac {r_{\text{adj}}\left(1-r_{\text{adj}}^{2}\right)}{2n}}.$ ( 2 )

Примерное решение к уравнению ( 2 ) есть

$r_{\text{adj}}\approx r\left[1+{\frac {1-r^{2}}{2n}}\right],$ ( 3 )

где в ( 3 )

• $r,n$ определяются, как указано выше,
• r _adj — субоптимальная оценка,
• r _adj также можно получить путем максимизации log( f ( r )),
• r _adj имеет минимальную дисперсию для больших значений n ,
• r _adj имеет смещение порядка 1 ⁄ ( п - 1) .

Еще один предложенный скорректированный коэффициент корреляции

$r_{\text{adj}}={\sqrt {1-{\frac {(1-r^{2})(n-1)}{(n-2)}}}}.$

r _adj ≈ r для больших значений n .

Взвешенный коэффициент корреляции

Предположим, что наблюдения, подлежащие корреляции, имеют разную степень важности, которую можно выразить с помощью весового вектора w . Чтобы вычислить корреляцию между векторами x и y с весовым вектором w (все длины n ),

• Взвешенное среднее: $$\operatorname {m} (x;w)={\frac {\sum _{i}w_{i}x_{i}}{\sum _{i}w_{i}}}.$$
• Взвешенная ковариация $$\operatorname {cov} (x,y;w)={\frac {\sum _{i}w_{i}\cdot (x_{i}-\operatorname {m} (x;w))(y_{i}-\operatorname {m} (y;w))}{\sum _{i}w_{i}}}.$$
• Взвешенная корреляция $$\operatorname {corr} (x,y;w)={\frac {\operatorname {cov} (x,y;w)}{\sqrt {\operatorname {cov} (x,x;w)\operatorname {cov} (y,y;w)}}}.$$

Коэффициент отражательной корреляции

Рефлексивная корреляция — это вариант корреляции Пирсона, в котором данные не сосредоточены вокруг их средних значений. Рефлективная корреляция населения

$\operatorname {corr} _{r}(X,Y)={\frac {\operatorname {\mathbb {E} } [\,X\,Y\,]}{\sqrt {\operatorname {\mathbb {E} } [\,X^{2}\,]\cdot \operatorname {\mathbb {E} } [\,Y^{2}\,]}}}.$

Рефлексивная корреляция симметрична, но не инвариантна при трансляции:

$\operatorname {corr} _{r}(X,Y)=\operatorname {corr} _{r}(Y,X)=\operatorname {corr} _{r}(X,bY)\neq \operatorname {corr} _{r}(X,a+bY),\quad a\neq 0,b>0.$

Выборочная отражательная корреляция эквивалентна косинусному подобию :

$rr_{xy}={\frac {\sum x_{i}y_{i}}{\sqrt {(\sum x_{i}^{2})(\sum y_{i}^{2})}}}.$

Взвешенная версия выборочной отражательной корреляции:

$rr_{xy,w}={\frac {\sum w_{i}x_{i}y_{i}}{\sqrt {(\sum w_{i}x_{i}^{2})(\sum w_{i}y_{i}^{2})}}}.$

Масштабированный коэффициент корреляции

Основная статья: Масштабированная корреляция

Масштабированная корреляция — это вариант корреляции Пирсона, в котором диапазон данных ограничивается намеренно и контролируемым образом, чтобы выявить корреляции между быстрыми компонентами временных рядов . Масштабированная корреляция определяется как средняя корреляция между короткими сегментами данных.

Позволять $K$ быть количеством сегментов, которые могут вписаться в общую длину сигнала $T$ для заданного масштаба $s$:

$K=\operatorname {round} \left({\frac {T}{s}}\right).$

Масштабированная корреляция по всем сигналам ${\bar {r}}_{s}$ затем вычисляется как

${\bar {r}}_{s}={\frac {1}{K}}\sum \limits _{k=1}^{K}r_{k},$

где $r_{k}$ - коэффициент корреляции Пирсона для сегмента $k$.

Выбрав параметр $s$, диапазон значений сокращается и корреляции на длительном временном масштабе отфильтровываются, выявляются только корреляции на коротких временных масштабах. Таким образом, вклады медленных компонент удаляются, а вклады быстрых компонент сохраняются.

Расстояние Пирсона

Метрика расстояния для двух переменных X и Y, известная как расстояние Пирсона, может быть определена на основе их коэффициента корреляции как

$d_{X,Y}=1-\rho _{X,Y}.$

Учитывая, что коэффициент корреляции Пирсона находится в диапазоне [−1, +1], расстояние Пирсона лежит в диапазоне [0, 2]. Расстояние Пирсона использовалось в кластерном анализе и обнаружении данных для связи и хранения с неизвестным усилением и смещением.

Определенное таким образом «расстояние» Пирсона присваивает расстояние больше 1 отрицательным корреляциям. В действительности, имеют значение как сильная положительная, так и отрицательная корреляция, поэтому необходимо соблюдать осторожность, когда «расстояние» Пирсона используется для алгоритма ближайшего соседа, поскольку такой алгоритм будет включать только соседей с положительной корреляцией и исключать соседей с отрицательной корреляцией. Альтернативно, абсолютное расстояние, $d_{X,Y}=1-|\rho _{X,Y}|$, который будет учитывать как положительные, так и отрицательные корреляции. Информацию о положительных и отрицательных ассоциациях можно будет извлечь позже отдельно.

Коэффициент круговой корреляции

Дополнительная информация: Круговая статистика.

Для переменных X = { x ₁ ,..., x _n } и Y = { y ₁ ,..., y _n }, которые определены на единичной окружности [0, 2π) , можно определить круговой аналог коэффициента Пирсона. Это делается путем преобразования точек данных по X и Y с помощью синусоидальной функции, так что коэффициент корреляции задается как:

$r_{\text{circular}}={\frac {\sum _{i=1}^{n}\sin(x_{i}-{\bar {x}})\sin(y_{i}-{\bar {y}})}{{\sqrt {\sum _{i=1}^{n}\sin(x_{i}-{\bar {x}})^{2}}}{\sqrt {\sum _{i=1}^{n}\sin(y_{i}-{\bar {y}})^{2}}}}}$

где ${\bar {x}}$ и ${\bar {y}}$ являются средними X Y и . круговыми Эта мера может быть полезна в таких областях, как метеорология, где важно угловое направление данных.

Частичная корреляция

Основная статья: Частичная корреляция

Если совокупность или набор данных характеризуются более чем двумя переменными, коэффициент частичной корреляции измеряет силу зависимости между парой переменных, которая не учитывается тем, как они обе изменяются в ответ на изменения в выбранном подмножестве. других переменных.

Декорреляция n случайных величин

Основная статья: Декорреляция

Всегда можно удалить корреляции между всеми парами произвольного числа случайных величин с помощью преобразования данных, даже если связь между переменными нелинейна. Представление этого результата для распределения населения дано Коксом и Хинкли.

Соответствующий результат существует для сведения выборочных корреляций к нулю. Предположим, что вектор из n случайных величин наблюдается m раз. Пусть X — матрица, где $X_{i,j}$ — j -я переменная наблюдения i . Позволять $Z_{m,m}$ быть m на квадратной матрицей размером m с каждым элементом 1. Тогда D — это данные, преобразованные так, что каждая случайная величина имеет нулевое среднее значение, а T — это данные, преобразованные так, чтобы все переменные имели нулевое среднее значение и нулевую корреляцию со всеми другими переменными — выборочная матрица корреляции. T . будет единичной матрицей Чтобы получить единичную дисперсию, это значение необходимо разделить на стандартное отклонение. Преобразованные переменные не будут коррелированы, даже если они не будут независимыми .

$D=X-{\frac {1}{m}}Z_{m,m}X$

$T=D(D^{\mathsf {T}}D)^{-{\frac {1}{2}}},$

где показатель степени − + 1 ⁄ 2 представляет матричный квадратный корень из обратной матрицы. Корреляционная матрица T будет единичной матрицей. Если новое наблюдение данных x представляет собой вектор-строку из n элементов, то то же преобразование можно применить к x, чтобы получить преобразованные векторы d и t :

$d=x-{\frac {1}{m}}Z_{1,m}X,$

$t=d(D^{\mathsf {T}}D)^{-{\frac {1}{2}}}.$

Эта декорреляция связана с анализом главных компонент многомерных данных.

Реализации программного обеспечения

• R реализует коэффициент корреляции с Базовый пакет статистики cor(x, y), или (также со значением P) с cor.test(x, y).
• Библиотека SciPy Python через pearsonr(x, y).
• Библиотека Pandas Python реализует расчет коэффициента корреляции Пирсона в качестве опции по умолчанию для метода. pandas.DataFrame.corr
• Wolfram Mathematica через Correlation функции, или (со значением P) с CorrelationTest.
• Библиотека Boost C++ через correlation_coefficient функция.
• Excel имеет встроенный correl(array1, array2) функция для расчета коэффициента корреляции Пирсона.

См. также

• квартет Анскомба
• Ассоциация (статистика)
• Коэффициент корреляции
  • Вопрос Йоля
  • Йольский Y
• Коэффициент множественной корреляции
• Коэффициент согласованности корреляции
• Корреляция и зависимость
• Коэффициент корреляции
• Ослабление
• Корреляция расстояний
• Максимальный информационный коэффициент
• Множественная корреляция
• Нормально распределенные и некоррелированные не означают независимости.
• Коэффициент шансов
• Частичная корреляция
• Полихорическая корреляция
• Соотношение количества квадрантов
• Коэффициент РВ
• Коэффициент ранговой корреляции Спирмена

Внешние ссылки

• «кокор» . сайт сравнения корреляций . – Бесплатный веб-интерфейс и пакет R для статистического сравнения двух зависимых или независимых корреляций с перекрывающимися или непересекающимися переменными.
• «Корреляция» . nagysandor.eu . – интерактивное Flash-моделирование корреляции двух нормально распределенных переменных.
• «Калькулятор коэффициентов корреляции» . hackmath.net . Линейная регрессия.
• «Критические значения коэффициента корреляции Пирсона» (PDF) . Frank.mtsu.edu/~dkfuller . – большой стол.
• «Угадай соотношение» . – Игра, в которой игроки угадывают, насколько коррелируют две переменные на диаграмме рассеяния, чтобы лучше понять концепцию корреляции.