Предел функции

О математической концепции в целом см. Предел (математика) .

$x$	${\frac {\sin x}{x}}$
1	0.841471...
0.1	0.998334...
0.01	0.999983...

Хотя функция ${\tfrac {\sin x}{x}}$ не определяется в нуле, поскольку x становится все ближе и ближе к нулю, ${\tfrac {\sin x}{x}}$ становится сколь угодно близким к 1. Другими словами, предел ${\tfrac {\sin x}{x}},$ когда x приближается к нулю, равно 1.

В математике предел функции — это фундаментальная концепция исчисления и анализа, касающаяся поведения этой функции вблизи определенного входного сигнала , который может находиться или не находиться в области определения функции.

Ниже приведены формальные определения, впервые разработанные в начале XIX века. Неформально, функция f назначает выход f ( x ) каждому входу x . Мы говорим, что функция имеет предел L на входе p , если f ( x ) становится всё ближе и ближе к L по мере того, как x приближается всё ближе и ближе к p . Более конкретно, выходное значение может быть сделано сколь угодно близким к L, если входные данные f взяты достаточно близкими к p . С другой стороны, если некоторые входные данные, очень близкие к p, преобразуются в выходные данные, находящиеся на фиксированном расстоянии друг от друга, то мы говорим, что предела не существует .

Понятие предела имеет множество применений в современном исчислении . В частности, во многих определениях непрерывности используется концепция предела: грубо говоря, функция является непрерывной, если все ее пределы совпадают со значениями функции. Понятие предела появляется и в определении производной : в исчислении одной переменной это предельное значение наклона секущих линий к графику функции.

История

хотя и неявно присутствовала в развитии исчисления Современная идея предела функции, 17 и 18 веков, восходит к Больцано , который в 1817 году представил основы техники эпсилон-дельта (см. (ε, δ)-определение предела ниже) для определения непрерывных функций. Однако при жизни его работы не были известны.

В своей книге «Кур анализа» 1821 года Огюстен-Луи Коши обсуждал переменные величины, бесконечно малые величины и пределы, а также определял непрерывность $y=f(x)$ говоря, что бесконечно малое изменение x обязательно приводит к бесконечно малому изменению y , в то время как Грабинер утверждает, что он использовал строгое определение эпсилон-дельта в доказательствах. В 1861 году Вейерштрасс впервые представил определение предела эпсилон-дельта в той форме, в которой оно обычно пишется сегодня. Он также ввел обозначения ${\textstyle \lim }$ и ${\textstyle \textstyle \lim _{x\to x_{0}}\displaystyle .}$

Современное обозначение размещения стрелки ниже предельного символа принадлежит Харди , которое введено в его книге «Курс чистой математики» в 1908 году.

Мотивация

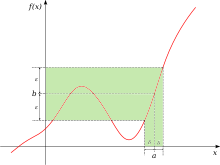
Представьте себе человека, идущего по ландшафту, представленному графиком y = f ( x ) . Их горизонтальное положение определяется x , во многом аналогично положению, заданному на карте местности или в глобальной системе позиционирования . Их высота задается координатой y . Предположим, они идут к позиции x = p по мере приближения к этой точке они заметят, что их высота приближается к определенному значению L. , и соответствующей x = p , они бы ответили: y = L. Если бы их спросили о высоте ,

Что же тогда значит, когда говорят, что их высота приближается к L ? Это означает, что их высота становится все ближе и ближе к L — за исключением возможной небольшой погрешности в точности. Например, предположим, что мы установили для нашего путешественника конкретную цель по точности: он должен находиться в пределах десяти метров от L . Они сообщают, что действительно могут оказаться в пределах десяти метров по вертикали от L что пока они находятся в пределах пятидесяти метров по горизонтали от p , их высота всегда находится в пределах десяти метров от L. , утверждая ,

Затем цель точности меняется: смогут ли они попасть в пределах одного вертикального метра? что они могут двигаться в пределах пяти метров по горизонтали от p , их высота всегда будет оставаться в пределах одного метра от целевой высоты L. Да, если предположить , Суммируя вышеупомянутую концепцию, мы можем сказать, что высота путешественника приближается к L по мере того, как его горизонтальное положение приближается к p , то есть для каждой цели целевой точности, какой бы маленькой она ни была, существует некоторая окрестность p , где все (а не только некоторые) высоты соответствуют всем горизонтальным положениям, за исключением, возможно, самого горизонтального положения p , в этой окрестности достигают этой цели точности.

Первоначальное неформальное утверждение теперь можно объяснить:

Пределом функции f ( x ) при x приближении к p является число L со следующим свойством: при любом целевом расстоянии от L существует расстояние от p, в пределах которого значения f ( x ) остаются в пределах целевого расстояния.

Фактически, это явное утверждение весьма близко к формальному определению предела функции со значениями в топологическом пространстве .

Точнее сказать, что

$$\lim _{x\to p}f(x)=L,$$

То есть, f ( x ) можно сделать настолько близким к L , насколько это необходимо, сделав x достаточно близким, но не равным p .

Следующие определения, известные как ( ε , δ ) -определения, являются общепринятыми определениями предела функции в различных контекстах.

Функции одной переменной

( e , d ) - определение предела

Для изображенных f , a и b мы можем гарантировать, что значение f ( x ) находится в пределах сколь угодно малого интервала ( b – ε, b + ε), ограничивая x достаточно малым интервалом ( a – δ, a + δ). Следовательно, f ( x ) → b как x → a .

Предполагать $f:\mathbb {R} \rightarrow \mathbb {R}$ — функция, определенная на прямой , и существуют два действительных числа p и L. действительной Можно было бы сказать, что предел f , когда x приближается к p , равен L и записан

$$\lim _{x\to p}f(x)=L,$$

или, альтернативно, скажем, f ( x ) стремится к L, поскольку x стремится к p , и записано:

$$f(x)\to L{\text{ as }}x\to p,$$

если выполняется следующее свойство: для каждого вещественного ε > 0 существует вещественное число δ > 0 такое, что для всех вещественных x 0 < | Икс - р | < δ подразумевает | ж ( Икс ) - L | < е . Символически,

$$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in \mathbb {R} )\,(0<|x-p|<\delta \implies |f(x)-L|<\varepsilon ).$$

Например, мы можем сказать

$$\lim _{x\to 2}(4x+1)=9$$

потому что для каждого вещественного ε > 0 мы можем взять δ = ε /4 , так что для всех вещественных x , если 0 < | х - 2 | < δ , то | 4 х + 1 − 9 | < е .

Более общее определение применяется к функциям, определенным на подмножествах реальной линии. Пусть S — подмножество $\mathbb {R} .$ Позволять $f:S\to \mathbb {R}$ быть вещественной функцией . Пусть p — такая точка, что существует некоторый открытый интервал ( a , b ), содержащий p с $(a,p)\cup (p,b)\subset S.$ Тогда говорят, что предел f при x приближении к p равен L , если:

Для каждого действительного ε > 0 существует вещественное число δ > 0 такое, что для всех x ∈ ( a , b ) , 0 < | Икс - р | < δ означает, что | ж ( Икс ) - L | < е .

Или, символически:

$$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in (a,b))\,(0<|x-p|<\delta \implies |f(x)-L|<\varepsilon ).$$

Например, мы можем сказать

$$\lim _{x\to 1}{\sqrt {x+3}}=2$$

потому что для любого действительного ε > 0 мы можем взять δ = ε , так что для всех вещественных x ≥ −3 , если 0 < | х - 1 | < δ , то | ж ( Икс ) - 2 | < е . В этом примере S = [−3, ∞) содержит открытые интервалы вокруг точки 1 (например, интервал (0, 2)).

Здесь обратите внимание, что значение предела не зависит ни от того, f определено ли в точке p , ни от значения f ( p ) — если оно определено. Например, пусть $f:[0,1)\cup (1,2]\to \mathbb {R} ,f(x)={\tfrac {2x^{2}-x-1}{x-1}}.$

$$\lim _{x\to 1}f(x)=3$$

потому что для любого ε > 0 мы можем взять δ = ε /2 , так что для всех действительных x ≠ 1 , если 0 < | х - 1 | < δ , то | ж ( Икс ) - 3 | < е . Обратите внимание, что здесь f (1) не определена.

В действительности предел может существовать в $\{x\in \mathbb {R} \,|\,\exists (a,b)\subset \mathbb {R} \quad p\in (a,b){\text{ and }}(a,p)\cup (p,b)\subset S\},$ что равно $\operatorname {int} S\cup \operatorname {iso} S^{c},$ где int S — внутренняя часть S , а iso S ^с являются изолированными точками дополнения к S . В нашем предыдущем примере, где $S=[0,1)\cup (1,2],$ $\operatorname {int} S=(0,1)\cup (1,2),$ $\operatorname {iso} S^{c}=\{1\}.$ В частности, мы видим, что это определение предела допускает существование предела в 1, но не в 0 или 2.

Буквы ε и δ можно понимать как «ошибка» и «расстояние». Фактически, Коши использовал ε как сокращение от слова «ошибка» в некоторых своих работах. хотя в своем определении непрерывности он использовал бесконечно малую величину $\alpha$ а не ε или δ (см. Курс анализа ). В этих терминах погрешность ( ε ) измерения предельного значения можно сделать настолько малой, насколько это необходимо, за счет уменьшения расстояния ( δ ) до предельной точки. Как обсуждается ниже, это определение также работает для функций в более общем контексте. Идея о том, что δ и ε представляют расстояния, помогает предположить эти обобщения.

Существование и односторонние ограничения

Основная статья: Односторонний лимит

Предел как $x\to x_{0}^{+}$ отличается от этого тем, что $x\to x_{0}^{-}.$ Следовательно, предела при x → x ₀ не существует.

Альтернативно, x может приближаться к p сверху (справа) или снизу (слева), и в этом случае пределы можно записать как

$$\lim _{x\to p^{+}}f(x)=L$$

или

$$\lim _{x\to p^{-}}f(x)=L$$

Первые три функции имеют точки, для которых предел не существует, а функция

$$f(x)={\frac {\sin(x)}{x}}$$

не определяется в $x=0$, но его предел существует.

соответственно. p и там равны, то это можно назвать пределом f Если эти пределы существуют в точке ( x ) в точке p . Если односторонние пределы существуют в точке p нет , но неравны, то предела в точке p (т. е. предела в точке p не существует). Если какой-либо односторонний предел не существует в точке p , то и предел в точке p также не существует.

Формальное определение следующее. Предел когда f, x приближается к p сверху, равен L , если:

Для любого ε > 0 существует δ > 0 такое, что всякий раз, когда 0 < x − p < δ , мы имеем | ж ( Икс ) - L | < е .

$$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in (a,b))\,(0<x-p<\delta \implies |f(x)-L|<\varepsilon ).$$

Предел когда f, x приближается к p снизу, равен L , если:

Для каждого ε > 0 существует δ > 0 такое, что всякий раз, когда 0 < p − x < δ , мы имеем | ж ( Икс ) - L | < е .

$$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in (a,b))\,(0<p-x<\delta \implies |f(x)-L|<\varepsilon ).$$

предел не существует, то колебание f Если в точке p не равно нулю.

Более общее определение с использованием предельных точек и подмножеств

Дополнительная информация: Предельная точка.

Пределы также могут быть определены путем подхода к подмножествам предметной области.

В общем: Позволять $f:S\to \mathbb {R}$ быть вещественной функцией, определенной на некотором $S\subseteq \mathbb {R} .$ Пусть p — предельная точка некоторого $T\subset S$— то есть, p — предел некоторой последовательности элементов T , отличной от p . Тогда мы говорим, что предел f , когда x приближается к p от значений в T , равен L , записанный

$$\lim _{{x\to p} \atop {x\in T}}f(x)=L$$

если имеет место следующее:

Для любого ε > 0 существует δ > 0 такое, что для всех x ∈ T 0 < | Икс - р | < δ означает, что | ж ( Икс ) - L | < е .

$$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in T)\,(0<|x-p|<\delta \implies |f(x)-L|<\varepsilon ).$$

Обратите внимание: T может быть любым подмножеством S , областью определения f . И предел может зависеть от выбора T . Это обобщение включает в себя в качестве частных случаев пределы на интервале, а также левые пределы вещественных функций (например, если взять T в качестве открытого интервала вида (–∞, a ) ) и правые пределы (например, взяв T в качестве открытого интервала формы ( a , ∞) ). Он также расширяет понятие односторонних пределов на включенные конечные точки (полу)замкнутых интервалов, поэтому функция квадратного корня $f(x)={\sqrt {x}}$ может иметь предел 0, когда x приближается к 0 сверху:

$$\lim _{{x\to 0} \atop {x\in [0,\infty )}}{\sqrt {x}}=0$$

поскольку для любого ε > 0 мы можем взять δ = ε такое, что для всех x ≥ 0 , если 0 < | Икс - 0 | < δ , то | ж ( Икс ) - 0 | < е .

Это определение позволяет определить предел в предельных точках области S подходящее подмножество T , если выбрано , имеющее ту же предельную точку.

Примечательно, что предыдущее двустороннее определение работает $\operatorname {int} S\cup \operatorname {iso} S^{c},$ которое является подмножеством предельных точек S .

Например, пусть $S=[0,1)\cup (1,2].$ Предыдущее двустороннее определение будет работать при $1\in \operatorname {iso} S^{c}=\{1\},$ но это не сработает при значениях 0 или 2, которые являются предельными точками S .

Удаленные и неудаленные лимиты

Определение предела, данное здесь, не зависит от того, как (или ли) f определяется в точке p . Бартл называет это удаленным пределом , поскольку исключает значение f в точке p . Соответствующий неудаленный предел действительно зависит от значения f в точке p , если p находится в области определения f . Позволять $f:S\to \mathbb {R}$ быть вещественной функцией. Неудаленный предел f , когда x приближается к p , равен L , если

Для любого ε > 0 существует δ > 0 что для всех x ∈ S | такое , Икс - р | < δ подразумевает | ж ( Икс ) - L | < е .

$$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(|x-p|<\delta \implies |f(x)-L|<\varepsilon ).$$

Определение то же самое, за исключением того, что окрестность | Икс - р | < δ теперь включает точку p , в отличие от удаленной окрестности 0 < | Икс - р | < δ . Это делает определение неудаляемого лимита менее общим. Одним из преимуществ работы с неудаляемыми пределами является то, что они позволяют сформулировать теорему о пределах композиции без каких-либо ограничений на функции (кроме существования их неудаляемых пределов).

Бартл отмечает, что, хотя под «пределом» некоторые авторы подразумевают неудаляемый лимит, удаленные лимиты являются наиболее популярными.

Примеры

Отсутствие одностороннего лимита(ов)

Функция без предела при существенном разрыве

Функция

$$f(x)={\begin{cases}\sin {\frac {5}{x-1}}&{\text{ for }}x<1\\0&{\text{ for }}x=1\\[2pt]{\frac {1}{10x-10}}&{\text{ for }}x>1\end{cases}}$$

не имеет предела при x ₀ = 1 (левый предел не существует из-за колебательного характера синусоидальной функции, а правый предел не существует из-за асимптотического поведения обратной функции, см. рисунок), но имеет предел по каждой второй координате x .

Функция

$$f(x)={\begin{cases}1&x{\text{ rational }}\\0&x{\text{ irrational }}\end{cases}}$$

(она же функция Дирихле ) не имеет предела ни в одной координате x .

Неравенство односторонних пределов

Функция

$$f(x)={\begin{cases}1&{\text{ for }}x<0\\2&{\text{ for }}x\geq 0\end{cases}}$$

имеет предел в каждой ненулевой координате x (предел равен 1 для отрицательного x и равен 2 для положительного x ). Предела при x = 0 не существует (левый предел равен 1, а правый предел равен 2).

Ограничения только в одной точке

Функции

$$f(x)={\begin{cases}x&x{\text{ rational }}\\0&x{\text{ irrational }}\end{cases}}$$

и

$$f(x)={\begin{cases}|x|&x{\text{ rational }}\\0&x{\text{ irrational }}\end{cases}}$$

оба имеют предел при x = 0 и он равен 0.

Пределы в счетном числе точек

Функция

$$f(x)={\begin{cases}\sin x&x{\text{ irrational }}\\1&x{\text{ rational }}\end{cases}}$$

имеет предел в любой координате x вида ${\tfrac {\pi }{2}}+2n\pi ,$ где n — любое целое число.

Пределы,

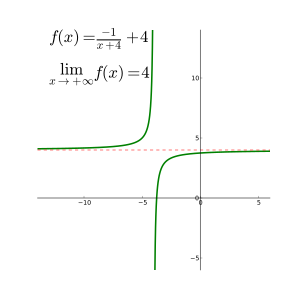
Пределы на бесконечности

Предел этой функции на бесконечности существует

Позволять $f:S\to \mathbb {R}$ быть функцией, определенной на $S\subseteq \mathbb {R} .$ Пределом f, когда x приближается к бесконечности, является L , обозначаемый

$$\lim _{x\to \infty }f(x)=L,$$

означает, что:

Для каждого ε > 0 существует c > 0 такое, что всякий раз, когда + x > c , мы имеем | ж ( Икс ) - L | < е .

$$(\forall \varepsilon >0)\,(\exists c>0)\,(\forall x\in S)\,(x>c\implies |f(x)-L|<\varepsilon ).$$

Аналогично, предел f при приближении x к минус бесконечности равен L , обозначаемый

$$\lim _{x\to -\infty }f(x)=L,$$

означает, что:

Для каждого ε > 0 существует c > 0 такой, что всякий раз, когда x < − c , мы имеем | ж ( Икс ) - L | < е .

$$(\forall \varepsilon >0)\,(\exists c>0)\,(\forall x\in S)\,(x<-c\implies |f(x)-L|<\varepsilon ).$$

Например,

$$\lim _{x\to \infty }\left(-{\frac {3\sin x}{x}}+4\right)=4$$

потому что для любого ε > 0 мы можем взять c = 3/ ε такое, что для всех вещественных x , если x > c , то | ж ( Икс ) - 4 | < е .

Другой пример заключается в том, что

$$\lim _{x\to -\infty }e^{x}=0$$

потому что для любого ε > 0 мы можем взять c = max{1, −ln( ε )} так, что для всех вещественных x , если x < − c , то | ж ( Икс ) - 0 | < е .

Бесконечные пределы

Для функции, значения которой неограниченно растут, функция расходится и обычного предела не существует. Однако в этом случае можно ввести пределы с бесконечными значениями.

Позволять $f:S\to \mathbb {R}$ быть функцией, определенной на $S\subseteq \mathbb {R} .$ Утверждение, что предел f при x приближении к p равен бесконечности , обозначается

$$\lim _{x\to p}f(x)=\infty ,$$

означает, что:

Для каждого N > 0 существует δ > 0 такое, что всякий раз, когда 0 < | Икс - р | < δ , мы имеем f ( x ) > N .

$$(\forall N>0)\,(\exists \delta >0)\,(\forall x\in S)\,(0<|x-p|<\delta \implies f(x)>N).$$

Утверждение, что предел f при x приближении к p равен минус бесконечности , обозначается

$$\lim _{x\to p}f(x)=-\infty ,$$

означает, что:

Для каждого N > 0 существует δ > 0 такое, что всякий раз, когда 0 < | Икс - р | < δ , мы имеем ж ( Икс ) < - N .

$$(\forall N>0)\,(\exists \delta >0)\,(\forall x\in S)\,(0<|x-p|<\delta \implies f(x)<-N).$$

Например,

$$\lim _{x\to 1}{\frac {1}{(x-1)^{2}}}=\infty$$

потому что для каждого N > 0 мы можем взять ${\textstyle \delta ={\tfrac {1}{{\sqrt {N}}\delta }}={\tfrac {1}{\sqrt {N}}}}$ такой, что для всех действительных x > 0 , если 0 < x − 1 < δ , то f ( x ) > N .

Эти идеи можно использовать вместе для создания определений различных комбинаций, таких как

$$\lim _{x\to \infty }f(x)=\infty ,$$

или $\lim _{x\to p^{+}}f(x)=-\infty .$

Например,

$$\lim _{x\to 0^{+}}\ln x=-\infty$$

потому что для любого N > 0 мы можем взять δ = e ^{− Н} такой, что для всех действительных x > 0 , если 0 < x − 0 < δ , то f ( x ) < − N .

Пределы, включающие бесконечность, связаны с понятием асимптот .

Эти понятия предела пытаются дать интерпретацию пределов на бесконечности в метрическом пространстве. Фактически, они согласуются с определением предела в топологическом пространстве, если

• окрестность −∞ определяется как содержащая интервал [−∞, c ) для некоторого $c\in \mathbb {R} ,$
• окрестность ∞ определяется как содержащая интервал ( c , ∞] , где $c\in \mathbb {R} ,$ и
• окрестности $a\in \mathbb {R}$ определяется обычным образом метрическое пространство $\mathbb {R} .$

В этом случае, ${\overline {\mathbb {R} }}$ является топологическим пространством и любая функция вида $f:X\to Y$ с $X,Y\subseteq {\overline {\mathbb {R} }}$ подлежит топологическому определению предела. Обратите внимание, что с помощью этого топологического определения легко определить бесконечные пределы в конечных точках, которые не были определены выше в метрическом смысле.

Альтернативное обозначение

Многие авторы позволяют проективно расширенную действительную линию использовать как способ включения бесконечных значений, а также расширенную действительную линию . В этих обозначениях расширенная действительная линия задается как $\mathbb {R} \cup \{-\infty ,+\infty \}$ а проективно продолженная действительная линия равна $\mathbb {R} \cup \{\infty \}$ где окрестность точки ∞ представляет собой множество вида $\{x:|x|>c\}.$ Преимущество состоит в том, что для охвата всех случаев достаточно всего трех определений пределов (левого, правого и центрального).Как было указано выше, для полностью строгого учета нам потребуется рассмотреть 15 отдельных случаев для каждой комбинации бесконечностей (пять направлений: −∞, левое, центральное, правое и +∞; три границы: −∞, конечная или + ∞). Есть и примечательные подводные камни. Например, при работе с расширенной действительной линией $x^{-1}$ не имеет центрального предела (что нормально):

$$\lim _{x\to 0^{+}}{1 \over x}=+\infty ,\quad \lim _{x\to 0^{-}}{1 \over x}=-\infty .$$

Напротив, при работе с проективной действительной линией бесконечности (как и 0) не имеют знака, поэтому центральный предел действительно существует в этом контексте:

$$\lim _{x\to 0^{+}}{1 \over x}=\lim _{x\to 0^{-}}{1 \over x}=\lim _{x\to 0}{1 \over x}=\infty .$$

На самом деле существует множество конфликтующих между собой формальных систем.В некоторых приложениях численного дифференцирования и интегрирования удобно иметь, например, нули со знаком . Простая причина связана с обратным утверждением $\lim _{x\to 0^{-}}{x^{-1}}=-\infty ,$ а именно, это удобно для $\lim _{x\to -\infty }{x^{-1}}=-0$ считать правдой.Такие нули можно рассматривать как приближение к бесконечно малым .

на бесконечности для

Горизонтальная асимптота относительно y = 4

Существует три основных правила оценки пределов на бесконечности для рациональной функции. $f(x)={\tfrac {p(x)}{q(x)}}$ (где p и q — полиномы):

• Если степень p q больше степени , то предел равен положительной или отрицательной бесконечности в зависимости от знаков старших коэффициентов;
• Если степени p и q равны, пределом является старший коэффициент p, деленный на старший коэффициент q ;
• Если степень p меньше степени q , предел равен 0.

Если предел на бесконечности существует, он представляет собой горизонтальную асимптоту y = L. при Полиномы не имеют горизонтальных асимптот; однако такие асимптоты могут возникать и с рациональными функциями.

Функции более чем одной переменной

Обычные ограничения

Отметив, что | Икс - р | представляет расстояние , определение предела может быть распространено на функции более чем одной переменной. В случае функции $f:S\times T\to \mathbb {R}$ определено на $S\times T\subseteq \mathbb {R} ^{2},$ мы определили предел следующим образом: предел f при ( x , y ) приближении к ( p , q ) равен L , записанный

$$\lim _{(x,y)\to (p,q)}f(x,y)=L$$

если выполняется следующее условие:

Для каждого ε > 0 существует δ > 0 такое, что для всех x в S и y в T , всякий раз, когда ${\textstyle 0<{\sqrt {(x-p)^{2}+(y-q)^{2}}}<\delta ,}$ у нас есть | ж ( Икс , y ) - L | < ε ,

или формально:

$$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(\forall y\in T)\,(0<{\sqrt {(x-p)^{2}+(y-q)^{2}}}<\delta \implies |f(x,y)-L|<\varepsilon )).$$

Здесь ${\textstyle {\sqrt {(x-p)^{2}+(y-q)^{2}}}}$ — евклидово расстояние между ( x , y ) и ( p , q ) . (Фактически это можно заменить любой нормой | | ( x , y ) − ( p , q ) | | и распространить на любое количество переменных.)

Например, мы можем сказать

$$\lim _{(x,y)\to (0,0)}{\frac {x^{4}}{x^{2}+y^{2}}}=0$$

потому что для каждого ε > 0 мы можем взять ${\textstyle \delta ={\sqrt {\varepsilon }}}$ такой, что для всех действительных x ≠ 0 и вещественных y ≠ 0 , если ${\textstyle 0<{\sqrt {(x-0)^{2}+(y-0)^{2}}}<\delta ,}$ тогда | ж ( Икс , y ) - 0 | < е .

Как и в случае с одной переменной, значение f в ( p , q ) не имеет значения в этом определении предела.

Для существования такого многовариантного предела это определение требует, чтобы значение f приближалось к L вдоль каждого возможного пути, приближающегося к ( p , q ) . В приведенном выше примере функция

$$f(x,y)={\frac {x^{4}}{x^{2}+y^{2}}}$$

удовлетворяет этому условию. В этом можно убедиться, рассматривая полярные координаты

$$(x,y)=(r\cos \theta ,r\sin \theta )\to (0,0),$$

что дает

$$\lim _{r\to 0}f(r\cos \theta ,r\sin \theta )=\lim _{r\to 0}{\frac {r^{4}\cos ^{4}\theta }{r^{2}}}=\lim _{r\to 0}r^{2}\cos ^{4}\theta .$$

Здесь θ = θ ( r ) — функция от r , которая управляет формой пути, по которому f приближается к ( p , q ) . Поскольку cos θ ограничен между [−1, 1] по сэндвич-теореме , этот предел стремится к 0.

Напротив, функция

$$f(x,y)={\frac {xy}{x^{2}+y^{2}}}$$

не имеет предела в (0, 0) . Пройдя путь ( x , y ) = ( t , 0) → (0, 0) , получаем

$$\lim _{t\to 0}f(t,0)=\lim _{t\to 0}{\frac {0}{t^{2}}}=0,$$

идя по пути ( x , y ) = ( t , t ) → (0, 0) , мы получаем

$$\lim _{t\to 0}f(t,t)=\lim _{t\to 0}{\frac {t^{2}}{t^{2}+t^{2}}}={\frac {1}{2}}.$$

Поскольку эти два значения не совпадают, f не стремится к одному значению, когда ( x , y ) приближается к (0, 0) .

Множественные ограничения

Хотя он используется реже, существует еще один тип предела для функции с несколькими переменными, известный как множественный предел . Для функции с двумя переменными это двойной предел . Позволять $f:S\times T\to \mathbb {R}$ быть определены на $S\times T\subseteq \mathbb {R} ^{2},$ мы говорим, что двойной предел f, когда x приближается к p, а y приближается к q, равен L , записанный

$$\lim _{{x\to p} \atop {y\to q}}f(x,y)=L$$

если выполняется следующее условие:

Для каждого ε > 0 существует δ > 0 такое, что для всех x в S и y в T всякий раз, когда 0 < | Икс - р | < δ и 0 < | у - д | < δ , мы имеем | ж ( Икс , y ) - L | < е .

$$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(\forall y\in T)\,((0<|x-p|<\delta )\land (0<|y-q|<\delta )\implies |f(x,y)-L|<\varepsilon ).$$

Для существования такого двойного предела это определение требует, чтобы значение f приближалось к L вдоль каждого возможного пути, приближающегося к ( p , q ) , исключая две линии x = p и y = q . В результате кратный предел является более слабым понятием, чем обычный предел: если обычный предел существует и равен , то кратный предел существует и также равен L. L Обратное неверно: существование множественных пределов не означает существования обычного предела. Рассмотрим пример

$$f(x,y)={\begin{cases}1\quad {\text{for}}\quad xy\neq 0\\0\quad {\text{for}}\quad xy=0\end{cases}}$$

где

$$\lim _{{x\to 0} \atop {y\to 0}}f(x,y)=1$$

но

$$\lim _{(x,y)\to (0,0)}f(x,y)$$

не существует.

Если область определения f ограничена $(S\setminus \{p\})\times (T\setminus \{q\}),$ тогда два определения пределов совпадают.

Множественные ограничения на бесконечности

Концепция множественного предела может распространяться на предел на бесконечности, аналогично функции с одной переменной. Для $f:S\times T\to \mathbb {R} ,$ мы говорим, что двойной предел f, когда x и y приближаются к бесконечности, равен L , записанный

$$\lim _{{x\to \infty } \atop {y\to \infty }}f(x,y)=L$$

если выполняется следующее условие:

Для каждого ε > 0 существует c > 0 такой, что для всех x в S и y в T , когда x > c и y > c , мы имеем | ж ( Икс , y ) - L | < е .

$$(\forall \varepsilon >0)\,(\exists c>0)\,(\forall x\in S)\,(\forall y\in T)\,((x>c)\land (y>c)\implies |f(x,y)-L|<\varepsilon ).$$

Мы говорим, что двойной предел f при приближении x и y к минус бесконечности равен L , записанный

$$\lim _{{x\to -\infty } \atop {y\to -\infty }}f(x,y)=L$$

если выполняется следующее условие:

Для каждого ε > 0 существует c > 0 такой, что x в S и y в T , всякий раз, когда x < − c и y < − c , мы имеем | ж ( Икс , y ) - L | < е .

$$(\forall \varepsilon >0)\,(\exists c>0)\,(\forall x\in S)\,(\forall y\in T)\,((x<-c)\land (y<-c)\implies |f(x,y)-L|<\varepsilon ).$$

Поточечные пределы и равномерные пределы

Основные статьи: Поточечная сходимость и Равномерная сходимость

Позволять $f:S\times T\to \mathbb {R} .$ Вместо того, чтобы брать предел как ( x , y ) → ( p , q ) , мы можем рассмотреть возможность принятия предела только одной переменной, скажем, x → p , чтобы получить функцию одной переменной y , а именно $g:T\to \mathbb {R} .$ Фактически, этот ограничивающий процесс может осуществляться двумя различными способами. Первый из них называется поточечным пределом . Мы говорим, что поточечный предел f при x приближении к p равен g , обозначаемый

$$\lim _{x\to p}f(x,y)=g(y),$$

или

$$\lim _{x\to p}f(x,y)=g(y)\;\;{\text{pointwise}}.$$

В качестве альтернативы мы можем сказать, что f стремится к g поточечно, когда x приближается к p , что обозначается

$$f(x,y)\to g(y)\;\;{\text{as}}\;\;x\to p,$$

или

$$f(x,y)\to g(y)\;\;{\text{pointwise}}\;\;{\text{as}}\;\;x\to p.$$

Этот предел существует, если выполняется следующее:

Для каждого ε > 0 и каждого фиксированного y в T существует δ ( ε , y ) > 0 такое, что для всех x в S , всякий раз, когда 0 < | Икс - р | < δ , мы имеем | ж ( Икс , y ) - грамм ( y ) | < е .

$$(\forall \varepsilon >0)\,(\forall y\in T)\,(\exists \delta >0)\,(\forall x\in S)\,(0<|x-p|<\delta \implies |f(x,y)-g(y)|<\varepsilon ).$$

Здесь δ = δ ( ε , y ) является функцией как ε, так и y . Каждый δ выбирается для конкретной y точки . Следовательно, мы говорим, что предел поточечен по y . Например,

$$f(x,y)={\frac {x}{\cos y}}$$

имеет поточечный предел постоянной нулевой функции

$$\lim _{x\to 0}f(x,y)=0(y)\;\;{\text{pointwise}}$$

потому что для каждого фиксированного y предел явно равен 0. Этот аргумент неверен, если y не фиксирован: если y очень близко к π /2 , значение дроби может отклоняться от 0.

Это приводит к другому определению предела, а именно к равномерному пределу . Мы говорим, что равномерный предел f на T при x приближении к p равен g , обозначаемый

$${\underset {{x\to p} \atop {y\in T}}{\mathrm {unif} \lim \;}}f(x,y)=g(y),$$

или

$$\lim _{x\to p}f(x,y)=g(y)\;\;{\text{uniformly on}}\;T.$$

В качестве альтернативы мы можем сказать, что f стремится к g равномерно на T, когда x приближается к p , что обозначается

$$f(x,y)\rightrightarrows g(y)\;{\text{on}}\;T\;\;{\text{as}}\;\;x\to p,$$

или

$$f(x,y)\to g(y)\;\;{\text{uniformly on}}\;T\;\;{\text{as}}\;\;x\to p.$$

Этот предел существует, если выполняется следующее:

Для каждого ε > 0 существует δ ( ε ) > 0 такое, что для всех x в S и y в T , всякий раз, когда 0 < | Икс - р | < δ , мы имеем | ж ( Икс , y ) - грамм ( y ) | < е .

$$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(\forall y\in T)\,(0<|x-p|<\delta \implies |f(x,y)-g(y)|<\varepsilon ).$$

Здесь δ = δ ( ε ) является функцией только ε , но не y . Другими словами, δ ко равномерно применимо всем y в T . Следовательно, мы говорим, что предел равномерен по y . Например,

$$f(x,y)=x\cos y$$

имеет равномерный предел постоянной нулевой функции

$$\lim _{x\to 0}f(x,y)=0(y)\;\;{\text{ uniformly on}}\;\mathbb {R}$$

потому что для всех реальных cos y y ограничен между [−1, 1] . Следовательно, независимо от того, как ведет себя y , мы можем использовать сэндвич-теорему, чтобы показать, что предел равен 0.

Итерированные пределы

Основная статья: Итерированные пределы

Позволять $f:S\times T\to \mathbb {R} .$ Мы можем рассмотреть возможность ограничения только одной переменной, скажем, x → p , чтобы получить функцию одной переменной от y , а именно $g:T\to \mathbb {R} ,$ а затем возьмем предел по другой переменной, а именно → q , чтобы получить число L. y Символически,

$$\lim _{y\to q}\lim _{x\to p}f(x,y)=\lim _{y\to q}g(y)=L.$$

Этот предел известен как повторный предел функции многих переменных. Порядок взятия пределов может повлиять на результат, т.е.

$$\lim _{y\to q}\lim _{x\to p}f(x,y)\neq \lim _{x\to p}\lim _{y\to q}f(x,y)$$

в общем.

Достаточное условие равенства даёт теорема Мура-Осгуда , которая требует предела $\lim _{x\to p}f(x,y)=g(y)$ быть равномерным на T .

Функции в метрических пространствах

Предположим, что и N — подмножества метрических пространств A и B соответственно, и f : M → N определено между M и N , причем x ∈ M , p предельная точка M — и L ∈ N. M Говорят, что предел f при x приближении к p равен L , и пишут

$$\lim _{x\to p}f(x)=L$$

если выполняется следующее свойство:

Для каждого ε > 0 существует δ > 0 такое, что для всех точек x ∈ M из 0 < d _A ( x , p ) < δ следует d _B ( f ( x ), L ) < ε .

$$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in M)\,(0<d_{A}(x,p)<\delta \implies d_{B}(f(x),L)<\varepsilon ).$$

что p не обязательно должен находиться в области определения f , а L не обязательно должен находиться в диапазоне f , и даже если f ( p ) определено, оно не обязательно должно быть равно L. Опять же, обратите внимание ,

Евклидова метрика

Предел в евклидовом пространстве является прямым обобщением пределов векторных функций . Например, мы можем рассмотреть функцию $f:S\times T\to \mathbb {R} ^{3}$ такой, что

$$f(x,y)=(f_{1}(x,y),f_{2}(x,y),f_{3}(x,y)).$$

Тогда в обычной евклидовой метрике

$$\lim _{(x,y)\to (p,q)}f(x,y)=(L_{1},L_{2},L_{3})$$

если имеет место следующее:

Для каждого ε > 0 существует δ > 0 такое, что для x в S и y в T всех ${\textstyle 0<{\sqrt {(x-p)^{2}+(y-q)^{2}}}<\delta }$ подразумевает ${\textstyle {\sqrt {(f_{1}-L_{1})^{2}+(f_{2}-L_{2})^{2}+(f_{3}-L_{3})^{2}}}<\varepsilon .}$

$$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(\forall y\in T)\,\left(0<{\sqrt {(x-p)^{2}+(y-q)^{2}}}<\delta \implies {\sqrt {(f_{1}-L_{1})^{2}+(f_{2}-L_{2})^{2}+(f_{3}-L_{3})^{2}}}<\varepsilon \right).$$

В этом примере рассматриваемая функция представляет собой конечномерную векторную функцию. В этом случае предельная теорема для векторной функции гласит, что если предел каждого компонента существует, то предел векторной функции равен вектору, каждый компонент которого принимает предел:

$$\lim _{(x,y)\to (p,q)}{\Bigl (}f_{1}(x,y),f_{2}(x,y),f_{3}(x,y){\Bigr )}=\left(\lim _{(x,y)\to (p,q)}f_{1}(x,y),\lim _{(x,y)\to (p,q)}f_{2}(x,y),\lim _{(x,y)\to (p,q)}f_{3}(x,y)\right).$$

Манхэттенская метрика

Можно также рассмотреть пространства, отличные от евклидова. Примером может служить пространство Манхэттена. Учитывать $f:S\to \mathbb {R} ^{2}$ такой, что

$$f(x)=(f_{1}(x),f_{2}(x)).$$

Тогда по метрике манхэттенской

$$\lim _{x\to p}f(x)=(L_{1},L_{2})$$

если имеет место следующее:

Для каждого ε > 0 существует δ > 0 такое, что для всех x в S 0 < | Икс - р | < δ подразумевает | ж ₁ - L ₁ | + | ж ₂ - L ₂ | < е .

$$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(0<|x-p|<\delta \implies |f_{1}-L_{1}|+|f_{2}-L_{2}|<\varepsilon ).$$

Поскольку это тоже конечномерная вектор-функция, применима и сформулированная выше предельная теорема.

Единая метрика

Наконец, мы обсудим предел в функциональном пространстве , которое имеет бесконечные измерения. Рассмотрим функцию f ( x , y ) в функциональном пространстве $S\times T\to \mathbb {R} .$ Мы хотим выяснить, как x приближается к p , как f ( x , y ) будет стремиться к другой функции g ( y ) , которая находится в функциональном пространстве $T\to \mathbb {R} .$ «Близость» в этом функциональном пространстве может быть измерена с помощью единой метрики . Тогда мы скажем, что равномерный предел f на T при x приближении к p равен g и напишем

$${\underset {{x\to p} \atop {y\in T}}{\mathrm {unif} \lim \;}}f(x,y)=g(y),$$

или

$$\lim _{x\to p}f(x,y)=g(y)\;\;{\text{uniformly on}}\;T,$$

если имеет место следующее:

Для каждого ε > 0 существует δ > 0 такое, что для всех x в S 0 < | Икс - р | < δ подразумевает $\sup _{y\in T}|f(x,y)-g(y)|<\varepsilon .$

$$(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(0<|x-p|<\delta \implies \sup _{y\in T}|f(x,y)-g(y)|<\varepsilon ).$$

Фактически можно видеть, что это определение эквивалентно определению равномерного предела функции многих переменных, введенному в предыдущем разделе.

Функции в топологических пространствах

См. Также: Фильтры в топологии § Пределы функций.

Предположим, что X и Y — топологические пространства , а Y — хаусдорфово пространство . Пусть p — точка предельная ⊆ X и L ∈ Y. Ω Для функции f : Ω → Y говорят, что предел f при x приближении к p равен L , записанный

$$\lim _{x\to p}f(x)=L,$$

если выполняется следующее свойство:

Для каждой открытой окрестности V точки L существует открытая окрестность U точки p такая, что f ( U ∩ Ω − { p }) ⊆ V .

Эту последнюю часть определения можно также сформулировать так: «существует открытая проколотая окрестность U точки p такая, что f ( U ∩ Ω) ⊆ V ».

Область определения f не обязательно должна содержать p . Если да, то значение f в точке p не имеет отношения к определению предела. В частности, если областью определения f является X − { p } (или все из X ), то предел f при x → p существует и равен L , если для всех подмножеств из X с предельной точкой p Ω предел ограничения f на Ω существует и равен L . Иногда этот критерий используют для установления отсутствия двустороннего предела функции на $\mathbb {R}$ показывая, что односторонние пределы либо не существуют, либо не согласуются друг с другом. Такой взгляд является фундаментальным в области общей топологии , где пределы и непрерывность в точке определяются в терминах специальных семейств подмножеств, называемых фильтрами , или обобщенных последовательностей, известных как сети .

Альтернативно, требование, чтобы Y было хаусдорфовым пространством, можно смягчить до предположения, что Y — общее топологическое пространство, но тогда предел функции может быть неединственным. В частности, уже можно говорить не о пределе функции в точке, а о пределе или множестве пределов в точке.

Функция непрерывна в предельной точке p и в своей области определения тогда и только тогда, когда f ( p ) является f (или, в общем случае, a ) пределом ( x ) , когда x стремится к p .

Существует еще один тип предела функции, а именно последовательный предел . Пусть f : X → Y — отображение топологического пространства X в хаусдорфово пространство Y , p ∈ X — точка X и L ∈ Y. предельная Последовательный предел f при x стремлении к p равен L, если

Для каждой последовательности ( x _n ) из X − { p } , которая сходится к p , последовательность f ( x _n ) сходится к L .

Если L является пределом (в указанном выше смысле) f при x приближении к p , то это также последовательный предел, однако в общем случае обратное не обязательно. Если, кроме того, , то X метризуемо L является последовательным пределом f при x приближении к p тогда и только тогда, когда это предел (в указанном выше смысле) f при x приближении к p .

Другие характеристики

С точки зрения последовательностей

Для функций на реальной прямой один из способов определить предел функции — это предел последовательностей. (Это определение обычно приписывают Эдуарду Гейне .) В такой обстановке:

$$\lim _{x\to a}f(x)=L$$

тогда и только тогда, когда для всех последовательностей x _n (где x _n не равен a для всех n ), сходящихся к a, последовательность f ( x _n ) сходится к L . показал В 1916 году Серпинский , что доказательство эквивалентности этого определения и приведенного выше определения требует и эквивалентно слабой форме аксиомы выбора . последовательности x _n Обратите внимание, что для определения того, что означает сходимость к a, требуется метод эпсилон, дельта .

Подобно определению Вейерштрасса, более общее определение Гейне применимо к функциям, определенным на подмножествах вещественной прямой. Пусть f — вещественная функция с областью определения Dm ( f ) . Пусть a — предел последовательности элементов из Dm ( f ) \ { a }. Тогда предел (в этом смысле) f равен L, когда x приближается к p если для каждой последовательности x _n ∈ Dm ( f ) \ { a } (так что для всех x n n _не равен a ), которая сходится к a , последовательность f ( x _n ) сходится к L . Это то же самое, что определение последовательного предела в предыдущем разделе, полученное при рассмотрении подмножества Dm ( f ) из $\mathbb {R}$ как метрическое пространство с индуцированной метрикой.

В нестандартном исчислении

В нестандартном исчислении предел функции определяется следующим образом:

$$\lim _{x\to a}f(x)=L$$

тогда и только тогда, когда для всех $x\in \mathbb {R} ^{*},$ $f^{*}(x)-L$ бесконечно мало, если x − a бесконечно мало. Здесь $\mathbb {R} ^{*}$ — гипердействительные числа , а f* — естественное расширение f до нестандартных действительных чисел. Кейслер доказал, что такое гиперреальное определение предела уменьшает сложность квантора на два квантора. С другой стороны, Хрбачек пишет, что для того, чтобы определения были действительными для всех гипердействительных чисел, они должны быть неявно основаны на методе ε-δ, и утверждает, что с педагогической точки зрения надежда на то, что нестандартное исчисление может быть без ε-δ методов невозможно реализовать в полной мере. Баащик и др. подробно опишите полезность микронепрерывности для разработки прозрачного определения единообразной непрерывности и охарактеризуйте критику Хрбачека как «сомнительную жалобу».

С точки зрения близости

На международном математическом конгрессе 1908 года Ф. Рисс представил альтернативный способ определения пределов и непрерывности понятия, названного «близостью». Точка x определяется как находящаяся рядом с множеством $A\subseteq \mathbb {R}$ если для любого r > 0 существует точка a ∈ A такая, что | Икс - а | < р . В этой обстановке

$$\lim _{x\to a}f(x)=L$$

тогда и только тогда, когда для всех $A\subseteq \mathbb {R} ,$ L находится рядом с f ( A ), a находится рядом с A. когда Здесь f ( A ) — множество $\{f(x)|x\in A\}.$ Это определение также можно распространить на метрические и топологические пространства.

Отношение

Основная статья: Непрерывная функция

Понятие предела функции очень тесно связано с понятием непрерывности. Функция f называется непрерывной в точке c, если она определена в точке c и ее значение в точке c равно пределу функции f при x приближении к c :

$$\lim _{x\to c}f(x)=f(c).$$

(Здесь мы предположили, что c является предельной точкой области определения f .)

Свойства

Если функция f вещественнозначна, то предел f в точке p равен L тогда и только тогда, когда и правый предел, и левый предел f в точке p существуют и равны L .

Функция f непрерывна тогда и только тогда , в точке p когда предел f ( x ) при x приближении к p существует и равен f ( p ) . Если f : M → N — функция между метрическими пространствами M и N , то это эквивалентно тому, что f преобразует каждую последовательность из M , которая сходится к p, в последовательность из N , которая сходится к f ( p ) .

Если N — нормированное векторное пространство , то предельная операция линейна в следующем смысле: если предел f ( x ) , когда x приближается к p, равен L , а предел g ( x ) , когда x приближается к p , равен P , то предел f ( x ) + g ( x ) при x приближении к p равен L + P . Если a является скаляром из базового поля , то пределом af ( x ) при x приближении к p является aL .

Если f и g — вещественные (или комплекснозначные) функции, то переход к пределу операции над f ( x ) и g ( x ) (например, f + g , f − g , f × g , f / г , ж ^г ) при определенных условиях совместимо с действием пределов f ( x ) и g ( x ) . Этот факт часто называют алгебраической предельной теоремой . Основным условием, необходимым для применения следующих правил, является наличие пределов в правых частях уравнений (другими словами, эти пределы представляют собой конечные значения, включая 0). Кроме того, тождество деления требует, чтобы знаменатель в правой части был ненулевым (деление на 0 не определено), а тождество возведения в степень требует, чтобы основание было положительным или нулевым, а показатель степени положителен (конечный ).

$${\begin{array}{lcl}\displaystyle \lim _{x\to p}(f(x)+g(x))&=&\displaystyle \lim _{x\to p}f(x)+\lim _{x\to p}g(x)\\\displaystyle \lim _{x\to p}(f(x)-g(x))&=&\displaystyle \lim _{x\to p}f(x)-\lim _{x\to p}g(x)\\\displaystyle \lim _{x\to p}(f(x)\cdot g(x))&=&\displaystyle \lim _{x\to p}f(x)\cdot \lim _{x\to p}g(x)\\\displaystyle \lim _{x\to p}(f(x)/g(x))&=&\displaystyle {\lim _{x\to p}f(x)/\lim _{x\to p}g(x)}\\\displaystyle \lim _{x\to p}f(x)^{g(x)}&=&\displaystyle {\lim _{x\to p}f(x)^{\lim _{x\to p}g(x)}}\end{array}}$$

Эти правила также действительны для односторонних пределов, в том числе когда p равно ∞ или −∞. В каждом приведенном выше правиле, когда один из пределов справа равен ∞ или −∞, предел слева иногда все еще может определяться следующими правилами.

$${\begin{array}{rcl}q+\infty &=&\infty {\text{ if }}q\neq -\infty \\[8pt]q\times \infty &=&{\begin{cases}\infty &{\text{if }}q>0\\-\infty &{\text{if }}q<0\end{cases}}\\[6pt]\displaystyle {\frac {q}{\infty }}&=&0{\text{ if }}q\neq \infty {\text{ and }}q\neq -\infty \\[6pt]\infty ^{q}&=&{\begin{cases}0&{\text{if }}q<0\\\infty &{\text{if }}q>0\end{cases}}\\[4pt]q^{\infty }&=&{\begin{cases}0&{\text{if }}0<q<1\\\infty &{\text{if }}q>1\end{cases}}\\[4pt]q^{-\infty }&=&{\begin{cases}\infty &{\text{if }}0<q<1\\0&{\text{if }}q>1\end{cases}}\end{array}}$$

(см. также Расширенная строка действительных чисел ).

В других случаях предел слева еще может существовать, хотя правая часть, называемая неопределенной формой , не позволяет определить результат. Это зависит от функций f и g . К неопределенным формам относятся:

$${\begin{array}{cc}\displaystyle {\frac {0}{0}}&\displaystyle {\frac {\pm \infty }{\pm \infty }}\\[6pt]0\times \pm \infty &\infty +-\infty \\[8pt]\qquad 0^{0}\qquad &\qquad \infty ^{0}\qquad \\[8pt]1^{\pm \infty }\end{array}}$$

См. далее правило Лопиталя ниже и неопределенную форму .

Пределы композиций функций

В общем, от знания этого $\lim _{y\to b}f(y)=c$ и $\lim _{x\to a}g(x)=b,$ из этого не следует, что $\lim _{x\to a}f(g(x))=c.$ Однако это «цепное правило» действует, если одно из следующих дополнительных выполняется условий:

• f ( b ) = c (то есть f непрерывен в точке b ), или
• g не принимает значение b вблизи a (то есть существует δ > 0 такое, что если 0 < | x − a | < δ , то | g ( x ) − b | > 0 ).

В качестве примера этого явления рассмотрим следующую функцию, которая нарушает оба дополнительных ограничения:

$$f(x)=g(x)={\begin{cases}0&{\text{if }}x\neq 0\\1&{\text{if }}x=0\end{cases}}$$

Поскольку значение в точке f (0) является устранимым разрывом ,

$$\lim _{x\to a}f(x)=0$$

для всех а .Таким образом, правило наивной цепочки предполагает, что предел f ( f ( x )) равен 0. Однако это тот случай, когда

$$f(f(x))={\begin{cases}1&{\text{if }}x\neq 0\\0&{\text{if }}x=0\end{cases}}$$

и так

$$\lim _{x\to a}f(f(x))=1$$

для всех а .

Пределы особого интереса

Основная статья: Список ограничений

Рациональные функции

Для n неотрицательное целое число и константы $a_{1},a_{2},a_{3},\ldots ,a_{n}$ и $b_{1},b_{2},b_{3},\ldots ,b_{n},$

$$\lim _{x\to \infty }{\frac {a_{1}x^{n}+a_{2}x^{n-1}+a_{3}x^{n-2}+\dots +a_{n}}{b_{1}x^{n}+b_{2}x^{n-1}+b_{3}x^{n-2}+\dots +b_{n}}}={\frac {a_{1}}{b_{1}}}$$

Это можно доказать, разделив числитель и знаменатель на x. ^н . Если числитель представляет собой многочлен более высокой степени, предела не существует. Если знаменатель имеет более высокую степень, предел равен 0.

Тригонометрические функции

$${\begin{array}{lcl}\displaystyle \lim _{x\to 0}{\frac {\sin x}{x}}&=&1\\[4pt]\displaystyle \lim _{x\to 0}{\frac {1-\cos x}{x}}&=&0\end{array}}$$

Экспоненциальные функции

$${\begin{array}{lcl}\displaystyle \lim _{x\to 0}(1+x)^{\frac {1}{x}}&=&\displaystyle \lim _{r\to \infty }\left(1+{\frac {1}{r}}\right)^{r}=e\\[4pt]\displaystyle \lim _{x\to 0}{\frac {e^{x}-1}{x}}&=&1\\[4pt]\displaystyle \lim _{x\to 0}{\frac {e^{ax}-1}{bx}}&=&\displaystyle {\frac {a}{b}}\\[4pt]\displaystyle \lim _{x\to 0}{\frac {c^{ax}-1}{bx}}&=&\displaystyle {\frac {a}{b}}\ln c\\[4pt]\displaystyle \lim _{x\to 0^{+}}x^{x}&=&1\end{array}}$$

Логарифмические функции

$${\begin{array}{lcl}\displaystyle \lim _{x\to 0}{\frac {\ln(1+x)}{x}}&=&1\\[4pt]\displaystyle \lim _{x\to 0}{\frac {\ln(1+ax)}{bx}}&=&\displaystyle {\frac {a}{b}}\\[4pt]\displaystyle \lim _{x\to 0}{\frac {\log _{c}(1+ax)}{bx}}&=&\displaystyle {\frac {a}{b\ln c}}\end{array}}$$

Правило Лопиталя

Основная статья: Правило больницы

Это правило использует производные для нахождения пределов неопределенных форм 0/0 или ±∞/∞ и применяется только к таким случаям. В эту форму можно манипулировать и другими неопределенными формами. Учитывая две функции f ( x ) и g ( x ) , определенные на открытом интервале I, содержащем желаемую предельную точку c , тогда если:

1. $\lim _{x\to c}f(x)=\lim _{x\to c}g(x)=0,$ или $\lim _{x\to c}f(x)=\pm \lim _{x\to c}g(x)=\pm \infty ,$ и
2. $f$ и $g$ дифференцируемы по $I\setminus \{c\},$ и
3. $g'(x)\neq 0$ для всех $x\in I\setminus \{c\},$ и
4. $\lim _{x\to c}{\tfrac {f'(x)}{g'(x)}}$ существует,

затем:

$$\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {f'(x)}{g'(x)}}.$$

Обычно первое условие является наиболее важным.

Например: $\lim _{x\to 0}{\frac {\sin(2x)}{\sin(3x)}}=\lim _{x\to 0}{\frac {2\cos(2x)}{3\cos(3x)}}={\frac {2\cdot 1}{3\cdot 1}}={\frac {2}{3}}.$

Суммы и интегралы

Указание бесконечной границы суммирования или интеграла является общепринятым сокращением для указания предела.

Короткий способ написать предел $\lim _{n\to \infty }\sum _{i=s}^{n}f(i)$является $\sum _{i=s}^{\infty }f(i).$ Важным примером пределов таких сумм являются ряды .

Короткий способ написать предел $\lim _{x\to \infty }\int _{a}^{x}f(t)\;dt$является $\int _{a}^{\infty }f(t)\;dt.$

Короткий способ написать предел $\lim _{x\to -\infty }\int _{x}^{b}f(t)\;dt$является $\int _{-\infty }^{b}f(t)\;dt.$

См. также

• Обозначение Big O — описывает предельное поведение функции.
• Правило Лопиталя - математическое правило для оценки некоторых пределов.
• Список лимитов
• Предел последовательности - значение, к которому стремится бесконечная последовательность.
• Предельная точка — точка кластера в топологическом пространстве. Страницы с краткими описаниями целей перенаправления.
• Ограничить верхний и нижний предел — границы последовательности. Страницы, отображающие краткие описания целей перенаправления.
• Сеть (математика) - обобщение последовательности точек.
• Нестандартное исчисление – современное применение бесконечно малых. Страницы с краткими описаниями целей перенаправления.
• Теорема о сжатии - метод поиска пределов в исчислении
• Последующий предел - предел некоторой подпоследовательности.

Ссылки

• Апостол, Том М. (1974). Математический анализ (2-е изд.). Аддисон-Уэсли. ISBN  0-201-00288-4 .
• Бартл, Роберт (1967). Элементы настоящего анализа . Уайли.
• Бартл, Роберт Г.; Шерберт, Дональд Р. (2000). Введение в реальный анализ . Уайли.
• Курант, Ришар (1924). Лекции по дифференциальному и интегральному исчислению (на немецком языке). Спрингер.
• Харди, GH (1921). Курс чистой математики . Издательство Кембриджского университета.
• Хаббард, Джон Х. (2015). Векторное исчисление, линейная алгебра и дифференциальные формы: единый подход (5-е изд.). Матричные издания.
• Пейдж, Уоррен; Херш, Рубен; Селден, Энни; и др., ред. (2002). «Актуальные новости СМИ». Математический колледж . 33 (2): 147–154. JSTOR   2687124 . .
• Рудин, Вальтер (1964). Принципы математического анализа . МакГроу-Хилл.
• Сазерленд, Вашингтон (1975). Введение в метрические и топологические пространства . Оксфорд: Издательство Оксфордского университета. ISBN  0-19-853161-3 .
• Уиттакер ; Уотсон (1904). Курс современного анализа . Издательство Кембриджского университета.

Внешние ссылки

• MacTutor История Вейерштрасса.
• MacTutor История Больцано
• Визуальное исчисление Лоуренса С. Хаша, Университет Теннесси (2001).