Метрика Шварцшильда

В относительности Эйнштейна теории общей метрика Шварцшильда (также известная как решение Шварцшильда ) является точным решением уравнений поля Эйнштейна , которое описывает гравитационное поле вне сферической массы, при условии, что электрический заряд массы, угловой момент массы и универсальная космологическая постоянная равны нулю. Решение является полезным приближением для описания медленно вращающихся астрономических объектов, таких как многие звезды и планеты , включая Землю и Солнце. Его нашел Карл Шварцшильд в 1916 году.

Согласно теореме Биркгофа , метрика Шварцшильда является наиболее общим сферически-симметричным вакуумным решением уравнений поля Эйнштейна. или Черная дыра Шварцшильда статическая черная дыра — это черная дыра , не имеющая ни электрического заряда, ни углового момента (невращающаяся). Черная дыра Шварцшильда описывается метрикой Шварцшильда, и ее нельзя отличить от любой другой черной дыры Шварцшильда, кроме как по ее массе.

Черная дыра Шварцшильда характеризуется окружающей сферической границей, называемой горизонтом событий , которая расположена на радиусе Шварцшильда ( $r_{\text{s}}$), часто называемый радиусом черной дыры. Граница не является физической поверхностью, и человек, провалившийся за горизонт событий (до того, как его разорвало приливные силы), не заметил бы никакой физической поверхности в этом положении; это математическая поверхность, которая важна для определения свойств черной дыры. Любая невращающаяся и незаряженная масса, меньшая ее радиуса Шварцшильда, образует черную дыру. Решение уравнений поля Эйнштейна справедливо для любой массы M , поэтому в принципе (в рамках общей теории относительности) черная дыра Шварцшильда любой массы могла бы существовать, если бы условия стали достаточно благоприятными, чтобы обеспечить ее образование.

Вблизи черной дыры Шварцшильда пространство искривляется настолько сильно, что даже лучи света отклоняются, а очень близкий свет может отклоняться настолько сильно, что он несколько раз проходит вокруг черной дыры.

Формулировка

Дополнительная информация: Вывод решения Шварцшильда.

Метрика Шварцшильда — это сферически симметричная лоренцева метрика (здесь с соглашением о сигнатурах (+, -, -, -) ), определенная на (подмножестве) $$\mathbb {R} \times \left(E^{3}-O\right)\cong \mathbb {R} \times (0,\infty )\times S^{2}$$ где $E^{3}$ представляет собой трехмерное евклидово пространство, а $S^{2}\subset E^{3}$ это две сферы. Группа ротации $\mathrm {SO} (3)=\mathrm {SO} (E^{3})$ действует на $E^{3}-O$ или $S^{2}$ фактор как вращение вокруг центра $O$, оставив первый $\mathbb {R}$ фактор не изменился. Метрика Шварцшильда представляет собой решение уравнений поля Эйнштейна в пустом пространстве, а это означает, что она действительна только вне гравитирующего тела. То есть для сферического тела радиуса $R$ решение справедливо для $r>R$. To describe the gravitational field both inside and outside the gravitating body the Schwarzschild solution must be matched with some suitable interior solution at . Чтобы описать гравитационное поле как внутри, так и снаружи гравитирующего тела, решение Шварцшильда должно быть сопоставлено с некоторым подходящим внутренним решением при $r=R$‍ , например, внутренняя метрика Шварцшильда .

В координатах Шварцшильда $(t,r,\theta ,\phi )$ метрика Шварцшильда (или, что то же самое, линейный элемент для собственного времени ) имеет вид $${ds}^{2}=c^{2}\,{d\tau }^{2}=\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)c^{2}\,dt^{2}-\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)^{-1}\,dr^{2}-r^{2}{d\Omega }^{2},$$где ${d\Omega }^{2}$ is the metric on the two sphere, i.e. – метрика на двух сферах, т.е. ${d\Omega }^{2}=\left(d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2}\right)$. Более того, . Furthermore,

• $d\tau ^{2}$ положителен для времениподобных кривых, и в этом случае $\tau$ — собственное время (время, измеряемое часами, движущимися вдоль одной мировой линии с пробной частицей ),
• $c$ это скорость света ,
• $t$ is, for есть, для $r>r_{\text{s}}$— временная координата (измеряется часами, находящимися бесконечно далеко от массивного тела и неподвижными по отношению к нему), , the time coordinate (measured by a clock located infinitely far from the massive body and stationary with respect to it),
• $r$ is, for есть, для $r>r_{\text{s}}$, , the radial coordinate (measured as the circumference, divided by 2 радиальная координата (измеряется как длина окружности, разделенная на 2 π , сферы с центром вокруг массивного тела),
• $\Omega$ is a point on the two sphere это точка на двух сферах $S^{2}$‍ ,
• $\theta$ это широта ​ $\Omega$ (угол с севера, в радианах ) , определяемый после произвольного выбора оси z ,
• $\phi$ долгота ​ ​ $\Omega$ (также в радианах) вокруг выбранной оси z и
• $r_{\text{s}}$ - радиус Шварцшильда массивного тела, масштабный коэффициент , связанный с его массой. $M$ by к $r_{\text{s}}={2GM}/{c^{2}}$‍где $G$ является гравитационной постоянной .

Метрика Шварцшильда имеет особенность при r = 0 , которая является особенностью внутренней кривизны. Похоже, что у него также есть сингулярность на горизонте событий r = r _s . Таким образом, в зависимости от точки зрения метрика определяется только во внешней области. $r>r_{\text{s}}$, только во внутренней области $r<r_{\text{s}}$ or their disjoint union. However, the metric is actually non-singular across the event horizon, as one sees in suitable coordinates (see below). For или их непересекающийся союз. Однако на самом деле метрика несингулярна на горизонте событий, как видно в подходящих координатах (см. ниже). Для $r\gg r_{\text{s}}$метрика Шварцшильда асимптотична стандартной метрике Лоренца в пространстве Минковского. Практически для всех астрофизических объектов соотношение , the Schwarzschild metric is asymptotic to the standard Lorentz metric on Minkowski space. For almost all astrophysical objects, the ratio ${\frac {r_{\text{s}}}{R}}$ чрезвычайно мал. Например, радиус Шварцшильда $r_{\text{s}}^{({\text{Earth}})}$ Земли составляет примерно 8,9 мм , а Солнца, которое составляет 3,3 × 10 ⁵ раз массивнее имеет радиус Шварцшильда $r_{\text{s}}^{({\text{Sun}})}$ около 3,0 км. Это соотношение становится большим только в непосредственной близости от черных дыр и других сверхплотных объектов, таких как нейтронные звезды .

Оказывается, радиальная координата имеет физическое значение как «собственное расстояние между двумя событиями, которые происходят одновременно относительно радиально движущихся геодезических часов, причем два события лежат на одной и той же радиальной координатной линии».

Решение Шварцшильда аналогично классической ньютоновской теории гравитации, которая соответствует гравитационному полю вокруг точечной частицы.Даже на поверхности Земли поправки к ньютоновской гравитации составляют лишь одну миллиардную часть.

История

Решение Шварцшильда названо в честь Карла Шварцшильда , который нашел точное решение в 1915 году и опубликовал его в январе 1916 года. чуть больше месяца после публикации общей теории относительности Эйнштейна.Это было первое точное решение уравнений поля Эйнштейна, отличное от тривиального решения в плоском пространстве . Шварцшильд умер вскоре после публикации своей статьи в результате болезни, которую он развил во время службы в немецкой армии во время Первой мировой войны .

Йоханнес Дросте в 1916 году. независимо предложил то же решение, что и Шварцшильд, используя более простой и прямой вывод.

В первые годы существования общей теории относительности существовало много путаницы относительно природы особенностей, обнаруженных в уравнениях Шварцшильда и других решениях уравнений поля Эйнштейна . В оригинальной статье Шварцшильд поместил то, что мы сейчас называем горизонтом событий, в начало своей системы координат. В этой статье он также ввел в качестве вспомогательной переменной то, что сейчас известно как радиальная координата Шварцшильда ( r в приведенных выше уравнениях). В своих уравнениях Шварцшильд использовал другую радиальную координату, равную нулю на радиусе Шварцшильда.

Более полный анализ структуры особенности дал Дэвид Гильберт. в следующем году, выявив особенности как при r = 0, так и при r = r _s . Хотя существовало общее мнение, что особенность при r = 0 была «настоящей» физической особенностью, природа особенности при r = r _s оставалась неясной.

В 1921 году Поль Пенлеве и в 1922 году Аллвар Галлстранд независимо друг от друга создали метрику, сферически симметричное решение уравнений Эйнштейна, которое, как мы теперь знаем, представляет собой координатное преобразование метрики Шварцшильда, координат Гулстранда – Пенлеве , в котором не было сингулярности при r = r. _с . Однако они не осознавали, что их решения были всего лишь преобразованиями координат, и фактически использовали свое решение, чтобы доказать, что теория Эйнштейна неверна. В 1924 году Артур Эддингтон произвел первое преобразование координат ( координаты Эддингтона-Финкельштейна ), которое показало, что сингулярность при r = r _s была координатным артефактом, хотя он, похоже, также не осознавал значения этого открытия. Позже, в 1932 году, Жорж Леметр дал другое преобразование координат ( координаты Леметра ) с тем же эффектом и был первым, кто осознал, что это означает, что сингулярность при r = r _s не является физической. В 1939 году Говард Робертсон показал, что свободно падающий наблюдатель, спускающийся в метрике Шварцшильда, пересечет r = r _s сингулярность за конечное количество собственного времени , хотя это заняло бы бесконечное количество времени с точки зрения координатного времени t .

В 1950 году Джон Синдж выпустил статью. это показало максимальное аналитическое расширение метрики Шварцшильда, снова показав, что особенность при r = r _s была координатным артефактом и представляла собой два горизонта. Подобный результат позже был заново открыт Джорджем Секересом . и независимо Мартин Крускал . Новые координаты, ныне известные как координаты Крускала – Секереса, были намного проще, чем координаты Синджа, но обе обеспечивали единый набор координат, охватывающий все пространство-время. Однако, возможно, из-за малоизвестности журналов, в которых были опубликованы статьи Леметра и Синга, их выводы остались незамеченными, поскольку многие крупные игроки в этой области, включая Эйнштейна, полагали, что сингулярность на радиусе Шварцшильда была физической. Более поздний вывод Synge метрического решения Краскала – Секереса, которое было мотивировано желанием избежать «использования «плохих» координат [Шварцшильда] для получения «хороших» координат [Краскала – Секереса]», в целом недооценивалось в литературе, но было принято Чандрасекаром в его монографии о черных дырах. .

Настоящий прогресс был достигнут в 1960-х годах, когда математически строгая формулировка, сформулированная в терминах дифференциальной геометрии, вошла в область общей теории относительности, позволив более точно определить, что означает лоренцева многообразия сингулярность . Это привело к окончательной идентификации особенности r = r _s в метрике Шварцшильда как горизонта событий , т. е. гиперповерхности в пространстве-времени, которую можно пересечь только в одном направлении.

Сингулярности и черные дыры

Решение Шварцшильда, по-видимому, имеет особенности при r = 0 и r = r _s ; некоторые компоненты метрики «раздуваются» (влекут за собой деление на ноль или умножение на бесконечность) на этих радиусах. Поскольку ожидается, что метрика Шварцшильда будет справедливой только для тех радиусов, которые больше радиуса R гравитирующего тела, проблем нет, пока R > r _s . Для обычных звезд и планет это всегда так. Например, радиус Солнца составляет примерно 700 000 км , тогда как его шварцшильдовский радиус всего 3 км .

Особенность в точке r = r _s делит координаты Шварцшильда на два несвязанных участка . Внешнее решение Шварцшильда с r > r _s связано с гравитационными полями звезд и планет. Внутреннее решение Шварцшильда с 0 ⩽ r < r _s , содержащее особенность в точке = 0 , полностью отделено от внешнего участка особенностью в точке r = rs _. r Таким образом, координаты Шварцшильда не дают физической связи между двумя участками, которые можно рассматривать как отдельные решения. Однако сингулярность в точке r = rs _— иллюзия; это пример того, что называется координатной сингулярностью . Как следует из названия, сингулярность возникает из-за неправильного выбора координат или координатных условий . При переходе на другую систему координат (например , координаты Леметра , координаты Эддингтона–Финкельштейна , координаты Крускала–Секереса , координаты Новикова или координаты Гулстранда–Пенлеве ) метрика становится регулярной при r = r _s и может расширять внешний патч до значений r меньше, чем r _s . Используя другое преобразование координат, можно затем связать расширенный внешний фрагмент с внутренним фрагментом.

Однако случай r = 0 отличается. Если кто-то спросит, что решение справедливо для всех r, он столкнется с истинной физической сингулярностью, или гравитационной сингулярностью , в начале координат. Чтобы увидеть, что это настоящая сингулярность, нужно посмотреть на величины, не зависящие от выбора координат. Одной из таких важных величин является инвариант Кречмана , который определяется выражением

$R^{\alpha \beta \gamma \delta }R_{\alpha \beta \gamma \delta }={\frac {12r_{\mathrm {s} }^{2}}{r^{6}}}={\frac {48G^{2}M^{2}}{c^{4}r^{6}}}\,.$

При r = 0 кривизна становится бесконечной, что указывает на наличие особенности. На этом этапе метрика не может быть расширена плавным образом (инвариант Кречмана включает вторые производные метрики), само пространство-время больше не является четко определенным. Кроме того, Сберский показал, что метрика не может быть расширена даже непрерывным образом. Долгое время считалось, что такое решение нефизично. Однако более глубокое понимание общей теории относительности привело к осознанию того, что такие особенности являются общей чертой теории, а не просто экзотическим частным случаем.

Решение Шварцшильда, которое считается справедливым для всех r > 0 , называется черной дырой Шварцшильда . Это совершенно правильное решение уравнений поля Эйнштейна, хотя (как и другие черные дыры) оно обладает довольно причудливыми свойствами. При r < r _s радиальная координата Шварцшильда r становится времениподобной , а временная координата t становится пространственноподобной . Кривая при постоянном r больше не является возможной мировой линией частицы или наблюдателя, даже если приложить силу, чтобы удержать ее там; это происходит потому, что пространство-время искривлено настолько, что направление причины и следствия (будущий световой конус частицы ) указывает на сингулярность. Поверхность r = r _s ограничивает то, что называется горизонтом событий черной дыры. Он представляет собой точку, после которой свет больше не может покинуть гравитационное поле. Любой физический объект, радиус R которого становится меньше или равен радиусу Шварцшильда, подвергся гравитационному коллапсу и стал черной дырой.

Альтернативные координаты

Решение Шварцшильда может быть выражено в диапазоне различных вариантов координат, помимо координат Шварцшильда, использованных выше. Различные варианты выбора, как правило, подчеркивают разные особенности решения. В таблице ниже показаны некоторые популярные варианты.

Альтернативные координаты

Координаты	Линейный элемент	Примечания	Функции
Координаты Эддингтона – Финкельштейна (входящий)	$\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)\,dv^{2}-2\,dv\,dr-r^{2}\,g_{\Omega }$		регулярный на горизонте будущего прошлый горизонт находится в точке v = −∞
Координаты Эддингтона – Финкельштейна (исходящий)	$\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)\,du^{2}+2\,du\,dr-r^{2}g_{\Omega }$		регулярный на прошлом горизонте простирается за прошлый горизонт горизонт будущего в точке u = ∞
Координаты Гулстранд – Пенлеве	$\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)\,dT^{2}\pm 2{\sqrt {\frac {r_{\mathrm {s} }}{r}}}\,dT\,dr-dr^{2}-r^{2}\,g_{\Omega }$		регулярный на прошлых и будущих горизонтах
Изотропные координаты	${\frac {\left(1-{\frac {r_{\mathrm {s} }}{4R}}\right)^{2}}{\left(1+{\frac {r_{\mathrm {s} }}{4R}}\right)^{2}}}\,{dt}^{2}-\left(1+{\frac {r_{\mathrm {s} }}{4R}}\right)^{4}\,\left(dx^{2}+dy^{2}+dz^{2}\right)$	$R={\sqrt {x^{2}+y^{2}+z^{2}}}$ Действительно только за пределами горизонта событий: $R>r_{\text{s}}/4$	изотропные световые конусы на срезах постоянного времени
Координаты Крускала – Секереса	${\frac {4r_{\mathrm {s} }^{3}}{r}}e^{-{\frac {r}{r_{\mathrm {s} }}}}\,\left(dT^{2}-dR^{2}\right)-r^{2}\,g_{\Omega }$	$T^{2}-R^{2}=\left(1-{\frac {r}{r_{\mathrm {s} }}}\right)e^{\frac {r}{r_{\mathrm {s} }}}$	регулярный на горизонте; максимально распространяется на полное пространство-время
Подробности о Леметре	$dT^{2}-{\frac {r_{\mathrm {s} }}{r}}\,dR^{2}-r^{2}\,g_{\Omega }$	$r=\left({\tfrac {3}{2}}(R\pm T)\right)^{\frac {2}{3}}r_{\mathrm {s} }^{\frac {1}{3}}$	регулярный либо на прошлом, либо на будущем горизонте
Гармонические координаты	${\frac {\rho -r_{\mathrm {s} }/2}{\rho +r_{\mathrm {s} }/2}}dt^{2}-{\frac {\rho +r_{\mathrm {s} }/2}{\rho -r_{\mathrm {s} }/2}}d\rho ^{2}-(\rho +r_{\mathrm {s} }/2)^{2}g_{\Omega }$	$\rho =r-r_{\mathrm {s} }/2$

В таблице выше для краткости введены некоторые сокращения. Скорость света c установлена ​​равной единице . Обозначения

$g_{\Omega }=d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}$

используется для метрики двумерной сферы единичного радиуса. Более того, в каждой записи R и T обозначают альтернативные варианты радиальной и временной координаты для конкретных координат. Обратите внимание, что R или T могут варьироваться от записи к записи.

Координаты Крускала–Секереша имеют вид, к которому преобразование Белинского–Захарова можно применить . Это означает, что черная дыра Шварцшильда представляет собой разновидность гравитационного солитона .

Параболоид Фламма

График параболоида Фламма. Его не следует путать с несвязанной с ним концепцией гравитационного колодца .

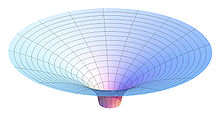
Пространственную кривизну решения Шварцшильда для r > r _s можно визуализировать, как показано на рисунке. с постоянным временем Рассмотрим экваториальный срез H через решение Шварцшильда, зафиксировав θ = π / 2 , t = константа, а остальные координаты Шварцшильда ( r , φ ) меняются. Представьте теперь, что существует дополнительное евклидово измерение w , которое не имеет физической реальности (оно не является частью пространства-времени). Затем замените плоскость ( r , φ ) поверхностью с ямочкой в ​​направлении w согласно уравнению ( параболоид Фламма )

$w=2{\sqrt {r_{\mathrm {s} }\left(r-r_{\mathrm {s} }\right)}}.$

Эта поверхность обладает тем свойством, что расстояния, измеренные внутри нее, соответствуют расстояниям в метрике Шварцшильда, поскольку согласно определению w, приведенному выше,

$dw^{2}+dr^{2}+r^{2}\,d\varphi ^{2}={\frac {dr^{2}}{1-{\frac {r_{\mathrm {s} }}{r}}}}+r^{2}\,d\varphi ^{2}=-ds^{2}$

Таким образом, параболоид Фламма полезен для визуализации пространственной кривизны метрики Шварцшильда. Однако не следует путать его с гравитационным колодцем . Ни одна обычная (массивная или безмассовая) частица не может иметь мировую линию, лежащую на параболоиде, так как все расстояния на ней пространственноподобны (это сечение в один момент времени, поэтому любая частица, движущаяся по нему, имела бы бесконечную скорость ). Тахион может иметь пространственноподобную мировую линию , полностью лежащую на одном параболоиде. Однако даже в этом случае его геодезический путь не является траекторией, которую можно пройти через аналогию гравитационного колодца с «резиновым листом»: в частности, если ямочка нарисована вверх, а не вниз, геодезический путь тахиона все равно изгибается в сторону центральной массы. , не прочь. см. в статье о гравитационных колодцах Дополнительную информацию .

Параболоид Фламма можно получить следующим образом. Евклидова метрика в цилиндрических координатах ( r , φ , w ) записывается

$-ds^{2}=dw^{2}+dr^{2}+r^{2}\,d\varphi ^{2}\,.$

Полагая поверхность описываться функцией w = w ( r ) , евклидову метрику можно записать как

$-ds^{2}=\left(1+\left({\frac {dw}{dr}}\right)^{2}\right)\,dr^{2}+r^{2}\,d\varphi ^{2}\,,$

Сравнивая это с метрикой Шварцшильда в экваториальной плоскости ( θ = π / 2 ) в фиксированное время ( t = константа, dt = 0 )

$-ds^{2}=\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)^{-1}\,dr^{2}+r^{2}\,d\varphi ^{2}\,,$

дает интегральное выражение для w ( r ) :

$w(r)=\int {\frac {dr}{\sqrt {{\frac {r}{r_{\mathrm {s} }}}-1}}}=2r_{\mathrm {s} }{\sqrt {{\frac {r}{r_{\mathrm {s} }}}-1}}+{\mbox{constant}}$

решением которого является параболоид Фламма.

Орбитальное движение

Сравнение орбиты пробной частицы в ньютоновском (слева) и шварцшильдовском (справа) пространстве-времени; обратите внимание на апсидальную прецессию справа.

Дополнительная информация: Шварцшильдовская геодезия.

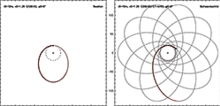
Частица, вращающаяся в метрике Шварцшильда, может иметь устойчивую круговую орбиту с r > 3 r _s . Круговые орбиты с r от 1,5 r _s до 3 r _s неустойчивы, и круговых орбит с r < 1,5 r _s не существует . Круговая орбита минимального радиуса 1,5 r _s соответствует орбитальной скорости, приближающейся к скорости света. Частица может иметь постоянное значение r между rs _s и 1,5 r _{, но только если действует некоторая сила ,} удерживающая ее на этом уровне.

Некруговые орбиты, такие как орбита Меркурия , живут на малых радиусах дольше, чем можно было бы ожидать в условиях ньютоновской гравитации . Это можно рассматривать как менее крайнюю версию более драматичного случая, когда частица проходит через горизонт событий и навсегда остается внутри него. Промежуточным между случаем Меркурия и случаем падения объекта за горизонт событий существуют экзотические возможности, такие как ножевые орбиты, при которых спутник можно заставить совершать сколь угодно большое количество почти круговых орбит, после чего он улетает обратно наружу.

Симметрии

The isometry group of the Schwarzchild metric is Группа изометрии метрики Шварцшильда : $\mathbb {R} \times \mathrm {O} (3)\times \{\pm 1\}$‍где $\mathrm {O} (3)$ - ортогональная группа вращений и отражений в трех измерениях, $\mathbb {R}$ включает в себя переводы времени, и $\{\pm 1\}$ — группа, порожденная обращением времени.

Таким образом, это подгруппа десятимерной группы Пуанкаре , которая принимает ось времени (траекторию звезды) к себе. Он опускает пространственные перемещения (трехмерные измерения) и усиливает (трехмерные измерения). Он сохраняет перевод времени (одно измерение) и вращение (трехмерное). Таким образом, он имеет четыре измерения. Как и группа Пуанкаре, она имеет четыре связных компонента: компонент тождества; компонент, обращенный во времени; компонент пространственной инверсии; и компонент, который одновременно обращен во времени и в пространстве.

Кривизны

Скаляр кривизны Риччи и тензор кривизны Риччи равны нулю. Ненулевые компоненты тензора кривизны Римана :

$R^{t}{}_{rrt}=2R^{\theta }{}_{r\theta r}=2R^{\phi }{}_{r\phi r}={\frac {r_{\text{s}}}{r^{2}(r_{\text{s}}-r)}},$

$2R^{t}{}_{\theta \theta t}=2R^{r}{}_{\theta \theta r}=R^{\phi }{}_{\theta \phi \theta }={\frac {r_{\text{s}}}{r}},$

$2R^{t}{}_{\phi \phi t}=2R^{r}{}_{\phi \phi r}=-R^{\theta }{}_{\phi \phi \theta }={\frac {r_{\text{s}}\sin ^{2}(\theta )}{r}},$

$R^{r}{}_{trt}=-2R^{\theta }{}_{t\theta t}=-2R^{\phi }{}_{t\phi t}=c^{2}{\frac {r_{\text{s}}(r_{\text{s}}-r)}{r^{4}}}$

Компоненты, которые можно получить с помощью симметрий тензора Римана, не отображаются.

Чтобы понять физический смысл этих величин, полезно выразить тензор кривизны в ортонормированном базисе. В ортонормированном базисе наблюдателя ненулевые компоненты в геометрических единицах равны

$R^{\hat {r}}{}_{{\hat {t}}{\hat {r}}{\hat {t}}}=-R^{\hat {\theta }}{}_{{\hat {\phi }}{\hat {\theta }}{\hat {\phi }}}=-{\frac {r_{\text{s}}}{r^{3}}},$

$R^{\hat {\theta }}{}_{{\hat {t}}{\hat {\theta }}{\hat {t}}}=R^{\hat {\phi }}{}_{{\hat {t}}{\hat {\phi }}{\hat {t}}}=-R^{\hat {r}}{}_{{\hat {\theta }}{\hat {r}}{\hat {\theta }}}=-R^{\hat {r}}{}_{{\hat {\phi }}{\hat {r}}{\hat {\phi }}}={\frac {r_{\text{s}}}{2r^{3}}}.$

Опять же, компоненты, которые можно получить с помощью симметрии тензора Римана, не отображаются. Эти результаты инвариантны к любому повышению Лоренца, поэтому компоненты не изменяются для нестатических наблюдателей. Уравнение геодезического отклонения показывает, что приливное ускорение между двумя наблюдателями, разделенными расстоянием $\xi ^{\hat {j}}$ является $D^{2}\xi ^{\hat {j}}/D\tau ^{2}=-R^{\hat {j}}{}_{{\hat {t}}{\hat {k}}{\hat {t}}}\xi ^{\hat {k}}$, поэтому тело длиной $L$ растягивается в радиальном направлении под действием кажущегося ускорения $(r_{\text{s}}/r^{3})c^{2}L$ и сжимается в перпендикулярных направлениях $-(r_{\text{s}}/(2r^{3}))c^{2}L$.

См. также

• Вывод решения Шварцшильда
• Метрика Рейсснера – Нордстрема (заряженное, невращающееся решение)
• Метрика Керра (незаряженное, вращающееся решение)
• Метрика Керра – Ньюмана (заряженное вращающееся решение)
• Черная дыра , общий обзор
• Координаты Шварцшильда
• Координаты Крускала – Секереса
• Координаты Эддингтона – Финкельштейна
• Координаты Гулстранд – Пенлеве
• Координаты Леметра (решение Шварцшильда в синхронных координатах )
• Поля системы отсчета в общей теории относительности (наблюдатели Леметра в вакууме Шварцшильда)
• Уравнение Толмана – Оппенгеймера – Волкова (уравнения метрики и давления статического и сферически симметричного тела из изотропного материала)
• Планковская длина

Ссылки

• Шварцшильд, К. (1916). «О гравитационном поле точки массы по теории Эйнштейна» . Труды Королевской прусской академии наук . 7 : 189-196. Бибкод : 1916AbhKP1916..189S .

• Текст оригинальной статьи в Wikisource.
• Перевод: Анточи, С.; Лойнгер, А. (1999). «О гравитационном поле массовой точки по теории Эйнштейна». arXiv : физика/9905030 .
• Комментарий к статье, дающий более простой вывод: Бел, Л. (2007). «О гравитационном поле массовой точки по теории Эйнштейна». arXiv : 0709.2257 [ gr-qc ].

• Шварцшильд, К. (1916). «О гравитационном поле сферы несжимаемой жидкости» . Труды Королевской прусской академии наук . 1 :424.

• Текст оригинальной статьи в Wikisource.
• Перевод: Анточи, С. (1999). «О гравитационном поле сферы несжимаемой жидкости по теории Эйнштейна». arXiv : физика/9912033 .

• Фламм, Л. (1916). «Вклад в теорию гравитации Эйнштейна». Физический журнал . 17 :448.
• Адлер, Р.; Базен, М.; Шиффер, М. (1975). Введение в общую теорию относительности (2-е изд.). МакГроу-Хилл . Глава 6. ISBN  0-07-000423-4 .
• Ландау, Л.Д.; Лифшиц, Э.М. (1951). Классическая теория полей . Курс теоретической физики . Том. 2 (4-е исправленное английское изд.). Пергамон Пресс . Глава 12. ISBN  0-08-025072-6 .
• Миснер, CW; Торн, Канзас; Уилер, Дж. А. (1970). Гравитация . У. Х. Фриман . Главы 31 и 32. ISBN.  0-7167-0344-0 .
• Вайнберг, С. (1972). Гравитация и космология: принципы и приложения общей теории относительности . Джон Уайли и сыновья . Глава 8. ISBN  0-471-92567-5 .
• Тейлор, EF; Уилер, Дж. А. (2000). Исследование черных дыр: введение в общую теорию относительности . Аддисон-Уэсли . ISBN  0-201-38423-Х .
• Хайнцле, Дж. М.; Штайнбауэр, Р. (2002). «Замечания о распределительной геометрии Шварцшильда». Журнал математической физики . 43 (3): 1493–1508. arXiv : gr-qc/0112047 . Бибкод : 2002JMP....43.1493H . дои : 10.1063/1.1448684 . S2CID   119677857 .