Хроматическая шкала
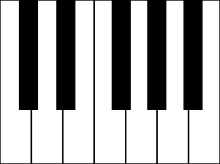
Хроматическая гамма (или двенадцатитоновая шкала ) — набор из двенадцати тонов (более полно — высотных классов ), используемых в тональной музыке, с нотами, разделенными интервалом в полутон . Хроматические инструменты , такие как фортепиано , созданы для создания хроматической гаммы, в то время как другие инструменты, способные плавно изменять высоту звука, такие как тромбон и скрипка , также могут воспроизводить микротона или ноты между теми, которые доступны на фортепиано.
В большинстве музыкальных произведений используются подмножества хроматической гаммы, такие как диатонические гаммы . Хотя хроматическая гамма является фундаментальной в западной теории музыки , она редко используется целиком в музыкальных композициях или импровизации .
Определение
[ редактировать ]Хроматическая гамма — это музыкальная гамма с двенадцатью тонами , каждый на полутон , также известный как полутон, выше или ниже соседних тонов. В результате в 12-тоновой равнотемперированной настройке (наиболее распространенной настройке в западной музыке) хроматическая гамма охватывает все 12 доступных тонов. Таким образом, существует только одна хроматическая гамма. [а] Отношение частоты одной ноты в гамме к частоте предыдущей ноты определяется выражением . [1]
![{\displaystyle {\sqrt[{12}]{2}}\approxeq 1.06}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1241dd2aeab3b8ebf705cfe7d1ca86f0c07d905b)
При равной темперации все полутона имеют одинаковую величину (100 центов двенадцать полутонов ), а в октаве (1200 центов). В результате ноты равнотемперированной хроматической гаммы располагаются на одинаковом расстоянии друг от друга.
Хроматическая гамма ... представляет собой серию полутонов, включающую все высоты нашей [12-тоновой] равнотемперированной системы.
- Аллен Форте (1979) [2]
Все общепринятые высоты звука, рассматриваемые вместе, составляют хроматическую гамму . Она полностью состоит из последовательных полутонов, самого маленького интервала в западной музыке.... Считая полутонами, октава включает двенадцать различных тонов, белые и черные клавиши вместе. Таким образом, хроматическая гамма представляет собой совокупность всех доступных тонов в порядке увеличения или уменьшения, по октаве за другой.
- Уолтер Пистон (1987) [3]
Хроматическая гамма – это недиатоническая гамма, состоящая полностью из полутоновых интервалов. Поскольку каждый тон гаммы равноудалён от следующего [ симметрии ], у него нет тоники [ тональности ]. [4] ...
Хроматизм [является] введением некоторых нот хроматической гаммы в музыку, которая в основном диатоническая по ориентации, или музыку, основанную на хроматической гамме вместо диатонических гамм. [5]- Бенвард и Сейкер (2003)
Восходящая и нисходящая хроматическая гамма показана ниже. [4]
Двенадцать нот октавы — все черные и белые клавиши одной октавы фортепиано — образуют хроматическую гамму . Все тона хроматической гаммы (в отличие от мажорной или минорной гаммы) находятся на одинаковом расстоянии друг от друга, в полшага.Слово хроматический происходит от греческого chroma — цвет ; а традиционная функция хроматической гаммы — окрашивать или украшать тона мажорной и минорной гамм. Он не определяет тональность, но дает ощущение движения и напряжения. Издавна его использовали, чтобы вызвать горе, потерю или печаль. В ХХ веке он также стал независимым от мажорных и минорных гамм и используется как основа целых композиций.
Обозначения
[ редактировать ]
Хроматическая гамма не имеет установленного энгармонического написания , которое всегда используется. Однако его написание часто зависит от мажорных или минорных тональностей, а также от того, является ли шкала восходящей или нисходящей. В целом хроматическая гамма обычно обозначается резкими знаками при восхождении и плоскими знаками при нисхождении. Это также обозначается так, что ни одна ступень шкалы не используется более двух раз подряд (например, G ♭ – G ♮ – G ♯ ).
Точно так же некоторые ноты хроматической гаммы имеют энгармонические эквиваленты в сольфеджио . Восходящая шкала — До, Ди, Ре, Ри, Ми, Фа, Фи, Соль, Си, Ла, Ли, Ти, нисходящая — Ти, Те/Та, Ла, Ле/Ло, Соль, Се, Фа, Ми. , Me/Ma, Re, Ra, Do, Однако, как только ноте присвоен 0, из-за октавной эквивалентности хроматическая гамма может быть однозначно обозначена числами 0-11 по модулю двенадцать . Таким образом, две идеальные пятые составляют 0-7-2. Тональные ряды , порядки, используемые в двенадцатитоновой технике , часто рассматриваются именно так из-за повышенной простоты сравнения обратных интервалов и форм ( инверсионная эквивалентность ).
Рациональная настройка высоты звука
[ редактировать ]Пифагорейский
[ редактировать ]Наиболее распространенной концепцией хроматической гаммы до 13 века была пифагорейская хроматическая гамма ( ). Из-за другой техники настройки двенадцать полутонов в этой гамме имеют два немного разных размера. Таким образом, масштаб не является совершенно симметричным. Многие другие системы настройки , разработанные в последующие столетия, имеют аналогичную асимметрию.
В пифагорейской настройке (т.е. 3-предельная просто интонация ) хроматическая гамма настраивается следующим образом: в идеальных квинтах от G ♭ до A ♯ с центром в D (жирным шрифтом) (G ♭ –D ♭ –A ♭ –E ♭ –B ♭ –F–C–G– D –A–E–B–F ♯ –C ♯ –G ♯ –D ♯ –A ♯ ), с диезами выше, чем их энгармонические бемоли (центы округлены до одной десятичной):
С D ♭ C ♯ Д E ♭ D ♯ И Ф G ♭ F ♯ Г A ♭ G ♯ А B ♭ A ♯ Б С Подача
соотношение1 256 ⁄ 243 2187 ⁄ 2048 9 ⁄ 8 32 ⁄ 27 19683 ⁄ 16384 81 ⁄ 64 4 ⁄ 3 1024 ⁄ 729 729 ⁄ 512 3 ⁄ 2 128 ⁄ 81 6561 ⁄ 4096 27 ⁄ 16 16 ⁄ 9 59049 ⁄ 32768 243 ⁄ 128 2 центы 0 90.2 113.7 203.9 294.1 317.6 407.8 498 588.3 611.7 702 792.2 815.6 905.9 996.1 1019.6 1109.8 1200
где 256/243 и пифагорейская — диатонический полутон ( лимма ) 2187/2048 ) пифагоров — хроматический полутон ( апотом .
Хроматическая гамма в пифагорейской настройке может быть смягчена до настройки 17-EDO (P5 = 10 шагов = 705,88 цента).
Просто интонация
[ редактировать ]В 5-предельной просто интонационной хроматической гамме, интенсивной хроматической гамме Птолемея. [ нужна ссылка ] , выглядит следующим образом: бемоли выше, чем их энгармонические диезы, и новые ноты между E – F и B – C (центы округлены до одного десятичного):
С C ♯ D ♭ Д D ♯ E ♭ И E ♯ /F ♭ Ф F ♯ G ♭ Г G ♯ A ♭ А A ♯ B ♭ Б B ♯ /C ♭ С Коэффициент шага 1 25 ⁄ 24 16 ⁄ 15 9 ⁄ 8 75 ⁄ 64 6 ⁄ 5 5 ⁄ 4 32 ⁄ 25 4 ⁄ 3 25 ⁄ 18 36 ⁄ 25 3 ⁄ 2 25 ⁄ 16 8 ⁄ 5 5 ⁄ 3 125 ⁄ 72 9 ⁄ 5 15 ⁄ 8 48 ⁄ 25 2 центы 0 70.7 111.7 203.9 274.6 315.6 386.3 427.4 498 568.7 631.3 702 772.6 813.7 884.4 955 1017.6 1088.3 1129.3 1200
Фракции 9 ⁄ 8 и 10 ⁄ 9 , 6 ⁄ 5 и 32 ⁄ 27 , 5 ⁄ 4 и 81 ⁄ 64 , 4 ⁄ 3 и 27 ⁄ 20 и многие другие пары взаимозаменяемы, например 81/80 ( синтонная запятая ) смягчается. [ нужны разъяснения ]
Просто настройку интонации можно аппроксимировать настройкой 19-EDO (P5 = 11 шагов = 694,74 цента).
Незападные культуры
[ редактировать ]Древняя китайская хроматическая гамма называется Ши-эр-лу . Однако «не следует думать, что эта гамма когда-либо функционировала как гамма , и ошибочно ссылаться на «китайскую хроматическую гамму», как это делали некоторые западные писатели. Серия из двенадцати нот, известная как двенадцать лю, была просто ряд фундаментальных нот, из которых можно построить гаммы». [8] Однако «с точки зрения тональной музыки [хроматическая гамма] не является самостоятельной гаммой, а происходит от диатонической гаммы». [2] превратив западную хроматическую гамму в гамму основных нот, из которых также можно было бы строить гаммы.
См. также
[ редактировать ]- Атональность
- хроматизм
- Двенадцатитоновая техника
- Музыка 20 века # Классика
- «All Through the Night» (песня Коула Портера)
Примечания
[ редактировать ]- ^ Поскольку каждая хроматическая гамма при транспозиции , инверсии и ретроградности . идентична любой другой
Определения из Викисловаря 
СМИ из Commons 
Цитаты из Wikiquote 
Учебники из Wikibooks 
Данные из Викиданных
Источники
[ редактировать ]- ^ Джинсы, Джеймс (1923). Наука и музыка . Издательство Кембриджского университета. стр. 24–25 – из Интернет-архива .
- ^ Jump up to: а б с Форте, Аллен , Тональная гармония , третье издание (Sl: Холт, Райнхарт и Уилсон, 1979): стр. 4–5. ISBN 0-03-020756-8 .
- ^ Поршень, Уолтер (1987/1941). Гармония , с. 5. 5-е изд. отредактировано ДеВото, Марк. WW Нортон, Нью-Йорк/Лондон. ISBN 0-393-95480-3 .
- ^ Jump up to: а б Бенвард, Брюс; Сейкер, Мэрилин Надин (2003). Музыка в теории и практике . Том. Я (7-е изд.). МакГроу-Хилл. п. 37. ИСБН 978-0-07-294262-0 .
- ^ Бенвард и Сакер (2003). «Глоссарий», с. 359.
- ^ Камен, Роджер (1990). Музыка: Признательность , с. 44. Краткое издание. МакГроу-Хилл. ISBN 0-07-033568-0 .
- ^ Маккартин, Брайан Дж. (ноябрь 1998 г.). «Прелюдия к музыкальной геометрии». Математический журнал колледжа . 29 (5): 354–370 (364). дои : 10.1080/07468342.1998.11973971 . JSTOR 2687250 .
- ^ Нидхэм, Джозеф (1962/2004). Наука и цивилизация в Китае, Vol. IV: Физика и физическая технология , стр. 170–171. ISBN 978-0-521-05802-5 .
Дальнейшее чтение
[ редактировать ]- Хьюитт, Майкл. 2013. Музыкальные гаммы мира . Дерево заметок. ISBN 978-0957547001
