Цепная линия

Эта статья о математической кривой. Чтобы узнать о других значениях, см. Цепная линия (значения) .

«Шенетта» перенаправляется сюда. Чтобы узнать о винном винограде, также известном как Шенетт, см. Синсо .

Цепь , свисающая с точек, образует контактную сеть.

Свободно висящие воздушные линии электропередачи также образуют контактную сеть (наиболее заметно на высоковольтных линиях и с некоторыми дефектами вблизи изоляторов ) .

Шелк паутины образует множество эластичных цепей.

В физике и геометрии сеть контактная ( США : / ˈ k æ t ən ɛr i / KAT -ən-err-ee , Великобритания : / k ə ˈ t iː n ər i / kə- TEE -nər-ee ) — это кривая , которую идеализированная висящая цепь или трос принимает под собственным весом , когда поддерживается только на своих концах в однородном гравитационном поле.

Цепная кривая имеет U-образную форму, внешне похожую на параболу , которой она не является.

Кривая появляется в конструкции некоторых типов арок и как поперечное сечение катеноида — формы, которую принимает мыльная пленка, ограниченная двумя параллельными круглыми кольцами.

Цепную сеть еще называют ализоидом , цепочкой , или, особенно в области материаловедения, пример фуникулера . Статика веревок описывает контактные сети в классической задаче статики, связанной с висящей веревкой.

Математически цепная кривая представляет собой график гиперболической функции косинуса . Поверхность вращения цепной кривой, катеноид , является минимальной поверхностью , в частности, минимальной поверхностью вращения . Висящая цепь примет форму с наименьшей потенциальной энергией, то есть цепную связь. Галилео Галилей в 1638 году обсуждал цепную линию в книге «Две новые науки», признавая, что она отличается от параболы . Математические свойства цепной линии изучал Роберт Гук в 1670-х годах, а ее уравнение вывели Лейбниц , Гюйгенс и Иоганн Бернулли в 1691 году.

Контактные сети и связанные с ними кривые используются в архитектуре и технике (например, при проектировании мостов и арок , чтобы силы не приводили к изгибающим моментам). В морской нефтегазовой отрасли термин «цепная линия» относится к стальному стояку цепной линии , трубопроводу, подвешенному между добывающей платформой и морским дном, который принимает форму, приближенную к цепной линии. В железнодорожной отрасли это относится к воздушной проводке , передающей электроэнергию поездам. (Часто он поддерживает контактный провод, и в этом случае он не следует истинной цепной линии.)

В оптике и электромагнетике гиперболические функции косинуса и синуса являются основными решениями уравнений Максвелла. Симметричные моды, состоящие из двух затухающих волн, будут образовывать цепную форму.

История

Антонио Гауди Модель цепной линии в Доме Мила

Слово «цепочка» происходит от латинского слова catēna , что означает « цепь ». Английское слово «цепная цепь» обычно приписывают Томасу Джефферсону . который писал в письме Томасу Пейну о строительстве арки для моста:

Недавно я получил из Италии трактат о равновесии аббата Маскерони арок. Кажется, это очень научная работа. Я еще не успел этим заняться; но я нахожу, что выводы его доказательств таковы, что каждая часть цепной цепи находится в совершенном равновесии.

Часто говорят что Галилей считал кривую висящей цепи параболической. Однако в своей книге «Две новые науки » (1638 г.) Галилей писал, что висящий шнур представляет собой лишь приблизительную параболу, правильно отмечая, что это приближение улучшается в точности по мере уменьшения кривизны и становится почти точным, когда угол возвышения меньше 45 °. Тот факт, что кривая, за которой следует цепочка, не является параболой, доказал Иоахим Юнгиус (1587–1657); этот результат был опубликован посмертно в 1669 году.

Применение контактной сети для строительства арок приписывается Роберту Гуку , чья «истинная математическая и механическая форма» в контексте восстановления собора Святого Павла намекала на контактную сеть. Некоторые гораздо более старые арки приближаются к контактным сетям, примером которых является арка Так-и Кисра в Ктесифоне .

Аналогия между аркой и висящей цепью и сравнение с куполом базилики Святого Петра в Риме ( Джованни Полени , 1748 г.)

В 1671 году Гук объявил Королевскому обществу , что решил проблему оптимальной формы арки, а в 1675 году опубликовал зашифрованное решение в виде латинской анаграммы. в приложении к его «Описанию гелиоскопов» где он написал, что нашел «истинную математическую и механическую форму всех видов строительных арок». Он не опубликовал решение этой анаграммы. при его жизни, но в 1705 году его душеприказчик представил его как ut pendet continuum flexile, sic stabit contiguumrigidum inversum , что означает «Как висит гибкий трос, так, в перевернутом виде, стоят соприкасающиеся части арки».

В 1691 году Готфрид Лейбниц , Христиан Гюйгенс и Иоганн Бернулли вывели уравнение в ответ на вызов Якоба Бернулли ; их решения были опубликованы в Acta Eruditorum за июнь 1691 года. Дэвид Грегори написал трактат о контактной сети в 1697 году. в котором он дал неправильный вывод правильного дифференциального уравнения.

Эйлер доказал в 1744 году, что цепная линия — это кривая, которая при вращении вокруг оси x дает поверхность с минимальной площадью поверхности ( катеноид ) для данных ограничивающих кругов. Николя Фусс в 1796 году дал уравнения, описывающие равновесие цепи под действием любой силы .

Перевернутая цепная арка

Цепные арки часто используются при строительстве печей . Чтобы создать желаемую кривую, форму подвесной цепи нужных размеров переносят в форму, которая затем используется в качестве ориентира для размещения кирпичей или другого строительного материала.

Арку Ворот в Сент-Луисе, штат Миссури , США, иногда называют (перевернутой) цепной линией, но это неверно. Это близко к более общей кривой, называемой сплющенной цепной линией, с уравнением y = A cosh( Bx ) , которая является цепной цепью, если AB = 1 . В то время как цепная связь является идеальной формой для отдельно стоящей арки постоянной толщины, Арка Ворот уже ближе к вершине. Согласно Национальный исторический памятник номинации арки в номинации « США», вместо этого она представляет собой « взвешенную цепную связь ». Ее форма соответствует форме, которую могла бы образовать утяжеленная цепь, имеющая более легкие звенья посередине.

• 
  Цепная линия арки под крышей , Гауди Дома Мила работы Барселона , Испания.
• 
  окружен Зимний сад Шеффилда серией цепных арок .
• 
  Арка Ворот ( Сент-Луис, Миссури ) представляет собой сплющенную контактную сеть.
• 
  Строящаяся печь с цепной аркой поверх временной формы

Цепные мосты

Простые подвесные мосты по сути представляют собой утолщенные тросы и следуют по цепной линии.

Напряженные ленточные мосты , такие как мост Леонеля Виера в Мальдонадо, Уругвай , также следуют по цепной линии с кабелями, встроенными в жесткое настил.

В свободно висящих цепях прилагаемая сила одинакова по длине цепи, поэтому цепь следует цепной кривой. То же самое относится и к простому подвесному мосту или «цепному мосту», где проезжая часть следует за тросом.

Напряженный ленточный мост представляет собой более сложную конструкцию с такой же цепной формой.

Однако в подвесном мосту с подвесной проезжей частью цепи или тросы выдерживают вес моста и поэтому не висят свободно. В большинстве случаев проезжая часть плоская, поэтому, когда вес кабеля пренебрежимо мал по сравнению с поддерживаемым весом, прикладываемая сила однородна по отношению к горизонтальному расстоянию, и результатом является парабола , как обсуждается ниже (хотя термин « контактная сеть» часто до сих пор используется в неформальном смысле). Если кабель тяжелый, то результирующая кривая находится между цепной линией и параболой.

Сравнение цепной арки (черная пунктирная кривая) и параболической арки (красная сплошная кривая) с одинаковым пролетом и провисанием. Цепная сеть представляет собой профиль простого подвесного моста или трос подвесного подвесного моста, на котором его настил и подвески имеют пренебрежимо малый вес по сравнению с его тросом. Парабола представляет собой профиль троса висячего моста, на котором его трос и подвески имеют пренебрежимо малый вес по сравнению с его палубой. Профиль троса реального подвесного моста с одинаковым пролетом и провисанием лежит между двумя кривыми. Уравнения цепной связи и параболы соответственно: $y={\text{cosh }}x$ и $y=x^{2}[({\text{cosh }}1)-1]+1$

Закрепление морских объектов

Тяжелая якорная цепь образует контактную сеть с небольшим углом натяжения якоря.

Цепная связь, создаваемая силой тяжести, дает преимущество тяжелым якорным канатам . Якорная тяга (или якорный канат) обычно состоит из цепи или троса, или того и другого. Якорные тросы используются на кораблях, нефтяных вышках, доках, плавучих ветряных турбинах и другом морском оборудовании, которое необходимо закрепить на морском дне.

Когда веревка провисает, кривая цепной линии представляет собой меньший угол натяжения якоря или швартовочного устройства, чем это было бы в случае, если бы она была почти прямой. Это повышает эффективность якоря и повышает уровень силы, которой он будет сопротивляться перед перетаскиванием. Для сохранения формы цепной цепи при наличии ветра необходима тяжелая цепь, так что на этот эффект могут рассчитывать только более крупные корабли, находящиеся на большей глубине. Лодки меньшего размера также полагаются на контактную сеть для поддержания максимальной удерживающей силы.

Канатные паромы и цепные лодки представляют собой особый случай морских транспортных средств, движущихся, хотя они и пришвартованы двумя контактными сетями, каждый из которых состоит из одного или нескольких тросов (тросов или цепей), проходящих через транспортное средство и перемещаемых моторизованными шкивами. Цепные линии можно оценить графически.

Математическое описание

Уравнение

Контактные сети для разных значений a

Уравнение контактной сети в декартовых координатах имеет вид

$$y=a\cosh \left({\frac {x}{a}}\right)={\frac {a}{2}}\left(e^{\frac {x}{a}}+e^{-{\frac {x}{a}}}\right),$$где cosh — функция гиперболического косинуса , и где a — расстояние до самой низкой точки над осью x. Все цепные кривые подобны друг другу, поскольку изменение параметра a эквивалентно равномерному масштабированию кривой.

Уравнение Уэвелла для контактной сети: $$\tan \varphi ={\frac {s}{a}},$$где $\varphi$ — тангенциальный угол , а — дуги длина .

Дифференциация дает $${\frac {d\varphi }{ds}}={\frac {\cos ^{2}\varphi }{a}},$$и устранение $\varphi$ дает уравнение Чезаро $$\kappa ={\frac {a}{s^{2}+a^{2}}},$$где $\kappa$ это кривизна .

радиус кривизны Тогда $$\rho =a\sec ^{2}\varphi ,$$что является длиной нормали между кривой и осью x .

Связь с другими кривыми

Когда парабола катится по прямой, кривая рулетки , очерченная ее фокусом, представляет собой цепную линию. Огибающая . директрисы линией параболы также является цепной Эвольвента является из вершины, то есть рулетка, прослеживаемая точкой, начинающейся в вершине, когда линия катится по цепной линии, трактрисой .

Другая рулетка, образованная путем перекатывания линии по цепной линии, является еще одной линией. Это означает, что квадратные колеса могут совершенно плавно катиться по дороге, состоящей из ряда неровностей в форме перевернутой цепной цепи. Колеса могут быть любым правильным многоугольником, кроме треугольника, но цепная связь должна иметь параметры, соответствующие форме и размерам колес.

Геометрические свойства

На любом горизонтальном интервале отношение площади под цепной линией к ее длине равно a независимо от выбранного интервала. Цепная линия — единственная плоская кривая, кроме горизонтальной линии, обладающая этим свойством. Кроме того, геометрический центр тяжести области под участком контактной сети является средней точкой перпендикулярного сегмента, соединяющего центр тяжести самой кривой и X. ось

Наука

Движущийся заряд в однородном электрическом поле движется по цепной линии (которая стремится к параболе, если скорость заряда много меньше скорости света с ).

Поверхность вращения с фиксированными радиусами на обоих концах и минимальной площадью поверхности представляет собой цепную линию, вращающуюся вокруг оси x .

Анализ

Модель цепей и арок

В математической модели цепь (или шнур, трос, веревка, веревка и т. д.) идеализируется, предполагая, что она настолько тонка, что ее можно рассматривать как кривую, и что она настолько гибка, что любая сила натяжения, оказываемая цепью параллелен цепи. Анализ кривой оптимальной арки аналогичен, за исключением того, что силы растяжения становятся силами сжатия , и все переворачивается. Основной принцип заключается в том, что цепь можно считать твердым телом, как только она достигнет равновесия. Уравнения, определяющие форму кривой и натяжение цепи в каждой точке, могут быть получены путем тщательного изучения различных сил, действующих на сегмент, используя тот факт, что эти силы должны находиться в равновесии, если цепь находится в статическом равновесии .

Пусть путь, по которому следует цепь, задан параметрически как r = ( x , y ) = ( x ( s ), y ( s )), где s представляет длину дуги , а r — вектор положения . Это естественная параметризация , обладающая тем свойством, что

$${\frac {d\mathbf {r} }{ds}}=\mathbf {u}$$

где u — единичный касательный вектор .

Схема сил, действующих на участок цепной линии от c до r . Силы — это натяжение T ₀ в точке c , натяжение T в точке r и вес цепи (0, − ws ) . Поскольку цепь покоится, сумма этих сил должна быть равна нулю.

кривой Дифференциальное уравнение можно вывести следующим образом. Пусть c — самая нижняя точка цепи, называемая вершиной цепной линии. Склон ⁠ dy / dx ⁠ кривой равна нулю в точке c, поскольку это точка минимума. Предположим, что r находится справа от c, поскольку другой случай подразумевается симметрией. Силы, действующие на участок цепи от c до r, — это натяжение цепи в точке c , натяжение цепи в точке r и вес цепи. Натяжение в точке c касается кривой в точке c и, следовательно, горизонтально без какой-либо вертикальной составляющей и тянет секцию влево, поэтому ее можно записать (− T ₀ , 0) , где T ₀ — величина силы. Натяжение в точке r параллельно кривой в точке r и тянет секцию вправо. Натяжение в точке r можно разделить на две составляющие, поэтому ее можно записать T u = ( T cos φ , T sin φ ) , где T величина силы, а φ — угол между кривой в точке r и x- — ось (см. Тангенциальный угол ). Наконец, вес цепи представлен как (0, − ws ), где w — вес на единицу длины, а s — длина сегмента цепи между c и r .

Цепь находится в равновесии, поэтому сумма трех сил равна 0 , следовательно

$$T\cos \varphi =T_{0}$$и $$T\sin \varphi =ws\,,$$

и деление этих дает

$${\frac {dy}{dx}}=\tan \varphi ={\frac {ws}{T_{0}}}\,.$$

Удобно писать

$$a={\frac {T_{0}}{w}}$$

которая представляет собой длину цепи, вес которой равен по величине натяжению в точке с . Затем

$${\frac {dy}{dx}}={\frac {s}{a}}$$

представляет собой уравнение, определяющее кривую.

Горизонтальная составляющая напряжения T cos φ = T ₀ является постоянной, а вертикальная составляющая напряжения T sin φ = ws пропорциональна длине цепи между r и вершиной.

Вывод уравнений кривой

Дифференциальное уравнение $dy/dx=s/a$, данное выше, можно решитьсоставить уравнения для кривой. Решим уравнение, используя граничное условие, котороевершина расположена в $s_{0}=0$ и $(x,y)=(x_{0},y_{0})$.

Сначала вызовите формулу для длина дуги получить $${\frac {ds}{dx}}={\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}={\sqrt {1+\left({\frac {s}{a}}\right)^{2}}}\,,$$затем отдельные переменные чтобы получить $${\frac {ds}{\sqrt {1+(s/a)^{2}}}}=dx\,.$$

Достаточно простой подход к интеграции заключается в использовании гиперболическая замена ,что дает $$a\sinh ^{-1}{\frac {s}{a}}+x_{0}=x$$(где $x_{0}$ – константа интегрирования ),и, следовательно, $${\frac {s}{a}}=\sinh {\frac {x-x_{0}}{a}}\,.$$

Но ${\textstyle s/a=dy/dx}$, так $${\frac {dy}{dx}}=\sinh {\frac {x-x_{0}}{a}}\,,$$который интегрируется как $$y=a\cosh {\frac {x-x_{0}}{a}}+\delta$$(с $\delta =y_{0}-a$ — константа интегрирования, удовлетворяющая граничному условию).

Поскольку основной интерес здесь представляет просто форма кривой,размещение осей координат произвольное;так что сделайте удобный выбор ${\textstyle x_{0}=0=\delta }$упростить результат до $$y=a\cosh {\frac {x}{a}}\quad \square$$

Для полноты картины $y\leftrightarrow s$ отношение может быть получено путемрешение каждого из $x\leftrightarrow y$ и $x\leftrightarrow s$ отношения для $x/a$, давая: $$\cosh ^{-1}{\frac {y-\delta }{a}}={\frac {x-x_{0}}{a}}=\sinh ^{-1}{\frac {s}{a}}\,,$$так $$y-\delta =a\cosh \left(\sinh ^{-1}{\frac {s}{a}}\right)\,,$$который можно переписать как $$y-\delta =a{\sqrt {1+\left({\frac {s}{a}}\right)^{2}}}={\sqrt {a^{2}+s^{2}}}\,.$$

Альтернативный вывод

Дифференциальное уравнение можно решить, используя другой подход. От

$$s=a\tan \varphi$$

отсюда следует, что

$${\frac {dx}{d\varphi }}={\frac {dx}{ds}}{\frac {ds}{d\varphi }}=\cos \varphi \cdot a\sec ^{2}\varphi =a\sec \varphi$$и $${\frac {dy}{d\varphi }}={\frac {dy}{ds}}{\frac {ds}{d\varphi }}=\sin \varphi \cdot a\sec ^{2}\varphi =a\tan \varphi \sec \varphi \,.$$

Интеграция дает,

$$x=a\ln(\sec \varphi +\tan \varphi )+\alpha$$и $$y=a\sec \varphi +\beta \,.$$

Как и раньше, оси x и y можно сместить, так что α и β можно принять равными 0. Тогда

$$\sec \varphi +\tan \varphi =e^{\frac {x}{a}}\,,$$и принимая взаимность обеих сторон $$\sec \varphi -\tan \varphi =e^{-{\frac {x}{a}}}\,.$$

Сложение и вычитание последних двух уравнений дает решение $$y=a\sec \varphi =a\cosh \left({\frac {x}{a}}\right)\,,$$и $$s=a\tan \varphi =a\sinh \left({\frac {x}{a}}\right)\,.$$

Определение параметров

Три контактные сети, проходящие через одни и те же две точки, в зависимости от горизонтальной силы T _H .

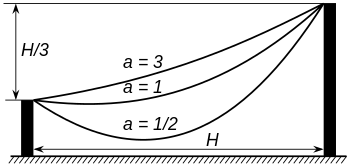
В общем случае параметр a — это положение оси. Уравнение в этом случае можно определить следующим образом:

При необходимости измените маркировку так, чтобы находилась _v слева от P2 _, и пусть H горизонтальное расстояние, а — вертикальное расстояние от P1 _P1 до P2 _— . Переведите оси так, чтобы вершина цепной линии лежала на оси y , а ее высота a была отрегулирована так, чтобы цепная связь удовлетворяла стандартному уравнению кривой.

$$y=a\cosh \left({\frac {x}{a}}\right)$$

и пусть координаты P ₁ и P ₂ будут ( x ₁ , y ₁ ) и ( x ₂ , y ₂ ) соответственно. Кривая проходит через эти точки, поэтому разница высот равна

$$v=a\cosh \left({\frac {x_{2}}{a}}\right)-a\cosh \left({\frac {x_{1}}{a}}\right)\,.$$

а длина кривой от P ₁ до P ₂ равна

$$L=a\sinh \left({\frac {x_{2}}{a}}\right)-a\sinh \left({\frac {x_{1}}{a}}\right)\,.$$

Когда Л ² − v ² расширяется с использованием этих выражений, результат:

$$L^{2}-v^{2}=2a^{2}\left(\cosh \left({\frac {x_{2}-x_{1}}{a}}\right)-1\right)=4a^{2}\sinh ^{2}\left({\frac {H}{2a}}\right)\,,$$так $${\frac {1}{H}}{\sqrt {L^{2}-v^{2}}}={\frac {2a}{H}}\sinh \left({\frac {H}{2a}}\right)\,.$$

Это трансцендентное уравнение относительно a и его необходимо решать численно . С $\sinh(x)/x$ строго монотонна на $x>0$, существует не более одного решения с a > 0 , следовательно, существует не более одного положения равновесия.

оба конца кривой ( P1 _что и P2 ₎ находятся на одном уровне ( y1 _{, если} = y2 _Однако ), можно показать, $$a={\frac {{\frac {1}{4}}L^{2}-h^{2}}{2h}}\,$$где L — общая длина кривой между P1 _P1 и P2 _, а h — прогиб (расстояние по вертикали между вершиной _и кривой ) _{, P2} .

Также можно показать, что $$L=2a\sinh {\frac {H}{2a}}\,$$и $$H=2a\operatorname {arcosh} {\frac {h+a}{a}}\,$$где H — горизонтальное расстояние между P ₁ и P ₂ , расположенными на одном уровне ( H = x ₂ − x ₁ ).

Горизонтальная тяговая сила при Р ₁ и Р ₂ равна Т ₀ = wa , где w — вес на единицу длины цепи или троса.

Напряженные отношения

Существует простая зависимость между натяжением кабеля в точке и его x и/или y координатой . Начнем с объединения квадратов векторных составляющих натяжения: $$(T\cos \varphi )^{2}+(T\sin \varphi )^{2}=T_{0}^{2}+(ws)^{2}$$который (напоминая, что $T_{0}=wa$) можно переписать как $${\begin{aligned}T^{2}(\cos ^{2}\varphi +\sin ^{2}\varphi )&=(wa)^{2}+(ws)^{2}\\[6pt]T^{2}&=w^{2}(a^{2}+s^{2})\\[6pt]T&=w{\sqrt {a^{2}+s^{2}}}\,.\end{aligned}}$$Но, как было показано выше , $y={\sqrt {a^{2}+s^{2}}}$ (предполагая, что $y_{0}=a$), поэтому мы получаем простые соотношения $$T=wy=wa\cosh {\frac {x}{a}}\,.$$

Вариационная формулировка

Рассмотрим цепочку длиной $L$ подвешивается в двух точках одинаковой высоты и на расстоянии $D$. Кривая должна минимизировать свою потенциальную энергию. $$U=\int _{0}^{D}wy{\sqrt {1+y'^{2}}}dx$$(где w — вес на единицу длины) и подчиняется ограничению $$\int _{0}^{D}{\sqrt {1+y'^{2}}}dx=L\,.$$

модифицированный лагранжиан Таким образом, $${\mathcal {L}}=(wy-\lambda ){\sqrt {1+y'^{2}}}$$где $\lambda$ – множитель Лагранжа, который необходимо определить. В качестве независимой переменной $x$ не появляется в лагранжиане, мы можем использовать тождество Бельтрами $${\mathcal {L}}-y'{\frac {\partial {\mathcal {L}}}{\partial y'}}=C$$где $C$ — константа интегрирования, чтобы получить первый интеграл $${\frac {(wy-\lambda )}{\sqrt {1+y'^{2}}}}=-C$$

Это обыкновенное дифференциальное уравнение первого порядка, которое можно решить методом разделения переменных . Его решением является обычный гиперболический косинус, параметры которого получены из ограничений.

Обобщения с вертикальной силой

Неоднородные цепи

Если плотность цепи является переменной, то приведенный выше анализ можно адаптировать для получения уравнений для кривой с учетом плотности или с учетом кривой для определения плотности.

Обозначим через w вес единицы длины цепи, тогда вес цепи имеет величину

$$\int _{\mathbf {c} }^{\mathbf {r} }w\,ds\,,$$

где пределы интегрирования — c и r . Балансирующие силы, как и в единой цепочке, производят

$$T\cos \varphi =T_{0}$$и $$T\sin \varphi =\int _{\mathbf {c} }^{\mathbf {r} }w\,ds\,,$$и поэтому $${\frac {dy}{dx}}=\tan \varphi ={\frac {1}{T_{0}}}\int _{\mathbf {c} }^{\mathbf {r} }w\,ds\,.$$

Тогда дифференцирование дает

$$w=T_{0}{\frac {d}{ds}}{\frac {dy}{dx}}={\frac {T_{0}{\dfrac {d^{2}y}{dx^{2}}}}{\sqrt {1+\left({\dfrac {dy}{dx}}\right)^{2}}}}\,.$$

С точки зрения φ и радиуса кривизны ρ это становится

$$w={\frac {T_{0}}{\rho \cos ^{2}\varphi }}\,.$$

Кривая подвесного моста

Мост Золотые Ворота . Большинство тросов подвесного моста следуют по параболической, а не по цепной линии, поскольку проезжая часть намного тяжелее троса.

Аналогичный анализ можно провести, чтобы найти кривую, по которой следует трос, поддерживающий подвесной мост с горизонтальной проезжей частью. Если вес проезжей части на единицу длины равен w и вес троса и троса, поддерживающего мост, по сравнению с ним пренебрежимо мал, то вес на тросе (см. рисунок в Контактной сети#Модель цепей и арок ) от с до r — это wx , где x — горизонтальное расстояние между c и r . Продолжая, как и раньше, получаем дифференциальное уравнение

$${\frac {dy}{dx}}=\tan \varphi ={\frac {w}{T_{0}}}x\,.$$

Это решается простым интегрированием, чтобы получить

$$y={\frac {w}{2T_{0}}}x^{2}+\beta$$

и поэтому кабель следует по параболе. Если вес кабеля и поддерживающих проводов незначителен, анализ становится более сложным.

Цепная связь равной силы

В контактной сети равной прочности трос усиливается по величине натяжения в каждой точке, поэтому его сопротивление разрыву постоянно по длине. Полагая, что прочность троса пропорциональна его плотности на единицу длины, можно записать вес w на единицу длины цепи: ⁠ T / c ⁠ , где c — константа, и можно применить анализ неоднородных цепей.

В этом случае уравнения для натяжения имеют вид

$${\begin{aligned}T\cos \varphi &=T_{0}\,,\\T\sin \varphi &={\frac {1}{c}}\int T\,ds\,.\end{aligned}}$$

Объединение дает

$$c\tan \varphi =\int \sec \varphi \,ds$$

и путем дифференцирования

$$c=\rho \cos \varphi$$

где ρ — радиус кривизны.

Решение этой проблемы

$$y=c\ln \left(\sec \left({\frac {x}{c}}\right)\right)\,.$$

В этом случае кривая имеет вертикальные асимптоты, и это ограничивает диапазон до π c . Другие отношения

$$x=c\varphi \,,\quad s=\ln \left(\tan \left({\frac {\pi +2\varphi }{4}}\right)\right)\,.$$

Кривая была изучена в 1826 году Дэвисом Гилбертом и, очевидно, независимо, Гаспаром-Гюставом Кориолисом в 1836 году.

Недавно было показано, что этот тип цепной линии может выступать в качестве строительного блока электромагнитной метаповерхности и был известен как «цепная цепь равного фазового градиента».

Эластичная контактная цепь

В эластичной контактной сети цепь заменена пружиной , которая может растягиваться в ответ на натяжение. Предполагается, что пружина растягивается в соответствии с законом Гука . В частности, если p — естественная длина секции пружины, то длина пружины с приложенным натяжением T имеет длину

$$s=\left(1+{\frac {T}{E}}\right)p\,,$$

где E — константа, равная kp , где k — жесткость пружины. В цепной цепи значение T является переменным, но соотношение остается действительным на локальном уровне, поэтому $${\frac {ds}{dp}}=1+{\frac {T}{E}}\,.$$Кривую, которой соответствует упругая пружина, теперь можно получить, используя тот же метод, что и для неупругой пружины.

Уравнения натяжения пружины имеют вид

$$T\cos \varphi =T_{0}\,,$$и $$T\sin \varphi =w_{0}p\,,$$

откуда

$${\frac {dy}{dx}}=\tan \varphi ={\frac {w_{0}p}{T_{0}}}\,,\quad T={\sqrt {T_{0}^{2}+w_{0}^{2}p^{2}}}\,,$$

где p — естественная длина отрезка от c до r , а w ₀ — вес на единицу длины пружины в ненапряженном состоянии. Писать $$a={\frac {T_{0}}{w_{0}}}$$так $${\frac {dy}{dx}}=\tan \varphi ={\frac {p}{a}}\quad {\text{and}}\quad T={\frac {T_{0}}{a}}{\sqrt {a^{2}+p^{2}}}\,.$$

Затем $${\begin{aligned}{\frac {dx}{ds}}&=\cos \varphi ={\frac {T_{0}}{T}}\\[6pt]{\frac {dy}{ds}}&=\sin \varphi ={\frac {w_{0}p}{T}}\,,\end{aligned}}$$откуда $${\begin{alignedat}{3}{\frac {dx}{dp}}&={\frac {T_{0}}{T}}{\frac {ds}{dp}}&&=T_{0}\left({\frac {1}{T}}+{\frac {1}{E}}\right)&&={\frac {a}{\sqrt {a^{2}+p^{2}}}}+{\frac {T_{0}}{E}}\\[6pt]{\frac {dy}{dp}}&={\frac {w_{0}p}{T}}{\frac {ds}{dp}}&&={\frac {T_{0}p}{a}}\left({\frac {1}{T}}+{\frac {1}{E}}\right)&&={\frac {p}{\sqrt {a^{2}+p^{2}}}}+{\frac {T_{0}p}{Ea}}\,.\end{alignedat}}$$

Интегрирование дает параметрические уравнения

$${\begin{aligned}x&=a\operatorname {arsinh} \left({\frac {p}{a}}\right)+{\frac {T_{0}}{E}}p+\alpha \,,\\[6pt]y&={\sqrt {a^{2}+p^{2}}}+{\frac {T_{0}}{2Ea}}p^{2}+\beta \,.\end{aligned}}$$

Опять же, оси x и y можно сместить, так что α и β можно принять равными 0. Итак,

$${\begin{aligned}x&=a\operatorname {arsinh} \left({\frac {p}{a}}\right)+{\frac {T_{0}}{E}}p\,,\\[6pt]y&={\sqrt {a^{2}+p^{2}}}+{\frac {T_{0}}{2Ea}}p^{2}\end{aligned}}$$

являются параметрическими уравнениями кривой. В жестком пределе , когда E велико, форма кривой сводится к форме неупругой цепи.

Другие обобщения

Цепь под общей силой

Не делая никаких предположений относительно силы G, действующей на цепь, можно провести следующий анализ.

Во-первых, пусть T = T ( s ) — сила натяжения как функция s . Цепь гибкая, поэтому она может прилагать силу только параллельно самой себе. Поскольку натяжение определяется как сила, которую цепь оказывает на себя, T должно быть параллельно цепи. Другими словами,

$$\mathbf {T} =T\mathbf {u} \,,$$

где T — величина T , а u — единичный касательный вектор.

Во-вторых, пусть G = G ( s ) — внешняя сила на единицу длины, действующая на небольшой участок цепи как функция s . Силы, действующие на отрезок цепи между s и s + Δ s, представляют собой силу натяжения T ( s + Δ s ) на одном конце отрезка, почти противоположную силу - T ( s ) на другом конце и внешняя сила, действующая на сегмент, равна примерно G Δ s . Эти силы должны уравновешиваться так

$$\mathbf {T} (s+\Delta s)-\mathbf {T} (s)+\mathbf {G} \Delta s\approx \mathbf {0} \,.$$

Разделите на Δ s и примите предел при Δ s → 0 , чтобы получить

$${\frac {d\mathbf {T} }{ds}}+\mathbf {G} =\mathbf {0} \,.$$

Эти уравнения можно использовать в качестве отправной точки при анализе гибкой цепи, действующей под действием любой внешней силы. В случае стандартной контактной сети G = (0, − w ) , где цепь имеет вес w на единицу длины.

См. также

• Цепная арка
• Цепочка-фонтан или самовыкачивающиеся бусины.
• Воздушная контактная сеть - линии электропередачи, подвешенные над железнодорожными или трамвайными транспортными средствами.
• Рулетка (кривая) – эллиптическая/гиперболическая цепная линия.
• Тропоскейн – форма скрученной веревки.
• Взвешенная контактная сеть

Библиография

• Локвуд, Э.Х. (1961). «Глава 13: Трактрикс и цепная линия» . Книга кривых . Кембридж.
• Салмон, Джордж (1879). Высшие плоские кривые . Ходжес, Фостер и Фиггис. стр. 287–289 .
• Раут, Эдвард Джон (1891). «Глава X: О струнах» . Трактат по аналитической статике . Университетское издательство.
• Маурер, Эдвард Роуз (1914). «Статья 26 Цепной кабель» . Техническая механика . Дж. Уайли и сыновья.
• Лэмб, сэр Гораций (1897). «Статья 134 Трансцендентных кривых; Цепная линия, Tractrix» . Элементарный курс исчисления бесконечно малых . Университетское издательство.
• Тодхантер, Исаак (1858). «XI Гибкие струны. Нерастяжимые, XII Гибкие струны. Растяжимые» . Трактат по аналитической статике . Макмиллан.
• Уэвелл, Уильям (1833). «Глава V: Равновесие гибкого тела» . Аналитическая статика . Дж. и Джей Джей Дейтон. п. 65.
• Вайсштейн, Эрик В. «Цепная линия» . Математический мир .

Дальнейшее чтение

• Свец, Фрэнк (1995). Учитесь у Мастеров . МАА. стр. 128–9. ISBN  978-0-88385-703-8 .
• Вентуроли, Джузеппе (1822). «Глава XXIII: О цепной линии» . Элементы теории механики . Пер. Дэниел Крессвелл. Дж. Николсон и сын.

Внешние ссылки

• О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Цепная линия» , Архив истории математики MacTutor , Университет Сент-Эндрюс
• Цепная линия в PlanetMath .
• Калькулятор контактной кривой
• Цепная линия в Центре геометрии
• «Цепная сеть» в Визуальном словаре специальных плоских кривых
• Цепная линия — цепи, арки и мыльная пленка.
• Калькулятор ошибки провисания кабеля – рассчитывает отклонение от прямой линии цепной линии и обеспечивает расчет калькулятора и справочных данных.
• Выведены динамические, а также статические уравнения столетней кривой. Выводятся уравнения, определяющие форму (статический случай), а также динамику (динамический случай) столетней годовщины. Решение обсуждаемых уравнений.
• Прямая линия, цепная линия, брахистохрона, круг и унифицированный подход Ферма к некоторым геодезическим.
• Ира Фриман «Общая форма контактной сети подвесного моста» Бюллетень AMS