Динамическая система

Эта статья посвящена общим аспектам динамических систем. Информацию о области исследования см. в разделе Теория динамических систем .

«Динамический» перенаправляется сюда. Чтобы узнать о других значениях, см. Динамический (значения) .

Аттрактор Лоренца возникает при исследовании осциллятора Лоренца — динамической системы.

В математике динамическая система — это система, в которой функция описывает временную зависимость точки в окружающем пространстве , например, в параметрической кривой . Примеры включают математические модели , описывающие раскачивание маятника часов , течение воды в трубе , случайное движение частиц в воздухе и количество рыбы каждую весну в озере . Самое общее определение объединяет несколько концепций математики, таких как обыкновенные дифференциальные уравнения и эргодическая теория, позволяя по-разному выбирать пространство и способы измерения времени. Время может измеряться целыми числами, действительными или комплексными числами или может быть более общим алгебраическим объектом, теряющим память о своем физическом происхождении, а пространство может быть многообразием или просто множеством , без необходимости гладкого пространства-времени. определенная на нем структура.

В любой момент времени динамическая система имеет состояние , представляющее точку в соответствующем пространстве состояний . Это состояние часто задается набором действительных чисел или вектором в геометрическом многообразии. Правило эволюции динамической системы — это функция, которая описывает, какие будущие состояния следуют из текущего состояния. Часто функция является детерминированной , то есть за заданный интервал времени из текущего состояния следует только одно будущее состояние. Однако некоторые системы являются стохастическими , поскольку случайные события также влияют на эволюцию переменных состояния.

В физике динамическая система описывается как «частица или ансамбль частиц, состояние которых меняется со временем и, таким образом, подчиняется дифференциальным уравнениям , включающим производные по времени». Чтобы сделать прогноз о будущем поведении системы, реализуется аналитическое решение таких уравнений или их интегрирование во времени посредством компьютерного моделирования.

Изучение динамических систем находится в центре внимания теории динамических систем , которая имеет приложения в самых разных областях, таких как математика, физика, биология , химия , инженерия , экономика , история и медицина . Динамические системы являются фундаментальной частью теории хаоса , динамики логистических карт , теории бифуркаций , процессов самосборки и самоорганизации , а также границы концепции хаоса .

Обзор

Понятие динамической системы берет свое начало в механике Ньютона . Здесь, как и в других естественных и инженерных дисциплинах, правило эволюции динамических систем представляет собой неявное соотношение, которое определяет состояние системы лишь на короткое время в будущем. (Отношение представляет собой либо дифференциальное уравнение , либо разностное уравнение , либо другую временную шкалу .) Чтобы определить состояние для всех будущих моментов времени, требуется многократная итерация соотношения — каждое продвижение вперед представляет собой небольшой шаг. Итерационная процедура называется решением системы или интеграцией системы . Если систему можно решить, то, зная начальную точку, можно определить все ее будущие положения — набор точек, известный как траектория или орбита .

До появления компьютеров нахождение орбиты требовало сложных математических методов и могло быть выполнено только для небольшого класса динамических систем. Численные методы, реализованные на электронных вычислительных машинах, упростили задачу определения орбит динамической системы.

Для простых динамических систем часто достаточно знания траектории, но большинство динамических систем слишком сложны, чтобы их можно было понять с точки зрения отдельных траекторий. Трудности возникают потому, что:

• Исследуемые системы могут быть известны только приблизительно: параметры системы могут быть неизвестны точно или в уравнениях могут отсутствовать члены. Используемые приближения ставят под сомнение обоснованность или актуальность численных решений. Для решения этих вопросов при изучении динамических систем было введено несколько понятий устойчивости, таких как устойчивость по Ляпунову или структурная устойчивость . Устойчивость динамической системы предполагает наличие класса моделей или начальных условий, для которых траектории будут эквивалентны. Операция сравнения орбит для установления их эквивалентности меняется при различных понятиях устойчивости.
• Тип траектории может быть более важным, чем одна конкретная траектория. Некоторые траектории могут быть периодическими, тогда как другие могут проходить через множество различных состояний системы. Приложения часто требуют перечисления этих классов или поддержания системы в пределах одного класса. Классификация всех возможных траекторий привела к качественному изучению динамических систем, то есть свойств, не изменяющихся при изменении координат. Линейные динамические системы и системы, имеющие два числа, описывающие состояние, являются примерами динамических систем, в которых понимаются возможные классы орбит.
• Поведение траекторий как функция параметра может быть тем, что необходимо для приложения. При изменении параметра динамические системы могут иметь точки бифуркации , в которых меняется качественное поведение динамической системы. Например, он может перейти от периодических движений к явно беспорядочному поведению, как при переходе к турбулентности жидкости .
• Траектории системы могут показаться беспорядочными, как бы случайными. В этих случаях может оказаться необходимым вычислить средние значения, используя одну очень длинную траекторию или множество различных траекторий. Средние значения хорошо определены для эргодических систем , а более детальное понимание было разработано для гиперболических систем . Понимание вероятностных аспектов динамических систем помогло заложить основы статистической механики и хаоса .

История

Многие считают французского математика Анри Пуанкаре . основателем динамических систем Пуанкаре опубликовал две ставшие классическими монографии: «Новые методы небесной механики» (1892–1899) и «Лекции по небесной механике» (1905–1910). В них он успешно применил результаты своих исследований к задаче о движении трех тел и подробно изучил поведение решений (частоту, устойчивость, асимптотику и т. д.). В число этих работ входила теорема о возврате Пуанкаре , которая утверждает, что некоторые системы через достаточно долгое, но конечное время вернутся в состояние, очень близкое к исходному.

Александр Ляпунов разработал множество важных методов аппроксимации. Его методы, разработанные им в 1899 г., позволяют определять устойчивость систем обыкновенных дифференциальных уравнений. Он создал современную теорию устойчивости динамической системы.

В 1913 году Джордж Дэвид Биркгоф » Пуанкаре доказал « Последнюю геометрическую теорему , частный случай задачи трёх тел , результат, который принес ему мировую известность. В 1927 году он опубликовал свою работу «Динамические системы» . Самым устойчивым результатом Биркгофа стало открытие в 1931 году того, что сейчас называется эргодической теоремой . Объединив идеи физики об эргодической гипотезе с теорией меры , эта теорема решила, по крайней мере в принципе, фундаментальную проблему статистической механики . Эргодическая теорема также имела последствия для динамики.

Стивен Смейл также добился значительных успехов. Его первым вкладом стала подкова Смейла , которая положила начало значительным исследованиям в области динамических систем. Он также рассказал об исследовательской программе, проводимой многими другими.

Александр Николаевич Шарковский разработал теорему Шарковского о периодах дискретных динамических систем в 1964 году. Одним из следствий теоремы является то, что если дискретная динамическая система на действительной прямой имеет периодическую точку периода 3, то она должна иметь периодические точки каждого другой период.

В конце 20-го века взгляд на динамические системы уравнений в частных производных начал набирать популярность. Палестинский инженер-механик Али Х. Найфе применил нелинейную динамику в механических и инженерных системах. Его новаторские работы в области прикладной нелинейной динамики оказали влияние на строительство и обслуживание машин и конструкций , которые используются в повседневной жизни, таких как корабли , краны , мосты , здания , небоскребы , реактивные двигатели , ракетные двигатели , самолеты и космические корабли .

Формальное определение

В самом общем смысле, динамическая система — это набор ( T , X , Φ), где T — моноид , записанный аддитивно, X — непустое множество , а Φ — функция

$\Phi :U\subseteq (T\times X)\to X$

с

$\mathrm {proj} _{2}(U)=X$ (где $\mathrm {proj} _{2}$ это вторая карта проекции )

и для любого x в X :

$\Phi (0,x)=x$

$\Phi (t_{2},\Phi (t_{1},x))=\Phi (t_{2}+t_{1},x),$

для $\,t_{1},\,t_{2}+t_{1}\in I(x)$ и $\ t_{2}\in I(\Phi (t_{1},x))$, где мы определили множество $I(x):=\{t\in T:(t,x)\in U\}$ для любого x в X .

В частности, в случае, когда $U=T\times X$ у нас есть для каждого x в X, что $I(x)=T$ определяет моноидное действие T и, таким образом, Φ на X .

Функция Φ( t , x ) называется функцией эволюции динамической системы: она ставит в соответствие каждой точке x множества X уникальный образ, зависящий от переменной t , называемый параметром эволюции . X называется фазовым пространством или пространством состояний , а переменная x представляет начальное состояние системы.

Мы часто пишем

$\Phi _{x}(t)\equiv \Phi (t,x)$

$\Phi ^{t}(x)\equiv \Phi (t,x)$

если мы примем одну из переменных постоянной. Функция

$\Phi _{x}:I(x)\to X$

называется потоком через x , а его график называется траекторией через x . Набор

$\gamma _{x}\equiv \{\Phi (t,x):t\in I(x)\}$

называется орбитой через x .Орбита через x — это образ потока через x .Подмножество S пространства состояний X называется Φ- инвариантным , если для всех x в S и всех t в T

$\Phi (t,x)\in S.$

Таким образом, в частности, если S Φ- инвариантно , $I(x)=T$ для x в S. всех То есть поток через x должен быть определен на все времена для каждого S. элемента

Чаще всего существует два класса определений динамической системы: одно основано на обыкновенных дифференциальных уравнениях и имеет геометрический характер; а другой мотивирован эргодической теорией и по своей сути является теоретической мерой .

Геометрическое определение

В геометрическом определении динамическая система — это набор $\langle {\mathcal {T}},{\mathcal {M}},f\rangle$. ${\mathcal {T}}$ это область времени – есть много вариантов, обычно действительные или целые числа, возможно, ограниченные неотрицательными числами. ${\mathcal {M}}$ является многообразием , т.е. локально банаховым пространством или евклидовым пространством, или в дискретном случае графом . f — правило эволюции t → f  ^т (с $t\in {\mathcal {T}}$) такой, что f ^т является диффеоморфизмом многообразия в себя. Итак, f — «гладкое» отображение временной области. ${\mathcal {T}}$ в пространство диффеоморфизмов многообразия на себя. Другими словами, f ( t ) является диффеоморфизмом для каждого времени t в области ${\mathcal {T}}$ .

Реальная динамическая система

Реальная динамическая система , динамическая система реального времени , с непрерывным временем динамическая система или поток — это кортеж ( T , M , Φ), где T — многообразие открытый интервал в действительных числах R , M — , локально диффеоморфное банаховому пространству , и Φ — непрерывная функция . Если Ф непрерывно дифференцируема, мы говорим, что система является дифференцируемой динамической системой . Если многообразие M локально диффеоморфно R ^н , динамическая система конечномерна ; в противном случае динамическая система бесконечномерна . Это не предполагает симплектической структуры . Когда T считается действительным, динамическая система называется глобальной или потоковой ; и если T ограничено неотрицательными действительными числами, то динамическая система является полупотоком .

Дискретная динамическая система

Дискретная динамическая система , с дискретным временем динамическая система — это набор ( T , M , Φ), где M — многообразие, локально диффеоморфное банаховому пространству , а Φ — функция. Когда T принимается за целые числа, это каскад или карта . Если T ограничено целыми неотрицательными числами, мы называем систему полукаскадом .

Клеточный автомат

Клеточный автомат — это кортеж ( T , M , Φ), где T целых — это решетка чисел или многомерная целочисленная сетка , M — это набор функций из целочисленной решетки (опять же, с одним или несколькими измерениями) до конечное множество и Φ (локально определенная) эволюционная функция. Таким образом, клеточные автоматы являются динамическими системами. Решетка в M представляет собой решетку «пространства», а решетка в T представляет решетку «времени».

Многомерное обобщение

Динамические системы обычно определяются по одной независимой переменной, называемой временем. Более общий класс систем определяется по множеству независимых переменных и поэтому называется многомерными системами . Такие системы полезны для моделирования, например, обработки изображений .

Компактификация динамической системы.

Учитывая глобальную динамическую систему ( R , X , Φ ) на локально компактном и хаусдорфовом топологическом пространстве X , часто бывает полезно изучить непрерывное расширение Φ* Φ до одноточечной компактификации X* пространства X . Хотя мы теряем дифференциальную структуру исходной системы, теперь мы можем использовать аргументы компактности для анализа новой системы ( R , X* , Φ*).

В компактных динамических системах предельное множество любой орбиты непусто , компактно и односвязно .

Теоретическое определение меры

Основная статья: Динамическая система, сохраняющая меру

Динамическую систему можно формально определить как сохраняющее меру преобразование пространства с мерой , тройку ( T , ( X , Σ, µ ), Φ). Здесь T — моноид (обычно неотрицательные целые числа), X — множество , а ( X , Σ, µ ) — вероятностное пространство , что означает, что Σ — сигма-алгебра на X , а µ — конечная мера на X. ( Икс , Σ). Отображение Φ: X → X называется Σ-измеримым тогда и только тогда, когда для любого σ из Σ выполнено $\Phi ^{-1}\sigma \in \Sigma$. Говорят, что отображение Φ сохраняет меру тогда и только тогда, когда для любого σ из Σ выполнено $\mu (\Phi ^{-1}\sigma )=\mu (\sigma )$. Объединяя вышесказанное, отображение Φ называется сохраняющим меру преобразованием X , если оно является отображением X в себя, оно Σ-измеримо и сохраняет меру. Тройка ( T , ( X , Σ, µ ), Φ) для такого Φ тогда определяется как динамическая система .

Отображение Φ воплощает временную эволюцию динамической системы. Таким образом, для дискретных динамических систем итерации $\Phi ^{n}=\Phi \circ \Phi \circ \dots \circ \Phi$ для каждого целого числа n изучаются. Для непрерывных динамических систем отображение Φ понимается как отображение эволюции за конечное время, и его конструкция усложняется.

Связь с геометрическим определением

Теоретическое определение меры предполагает существование преобразования, сохраняющего меру. С любым правилом эволюции может быть связано множество различных инвариантных мер. Если динамическая система задана системой дифференциальных уравнений, необходимо определить соответствующую меру. Это затрудняет разработку эргодической теории, начиная с дифференциальных уравнений, поэтому становится удобным иметь в эргодической теории определение, мотивированное динамическими системами, которое обходит выбор меры и предполагает, что выбор уже сделан. Простая конструкция (иногда называемая теоремой Крылова–Боголюбова ) показывает, что для большого класса систем всегда можно построить меру так, чтобы правило эволюции динамической системы стало преобразованием, сохраняющим меру. При построении заданная мера пространства состояний суммируется для всех будущих точек траектории, обеспечивая инвариантность.

Некоторые системы имеют естественную меру, такую ​​как мера Лиувилля в гамильтоновых системах , выбранную среди других инвариантных мер, таких как меры, поддерживаемые на периодических орбитах гамильтоновой системы. Для хаотических диссипативных систем выбор инвариантной меры технически более сложен. Меру необходимо поддерживать на аттракторе , но аттракторы имеют нулевую меру Лебега , а инвариантные меры должны быть сингулярными относительно меры Лебега. Небольшая область фазового пространства сжимается во времени.

Для гиперболических динамических систем меры Синая–Рюэля–Боуэна кажутся естественным выбором. Они построены на геометрической структуре устойчивых и неустойчивых многообразий динамической системы; они физически ведут себя при малых возмущениях; и они объясняют многие из наблюдаемых статистических данных гиперболических систем.

Построение динамических систем

Концепция эволюции во времени занимает центральное место в теории динамических систем, как было показано в предыдущих разделах: основная причина этого факта заключается в том, что исходной мотивацией теории было изучение поведения классических механических систем во времени . Но прежде чем система обыкновенных дифференциальных уравнений станет динамической системой, ее необходимо решить. Например, рассмотрим задачу начального значения, такую ​​как следующая:

${\dot {\boldsymbol {x}}}={\boldsymbol {v}}(t,{\boldsymbol {x}})$

${\boldsymbol {x}}|_{t=0}={\boldsymbol {x}}_{0}$

где

• ${\dot {\boldsymbol {x}}}$ представляет скорость материальной точки x
• M — конечномерное многообразие
• v : T × M → TM — векторное поле в R ^н или С ^н и представляет собой изменение скорости, вызванное известными силами, действующими на данную материальную точку в фазовом пространстве M . Изменение не является вектором в фазовом пространстве M , а находится в касательном пространстве TM .

В уравнении нет необходимости ни в производных более высокого порядка, ни в параметре t в v ( t , x ), поскольку их можно устранить, рассматривая системы более высоких размерностей.

В зависимости от свойств этого векторного поля механическая система называется

• автономный , когда v ( т , x ) = v ( x )
• однородный , когда v ( t , 0 ) = 0 для всех t

Решение может быть найдено с использованием стандартных методов ОДУ и обозначается как уже введенная выше функция эволюции.

${\boldsymbol {x}}(t)=\Phi (t,{\boldsymbol {x}}_{0})$

Тогда динамическая система — это ( T , M , Φ).

Некоторые формальные манипуляции с системой дифференциальных уравнений, показанные выше, дают более общую форму уравнений, которой должна удовлетворять динамическая система.

${\dot {\boldsymbol {x}}}-{\boldsymbol {v}}(t,{\boldsymbol {x}})=0\qquad \Leftrightarrow \qquad {\mathfrak {G}}\left(t,\Phi (t,{\boldsymbol {x}}_{0})\right)=0$

где ${\mathfrak {G}}:{{(T\times M)}^{M}}\to \mathbf {C}$ – функционал от множества эволюционных функций к полю комплексных чисел.

Это уравнение полезно при моделировании механических систем со сложными ограничениями.

Многие концепции динамических систем могут быть распространены на бесконечномерные многообразия — те, которые являются локально банаховыми пространствами — и в этом случае дифференциальные уравнения являются уравнениями в частных производных .

Примеры

• Карта кошек Арнольда
• Карта Бейкера является примером хаотического кусочно-линейного отображения .
• Бильярд и внешний бильярд
• Динамика прыгающего мяча
• Круговая карта
• Комплексный квадратичный полином
• Двойной маятник
• Диадическая трансформация
• Карта Хенона
• Иррациональное вращение
• Карта Каплана – Йорка
• Список хаотичных карт
• система Лоренца
• Система моделирования квадратичных карт
• Карта Рёсслера
• Качающаяся машина Этвуда
• Карта палаток

Линейные динамические системы

Основная статья: Линейная динамическая система

Линейные динамические системы можно решать с точки зрения простых функций и поведения всех классифицированных орбит. В линейной системе фазовое пространство представляет собой N -мерное евклидово пространство, поэтому любая точка фазового пространства может быть представлена ​​вектором с N числами. Анализ линейных систем возможен, поскольку они удовлетворяют принципу суперпозиции : если u ( t ) и w ( t ) удовлетворяют дифференциальному уравнению для векторного поля (но не обязательно начальному условию), то то же самое будет и с u ( t ) + w ( т ).

Потоки

Для потока векторное поле v( x ) является аффинной функцией положения в фазовом пространстве, т.е.

${\dot {x}}=v(x)=Ax+b,$

где A — матрица, b — вектор чисел, а x — вектор положения. Решение этой системы можно найти, используя принцип суперпозиции (линейности).Случай b ≠ 0 с A = 0 представляет собой просто прямую линию в направлении b :

$\Phi ^{t}(x_{1})=x_{1}+bt.$

Когда b равно нулю и A ≠ 0, начало координат является равновесной (или особой) точкой потока, т. е. если x ₀ = 0, то орбита остается там.Для других начальных условий уравнение движения задается экспонентой матрицы : для начальной точки x ₀ ,

$\Phi ^{t}(x_{0})=e^{tA}x_{0}.$

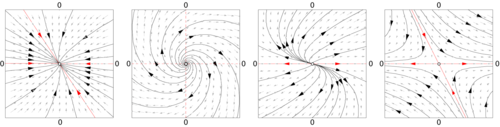
Когда b = 0, определяют структуру собственные значения A фазового пространства. По собственным значениям и собственным векторам можно A определить, будет ли начальная точка сходиться или расходиться к точке равновесия в начале координат.

Расстояние между двумя различными начальными условиями в случае A ≠ 0 в большинстве случаев будет меняться экспоненциально, либо экспоненциально быстро сходясь к точке, либо экспоненциально быстро расходясь. В случае дивергенции линейные системы демонстрируют чувствительную зависимость от начальных условий. Для нелинейных систем это одно из (необходимых, но не достаточных) условий хаотического поведения .

Линейные векторные поля и несколько траекторий.

Карты

дискретным временем динамическая система с Аффинная имеет форму матричного разностного уравнения :

$x_{n+1}=Ax_{n}+b,$

где A — матрица, а b — вектор. Как и в непрерывном случае, замена координат x → x + (1 − A )  ^–1 b удаляет член b из уравнения. В новой системе координат начало координат — фиксированная точка карты, а решения — линейной системы A.  ^н х ₀ .Решениями для карты больше не являются кривые, а точки, прыгающие в фазовом пространстве. Орбиты организованы в виде кривых или волокон, которые представляют собой наборы точек, которые преобразуются сами в себя под действием карты.

Как и в непрерывном случае, собственные значения и собственные векторы A определяют структуру фазового пространства. Например, если u ₁ является собственным вектором A с вещественным собственным значением меньше единицы, то прямые линии, заданные точками вдоль α   u ₁ , с α ∈ R , являются инвариантной кривой отображения. Точки этой прямой линии сходятся в фиксированную точку.

Существует также множество других дискретных динамических систем .

Локальная динамика

Качественные свойства динамических систем не изменяются при плавном изменении координат (иногда это принимают за определение качественных): особая точка векторного поля (точка, где v ( x ) = 0) останется особой точкой при плавных преобразованиях; периодическая орбита представляет собой петлю в фазовом пространстве, и плавные деформации фазового пространства не могут изменить ее статус петли. Именно в окрестности особых точек и периодических орбит можно хорошо понять структуру фазового пространства динамической системы. При качественном исследовании динамических систем подход заключается в том, чтобы показать, что происходит изменение координат (обычно неуказанное, но вычислимое), которое делает динамическую систему максимально простой.

Исправление

Течение в большинстве небольших участков фазового пространства можно сделать очень простым. Если y — это точка, где векторное поле v ( y ) ≠ 0, то происходит изменение координат области вокруг y , где векторное поле становится серией параллельных векторов одной и той же величины. Это известно как теорема о выпрямлении.

Теорема о выпрямлении гласит, что вдали от особых точек динамика точки на небольшом участке представляет собой прямую линию. Иногда патч можно увеличить, сшивая несколько патчей вместе, и когда это получается во всем фазовом пространстве M, динамическая система становится интегрируемой . В большинстве случаев патч не может быть распространен на все фазовое пространство. В векторном поле могут быть особые точки (где v ( x ) = 0); или пятна могут становиться все меньше и меньше по мере приближения к какой-то точке. Более тонкая причина — глобальное ограничение, при котором траектория начинается с одного участка и после посещения ряда других участков возвращается к исходному. Если в следующий раз орбита обойдет фазовое пространство другим образом, то выпрямить векторное поле во всей серии патчей будет невозможно.

Близкие периодические орбиты

Вообще говоря, в окрестности периодической орбиты теорему о выпрямлении применить нельзя. Пуанкаре разработал подход, который превращает анализ вблизи периодической орбиты в анализ карты. Выберите точку x ₀ на орбите γ и рассмотрите точки фазового пространства в этой окрестности, перпендикулярные v ( x ₀ ). Эти точки представляют собой сечение Пуанкаре S ( γ , x ₀ ) орбиты. Теперь поток определяет карту Пуанкаре F : S → S для точек, начинающихся в S и возвращающихся в S . Не всем этим точкам потребуется одинаковое количество времени, чтобы вернуться, но время будет близко к времени, которое требуется x ₀ .

Пересечение периодической орбиты с сечением Пуанкаре является неподвижной точкой отображения F. Пуанкаре Путем перевода можно предположить, что точка находится в точке x = 0. Ряд Тейлора карты равен F ( x ) = J · x + O( x ² изменение координат h ), поэтому можно ожидать, что приведет только к упрощению F до его линейной части

$h^{-1}\circ F\circ h(x)=J\cdot x.$

Это известно как уравнение сопряжения. Поиск условий выполнения этого уравнения был одной из основных задач исследования динамических систем. Пуанкаре впервые подошел к этому, предположив, что все функции аналитичны, и в процессе обнаружил нерезонансное условие. Если λ ₁ , ..., λ _ν являются собственными значениями J , они будут резонансными, если одно собственное значение представляет собой целочисленную линейную комбинацию двух или более других. Поскольку члены формы λ _i – Σ (кратные другим собственным значениям) встречаются в знаменателе членов функции h , нерезонансное условие также известно как проблема малого делителя.

Результаты конъюгации

Результаты о существовании решения уравнения сопряжения зависят от собственных значений J степени гладкости и требуемой от h . Поскольку J не обязательно должен иметь какие-либо особые симметрии, его собственные значения обычно будут комплексными числами. Когда собственные значения J не находятся в единичном круге, динамика вблизи неподвижной точки x0 _{функции} F , а когда собственные значения находятся на единичном круге и являются называется гиперболической комплексными, динамика называется эллиптической .

В гиперболическом случае теорема Хартмана–Гробмана дает условия существования непрерывной функции, отображающей окрестность неподвижной точки отображения в линейное отображение J · x . Гиперболический случай также структурно устойчив . Небольшие изменения в векторном поле приведут лишь к небольшим изменениям в карте Пуанкаре, и эти небольшие изменения отразятся на небольших изменениях положения собственных значений J в комплексной плоскости, подразумевая, что карта по-прежнему является гиперболической.

Теорема Колмогорова -Арнольда-Мозера (КАМ) дает поведение вблизи эллиптической точки.

Теория бифуркации

Основная статья: Теория бифуркации

Когда карта эволюции Φ ^т (или векторное поле, из которого оно получено) зависит от параметра ц, структура фазового пространства также будет зависеть от этого параметра. Небольшие изменения могут не привести к качественным изменениям в фазовом пространстве до тех пор, пока не будет достигнуто особое значение µ ₀ . В этот момент фазовое пространство качественно меняется, и говорят, что динамическая система претерпела бифуркацию.

Теория бифуркаций рассматривает структуру в фазовом пространстве (обычно фиксированную точку , периодическую орбиту или инвариантный тор ) и изучает ее поведение в зависимости от параметра μ . В точке бифуркации структура может изменить свою устойчивость, распасться на новые структуры или слиться с другими структурами. Используя аппроксимации карт рядами Тейлора и понимание различий, которые можно устранить заменой координат, можно каталогизировать бифуркации динамических систем.

Бифуркации гиперболической неподвижной точки x ₀ семейства систем F _µ можно охарактеризовать собственными значениями первой производной системы DF _µ ( x ₀ ), вычисленными в точке бифуркации. Для отображения бифуркация произойдет, когда найдутся собственные значения DF _μ на единичной окружности . Для потока это произойдет при наличии собственных значений на мнимой оси. Дополнительную информацию можно найти в основной статье по теории бифуркаций .

Некоторые бифуркации могут привести к очень сложным структурам в фазовом пространстве. Например, сценарий Рюэля-Такенса описывает, как периодическая орбита разветвляется на тор, а тор - на странный аттрактор . В другом примере удвоение периода Фейгенбаума описывает, как устойчивая периодическая орбита проходит через серию бифуркаций удвоения периода .

Эргодические системы

Основная статья: Эргодическая теория

Во многих динамических системах можно выбрать координаты системы так, чтобы объем (на самом деле ν-мерный объем) в фазовом пространстве был инвариантным. Это происходит с механическими системами, полученными на основе законов Ньютона, если координатами являются положение и импульс, а объем измеряется в единицах (положение) × (импульс). Поток переводит точки подмножества A в точки Φ  ^т ( A ) и инвариантность фазового пространства означает, что

$\mathrm {vol} (A)=\mathrm {vol} (\Phi ^{t}(A)).$

В гамильтоновом формализме по координате можно получить соответствующий (обобщенный) импульс такой, что соответствующий объем сохраняется потоком. Говорят, что объем вычисляется по мере Лиувилля .

В гамильтоновой системе не все возможные конфигурации положения и импульса могут быть достигнуты из начальных условий. Из-за сохранения энергии доступны только состояния с той же энергией, что и начальное состояние. Состояния с одинаковой энергией образуют энергетическую оболочку Ω — подмногообразие фазового пространства. Объем энергетической оболочки, рассчитанный с помощью меры Лиувилля, сохраняется при эволюции.

Для систем, в которых объем сохраняется потоком, Пуанкаре открыл теорему о возврате : предположим, что фазовое пространство имеет конечный объем Лиувилля, и пусть F — отображение, сохраняющее объем фазового пространства, а A — подмножество фазового пространства. Тогда почти каждая точка А возвращается в А. бесконечно часто Теорема о возврате Пуанкаре была использована Цермело, чтобы возразить против вывода Больцмана об увеличении энтропии в динамической системе сталкивающихся атомов.

Одним из вопросов, поднятых в работе Больцмана, было возможное равенство между средними по времени и средними по пространству, то, что он назвал эргодической гипотезой . Гипотеза утверждает, что продолжительность времени, которое типичная траектория проводит в регионе A, равна vol( A )/vol(Ω).

Эргодическая гипотеза оказалась не существенным свойством, необходимым для развития статистической механики , и был введен ряд других эргодических свойств, чтобы охватить соответствующие аспекты физических систем. Купман подошел к изучению эргодических систем с помощью функционального анализа . Наблюдаемая a — это функция, которая каждой точке фазового пространства сопоставляет число (скажем, мгновенное давление или среднюю высоту). Значение наблюдаемой можно вычислить в другое время, используя функцию эволюции φ ^т . Это вводит оператор U  ^т , оператор трансфера ,

$(U^{t}a)(x)=a(\Phi ^{-t}(x)).$

Изучая спектральные свойства линейного оператора U, становится возможным классифицировать эргодические свойства Φ  ^т . При использовании подхода Купмана к рассмотрению действия потока на наблюдаемую функцию решается конечномерная нелинейная задача, включающая Φ  ^т преобразуется в бесконечномерную линейную задачу, включающую U .

Мера Лиувилля, ограниченная энергетической поверхностью Ω, является основой для средних значений, вычисляемых в равновесной статистической механике . Среднее значение по времени по траектории эквивалентно среднему значению в пространстве, вычисленному с помощью фактора Больцмана exp(−β H ) . Эта идея была обобщена Синаем, Боуэном и Рюэлем (SRB) на более широкий класс динамических систем, включающий диссипативные системы. Меры SRB заменяют фактор Больцмана и определяются на аттракторах хаотических систем.

Нелинейные динамические системы и хаос

Основная статья: Теория хаоса

Простые нелинейные динамические системы и даже кусочно-линейные системы могут демонстрировать совершенно непредсказуемое поведение, которое может показаться случайным, несмотря на то, что они принципиально детерминированы. Это, казалось бы, непредсказуемое поведение было названо хаосом . Гиперболические системы — это точно определенные динамические системы, обладающие свойствами, приписываемыми хаотическим системам. В гиперболических системах касательное пространство, перпендикулярное траектории, можно хорошо разделить на две части: одну с точками, сходящимися к орбите ( стабильное многообразие ), и другую с точками, расходящимися от орбиты ( неустойчивое многообразие ).

Этот раздел математики занимается долгосрочным качественным поведением динамических систем. Здесь основное внимание уделяется не поиску точных решений уравнений, определяющих динамическую систему (что часто безнадежно), а, скорее, ответам на такие вопросы, как «Установится ли система в устойчивое состояние в долгосрочной перспективе, и если да, то что?» возможные аттракторы ?» или «Зависит ли долгосрочное поведение системы от ее начального состояния?»

Проблема не в хаотичном поведении сложных систем. Уже много лет известно, что метеорология характеризуется сложным и даже хаотичным поведением. Теория хаоса оказалась настолько удивительной, потому что хаос можно обнаружить внутри почти тривиальных систем. представляет Логистическая карта собой всего лишь полином второй степени; отображение подковы кусочно-линейно.

Решения конечной длительности.

Для нелинейных автономных ОДУ при некоторых условиях возможно разработать решения конечной длительности: Здесь имеется в виду, что в силу своей собственной динамики система достигнет нулевого значения в конечный момент времени и после этого останется в этом нулевом значении навсегда. Эти решения конечной длительности не могут быть аналитическими функциями на всей вещественной прямой, и поскольку они не являются липшицевыми функциями в момент окончания, они не являются уникальными решениями дифференциальных уравнений Липшица.

Например, уравнение:

$y'=-{\text{sgn}}(y){\sqrt {|y|}},\,\,y(0)=1$

Допускает решение конечной длительности:

$y(x)={\frac {1}{4}}\left(1-{\frac {x}{2}}+\left|1-{\frac {x}{2}}\right|\right)^{2}$

См. также

• Поведенческое моделирование
• Когнитивное моделирование
• Сложная динамика
• Динамический подход к развитию второго языка
• Пассивация обратной связи
• Бесконечные композиции аналитических функций
• Список тем динамических систем
• Колебания
• Люди в системах и управлении
• Теорема Шарковского
• Фундаментальная теорема Конли о динамических системах
• Системная динамика
• Теория систем
• Принцип максимального калибра

Ссылки

• Арнольд, Владимир И. (2006). «Основные понятия». Обыкновенные дифференциальные уравнения . Берлин: Springer Verlag. ISBN  3-540-34563-9 .
• Чуешов И.Д. Введение в теорию бесконечномерных диссипативных систем . онлайн-версия первого издания на сайте ЭМИС [1] .
• Темам, Роджер (1997) [1988]. Бесконечномерные динамические системы в механике и физике . Спрингер Верлаг.

Дальнейшее чтение

Работы, обеспечивающие широкий охват:

• Ральф Абрахам и Джеррольд Э. Марсден (1978). Основы механики . Бенджамин-Каммингс. ISBN  978-0-8053-0102-1 . (доступно в виде перепечатки: ISBN   0-201-40840-6 )
• Энциклопедия математических наук ( ISSN   0938-0396 ) имеет подсерию по динамическим системам с обзорами текущих исследований.
• Кристиан Бонатти; Лоренцо Х. Диас; Марсело Виана (2005). Динамика за пределами однородной гиперболичности: глобальная геометрическая и вероятностная перспектива . Спрингер. ISBN  978-3-540-22066-4 .
• Стивен Смейл (1967). «Дифференцируемые динамические системы» . Бюллетень Американского математического общества . 73 (6): 747–817. дои : 10.1090/S0002-9904-1967-11798-1 .

Вводные тексты с уникальной точки зрения:

• В.И. Арнольд (1982). Математические методы классической механики . Спрингер-Верлаг. ISBN  978-0-387-96890-2 .
• Джейкоб Палис и Веллингтон де Мело (1982). Геометрическая теория динамических систем: введение . Спрингер-Верлаг. ISBN  978-0-387-90668-3 .
• Дэвид Рюэль (1989). Элементы дифференцируемой динамики и теории бифуркаций . Академическая пресса. ISBN  978-0-12-601710-6 .
• Тим Бедфорд, Майкл Кин и Кэролайн Ряд, ред. (1991). Эргодическая теория, символическая динамика и гиперболические пространства . Издательство Оксфордского университета. ISBN  978-0-19-853390-0 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
• Ральф Х. Абрахам и Кристофер Д. Шоу (1992). Динамика — геометрия поведения, 2-е изд . Аддисон-Уэсли. ISBN  978-0-201-56716-8 .

Учебники

• Кэтлин Т. Аллигуд, Тим Д. Зауэр и Джеймс А. Йорк (2000). Хаос. Введение в динамические системы . Спрингер Верлаг. ISBN  978-0-387-94677-1 .
• Одед Галор (2011). Дискретные динамические системы . Спрингер. ISBN  978-3-642-07185-0 .
• Моррис В. Хирш , Стивен Смейл и Роберт Л. Девани (2003). Дифференциальные уравнения, динамические системы и введение в хаос . Академическая пресса. ISBN  978-0-12-349703-1 .
• Анатоль Каток; Борис Хассельблатт (1996). Введение в современную теорию динамических систем . Кембридж. ISBN  978-0-521-57557-7 .
• Стивен Линч (2010). Динамические системы с приложениями, использующими Maple, 2-е изд . Спрингер. ISBN  978-0-8176-4389-8 .
• Стивен Линч (2014). Динамические системы с приложениями, использующими MATLAB, 2-е издание . Международное издательство Спрингер. ISBN  978-3319068190 .
• Стивен Линч (2017). Динамические системы с приложениями с использованием Mathematica, 2-е изд . Спрингер. ISBN  978-3-319-61485-4 .
• Стивен Линч (2018). Динамические системы с приложениями, использующими Python . Международное издательство Спрингер. ISBN  978-3-319-78145-7 .
• Джеймс Мейсс (2007). Дифференциальные динамические системы . СИАМ. ISBN  978-0-89871-635-1 .
• Дэвид Д. Нолти (2015). Введение в современную динамику: хаос, сети, пространство и время . Издательство Оксфордского университета. ISBN  978-0199657032 .
• Жюльен Клинтон Спротт (2003). Хаос и анализ временных рядов . Издательство Оксфордского университета. ISBN  978-0-19-850839-7 .
• Стивен Х. Строгац (1994). Нелинейная динамика и хаос: с приложениями к физике, биологии, химии и технике . Эддисон Уэсли. ISBN  978-0-201-54344-5 .
• Тешль, Джеральд (2012). Обыкновенные дифференциальные уравнения и динамические системы . Провиденс : Американское математическое общество . ISBN  978-0-8218-8328-0 .
• Стивен Виггинс (2003). Введение в прикладные динамические системы и хаос . Спрингер. ISBN  978-0-387-00177-7 .

Популяризации:

• Флорин Диаку и Филип Холмс (1996). Небесные встречи . Принстон. ISBN  978-0-691-02743-2 .
• Джеймс Глейк (1988). Хаос: создание новой науки . Пингвин. ISBN  978-0-14-009250-9 .
• Ивар Экеланд (1990). Математика и неожиданное (Мягкая обложка) . Издательство Чикагского университета. ISBN  978-0-226-19990-0 .
• Ян Стюарт (1997). Играет ли Бог в кости? Новая математика хаоса . Пингвин. ISBN  978-0-14-025602-4 .

Внешние ссылки

• Сервер препринтов Arxiv ежедневно отправляет (не рецензируемые) рукописи в динамические системы.
• Энциклопедия динамических систем. Часть Scholarpedia — рецензируемая и написанная приглашенными экспертами.
• Нелинейная динамика . Модели бифуркации и хаоса Элмера Г. Винса
• Sci.Nonlinear FAQ 2.0 (сентябрь 2003 г.) содержит определения, объяснения и ресурсы, связанные с нелинейной наукой.

Онлайн-книги или конспекты лекций

• Геометрическая теория динамических систем . Конспекты лекций Нильса Берглунда для курса ETH на продвинутом уровне бакалавриата.
• Динамические системы . В книге Джорджа Д. Биркгофа 1927 года уже используется современный подход к динамическим системам.
• Хаос: классический и квантовый . Введение в динамические системы с точки зрения периодической орбиты.
• Изучение динамических систем . Учебное пособие по изучению динамических систем.
• Обыкновенные дифференциальные уравнения и динамические системы . Конспекты лекций Джеральда Тешля

Исследовательские группы

• Группа динамических систем Гронингена , IWI, Гронингенский университет.
• Хаос @ UMD . Концентрируется на приложениях динамических систем.
• [2] , SUNY Стоуни-Брук. Списки конференций, исследователей и некоторых открытых проблем.
• Центр динамики и геометрии , штат Пенсильвания.
• Управление и динамические системы , Калифорнийский технологический институт.
• Лаборатория нелинейных систем Федеральной политехнической школы Лозанны (EPFL).
• Центр динамических систем Бременского университета
• Группа системного анализа, моделирования и прогнозирования , Оксфордский университет
• Группа нелинейной динамики , Высший технический институт, Технический университет Лиссабона
• Динамические системы. Архивировано 2 июня 2017 г. в Wayback Machine , IMPA, Национальный институт чистой и прикладной математики.
• Рабочая группа по нелинейной динамике. Архивировано 21 января 2015 г. в Wayback Machine , Институт компьютерных наук Чешской академии наук.
• Группа динамических систем UPC Барселона , Политехнический университет Каталонии.
• Центр управления, динамических систем и вычислений , Калифорнийский университет, Санта-Барбара.