Шестиугольная плитка порядка 4

Шестиугольная плитка порядка 4
Модель диска Пуанкаре гиперболической плоскости
Тип	Гиперболическая регулярная мозаика
Конфигурация вершин	6 ⁴
Символ Шлефли	{6,4}
Символ Витхоффа	4 \| 6 2
Диаграмма Кокстера
Группа симметрии	[6,4], (*642)
Двойной	Укладка плитки порядка 6 квадратов
Характеристики	Вершинно-транзитивный , реберно-транзитивный , грани-транзитивный

В геометрии представляет шестиугольная мозаика четвертого порядка собой правильную мозаику гиперболической плоскости . Он имеет символ Шлефли {6,4}.

Симметрия

Эта мозаика представляет собой гиперболический калейдоскоп из 6 зеркал, определяющих фундаментальную область правильного шестиугольника. Эта симметрия в обозначениях орбифолда называется * 222222 с 6 зеркальными пересечениями второго порядка. В обозначениях Кокстера их можно представить в виде [6 ^*,4], сняв два зеркала из трёх (проходя через центр шестиугольника). Добавление биссектрисы через 2 вершины шестиугольной фундаментальной области определяет трапецоэдрическую симметрию *4422 . Добавление трех зеркал пополам через вершины определяет симметрию *443 . Добавление трех зеркал пополам по краю определяет симметрию *3222 . Добавление всех 6 биссектрис приводит к полной симметрии *642 .

*222222	*443	*3222	*642

Равномерные раскраски

существует семь различных однородных раскрасок Для шестиугольной мозаики четвертого порядка . Они подобны семи однородным раскраскам квадратной мозаики , но исключают два случая с вращательной симметрией второго порядка. Четыре из них имеют светоотражающие конструкции и диаграммы Кокстера , а три — подкрашены.

Однородные конструкции 6.6.6.6
	1 цвет	2 цвета	3 и 2 цвета		4, 3 и 2 цвета
Униформа Раскраска	(1111)	(1212)	(1213)	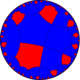(1113)	(1234)	(1123)	(1122)
Симметрия	[6,4] ( *642 )	[6,6] ( *662 ) =	[(6,6,3)] = [6,6,1 ⁺] ( *663 ) =		[1 ⁺,6,6,1 ⁺] ( *3333 ) = =
Символ	{6,4}	г{6,6} = {6,4} ¹/ ₂	г(6,3,6) = г{6,6} ¹/ ₂		г{6,6} ¹/ ₄
Коксетер диаграмма		=	=		= =

Обычные карты

Обычную карту {6,4} ₃ или {6,4} _(4,0) можно рассматривать как 4-раскраску на мозаике {6,4}. Он также имеет представление в виде петриального октаэдра {3,4}. ^$п$, абстрактный многогранник с вершинами и ребрами октаэдра , но вместо этого соединенный четырьмя гранями многоугольника Петри .

Связанные многогранники и мозаика

Это замощение топологически связано как часть последовательности правильных замощений с шестиугольными гранями, начиная с шестиугольного замощения , с символом Шлефли {6,n} и диаграммой Кокстера. , стремясь к бесконечности.

* n 62 мутация симметрии правильных мозаик: {6, n } v т и
Spherical	Euclidean	Hyperbolic tilings
{6,2}	{6,3}	{6,4}	{6,5}	{6,6}	{6,7}	{6,8}	...	{6,∞}

Это замощение также топологически связано как часть последовательности правильных многогранников и замощений с четырьмя гранями на вершину, начиная с октаэдра , с символом Шлефли {n, 4} и диаграммой Коксетера. , где n стремится к бесконечности.

* n 42 мутация симметрии регулярных мозаик: { n ,4} v т и
Spherical		Euclidean	Hyperbolic tilings

2⁴	3⁴	4⁴	5⁴	6⁴	7⁴	8⁴	...∞⁴

Мутация симметрии квазирегулярных мозаик: 6.n.6.n v т и
Symmetry *6n2 [n,6]	Euclidean	Compact hyperbolic					Paracompact	Noncompact
Symmetry *6n2 [n,6]	*632 [3,6]	*642 [4,6]	*652 [5,6]	*662 [6,6]	*762 [7,6]	*862 [8,6]...	*∞62 [∞,6]	[iπ/λ,6]
Quasiregular figures configuration	6.3.6.3	6.4.6.4	6.5.6.5	6.6.6.6	6.7.6.7	6.8.6.8	6.∞.6.∞	6.∞.6.∞
Dual figures
Rhombic figures configuration	V6.3.6.3	V6.4.6.4	V6.5.6.5	V6.6.6.6	V6.7.6.7	V6.8.6.8	V6.∞.6.∞

Однородные тетрагексагональные мозаики v т и
*Symmetry: [6,4], (642)** (with [6,6] (662), [(4,3,3)] (443) , [∞,3,∞] (3222) index 2 subsymmetries) (And [(∞,3,∞,3)] (3232) index 4 subsymmetry)
= = =	=	= = =	=	= = =	=

{6,4}	t{6,4}	r{6,4}	t{4,6}	{4,6}	rr{6,4}	tr{6,4}
Uniform duals


V6⁴	V4.12.12	V(4.6)²	V6.8.8	V4⁶	V4.4.4.6	V4.8.12
Alternations
[1⁺,6,4] (*443)	[6⁺,4] (6*2)	[6,1⁺,4] (*3222)	[6,4⁺] (4*3)	[6,4,1⁺] (*662)	[(6,4,2⁺)] (2*32)	[6,4]⁺ (642)
=	=	=	=	=	=

h{6,4}	s{6,4}	hr{6,4}	s{4,6}	h{4,6}	hrr{6,4}	sr{6,4}

Равномерные шестиугольные мозаики v т и
Symmetry: [6,6], (*662)
= =	= =	= =	= =	= =	= =	= =

{6,6} = h{4,6}	t{6,6} = h₂{4,6}	r{6,6} {6,4}	t{6,6} = h₂{4,6}	{6,6} = h{4,6}	rr{6,6} r{6,4}	tr{6,6} t{6,4}
Uniform duals


V6⁶	V6.12.12	V6.6.6.6	V6.12.12	V6⁶	V4.6.4.6	V4.12.12
Alternations
[1⁺,6,6] (*663)	[6⁺,6] (6*3)	[6,1⁺,6] (*3232)	[6,6⁺] (6*3)	[6,6,1⁺] (*663)	[(6,6,2⁺)] (2*33)	[6,6]⁺ (662)
=		=		=


h{6,6}	s{6,6}	hr{6,6}	s{6,6}	h{6,6}	hrr{6,6}	sr{6,6}

Подобные мозаики H2 в симметрии *3232 v т и
Coxeter diagrams


Vertex figure	6⁶	(3.4.3.4)²	3.4.6.6.4	6.4.6.4
Image
Dual

Однородные мозаики по симметрии *3222 v т и
6⁴	6.6.4.4	(3.4.4)²	4.3.4.3.3.3
6.6.4.4	6.4.4.4	3.4.4.4.4
(3.4.4)²	3.4.4.4.4	4⁶

См. также

Ссылки

Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
«Глава 10: Правильные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе . Дуврские публикации. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .

Внешние ссылки