5-клеточный

5-клеточный
(4-симплекс)
5-клеточный ; (4-симплекс)
	Диаграмма Шлегеля ; (вершины и ребра)
Тип	Выпуклый правильный 4-многогранник
Символ Шлефли	{3,3,3}
Диаграмма Кокстера
Клетки	5 {3,3}
Лица	10 {3}
Края	10
Вершины	5
Вершинная фигура	; ( тетраэдр )
Полигон Петри	пятиугольник
Группа Коксетера	A 4 , [3,3,3]
Двойной	Самодвойственный
Характеристики	выпуклый , изогональный , изотоксальный , изоэдральный
Единый индекс	1

3D-проекция 5-клеточного элемента, выполняющего простое вращение.

В геометрии — 5-ячейка это выпуклый 4-многогранник с символом Шлефли {3,3,3}. Это 5-вершинный четырехмерный объект, ограниченный пятью тетраэдрическими ячейками. ^[а] Он также известен C5 _, . пентахорон как ^[1] пентатоп , пентаэдроид , ^[2] или четырехгранная пирамида . Это 4- симплекс (Коксетера). $\alpha _{4}$ многогранник), ^[3] простейший выпуклый 4-мерный многогранник, аналог тетраэдра в трех измерениях и треугольника в двух измерениях. 5-ячеечная представляет собой 4-мерную пирамиду с четырехгранным основанием и четырьмя тетраэдрическими сторонами.

Правильная 5-ячейка ограничена пятью правильными тетраэдрами и является одним из шести правильных выпуклых 4-многогранников (четырехмерных аналогов Платоновых тел ). Правильную пятиклетку можно построить из правильного тетраэдра, добавив пятую вершину, расположенную на расстоянии одной ребра от всех вершин тетраэдра. Это невозможно сделать в трехмерном пространстве. Обычная 5-ячеечная клетка — это решение проблемы: сделайте 10 равносторонних треугольников одинакового размера, используя 10 спичек, где каждая сторона каждого треугольника представляет собой ровно одну спичку, и ни один из треугольников и спичек не пересекается друг с другом. В трех измерениях решения не существует.

Альтернативные названия

Пентахорон (5-точечный 4-многогранник)
Гипертетраэдр (4-мерный аналог тетраэдра )
4-симплекс (4-мерный симплекс )
Тетраэдрическая пирамида (4-мерная гиперпирамида с тетраэдрическим основанием)
Пентатоп
Пентаэдроид (Генри Паркер Мэннинг)
Ручка (Джонатан Бауэрс: для пентахорона) ^[4]

Геометрия

5-ячейка — это 4-мерный симплекс , простейший возможный 4-многогранник . По существу, он является первым в последовательности из 6 выпуклых правильных 4-многогранников (в порядке размера и сложности). ^[б]

Правильные выпуклые 4-многогранники
Symmetry group	A₄	B₄		F₄	H₄
Name	5-cell Hyper-tetrahedron 5-point	16-cell Hyper-octahedron 8-point	8-cell Hyper-cube 16-point	24-cell 24-point	600-cell Hyper-icosahedron 120-point	120-cell Hyper-dodecahedron 600-point
Schläfli symbol	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Coxeter mirrors
Mirror dihedrals	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/4⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/4⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/4⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/5⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/5⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠
Graph
Vertices	5 tetrahedral	8 octahedral	16 tetrahedral	24 cubical	120 icosahedral	600 tetrahedral
Edges	10 triangular	24 square	32 triangular	96 triangular	720 pentagonal	1200 triangular
Faces	10 triangles	32 triangles	24 squares	96 triangles	1200 triangles	720 pentagons
Cells	5 tetrahedra	16 tetrahedra	8 cubes	24 octahedra	600 tetrahedra	120 dodecahedra
Tori	1 5-tetrahedron	2 8-tetrahedron	2 4-cube	4 6-octahedron	20 30-tetrahedron	12 10-dodecahedron
Inscribed	120 in 120-cell	675 in 120-cell	2 16-cells	3 8-cells	25 24-cells	10 600-cells
Great polygons		2 squares x 3	4 rectangles x 4	4 hexagons x 4	12 decagons x 6	100 irregular hexagons x 4
Petrie polygons	1 pentagon x 2	1 octagon x 3	2 octagons x 4	2 dodecagons x 4	4 30-gons x 6	20 30-gons x 4
Long radius	$1$	$1$	$1$	$1$	$1$	$1$
Edge length	${\sqrt {\tfrac {5}{2}}}\approx 1.581$	${\sqrt {2}}\approx 1.414$	$1$	$1$	${\tfrac {1}{\phi }}\approx 0.618$	${\tfrac {1}{\phi ^{2}{\sqrt {2}}}}\approx 0.270$
Short radius	${\tfrac {1}{4}}$	${\tfrac {1}{2}}$	${\tfrac {1}{2}}$	${\sqrt {\tfrac {1}{2}}}\approx 0.707$	${\sqrt {\tfrac {\phi ^{4}}{8}}}\approx 0.926$	${\sqrt {\tfrac {\phi ^{4}}{8}}}\approx 0.926$
Area	$10\left({\tfrac {5{\sqrt {3}}}{8}}\right)\approx 10.825$	$32\left({\sqrt {\tfrac {3}{4}}}\right)\approx 27.713$	$24$	$96\left({\sqrt {\tfrac {3}{16}}}\right)\approx 41.569$	$1200\left({\tfrac {\sqrt {3}}{4\phi ^{2}}}\right)\approx 198.48$	$720\left({\tfrac {\sqrt {25+10{\sqrt {5}}}}{8\phi ^{4}}}\right)\approx 90.366$
Volume	$5\left({\tfrac {5{\sqrt {5}}}{24}}\right)\approx 2.329$	$16\left({\tfrac {1}{3}}\right)\approx 5.333$	$8$	$24\left({\tfrac {\sqrt {2}}{3}}\right)\approx 11.314$	$600\left({\tfrac {\sqrt {2}}{12\phi ^{3}}}\right)\approx 16.693$	$120\left({\tfrac {15+7{\sqrt {5}}}{4\phi ^{6}{\sqrt {8}}}}\right)\approx 18.118$
4-Content	${\tfrac {\sqrt {5}}{24}}\left({\tfrac {\sqrt {5}}{2}}\right)^{4}\approx 0.146$	${\tfrac {2}{3}}\approx 0.667$	$1$	$2$	${\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 3.863$	${\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 4.193$

5-ячейка образована любыми пятью точками, не все из которых находятся в одной гиперплоскости (как тетраэдр образован любыми четырьмя точками, не все из которых находятся в одной плоскости, а треугольник образован любыми тремя точками, не все из которых находятся в одной плоскости). в той же строке). Любые такие пять точек составляют 5-ячейку, хотя обычно это не обычная 5-ячейка. Правильный с 600 вершинами представляет 5-клеточный не встречается ни в одном из других правильных выпуклых 4-клеток, кроме одного: 120-клеточный собой соединение 120 правильных 5-клеточных. ^[с]

Структура

Когда сеть из пяти тетраэдров складывается в 4-мерном пространстве так, что каждый тетраэдр связан гранями с четырьмя другими, в результате получается 5-ячейка, имеющая в общей сложности 5 вершин, 10 ребер и 10 граней. В каждой вершине сходятся четыре ребра, а на каждом ребре встречаются три тетраэдрические ячейки.

5-ячейка самодвойственна (как и все симплексы ), а ее вершинная фигура — тетраэдр . ^[и] Ее максимальное пересечение с трехмерным пространством — треугольная призма . Его двугранный угол равен cos ⁻¹( ⁠ 1/4 . ⁠ ) , или примерно 75,52°

Выпуклая оболочка двух 5-клеток в двойной конфигурации представляет собой дисфеноидальную 30-клетку , двойственную усеченной 5-клетке .

В качестве конфигурации

Эта матрица конфигурации представляет собой 5-ячеечную структуру. Строки и столбцы соответствуют вершинам, ребрам, граням и ячейкам. Диагональные числа говорят, сколько каждого элемента встречается во всей 5-клетке. Недиагональные числа показывают, сколько элементов столбца встречается в элементе строки или рядом с ним. Матрица этого самодвойственного многогранника идентична его повороту на 180 градусов. ^[7] - грани k можно читать как строки слева от диагонали, а k -цифры читаются как строки после диагонали. ^[8]

к -лицо	ж _к	ж ₀	ж ₁	f_f2	f ₃	к -инжир
( )	ж ₀	5	4	6	4	{3,3}
{ }	ж ₁	2	10	3	3	{3}
{3}	f_f2	3	3	10	2	{ }
{3,3}	f ₃	4	6	4	5	( )

Все эти элементы 5-клетки перечислены в Грюнбаума Бранко пятиточечной диаграмме Венна , которая буквально является иллюстрацией правильной 5-клетки в проекции на плоскость.

Координаты

Простейший набор декартовых координат : (2,0,0,0), (0,2,0,0), (0,0,2,0), (0,0,0,2), (𝜙 ,𝜙,𝜙,𝜙), с длиной ребра 2 √ 2 , где 𝜙 — золотое сечение . ^[9] Хотя эти координаты не сосредоточены в центре начала координат, вычитание $(1,1,1,1)/(2-{\tfrac {1}{\phi }})$ 4-многогранника из каждого переводит центр описанной окружности в начало координат с радиусом $2(\phi -1/(2-{\tfrac {1}{\phi }}))={\sqrt {\tfrac {16}{5}}}\approx 1.7888$ , со следующими координатами:

\left({\tfrac {2}{\phi }}-3,1,1,1\right)/({\tfrac {1}{\phi }}-2)

\left(1,{\tfrac {2}{\phi }}-3,1,1\right)/({\tfrac {1}{\phi }}-2)

\left(1,1,{\tfrac {2}{\phi }}-3,1\right)/({\tfrac {1}{\phi }}-2)

\left(1,1,1,{\tfrac {2}{\phi }}-3\right)/({\tfrac {1}{\phi }}-2)

\left({\tfrac {2}{\phi }},{\tfrac {2}{\phi }},{\tfrac {2}{\phi }},{\tfrac {2}{\phi }}\right)/({\tfrac {1}{\phi }}-2)

Следующий набор координат с центром в начале координат с тем же радиусом и длиной ребра, что и выше, можно рассматривать как гиперпирамиду с правильным тетраэдрическим основанием в трехмерном пространстве:

\left(1,1,1,{\frac {-1}{\sqrt {5}}}\right)

\left(1,-1,-1,{\frac {-1}{\sqrt {5}}}\right)

\left(-1,1,-1,{\frac {-1}{\sqrt {5}}}\right)

\left(-1,-1,1,{\frac {-1}{\sqrt {5}}}\right)

\left(0,0,0,{\frac {4}{\sqrt {5}}}\right)

Масштабирование этих или предыдущего набора координат путем ${\tfrac {\sqrt {5}}{4}}$ дать единичным радиусом , центрированными в начале координат, с длинами ребер регулярные 5 ячеек с ${\sqrt {\tfrac {5}{2}}}$ . Гиперпирамида имеет координаты:

\left({\sqrt {5}},{\sqrt {5}},{\sqrt {5}},-1\right)/4

\left({\sqrt {5}},-{\sqrt {5}},-{\sqrt {5}},-1\right)/4

\left(-{\sqrt {5}},{\sqrt {5}},-{\sqrt {5}},-1\right)/4

\left(-{\sqrt {5}},-{\sqrt {5}},{\sqrt {5}},-1\right)/4

\left(0,0,0,1\right)

Координаты вершин другой правильной 5-ячейки с центром в начале координат с длиной ребра 2 и радиусом ${\sqrt {\tfrac {8}{5}}}\approx 1.265$ являются:

\left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)

\left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {-2}{\sqrt {3}}},\ 0\right)

\left({\frac {1}{\sqrt {10}}},\ -{\sqrt {\frac {3}{2}}},\ 0,\ 0\right)

\left(-2{\sqrt {\frac {2}{5}}},\ 0,\ 0,\ 0\right)

Масштабируя их по ${\sqrt {\tfrac {5}{8}}}$ к единичному радиусу и длине ребра ${\sqrt {\tfrac {5}{2}}}$ дает:

\left({\sqrt {3}},{\sqrt {5}},{\sqrt {10}},\pm {\sqrt {30}}\right)/(4{\sqrt {3}})

\left({\sqrt {3}},{\sqrt {5}},-{\sqrt {40}},0\right)/(4{\sqrt {3}})

\left({\sqrt {3}},-{\sqrt {45}},0,0\right)/(4{\sqrt {3}})

\left(-1,0,0,0\right)

Вершины 4-симплекса (с ребром √ 2 и радиусом 1) проще построить на гиперплоскости в 5-пространстве как (отдельные) перестановки (0,0,0,0,1) или (0, 1,1,1,1); в этих позициях это грань соответственно 5-ортоплекса или выпрямленного пентеракта .

Геодезические и вращения

Трехмерная проекция пятиклеточной ячейки, совершающей двойное вращение . ^[ф]

Пятиклетка имеет только центральные плоскости двуугольников, проходящие через вершины. Он имеет 10 центральных плоскостей двуугольников, где каждая пара вершин является ребром, а не осью 5-ячейки. ^[д] Каждая двуугольная плоскость ортогональна трем другим, но не ортогональна ни одной из них полностью. ^[час] Характерное изоклиническое вращение 5-клеточной клетки имеет в качестве пар инвариантных плоскостей эти 10-угольные плоскости и их полностью ортогональные центральные плоскости, которые представляют собой 0-угольные плоскости, не пересекающие ни одной 5-клеточной вершины.

Есть только два способа обойти 5 -клетку через все 5 вершин по 5 ребрам: ^[и] таким образом, существуют два дискретных расслоения Хопфа больших двуугольников 5-клетки. Каждое из двух расслоений соответствует паре изоклинических вращений влево-вправо, каждое из которых вращает все 5 вершин в контуре периода 5. 5-ячейка имеет только две различные изоклины периода 5 (эти окружности, проходящие через все 5 вершин), каждая из которая действует как единственная изоклина правого вращения и единственная изоклина левого вращения в двух разных расслоениях. ^[г]

Ниже изображена вращающаяся 5-ячейка со сдавленным четвертым измерением и отображена в цвете. изображен Тор Клиффорда в прямоугольной (оберточной) форме.

Визуализация 4D-вращений
Простое вращение в плоскости XY
Простое вращение в плоскости ZW
Двойное вращение в плоскостях XY и ZW с угловыми скоростями в соотношении 4:3.
Левое изоклиническое вращение
Правое изоклиническое вращение

Спираль Бурдейка – Кокстера

5-ячейку можно построить как спираль Бурдейка – Кокстера из пяти цепных тетраэдров, свернутых в 4-мерное кольцо. ^[10] 10 треугольных граней можно увидеть в двумерной сети внутри треугольной мозаики с шестью треугольниками вокруг каждой вершины, хотя сворачивание в 4 измерения приводит к совпадению ребер. Пурпурные края образуют правильный пятиугольник , который является многоугольником Петри 5-клеточного элемента. Синие края соединяют каждую вторую вершину, образуя пентаграмму , которая представляет собой многоугольник Клиффорда из 5 ячеек. Синие края пентаграммы — это хорды изоклины 5-клеток , круговой путь вращения ее вершин во время изоклинического вращения , также известного как смещение Клиффорда . ^[я]

Прогнозы

Плоскость Кокстера A ₄ проецирует 5-клетку в правильный пятиугольник и пентаграмму . А ₃ Проекция 5-клетки на плоскость Кокстера представляет собой проекцию квадратной пирамиды . А ₂ Проекция правильной пятиклеточной ячейки на плоскость Кокстера представляет собой проекцию треугольной бипирамиды (два тетраэдра, соединенных лицом к лицу) с двумя противоположными вершинами, расположенными по центру.

орфографические проекции
А _q Самолет Коксетера	A ₄	A_А3	A_А2
График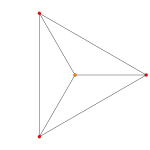
Двугранная симметрия	[5]	[4]	[3]

Проекции в 3 измерения
Проекция 5-ячейки в 3 измерения, первая из вершин, имеет тетраэдрическую оболочку проекции. Ближайшая вершина 5-клеток выступает к центру тетраэдра, как показано здесь красным. Самая дальняя ячейка выступает на саму оболочку тетраэдра, а остальные 4 ячейки проецируются на 4 уплощенные области тетраэдра, окружающие центральную вершину.	Проекция 5-клеточной ячейки в трех измерениях, направленная вперед, имеет треугольную дипирамидальную оболочку. Ближайший край (показанный здесь красным) выступает на ось дипирамиды, а три окружающие его ячейки образуют 3 тетраэдрических объема, расположенных вокруг этой оси под углом 120 градусов друг к другу. Остальные 2 ячейки выступают на две половины дипирамиды и находятся на дальней стороне пентатопа.
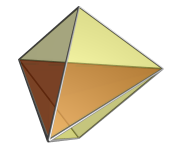Проекция 5-клеточной клетки в трех измерениях, обращенная лицом вперед, также имеет треугольную дипирамидальную оболочку. Ближайшее лицо показано здесь красным. Две ячейки, которые встречаются на этой грани, проецируются на две половины дипирамиды. Остальные три ячейки находятся на дальней стороне пентатопа с точки зрения 4D и для ясности вырезаны из изображения. Они располагаются вокруг центральной оси дипирамиды, как и в проекции «ребро вперед».	Проекция 5-клетки в трех измерениях, первая из ячеек, имеет тетраэдрическую оболочку. Ближайшая ячейка проецируется на всю оболочку и с точки зрения 4D закрывает остальные 4 ячейки; следовательно, они здесь не отображаются.

Неправильные 5-клеточные

В случае симплексов, таких как 5-клеточный, некоторые неправильные формы в некотором смысле более фундаментальны, чем правильная форма. Хотя обычные 5-клетки не могут заполнить 4-мерное пространство или правильные 4-многогранники, существуют неправильные 5-клетки, которые это делают. Эти характеристические 5-ячейки являются фундаментальными областями различных групп симметрии , которые порождают различные 4-многогранники.

Ортосхемы

— 4-ортосхема это 5-ячеечная структура, все 10 граней которой представляют собой прямоугольные треугольники . ^[а] Ортосхема , все ребра — неправильный симплекс , представляющий собой выпуклую оболочку дерева которого взаимно перпендикулярны. ^[Дж] В 4-мерной ортосхеме дерево состоит из четырех перпендикулярных ребер, соединяющих все пять вершин в линейном пути, совершающем три поворота под прямым углом. Элементы ортосхемы также являются ортосхемами (так же, как элементы правильного симплекса также являются правильными симплексами). Каждая тетраэдрическая ячейка 4-ортосхемы является 3-ортосхемой , а каждая треугольная грань — 2-ортосхемой (прямоугольный треугольник).

Ортосхемы являются характеристическими симплексами правильных многогранников, поскольку каждый правильный многогранник порождается отражениями в ограничивающих гранях его конкретной характеристической ортосхемы. ^[11] Например, частным случаем 4-ортосхемы с перпендикулярными ребрами одинаковой длины является характеристическая ортосхема 4-куба (также называемая тессерактом или 8-клеткой ), 4-мерный аналог 3-мерного куба. Если три перпендикулярных ребра 4-ортосхемы имеют единичную длину, то все ее ребра имеют длину √ 1 , √ 2 , √ 3 или √ 4 , что в точности соответствует длине хорды единичного 4-куба (длины Ребра 4-куба и его различные диагонали). Следовательно, эта 4-ортосхема вписывается в 4-куб, и 4-куб (как и любой правильный выпуклый многогранник) можно разобрать на экземпляры его характеристической ортосхемы .

3-ортосхему легко проиллюстрировать, но 4-ортосхему визуализировать труднее. 4-ортосхема – это тетраэдрическая пирамида, в основании которой находится 3-ортосхема. У нее на четыре ребра больше, чем у 3-ортосхемы, соединяющей четыре вершины основания с ее вершиной (пятая вершина 5-клетки). Выберите любую из трех ортосхем из шести, показанных на иллюстрации трех кубов. Обратите внимание, что он касается четырех из восьми вершин куба, и эти четыре вершины соединены трехреберным путем, который делает два поворота под прямым углом. Представьте, что эта 3-ортосхема является основанием 4-ортосхемы, так что из каждой из этих четырех вершин невидимое ребро 4-ортосхемы соединяется с пятой вершиной вершины (которая находится вне 3-куба и не появляется в кубе). иллюстрация вообще). Хотя все четыре дополнительных ребра достигают одной и той же вершины, все они будут иметь разную длину. Первый из них, на одном конце ортогонального пути с 3 ребрами, расширяет этот путь четвертым ортогональным √ 1 ребром, делая третий поворот на 90 градусов и достигая перпендикулярно четвертому измерению к вершине. Второе из четырех дополнительных ребер — это √ 2 диагонали грани куба (не иллюстрированного 3-куба, а другого из восьми 3-кубов тессеракта). ^[к] Третье дополнительное ребро представляет собой диагональ √ 3 3-куба (опять же, не исходного иллюстрированного 3-куба). Четвертое дополнительное ребро (на другом конце ортогонального пути) представляет собой длинный диаметр самого тессеракта длиной √ 4 . Он проходит через точный центр тессеракта к антиподальной вершине (вершине противоположного трехмерного куба), которая является вершиной. Таким образом, характеристическая 5-ячейка 4-куба имеет четыре ребра √ 1 , три ребра √ 2 , два ребра √ 3 и одно ребро √ 4 .

4-куб можно разбить на 24 таких 4-ортосхемы. восемью различными способами, с шестью 4-ортосхемами, окружающими каждый из четырех ортогональных √ 4 диаметров тессеракта. 4-куб также можно разделить на 384 меньших экземпляра той же самой характеристической 4-ортосхемы, только в одном направлении, с помощью всех его гиперплоскостей симметрии одновременно, которые делят его на 384 4-ортосхемы, которые все встречаются в центре 4-ортосхемы. -куб. ^[л]

В более общем смысле любой правильный многогранник можно разбить на g экземпляров его характеристической ортосхемы, которые все встречаются в центре правильного многогранника. ^[12] Число g - это порядок многогранника, количество отраженных экземпляров его характерной ортосхемы, составляющих многогранник, когда один экземпляр ортосхемы с зеркальной поверхностью отражается в своих собственных гранях. ^[м] В более общем смысле характеристические симплексы способны заполнять однородные многогранники, поскольку обладают всеми необходимыми элементами многогранника. Они также обладают всеми необходимыми углами между элементами (от 90 градусов и ниже). Характерные симплексы представляют собой генетические коды многогранников: подобно швейцарскому армейскому ножу , они содержат все необходимое для построения многогранника путем репликации.

Каждый правильный многогранник, в том числе правильный 5-клеточный, имеет свою характерную ортосхему. ^[н] Существует 4-ортосхема, которая является характерной 5-клеточной для обычной 5-клеточной . Это тетраэдрическая пирамида, основанная на характерном тетраэдре правильного тетраэдра . Обычный 5-клеточный можно разделить на 120 экземпляров этой характерной 4-ортосхемы. только одним способом, всеми гиперплоскостями симметрии одновременно, которые делят его на 120 4-ортосхем, которые все встречаются в центре обычной 5-клетки. ^[the]

Характеристики обычного 5-клеточного ^[16]
	край ^[17]	дуга		двугранный ^[18]
𝒍	${\sqrt {\tfrac {5}{2}}}\approx 1.581$	104°30′40″	$\pi -2{\text{𝜂}}$	75°29′20″	$\pi -2{\text{𝟁}}$

𝟀	${\sqrt {\tfrac {1}{10}}}\approx 0.316$	75°29′20″	$2{\text{𝜂}}$	60°	${\tfrac {\pi }{3}}$
𝝉 ^[п]	${\sqrt {\tfrac {1}{30}}}\approx 0.183$	52°15′20″	${\tfrac {\pi }{2}}-{\text{𝜂}}$	60°	${\tfrac {\pi }{3}}$
𝟁	${\sqrt {\tfrac {2}{15}}}\approx 0.103$	52°15′20″	${\tfrac {\pi }{2}}-{\text{𝜂}}$	60°	${\tfrac {\pi }{3}}$

$_{0}R^{3}/l$	${\sqrt {\tfrac {3}{20}}}\approx 0.387$	75°29′20″	$2{\text{𝜂}}$	90°	${\tfrac {\pi }{2}}$
$_{1}R^{3}/l$	${\sqrt {\tfrac {1}{20}}}\approx 0.224$	52°15′20″	${\tfrac {\pi }{2}}-{\text{𝜂}}$	90°	${\tfrac {\pi }{2}}$
$_{2}R^{3}/l$	${\sqrt {\tfrac {1}{60}}}\approx 0.129$	52°15′20″	${\tfrac {\pi }{2}}-{\text{𝜂}}$	90°	${\tfrac {\pi }{2}}$

$_{0}R^{4}/l$	${\sqrt {1}}=1.0$
$_{1}R^{4}/l$	${\sqrt {\tfrac {3}{8}}}\approx 0.612$
$_{2}R^{4}/l$	${\sqrt {\tfrac {1}{6}}}\approx 0.408$
$_{3}R^{4}/l$	${\sqrt {\tfrac {1}{16}}}=0.25$

${\text{𝜼}}$		37°44′40″	${\tfrac {{\text{arc sec }}4}{2}}$

Характеристическая 5-ячейка (4-ортосхема) правильной 5-клетки имеет на четыре ребра больше, чем ее базовый характеристический тетраэдр (3-ортосхема), которые соединяют четыре вершины основания с его вершиной (пятая вершина 4-ортосхемы). ортосхема, в центре правильной 5-клеточной). ^[д] Если обычная 5-ячеечная клетка имеет единичный радиус и длину ребра ${\sqrt {\tfrac {5}{2}}}$ , десять ребер его характерной 5-ячейки имеют длину ${\sqrt {\tfrac {1}{10}}}$ , ${\sqrt {\tfrac {1}{30}}}$ , ${\sqrt {\tfrac {2}{15}}}$ вокруг его внешней грани прямоугольного треугольника (ребра, противоположные характерным углам 𝟀, 𝝉, 𝟁), ^[п] плюс ${\sqrt {\tfrac {3}{20}}}$ , ${\sqrt {\tfrac {1}{20}}}$ , ${\sqrt {\tfrac {1}{60}}}$ (остальные три ребра внешней 3-ортосхемы ограняют характеристический тетраэдр, которые являются характеристическими радиусами правильного тетраэдра), плюс ${\sqrt {1}}$ , ${\sqrt {\tfrac {3}{8}}}$ , ${\sqrt {\tfrac {1}{6}}}$ , ${\sqrt {\tfrac {1}{16}}}$ (ребра, являющиеся характерными радиусами правильной 5-клетки). Путь с 4 ребрами вдоль ортогональных ребер ортосхемы равен ${\sqrt {\tfrac {1}{30}}}$ , ${\sqrt {\tfrac {2}{15}}}$ , ${\sqrt {\tfrac {1}{60}}}$ , ${\sqrt {\tfrac {1}{16}}}$ , сначала от обычной 5-ячеечной вершины к регулярному 5-ячеечному реберному центру, затем поворот на 90° к обычному 5-ячеечному центру грани, затем поворот на 90° к обычному 5-ячеечному тетраэдрическому центру ячейки, затем поворот на 90° к обычный 5-клеточный центр. ^[р]

Изометрии

Существует множество форм более низкой симметрии 5-клеточной ячейки, в том числе те, которые встречаются в виде однородных вершинных фигур многогранника :

Симметрия	[3,3,3] Заказать 120	[3,3,1] Заказ 24	[3,2,1] Заказ 12	[3,1,1] Заказ 6	~[5,2] ⁺ Заказать 10
Имя	Обычный 5-клеточный	Тетраэдрическая пирамида		Треугольная пирамидальная пирамида
Шлефли	{3,3,3}	{3,3}∨( )	{3}∨{ }	{3}∨( )∨( )
Пример Вертекс фигура	5-симплекс	Усеченный 5-симплекс	Битусеченный 5-симплекс	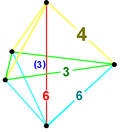Количественно усеченный 5-симплекс	Всеусеченные 4-симплексные соты

Тетраэдрическая пирамида — это частный случай 5-клеточной многогранной пирамиды основание правильного тетраэдра в трехмерной гиперплоскости и вершина над , построенной как гиперплоскостью. Четыре стороны пирамиды состоят из треугольных пирамидальных ячеек.

Многие однородные 5-многогранники имеют тетраэдрических пирамид вершинные фигуры с символами Шлефли ( )∨{3,3}.

Симметрия [3,3,1], порядок 24
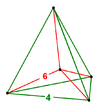Имя Коксетер	{ }×{3,3,3}	{ }×{4,3,3}	{ }×{5,3,3}	т{3,3,3,3}	т{4,3,3,3}	т{3,4,3,3}
Шлегель диаграмма

Другие однородные 5-многогранники имеют неправильные 5-клеточные вершинные фигуры. Симметрия вершинной фигуры однородного многогранника выражается удалением окольцованных узлов диаграммы Коксетера.

Симметрия	[3,2,1], порядок 12		[3,1,1], порядок 6		[2 ⁺,4,1], порядок 8	[2,1,1], порядок 4
Шлефли	{3}∨{ }		{3}∨( )∨( )		{ }∨{ }∨( )
Шлегель диаграмма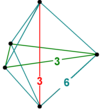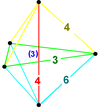
Имя Коксетер	т ₁₂ α ₅	т ₁₂ в ₅	т ₀₁₂ а ₅	т ₀₁₂ с ₅	т ₁₂₃ α ₅	т ₁₂₃ γ ₅

Симметрия	[2,1,1], порядок 2			[2 ⁺,1,1], порядок 2	[ ] ⁺, заказ 1
Шлефли	{ }∨( )∨( )∨( )			( )∨( )∨( )∨( )∨( )
Шлегель диаграмма
Имя Коксетер	т ₀₁₂₃ α ₅	т ₀₁₂₃ γ ₅	т ₀₁₂₃ б ₅	т ₀₁₂₃₄ а ₅	т ₀₁₂₃₄ с ₅

Сложный

Соединение двух 5-ячеек в двойной конфигурации можно увидеть на этой проекции плоскости Кокстера A5 с красными и синими 5-ячеечными вершинами и краями. Это соединение имеет симметрию [[3,3,3]] порядка 240. Пересечение этих двух 5-ячеек представляет собой однородную усеченную 5-ячейку . = ∩ .

Это соединение можно рассматривать как четырехмерный аналог двумерной гексаграммы { ⁠ 6/2 } ⁠ и трёхмерное соединение двух тетраэдров .

Связанные многогранники и соты

Пентахорон (5-клеточный) — простейшая из 9 однородных полихор, построенных из [3,3,3] группы Кокстера .

Шлефли	{3,3,3}	т{3,3,3}	г {3,3,3}	рр{3,3,3}	2т{3,3,3}	тр{3,3,3}	т _0,3 {3,3,3}	т _0,1,3 {3,3,3}	т _0,1,2,3 {3,3,3}
Коксетер
Шлегель

1 _k2 фигур в n измерениях
Space	Finite						Euclidean	Hyperbolic
n	3	4	5	6	7	8	9	10
Coxeter group	E₃=A₂A₁	E₄=A₄	E₅=D₅	E₆	E₇	E₈	E₉ = ${\tilde {E}}_{8}$ = E₈⁺	E₁₀ = ${\bar {T}}_{8}$ = E₈⁺⁺
Coxeter diagram
Symmetry (order)	[3^−1,2,1]	[3^0,2,1]	[3^1,2,1]	[[3^2,2,1]]	[3^3,2,1]	[3^4,2,1]	[3^5,2,1]	[3^6,2,1]
Order	12	120	1,920	103,680	2,903,040	696,729,600	∞
Graph							-	-
Name	1_−1,2	1₀₂	1₁₂	1₂₂	1₃₂	1₄₂	1₅₂	1₆₂

2 _{k 1} фигур в n измерениях
Space	Finite						Euclidean	Hyperbolic
n	3	4	5	6	7	8	9	10
Coxeter group	E₃=A₂A₁	E₄=A₄	E₅=D₅	E₆	E₇	E₈	E₉ = ${\tilde {E}}_{8}$ = E₈⁺	E₁₀ = ${\bar {T}}_{8}$ = E₈⁺⁺
Coxeter diagram
Symmetry	[3^−1,2,1]	[3^0,2,1]	[[3^1,2,1]]	[3^2,2,1]	[3^3,2,1]	[3^4,2,1]	[3^5,2,1]	[3^6,2,1]
Order	12	120	384	51,840	2,903,040	696,729,600	∞
Graph							-	-
Name	2_−1,1	2₀₁	2₁₁	2₂₁	2₃₁	2₄₁	2₅₁	2₆₁

Это последовательность {p,3,3} правильной полихоры с тетраэдрической вершинной фигурой : тессеракт {4,3,3} и 120 ячеек {5,3,3} евклидова 4-мерного пространства и гексагональное замощение сот {6,3,3} гиперболического пространства. ^[и]

{p,3,3} многогранники
Space	S³			H³
Form	Finite			Paracompact	Noncompact
Name	{3,3,3}	{4,3,3}	{5,3,3}	{6,3,3}	{7,3,3}	{8,3,3}	...{∞,3,3}
Image
Cells {p,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Это один из трех правильных 4-многогранников {3,3,p} с тетраэдрическими ячейками, а также 16-ячеечный {3,3,4} и 600-ячеечный {3,3,5}. { Тетраэдрические соты 6-го порядка 3,3,6} гиперболического пространства также имеют тетраэдрические ячейки.

{3,3,p} многогранники
Space	S³			H³
Form	Finite			Paracompact	Noncompact
Name	{3,3,3}	{3,3,4}	{3,3,5}	{3,3,6}	{3,3,7}	{3,3,8}	... {3,3,∞}
Image
Vertex figure	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Он самодуален, как и 24-клеточный {3,4,3}, имеющий палиндромный {3,p,3} символ Шлефли .

{3, p , 3} многогранники
Space	S³		H³
Form	Finite		Compact	Paracompact	Noncompact
{3,p,3}	{3,3,3}	{3,4,3}	{3,5,3}	{3,6,3}	{3,7,3}	{3,8,3}	... {3,∞,3}
Image
Cells	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}
Vertex figure	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

{p,3,p} обычные соты
Space	S³	Euclidean E³	H³
Form	Finite	Affine	Compact	Paracompact	Noncompact
Name	{3,3,3}	{4,3,4}	{5,3,5}	{6,3,6}	{7,3,7}	{8,3,8}	...{∞,3,∞}
Image
Cells	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}
Vertex figure	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Примечания

↑ Перейти обратно: Перейти обратно: ^а ^б 5 вершин 5-клеточного элемента образуют 5 тетраэдрических ячеек , соединенных гранями друг с другом, всего с 10 ребрами и 10 треугольными гранями.
^ Выпуклые правильные 4-многогранники можно упорядочить по размеру как мере четырехмерного содержимого (гиперобъема) для того же радиуса. Каждый больший многогранник в последовательности более круглый , чем его предшественник, и содержит больше содержимого. ^[5] в том же радиусе. 4-симплекс (5-ячеечный) — это наименьший случай, а 120-ячеечный — самый большой. Сложность (измеряемая путем сравнения матриц конфигурации или просто количества вершин) следует тому же порядку. Это обеспечивает альтернативную схему числового именования для правильных многогранников, в которой 5-ячеечный является 4-точечным многогранником с 5 точками: сначала в возрастающей последовательности, ведущей к 4-точечному многограннику с 600 точками.
^ Правильная 120-ячеечная имеет изогнутую трехмерную граничную поверхность, состоящую из 120 правильных ячеек додекаэдра. В него также вписано 120 непересекающихся правильных 5-клеток. ^[6] Это не трехмерные ячейки, а четырехмерные объекты, которые имеют общую центральную точку из 120 ячеек и в совокупности покрывают все 600 ее вершин.
↑ Перейти обратно: Перейти обратно: ^а ^б В многограннике с четырехгранной вершинной фигурой ^[и] геодезический путь вдоль ребер не лежит на обычном большом круге в одной центральной плоскости: каждое последующее ребро лежит в другой центральной плоскости, чем предыдущее ребро. с реберной траекторией Тем не менее, многоугольник Клиффорда представляет собой набор косых хорд истинного геодезического большого круга, проходящего через четыре измерения, а не только через два измерения: но это не обычный «плоский» большой круг окружности 2𝝅𝑟, это изоклина . ^[г]
↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и Диаграмма Шлегеля 5-клетки (вверху этой статьи) иллюстрирует ее тетраэдрическую вершинную фигуру . Шесть из 10 ребер 5-клетки являются ограничивающими рёбрами правильного тетраэдра Шлегеля. Остальные четыре ребра сходятся в пятой вершине, в центре объема тетраэдра. Рассмотрим любой круговой геодезический (кратчайший) путь вдоль ребер. ^[д] Есть четыре способа добраться до вершины (например, пятой «центральной» вершины), путешествуя по ребру. В 5-ячейке есть ровно два различных пятиугольных геодезических круга, и четыре направления прибытия в вершину соответствуют прибытию по одному из двух контуров, двигаясь в одном из двух направлений вращения на контуре. из 5 ячеек Эти два геодезических косых пятиугольника представляют собой два отдельных многоугольника Петри . В графе ортогональной проекции один выглядит как периметр пятиугольника (последовательность вершин 1 2 3 4 5), а другой — вписанная пентаграмма (последовательность вершин 1 3 5 2 4), но на самом деле это идентичные правильные косые пятиугольники, каждый из которых искажается по всем 4 измерениям. Каждый из них представляет собой отдельную последовательность из 5 из 10 ребер, и таких различных последовательностей только две.
^ Общее вращение в 4-мерном пространстве — это двойное вращение на отдельный угол в каждой из двух полностью ортогональных плоскостей вращения. Существует два особых случая двойного вращения: простое вращение (с одним углом поворота 0 °) и изоклиническое вращение (с двумя равными углами поворота).
↑ Перейти обратно: Перейти обратно: ^а ^б ^с 5-клеточный (4-симплекс) уникален среди правильных 4-многогранников тем, что его изоклинные хорды ^[я] являются его собственными краями. В других правильных 4-многогранниках хорда изоклины представляет собой более длинное ребро другого вписанного правильного многогранника. Другой аспект этой уникальности заключается в том, что изоклинальный многоугольник Клиффорда из 5 ячеек (косая пентаграмма) и ее зигзагообразный многоугольник Петри (косой пятиугольник) представляют собой один и тот же объект; в остальных правильных 4-многогранниках они совсем другие.
^ Каждое ребро пересекает 6 других (по 3 на каждом конце) и не пересекается с тремя другими, которым оно ортогонально, как ребро тетраэдра его противоположному ребру.
↑ Перейти обратно: Перейти обратно: ^а ^б Каждая хорда изоклины ( синяя грань пентаграммы ) проходит от одной из 5 вершин через внутренний объем одной из 5 тетраэдрических ячеек, через треугольную грань ячейки, противоположную вершине, а затем прямо через объем соседней ячейки, которая разделяет лицо, до его вершины, противоположной лицу. Хорда изоклины — это прямая линия между двумя вершинами, проходящая через объем двух ячеек. Как вы можете видеть на иллюстрации , синяя хорда изоклины проходит не через точный центр общей грани, а через точку, расположенную ближе к вершине одной грани. На самом деле в 5-ячейке есть две разные пентаграммы изоклин, одна из которых на иллюстрации изображена как синяя пентаграмма. Каждая из этих двух пентаграмм Клиффорда представляет собой различную круговую последовательность 5 из 10 ребер 5-ячейки. ^[и] Все 10 ребер присутствуют в каждой из 5 ячеек тетраэдра: каждая ячейка ограничена 6 из 10 ребер, а остальные 4 из 10 ребер проходят через ее объем как хорды изоклины, от ее 4 вершин и через 4 их противоположные стороны. лица. ^[г]
^ Прямоугольный треугольник — это двумерная ортосхема; ортосхемы — это обобщение прямоугольных треугольников на n измерений. Трехмерная ортосхема представляет собой тетраэдр с четырьмя прямоугольными гранями (не обязательно одинаковыми).
^ 4-куб (тессеракт) содержит восемь 3-кубов (поэтому его еще называют 8-клеточным). Каждый 3-куб соединен гранями с шестью другими (которые полностью окружают его), но полностью отделен от другого 3-куба, который лежит напротив и параллельно ему на другой стороне 8-клетки.
^ Расчленение 4-куба на 384 4-ортосхемы представляет собой 16 расчленений на 24 4-ортосхемы. Сначала каждое ребро 4-куба делится на 2 меньших ребра, поэтому каждая квадратная грань делится на 4 меньших квадрата, каждая кубическая ячейка делится на 8 меньших кубов, а весь 4-куб делится на 16 меньших 4-кубов. Затем каждый меньший 4-куб делится на 24 4-ортосхемы, которые встречаются в центре исходного 4-куба.
^ Для правильного k -многогранника диаграмма Кокстера-Дынкина характеристической k- ортосхемы представляет собой диаграмму k -многогранника без кольца образующих точек . Правильный k- многогранник подразделяется по его ( k -1)-элементам симметрии на g экземпляров его характеристической k -ортосхемы, окружающей его центр, где g — порядок k - многогранника группы симметрии . ^[13]
^ Правильный многогранник размерности k имеет характеристическую k -ортосхему, а также характеристическую ( k -1)-ортосхему. Правильный 4-многогранник имеет характерную 5-ячейку (4-ортосхему), на которую он подразделяется своими (3-мерными) гиперплоскостями симметрии, а также характерный тетраэдр (3-ортосхему), на который подразделяется его поверхность (2-мерные) плоскости симметрии ячеек. После разделения его (3-мерной) поверхности на характеристические тетраэдры, окружающие центр каждой ячейки, его (4-мерную) внутреннюю часть можно разделить на характеристические 5-ячейки путем добавления радиусов, соединяющих вершины характеристических тетраэдров поверхности с центром 4-мерного многогранника. ^[14] Образовавшиеся таким образом внутренние тетраэдры и треугольники также будут ортосхемами.
^ 120 конгруэнтных ^[15] 4-ортосхемы правильной 5-клетки встречаются в двух зеркальных формах, по 60 штук в каждой. Каждая 4-ортосхема связана с 4 другими клетками противоположной хиральности (4 из 5 тетраэдрических ячеек, лежащих внутри правильной 5-клетки). Если 60 левых 4-ортосхем окрашены в красный цвет, а 60 правых 4-ортосхем окрашены в черный цвет, то каждая красная 5-клетка окружена 4 черными 5-клетками и наоборот, в четырехмерном узоре, аналогичном шахматная доска (если на шахматной доске вместо квадратов были прямоугольные треугольники).
↑ Перейти обратно: Перейти обратно: ^а ^б ( Коксетер 1973 ) использует греческую букву 𝝓 (фи) для обозначения одного из трех характеристических углов 𝟀, 𝝓, 𝟁 правильного многогранника. Поскольку 𝝓 обычно используется для обозначения константы золотого сечения ≈ 1,618, для которой Коксетер использует 𝝉 (тау), мы переворачиваем соглашения Кокстера и используем 𝝉 для обозначения характеристического угла.
^ Четыре ребра каждой 4-ортосхемы, которые встречаются в центре правильного 4-многогранника, имеют неравную длину, поскольку они представляют собой четыре характерных радиуса правильного 4-многогранника: радиус вершины, радиус центра ребра, грань радиус центра и радиус центра ячейки. Пять вершин 4-ортосхемы всегда включают в себя одну вершину правильного 4-многогранника, один центр ребра правильного 4-многогранника, один центр грани правильного 4-многогранника, один центр ячейки правильного 4-многогранника и центр правильного 4-многогранника. Эти пять вершин (именно в таком порядке) составляют путь вдоль четырех взаимно перпендикулярных ребер (что делает три поворота под прямым углом), что является характерной особенностью 4-ортосхемы. 4-ортосхема имеет пять различных граней 3-ортосхемы.
^ Если обычная 5-ячеечная клетка имеет длину ребра $2$ и радиус $2{\sqrt {\tfrac {2}{5}}}\approx 1.265$ , десять ребер его характерной 5-ячейки имеют длину ${\sqrt {\tfrac {1}{3}}}\approx 0.577$ , ${\sqrt {\tfrac {1}{4}}}{=}0.5$ , ${\sqrt {\tfrac {1}{12}}}\approx 0.289$ (внешняя грань прямоугольного треугольника, характеристический треугольник ), плюс ${\sqrt {\tfrac {3}{8}}}\approx 0.612$ , ${\sqrt {\tfrac {1}{8}}}\approx 0.354$ , ${\sqrt {\tfrac {1}{24}}}\approx 0.204$ (остальные три ребра внешней 3-ортосхемы ограняют характерный тетраэдр ), плюс $2{\sqrt {\tfrac {2}{5}}}\approx 1.265$ , ${\sqrt {\tfrac {3}{5}}}\approx 0.775$ , ${\sqrt {\tfrac {4}{15}}}\approx 0.516$ , ${\sqrt {\tfrac {1}{10}}}=0.316$ (ребра, являющиеся характерными радиусами правильной 5-клетки). ^[16] Путь с 4 ребрами вдоль ортогональных ребер ортосхемы равен ${\sqrt {\tfrac {1}{4}}}$ , ${\sqrt {\tfrac {1}{12}}}$ , ${\sqrt {\tfrac {1}{24}}}$ , ${\sqrt {\tfrac {1}{10}}}$ .

Цитаты

^ Н. В. Джонсон : Геометрии и трансформации , (2018) ISBN 978-1-107-10340-5 Глава 11: Группы конечной симметрии , 11.5 Сферические группы Кокстера , стр.249
^ Матила Гика, Геометрия искусства и жизни (1977), стр.68
^ Коксетер 1973 , с. 120, §7.2. рисунок Рис. 7.2 A. см .
^ Категория 1: Обычная полихора.
^ Coxeter 1973 , стр. 292–293, Таблица I(ii): Шестнадцать правильных многогранников { p,q,r } в четырех измерениях; Бесценная таблица, предоставляющая все 20 метрик каждого 4-многогранника в единицах длины ребра. Их необходимо алгебраически преобразовать для сравнения многогранников единичного радиуса.
^ Коксетер 1973 , с. 305, Таблица VII: Регулярные соединения в четырех измерениях.
^ Коксетер 1973 , с. 12, §1.8. Конфигурации.
^ "Ручка" .
^ Коксетер 1991 , с. 30, §4.2. Кристаллографические правильные многогранники.
^ Банчофф 2013 .
^ Coxeter 1973 , стр. 198–202, §11.7 Правильные фигуры и их усечения.
^ Kim & Rote 2016 , стр. 17–20, §10 Классификация Кокстера четырехмерных точечных групп.
^ Coxeter 1973 , стр. 130–133, §7.6 Группа симметрии общего правильного многогранника.
^ Коксетер 1973 , с. 130, §7.6; «симплициальное подразделение».
^ Коксетер 1973 , §3.1 Конгруэнтные преобразования.
↑ Перейти обратно: Перейти обратно: ^а ^б Coxeter 1973 , стр. 292–293, Таблица I(ii); «5-клеточный, 𝛼 ₄ ».
^ Коксетер 1973 , с. 139, §7.9 Характеристический симплекс.
^ Коксетер 1973 , с. 290, таблица I(ii); «двугранные углы».

Ссылки

Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики, Макмиллан, 1900 г.
ХСМ Коксетер :
- Коксетер, HSM (1973). Правильные многогранники (3-е изд.). Нью-Йорк: Дувр.
  - п. 120, §7.2. см. рисунок Рис. 7.2 A
  - п. 296, Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерностях (n≥5).
- Коксетер, HSM (1991), Правильные комплексные многогранники (2-е изд.), Кембридж: Издательство Кембриджского университета
- Калейдоскопы: Избранные сочинения HSM Коксетера, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
  - (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
  - (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
Ким, Хына; Роте, Г. (2016). «Проверка конгруэнтности наборов точек в 4 измерениях». arXiv : 1603.07269 [ cs.CG ].
Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26. стр. 409: Гемикубы: 1 _n1 )
Нормана Джонсона Равномерные многогранники , Рукопись (1991)
- Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии. (1966)
Банчофф, Томас Ф. (2013). «Разложения тора правильных многогранников в 4-мерном пространстве». В Сенешале, Марджори (ред.). Формирование пространства . Спрингер Нью-Йорк. стр. 257–266 . дои : 10.1007/978-0-387-92714-5_20 . ISBN 978-0-387-92713-8 .

Внешние ссылки

Вайсштейн, Эрик В. «Пентатоп» . Математический мир .
Клитцинг, Ричард. «4D однородные многогранники (полихора) x3o3o3o — перо» .
Der 5-Zeller (5-клеточные) Правильные многогранники Марко Мёллера в R ⁴ (Немецкий)
Джонатан Бауэрс, Регулярная полихора
Java3D-апплеты
пирохорон

v т и Фундаментальные выпуклые правильные и однородные многогранники размерностей 2–10.
Семья	н	Б _н	И ₂ (п) / Д _н	Е ₆ / Е ₇ / Е ₈ / Ж ₄ / Г ₂	Ч _н
Правильный многоугольник	Треугольник	Квадрат	п-гон	Шестиугольник	Пентагон
Однородный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный полихорон	Пентахорон	16 ячеек • Тессеракт	Демитессеракт	24-ячеечный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-демикуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-демикуб	1 ₂₂ • 2 ₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-демикуб	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-демикуб	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-демикуб
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-демикуб
Равномерный n - многогранник	n - симплекс	n - ортоплекс • n - куб	n - демикуб	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁	n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений.

[elements-1] Перейти обратно: Перейти обратно: ^а ^б 5 вершин 5-клеточного элемента образуют 5 тетраэдрических ячеек , соединенных гранями друг с другом, всего с 10 ребрами и 10 треугольными гранями.

[polytopes_ordered_by_size_and_complexity-7] Выпуклые правильные 4-многогранники можно упорядочить по размеру как мере четырехмерного содержимого (гиперобъема) для того же радиуса. Каждый больший многогранник в последовательности более круглый , чем его предшественник, и содержит больше содержимого. ^[5] в том же радиусе. 4-симплекс (5-ячеечный) — это наименьший случай, а 120-ячеечный — самый большой. Сложность (измеряемая путем сравнения матриц конфигурации или просто количества вершин) следует тому же порядку. Это обеспечивает альтернативную схему числового именования для правильных многогранников, в которой 5-ячеечный является 4-точечным многогранником с 5 точками: сначала в возрастающей последовательности, ведущей к 4-точечному многограннику с 600 точками.

[9] Правильная 120-ячеечная имеет изогнутую трехмерную граничную поверхность, состоящую из 120 правильных ячеек додекаэдра. В него также вписано 120 непересекающихся правильных 5-клеток. ^[6] Это не трехмерные ячейки, а четырехмерные объекты, которые имеют общую центральную точку из 120 ячеек и в совокупности покрывают все 600 ее вершин.

[non-planar_geodesic_circle_along_edges-10] Перейти обратно: Перейти обратно: ^а ^б В многограннике с четырехгранной вершинной фигурой ^[и] геодезический путь вдоль ребер не лежит на обычном большом круге в одной центральной плоскости: каждое последующее ребро лежит в другой центральной плоскости, чем предыдущее ребро. с реберной траекторией Тем не менее, многоугольник Клиффорда представляет собой набор косых хорд истинного геодезического большого круга, проходящего через четыре измерения, а не только через два измерения: но это не обычный «плоский» большой круг окружности 2𝝅𝑟, это изоклина . ^[г]

[vertex_figure-11] Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и Диаграмма Шлегеля 5-клетки (вверху этой статьи) иллюстрирует ее тетраэдрическую вершинную фигуру . Шесть из 10 ребер 5-клетки являются ограничивающими рёбрами правильного тетраэдра Шлегеля. Остальные четыре ребра сходятся в пятой вершине, в центре объема тетраэдра. Рассмотрим любой круговой геодезический (кратчайший) путь вдоль ребер. ^[д] Есть четыре способа добраться до вершины (например, пятой «центральной» вершины), путешествуя по ребру. В 5-ячейке есть ровно два различных пятиугольных геодезических круга, и четыре направления прибытия в вершину соответствуют прибытию по одному из двух контуров, двигаясь в одном из двух направлений вращения на контуре. из 5 ячеек Эти два геодезических косых пятиугольника представляют собой два отдельных многоугольника Петри . В графе ортогональной проекции один выглядит как периметр пятиугольника (последовательность вершин 1 2 3 4 5), а другой — вписанная пентаграмма (последовательность вершин 1 3 5 2 4), но на самом деле это идентичные правильные косые пятиугольники, каждый из которых искажается по всем 4 измерениям. Каждый из них представляет собой отдельную последовательность из 5 из 10 ребер, и таких различных последовательностей только две.

[15] Общее вращение в 4-мерном пространстве — это двойное вращение на отдельный угол в каждой из двух полностью ортогональных плоскостей вращения. Существует два особых случая двойного вращения: простое вращение (с одним углом поворота 0 °) и изоклиническое вращение (с двумя равными углами поворота).

[4-simplex_isoclines_are_edges-16] Перейти обратно: Перейти обратно: ^а ^б ^с 5-клеточный (4-симплекс) уникален среди правильных 4-многогранников тем, что его изоклинные хорды ^[я] являются его собственными краями. В других правильных 4-многогранниках хорда изоклины представляет собой более длинное ребро другого вписанного правильного многогранника. Другой аспект этой уникальности заключается в том, что изоклинальный многоугольник Клиффорда из 5 ячеек (косая пентаграмма) и ее зигзагообразный многоугольник Петри (косой пятиугольник) представляют собой один и тот же объект; в остальных правильных 4-многогранниках они совсем другие.

[17] Каждое ребро пересекает 6 других (по 3 на каждом конце) и не пересекается с тремя другими, которым оно ортогонально, как ребро тетраэдра его противоположному ребру.

[Clifford_polygon-19] Перейти обратно: Перейти обратно: ^а ^б Каждая хорда изоклины ( синяя грань пентаграммы ) проходит от одной из 5 вершин через внутренний объем одной из 5 тетраэдрических ячеек, через треугольную грань ячейки, противоположную вершине, а затем прямо через объем соседней ячейки, которая разделяет лицо, до его вершины, противоположной лицу. Хорда изоклины — это прямая линия между двумя вершинами, проходящая через объем двух ячеек. Как вы можете видеть на иллюстрации , синяя хорда изоклины проходит не через точный центр общей грани, а через точку, расположенную ближе к вершине одной грани. На самом деле в 5-ячейке есть две разные пентаграммы изоклин, одна из которых на иллюстрации изображена как синяя пентаграмма. Каждая из этих двух пентаграмм Клиффорда представляет собой различную круговую последовательность 5 из 10 ребер 5-ячейки. ^[и] Все 10 ребер присутствуют в каждой из 5 ячеек тетраэдра: каждая ячейка ограничена 6 из 10 ребер, а остальные 4 из 10 ребер проходят через ее объем как хорды изоклины, от ее 4 вершин и через 4 их противоположные стороны. лица. ^[г]

[20] Прямоугольный треугольник — это двумерная ортосхема; ортосхемы — это обобщение прямоугольных треугольников на n измерений. Трехмерная ортосхема представляет собой тетраэдр с четырьмя прямоугольными гранями (не обязательно одинаковыми).

[22] 4-куб (тессеракт) содержит восемь 3-кубов (поэтому его еще называют 8-клеточным). Каждый 3-куб соединен гранями с шестью другими (которые полностью окружают его), но полностью отделен от другого 3-куба, который лежит напротив и параллельно ему на другой стороне 8-клетки.

[23] Расчленение 4-куба на 384 4-ортосхемы представляет собой 16 расчленений на 24 4-ортосхемы. Сначала каждое ребро 4-куба делится на 2 меньших ребра, поэтому каждая квадратная грань делится на 4 меньших квадрата, каждая кубическая ячейка делится на 8 меньших кубов, а весь 4-куб делится на 16 меньших 4-кубов. Затем каждый меньший 4-куб делится на 24 4-ортосхемы, которые встречаются в центре исходного 4-куба.

[26] Для правильного k -многогранника диаграмма Кокстера-Дынкина характеристической k- ортосхемы представляет собой диаграмму k -многогранника без кольца образующих точек . Правильный k- многогранник подразделяется по его ( k -1)-элементам симметрии на g экземпляров его характеристической k -ортосхемы, окружающей его центр, где g — порядок k - многогранника группы симметрии . ^[13]

[28] Правильный многогранник размерности k имеет характеристическую k -ортосхему, а также характеристическую ( k -1)-ортосхему. Правильный 4-многогранник имеет характерную 5-ячейку (4-ортосхему), на которую он подразделяется своими (3-мерными) гиперплоскостями симметрии, а также характерный тетраэдр (3-ортосхему), на который подразделяется его поверхность (2-мерные) плоскости симметрии ячеек. После разделения его (3-мерной) поверхности на характеристические тетраэдры, окружающие центр каждой ячейки, его (4-мерную) внутреннюю часть можно разделить на характеристические 5-ячейки путем добавления радиусов, соединяющих вершины характеристических тетраэдров поверхности с центром 4-мерного многогранника. ^[14] Образовавшиеся таким образом внутренние тетраэдры и треугольники также будут ортосхемами.

[30] 120 конгруэнтных ^[15] 4-ортосхемы правильной 5-клетки встречаются в двух зеркальных формах, по 60 штук в каждой. Каждая 4-ортосхема связана с 4 другими клетками противоположной хиральности (4 из 5 тетраэдрических ячеек, лежащих внутри правильной 5-клетки). Если 60 левых 4-ортосхем окрашены в красный цвет, а 60 правых 4-ортосхем окрашены в черный цвет, то каждая красная 5-клетка окружена 4 черными 5-клетками и наоборот, в четырехмерном узоре, аналогичном шахматная доска (если на шахматной доске вместо квадратов были прямоугольные треугольники).

[reversed_greek_symbols-34] Перейти обратно: Перейти обратно: ^а ^б ( Коксетер 1973 ) использует греческую букву 𝝓 (фи) для обозначения одного из трех характеристических углов 𝟀, 𝝓, 𝟁 правильного многогранника. Поскольку 𝝓 обычно используется для обозначения константы золотого сечения ≈ 1,618, для которой Коксетер использует 𝝉 (тау), мы переворачиваем соглашения Кокстера и используем 𝝉 для обозначения характеристического угла.

[characteristic_radii-35] Четыре ребра каждой 4-ортосхемы, которые встречаются в центре правильного 4-многогранника, имеют неравную длину, поскольку они представляют собой четыре характерных радиуса правильного 4-многогранника: радиус вершины, радиус центра ребра, грань радиус центра и радиус центра ячейки. Пять вершин 4-ортосхемы всегда включают в себя одну вершину правильного 4-многогранника, один центр ребра правильного 4-многогранника, один центр грани правильного 4-многогранника, один центр ячейки правильного 4-многогранника и центр правильного 4-многогранника. Эти пять вершин (именно в таком порядке) составляют путь вдоль четырех взаимно перпендикулярных ребер (что делает три поворота под прямым углом), что является характерной особенностью 4-ортосхемы. 4-ортосхема имеет пять различных граней 3-ортосхемы.

[36] Если обычная 5-ячеечная клетка имеет длину ребра $2$ и радиус $2{\sqrt {\tfrac {2}{5}}}\approx 1.265$ , десять ребер его характерной 5-ячейки имеют длину ${\sqrt {\tfrac {1}{3}}}\approx 0.577$ , ${\sqrt {\tfrac {1}{4}}}{=}0.5$ , ${\sqrt {\tfrac {1}{12}}}\approx 0.289$ (внешняя грань прямоугольного треугольника, характеристический треугольник ), плюс ${\sqrt {\tfrac {3}{8}}}\approx 0.612$ , ${\sqrt {\tfrac {1}{8}}}\approx 0.354$ , ${\sqrt {\tfrac {1}{24}}}\approx 0.204$ (остальные три ребра внешней 3-ортосхемы ограняют характерный тетраэдр ), плюс $2{\sqrt {\tfrac {2}{5}}}\approx 1.265$ , ${\sqrt {\tfrac {3}{5}}}\approx 0.775$ , ${\sqrt {\tfrac {4}{15}}}\approx 0.516$ , ${\sqrt {\tfrac {1}{10}}}=0.316$ (ребра, являющиеся характерными радиусами правильной 5-клетки). ^[16] Путь с 4 ребрами вдоль ортогональных ребер ортосхемы равен ${\sqrt {\tfrac {1}{4}}}$ , ${\sqrt {\tfrac {1}{12}}}$ , ${\sqrt {\tfrac {1}{24}}}$ , ${\sqrt {\tfrac {1}{10}}}$ .

[2] Н. В. Джонсон : Геометрии и трансформации , (2018) ISBN 978-1-107-10340-5 Глава 11: Группы конечной симметрии , 11.5 Сферические группы Кокстера , стр.249

[3] Матила Гика, Геометрия искусства и жизни (1977), стр.68

[FOOTNOTECoxeter1973120§7.2._see_illustration_Fig_7.2<small>A</small>-4] Коксетер 1973 , с. 120, §7.2. рисунок Рис. 7.2 A. см .

[5] Категория 1: Обычная полихора.

[FOOTNOTECoxeter1973292–293Table_I(ii):_The_sixteen_regular_polytopes_{''p,q,r''}_in_four_dimensions-6] Coxeter 1973 , стр. 292–293, Таблица I(ii): Шестнадцать правильных многогранников { p,q,r } в четырех измерениях; Бесценная таблица, предоставляющая все 20 метрик каждого 4-многогранника в единицах длины ребра. Их необходимо алгебраически преобразовать для сравнения многогранников единичного радиуса.

[FOOTNOTECoxeter1973305Table_VII:_Regular_Compounds_in_Four_Dimensions-8] Коксетер 1973 , с. 305, Таблица VII: Регулярные соединения в четырех измерениях.

[FOOTNOTECoxeter197312§1.8._Configurations-12] Коксетер 1973 , с. 12, §1.8. Конфигурации.

[13] "Ручка" .

[FOOTNOTECoxeter199130§4.2._The_Crystallographic_regular_polytopes-14] Коксетер 1991 , с. 30, §4.2. Кристаллографические правильные многогранники.

[FOOTNOTEBanchoff2013-18] Банчофф 2013 .

[FOOTNOTECoxeter1973198–202§11.7_Regular_figures_and_their_truncations-21] Coxeter 1973 , стр. 198–202, §11.7 Правильные фигуры и их усечения.

[FOOTNOTEKimRote201617–20§10_The_Coxeter_Classification_of_Four-Dimensional_Point_Groups-24] Kim & Rote 2016 , стр. 17–20, §10 Классификация Кокстера четырехмерных точечных групп.

[FOOTNOTECoxeter1973130–133§7.6_The_symmetry_group_of_the_general_regular_polytope-25] Coxeter 1973 , стр. 130–133, §7.6 Группа симметрии общего правильного многогранника.

[FOOTNOTECoxeter1973130§7.6-27] Коксетер 1973 , с. 130, §7.6; «симплициальное подразделение».

[FOOTNOTECoxeter1973§3.1_Congruent_transformations-29] Коксетер 1973 , §3.1 Конгруэнтные преобразования.

[FOOTNOTECoxeter1973292–293Table_I(ii);_"5-cell,_𝛼<sub>4</sub>"-31] Перейти обратно: Перейти обратно: ^а ^б Coxeter 1973 , стр. 292–293, Таблица I(ii); «5-клеточный, 𝛼 ₄ ».

[FOOTNOTECoxeter1973139§7.9_The_characteristic_simplex-32] Коксетер 1973 , с. 139, §7.9 Характеристический симплекс.

[FOOTNOTECoxeter1973290Table_I(ii);_"dihedral_angles"-33] Коксетер 1973 , с. 290, таблица I(ii); «двугранные углы».

[а]

[1]

[2]

[3]

[4]

[б]

[с]

[и]

[7]

[8]

[9]

[ф]

[д]

[час]

[г]

[10]

[я]

[Дж]

[11]

[к]

[л]

[12]

[м]

[н]

[the]

[16]

[17]

[18]

[п]

[д]

[р]

[5]

[6]

[13]

[14]

[15]