Квантовая запутанность

Процесс спонтанного параметрического понижающего преобразования может разделять фотоны на пары фотонов типа II со взаимно перпендикулярной поляризацией.

Квантовая запутанность — это явление, когда группа частиц генерируется, взаимодействует или разделяет пространственную близость таким образом, что квантовое состояние каждой частицы группы не может быть описано независимо от состояния других, в том числе когда частицы разделены. на большое расстояние. Тема квантовой запутанности лежит в основе несоответствия между классической и квантовой физикой : запутанность — это основная особенность квантовой механики, отсутствующая в классической механике.

Измерения физических свойств, таких как положение , импульс , спин и поляризация, выполненные на запутанных частицах, в некоторых случаях могут оказаться идеально коррелированными . Например, если пара запутанных частиц генерируется так, что их общий спин равен нулю, и обнаружено, что одна частица имеет вращение по часовой стрелке на первой оси, то спин другой частицы, измеренный на той же оси, оказывается против часовой стрелки. Однако такое поведение приводит к, казалось бы, парадоксальным эффектам: любое измерение свойств частицы приводит к кажущемуся и необратимому коллапсу волновой функции этой частицы и изменяет исходное квантовое состояние. В случае запутанных частиц такие измерения влияют на запутанную систему в целом.

Такие явления были предметом статьи 1935 года Альберта Эйнштейна , Бориса Подольского и Натана Розена . и несколько статей Эрвина Шрёдингера вскоре после этого, описывающее то, что стало известно как парадокс ЭПР . Эйнштейн и другие считали такое поведение невозможным, поскольку оно нарушало взгляд на причинность локального реализма (Эйнштейн называл это «жутким действием на расстоянии »). и утверждал, что принятая формулировка квантовой механики , следовательно, должна быть неполной.

Однако позже контринтуитивные предсказания квантовой механики подтвердились. в тестах, где поляризация или спин запутанных частиц измерялись в разных местах, что статистически нарушало неравенство Белла . В более ранних тестах нельзя было исключить, что результат в одной точке мог быть незаметно передан в удаленную точку, влияя на результат во второй точке. Однако с тех пор были проведены так называемые тесты Белла «без лазеек», в которых локации были достаточно разделены, так что связь со скоростью света заняла бы больше времени - в одном случае в 10 000 раз больше, - чем интервал между измерениями.

Согласно некоторым интерпретациям квантовой механики , эффект одного измерения наступает мгновенно. Другие интерпретации, не признающие коллапс волновой функции , оспаривают существование какого-либо «эффекта» вообще. Однако все интерпретации сходятся во мнении, что запутанность приводит к корреляции между измерениями и что взаимная информация между запутанными частицами может быть использована, но любая передача информации со скоростью, превышающей скорость света, невозможна. Таким образом, несмотря на распространенное мнение об обратном, квантовую запутанность нельзя использовать для связи со скоростью, превышающей скорость света .

Квантовая запутанность была продемонстрирована экспериментально на фотонах . электроны , высшие кварки, молекулы и даже небольшие бриллианты. Использование запутанности в коммуникациях , вычислениях и квантовом радаре является активной областью исследований и разработок.

История

Дополнительная информация: Теория скрытых переменных.

Заголовок статьи о парадоксе Эйнштейна-Подольского-Розена (ЭПР) в номере The New York Times от 4 мая 1935 года.

В 1935 году Альберт Эйнштейн , Борис Подольский и Натан Розен опубликовали статью о противоречивых предсказаниях, которые квантовая механика делает для пар объектов, приготовленных вместе определенным образом. В этом исследовании все трое сформулировали парадокс Эйнштейна-Подольского-Розена (парадокс ЭПР), мысленный эксперимент , который пытался показать, что « квантово-механическое описание физической реальности, данное волновыми функциями, не является полным». Однако эти трое учёных не придумали слово « запутанность » и не обобщили особые свойства рассматриваемого ими квантового состояния . После статьи об ЭПР Эрвин Шрёдингер написал письмо Эйнштейну на немецком языке , в котором он использовал слово Verschränkung (переведенное им самим как запутанность ) «для описания корреляций между двумя частицами, которые взаимодействуют, а затем разделяются, как в эксперименте ЭПР». Однако Шредингер обсуждал это явление еще в 1932 году.

Вскоре после этого Шрёдингер опубликовал основополагающую статью, определяющую и обсуждающую понятие «запутывания». В статье он признал важность этой концепции и заявил: «Я бы назвал [запутывание] не таковым , а скорее характерной чертой квантовой механики, той, которая обеспечивает полный ее отход от классических направлений мысли». Как и Эйнштейн, Шредингер был недоволен концепцией запутанности, поскольку она, казалось, нарушала ограничение скорости передачи информации, подразумеваемое теорией относительности . Позднее Эйнштейн высмеял запутанность, назвав ее « spukhafte Fernwirkung ». или « жуткое действие на расстоянии ».

Статья ЭПР вызвала значительный интерес среди физиков, что вызвало много дискуссий об основах квантовой механики и интерпретации Бома в частности, но произвело относительно мало других опубликованных работ. Несмотря на интерес, слабое место в аргументах ЭПР не было обнаружено до 1964 года, когда Джон Стюарт Белл доказал, что одно из их ключевых предположений, принцип локальности , применительно к интерпретации скрытых переменных, на которую надеялась ЭПР, было математически противоречивым. с предсказаниями квантовой теории.

В частности, Белл продемонстрировал верхний предел, наблюдаемый в неравенстве Белла , относительно силы корреляций, которые могут быть получены в любой теории, подчиняющейся локальному реализму , и показал, что квантовая теория предсказывает нарушения этого предела для определенных запутанных систем. Его неравенство поддается экспериментальной проверке, и было проведено множество соответствующих экспериментов , начиная с новаторской работы Стюарта Фридмана и Джона Клаузера в 1972 году. и Алена Аспекта в 1982 году. эксперименты

Ранний экспериментальный прорыв был сделан Карлом Кохером. который уже в 1967 году представил аппарат, в котором было показано, что два фотона, последовательно испускаемые из атома кальция, запутаны – первый случай запутанного видимого света. Два фотона прошли через диаметрально расположенные параллельные поляризаторы с более высокой вероятностью, чем предсказывалось классически, но с корреляциями, количественно согласующимися с квантово-механическими расчетами. Он также показал, что корреляция изменяется как квадрат косинуса угла между настройками поляризатора. и уменьшался экспоненциально с задержкой во времени между испускаемыми фотонами. Аппарат Кохера, оснащенный лучшими поляризаторами, использовался Фридманом и Клаузером, которые смогли подтвердить косинус-квадратическую зависимость и использовать ее для демонстрации нарушения неравенства Белла для набора фиксированных углов. Все эти эксперименты показали согласие с квантовой механикой, а не с принципом локального реализма.

На протяжении десятилетий каждая из них оставляла открытой по крайней мере одну лазейку , с помощью которой можно было поставить под сомнение достоверность результатов. Однако в 2015 году был проведен эксперимент, который одновременно закрыл лазейки как в обнаружении, так и в определении местоположения, и был объявлен «без лазеек»; этот эксперимент с уверенностью исключил большой класс теорий локального реализма. Аспект пишет, что «... ни один эксперимент... можно сказать, что он полностью лишен лазеек», но он говорит, что эксперименты «устраняют последние сомнения в том, что нам следует отказаться» от локальных скрытых переменных, и ссылается на примеры оставшихся лазеек как будучи «надуманным» и «чуждым обычному способу рассуждений в физике».

Работа Белла открыла возможность использования этих сверхсильных корреляций в качестве ресурса для общения. Это привело к открытию в 1984 году протоколов квантового распределения ключей , наиболее известный из которых — BB84 Чарльза Х. Беннета и Жиля Брассара. и E91 Артура Экерта . Хотя BB84 не использует запутанность, протокол Экерта использует нарушение неравенства Белла в качестве доказательства безопасности.

В 2022 году Нобелевская премия по физике была присуждена Алену Аспекту , Джону Клаузеру и Антону Цайлингеру «за эксперименты со запутанными фотонами, установление нарушения неравенств Белла и новаторство в области квантовой информатики».

Концепция

Значение запутанности

Запутанную систему можно определить как систему, квантовое состояние которой нельзя рассматривать как произведение состояний ее локальных составляющих; то есть они не являются отдельными частицами, а представляют собой неразделимое целое. В запутанности одну составляющую невозможно полностью описать без учета другой(их). Состояние сложной системы всегда выражается как сумма или суперпозиция произведений состояний локальных составляющих; он запутан, если эту сумму нельзя записать как одно произведение.

Квантовые системы могут запутываться в результате различных типов взаимодействий. Некоторые способы достижения запутанности в экспериментальных целях см. в разделе « Методы» ниже . Запутывание нарушается, когда запутанные частицы декогерируют за счет взаимодействия с окружающей средой; например, когда производится измерение.

В качестве примера запутанности: субатомная частица распадается на запутанную пару других частиц. События распада подчиняются различным законам сохранения , и в результате результаты измерений одной дочерней частицы должны быть сильно коррелированы с результатами измерений другой дочерней частицы (так, чтобы полный импульс, угловой момент, энергия и т. д. оставался неизменным). примерно одинаково до и после этого процесса). Например, частица со спином ноль может распасться на пару частиц со спином 1/2. Поскольку общий спин до и после этого распада должен быть равен нулю (сохранение углового момента), всякий раз, когда измеряется, что первая частица имеет спин вверх по какой-то оси, вторая частица, измеренная по той же оси, всегда оказывается со спином вниз. . (Это называется случаем спиновой антикорреляции; и если априорные вероятности измерения каждого спина равны, говорят, что пара находится в синглетном состоянии .)

Приведенный выше результат может быть воспринят как неожиданный. Классическая система будет обладать тем же свойством, и теория скрытых переменных для этого, безусловно, потребуется , основанная на сохранении углового момента как в классической, так и в квантовой механике. Разница в том, что классическая система всегда имеет определенные значения для всех наблюдаемых, а квантовая — нет. В некотором смысле, который будет обсуждаться ниже, рассматриваемая здесь квантовая система, по-видимому, приобретает распределение вероятностей для результата измерения спина вдоль любой оси другой частицы после измерения первой частицы. Это распределение вероятностей в целом отличается от того, каким оно было бы без измерения первой частицы. Это, конечно, может показаться удивительным в случае пространственно разделенных запутанных частиц.

Парадокс

Парадокс заключается в том, что измерение, произведенное на любой из частиц, по-видимому, разрушает состояние всей запутанной системы — и происходит это мгновенно, прежде чем какая-либо информация о результате измерения могла быть передана другой частице (при условии, что информация не может распространяться быстрее, чем свет ) и, следовательно, гарантировал «правильный» результат измерения другой части запутанной пары. В копенгагенской интерпретации результатом измерения спина одной из частиц является коллапс (волновой функции) в состояние, в котором каждая частица имеет определенный спин (либо вверх, либо вниз) вдоль оси измерения. Результат считается случайным, причем вероятность каждого варианта равна 50%. Однако, если оба спина измеряются вдоль одной и той же оси, они оказываются антикоррелированными. Это означает, что случайный результат измерения, сделанного на одной частице, по-видимому, был передан другой частице, так что она может сделать «правильный выбор», когда ее тоже будут измерять.

Расстояние и время измерений можно выбрать так, чтобы интервал между двумя измерениями был пространственным , следовательно, любой причинный эффект, связывающий события, должен был бы распространяться быстрее света. Согласно принципам специальной теории относительности , никакая информация не может перемещаться между двумя такими измерениями. Даже невозможно сказать, какое из измерений было первым. Для двух пространственно разделенных событий x ₁ и x ₂ существуют инерциальные системы отсчета , в которых x ₁ является первым, и другие, в которых x ₂ является первым. Следовательно, корреляцию между двумя измерениями нельзя объяснить как одно измерение, определяющее другое: разные наблюдатели расходятся во мнениях относительно роли причины и следствия.

(На самом деле подобные парадоксы могут возникнуть и без запутанности: положение отдельной частицы разбросано в пространстве, и два широко разнесенных детектора, пытающиеся обнаружить частицу в двух разных местах, должны мгновенно достичь соответствующей корреляции, чтобы они оба не обнаруживали частица.)

Теория скрытых переменных

Возможное решение парадокса состоит в том, чтобы предположить, что квантовая теория неполна, а результат измерений зависит от заранее определенных «скрытых переменных». Состояние измеряемых частиц содержит некоторые скрытые переменные , значения которых эффективно определяют, прямо с момента разделения, какими будут результаты измерений спина. Это означало бы, что каждая частица несет с собой всю необходимую информацию, и в момент измерения от одной частицы к другой ничего не нужно передавать. Эйнштейн и другие (см. предыдущий раздел) первоначально полагали, что это единственный выход из парадокса, а принятое квантовомеханическое описание (со случайным результатом измерения) должно быть неполным.

Нарушения неравенства Белла

Однако локальные теории скрытых переменных терпят неудачу, когда рассматриваются измерения вращения запутанных частиц вдоль разных осей. Если выполнено большое количество пар таких измерений (на большом количестве пар запутанных частиц), то статистически, если взгляд на локальный реалист или скрытые переменные верен, результаты всегда будут удовлетворять неравенству Белла . Ряд экспериментов на практике показал, что неравенство Белла не выполняется. Однако до 2015 года во всех этих экспериментах были проблемы с лазейками, которые сообщество физиков считало наиболее важными. Когда измерения запутанных частиц производятся в движущихся релятивистских системах отсчета, в которых каждое измерение (в своем релятивистском временном интервале) происходит раньше другого, результаты измерений остаются коррелированными.

Фундаментальная проблема измерения вращения по разным осям заключается в том, что эти измерения не могут иметь определенные значения одновременно — они несовместимы в том смысле, что максимальная одновременная точность этих измерений ограничена принципом неопределенности . Это противоречит тому, что наблюдается в классической физике, где любое количество свойств можно измерить одновременно с произвольной точностью. Математически доказано, что совместимые измерения не могут выявить корреляции, нарушающие неравенство Белла. и, таким образом, запутанность является фундаментально неклассическим явлением.

Известные экспериментальные результаты, доказывающие квантовую запутанность

Первый эксперимент, подтвердивший жуткое действие Эйнштейна на расстоянии (запутывание), был успешно подтвержден в лаборатории Чиен-Шиунг Ву и его коллегой И. Шакновым в 1949 году и был опубликован в первый день Нового года в 1950 году. Результат конкретно доказал квантовые корреляции. пары фотонов. В экспериментах 2012 и 2013 годов была создана поляризационная корреляция между фотонами, которые никогда не сосуществовали во времени. Авторы утверждали, что этот результат был достигнут путем обмена запутанностью между двумя парами запутанных фотонов после измерения поляризации одного фотона ранней пары, и что это доказывает, что квантовая нелокальность применима не только к пространству, но и ко времени.

В трех независимых экспериментах в 2013 году было показано, что классически передаваемые разделимые квантовые состояния могут использоваться для переноса запутанных состояний. Первый тест Белла без лазеек был проведен Рональдом Хэнсоном из Делфтского технологического университета в 2015 году, подтвердив нарушение неравенства Белла.

В августе 2014 года бразильский исследователь Габриэла Баррето Лемос и его команда смогли «сфотографировать» объекты, используя фотоны, которые не взаимодействовали с объектами, но были запутаны фотонами, которые взаимодействовали с такими объектами. Лемос из Венского университета уверен, что этот новый метод квантовой визуализации может найти применение там, где получение изображений при слабом освещении является обязательным, в таких областях, как биологическая или медицинская визуализация.

С 2016 года различные компании, например IBM и Microsoft, создали квантовые компьютеры, которые позволили разработчикам и техническим энтузиастам свободно экспериментировать с концепциями квантовой механики, включая квантовую запутанность.

Возникновение времени из квантовой запутанности

Существует фундаментальный конфликт, называемый проблемой времени , между тем, как понятие времени используется в квантовой механике , и той ролью, которую оно играет в общей теории относительности . В стандартных квантовых теориях время действует как независимый фон, на котором развиваются состояния, а оператор Гамильтона действует как генератор бесконечно малых перемещений квантовых состояний во времени.

Напротив, общая теория относительности рассматривает время как динамическую переменную , которая напрямую связана с материей и, кроме того, требует гамильтонова ограничения исчезновения . В квантовой общей теории относительности квантовая версия гамильтонова ограничения с использованием метрических переменных приводит к уравнению Уиллера-ДеВитта :

${\hat {H}}(x)|\psi \rangle =0$

где ${\hat {H}}(x)$ является гамильтоновым ограничением и $|\psi \rangle$ обозначает волновую функцию Вселенной . Оператор ${\hat {H}}$ действует в гильбертовом пространстве волновых функций, но это не то же самое гильбертово пространство, что и в нерелятивистском случае. Этот гамильтониан больше не определяет эволюцию системы, поскольку уравнение Шрёдингера : ${\hat {H}}|\psi \rangle =i\hbar {\partial \over {\partial t}}|\psi \rangle$, перестает быть действительным. Это свойство известно как безвременье. Были предприняты различные попытки включить время в полностью квантовую структуру, начиная с механизма Пейджа и Вуттерса и других последующих предложений.

Возникновение времени также было предложено как результат квантовых корреляций между развивающейся системы и эталонной системы квантовых часов, концепция запутанности системного времени вводится как квантификатор фактической различимой эволюции, претерпеваемой системой.

Возникающая гравитация

Основываясь на переписке AdS/CFT , Марк Ван Раамсдонк предположил, что пространство-время возникает как возникающий феномен квантовых степеней свободы, которые запутаны и живут на границе пространства-времени. Индуцированная гравитация может возникнуть из первого закона запутанности.

Нелокальность и запутанность

В средствах массовой информации и популярной науке квантовая нелокальность часто изображается как эквивалент запутанности. Хотя это верно для чистых двудольных квантовых состояний, в целом запутанность необходима только для нелокальных корреляций, но существуют смешанные запутанные состояния, которые не создают таких корреляций. Хорошо известным примером являются состояния Вернера , запутанные при определенных значениях $p_{sym}$, но всегда может быть описан с использованием локальных скрытых переменных. Более того, было показано, что для произвольного числа частиц существуют состояния, которые действительно запутаны, но допускают локальную модель.

Упомянутые доказательства существования локальных моделей предполагают, что одновременно доступна только одна копия квантового состояния. Если частицам позволить выполнять локальные измерения во многих копиях таких состояний, то многие явно локальные состояния (например, кубитные состояния Вернера) больше не могут быть описаны локальной моделью. Это, в частности, справедливо для всех дистиллируемых состояний. Однако остается открытым вопрос, станут ли все запутанные состояния нелокальными при наличии достаточного количества копий.

Запутывание состояния, разделяемого двумя частицами, необходимо, но недостаточно для того, чтобы это состояние было нелокальным. Запутанность чаще рассматривается как алгебраическая концепция, известная как предпосылка нелокальности, а также квантовой телепортации и сверхплотного кодирования , тогда как нелокальность определяется в соответствии с экспериментальной статистикой и гораздо больше связана с основами и интерпретациями. квантовой механики .

Квантово-механическая основа

Следующие подразделы предназначены для тех, кто хорошо разбирается в формальном математическом описании квантовой механики, включая знакомство с формализмом и теоретической базой, разработанной в статьях: нотация Бракета и математическая формулировка квантовой механики .

Чистые состояния

Рассмотрим две произвольные квантовые системы A и B соответственно с гильбертовыми пространствами H _A и H _B . Гильбертово пространство сложной системы представляет собой тензорное произведение

$H_{A}\otimes H_{B}.$

Если первая система находится в состоянии $|\psi \rangle _{A}$ и второй в штате $|\phi \rangle _{B}$, состояние сложной системы

$|\psi \rangle _{A}\otimes |\phi \rangle _{B}.$

Состояния сложной системы, которые можно представить в таком виде, называются сепарабельными состояниями, или состояниями-продуктами .

Не все состояния являются отделимыми состояниями (и, следовательно, состояниями-продуктами). Закрепить основу $\{|i\rangle _{A}\}$ для H _A и базиса $\{|j\rangle _{B}\}$ для ХБ _​ . Наиболее общее состояние в H _A ⊗ H _B имеет вид

$|\psi \rangle _{AB}=\sum _{i,j}c_{ij}|i\rangle _{A}\otimes |j\rangle _{B}$.

Это состояние сепарабельно, если существуют векторы $[c_{i}^{A}],[c_{j}^{B}]$ так что $c_{ij}=c_{i}^{A}c_{j}^{B},$ уступчивость ${\textstyle |\psi \rangle _{A}=\sum _{i}c_{i}^{A}|i\rangle _{A}}$ и ${\textstyle |\phi \rangle _{B}=\sum _{j}c_{j}^{B}|j\rangle _{B}.}$ Оно неразделимо, если для любых векторов $[c_{i}^{A}],[c_{j}^{B}]$ хотя бы для одной пары координат $c_{i}^{A},c_{j}^{B}$ у нас есть $c_{ij}\neq c_{i}^{A}c_{j}^{B}.$ Если государство неразделимо, его называют «запутанным государством».

Например, учитывая два базисных вектора $\{|0\rangle _{A},|1\rangle _{A}\}$ из H _A и двух базисных векторов $\{|0\rangle _{B},|1\rangle _{B}\}$ из H _B следующее состояние является запутанным:

${\tfrac {1}{\sqrt {2}}}\left(|0\rangle _{A}\otimes |1\rangle _{B}-|1\rangle _{A}\otimes |0\rangle _{B}\right).$

нельзя приписать Если сложная система находится в этом состоянии, то ни системе А , ни системе В определенное чистое состояние . Другими словами, хотя энтропия фон Неймана всего состояния равна нулю (как и для любого чистого состояния), энтропия подсистем больше нуля. В этом смысле системы «запутаны». Это имеет конкретные эмпирические последствия для интерферометрии. пример является одним из четырех состояний Белла , которые являются (максимально) запутанными чистыми состояниями (чистыми состояниями пространства ⊗ _B H Приведенный выше _, но которые не могут быть разделены на чистые состояния каждого HA _и HA H _B ).

что Алиса является наблюдателем системы A , а Боб — наблюдателем системы B. Теперь предположим , Если в приведенном выше состоянии запутанности Алиса производит измерение в $\{|0\rangle ,|1\rangle \}$ В соответствии с собственным базисом A существует два возможных исхода, происходящих с равной вероятностью:

1. Алиса измеряет 0, и состояние системы снижается до $|0\rangle _{A}|1\rangle _{B}$.
2. Алиса измеряет 1, и состояние системы схлопывается до $|1\rangle _{A}|0\rangle _{B}$.

Если произойдет первое, то любое последующее измерение, выполненное Бобом на том же базисе, всегда будет возвращать 1. Если произойдет последнее (Алиса измеряет 1), то измерение Боба с уверенностью вернет 0. Таким образом, система B была изменена Алисой, выполнившей локальное измерение A. системы Это остается верным, даже если системы A и B пространственно разделены. Это основа парадокса ЭПР.

Результат измерения Алисы случайен. Алиса не может решить, в какое состояние свернуть составную систему, и, следовательно, не может передавать информацию Бобу, воздействуя на свою систему. Таким образом, в этой конкретной схеме причинность сохраняется. Общий аргумент см. в теореме об отсутствии связи .

Ансамбли

Как упоминалось выше, состояние квантовой системы задается единичным вектором в гильбертовом пространстве. В более общем смысле, если у кого-то меньше информации о системе, то ее называют «ансамблем» и описывают ее с помощью матрицы плотности , которая представляет собой положительно-полуопределенную матрицу , или следового класса , когда пространство состояний бесконечномерно, и имеет след 1. Опять же по спектральной теореме такая матрица принимает общий вид:

$\rho =\sum _{i}w_{i}|\alpha _{i}\rangle \langle \alpha _{i}|,$

где w _i — положительнозначные вероятности (их сумма равна 1), векторы α _i — единичные векторы, и в бесконечномерном случае мы бы взяли замыкание таких состояний в норме следа. Мы можем интерпретировать ρ как представление ансамбля, где $w_{i}$ – это доля ансамбля, состояния которого $|\alpha _{i}\rangle$. Таким образом, когда смешанное состояние имеет ранг 1, оно описывает «чистый ансамбль». Когда информации о состоянии квантовой системы недостаточно, нам нужны матрицы плотности для представления состояния.

Экспериментально смешанный ансамбль можно реализовать следующим образом. Рассмотрим аппарат «черный ящик», который выбрасывает электроны в сторону наблюдателя. Гильбертовы пространства электронов идентичны . Аппарат мог бы производить электроны, находящиеся в одном и том же состоянии; в этом случае электроны, полученные наблюдателем, представляют собой чистый ансамбль. Однако аппарат мог производить электроны в разных состояниях. Например, он мог бы произвести две популяции электронов: одну с состоянием $|\mathbf {z} +\rangle$ со спинами, выровненными в положительном направлении z , а другой с состоянием $|\mathbf {y} -\rangle$ со спинами, выровненными в отрицательном направлении y . Как правило, это смешанный ансамбль, поскольку может быть любое количество популяций, каждая из которых соответствует отдельному штату.

Следуя приведенному выше определению, для двудольной составной системы смешанные состояния представляют собой просто матрицы плотности HA _H ⊗ на _B . То есть он имеет общий вид

$\rho =\sum _{i}w_{i}\left[\sum _{j}{\bar {c}}_{ij}(|\alpha _{ij}\rangle \otimes |\beta _{ij}\rangle )\right]\left[\sum _{k}c_{ik}(\langle \alpha _{ik}|\otimes \langle \beta _{ik}|)\right]$

где w _i — положительно оцененные вероятности, ${\textstyle \sum _{j}|c_{ij}|^{2}=1}$, а векторы являются единичными векторами. Оно самосопряженное, положительное и имеет след 1.

Расширяя определение отделимости от чистого случая, мы говорим, что смешанное состояние является отделимым, если его можно записать как

$\rho =\sum _{i}w_{i}\rho _{i}^{A}\otimes \rho _{i}^{B},$

где w _i — положительно оцененные вероятности, а $\rho _{i}^{A}$'песок $\rho _{i}^{B}$Сами по себе являются смешанными состояниями (операторами плотности) в подсистемах A и B соответственно. Другими словами, состояние является отделимым, если оно представляет собой распределение вероятностей по некоррелированным состояниям или состояниям-продуктам. Записывая матрицы плотности в виде сумм чистых ансамблей и разлагая их, мы можем без ограничения общности считать, что $\rho _{i}^{A}$ и $\rho _{i}^{B}$ сами по себе являются чистыми ансамблями. В таком случае состояние называется запутанным, если оно неразделимо.

В общем, выяснить, запутано или нет смешанное состояние, считается затруднительным. Показано, что общий двудольный случай NP-труден . Для случаев 2 × 2 и 2 × 3 необходимым и достаточным критерием разделимости является знаменитое условие положительного частичного транспонирования (PPT) .

Матрицы уменьшенной плотности

Идею матрицы уменьшенной плотности предложил Поль Дирак в 1930 году. Рассмотрим, как указано выше, системы A и B, каждая из которых имеет гильбертово пространство H _A , H _B . Пусть состояние сложной системы будет

$|\Psi \rangle \in H_{A}\otimes H_{B}.$

Как указано выше, в общем случае невозможно связать чистое состояние с компонентной A. системой Однако связать матрицу плотности все же возможно. Позволять

$\rho _{T}=|\Psi \rangle \;\langle \Psi |$.

который является оператором проекции на это состояние. Состояние A является частичным следом ρ : _T базисе системы B на

$\rho _{A}\ {\stackrel {\mathrm {def} }{=}}\ \sum _{j}^{N_{B}}\left(I_{A}\otimes \langle j|_{B}\right)\left(|\Psi \rangle \langle \Psi |\right)\left(I_{A}\otimes |j\rangle _{B}\right)={\hbox{Tr}}_{B}\;\rho _{T}.$

Сумма происходит за $N_{B}:=\dim(H_{B})$ и $I_{A}$ оператор идентификации в $H_{A}$. ρ _A иногда называют приведенной матрицей плотности ρ на подсистеме A . В просторечии мы «отслеживаем» систему B , чтобы получить приведенную матрицу плотности на A .

Например, приведенная матрица плотности A для запутанного состояния

${\tfrac {1}{\sqrt {2}}}\left(|0\rangle _{A}\otimes |1\rangle _{B}-|1\rangle _{A}\otimes |0\rangle _{B}\right),$

обсуждалось выше

$\rho _{A}={\tfrac {1}{2}}\left(|0\rangle _{A}\langle 0|_{A}+|1\rangle _{A}\langle 1|_{A}\right).$

Это показывает, что, как и ожидалось, приведенная матрица плотности для запутанного чистого ансамбля представляет собой смешанный ансамбль. Также неудивительно, что матрица плотности A для состояния чистого продукта $|\psi \rangle _{A}\otimes |\phi \rangle _{B}$ обсуждалось выше

$\rho _{A}=|\psi \rangle _{A}\langle \psi |_{A}$.

В общем, двучастное чистое состояние ρ запутано тогда и только тогда, когда его приведенные состояния являются смешанными, а не чистыми.

Два приложения, которые их используют

Матрицы приведенной плотности были явно рассчитаны для различных спиновых цепочек с уникальным основным состоянием. Примером может служить одномерная спиновая цепочка AKLT : основное состояние можно разделить на блок и окружение. Приведенная матрица плотности блока пропорциональна проектору вырожденному основному состоянию другого гамильтониана.

Матрица приведенной плотности также оценивалась для спиновых цепочек XY , где она имеет полный ранг. Было доказано, что в термодинамическом пределе спектр приведенной матрицы плотности большого блока спинов представляет собой точную геометрическую последовательность в этом случае.

Запутанность как ресурс

В квантовой теории информации запутанные состояния считаются «ресурсом», то есть чем-то дорогостоящим в производстве и позволяющим осуществлять ценные преобразования. Наиболее очевидна эта перспектива в условиях «отдаленных лабораторий», то есть двух квантовых систем, обозначенных «А» и «В», в каждой из которых могут выполняться произвольные квантовые операции , но которые не взаимодействуют друг с другом. механически. Единственное разрешенное взаимодействие — это обмен классической информацией, который в сочетании с наиболее общими локальными квантовыми операциями порождает класс операций, называемый LOCC (локальные операции и классическая коммуникация). Эти операции не позволяют создавать запутанные состояния между системами A и B. Но если A и B снабжены запасом запутанных состояний, то они вместе с операциями LOCC могут обеспечить более широкий класс преобразований. Например, взаимодействие между кубитом A и кубитом B можно реализовать, сначала телепортировав кубит A в B, а затем позволив ему взаимодействовать с кубитом B (что теперь является операцией LOCC, поскольку оба кубита находятся в лаборатории B) и затем телепортируем кубит обратно в A. В этом процессе используются два максимально запутанных состояния двух кубитов. Таким образом, запутанные состояния — это ресурс, который позволяет реализовать квантовые взаимодействия (или квантовые каналы) в условиях, когда доступны только LOCC, но они расходуются в процессе. Существуют и другие приложения, в которых запутанность можно рассматривать как ресурс, например, частное общение или различение квантовых состояний.

Классификация запутывания

Не все квантовые состояния одинаково ценны как ресурс. Для количественной оценки этого значения можно использовать различные меры запутанности (см. Ниже), которые присваивают числовое значение каждому квантовому состоянию. Однако часто бывает интересно остановиться на более грубом способе сравнения квантовых состояний. Это приводит к появлению различных схем классификации. Большинство классов запутанности определяются на основе того, можно ли преобразовать состояния в другие состояния с помощью LOCC или подкласса этих операций. Чем меньше набор разрешенных операций, тем точнее классификация. Важными примерами являются:

• Если два состояния могут быть преобразованы друг в друга с помощью локальной унитарной операции, говорят, что они находятся в одном классе LU . Это лучший из обычно рассматриваемых классов. Два состояния в одном классе LU имеют одинаковое значение для мер запутанности и то же значение, что и ресурс в настройке удаленных лабораторий. Существует бесконечное количество различных классов LU (даже в простейшем случае двух кубитов в чистом состоянии).
• Если два состояния могут быть преобразованы друг в друга с помощью локальных операций, включая измерения с вероятностью больше 0, говорят, что они принадлежат к одному и тому же «классу SLOCC» («стохастический LOCC»). Качественно два состояния $\rho _{1}$ и $\rho _{2}$ в одном и том же классе SLOCC одинаково эффективны (поскольку я могу преобразовать одно в другое, а затем делать все, что оно позволяет мне делать), но поскольку преобразования $\rho _{1}\to \rho _{2}$ и $\rho _{2}\to \rho _{1}$ могут добиться успеха с разной вероятностью, они уже не одинаково ценны. Например, для двух чистых кубитов существует только два класса SLOCC: запутанные состояния (которые содержат как (максимально запутанные) состояния Белла, так и слабо запутанные состояния, такие как $|00\rangle +0.01|11\rangle$) и отделимые (т.е. состояния продукта типа $|00\rangle$).
• Вместо рассмотрения преобразований отдельных копий состояния (например, $\rho _{1}\to \rho _{2}$) можно определять классы на основе возможности многокопийных преобразований. Например, есть примеры, когда $\rho _{1}\to \rho _{2}$ невозможно по LOCC, но $\rho _{1}\otimes \rho _{1}\to \rho _{2}$ возможно. Очень важная (и очень грубая) классификация основана на свойстве можно ли преобразовать сколь угодно большое количество копий состояния $\rho$ хотя бы в одно чисто запутанное состояние. Состояния, обладающие этим свойством, называются дистилляционными. Эти состояния являются наиболее полезными квантовыми состояниями, поскольку, если их достаточно, их можно преобразовать (с помощью локальных операций) в любое запутанное состояние и, следовательно, обеспечить все возможные варианты использования. Поначалу стало неожиданностью, что не все запутанные состояния поддаются дистилляции, а те, которые таковыми не являются, называются « связанными запутанными ».

Другая классификация запутанности основана на том, что квантовые корреляции, присутствующие в состоянии, позволяют делать A и B: различают три подмножества запутанных состояний: (1) нелокальные состояния , которые производят корреляции, которые не могут быть объяснены локальными скрытыми состояниями. переменную модель и, таким образом, нарушают неравенство Белла, (2) управляемые состояния , которые содержат достаточные корреляции для A, чтобы модифицировать («управлять») посредством локальных измерений условное приведенное состояние B таким образом, что A может доказать B, что состояние, которым они обладают, действительно запутано, и, наконец, (3) те запутанные состояния, которые не являются ни нелокальными, ни управляемыми. Все три множества непусты.

Энтропия

В этом разделе обсуждается энтропия смешанного состояния, а также то, как ее можно рассматривать как меру квантовой запутанности.

Определение

График зависимости энтропии фон Неймана от собственного значения для двудольного двухуровневого чистого состояния. Когда собственное значение имеет значение 0,5, энтропия фон Неймана максимальна, что соответствует максимальной запутанности.

В классической теории информации H , энтропия Шеннона , связана с распределением вероятностей, $p_{1},\cdots ,p_{n}$, следующим образом:

$H(p_{1},\cdots ,p_{n})=-\sum _{i}p_{i}\log _{2}p_{i}.$

Поскольку смешанное состояние ρ представляет собой распределение вероятностей по ансамблю, это естественным образом приводит к определению энтропии фон Неймана :

$S(\rho )=-{\hbox{Tr}}\left(\rho \log _{2}{\rho }\right).$

используется В общем, функциональное исчисление Бореля для вычисления неполиномиальной функции, такой как log ₂ ( ρ ) . Если неотрицательный оператор ρ действует в конечномерном гильбертовом пространстве и имеет собственные значения $\lambda _{1},\cdots ,\lambda _{n}$, log ₂ ( ρ ) оказывается не чем иным, как оператором с теми же собственными векторами, но собственными значениями $\log _{2}(\lambda _{1}),\cdots ,\log _{2}(\lambda _{n})$. Тогда энтропия Шеннона равна:

$S(\rho )=-{\hbox{Tr}}\left(\rho \log _{2}{\rho }\right)=-\sum _{i}\lambda _{i}\log _{2}\lambda _{i}$.

Поскольку событие с вероятностью 0 не должно вносить вклад в энтропию, и учитывая, что

$\lim _{p\to 0}p\log p=0,$

соглашение 0 log(0) = 0 принимается . Это распространяется и на бесконечномерный случай: если ρ имеет спектральное разрешение

$\rho =\int \lambda dP_{\lambda },$

примите то же соглашение при вычислении

$\rho \log _{2}\rho =\int \lambda \log _{2}\lambda dP_{\lambda }.$

Как и в статистической механике , чем большей неопределенностью (количеством микросостояний) должна обладать система, тем больше энтропия. Например, энтропия любого чистого состояния равна нулю, что неудивительно, поскольку нет никакой неопределенности относительно системы в чистом состоянии. Энтропия любой из двух подсистем запутанного состояния, обсуждавшегося выше, равна log(2) (можно показать, что это максимальная энтропия для 2 × 2 смешанных состояний ).

Как мера запутанности

Энтропия предоставляет один инструмент, который можно использовать для количественной оценки запутанности, хотя существуют и другие меры запутанности. Если вся система чиста, энтропию одной подсистемы можно использовать для измерения степени ее запутанности с другими подсистемами. Для двудольных чистых состояний энтропия фон Неймана приведенных состояний является уникальной мерой запутанности в том смысле, что это единственная функция в семействе состояний, которая удовлетворяет определенным аксиомам, необходимым для меры запутанности.

Классический результат состоит в том, что энтропия Шеннона достигает максимума при и только при равномерном распределении вероятностей {1/ n ,...,1/ n }. Поэтому двудольное чистое состояние ρ ∈ HA _если ⊗ H _B называется максимально запутанным состоянием, приведенное состояние каждой подсистемы ρ является диагональной матрицей

${\begin{bmatrix}{\frac {1}{n}}&&\\&\ddots &\\&&{\frac {1}{n}}\end{bmatrix}}.$

Для смешанных состояний пониженная энтропия фон Неймана не является единственной разумной мерой запутанности.

Кроме того, теоретико-информационное определение тесно связано с энтропией в смысле статистической механики. принято считать (сравнивая два определения в данном контексте, константу Больцмана k = 1 ). Например, по свойствам функционального исчисления Бореля мы видим, что для любого унитарного U оператора

$S(\rho )=S\left(U\rho U^{*}\right).$

Действительно, без этого свойства энтропия фон Неймана не была бы четко определена.

В частности, U мог бы быть оператором эволюции системы во времени, т. е.

$U(t)=\exp \left({\frac {-iHt}{\hbar }}\right),$

где H — гамильтониан системы. Здесь энтропия не меняется.

Энтропию Реньи также можно использовать как меру запутанности.

Меры по запутыванию

Меры запутанности количественно определяют степень запутанности в квантовом состоянии (часто рассматриваемом как двудольное). Как уже упоминалось, энтропия запутанности является стандартной мерой запутанности для чистых состояний (но больше не является мерой запутанности для смешанных состояний). Для смешанных состояний в литературе есть некоторые меры запутанности. и ни один из них не является стандартным.

• Стоимость запутывания
• Дистилляционная запутанность
• Запутывание образования
• Совпадение
• Относительная энтропия запутанности
• Раздавленное запутывание
• Логарифмическая отрицательность

Большинство (но не все) этих мер запутанности сводятся для чистых состояний к энтропии запутанности, и их трудно ( NP-трудно ) вычислить для смешанных состояний по мере роста размерности запутанной системы.

Квантовая теория поля

Теорему Риха -Шлидера квантовой теории поля иногда рассматривают как аналог квантовой запутанности.

Приложения

Запутанность имеет множество приложений в квантовой теории информации . С помощью запутанности можно достичь невыполнимых иначе задач.

Среди наиболее известных применений запутанности — сверхплотное кодирование и квантовая телепортация.

Большинство исследователей считают, что запутанность необходима для реализации квантовых вычислений (хотя некоторые это оспаривают).

Запутывание используется в некоторых протоколах квантовой криптографии . но для доказательства безопасности квантового распределения ключей (QKD) при стандартных предположениях не требуется запутанность. Однако независимая от устройства безопасность QKD, использующая запутанность между партнерами по связи. показана

Запутанные состояния

Существует несколько канонических запутанных состояний, которые часто возникают в теории и экспериментах.

Для двух кубитов таковы состояния Белла :

$|\Phi ^{\pm }\rangle ={\frac {1}{\sqrt {2}}}(|0\rangle _{A}\otimes |0\rangle _{B}\pm |1\rangle _{A}\otimes |1\rangle _{B})$

$|\Psi ^{\pm }\rangle ={\frac {1}{\sqrt {2}}}(|0\rangle _{A}\otimes |1\rangle _{B}\pm |1\rangle _{A}\otimes |0\rangle _{B}).$

Все эти четыре чистых состояния максимально запутаны (в соответствии с энтропией запутанности ) и образуют ортонормированный базис (линейную алгебру) гильбертова пространства двух кубитов. Они играют фундаментальную роль в теореме Белла .

Для кубитов M>2 состояние GHZ равно

$|\mathrm {GHZ} \rangle ={\frac {|0\rangle ^{\otimes M}+|1\rangle ^{\otimes M}}{\sqrt {2}}},$

что сводится к состоянию Белла $|\Phi ^{+}\rangle$ для $M=2$. Традиционное состояние GHZ было определено для $M=3$. Состояния ГГц иногда расширяются до кудитов , т. е. систем d , а не двухмерных систем.

Также для кубитов M>2 существуют спиновые сжатые состояния — класс сжатых когерентных состояний, удовлетворяющих определённым ограничениям на неопределённость измерений спина, которые обязательно запутаны. Состояния со сжатием спина являются хорошими кандидатами для повышения точности измерений с использованием квантовой запутанности.

Для двух бозонных мод ПОЛДЕНЬ состояние

$|\psi _{\text{NOON}}\rangle ={\frac {|N\rangle _{a}|0\rangle _{b}+|{0}\rangle _{a}|{N}\rangle _{b}}{\sqrt {2}}},\,$

Это похоже на состояние Белла $|\Psi ^{+}\rangle$ за исключением того, что базисные кеты 0 и 1 были заменены на « N фотонов находятся в одном режиме» и « N фотонов находятся в другом режиме».

Наконец, существуют также двойные состояния Фока для бозонных мод, которые можно создать, подав состояние Фока в два плеча, ведущих к светоделителю. Они представляют собой сумму нескольких состояний NOON и могут использоваться для достижения предела Гейзенберга.

При правильно выбранных мерах запутанности состояния Белла, GHZ и NOON максимально запутаны, в то время как спин-сжатые и двойные состояния Фока запутаны лишь частично. Частично запутанные состояния обычно легче получить экспериментально.

Способы создания запутанности

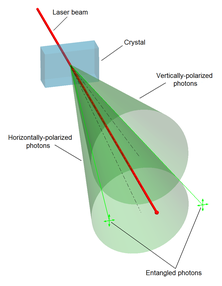
Запутывание обычно создается прямым взаимодействием между субатомными частицами. Эти взаимодействия могут принимать различные формы. Одним из наиболее часто используемых методов является спонтанное параметрическое преобразование с понижением частоты для генерации пары фотонов, запутанных в поляризации. Другие методы включают использование волоконного соединителя для удержания и смешивания фотонов, фотонов, испускаемых каскадом распада биэкситона в квантовой точке . использование эффекта Хонга-Оу-Манделя и др. Квантовая запутанность частицы и ее античастицы , такой как электрон и позитрон , может быть создана путем частичного перекрытия соответствующих квантовых волновых функций в интерферометре Харди . В самых ранних проверках теоремы Белла запутанные частицы генерировались с помощью атомных каскадов .

Также возможно создать запутанность между квантовыми системами, которые никогда напрямую не взаимодействовали, с помощью замены запутанности . Две независимо приготовленные идентичные частицы также могут быть запутаны, если их волновые функции просто перекрываются в пространстве, по крайней мере частично.

Тестирование системы на запутывание

Матрица плотности ρ называется сепарабельной, если ее можно записать в виде выпуклой суммы состояний-продуктов, а именно $${\rho =\sum _{j}p_{j}\rho _{j}^{(A)}\otimes \rho _{j}^{(B)}}$$ с $0\leq p_{j}\leq 1$ вероятности. По определению, состояние запутано, если оно неразделимо.

Для систем 2-кубит и кубит-кутрит (2 × 2 и 2 × 3 соответственно) простой критерий Переса – Городецкого обеспечивает как необходимый, так и достаточный критерий разделимости и, следовательно, — непреднамеренно — для обнаружения запутанности. Однако в общем случае критерий просто необходим для разделимости, поскольку при обобщении проблема становится NP-трудной. Другие критерии разделимости включают (но не ограничиваются ими) критерий диапазона , критерий редукции и критерии, основанные на соотношениях неопределенности. См. ссылку. за обзор критериев разделимости в системах с дискретными переменными и работу 1. за обзор методов и проблем экспериментальной сертификации запутанности в системах с дискретными переменными.

Численный подход к проблеме предложен Йоном Магне Лейнаасом , Яном Мирхеймом и Эйриком Оврумом в их статье «Геометрические аспекты запутанности». Лейнаас и др. предложить численный подход, итеративно уточняя предполагаемое разделимое состояние до целевого состояния, подлежащего тестированию, и проверяя, действительно ли целевое состояние может быть достигнуто. Реализацией алгоритма (включая встроенный критерий Переса-Городецкого ) является веб-приложение StateSeparator.

В системах с непрерывными переменными также применяется критерий Переса-Городецкого. В частности, Саймон сформулировал частный вариант критерия Переса-Городецкого в терминах моментов второго порядка канонических операторов и показал, что он необходим и достаточен для $1\oplus 1$-модальные гауссовы состояния (см. для, казалось бы, другого, но по сути эквивалентного подхода). Позже было найдено что условие Саймона также необходимо и достаточно для $1\oplus n$-модные гауссовы состояния, но уже недостаточны для $2\oplus 2$-режимные гауссовы состояния. Условие Саймона можно обобщить, приняв во внимание моменты высших порядков канонических операторов. или с помощью энтропийных мер.

был запущен первый в мире спутник квантовой связи 16 августа 2016 года с космодрома Цзюцюань в Китае в рамках миссии «Квантовые эксперименты в космическом масштабе » (QUESS), получивший прозвище « Миций » в честь древнего китайского философа. Спутник был предназначен для демонстрации возможности квантовой связи между Землей и космосом и проверки квантовой запутанности на беспрецедентных расстояниях.

от 16 июня 2017 г. В номере журнала Science Инь и др. отчет, устанавливающий новый рекорд расстояния квантовой запутанности в 1203 км, демонстрирующий выживание двухфотонной пары и нарушение неравенства Белла, достигая оценки CHSH 2,37 ± 0,09 при строгих условиях локальности Эйнштейна, от спутника Мициуса до баз. в Лицзяне, Юньнань и Делинге, Квинхай, что на порядок повышает эффективность передачи по сравнению с предыдущими оптоволоконными экспериментами.

Естественно запутанные системы

Электронные оболочки многоэлектронных атомов всегда состоят из запутанных электронов. Правильную энергию ионизации можно рассчитать только с учетом электронной запутанности.

Запутывание макроскопических объектов

В 2020 году исследователи сообщили о квантовой запутанности между движением механического осциллятора миллиметрового размера и несопоставимой удаленной спиновой системой облака атомов. Более поздняя работа дополнила эту работу квантовой запутанностью двух механических осцилляторов.

Запутывание элементов живых систем

В октябре 2018 года физики сообщили о создании квантовой запутанности с использованием живых организмов , в частности, между фотосинтезирующими молекулами внутри живых бактерий и квантованным светом .

Живые организмы (зеленые серные бактерии) изучались как медиаторы для создания квантовой запутанности между невзаимодействующими световыми модами, что демонстрирует высокую степень запутанности между световыми и бактериальными модами и, в некоторой степени, даже запутанность внутри бактерий.

См. также

• Связанное запутывание
• Совпадение
• ворота CNOT
• Мысленные эксперименты Эйнштейна
• Перегонка перепутывания
• Свидетель запутанности
• ЭР = ЭПР
• Связь быстрее света
• Многосторонняя запутанность
• Нормально распределенные и некоррелированные не подразумевают независимость.
• Принцип исключения Паули
• Квантовая когерентность
• Квантовые вычисления
• Квантовый диссонанс
• Квантовая сеть
• Квантовый фазовый переход
• Квантовая псевдотелепатия
• Квантовая телепортация
• Ретропричинность
• Сепарабельное состояние
• Спонтанное параметрическое преобразование с понижением частоты
• Раздавленное запутывание
• Эксперимент Штерна-Герлаха
• Амплитуда вероятности Уорда

Дальнейшее чтение

• Альберт, Дэвид З.; Галчен, Ривка (2009). «Был ли Эйнштейн неправ?: Квантовая угроза специальной теории относительности» . Научный американец . 300 (3): 32–39. doi : 10.1038/scientificamerican0309-32 . ПМИД   19253771 .
• Бенгтссон И.; Жичковский К. (2006). «Геометрия квантовых состояний». Введение в квантовую запутанность . Кембридж: Издательство Кембриджского университета. второе, исправленное издание (2017 г.)
• Баб, Джеффри (2019). «Квантовая запутанность и информация» . Стэнфордская энциклопедия философии . Стэнфорд, Калифорния: Стэнфордский университет.
• Крамер Дж.Г. (2015). Квантовое рукопожатие: запутанность, нелокальность и транзакции . Спрингер Верлаг. ISBN  978-3-319-24642-0 .
• Дуарте Ф.Дж. (2019). Основы квантовой запутанности . Бристоль, Великобритания: Институт физики. ISBN  978-0-7503-2226-3 .
• Гюне О, Тот Г (2009). «Обнаружение запутывания». Отчеты по физике . 474 (1–6): 1–75. arXiv : 0811.2803 . Бибкод : 2009ФР...474....1Г . дои : 10.1016/j.physrep.2009.02.004 . S2CID   119288569 .
• Бхаскара В.С., Паниграхи ПК (2017). «Обобщенная мера совпадения для точной количественной оценки многочастичной запутанности в чистом состоянии с использованием тождества Лагранжа и клинового произведения». Квантовая обработка информации . 16 (5): 118. arXiv : 1607.00164 . Бибкод : 2017QuIP...16..118B . дои : 10.1007/s11128-017-1568-0 . S2CID   43754114 .
• Суэйн С.Н., Бхаскара В.С., Паниграхи ПК (2022 г.). «Обобщенная мера запутанности для систем с непрерывными переменными». Физ. Преподобный А. 105 (5): 052441. arXiv : 1706.01448 . Бибкод : 2022PhRvA.105e2441S . дои : 10.1103/PhysRevA.105.052441 . S2CID   239885759 .
• Джагер Г (2009). Запутывание, информация и интерпретация квантовой механики . Гейдельберг: Спрингер. ISBN  978-3-540-92127-1 .
• Стюард Э.Г. (2008). Квантовая механика: ее раннее развитие и путь к запутанности . Издательство Имперского колледжа. ISBN  978-1-86094-978-4 .

Внешние ссылки

• Пояснительное видео от Scientific American журнала
• Эксперимент по запутанности пар фотонов – интерактивный
• Аудио – Каин/Гей (2009) актеров астрономии Запутывание
• «Жуткие действия на расстоянии?»: Лекция Оппенгеймера, профессор Дэвид Мермин (Корнельский университет), ун. Калифорния, Беркли, 2008 г. Нематематическая популярная лекция на YouTube, опубликована в марте 2008 г.
• «Квантовая запутанность против классической корреляции» (интерактивная демонстрация)