Вязкость
| Вязкость | |
|---|---|
 Моделирование жидкостей различной вязкости. Жидкость слева имеет меньшую вязкость, чем жидкость справа. | |
Общие символы | ч , м |
Выводы из другие количества | µ = G · t |
| Измерение | |
| Часть серии о |
| Механика сплошных сред |
|---|
Вязкость жидкости сопротивления является мерой ее деформации при заданной скорости. [1] Для жидкостей это соответствует неформальному понятию «густота»: например, сироп имеет более высокую вязкость, чем вода . [2] Вязкость определяется с научной точки зрения как сила, умноженная на время, разделенное на площадь. Таким образом, единицей измерения в системе СИ являются ньютоны-секунды на квадратный метр или паскаль-секунды. [1]
Вязкость количественно определяет силу внутреннего трения между соседними слоями жидкости, находящимися в относительном движении. [1] Например, когда вязкая жидкость проталкивается через трубку, она течет быстрее вблизи центральной линии трубки, чем вблизи ее стенок. [3] Эксперименты показывают, что для поддержания потока необходимо некоторое напряжение (например, разница давлений между двумя концами трубки). Это связано с тем, что для преодоления трения между слоями жидкости, находящимися в относительном движении, требуется сила. Для трубки с постоянной скоростью потока сила компенсирующей силы пропорциональна вязкости жидкости.
В общем, вязкость зависит от состояния жидкости, например, от ее температуры, давления и скорости деформации. Однако в некоторых случаях зависимость от некоторых из этих свойств незначительна. Например, вязкость ньютоновской жидкости существенно не меняется в зависимости от скорости деформации.
Нулевая вязкость (отсутствие сопротивления сдвиговому напряжению ) наблюдается только при очень низких температурах в сверхтекучих средах ; в противном случае второй закон термодинамики требует, чтобы все жидкости имели положительную вязкость. [4] [5] Жидкость, имеющая нулевую вязкость (невязкая), называется идеальной или невязкой .
Этимология
[ редактировать ]Слово «вязкость» происходит от латинского viscum (« омела »). Вискум также назывался вязким клеем, полученным из ягод омелы. [6]
Определения
[ редактировать ]Динамическая вязкость
[ редактировать ]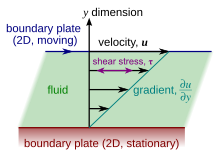

В материаловедении и инженерии часто возникает интерес к пониманию сил или напряжений, участвующих в деформации материала. Например, если бы материал был простой пружиной, ответ был бы дан законом Гука , который гласит, что сила, испытываемая пружиной, пропорциональна расстоянию, смещенному от равновесия. Напряжения, которые можно объяснить деформацией материала из некоторого состояния покоя, называются упругими напряжениями. В других материалах присутствуют напряжения, которые можно объяснить скоростью деформации с течением времени . Их называют вязкими напряжениями. Например, в такой жидкости, как вода, напряжения, возникающие при сдвиге жидкости, не зависят от расстояния, на которое жидкость была сдвинута; скорее, они зависят от того, насколько быстро происходит сдвиг.
Вязкость — это свойство материала, которое связывает вязкие напряжения в материале со скоростью изменения деформации (скоростью деформации). Хотя это применимо к общим потокам, его легко визуализировать и определить в простом сдвиговом потоке, таком как плоское течение Куэтта .
В потоке Куэтта жидкость зажата между двумя бесконечно большими пластинами: одна неподвижна, а другая движется параллельно с постоянной скоростью. (см. иллюстрацию справа). Если скорость верхней пластины достаточно мала (во избежание турбулентности), то в установившемся режиме частицы жидкости движутся параллельно ей, а их скорость изменяется от внизу, чтобы наверху. [7] Каждый слой жидкости движется быстрее, чем тот, что находится непосредственно под ним, и трение между ними порождает силу, сопротивляющуюся их относительному движению. В частности, жидкость прикладывает к верхней пластине силу в направлении, противоположном ее движению, и равную, но противоположную силу к нижней пластине. Поэтому требуется внешняя сила, чтобы поддерживать движение верхней пластины с постоянной скоростью.
Во многих жидкостях наблюдается линейное изменение скорости потока от нуля внизу до наверху. Кроме того, величина силы, , действующее на верхнюю пластину оказывается пропорциональным скорости и площадь каждой пластины и обратно пропорциональна их расстоянию :
Коэффициент пропорциональности — это динамическая вязкость жидкости, часто называемая просто вязкостью . Обозначается греческой буквой мю ( μ ). Динамическая вязкость имеет размеры , что приводит к единицам СИ и производным единицам :
Вышеупомянутое соотношение называется скоростью сдвиговой деформации или скоростью сдвига и является производной скорости жидкости в направлении, параллельном вектору нормали пластин (см. иллюстрации справа). Если скорость не изменяется линейно с , то подходящее обобщение таково:
где , и - локальная скорость сдвига. Это выражение называется законом вязкости Ньютона . В сдвиговых потоках с плоской симметрией именно это определяет . Это частный случай общего определения вязкости (см. ниже), которое можно выразить в бескоординатной форме.
Использование греческой буквы мю ( ) для динамической вязкости (иногда также называемой абсолютной вязкостью ) распространено среди инженеров -механиков и химиков , а также математиков и физиков. [8] [9] [10] Однако греческая буква эта ( ) также используется химиками, физиками и ИЮПАК . [11] Вязкость иногда также называют сдвиговой вязкостью . Однако по крайней мере один автор не одобряет использование этой терминологии, отмечая, что могут появляться не только в сдвиговых течениях, но и в несдвиговых течениях. [12]
Кинематическая вязкость
[ редактировать ]В гидродинамике иногда более уместно работать с терминами кинематической вязкости (иногда также называемой коэффициентом диффузии импульса ), определяемой как отношение динамической вязкости ( μ ) к плотности жидкости ( ρ ). Обычно его обозначают греческой буквой nu ( ν ):
и имеет размеры , что приводит к единицам СИ и производным единицам :
- удельная энергия, умноженная на время энергия единицы массы, умноженная на время.
Общее определение
[ редактировать ]В самых общих чертах вязкие напряжения в жидкости определяются как напряжения, возникающие в результате относительной скорости различных частиц жидкости. Таким образом, вязкие напряжения должны зависеть от пространственных градиентов скорости потока. Если градиенты скорости малы, то вязкие напряжения в первом приближении зависят только от первых производных скорости. [13] (Для ньютоновских жидкостей это также линейная зависимость.) В декартовых координатах общее соотношение тогда можно записать как
где - тензор вязкости, отображающий градиента скорости тензор на тензор вязких напряжений . [14] Поскольку индексы в этом выражении могут варьироваться от 1 до 3, то существует 81 «коэффициент вязкости». всего. Однако если предположить, что тензор вязкости ранга 2 изотропен , эти 81 коэффициент сводится к трем независимым параметрам. , , :
и, кроме того, предполагается, что никакие вязкие силы не могут возникнуть, когда жидкость подвергается простому вращению твердого тела, таким образом , оставив только два независимых параметра. [13] Наиболее обычное разложение происходит по стандартной (скалярной) вязкости. и объемная вязкость такой, что и . В векторной записи это выглядит так:
где – единичный тензор. [12] [15] Это уравнение можно рассматривать как обобщенную форму закона вязкости Ньютона.
Объемная вязкость (также называемая объемной вязкостью) отражает тип внутреннего трения, которое препятствует сжатию или расширению жидкости без сдвига. Знание часто не требуется в задачах гидродинамики. Например, несжимаемая жидкость удовлетворяет условию и поэтому термин, содержащий выпадает. Более того, часто считается пренебрежимо малым для газов, поскольку в одноатомном идеальном газе . [12] Одна ситуация, в которой Важное значение может иметь расчет потерь энергии в звуковых и ударных волнах , описываемых законом затухания звука Стокса , поскольку эти явления связаны с быстрым расширением и сжатием.
Определяющие уравнения вязкости не являются фундаментальными законами природы, поэтому их полезность, а также методы измерения или расчета вязкости должны устанавливаться отдельными средствами. Потенциальная проблема заключается в том, что вязкость, в принципе, зависит от полного микроскопического состояния жидкости, которое включает в себя положение и импульс каждой частицы в системе. [16] Такая подробная информация обычно недоступна в реалистичных системах. Однако при определенных условиях большая часть этой информации может оказаться незначительной. В частности, для ньютоновских жидкостей вблизи равновесия и вдали от границ (объемное состояние) вязкость зависит только от пространственно-временных макроскопических полей (таких как температура и плотность), определяющих локальное равновесие. [16] [17]
Тем не менее, вязкость все еще может иметь существенную зависимость от нескольких свойств системы, таких как температура, давление, а также амплитуда и частота любого внешнего воздействия. Таким образом, прецизионные измерения вязкости определяются толькоотносительно конкретного состояния жидкости. [18] Чтобы стандартизировать сравнения экспериментов и теоретических моделей, данные о вязкости иногда экстраполируются на идеальные предельные случаи, такие как предел нулевого сдвига или (для газов) предел нулевой плотности .
Импульсный транспорт
[ редактировать ]Теория переноса предлагает альтернативную интерпретацию вязкости с точки зрения переноса импульса: вязкость — это свойство материала, которое характеризует перенос импульса внутри жидкости, точно так же, как теплопроводность характеризует перенос тепла , а коэффициент диффузии (массовой) характеризует перенос массы. [19] Эта точка зрения неявно заложена в законе вязкости Ньютона: , поскольку напряжение сдвига имеет единицы измерения, эквивалентные потоку импульса , т. е. импульсу в единицу времени на единицу площади. Таким образом, можно интерпретировать как определение потока импульса в направлении от одного слоя жидкости к другому. Согласно закону вязкости Ньютона, этот поток импульса происходит поперек градиента скорости, и величина соответствующего потока импульса определяется вязкостью.
Можно провести явную аналогию с тепломассопереносом. Точно так же, как тепло течет от высокой температуры к низкой температуре, а масса течет от высокой плотности к низкой, импульс течет от высокой скорости к низкой скорости. Все эти поведения описываются компактными выражениями, называемыми определяющими отношениями , одномерные формы которых приведены здесь:
где плотность, и – потоки массы и тепла, а и – массопроводность и теплопроводность. [20] Тот факт, что перенос массы, импульса и энергии (тепла) являются одними из наиболее важных процессов в механике сплошной среды, не является совпадением: это одни из немногих физических величин, которые сохраняются на микроскопическом уровне при межчастичных столкновениях. Таким образом, их динамика не диктуется быстрым и сложным микроскопическим временным масштабом взаимодействия, а происходит в макроскопических временных масштабах, как описывается различными уравнениями теории переноса и гидродинамики.
Ньютоновские и неньютоновские жидкости
[ редактировать ]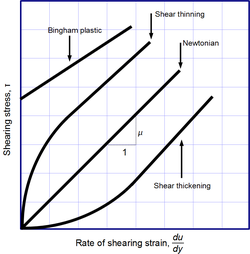
Закон вязкости Ньютона не является фундаментальным законом природы, а скорее определяющим уравнением (подобно закону Гука , закону Фика и закону Ома ), которое служит для определения вязкости. . Его форма обусловлена экспериментами, которые показывают, что для широкого диапазона жидкостей не зависит от скорости деформации. Такие жидкости называются ньютоновскими . Газы , воду и многие обычные жидкости можно считать ньютоновскими в обычных условиях и контекстах. Однако существует множество неньютоновских жидкостей , поведение которых значительно отклоняется от такого поведения. Например:
- Загущающиеся при сдвиге (дилатантные) жидкости, вязкость которых увеличивается со скоростью сдвиговой деформации.
- Жидкости , разжижающие сдвиг , вязкость которых уменьшается со скоростью деформации сдвига.
- Тиксотропные жидкости, которые со временем становятся менее вязкими при встряхивании, взбалтывании или ином воздействии.
- Реопектические жидкости, которые со временем становятся более вязкими при встряхивании, взбалтывании или ином воздействии.
- Пластики Бингама , которые ведут себя как твердое тело при низких напряжениях, но текут как вязкая жидкость при высоких напряжениях.
Коэффициент Трутона представляет собой отношение вязкости при растяжении к вязкости при сдвиге . Для ньютоновской жидкости коэффициент Трутона равен 3. [21] [22] Жидкости, разжижающие сдвиг, очень часто, но ошибочно, называют тиксотропными. [23]
Вязкость также может зависеть от физического состояния жидкости (температуры и давления) и других внешних факторов. Для газов и других сжимаемых жидкостей оно зависит от температуры и очень медленно меняется с давлением. Вязкость некоторых жидкостей может зависеть от других факторов. магнитного поля Например, магнитореологическая жидкость становится толще под воздействием , возможно, до такой степени, что ведет себя как твердое тело.
В твердых телах
[ редактировать ]Силы вязкости, возникающие при течении жидкости, отличаются от сил упругости , возникающих в твердом теле в ответ на напряжения сдвига, сжатия или растяжения. В то время как в последнем случае напряжение пропорционально величине деформации сдвига, в жидкости оно пропорционально скорости деформации с течением времени. По этой причине Джеймс Клерк Максвелл использовал термин «бегущая эластичность» для обозначения вязкости жидкости.
Однако многие жидкости (включая воду) кратковременно реагируют как упругие твердые тела при внезапном напряжении. И наоборот, многие «твердые тела» (даже гранит ) будут течь как жидкости, хотя и очень медленно, даже при сколь угодно малом напряжении. [24] Такие материалы лучше всего охарактеризовать как вязкоупругие , то есть обладающие как эластичностью (реакция на деформацию), так и вязкостью (реакция на скорость деформации).
Вязкоупругие твердые вещества могут проявлять как сдвиговую вязкость, так и объемную вязкость. Вязкость при растяжении представляет собой линейную комбинацию сдвиговой и объемной вязкостей, которая описывает реакцию твердого эластичного материала на удлинение. Он широко используется для характеристики полимеров.
В геологии земные материалы, демонстрирующие вязкую деформацию, по крайней мере на три порядка превышающую их упругую деформацию, иногда называют рейдами . [25]
Измерение
[ редактировать ]Вязкость измеряют различными типами вискозиметров и реометров . Тщательный контроль температуры жидкости необходим для получения точных измерений, особенно для таких материалов, как смазочные материалы, вязкость которых может удвоиться при изменении всего на 5 °C. Реометр используется для жидкостей, вязкость которых невозможно определить по одному значению и поэтому требуется установка и измерение большего количества параметров, чем в случае вискозиметра. [26]
Для некоторых жидкостей вязкость постоянна в широком диапазоне скоростей сдвига ( ньютоновские жидкости ). Жидкости без постоянной вязкости ( неньютоновские жидкости ) не могут быть описаны одним числом. Неньютоновские жидкости демонстрируют множество различных корреляций между напряжением сдвига и скоростью сдвига.
Одним из наиболее распространенных приборов для измерения кинематической вязкости является стеклянный капиллярный вискозиметр.
В промышленности по нанесению покрытий вязкость можно измерять с помощью чашки, в которой время истечения измеряется . Существует несколько типов чашек, таких как чашка Зана и чашка вязкости Форда , причем использование каждого типа варьируется в основном в зависимости от отрасли.
, также используемый в покрытиях, Вискозиметр Штормера использует вращение в зависимости от нагрузки для определения вязкости. Вязкость указывается в единицах Кребса (КУ), которые являются уникальными для вискозиметров Штормера.
Вибрационные вискозиметры также можно использовать для измерения вязкости. Резонансные или вибрационные вискозиметры работают за счет создания поперечных волн в жидкости. В этом методе датчик погружается в жидкость и заставляет его резонировать на определенной частоте. Когда поверхность датчика проходит через жидкость, энергия теряется из-за ее вязкости. Затем эта рассеиваемая энергия измеряется и преобразуется в показания вязкости. Более высокая вязкость приводит к большим потерям энергии. [ нужна ссылка ]
Вязкость при растяжении можно измерить с помощью различных реометров , создающих напряжение при растяжении .
Объемную вязкость можно измерить акустическим реометром .
Кажущаяся вязкость — это расчет, полученный на основе испытаний, проведенных с буровым раствором, используемым при разработке нефтяных или газовых скважин. Эти расчеты и испытания помогают инженерам разрабатывать и поддерживать свойства бурового раствора в соответствии с требуемыми спецификациями.
Нановязкость (вязкость, измеряемая нанозондами) можно измерить с помощью флуоресцентной корреляционной спектроскопии . [27]
Единицы
[ редактировать ]Единицей в системе СИ динамической вязкости является ньютон -секунда на квадратный метр (Н·с/м). 2 ), также часто выражается в эквивалентных формах паскаль - секунда (Па·с), килограмм на метр в секунду (кг·м −1 ·с −1 ) и пуазейль (Пл.). Единицей СГС является пуаз (П или г·см). −1 ·с −1 = 0,1 Па·с), [28] назван в честь Жана Леонара Мари Пуазейля . Обычно его выражают, особенно в ASTM стандартах , в сантипуазах (сП). Сантипуаз удобен тем, что вязкость воды при 20 °C составляет около 1 сП, а один сантипуаз равен миллипаскалю-секунде системы СИ (мПа·с).
Единицей кинематической вязкости в системе СИ является квадратный метр в секунду (м 2 /с), тогда как единицей СГС для кинематической вязкости является стокс (Ст или см). 2 ·с −1 = 0,0001 м 2 ·с −1 ), названный в честь сэра Джорджа Габриэля Стоукса . [29] В США слово «стоук» иногда используется в единственном числе. 1 . мм Вместо этого часто используются дробные сантистоксы (сСт), 1 сСт = 2 ·с −1 = 10 −6 м 2 ·с −1 . 1 сСт равен 1 сП, разделенному на 1000 кг/м^3, что близко к плотности воды. Кинематическая вязкость воды при 20 °С составляет около 1 сСт.
Наиболее часто используемые системы обычных или имперских единиц США — это британская гравитационная (BG) и английская инженерная (EE). В системе BG динамическая вязкость измеряется в фунтах -секундах на квадратный фут (фунт·с/фут). 2 ), а в системе EE он имеет единицы фунт-сила -секунды на квадратный фут (фунт-сила·с/фут 2 ). Фунт и фунт-сила эквивалентны; две системы различаются только тем, как определяются сила и масса. В системе BG фунт является основной единицей, из которой единица массы (снаряд ) определяется вторым законом Ньютона , тогда как в системе EE единицы силы и массы (фунт-сила и фунт-масса соответственно) равны определяется независимо посредством Второго закона с использованием константы пропорциональности g c .
Кинематическая вязкость измеряется в квадратных футах в секунду (футах). 2 /s) как в системах BG, так и в EE.
К нестандартным единицам измерения относятся рейн (фунт-сила·с/дюйм). 2 ), британская единица динамической вязкости. [30] В автомобильной промышленности индекс вязкости используется для описания изменения вязкости с температурой.
Обратной , вязкостью является текучесть обычно обозначаемая или , в зависимости от используемого соглашения, измеряется в обратном равновесии (P −1 , или см · с · г −1 ), иногда называемый rhe . Текучесть редко используется в инженерной практике. [ нужна ссылка ]
Одно время нефтяная промышленность полагалась на измерение кинематической вязкости с помощью вискозиметра Сейболта и выражение кинематической вязкости в единицах универсальных секунд Сейболта (SUS). [31] и другие сокращения, такие как SSU ( универсальные секунды Saybolt ) или SUV ( универсальная вязкость Saybolt Иногда используются ). Кинематическая вязкость в сантистоксах может быть преобразована из SUS в соответствии с арифметикой и справочной таблицей, приведенной в ASTM D 2161.
Молекулярное происхождение
[ редактировать ]Перенос импульса в газах осуществляется дискретными столкновениями молекул, а в жидкостях — силами притяжения, которые связывают молекулы близко друг к другу. [19] Из-за этого динамическая вязкость жидкостей обычно намного больше, чем у газов. Кроме того, вязкость имеет тенденцию увеличиваться с температурой в газах и уменьшаться с температурой в жидкостях.
жидкость-газ Выше критической точки жидкая и газовая фазы заменяются одной сверхкритической фазой . В этом режиме механизмы переноса импульса интерполируют поведение жидкости и газа.Например, вдоль сверхкритической изобары (поверхности постоянного давления) кинематическая вязкость уменьшается при низкой температуре и увеличивается при высокой температуре с минимумом между ними. [32] [33] Приблизительная оценка стоимостикак минимум это
где — постоянная Планка , - масса электрона , а это молекулярная масса. [33]
Однако вообще вязкость системы в деталях зависит от того, как взаимодействуют молекулы, составляющие систему, и для нее не существует простых, но правильных формул. Простейшими точными выражениями являются соотношения Грина-Кубо для линейной сдвиговой вязкости или выражения нестационарной временной корреляционной функции, полученные Эвансом и Морриссом в 1988 году. [34] Хотя каждое из этих выражений является точным, расчет вязкости плотной жидкости с использованием этих соотношений в настоящее время требует использования компьютерного моделирования молекулярной динамики . Несколько большего прогресса можно добиться для разбавленного газа, поскольку элементарные предположения о том, как движутся и взаимодействуют молекулы газа, приводят к базовому пониманию молекулярной природы вязкости. Более сложные методы лечения могут быть построены путем систематического уточнения уравнений движения молекул газа. Примером такой трактовки является теория Чепмена-Энскога , которая выводит выражения для вязкости разбавленного газа из уравнения Больцмана . [17]
Чистые газы
[ редактировать ]Элементарный расчет вязкости разбавленного газа
Вязкость газов возникает главным образом из-за молекулярной диффузии , которая передает импульс между слоями потока. Элементарный расчет для разбавленного газа при температуре и плотность дает
где — постоянная Больцмана , молекулярная масса и числовая константа порядка . Количество , средняя длина свободного пробега , измеряет среднее расстояние, которое молекула проходит между столкновениями. Даже без предварительного знания , это выражение имеет нетривиальные последствия. В частности, поскольку обычно обратно пропорциональна плотности и увеличивается с температурой, сама по себе должна увеличиваться с температурой и не зависеть от плотности при фиксированной температуре. Фактически, оба этих предсказания сохраняются при более сложных методах лечения и точно описывают экспериментальные наблюдения. Напротив, вязкость жидкости обычно уменьшается с температурой. [19] [35]
Для жестких упругих сфер диаметром , можно вычислить, дав
В этом случае не зависит от температуры, поэтому . Однако для более сложных молекулярных моделей зависит от температуры нетривиальным образом, и используемые здесь простые кинетические аргументы недостаточны. Более фундаментально, понятие средней длины свободного пробега становится неточным для частиц, которые взаимодействуют в конечном диапазоне, что ограничивает полезность концепции для описания реальных газов. [36]
Теория Чепмена – Энскога
[ редактировать ]Методика, разработанная Сиднеем Чепменом и Дэвидом Энскогом в начале 1900-х годов, позволяет более точно рассчитать . [17] Оно основано на уравнении Больцмана , которое дает статистическое описание разреженного газа с точки зрения межмолекулярных взаимодействий. [37] Методика позволяет точно рассчитать для молекулярных моделей, которые более реалистичны, чем жесткие упругие сферы, например модели, включающие межмолекулярное притяжение. Это необходимо для воспроизведения правильной температурной зависимости , который, как показывают эксперименты, увеличивается быстрее, чем тенденция, предсказанная для жестких упругих сфер. [19] Действительно, анализ Чепмена-Энскога показывает, что предсказанную температурную зависимость можно настроить, варьируя параметры в различных молекулярных моделях. Простой пример — модель Сазерленда. [а] которое описывает жесткие упругие сферы со слабым взаимным притяжением. В таком случае силу притяжения можно рассматривать пертурбативно , что приводит к простому выражению для :
где не зависит от температуры и определяется только параметрами межмолекулярного притяжения. Для связи с экспериментом удобно переписать в виде
где вязкость при температуре . Это выражение обычно называют формулой Сазерленда. [38] Если известно из экспериментов и хотя бы еще одна температура, тогда можно рассчитать. Выражения для полученные таким образом качественно точны для ряда простых газов. Немного более сложные модели, такие как потенциал Леннарда-Джонса или более гибкий потенциал Ми , могут обеспечить лучшее согласие с экспериментами, но только за счет более непрозрачной зависимости от температуры. Еще одним преимуществом этих более сложных потенциалов взаимодействия является то, что их можно использовать для разработки точных моделей для широкого спектра свойств с использованием одних и тех же потенциальных параметров. В ситуациях, когда доступно мало экспериментальных данных, это позволяет получить параметры модели путем подгонки к таким свойствам, как равновесие пар-жидкость чистой жидкости , прежде чем использовать полученные таким образом параметры для прогнозирования интересующей вязкости с разумной точностью.
В некоторых системах необходимо отказаться от предположения о сферической симметрии это происходит в случае паров с высокополярными молекулами типа H 2 O. , как В этих случаях анализ Чепмена–Энскога значительно сложнее. [39] [40]
Объемная вязкость
[ редактировать ]В кинетически-молекулярной картине ненулевая объемная вязкость возникает в газах всякий раз, когда существуют существенные релаксационные временные масштабы, управляющие обменом энергией между поступательной энергией молекул и их внутренней энергией, например вращательной и колебательной . Таким образом, объемная вязкость равна для одноатомного идеального газа, в котором внутренняя энергия молекул незначительна, но отлична от нуля для газа типа углекислого газа , молекулы которого обладают как вращательной, так и колебательной энергией. [41] [42]
Чистые жидкости
[ редактировать ]В отличие от газов, в жидкостях не существует простой, но точной картины молекулярного происхождения вязкости.
На простейшем уровне описания относительному движению соседних слоев в жидкости противодействуют прежде всего молекулярные силы притяжения.действующий через границу слоя. На этой картине можно (и правильно) ожидать, что вязкость уменьшится с повышением температуры. Это потому, чтоповышение температуры увеличивает случайное тепловое движение молекул, что облегчает им преодоление притягивающих взаимодействий. [43]
Основываясь на этой визуализации, можно построить простую теорию по аналогии с дискретной структурой твердого тела: группы молекул в жидкости. визуализируются как образующие «клетки», окружающие и заключающие в себе отдельные молекулы. [44] Эти клетки могут быть заняты или незаняты, иболее сильное молекулярное притяжение соответствует более сильным клеткам.Из-за случайного теплового движения молекула «прыгает» между клетками со скоростью, которая обратно пропорциональна силе молекулярного притяжения. В равновесии эти «прыжки» не смещены ни в каком направлении.С другой стороны, чтобы два соседних слоя могли двигаться относительно друг друга, «прыжки» должны быть смещены в сторонуотносительного движения. Силу, необходимую для поддержания этого направленного движения, можно оценить для заданной скорости сдвига, что приводит к
| ( 1 ) |
где – постоянная Авогадро , — постоянная Планка , - объем моля жидкости , а это нормальная температура кипения . Этот результат имеет тот же вид, что и известное эмпирическое соотношение
| ( 2 ) |
где и константы, соответствующие данным. [44] [45] С другой стороны, некоторые авторы выражают осторожность в отношении этой модели. ) могут возникнуть ошибки до 30% При использовании уравнения ( 1 по сравнению с уравнением подгонки ( 2 ) к экспериментальным данным. [44] физические предположения, лежащие в основе уравнения ( 1 ). В более фундаментальном плане подверглись критике [46] Также утверждалось, что экспоненциальная зависимость в уравнении ( 1 ) не обязательно описывает экспериментальные наблюдения более точно, чем более простые неэкспоненциальные выражения. [47] [48]
В свете этих недостатков разработка менее специальной модели представляет практический интерес. Отказ от простоты в пользу точности позволяет написать строгие выражения для вязкости, исходя из фундаментальных уравнений движения молекул. Классическим примером такого подхода является теория Ирвинга–Кирквуда. [49] С другой стороны, такие выражения задаются как средние по многочастичным корреляционным функциям и поэтому их трудно применять на практике.
В целом, выражения, полученные эмпирическим путем (основанные на существующих измерениях вязкости), кажутся единственным неизменно надежным средством расчета вязкости жидкостей. [50]
Изменения локальной атомной структуры наблюдаются в переохлажденных жидкостях при охлаждении ниже равновесной температуры плавления либо через функцию радиального распределения g ( r ) [51] или структурный фактор S ( Q ) [52] Установлено, что они напрямую ответственны за хрупкость жидкости: отклонение температурной зависимости вязкости переохлажденной жидкости от уравнения Аррениуса (2) за счет модификации энергии активации вязкого течения. В то же время равновесные жидкости подчиняются уравнению Аррениуса.
Смеси и смеси
[ редактировать ]Газовые смеси
[ редактировать ]Ту же молекулярно-кинетическую картину однокомпонентного газа можно применить и к газовой смеси. Например, в подходе Чепмена–Энскога вязкость бинарной смеси газов можно записать через вязкости отдельных компонентов , их соответствующие объемные доли и межмолекулярные взаимодействия. [17]
Что касается однокомпонентного газа, то зависимость На параметры межмолекулярных взаимодействий входит через различные интегралы столкновений, которые не могут быть выражены в замкнутой форме . Чтобы получить полезные выражения для которые разумно соответствуют экспериментальным данным, интегралы столкновений могут быть рассчитаны численно или на основе корреляций. [53] В некоторых случаях интегралы столкновений рассматриваются как подгоночные параметры и подгоняются непосредственно к экспериментальным данным. [54] Это распространенный подход при разработке эталонных уравнений вязкости газовой фазы. Примером такой процедуры является подход Сазерленда для однокомпонентного газа, обсуждавшийся выше.
Было показано , что для газовых смесей, состоящих из простых молекул, пересмотренная теория Энскога точно отражает зависимость вязкости как от плотности, так и от температуры в широком диапазоне условий. [55] [53]
Смеси жидкостей
[ редактировать ]Что касается чистых жидкостей, вязкость смеси жидкостей трудно предсказать с помощью молекулярных принципов. Один из методов — расширить представленную выше теорию молекулярной «клетки» на случай чистой жидкости. Это можно сделать с разной степенью сложности. Одним из выражений, полученных в результате такого анализа, является уравнение Ледерера – Регирса для бинарной смеси:
где является эмпирическим параметром, и и – соответствующие мольные доли и вязкости составляющих жидкостей. [56]
Поскольку смешивание является важным процессом в смазочной и нефтяной промышленности, существует множество эмпирических и частных уравнений для прогнозирования вязкости смеси. [56]
Растворы и суспензии
[ редактировать ]Водные растворы
[ редактировать ]В зависимости от растворенного вещества и диапазона концентраций водный раствор электролита может иметь большую или меньшую вязкость по сравнению с чистой водой при той же температуре и давлении. Например, 20%-ный солевой раствор ( хлорид натрия ) имеет вязкость более чем в 1,5 раза больше, чем чистая вода, тогда как 20%-ный раствор йодида калия имеет вязкость примерно в 0,91 раза больше, чем чистая вода.
Идеализированная модель разбавленных электролитических растворов приводит к следующему предсказанию вязкости: решения: [57]
где вязкость растворителя, это концентрация, и – положительная константа, которая зависит как от свойств растворителя, так и от свойств растворенного вещества. Однако это выражение справедливо только для очень разбавленных растворов, имеющих менее 0,1 моль/л. [58] Для более высоких концентраций необходимы дополнительные члены, которые учитывают молекулярные корреляции более высокого порядка:
где и подбираются по данным. В частности, отрицательное значение способен объяснить уменьшение вязкости, наблюдаемое в некоторых растворах. Ниже приведены расчетные значения этих констант для хлорида натрия и йодида калия при температуре 25 °C (моль = моль , L = литр ). [57]
| растворенное вещество | (моль −1/2 л 1/2 ) | (моль −1 Л) | (моль −2 л 2 ) |
|---|---|---|---|
| Хлорид натрия (NaCl) | 0.0062 | 0.0793 | 0.0080 |
| Йодид калия (KI) | 0.0047 | −0.0755 | 0.0000 |
Подвески
[ редактировать ]В суспензии твердых частиц (например, сфер микронного размера, взвешенных в масле) эффективная вязкость могут быть определены через компоненты напряжения и деформации, которые усреднены по объему, большому по сравнению с расстоянием между взвешенными частицами, но малому по отношению к макроскопическим размерам. [59] Такие суспензии обычно демонстрируют неньютоновское поведение. Однако для разбавленных систем в установившихся потоках поведение является ньютоновским, и выражения для могут быть получены непосредственно из динамики частиц. В очень разбавленной системе с объемной долей взаимодействием между взвешенными частицами можно пренебречь. В таком случае можно явно рассчитать поле течения вокруг каждой частицы независимо и объединить результаты, чтобы получить . Для сфер это приводит к формуле эффективной вязкости Эйнштейна:
где – вязкость суспендирующей жидкости. Линейная зависимость от является следствием пренебрежения межчастичными взаимодействиями. Для разбавленных систем в целом можно ожидать принять форму
где коэффициент может зависеть от формы частиц (например, сферы, стержни, диски). [60] Экспериментальное определение точного значения однако сложно: даже предсказание для сфер не было окончательно подтверждено: в различных экспериментах были обнаружены значения в диапазоне . Этот недостаток объясняется сложностью контроля условий эксперимента. [61]
В более плотных суспензиях приобретает нелинейную зависимость от , что указывает на важность межчастичных взаимодействий. Существуют различные аналитические и полуэмпирические схемы для определения этого режима. На самом базовом уровне термин, квадратичный по добавляется в :
и коэффициент подбирается на основе экспериментальных данных или аппроксимируется микроскопической теорией. Однако некоторые авторы советуют с осторожностью применять такие простые формулы, поскольку неньютоновское поведение проявляется в плотных суспензиях ( для сфер), [61] или в суспензиях удлиненных или гибких частиц. [59]
Существует различие между суспензией твердых частиц, описанной выше, и эмульсией . Последний представляет собой суспензию мельчайших капель, которые сами по себе могут проявлять внутреннюю циркуляцию. Наличие внутренней циркуляции может снизить наблюдаемую эффективную вязкость, поэтому необходимо использовать различные теоретические или полуэмпирические модели. [62]
Аморфные материалы
[ редактировать ]
В пределах высоких и низких температур вязкое течение в аморфных материалах (например, в стеклах и расплавах) [64] [65] [66] имеет форму Аррениуса :
где Q — соответствующая энергия активации , выраженная в молекулярных параметрах; Т – температура; R — молярная газовая постоянная ; и A приблизительно постоянна. Энергия активации Q принимает различное значение в зависимости от того, рассматривается ли верхний или нижний температурный предел: она меняется от высокого значения Q H при низких температурах (в стеклообразном состоянии) до низкого значения Q L при высоких температурах (в жидкое состояние).

Для промежуточных температур нетривиально меняется с температурой, и простая форма Аррениуса не работает. С другой стороны, двухэкспоненциальное уравнение
где , , , все являются константами, обеспечивает хорошее соответствие экспериментальным данным во всем диапазоне температур, в то же время приводя к правильной форме Аррениуса в низком и высоком температурном пределах. Это выражение можно мотивировать различными теоретическими моделями аморфных материалов на атомном уровне. [65]
Двухэкспоненциальное уравнение для вязкости можно вывести в рамках модели выталкивания Дайра для переохлажденных жидкостей, где энергетический барьер Аррениуса идентифицируется как высокочастотный модуль сдвига, умноженный на характерный объем выталкивания. [67] [68] При задании температурной зависимости модуля сдвига через тепловое расширение и отталкивающую часть межмолекулярного потенциала получается еще одно двухэкспоненциальное уравнение: [69]
где обозначает высокочастотный модуль сдвига материала, рассчитанный при температуре, равной стеклования . температуре , - это так называемый объем выталкивания, т.е. это характерный объем группы атомов, участвующих в событии выталкивания, при котором атом/молекула вырывается из клетки ближайших соседей, обычно порядка объема, занимаемого несколькими атомами . Более того, - коэффициент теплового расширения материала, — параметр, измеряющий крутизну степенного подъема восходящего фланга первого пика функции радиального распределения и количественно связанный с отталкивающей частью межатомного потенциала . [69] Окончательно, обозначает постоянную Больцмана .
Вихревая вязкость
[ редактировать ]При изучении турбулентности в жидкостях общепринятая практическая стратегия состоит в том, чтобы игнорировать мелкомасштабные вихри (или завихрения ) в движении и рассчитывать крупномасштабное движение с эффективной вязкостью, называемой «вихревой вязкостью», которая характеризует перенос и рассеивание энергии в потоке меньшего масштаба (см. Моделирование больших вихрей ). [70] [71] В отличие от вязкости самой жидкости, которая по второму закону термодинамики должна быть положительной , вихревая вязкость может быть отрицательной. [72] [73]
Прогноз
[ редактировать ]Поскольку вязкость непрерывно зависит от температуры и давления, ее нельзя полностью охарактеризовать с помощью конечного числа экспериментальных измерений. Прогнозирующие формулы становятся необходимыми, если экспериментальные значения недоступны при интересующих температурах и давлениях. Эта возможность важна для теплофизического моделирования. в котором температура и давление жидкости могут непрерывно изменяться в пространстве и времени. Аналогичная ситуация наблюдается и для смесей чистых жидкостей, где вязкость непрерывно зависит от соотношения концентраций составляющих жидкостей.
Для простейших жидкостей, таких как разбавленные одноатомные газы и их смеси, вычисления ab initio квантово-механические могут точно предсказать вязкость с точки зрения фундаментальных атомных констант, т.е. без ссылки на существующие измерения вязкости. [74] Для частного случая разбавленного гелия неопределенности в расчетной вязкости ab initio на два порядка меньше, чем неопределенности в экспериментальных значениях. [75]
Для немного более сложных жидкостей и смесей при умеренных плотностях (т.е. докритических плотностях ) пересмотренная теория Энскога может использоваться для прогнозирования вязкости с некоторой точностью. [53] Пересмотренная теория Энскога является прогнозирующей в том смысле, что прогнозы вязкости могут быть получены с использованием параметров, соответствующих другим термодинамическим свойствам или транспортным свойствам чистой жидкости , что не требует априорных экспериментальных измерений вязкости.
Для большинства жидкостей высокоточные расчеты из первых принципов невозможны. Скорее, теоретические или эмпирические выражения должны соответствовать существующим измерениям вязкости. Если такое выражение подходит для высокоточных данных в широком диапазоне температур и давлений, то оно называется «эталонной корреляцией» для этой жидкости. Справочные корреляции были опубликованы для многих чистых жидкостей; несколькими примерами являются вода , углекислый газ , аммиак , бензол и ксенон . [76] [77] [78] [79] [80] Многие из них охватывают диапазоны температур и давлений, охватывающие газовые, жидкие и сверхкритические фазы.
Программное обеспечение для теплофизического моделирования часто опирается на эталонные корреляции для прогнозирования вязкости при заданных пользователем температуре и давлении.Эти корреляции могут быть собственными . Примеры: REFPROP. [81] (собственность) и CoolProp [82] (с открытым исходным кодом).
Вязкость также можно рассчитать с помощью формул, которые выражают ее через статистику отдельных частиц.траектории. Эти формулы включают соотношения Грина-Кубо для линейной сдвиговой вязкости и выражения временной корреляционной функции, полученные Эвансом и Морриссом в 1988 году. [83] [34] Преимущество этих выражений состоит в том, что они формально точны и справедливы для общих систем. Недостатком является то, что они требуют детального знания траекторий частиц, доступного только в дорогостоящих с точки зрения вычислений симуляциях, таких как молекулярная динамика . Также необходима точная модель межчастичных взаимодействий, которую может быть сложно получить для сложных молекул. [84]
Выбранные вещества
[ редактировать ]
Наблюдаемые значения вязкости различаются на несколько порядков даже для обычных веществ (см. таблицу порядков величин ниже). Например, вязкость 70%-ного раствора сахарозы (сахара) более чем в 400 раз выше вязкости воды и в 26 000 раз выше вязкости воздуха. [86] Более того, по оценкам, вязкость смолы в 230 миллиардов раз выше вязкости воды. [85]
Вода
[ редактировать ]Динамическая вязкость воды составляет около 0,89 мПа·с при комнатной температуре (25 ° C ). Вязкость как функцию температуры в Кельвинах можно оценить с помощью полуэмпирического уравнения Фогеля-Фульчера-Таммана :
где А = 0,02939 мПа·с, В = 507,88 К и С = 149,3 К. [87] Экспериментально определенные значения вязкости также приведены в таблице ниже. Полезными являются значения при 20 °C: здесь динамическая вязкость составляет около 1 сП, а кинематическая вязкость — около 1 сСт.
| Температура (°С) | Вязкость (мПа·с или сП) |
|---|---|
| 10 | 1.305 9 |
| 20 | 1.001 6 |
| 30 | 0.797 22 |
| 50 | 0.546 52 |
| 70 | 0.403 55 |
| 90 | 0.314 17 |
Воздух
[ редактировать ]При стандартных атмосферных условиях (25 °C и давлении 1 бар) динамическая вязкость воздуха составляет 18,5 мкПа·с, что примерно в 50 раз меньше вязкости воды при той же температуре. За исключением очень высокого давления, вязкость воздуха зависит главным образом от температуры. Среди множества возможных приближенных формул температурной зависимости (см. Температурная зависимость вязкости ) есть одна: [88]
что соответствует точности в диапазоне от -20 °C до 400 °C. Чтобы эта формула была действительна, температура должна быть указана в кельвинах ; тогда соответствует вязкости в Па·с.

Другие распространенные вещества
[ редактировать ]| Вещество | Вязкость (мПа·с) | Температура (°С) | Ссылка. |
|---|---|---|---|
| Бензол | 0.604 | 25 | [86] |
| Вода | 1.0016 | 20 | |
| Меркурий | 1.526 | 25 | |
| Цельное молоко | 2.12 | 20 | [89] |
| Темное пиво | 2.53 | 20 | |
| Оливковое масло | 56.2 | 26 | [89] |
| Мед | 2,000–10,000 | 20 | [90] |
| Кетчуп [б] | 5,000–20,000 | 25 | [91] |
| Арахисовое масло [б] | 10 4 –10 6 | [92] | |
| Подача | 2.3 × 10 11 | 10–30 (переменная) | [85] |
Оценки порядка величины
[ редактировать ]В следующей таблице показан диапазон значений вязкости, наблюдаемый в обычных веществах. Если не указано иное, предполагается температура 25 °C и давление 1 атмосфера.
Перечисленные значения являются лишь репрезентативными оценками, поскольку они не учитывают неопределенности измерений, изменчивость определений материалов или неньютоновское поведение.
| Фактор (Па·с) | Описание | Примеры | Значения (Па·с) | Ссылка. |
|---|---|---|---|---|
| 10 −6 | Нижний диапазон вязкости газа | Бутан | 7.49 × 10 −6 | [93] |
| Водород | 8.8 × 10 −6 | [94] | ||
| 10 −5 | Верхний диапазон вязкости газа | Криптон | 2.538 × 10 −5 | [95] |
| Неон | 3.175 × 10 −5 | |||
| 10 −4 | Нижний диапазон вязкости жидкости | Пентан | 2.24 × 10 −4 | [86] |
| Бензин | 6 × 10 −4 | |||
| Вода | 8.90 × 10 −4 | [86] | ||
| 10 −3 | Типичный диапазон для малых молекул Ньютоновские жидкости | Этанол | 1.074 × 10 −3 | |
| Меркурий | 1.526 × 10 −3 | |||
| Цельное молоко (20 °C) | 2.12 × 10 −3 | [89] | ||
| Кровь | 3 × 10 −3 до 6 × 10 −3 | [96] | ||
| Жидкая сталь (1550 °С) | 6 × 10 −3 | [97] | ||
| 10 −2 – 10 0 | Нефти и длинноцепочечные углеводороды | Льняное масло | 0.028 | |
| Олеиновая кислота | 0.036 | [98] | ||
| Оливковое масло | 0.084 | [89] | ||
| SAE 10 Моторное масло | от 0,085 до 0,14 | |||
| Касторовое масло | 0.1 | |||
| SAE 20 Моторное масло | от 0,14 до 0,42 | |||
| SAE 30 Моторное масло | от 0,42 до 0,65 | |||
| SAE 40 Моторное масло | от 0,65 до 0,90 | |||
| Глицерин | 1.5 | |||
| Блинный сироп | 2.5 | |||
| 10 1 – 10 3 | Пасты, гели и другие полутвердые вещества (обычно неньютоновский) | Кетчуп | ≈ 10 1 | [91] |
| Горчица | ||||
| Сметана | ≈ 10 2 | |||
| Арахисовое масло | [92] | |||
| Сало | ≈ 10 3 | |||
| ≈10 8 | Вязкоэластичные полимеры | Подача | 2.3 × 10 8 | [85] |
| ≈10 21 | Некоторые твердые вещества под вязкоупругим слоем описание | Мантия (геология) | ≈ 10 19 до 10 24 | [99] |
См. также
[ редактировать ]- Дашпот
- Номер Деборы
- расширение
- Жидкость Гершеля – Балкли
- Миксер высокой вязкости
- Синдром гипервязкости
- Внутренняя вязкость
- Невязкое течение
- Метод Джобака (оценка вязкости жидкости по молекулярной структуре)
- Эффект Кея
- Микровязкость
- число Мортона
- Давление масла
- Квазитвердый
- Реология
- Стоксов поток
- Сверхтекучий гелий-4
- Вязкопластичность
- Модели вязкости смесей
- Кубок Зана
Ссылки
[ редактировать ]Сноски
[ редактировать ]- ^ Последующее обсуждение основано на Chapman & Cowling 1970 , стр. 232–237.
- ^ Перейти обратно: а б Эти материалы в высшей степени неньютоновские .
Цитаты
[ редактировать ]- ^ Перейти обратно: а б с «Вязкость» . Британская энциклопедия . 26 июня 2023 г. Проверено 4 августа 2023 г.
- ^ Растём вместе с наукой . Маршалл Кавендиш . 2006. с. 1928. ISBN 978-0-7614-7521-7 .
- ^ Э. Дейл Мартин (1961). Исследование ламинарного течения сжимаемой вязкой жидкости в трубе, ускоренного осевой объемной силой, с применением к магнитогазодинамике . НАСА . п. 7.
- ^ Балеску 1975 , стр. 428–429.
- ^ Ландау и Лифшиц 1987 .
- ^ Харпер, Дуглас (nd). «вязкий (прилаг.)» . Интернет-словарь этимологии . Архивировано из оригинала 1 мая 2019 года . Проверено 19 сентября 2019 г.
- ^ Мьюис и Вагнер 2012 , с. 19.
- ^ Стритер, Уайли и Бедфорд 1998 .
- ^ Холман 2002 .
- ^ Incropera et al. 2007
- ^ Ничего и др. 1997 год .
- ^ Перейти обратно: а б с Бёрд, Стюарт и Лайтфут, 2007 , с. 19.
- ^ Перейти обратно: а б Ландау и Лифшиц 1987 , стр. 44–45.
- ^ Берд, Стюарт и Лайтфут 2007 , стр. 18: В этом источнике используется альтернативное соглашение о знаках, которое здесь изменено на противоположное.
- ^ Ландау и Лифшиц 1987 , с. 45.
- ^ Перейти обратно: а б Балеску 1975 .
- ^ Перейти обратно: а б с д Чепмен и Коулинг, 1970 .
- ^ Нация 1996 .
- ^ Перейти обратно: а б с д и Бёрд, Стюарт и Лайтфут, 2007 .
- ^ Шредер 1999 .
- ^ Ружанска и др. 2014 , стр. 47–55.
- ^ Траутон 1906 , стр. 426–440.
- ^ Мьюис и Вагнер 2012 , с. 228–230.
- ^ Кумагай, Сасадзима и Ито 1978 , стр. 157–161.
- ^ Шерер, Парденек и Святек 1988 , с. 14.
- ^ Ханнан 2007 .
- ^ Квапишевска и др. 2020 .
- ^ Макнот и Уилкинсон 1997 , уравновешенность.
- ^ Гилленбок 2018 , стр. 213.
- ^ «Какая единица называется рейн?» . Размеры.com . Проверено 23 декабря 2023 г.
- ^ ASTM D2161: Стандартная практика преобразования кинематической вязкости в универсальную вязкость по Сейболту или вязкость по Сейболту по фуролу , ASTM , 2005, стр. 1
- ^ Траченко и Бражкин 2020 .
- ^ Перейти обратно: а б Траченко и Бражкин 2021 .
- ^ Перейти обратно: а б Эванс и Моррис, 1988 .
- ^ Перейти обратно: а б Беллак, Мортессань и Батруни, 2004 г.
- ^ Чепмен и Коулинг 1970 , с. 103.
- ^ Черчиньяни 1975 .
- ^ Сазерленд 1893 , стр. 507–531.
- ^ Берд, Стюарт и Лайтфут 2007 , стр. 25–27.
- ^ Чепмен и Коулинг 1970 , стр. 235–237.
- ^ Чепмен и Коулинг 1970 , стр. 197, 214–216.
- ^ Крамер 2012 , с. 066102-2.
- ^ Рид и Шервуд 1958 , с. 202.
- ^ Перейти обратно: а б с Бёрд, Стюарт и Лайтфут, 2007 , стр. 29–31.
- ^ Рид и Шервуд 1958 , стр. 203–204.
- ^ Хильдебранд 1977 .
- ^ Хильдебранд 1977 , с. 37.
- ^ Эгельстафф 1992 , с. 264.
- ^ Ирвинг и Кирквуд 1949 , стр. 817–829.
- ^ Рид и Шервуд 1958 , стр. 206–209.
- ^ Лузгин-Лузгин, Д.В. (18 октября 2022 г.). «Структурные изменения металлических стеклообразующих жидкостей при охлаждении и последующем стекловании во взаимосвязи с их свойствами» . Материалы . 15 (20): 7285. Бибкод : 2022Mate...15.7285L . дои : 10.3390/ma15207285 . ISSN 1996-1944 гг . ПМЦ 9610435 . ПМИД 36295350 .
- ^ Келтон, КФ (18 января 2017 г.). «Кинетическая и структурная хрупкость — корреляция между структурой и динамикой в металлических жидкостях и стеклах» . Физический журнал: конденсированное вещество . 29 (2): 023002. Бибкод : 2017JPCM...29b3002K . дои : 10.1088/0953-8984/29/2/023002 . ISSN 0953-8984 . ПМИД 27841996 .
- ^ Перейти обратно: а б с Джервелл, Вегард Г.; Вильгельмсен, Ойвинд (08 июня 2023 г.). «Пересмотренная теория Энскога для жидкостей Ми: прогнозирование коэффициентов диффузии, коэффициентов термодиффузии, вязкости и теплопроводности» . Журнал химической физики . 158 (22). Бибкод : 2023JChPh.158v4101J . дои : 10.1063/5.0149865 . ISSN 0021-9606 . ПМИД 37290070 . S2CID 259119498 .
- ^ Леммон, EW; Якобсен, RT (1 января 2004 г.). «Уравнения вязкости и теплопроводности азота, кислорода, аргона и воздуха» . Международный журнал теплофизики . 25 (1): 21–69. Бибкод : 2004IJT....25...21L . дои : 10.1023/B:IJOT.0000022327.04529.f3 . ISSN 1572-9567 . S2CID 119677367 .
- ^ Лопес де Аро, М.; Коэн, EGD; Кинкейд, Дж. М. (1 марта 1983 г.). «Теория Энскога для многокомпонентных смесей. I. Теория линейного переноса» . Журнал химической физики . 78 (5): 2746–2759. Бибкод : 1983JChPh..78.2746L . дои : 10.1063/1.444985 . ISSN 0021-9606 .
- ^ Перейти обратно: а б Жмудь 2014 , с. 22.
- ^ Перейти обратно: а б Вишванат и др. 2007 .
- ^ Абдулагатов, Зейналова и Азизов 2006 , стр. 75–88.
- ^ Перейти обратно: а б Бёрд, Стюарт и Лайтфут, 2007 , стр. 31–33.
- ^ Берд, Стюарт и Лайтфут 2007 , стр. 32.
- ^ Перейти обратно: а б Мюллер, Ллевеллин и Мэдер, 2009 г. , стр. 1201–1228.
- ^ Берд, Стюарт и Лайтфут 2007 , стр. 33.
- ^ Флюгель 2007 .
- ^ Доремус 2002 , стр. 7619–7629.
- ^ Перейти обратно: а б Оджован, Трэвис и Хэнд 2007 , стр. 415107.
- ^ Оджован и Ли 2004 , стр. 3803–3810.
- ^ Дайр, Олсен и Кристенсен 1996 , стр. 2171.
- ^ Хекшер и Дайр 2015 .
- ^ Перейти обратно: а б Крауссер, Самвер и Закконе, 2015 , с. 13762.
- ^ Берд, Стюарт и Лайтфут 2007 , стр. 163.
- ^ Лесье 2012 , стр. 2–.
- ^ Сивашинский и Яхот 1985 , с. 1040.
- ^ Се и Левченко 2019 , с. 045434.
- ^ Sharipov & Benites 2020 .
- ^ Роуленд, Аль Гафри и май 2020 г ..
- ^ Хубер и др. 2009 .
- ^ Лазеке и Музный 2017 .
- ^ Моногениду, Ассаэль и Хубер 2018 .
- ^ Авгери и др. 2014 .
- ^ Веллиаду и др. 2021 .
- ^ «Рефпроп» . НИСТ . Nist.gov. 18 апреля 2013 г. Архивировано из оригинала 9 февраля 2022 г. Проверено 15 февраля 2022 г.
- ^ Белл и др. 2014 .
- ^ Эванс и Моррис 2007 .
- ^ Магинн и др. 2019 .
- ^ Перейти обратно: а б с д Эджворт, Далтон и Парнелл, 1984 , стр. 198–200.
- ^ Перейти обратно: а б с д и Рамбл 2018 .
- ^ Вишванатх и Натараджан 1989 , стр. 714–715.
- ^ техническая наука (25 марта 2020 г.). «Вязкость жидкостей и газов» . техническая наука . Архивировано из оригинала 19 апреля 2020 г. Проверено 7 мая 2020 г.
- ^ Перейти обратно: а б с д Стипендиаты 2009 года .
- ^ Янниотис, Скальци и Карабурниоти 2006 , стр. 372–377.
- ^ Перейти обратно: а б Кучеки и др. 2009 , стр. 596–602.
- ^ Перейти обратно: а б Цистерна, Карро и Стон 2001 , стр. 86–96.
- ^ Кестин, Халифа и Уэйкхэм 1977 .
- ^ Ассаэль и др. 2018 .
- ^ Кестин, Ро и Уэйкхэм 1972 .
- ^ Розенсон, Маккормик и Урец 1996 .
- ^ Чжао и др. 2021 .
- ^ Сагдеев и др. 2019 .
- ^ Вальс, Хендель и Баумгарднер .
Источники
[ редактировать ]- Абдулагатов Ильмутдин М.; Зейналова Аделя Б.; Азизов, Назим Д. (2006). «Экспериментальные B-коэффициенты вязкости водных растворов LiCl». Журнал молекулярных жидкостей . 126 (1–3): 75–88. дои : 10.1016/j.molliq.2005.10.006 . ISSN 0167-7322 .
- Ассаэль, MJ; и др. (2018). «Справочные значения и эталонные корреляции теплопроводности и вязкости жидкостей» . Журнал физических и химических справочных данных . 47 (2): 021501. Бибкод : 2018JPCRD..47b1501A . дои : 10.1063/1.5036625 . ISSN 0047-2689 . ПМК 6463310 . ПМИД 30996494 .
- Авгери, С.; Ассаэль, MJ; Хубер, МЛ; Перкинс, Р.А. (2014). «Эталонная корреляция вязкости бензола от тройной точки до 675 К и до 300 МПа». Журнал физических и химических справочных данных . 43 (3). Издательство AIP: 033103. Бибкод : 2014JPCRD..43c3103A . дои : 10.1063/1.4892935 . ISSN 0047-2689 .
- Балеску, Раду (1975). Равновесная и неравновесная статистическая механика . Джон Уайли и сыновья. ISBN 978-0-471-04600-4 . Архивировано из оригинала 16 марта 2020 г. Проверено 18 сентября 2019 г.
- Белл, Ян Х.; Вронский, Йоррит; Куойлин, Сильвен; Леморт, Винсент (27 января 2014 г.). «Оценка теплофизических свойств чистых и псевдочистых жидкостей и открытая библиотека теплофизических свойств CoolProp» . Исследования в области промышленной и инженерной химии . 53 (6). Американское химическое общество (ACS): 2498–2508. дои : 10.1021/ie4033999 . ISSN 0888-5885 . ПМЦ 3944605 . ПМИД 24623957 .
- Беллак, Майкл; Мортессан, Фабрис; Батруни, Дж. Джордж (2004). Равновесная и неравновесная статистическая термодинамика . Издательство Кембриджского университета. ISBN 978-0-521-82143-8 .
- Берд, Р. Байрон; Стюарт, Уоррен Э.; Лайтфут, Эдвин Н. (2007). Транспортные явления (2-е изд.). Джон Уайли и сыновья, Inc. ISBN 978-0-470-11539-8 . Архивировано из оригинала 2 марта 2020 г. Проверено 18 сентября 2019 г.
- Берд, Р. Брайон; Армстронг, Роберт С.; Хассагер, Оле (1987), Динамика полимерных жидкостей, Том 1: Механика жидкости (2-е изд.), John Wiley & Sons
- Черчиньяни, Карло (1975). Теория и применение уравнения Больцмана . Эльзевир. ISBN 978-0-444-19450-3 .
- Чепмен, Сидней ; Коулинг, Т.Г. (1970). Математическая теория неоднородных газов (3-е изд.). Издательство Кембриджского университета. ISBN 978-0-521-07577-0 .
- Ситерн, Гийом П.; Карро, Пьер Ж.; Стон, Мишель (2001). «Реологические свойства арахисового масла». Реологика Акта . 40 (1): 86–96. дои : 10.1007/s003970000120 . S2CID 94555820 .
- Крамер, М.С. (2012). «Численные оценки объемной вязкости идеальных газов» . Физика жидкостей . 24 (6): 066102–066102–23. Бибкод : 2012PhFl...24f6102C . дои : 10.1063/1.4729611 . hdl : 10919/47646 . Архивировано из оригинала 15 февраля 2022 г. Проверено 19 сентября 2020 г.
- Доремус, Р.Х. (2002). «Вязкость кремнезема». Дж. Прил. Физ . 92 (12): 7619–7629. Бибкод : 2002JAP....92.7619D . дои : 10.1063/1.1515132 .
- Дайр, Джей Си; Олсен, Северная Каролина; Кристенсен, Т. (1996). «Модель локального упругого расширения для энергий активации вязкого течения стеклообразующих молекулярных жидкостей» . Физический обзор B . 53 (5): 2171–2174. Бибкод : 1996PhRvB..53.2171D . дои : 10.1103/PhysRevB.53.2171 . ПМИД 9983702 .
- Эджворт, Р.; Далтон, Би Джей; Парнелл, Т. (1984). «Эксперимент с падением высоты звука» . Европейский журнал физики . 5 (4): 198–200. Бибкод : 1984EJPh....5..198E . дои : 10.1088/0143-0807/5/4/003 . S2CID 250769509 . Архивировано из оригинала 28 марта 2013 г. Проверено 31 марта 2009 г.
- Эгельстафф, Пенсильвания (1992). Введение в жидкое состояние (2-е изд.). Издательство Оксфордского университета. ISBN 978-0-19-851012-3 .
- Эванс, Денис Дж .; Моррисс, Гэри П. (2007). Статистическая механика неравновесных жидкостей . АНУ Пресс. ISBN 978-1-921313-22-6 . JSTOR j.ctt24h99q . Архивировано из оригинала 10 января 2022 г. Проверено 10 января 2022 г.
- Эванс, Денис Дж.; Моррисс, Гэри П. (15 октября 1988 г.). «Корреляционные функции переходного процесса и реология жидкостей». Физический обзор А. 38 (8): 4142–4148. Бибкод : 1988PhRvA..38.4142E . дои : 10.1103/PhysRevA.38.4142 . ПМИД 9900865 .
- Товарищи, Пи Джей (2009). Технология пищевой промышленности: принципы и практика (3-е изд.). Вудхед. ISBN 978-1-84569-216-2 .
- Флюгель, Александр (2007). «Расчет вязкости стекол» . Glassproperties.com. Архивировано из оригинала 27 ноября 2010 г. Проверено 14 сентября 2010 г.
- Гиббс, Филип (январь 1997 г.). «Стекло жидкое или твердое?» . math.ucr.edu . Архивировано из оригинала 29 марта 2007 года . Проверено 19 сентября 2019 г.
- Гилленбок, январь (2018). «Энциклопедия исторической метрологии, весов и мер: Том 1». Энциклопедия исторической метрологии, весов и мер . Том. 1. Биркхойзер. ISBN 978-3-319-57598-8 .
- Ханнан, Генри (2007). Справочник технического специалиста по составу промышленных и бытовых чистящих средств . Уокеша, Висконсин: Kyral LLC. п. 7. ISBN 978-0-615-15601-9 .
- Хекшер, Тина; Дайр, Йеппе К. (01 января 2015 г.). «Обзор экспериментов по проверке модели толкания» . Журнал некристаллических твердых тел . 7-й IDMRCS: Релаксация в сложных системах. 407 : 14–22. Бибкод : 2015JNCS..407...14H . дои : 10.1016/j.jnoncrysol.2014.08.056 . ISSN 0022-3093 . Архивировано из оригинала 15 февраля 2022 г. Проверено 17 октября 2021 г.
- Хильдебранд, Джоэл Генри (1977). Вязкость и диффузия: прогнозное лечение . Джон Уайли и сыновья. ISBN 978-0-471-03072-0 .
- Холман, Джек Филип (2002). Теплопередача . МакГроу-Хилл. ISBN 978-0-07-112230-6 . Архивировано из оригинала 15 марта 2020 г. Проверено 18 сентября 2019 г.
- Хубер, МЛ; Перкинс, РА; Лазеке, А.; Друг, генеральный директор; Сенгерс, СП; Ассаэль, MJ; Метакса, Индиана; Фогель, Э.; Мареш, Р.; Миягава, К. (2009). «Новая международная формула вязкости H2O». Журнал физических и химических справочных данных . 38 (2). Издательство АИП: 101–125. Бибкод : 2009JPCRD..38..101H . дои : 10.1063/1.3088050 . ISSN 0047-2689 .
- Инкропера, Фрэнк П.; и др. (2007). Основы тепломассообмена . Уайли. ISBN 978-0-471-45728-2 . Архивировано из оригинала 11 марта 2020 г. Проверено 18 сентября 2019 г.
- Ирвинг, Дж. Х.; Кирквуд, Джон Г. (1949). «Статистическая механическая теория процессов переноса. IV. Уравнения гидродинамики». Дж. Хим. Физ . 18 (6): 817–829. дои : 10.1063/1.1747782 .
- Кестин, Дж.; Ро, СТ; Уэйкхэм, Вашингтон (1972). «Вязкость благородных газов в интервале температур 25–700 °С» . Журнал химической физики . 56 (8): 4119–4124. Бибкод : 1972ЖЧФ..56.4119К . дои : 10.1063/1.1677824 . ISSN 0021-9606 .
- Кестин, Дж.; Халифа, HE; Уэйкхэм, Вашингтон (1977). «Вязкость пяти газообразных углеводородов». Журнал химической физики . 66 (3): 1132. Бибкод : 1977ЖЧФ..66.1132К . дои : 10.1063/1.434048 .
- Кучеки, Араш; и др. (2009). «Реологические свойства кетчупа в зависимости от различных гидроколлоидов и температуры». Международный журнал пищевой науки и технологий . 44 (3): 596–602. дои : 10.1111/j.1365-2621.2008.01868.x .
- Краусер, Дж.; Самвер, К.; Закконе, А. (2015). «Мягкость межатомного отталкивания напрямую контролирует хрупкость переохлажденных металлических расплавов» . Труды Национальной академии наук США . 112 (45): 13762–13767. arXiv : 1510.08117 . Бибкод : 2015PNAS..11213762K . дои : 10.1073/pnas.1503741112 . ПМЦ 4653154 . ПМИД 26504208 .
- Кумагай, Наоичи; Сасадзима, Садао; Ито, Хидебуми (15 февраля 1978 г.). «Долговременная ползучесть горных пород: результаты с крупными образцами, полученные примерно за 20 лет, и результаты с мелкими образцами примерно за 3 года» . Журнал Общества материаловедения (Япония) . 27 (293): 157–161. НАИД 110002299397 . Архивировано из оригинала 21 мая 2011 г. Проверено 16 июня 2008 г.
- Квапишевская, Карина; Щепанский, Кшиштоф; Кальварчик, Томаш; Михальска, Бернадета; Паталас-Кравчик, Полина; Шиманский, Енджей; Андрышевский, Томаш; Иван, Михалина; Душиньский, Ежи; Холист, Роберт (2020). «Наномасштабная вязкость цитоплазмы сохраняется в клеточных линиях человека» . Журнал писем по физической химии . 11 (16): 6914–6920. doi : 10.1021/acs.jpclett.0c01748 . ПМК 7450658 . ПМИД 32787203 .
- Лазеке, Арно; Музный, Крис Д. (2017). «Эталонная корреляция вязкости углекислого газа» . Журнал физических и химических справочных данных . 46 (1). Издательство AIP: 013107. Бибкод : 2017JPCRD..46a3107L . дои : 10.1063/1.4977429 . ISSN 0047-2689 . ПМК 5514612 . ПМИД 28736460 .
- Ландау, LD ; Лифшиц, Э.М. (1987). Механика жидкости (2-е изд.). Эльзевир. ISBN 978-0-08-057073-0 . Архивировано из оригинала 21 марта 2020 г. Проверено 18 сентября 2019 г.
- Магинн, Эдвард Дж.; Мессерли, Ричард А.; Карлсон, Дэниел Дж.; Роу, Дэниел Р.; Эллиотт, Дж. Ричард (2019). «Лучшие методы расчета транспортных свойств 1. Самодиффузия и вязкость на основе равновесной молекулярной динамики [статья v1.0]» . Живой журнал вычислительной молекулярной науки . 1 (1). Университет Колорадо в Боулдере. дои : 10.33011/livecoms.1.1.6324 . ISSN 2575-6524 . S2CID 104357320 .
- Моногениду, SA; Ассаэль, MJ; Хубер, МЛ (2018). «Эталонная корреляция вязкости аммиака от тройной точки до 725 К и до 50 МПа» . Журнал физических и химических справочных данных . 47 (2). Издательство AIP: 023102. Бибкод : 2018JPCRD..47b3102M . дои : 10.1063/1.5036724 . ISSN 0047-2689 . ПМК 6512859 . ПМИД 31092958 .
- Лесье, Марсель (2012). Турбулентность в жидкостях: стохастическое и численное моделирование . Спрингер. ISBN 978-94-009-0533-7 . Архивировано из оригинала 14 марта 2020 г. Проверено 30 ноября 2018 г.
- Мьюис, Ян; Вагнер, Норман Дж. (2012). Реология коллоидной суспензии . Издательство Кембриджского университета. ISBN 978-0-521-51599-3 . Архивировано из оригинала 14 марта 2020 г. Проверено 10 декабря 2018 г.
- Макнот, AD; Уилкинсон, А. (1997). «уравновешенность». ИЮПАК. Сборник химической терминологии («Золотая книга») . С. Дж. Мел (2-е изд.). Оксфорд: Блэквелл Сайентифик. дои : 10.1351/goldbook . ISBN 0-9678550-9-8 .
- Миллат, Йорген (1996). Транспортные свойства жидкостей: их корреляция, прогноз и оценка . Кембридж: Издательство Кембриджского университета. ISBN 978-0-521-02290-3 . OCLC 668204060 .
- Мюллер, С.; Ллевеллин, EW; Мадер, HM (2009). «Реология суспензий твердых частиц» . Труды Королевского общества A: Математические, физические и технические науки . 466 (2116): 1201–1228. дои : 10.1098/rspa.2009.0445 . ISSN 1364-5021 .
- Нич, Милослав; и др., ред. (1997). «динамическая вязкость, η ». Сборник химической терминологии ИЮПАК . Оксфорд: Научные публикации Блэквелла. дои : 10.1351/goldbook . ISBN 978-0-9678550-9-7 .
- Оджован, Мичиган; Ли, МЫ (2004). «Вязкость сетевых жидкостей в рамках подхода Доремуса». Дж. Прил. Физ . 95 (7): 3803–3810. Бибкод : 2004JAP....95.3803O . дои : 10.1063/1.1647260 .
- Оджован, Мичиган; Трэвис, КП; Хэнд, Р.Дж. (2007). «Термодинамические параметры связей в стеклообразных материалах из зависимости вязкости от температуры» (PDF) . J. Phys.: Condens. Иметь значение . 19 (41): 415107. Бибкод : 2007JPCM...19O5107O . дои : 10.1088/0953-8984/19/41/415107 . ПМИД 28192319 . S2CID 24724512 . Архивировано (PDF) из оригинала 25 июля 2018 г. Проверено 27 сентября 2019 г.
- Пламб, Роберт К. (1989). «Античные оконные стекла и потоки переохлажденных жидкостей» . Журнал химического образования . 66 (12): 994. Бибкод : 1989ЖЧЭд..66..994П . дои : 10.1021/ed066p994 . Архивировано из оригинала 26 августа 2005 г. Проверено 25 декабря 2013 г.
- Рапапорт, округ Колумбия (2004). Искусство молекулярно-динамического моделирования (2-е изд.). Издательство Кембриджского университета. ISBN 978-0-521-82568-9 . Архивировано из оригинала 25 июня 2018 г. Проверено 10 января 2022 г.
- Рид, Роберт С.; Шервуд, Томас К. (1958). Свойства газов и жидкостей . МакГроу-Хилл.
- Рейф Ф. (1965), Основы статистической и теплофизики , McGraw-Hill . Передовое лечение.
- Розенсон, Р.С.; Маккормик, А; Урец, Э.Ф. (1 августа 1996 г.). «Распределение значений вязкости крови и биохимических коррелятов у здоровых взрослых» . Клиническая химия . 42 (8). Издательство Оксфордского университета (OUP): 1189–1195. дои : 10.1093/клинчем/42.8.1189 . ISSN 0009-9147 . ПМИД 8697575 .
- Роуленд, Даррен; Аль Гафри, Саиф З.С.; Мэй, Эрик Ф. (01 марта 2020 г.). «Широкомасштабные эталонные корреляции транспортных свойств разбавленного газа на основе неэмпирических расчетов и измерений коэффициента вязкости» . Журнал физических и химических справочных данных . 49 (1). Издательство AIP: 013101. Бибкод : 2020JPCRD..49a3101X . дои : 10.1063/1.5125100 . ISSN 0047-2689 . S2CID 213794612 .
- Рожанска, С.; Рожански, Ю.; Оховяк, М.; Митковский, PT (2014). «Измерение вязкости концентрированных эмульсий с использованием устройства с противоположными соплами» (PDF) . Бразильский журнал химической инженерии . 31 (1): 47–55. дои : 10.1590/S0104-66322014000100006 . ISSN 0104-6632 . Архивировано (PDF) из оригинала 8 мая 2020 г. Проверено 19 сентября 2019 г.
- Рамбл, Джон Р., изд. (2018). Справочник CRC по химии и физике (99-е изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1-138-56163-2 .
- Сагдеев, Дамир; Габитов, Ильгиз; Исьянов, Чингиз; Хайрутдинов, Венер; Фарахов, Мансур; Зарипов, Зуфар; Абдулагатов, Ильмутдин (22 апреля 2019 г.). «Плотность и вязкость олеиновой кислоты при атмосферном давлении». Журнал Американского общества нефтехимиков . 96 (6). Уайли: 647–662. дои : 10.1002/aocs.12217 . ISSN 0003-021X . S2CID 150156106 .
- Шерер, Джордж В.; Парденек, Сандра А.; Святек, Роуз М. (1988). «Вязкоупругость силикагеля». Журнал некристаллических твердых тел . 107 (1): 14. Бибкод : 1988JNCS..107...14S . дои : 10.1016/0022-3093(88)90086-5 .
- Шредер, Дэниел В. (1999). Введение в теплофизику . Эддисон Уэсли. ISBN 978-0-201-38027-9 . Архивировано из оригинала 10 марта 2020 г. Проверено 30 ноября 2018 г.
- Шарипов, Феликс; Бенитес, Виктор Дж. (01 июля 2020 г.). «Коэффициенты переноса многокомпонентных смесей благородных газов на основе ab initio потенциалов: вязкость и теплопроводность». Физика жидкостей . 32 (7). Издательство AIP: 077104. arXiv : 2006.08687 . Бибкод : 2020ФФл...32г7104С . дои : 10.1063/5.0016261 . ISSN 1070-6631 . S2CID 219708359 .
- Сивашинский В.; Яхот, Г. (1985). «Эффект отрицательной вязкости в крупномасштабных потоках». Физика жидкостей . 28 (4): 1040. Бибкод : 1985ФФл...28.1040С . дои : 10.1063/1.865025 .
- Стритер, Виктор Лайл; Уайли, Э. Бенджамин; Бедфорд, Кейт В. (1998). Механика жидкости . WCB/МакГроу Хилл. ISBN 978-0-07-062537-2 . Архивировано из оригинала 16 марта 2020 г. Проверено 18 сентября 2019 г.
- Сазерленд, Уильям (1893). «ЛИИ. Вязкость газов и молекулярная сила» (PDF) . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 36 (223): 507–531. дои : 10.1080/14786449308620508 . ISSN 1941-5982 . Архивировано (PDF) из оригинала 20 июля 2019 г. Проверено 18 сентября 2019 г.
- Саймон, Кейт Р. (1971). Механика (3-е изд.). Аддисон-Уэсли. ISBN 978-0-201-07392-8 . Архивировано из оригинала 11 марта 2020 г. Проверено 18 сентября 2019 г.
- Траченко К.; Бражкин, В.В. (22 апреля 2020 г.). «Минимальная квантовая вязкость из фундаментальных физических констант» . Достижения науки . 6 (17). Американская ассоциация содействия развитию науки (AAAS): eaba3747. arXiv : 1912.06711 . Бибкод : 2020SciA....6.3747T . дои : 10.1126/sciadv.aba3747 . ISSN 2375-2548 . ПМК 7182420 . ПМИД 32426470 .
- Траченко, Костя; Бражкин, Вадим В. (01 декабря 2021 г.). «Квантовая механика вязкости» (PDF) . Физика сегодня . 74 (12). Издательство АИП: 66–67. Бибкод : 2021ФТ....74л..66Т . дои : 10.1063/pt.3.4908 . ISSN 0031-9228 . S2CID 244831744 . Архивировано (PDF) из оригинала 10 января 2022 г. Проверено 10 января 2022 г.
- Траутон, Фред. Т. (1906). «О коэффициенте вязкой тяги и его связи с коэффициентом вязкости» . Труды Королевского общества A: Математические, физические и технические науки . 77 (519): 426–440. Бибкод : 1906RSPSA..77..426T . дои : 10.1098/rspa.1906.0038 . ISSN 1364-5021 .
- Веллиаду, Данай; Тасиду, Катерина А.; Антониадис, Константинос Д.; Ассаэль, Марк Дж.; Перкинс, Ричард А.; Хубер, Марсия Л. (25 марта 2021 г.). «Эталонная корреляция вязкости ксенона от тройной точки до 750 К и до 86 МПа» . Международный журнал теплофизики . 42 (5). Springer Science and Business Media LLC: 74. Бибкод : 2021IJT....42...74V . дои : 10.1007/s10765-021-02818-9 . ISSN 0195-928X . ПМЦ 8356199 . ПМИД 34393314 .
- Вишванатх, Д.С.; Натараджан, Г. (1989). Сборник данных по вязкости жидкостей . Издательская корпорация Hemisphere. ISBN 0-89116-778-1 .
- Вишванат, Дабир С.; и др. (2007). Вязкость жидкостей: теория, оценка, эксперимент и данные . Спрингер. ISBN 978-1-4020-5481-5 .
- Уолцер, Уве; Хендель, Роланд; Баумгарднер, Джон, «Мантийная вязкость и толщина конвективных нисходящих потоков» , igw.uni-jena.de , заархивировано из оригинала 11 июня 2007 г.
- Се, Хун-И; Левченко, Алексей (23 января 2019 г.). «Отрицательная вязкость и вихревое течение несбалансированной электронно-дырочной жидкости в графене». Физ. Преподобный Б. 99 (4): 045434. arXiv : 1807.04770 . Бибкод : 2019PhRvB..99d5434X . дои : 10.1103/PhysRevB.99.045434 . S2CID 51792702 .
- Янниотис, С.; Скальци, С.; Карабурниоти, С. (февраль 2006 г.). «Влияние влажности на вязкость меда при разных температурах». Журнал пищевой инженерии . 72 (4): 372–377. дои : 10.1016/j.jfoodeng.2004.12.017 .
- Чжао, Мэнцзин; Ван, Юн; Ян, Шуфэн; Ли, Цзинше; Лю, Вэй; Сун, Чжаоци (2021). «Текучесть и теплообмен жидкой стали в двухручьевом промковше, нагреваемом плазмой» . Журнал исследований материалов и технологий . 13 . Эльзевир Б.В.: 561–572. дои : 10.1016/j.jmrt.2021.04.069 . ISSN 2238-7854 . S2CID 236277034 .
- Жмудь, Борис (2014). «Уравнения смешивания вязкости» (PDF) . Лубе-Тех:93. Любэ . № 121. С. 22–27. Архивировано (PDF) из оригинала 1 декабря 2018 г. Проверено 30 ноября 2018 г.
- «База данных по термодинамическим и транспортным свойствам эталонных жидкостей NIST (REFPROP): версия 10» . НИСТ . 01.01.2018. Архивировано из оригинала 16 декабря 2021 г. Проверено 23 декабря 2021 г.
- техническая наука (25 марта 2020 г.). «Вязкость жидкостей и газов» . техническая наука . Архивировано из оригинала 19 апреля 2020 г. Проверено 7 мая 2020 г.
Внешние ссылки
[ редактировать ]- Вязкость - Фейнмановские лекции по физике
- Свойства жидкости – высокоточный расчет вязкости для часто встречающихся чистых жидкостей и газов.
- Таблица характеристик жидкости - таблица вязкости и давления пара для различных жидкостей.
- Gas Dynamics Toolbox – расчет коэффициента вязкости для смесей газов
- Измерение вязкости стекла – измерение вязкости, единицы вязкости и фиксированные точки, расчет вязкости стекла.
- Кинематическая вязкость – преобразование между кинематической и динамической вязкостью.
- Физические характеристики воды - таблица вязкости воды в зависимости от температуры.
- Расчет температурно-зависимой динамической вязкости для некоторых распространенных компонентов
- Искусственная вязкость
- Вязкость воздуха, динамическая и кинематическая, Engineers Edge









![{\displaystyle [\mu ]={\frac {\rm {kg}}{\rm {m{\cdot }s}}} = {\frac {\rm {N}}{\rm {m^{2 }}}}{\cdot }{\rm {s}}={\rm {Па{\cdot } с}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0505c4de127e4d762cc7174f9e205606cbef004)









![{\displaystyle [\nu ]=\mathrm {\frac {m^{2}}{s}} =\mathrm {{\frac {N{\cdot }m}{kg}}{\cdot }s} = \mathrm {{\frac {J}{kg}}{\cdot }s} =}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abefedddb99ec0896354cfcfcdffd26d00903265)













![{\displaystyle {\boldsymbol {\tau }}=\mu \left[\nabla \mathbf {v} +(\nabla \mathbf {v})^{\mathrm {T} }\right]-\left({ \frac {2}{3}}\mu -\kappa \right)(\nabla \cdot \mathbf {v} )\mathbf {\delta } ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c881ede5c0e043dbe36b7b5a30b4c6bf92204e5a)




![{\displaystyle {\begin{aligned}\mathbf {J} &=-D {\frac {\partial \rho }{\partial x}} && {\text{(закон диффузии Фика)}}\\[5pt ]\mathbf {q} &=-k_{t}{\frac {\partial T}{\partial x}}&& {\text{(закон теплопроводности Фурье)}}\\[5pt]\tau &= \mu {\frac {\partial u}{\partial y}}&&{\text{(закон вязкости Ньютона)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6380b89b0d24d9c9deb9ef04f333430b073c45cc)

































































![{\displaystyle \mu =AT\exp \left({\frac {B}{RT}}\right)\left[1+C\exp \left({\frac {D}{RT}}\right)\ верно],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38aa9224e9ac73624655cd20405e140af63a62eb)
![{\displaystyle \mu =\exp {\left\{{\frac {V_{c}C_{G}}{k_{B}T}}\exp {\left[(2+\lambda)\alpha _{ T}T_{g}\left(1-{\frac {T}{T_{g}}}\right)\right]}\right\}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7c6670713177337446c22a7976e9664d2008526)








