Законы движения планет Кеплера

- Орбиты представляют собой эллипсы с фокусами F 1 и F 2 для Планеты 1 и F 1 и F 3 для Планеты 2. Солнце находится в точке F 1 .
- Заштрихованные области A 1 и A 2 равны и охватываются орбитой Планеты 1 в одинаковое время.
- Отношение времени обращения Планеты 1 к времени обращения Планеты 2 равно .
| Часть серии о |
| Астродинамика |
|---|
В астрономии , законы движения планет Кеплера опубликованные Иоганном Кеплером , описывают орбиты планет между 1609 и 1619 годами вокруг Солнца . Законы изменяются изменили гелиоцентрическую теорию Николая Коперника , заменив ее круговые орбиты и эпициклы эллиптическими скорости и объяснив, как траекториями планет . Три закона гласят, что: [1] [2]
- Орбита в планеты представляет собой эллипс, которого находится Солнце одном из двух фокусов .
- соединяющий Отрезок линии, планету и Солнце, заметает равные площади за равные промежутки времени.
- планеты Квадрат периода обращения пропорционален кубу длины большой полуоси ее орбиты.
Эллиптические орбиты планет были указаны расчетами орбиты Марса . Из этого Кеплер сделал вывод, что другие тела Солнечной системы , в том числе находящиеся дальше от Солнца, также имеют эллиптические орбиты. Второй закон помогает установить, что когда планета находится ближе к Солнцу, она движется быстрее. Третий закон гласит, что чем дальше планета от Солнца, тем медленнее ее орбитальная скорость, и наоборот.
Исаак Ньютон показал в 1687 году, что соотношения, подобные тем, что были у Кеплера, будут применяться в Солнечной системе как следствие его собственных законов движения и закона всемирного тяготения .
Более точный исторический подход можно найти в Astronomia nova и Epitome Astronomiae Copernicanae .
Сравнение с Коперником
[ редактировать ]Законы Иоганна Кеплера усовершенствовали модель Коперника . По словам Коперника: [3] [4]
- Орбита планеты представляет собой круг с эпициклами.
- Солнце находится примерно в центре орбиты.
- Скорость планеты на главной орбите постоянна.
Несмотря на то, что Коперник был прав, утверждая, что планеты вращаются вокруг Солнца, он был неправ в определении их орбит. Предлагая физические объяснения движения в космосе, выходящие за рамки простой геометрии, Кеплер правильно определил орбиты планет следующим образом: [1] [2] [5] : 53–54
- Орбита планеты представляет собой не круг с эпициклами, а эллипс .
- Солнце находится не в центре, а в фокусе эллиптической орбиты.
- Ни линейная скорость, ни угловая скорость планеты на орбите не являются постоянными, но площадная скорость (тесно связанная исторически с понятием углового момента ). постоянна
Эксцентриситет , составляющее около орбиты Земли делает время от мартовского равноденствия до сентябрьского равноденствия 186 дней, не равным времени от сентябрьского равноденствия до мартовского равноденствия, составляющему около 179 дней. Диаметр разрезал бы орбиту на равные части, но плоскость, проходящая через Солнце, параллельная экватору Земли , делит орбиту на две части с площадями в соотношении 186 к 179, поэтому эксцентриситет орбиты Земли примерно равен
что близко к правильному значению (0,016710218). Точность этого расчета требует, чтобы две выбранные даты располагались вдоль малой оси эллиптической орбиты, а средние точки каждой половины - вдоль большой оси. Поскольку две выбранные здесь даты являются равноденствиями, это будет правильно, когда перигелий , дата, когда Земля находится ближе всего к Солнцу, приходится на солнцестояние . Текущий перигелий около 4 января довольно близок к солнцестоянию 21 или 22 декабря.
Номенклатура
[ редактировать ]Потребовалось почти два столетия, чтобы нынешняя формулировка работы Кеплера приняла устоявшуюся форму. « Книга Вольтера Элементы философии Ньютона» ( «Элементы философии Ньютона ») 1738 года была первой публикацией, в которой использовалась терминология «законов». [6] [7] Биографическая энциклопедия астрономов в своей статье о Кеплере (стр. 620) утверждает, что терминология научных законов для этих открытий была актуальна по крайней мере со времен Жозефа де Лаланда . [8] Именно изложение Роберта Смолла в «Отчёте об астрономических открытиях Кеплера» (1814 г.) составило набор трёх законов путём добавления третьего. [9] Смолл также утверждал, вопреки истории, что это были эмпирические законы , основанные на индуктивных рассуждениях . [7] [10]
Более того, нынешнее использование «Второго закона Кеплера» является своего рода неправильным употреблением. У Кеплера было две версии, родственные в качественном смысле: «закон расстояния» и «закон площади». «Закон территории» - это то, что стало Вторым законом в наборе из трех; но сам Кеплер не придавал этому особого значения. [11]
История
[ редактировать ]Кеплер опубликовал свои первые два закона движения планет в 1609 году. [12] обнаружив их путем анализа астрономических наблюдений Тихо Браге . [13] [14] [15] [5] : 53 Третий закон Кеплера был опубликован в 1619 году. [16] [14] Кеплер верил в коперниканскую модель Солнечной системы, которая требовала круговых орбит, но он не мог совместить высокоточные наблюдения Браге с круговым соответствием орбите Марса - Марс по совпадению имел самый высокий эксцентриситет среди всех планет, кроме Меркурия. [17] Его первый закон отразил это открытие.
что его третий закон применим к четырем ярчайшим спутникам Юпитера В 1621 году Кеплер отметил , . [Кол. 1] Годфруа Венделен также сделал это наблюдение в 1643 году. [Кол. 2] Второй закон в форме «закона площади» был оспорен Николаем Меркатором в книге 1664 года, но к 1670 году его «Философские труды» были в его пользу. [18] [19] В течение столетия оно получило более широкое признание. [20] Прием в Германии заметно изменился между 1688 годом, когда были опубликованы «Начала» Ньютона , которые были признаны в основном коперниканскими, и 1690 годом, когда работа Готфрида Лейбница о Кеплере. была опубликована [21]
Ньютону приписывали понимание того, что второй закон не является чем-то особенным по отношению к закону обратных квадратов гравитации, а является следствием только радиальной природы этого закона, тогда как другие законы действительно зависят от формы обратных квадратов притяжения. Карл Рунге и Вильгельм Ленц гораздо позже определили принцип симметрии в фазовом пространстве движения планет ( действующая ортогональная группа O(4)) который объясняет первый и третий законы в случае ньютоновской гравитации, как это делает сохранение углового момента через вращательная симметрия для второго закона. [22]
Формуляр
[ редактировать ]Математическая модель подчиняющейся законам кинематики планеты допускает большой диапазон дальнейших расчетов.
Первый закон
[ редактировать ]Орбита каждой планеты представляет собой эллипс, в одном из двух фокусов которого находится Солнце .


Математически эллипс можно представить формулой:
где — полуширокая прямая кишка , ε — эксцентриситет эллипса, r — расстояние от Солнца до планеты, а θ — угол к текущему положению планеты при ее наибольшем сближении, если смотреть с Солнца. Итак, ( r , θ ) — полярные координаты .
Для эллипса 0 < ε < 1; в предельном случае ε = 0 орбита представляет собой круг с Солнцем в центре (т. е. там, где эксцентриситет равен нулю).
При θ = 0°, перигелий , расстояние минимально.
При θ = 90° и при θ = 270° расстояние равно .
При θ = 180°, афелии , расстояние максимально (по определению афелий — это неизменно перигелий плюс 180°).
Большая полуось a представляет собой среднее арифметическое между r min и r max :
b Малая полуось представляет собой среднее геометрическое между r min и r max :
Полурасширенная прямая кишка p — это среднее гармоническое значение между r min и r max :
Эксцентриситет ε — это коэффициент вариации между r min и r max :
Площадь равна эллипса
Особым случаем круга является ε = 0, в результате чего r = p = r min = r max = a = b и A = πr. 2 .
Второй закон
[ редактировать ]Линия , соединяющая планету и Солнце, за равные промежутки времени охватывает равные площади. [23]

Радиус орбиты и угловая скорость планеты на эллиптической орбите будут меняться. Это показано в анимации: планета движется быстрее, когда ближе к Солнцу, и медленнее, когда дальше от Солнца. Второй закон Кеплера гласит, что синий сектор имеет постоянную площадь.
История и доказательства
[ редактировать ]Кеплер, в частности, пришел к этому закону на основе предположений, которые были либо лишь приблизительно верными, либо совершенно ложными, и их можно изложить следующим образом:
1. Планеты вращаются вокруг Солнца под действием солнечной силы. Это ложное предположение основано на неверной аристотелевской физике , согласно которой объект необходимо толкать, чтобы поддерживать движение.
2. Движущая сила Солнца обратно пропорциональна расстоянию от Солнца. Кеплер рассуждал так, полагая, что распространение гравитации в трех измерениях было бы напрасной тратой, поскольку планеты обитают в плоскости. Таким образом, обратный закон вместо [правильного] закона обратных квадратов.
3. Поскольку Кеплер считал, что сила пропорциональна скорости, из утверждений №1 и №2 следовало, что скорость будет обратно пропорциональна расстоянию от Солнца. Это также неверный принцип аристотелевской физики.
4. Поскольку скорость обратна времени, расстояние от Солнца будет пропорционально времени прохождения небольшого участка орбиты. Это примерно справедливо для эллиптических орбит.
5. Заметенная площадь пропорциональна общему времени. Это тоже примерно верно.
6. Орбиты планет круговые (Кеплер открыл свой Второй закон раньше Первого закона, что противоречит этому).
Тем не менее, результат Второго закона в точности верен, поскольку он логически эквивалентен сохранению углового момента, что справедливо для любого тела, на которое действует радиально-симметричная сила. [24] С помощью этого можно показать правильное доказательство. Поскольку векторное произведение двух векторов дает площадь параллелограмма, стороны которого равны этим векторам, площадь треугольника dA, выметенная за короткий период времени, равна половине векторного произведения векторов r и dx для некоторого короткого куска орбита, dx .
за небольшой участок орбиты dx и время его прохождения dt .
Таким образом
Поскольку окончательное выражение пропорционально полному угловому моменту Закон равновеликих площадей Кеплера справедлив для любой системы, сохраняющей угловой момент. Поскольку любая радиальная сила не будет создавать крутящего момента при движении планеты, угловой момент будет сохраняться.
По эллиптическим параметрам
[ редактировать ]За короткое время планета образует небольшой треугольник с базовой линией и высота и площадь , поэтому постоянная окружная скорость равна
Площадь, ограниченная эллиптической орбитой, равна . Итак, период удовлетворяет
и среднее движение планеты вокруг Солнца
удовлетворяет
И так,
Третий закон
[ редактировать ]Отношение квадрата периода обращения объекта к кубу большой полуоси его орбиты одинаково для всех объектов, вращающихся вокруг одной и той же главной звезды.
Это отражает взаимосвязь между расстоянием планет от Солнца и периодами их обращения.
Кеплер провозгласил в 1619 г. [16] этот третий закон в кропотливой попытке определить то, что он считал «музыкой сфер », согласно точным законам, и выразить это в терминах нотной записи. [25] Поэтому он был известен как гармонический закон . [26] Первоначальная форма этого закона (относящаяся не к большой полуоси, а к «среднему расстоянию») справедлива только для планет с небольшими эксцентриситетами, близкими к нулю. [27]
Используя закон тяготения Ньютона (опубликованный в 1687 г.), это соотношение можно найти в случае круговой орбиты, установив центростремительную силу равной гравитационной силе:
Тогда, выразив угловую скорость ω через орбитальный период а затем перестановка приводит к третьему закону Кеплера:
Более подробный вывод можно сделать, используя общие эллиптические орбиты вместо кругов, а также вращение вокруг центра масс, а не только большой массы. Это приводит к замене кругового радиуса, , с большой полуосью, , эллиптического относительного движения одной массы относительно другой, а также замены большой массы с . Однако, поскольку массы планет намного меньше Солнца, эту поправку часто игнорируют. Полная соответствующая формула:
где это масса Солнца , это масса планеты, гравитационная постоянная , - орбитальный период и — большая полуось эллипса, а — астрономическая единица , среднее расстояние от Земли до Солнца.
Стол
[ редактировать ]В следующей таблице показаны данные, которые Кеплер использовал для эмпирического вывода своего закона:
| Планета | Среднее расстояние к солнцу (AU) | Период (дней) | (10 -6 В 3 /день 2 ) |
|---|---|---|---|
| Меркурий | 0.389 | 87.77 | 7.64 |
| Венера | 0.724 | 224.70 | 7.52 |
| Земля | 1 | 365.25 | 7.50 |
| Марс | 1.524 | 686.95 | 7.50 |
| Юпитер | 5.20 | 4332.62 | 7.49 |
| Сатурн | 9.510 | 10759.2 | 7.43 |
Обнаружив эту закономерность, Кеплер написал: [28]
Сначала я поверил, что сплю... Но совершенно достоверно и точно то, что соотношение, существующее между периодами периодов любых двух планет, представляет собой в точности соотношение 3/2 степени среднего расстояния.
- перевод из «Гармонии мира» (1619 г.) книги Кеплера

Для сравнения вот современные оценки: [ нужна ссылка ]
| Планета | Большая полуось (АС) | Период (дни) | (10 -6 В 3 /день 2 ) |
|---|---|---|---|
| Меркурий | 0.38710 | 87.9693 | 7.496 |
| Венера | 0.72333 | 224.7008 | 7.496 |
| Земля | 1 | 365.2564 | 7.496 |
| Марс | 1.52366 | 686.9796 | 7.495 |
| Юпитер | 5.20336 | 4332.8201 | 7.504 |
| Сатурн | 9.53707 | 10775.599 | 7.498 |
| Уран | 19.1913 | 30687.153 | 7.506 |
| Нептун | 30.0690 | 60190.03 | 7.504 |
Планетарное ускорение
[ редактировать ]Исаак Ньютон в своей «Philosophiæ Naturalis Principia Mathematica» вычислил ускорение . планеты, движущейся в соответствии с первым и вторым законами Кеплера
- Направление . ускорения — к Солнцу
- Величина ускорения обратно пропорциональна квадрату расстояния планеты от Солнца ( закон обратных квадратов ).
Это означает, что Солнце может быть физической причиной ускорения планет. Однако Ньютон утверждает в своих «Началах» , что он рассматривает силы с математической, а не с физической точки зрения, тем самым придерживаясь инструменталистской точки зрения. [29] Более того, он не приписывает гравитации причину. [30]
Ньютон определил силу , действующую на планету, как произведение ее массы и ускорения (см. Законы движения Ньютона ). Так:
- Каждая планета притягивается к Солнцу.
- Сила, действующая на планету, прямо пропорциональна массе планеты и обратно пропорциональна квадрату ее расстояния от Солнца.
Солнце играет несимметричную роль, что неоправданно. Поэтому он предположил в законе всемирного тяготения Ньютона :
- Все тела Солнечной системы притягивают друг друга.
- Сила между двумя телами прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.
Поскольку планеты имеют малую массу по сравнению с массой Солнца, их орбиты примерно соответствуют законам Кеплера. Модель Ньютона является усовершенствованной моделью Кеплера и более точно соответствует реальным наблюдениям. (См. задачу двух тел .)
Ниже приводится подробный расчет ускорения планеты, движущейся по первому и второму законам Кеплера.
Вектор ускорения
[ редактировать ]С гелиоцентрической точки зрения рассмотрим вектор к планете где расстояние до планеты и — единичный вектор, направленный в сторону планеты.
где — единичный вектор, направление которого составляет 90 градусов против часовой стрелки. , и — полярный угол, и точка над переменной означает дифференцирование по времени.
Дважды продифференцируйте вектор положения, чтобы получить вектор скорости и вектор ускорения:
Так где ускорение радиальное а поперечное ускорение равно
Закон обратных квадратов
[ редактировать ]Второй закон Кеплера гласит, что является постоянным.
Поперечное ускорение равен нулю:
Итак, ускорение планеты, подчиняющейся второму закону Кеплера, направлено к Солнцу.
Радиальное ускорение является
Первый закон Кеплера гласит, что орбита описывается уравнением:
Дифференцирование по времени или
Дифференцируем еще раз
Радиальное ускорение удовлетворяет
Подстановка уравнения эллипса дает
Отношение дает простой конечный результат
Это означает, что вектор ускорения любая планета, подчиняющаяся первому и второму законам Кеплера, удовлетворяет закону обратных квадратов где является константой, и - единичный вектор, направленный от Солнца к планете, и расстояние между планетой и Солнцем.
Поскольку среднее движение где период, согласно третьему закону Кеплера, имеет одинаковое значение для всех планет. Таким образом, закон обратных квадратов для планетарных ускорений применяется во всей Солнечной системе.
Закон обратных квадратов представляет собой дифференциальное уравнение . Решения этого дифференциального уравнения включают, как показано, кеплеровы движения, но они также включают движения, орбита которых представляет собой гиперболу , параболу или прямую линию . (См. Орбиту Кеплера .)
Закон гравитации Ньютона
[ редактировать ]По второму закону Ньютона сила гравитации, действующая на планету, равна:
где это масса планеты и имеет одинаковое значение для всех планет Солнечной системы. Согласно третьему закону Ньютона , Солнце притягивается к планете силой такой же величины. Поскольку сила пропорциональна массе планеты, с точки зрения симметричности она также должна быть пропорциональна массе Солнца. . Так где является гравитационной постоянной .
Ускорение тела номер i Солнечной системы согласно законам Ньютона составляет: где — масса тела j , расстояние между телом i и телом j , — единичный вектор от тела i к телу j , а векторное суммирование производится по всем телам Солнечной системы, кроме самого i .
В частном случае, когда в Солнечной системе есть только два тела, Земля и Солнце, ускорение становится что является ускорением движения Кеплера. Итак, эта Земля движется вокруг Солнца по законам Кеплера.
Если двумя телами в Солнечной системе являются Луна и Земля, ускорение Луны становится
Итак, в этом приближении Луна движется вокруг Земли по законам Кеплера.
В случае трёх тел ускорения равны
Эти ускорения не соответствуют орбитам Кеплера, и проблема трех тел сложна. Но кеплерово приближение является основой для вычислений возмущений . (См. Теорию Луны .)
Позиция как функция времени
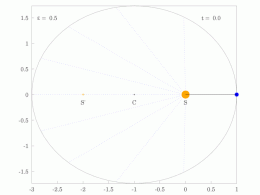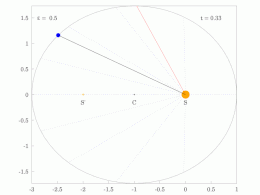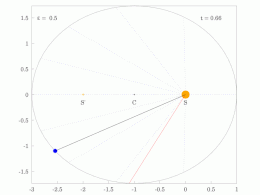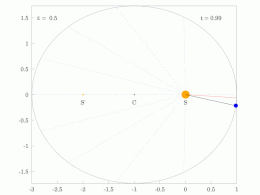
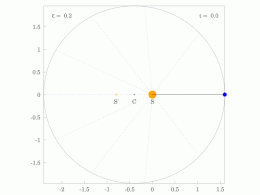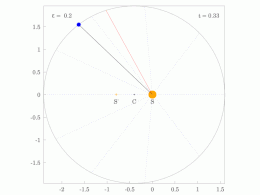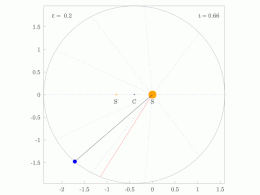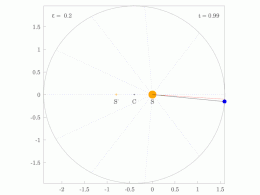
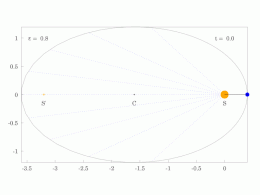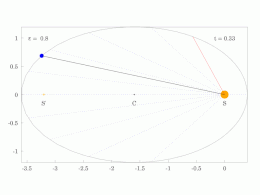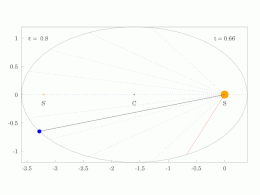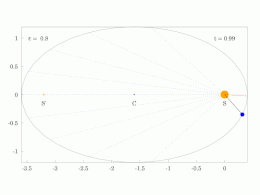
[ редактировать ]Кеплер использовал два своих первых закона для расчета положения планеты в зависимости от времени. Его метод предполагает решение трансцендентного уравнения, называемого уравнением Кеплера .
Процедура расчета гелиоцентрических полярных координат ( r , θ ) планеты как функции времени t с момента перигелия состоит из следующих пяти шагов:
- Вычислите среднее движение n = (2 π рад)/ P , где P — период.
- Вычислите среднюю аномалию M = nt , где t — время, прошедшее с момента перигелия.
- Вычислите эксцентрическую аномалию E, решив уравнение Кеплера: где это эксцентриситет.
- Вычислите истинную аномалию θ, решив уравнение:
- Вычислите гелиоцентрическое расстояние r : где является большой полуосью.
Полярные координаты положения ( r , θ ) теперь можно записать как декартов вектор. и тогда декартов вектор скорости можно рассчитать как , где — стандартный гравитационный параметр . [31]
Важный частный случай круговой орбиты, ε дает θ = E = M. = 0 , Поскольку равномерное круговое движение считалось нормальным , отклонение от этого движения считалось аномалией.
Доказательство этой процедуры показано ниже.
Средняя аномалия, М
[ редактировать ]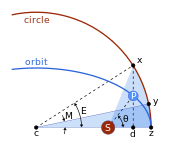
Задача Кеплера предполагает эллиптическую орбиту и четыре точки:
- s Солнце (в одном фокусе эллипса);
- z перигелий
- в центр эллипса
- п планета
и
- расстояние между центром и перигелием, большой полуосью,
- эксцентричность,
- малая полуось,
- расстояние между Солнцем и планетой.
- направление на планету, если смотреть со стороны Солнца, истинная аномалия .
Проблема состоит в том, чтобы вычислить полярные координаты ( r , θ ) планеты по времени, начиная с перигелия, t .
Решается поэтапно. Кеплер считал круг с большой осью диаметром, а
- проекция планеты на вспомогательный круг
- точка на окружности такая, что площади секторов | zcy | и | зсх | равны,
- средняя аномалия .
Области секторов связаны между собой
кругового сектора Площадь
Площадь, пройденная начиная с перигелия, по второму закону Кеплера пропорциональна времени, начиная с перигелия. Таким образом, средняя аномалия M пропорциональна времени, прошедшему с момента перигелия t . где n — среднее движение .
Эксцентрическая аномалия, E
[ редактировать ]Когда вычисляется средняя аномалия M , цель состоит в том, чтобы вычислить истинную аномалию θ . Однако функция θ = f ( M ) не является элементарной. [32] Решение Кеплера состоит в использовании x, если смотреть из центра, эксцентрическая аномалия в качестве промежуточной переменной и сначала вычислите E как функцию от M, приведенное ниже уравнение Кеплера, а затем вычислите истинную аномалию θ на основе эксцентрической аномалии E. решив Вот подробности.
на Разделение 2 /2 дает уравнение Кеплера
дает M как функцию E. Это уравнение Определение E для данного M является обратной задачей. Обычно используются итерационные численные алгоритмы.
После вычисления эксцентрической аномалии E следующим шагом будет вычисление истинной аномалии θ .
Но обратите внимание: декартовы координаты положения относительно центра эллипса: ( a cos E , b sin E )
По отношению к Солнцу (с координатами ( c ,0) = ( ae ,0)), r = ( a cos E – ae , b sin E )
Истинная аномалия будет arctan( r y / r x ), величина r будет √ r · r .
Истинная аномалия, θ
[ редактировать ]Обратите внимание на рисунок, что так что
Деление на и подстановка из первого закона Кеплера получить
Результатом является полезная связь между эксцентрической аномалией E и истинной аномалией θ .
Более удобная с вычислительной точки зрения форма получается путем подстановки в тригонометрическое тождество :
Получать
Умножение на 1 + ε дает результат
Это третий шаг в связи времени и положения на орбите.
Расстояние, р
[ редактировать ]Четвертый шаг — вычислить гелиоцентрическое расстояние r на основе истинной аномалии θ по первому закону Кеплера:
Используя приведенное выше соотношение между θ и E, окончательное уравнение для расстояния r будет следующим:
См. также
[ редактировать ]- Круговое движение
- Время свободного падения
- Гравитация
- Кеплер орбита
- проблема Кеплера
- Уравнение Кеплера
- Вектор Лапласа–Рунге–Ленца
- Удельный относительный угловой момент , относительно простой вывод законов Кеплера, начиная с сохранения углового момента.
Пояснительные примечания
[ редактировать ]- ↑ В 1621 году Иоганн Кеплер отметил, что спутники Юпитера подчиняются (приблизительно) его третьему закону в его Epitome Astronomiae Copernicanae [Воплощение коперниканской астрономии] (Линц («Lentiis ad Danubium»), (Австрия): Иоганн Планк, 1622), книга 4 , часть 2, страницы 554–555 . Со стр. 554–555: «... plane ut est cum sex Planet около Солема, ... prodit Marius in suo mundo Ioviali ista 3.5.8.13 (vel 14. Galilæo) ... Periodica vero tempora prodit idem Marius .. .sunt maiora simplis, minora vero duplis». (... так же, как это явно [истинно] среди шести планет вокруг Солнца, так же и среди четырех [спутников] Юпитера, потому что вокруг тела Юпитера любой [спутник], который может пройти дальше от него, вращается медленнее, да и тот [период орбиты] не в той же пропорции, а больше [расстояния от Юпитера], то есть 3/2 ( сескупла ) доли каждого из расстояний от Юпитера, что ясно; та самая [пропорция], которая использована для шести планет выше в его [книге] «Мир Юпитера» . [ Mundus Jovialis , 1614], [Саймон Майр или] «Мариус» [1573–1624] представляет эти расстояния от Юпитера четырех [спутников] Юпитера: 3, 5, 8, 13 (или 14 [по] Галилей) [Примечание: расстояния спутников Юпитера от Юпитера выражаются кратными диаметру Юпитера.] ... Майр представляет их периоды времени: 1 день 18 1/2 часа, 3 дня 13 1/3 часа, 7 дней 2 часа , 16 дней 18 часов: для всех [этих данных] пропорция больше чем в два раза, то есть больше, чем [доля] расстояний 3, 5, 8, 13 или 14, хотя и меньше, чем [доля] квадратов , которые удваивают пропорции расстояний, а именно 9, 25, 64, 169 или 196, точно так же, как [степень] 3/2 также больше 1, но меньше 2.)
- ↑ Годфруа Венделин написал письмо Джованни Баттисте Риччоли о взаимосвязи между расстояниями спутников Юпитера от Юпитера и периодами их орбит, показав, что периоды и расстояния соответствуют третьему закону Кеплера. См.: Джоан Баптиста Риччоли, Almagestum novum ... (Болонья (Бонония), (Италия): Виктор Бенати, 1651), том 1, стр. 492 Схолия III. На полях рядом с соответствующим абзацем напечатано: Vendelini ingeniosa speculatio circa motus & Intervalla satellitum Jovis . (Умное предположение Венделина о движении и расстояниях спутников Юпитера.) Со с. 492: «III. Non minus Kepleriana ingeniosa est Vendelini ... и D. 7. 164/1000. pro penextimo и D. 16. 756/1000. pro extimo». (Не менее умно [чем] Кеплера исследование самого проницательного астронома Венделина относительно пропорций периодов и расстояний спутников Юпитера, которое он с большой щедростью сообщил мне [в] очень длинном и очень ученом письме. Итак, просто как и в случае с более крупными планетами, средние расстояния планет от Солнца находятся соответственно в соотношении 3/2 их периодов, так же и расстояния этих малых планет Юпитера от Юпитера (которые равны 3, 5, 8); , и 14) находятся соответственно в соотношении 3/2 [их] периодов (что составляет 1,769 дня для самого внутреннего [Ио], 3,554 дня для ближайшего к самому внутреннему [Европы], 7,164 дня для ближайшего к самому внешнему [ Ганимед] и 16,756 дней для самого дальнего [Каллисто]).)
Цитаты
[ редактировать ]- ^ Перейти обратно: а б «Законы Кеплера» . гиперфизика.phy-astr.gsu.edu . Проверено 13 декабря 2022 г.
- ^ Перейти обратно: а б «Орбиты и законы Кеплера» . Исследование Солнечной системы НАСА . Проверено 13 декабря 2022 г.
- ^ «Движение планет: история идеи, положившей начало научной революции» . Earthobservatory.nasa.gov . 07.07.2009 . Проверено 13 декабря 2022 г.
- ^ «Николай Коперник» . история.com . Проверено 13 декабря 2022 г.
- ^ Перейти обратно: а б Джинджерич, Оуэн (2011). «Великая марсианская катастрофа и как ее исправил Кеплер» (PDF) . Физика сегодня . 64 (9): 50–54. Бибкод : 2011ФТ....64и..50Г . дои : 10.1063/PT.3.1259 . Проверено 27 июля 2023 г.
- ^ Вольтер, Элементы философии Ньютона (Лондон: 1738). См., например:
- Из стр. 162: «По одному из великих законов Кеплера каждая Планета описывает равные площади в одинаковое время; по другому, не менее достоверному закону, каждая Планета совершает свое обращение вокруг Солнца таким образом, что если ее среднее расстояние от Солнца равно 10 ... возьмем куб этого числа, которое будет 1000, и время обращения этой Планеты вокруг Солнца будет пропорционально квадратному корню из этого числа 1000». (По одному из великих законов Кеплера каждая планета описывает равные площади за равное время; по другому закону, не менее достоверному, каждая планета совершает свой оборот вокруг Солнца таким образом, что если ее среднее расстояние от Солнца равно 10, то куб этого числа, которое будет 1000, и время обращения этой планеты вокруг Солнца будет пропорционально квадратному корню из этого числа 1000.)
- Из стр. 205: «Il est donc prouvé par la loi de Kepler & par celle de Neuton, que chaque Planete gravite vers le Soleil,...» (Таким образом, законом Кеплера и законом Ньютона доказано, что каждая планета вращается вокруг Солнца...)
- ^ Перейти обратно: а б Уилсон, Кертис (май 1994 г.). «Так называемые законы Кеплера» (PDF) . HAD News (31): 1–2 . Проверено 27 декабря 2016 г.
- ^ Де ла Ланде, Астрономия , том. 1 (Париж: Десен и Сайян, 1764). См., например:
- Из стр. 390: "...но согласно знаменитому закону Кеплера, который будет объяснен в следующей Книге (892), отношение периодических времен всегда больше, чем соотношение расстояний, планета, в пять раз дальше от Солнца, пользуется совершить свой оборот в двенадцать раз за большее время или приблизительно..." (...но согласно знаменитому закону Кеплера, который будет объяснен в следующей книге [т.е. главе] (п. 892), соотношение периоды всегда больше, чем расстояния [так что, например] планете, находящейся в пять раз дальше от Солнца, требуется примерно в двенадцать раз больше времени, чтобы совершить свой оборот [вокруг Солнца]...)
- Из стр. 429: «Четверти периодических времен подобны кубам расстояний. 892. Самый известный закон движения планет, открытый Кеплером, — это закон соотношения между величинами их орбит и временем, которое они используют их, чтобы путешествовать...» (Квадраты периодов подобны кубам расстояний. 892. Самый известный закон движения планет, открытый Кеплером, — это закон соотношения размеров их орбит. и время, которое требуется [планетам] для прохождения их...)
- Из стр. 430: «Площади пропорциональны времени. 895. Этот общий закон движения планет, ставший столь важным в астрономии, а именно, что площади пропорциональны времени, до сих пор является одним из открытий Кеплера;...» («Площади » пропорциональны времени. 895. Этот общий закон движения планет, [который стал] столь важным в астрономии, а именно, что площади пропорциональны времени, является одним из открытий Кеплера...)
- Из стр. 435: «Этот закон площадей, пропорциональных времени, назвали законом Кеплера, как и закон статьи 892, по имени этого знаменитого изобретателя;...» (Этот закон площадей, пропорциональных времени, назвали законом Кеплера (законом Кеплер), а также п.
- ^ Роберт Смолл, Отчет об астрономических открытиях Кеплера (Лондон: Дж. Моуман, 1804), стр. 298–299.
- ^ Роберт Смолл, Отчет об астрономических открытиях Кеплера (Лондон: Дж. Моуман, 1804 г.).
- ^ Брюс Стивенсон (1994). Физическая астрономия Кеплера . Издательство Принстонского университета. п. 170. ИСБН 978-0-691-03652-6 .
- ^ Astronomy nova Aitiologitis, ou Physica Celestis traditio Commentarii de Tibus estella Martis из наблюдений Г. В. Тихона, Прага, 1609 г.; Английский тр. WH Донахью, Кембридж, 1992.
- ↑ В своей «Новой астрономии » Кеплер представил лишь доказательство того, что орбита Марса эллиптическая. Доказательства того, что орбиты других известных планет имеют эллиптическую форму, были представлены только в 1621 году.
См.: Иоганн Кеплер, Astronomia nova ... (1609), с. 285. Отвергнув круговую и овальную орбиты, Кеплер пришел к выводу, что орбита Марса должна быть эллиптической. В начале страницы 285: «Ergo ellipsis est Planetæ iter; ...» (Таким образом, эллипс — это путь планеты [т. е. Марса]; ...) Далее на той же странице: «... ut sequenti capite patescet: ubi simul etiam demostrabitur, nullam Planetæ relinqui figuram Orbitæ, præterquam perfecte ellipticam...» (... как будет показано в следующей главе: где также будет доказано, что любая фигура орбиты планеты должна быть следует отказаться, кроме идеального эллипса...) И затем: "Caput LIX. Demonstratio, quod Orbita Martis,..., fiat perfecta ellipsis:..." (Глава 59. Доказательство того, что орбита Марса,... представляет собой идеальный эллипс: ...) Геометрическое доказательство того, что орбита Марса представляет собой эллипс, содержится в Протеореме XI на страницах 289–290.
Кеплер заявил, что каждая планета движется по эллиптическим орбитам, в одном из фокусов которых находится Солнце: Иоганн Кеплер, Epitome Astronomiae Copernicanae [Краткий обзор коперниканской астрономии] (Линц («Lentiis ad Danubium»), (Австрия): Иоганн Планк, 1622), книга 5, часть 1, III. De Figura Orbitæ (III. О фигуре [то есть форме] орбит), страницы 658–665. Из стр. 658: «Ellipsin fieri Orbitam Planetæ…» (Из эллипса состоит орбита планеты…). Из стр. 659: "...Sole (Foco altero huius ellipsis)..." (...Солнце (другой фокус этого эллипса)...). - ^ Перейти обратно: а б Холтон, Джеральд Джеймс; Браш, Стивен Г. (2001). Физика, человеческое приключение: от Коперника до Эйнштейна и далее (3-е изд. в мягкой обложке). Пискатауэй, Нью-Джерси: Издательство Университета Рутгерса. стр. 40–41. ISBN 978-0-8135-2908-0 . Проверено 27 декабря 2009 г.
- ↑ В своей «Новой астрономии …» (1609 г.) Кеплер не представил свой второй закон в его современной форме. Он сделал это только в своем «Изложении 1621 года». Более того, в 1609 году он представил свой второй закон в двух разных формах, которые ученые называют «законом расстояния» и «законом площади».
- Его «закон расстояния» представлен в: «Caput XXXII. Virtutem quam Planetam moven in circulum attenuari cum discessu a Fonte». (Глава 32. Сила, перемещающая планету по кругу, ослабевает по мере удаления от источника.) См.: Иоганн Кеплер, Astronomia nova ... (1609), стр. 165–167. На странице 167 Кеплер утверждает: «…, quanto longior est αδ quam αε, tanto diutius moratur Planeta in certo aliquo arcui excentrici apud δ, quam in æquali arcu excentrici apud ε». (..., поскольку αδ длиннее αε, настолько дольше планета будет оставаться на определенной дуге эксцентрика вблизи δ, чем на равной дуге эксцентрика вблизи ε.) То есть, чем дальше планета находится от Солнце (в точке α) тем медленнее движется по своей орбите, поэтому радиус от Солнца до планеты проходит равные площади за равное время. Однако, как представил Кеплер, его аргумент верен только для кругов, а не для эллипсов.
- Его «закон площади» представлен в: «Caput LIX. Demonstratio, quod Orbita Martis,..., fiat perfecta ellipsis:...» (Глава 59. Доказательство того, что орбита Марса,..., представляет собой идеальный эллипс: ...), Протеоремы XIV и XV, стр. 291–295. На верхнем стр. 294, там написано: «Arcum ellipseos, cujus moras metitur area AKN, debere terminari в LK, ut sit AM». (Дуга эллипса, длительность которой ограничена [т. е. измерена] площадью АКМ, должна оканчиваться в ЛК, чтобы она [т. е. дуга] была АМ.) Другими словами, время, в течение которого Марс необходимого для перемещения по дуге АМ своей эллиптической орбиты, измеряется площадью отрезка АМН эллипса (где N – положение Солнца), которая в свою очередь пропорциональна сечению АКН круга, описывающего эллипс. и это имеет к этому отношение. Следовательно, площадь, охватываемая радиусом от Солнца до Марса при движении Марса по дуге своей эллиптической орбиты, пропорциональна времени, которое требуется Марсу для движения по этой дуге. Таким образом, радиус от Солнца до Марса за одинаковое время охватывает равные площади.
- ^ Перейти обратно: а б Иоганн Кеплер, Harmonices Mundi [Гармония мира] (Линц, (Австрия): Иоганн Планк, 1619), книга 5, глава 3, с. 189. Снизу п. 189: «Но совершенно достоверно и точно, что пропорция между периодами периодов любой пары планет составляет ровно половину пропорции средних расстояний...» (Но абсолютно достоверно и точно, что пропорция между время периодичности любых двух планет есть в точности полуторочередная пропорция [т. е. соотношение 3:2] их средних расстояний...")
Кеплера Английский перевод «Harmonices Mundi» доступен под названием: Йоханнес Кеплер с Э. Дж. Эйтоном, А. М. Дунканом и Дж. В. Филдом , пер., «Гармония мира» (Филадельфия, Пенсильвания: Американское философское общество, 1997); см. особенно стр. 411 . - ^ Национальная ассоциация учителей наук о Земле (9 октября 2008 г.). «Таблица данных для планет и карликовых планет» . Окна во Вселенную . Проверено 2 августа 2018 г.
- ^ Купец Николай (1664). Новая астрономическая гипотеза Николая Меркатора и ее согласие с наблюдениями на ( латыни). Лондон, Англия: Лейборн.
- ^ Меркатор, Ник. (25 марта 1670 г.). «Некоторые соображения г-на Ника Меркатора относительно геометрического и прямого метода старшего Кассини для нахождения апогеев, эксцентриситетов и аномалий планет; ...» . Философские труды Лондонского королевского общества (на латыни). 5 (57): 1168–1175. дои : 10.1098/rstl.1670.0018 . Меркатор раскритиковал метод Кассини, обнаруживший на основе трех наблюдений линию апсид орбиты. Кассини предполагал (ошибочно), что планеты движутся равномерно по своим эллиптическим орбитам. Из стр. 1174: «Sed cum id Observationibus nequaquam congruere animadverteret, mutavit sendentiam, & lineam veri motus Planetæ æqualibus temporibus æquales area Ellipticas verrere professus est: ...» (Но когда он заметил, что это совершенно не согласуется с наблюдениями, он изменил свое мышление, и он заявил, что линия [от Солнца до планеты, обозначающая] истинное движение планеты, охватывает равные площади эллипса за равные периоды времени: ... [что является формой «площади» Кеплера второй закон])
- ^ Уилбур Эпплбаум (2000). Энциклопедия научной революции: от Коперника до Ньютона . Рутледж. п. 603. Бибкод : 2000esrc.book.....A . ISBN 978-1-135-58255-5 .
- ^ Рой Портер (1992). Научная революция в национальном контексте . Издательство Кембриджского университета. п. 102 . ISBN 978-0-521-39699-8 .
- ^ Виктор Гиймен; Шломо Штернберг (2006). Вариации на тему Кеплера . Американское математическое соц. п. 5. ISBN 978-0-8218-4184-6 .
- ^ Брайант, Джефф; Павлик, Александр. « Второй закон Кеплера », Демонстрационный проект Вольфрама . Проверено 27 декабря 2009 г.
- ^ Холтон, Джеральд; Браш, Стивен (2001). Браш и Холтон - Физика: человеческое приключение . Издательство Принстонского университета. п. 42-43. ISBN 978-0813529080 .
- ^ Бертт, Эдвин . Метафизические основы современной физической науки . п. 52.
- ^ Джеральд Джеймс Холтон, Стивен Г. Браш (2001). Физика, человеческое приключение . Издательство Университета Рутгерса. п. 45. ИСБН 978-0-8135-2908-0 .
- ^ Виджая, ГК (2019). «Исходная форма третьего закона Кеплера и его неправильное применение в предложениях XXXII-XXXVII в «Началах» Ньютона (книга I)» . Гелион . 5 (2): e01274. Бибкод : 2019Хелий...501274В . дои : 10.1016/j.heliyon.2019.e01274 . ПМК 6395789 . ПМИД 30886926 .
- ^ Каспар, Макс (1993). Кеплер . Нью-Йорк: Дувр. ISBN 9780486676050 .
- ^ И. Ньютон, Principia , с. 408 в переводе И.Б. Коэна и А. Уитмена
- ^ И. Ньютон, Principia , с. 943 в переводе И.Б. Коэна и А. Уитмена
- ^ Шварц, Рене. «Меморандум № 1: Элементы кеплеровской орбиты → Декартовы векторы состояния» (PDF) . Проверено 4 мая 2018 г.
- ^ Мюллер, М (1995). «Уравнение времени – задача астрономии» . Acta Physica Polonica А. Проверено 23 февраля 2013 г.
Общая библиография
[ редактировать ]- Жизнь Кеплера кратко изложена на стр. 523–627, а пятая книга его великого опуса ( Harmonice Mundi « Гармонии мира ») переиздана на стр. 635–732 книги « На плечах гигантов : великие произведения физики и астрономии» ( работы Коперника, Кеплера , Галилея , Ньютона и Эйнштейна ). Стивен Хокинг , изд. 2002 г. ISBN 0-7624-1348-4
- Вывод третьего закона движения планет Кеплера — стандартная тема на уроках инженерной механики. См., например, стр. 161–164 из Мериам, Дж. Л. (1971) [1966]. Динамика (2-е изд.). Нью-Йорк: Джон Уайли. ISBN 978-0-471-59601-1 . .
- Мюррей и Дермотт, Динамика солнечной системы , издательство Кембриджского университета, 1999 г., ISBN 0-521-57597-4
- В. И. Арнольд, Математические методы классической механики , Гл. 2. Спрингер 1989, ISBN 0-387-96890-3
Внешние ссылки
[ редактировать ]- Б. Сурендранат Редди; анимация законов Кеплера: апплет. Архивировано 6 октября 2013 г. на Wayback Machine.
- Кроуэлл, Бенджамин, Свет и Материя , онлайн-книга , дающая доказательство первого закона без использования исчисления (см. раздел 15.7).
- Дэвид Макнамара и Джанфранко Видали, « Второй закон Кеплера – интерактивное руководство по Java », интерактивный Java-апплет, помогающий понять второй закон Кеплера.
- Каин, Гей (10 мая 2010 г.), Astronomy Cast , « Эпизод 189: Иоганн Кеплер и его законы движения планет »
- Факультет физики и астрономии Университета Теннесси: Астрономия 161, « Иоганн Кеплер: Законы движения планет ».
- Симулятор Солнечной системы ( интерактивный апплет ). Архивировано 13 декабря 2018 г. на Wayback Machine.
- « Кеплер и его законы » в От звездочетов до звездолетов» (10 октября 2016 г.) книге Дэвида П. Стерна «
- «Три закона движения планет Кеплера» на YouTube, автор Йенс Пуле (27 декабря 2023 г.) - видео, объясняющее и визуализирующее три закона движения планет Кеплера.






![{\displaystyle {\begin{aligned}a&={\frac {r_{\max }+r_{\min }}{2}}\\[3pt]a&={\frac {p}{1-\varepsilon ^ {2}}}\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82847fc5b12e705011877c295e4ed5b439a1ed30)
![{\displaystyle {\begin{aligned}b&={\sqrt {r_{\max }r_{\min }}}\\[3pt]b&={\frac {p}{\sqrt {1-\varepsilon ^{ 2}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03d3ca95934b7178477b3e16f3364de18f5fe6a9)

































































































![{\displaystyle {\begin{aligned}\tan ^{2}{\frac {E}{2}}&={\frac {1-\cos E}{1+\cos E}}={\frac { 1-{\frac {\varepsilon +\cos \theta }{1+\varepsilon \cos \theta }}}{1+{\frac {\varepsilon +\cos \theta }{1+\varepsilon \cos \theta }}}}\\[8pt]&={\frac {(1+\varepsilon \cos \theta )-(\varepsilon +\cos \theta )}{(1+\varepsilon \cos \theta )+(\ varepsilon +\cos \theta )}}={\frac {1-\varepsilon }{1+\varepsilon }}\cdot {\frac {1-\cos \theta }{1+\cos \theta }}={ \frac {1-\varepsilon }{1+\varepsilon }}\tan ^{2}{\frac {\theta }{2}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bc0a064e24ecffca17176902230ccd78625ad9a)

