Реп-плитка

В геометрии мозаики или реп -плитка на более мелкие рептилия — это форма, которую можно разделить копии той же формы. Этот термин был придуман как игра слов в отношении животных -рептилий математиком -любителем Соломоном В. Голомбом и популяризирован Мартином Гарднером в его колонке « Математические игры » в майском номере журнала Scientific American за 1963 год . ^[1] обобщение повторяющихся плиток, называемое наборами самозакрывающихся плиток представил В 2012 году Ли Сэллоуз в журнале Mathematics Magazine . ^[2]

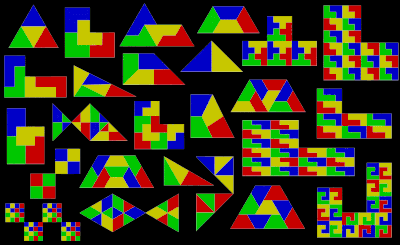
Терминология [ править ]

Плитка-реплик помечается как «реп- n» , если при вскрытии используется n копий. Такая форма обязательно образует прототип мозаики плоскости, во многих случаях апериодической мозаики . Рассечение рептилий с использованием разных размеров исходной формы называется нерегулярной рептилией или нерептилией. Если при рассечении используется n копий, форма называется неповторяющейся . Если все эти подплитки имеют разные размеры, то мозаику дополнительно называют идеальной. Форма, которая является Rep- n или IrRep- n, тривиально также является IrRep-( kn − k + n ) для любого k > 1 путем замены самой маленькой плитки в разрезе Rep- n на n еще меньших плиток. Порядок фигуры, независимо от того, используются ли повторяющиеся плитки или неповторяющиеся плитки, представляет собой наименьшее возможное количество плиток, которого будет достаточно. ^[3]

Примеры [ править ]

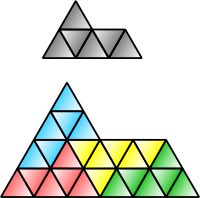
Каждый квадрат , прямоугольник , параллелограмм , ромб или треугольник представляет собой повторение-4. ( Гексиаммонд сфинкса самовоспроизводящихся показанный выше) имеет повторы 4 и повторения 9 и является одним из немногих известных пятиугольников . Остров Госпер имеет номер реп-7. Снежинка Коха имеет тип Irреп-7: шесть маленьких снежинок одинакового размера вместе с еще одной снежинкой, площадь которой в три раза превышает площадь меньших, могут объединиться в одну большую снежинку.

с Прямоугольный треугольник длинами сторон в соотношении 1:2 — это повтор-5, а его рассечение повтора-5 образует основу апериодической мозаики вертушки . По теореме Пифагора гипотенуза , или наклонная сторона треугольника Rep-5, имеет длину √ 5 .

Международный стандарт ISO 216 определяет размеры листов бумаги с помощью $\sqrt 2$ , в котором длинная сторона прямоугольного листа бумаги равна квадратному корню из двухкратной короткой стороны бумаги. Прямоугольники этой формы — это повтор 2. Прямоугольник (или параллелограмм) является повторением n, если его соотношение сторон равно √ n :1. Равнобедренный прямоугольный треугольник также является повтором-2.

Рептилии и симметрия [ править ]

Некоторые репродукции, такие как квадрат и равносторонний треугольник , симметричны и остаются идентичными при отражении в зеркале . Другие, такие как сфинкс , асимметричны и существуют в двух различных формах, связанных зеркальным отражением. Рассечение сфинкса и некоторых других асимметричных рептилий требует использования как исходной формы, так и ее зеркального отображения.

Рептилии и полиформы [ править ]

Некоторые рептилии основаны на полиформах, таких как полиромбы и полимино , или формах, созданных путем наложения равносторонних треугольников и квадратов от края к краю.

Квадраты [ править ]

Если полимино является спрямляемым, то есть способным замостить прямоугольник , то оно также будет повторяющейся плиткой, потому что прямоугольник будет иметь целое соотношение длин сторон и, таким образом, будет замостить квадрат . Это можно увидеть в октамино , которые состоят из восьми квадратов. Две копии некоторых октамино составят квадрат; следовательно, эти октамино также являются реп-плитами Rep-16.

Четыре копии некоторых нономино и нокингов замостит квадрат, поэтому эти полиформы также являются реп-тайлами Rep-36.

Рептилики, созданные из спрямляемых нономино и 9-поликоролей (нонакингов)

Равносторонние треугольники [ править ]

Аналогично, если полиалмаз замостит равносторонний треугольник, это также будет повторяющаяся плитка.

Прямоугольные треугольники [ править ]

– Прямоугольный треугольник это треугольник, содержащий один прямой угол 90°. Две конкретные формы прямоугольного треугольника привлекли внимание исследователей рептилий: треугольник 45°-90°-45° и треугольник 30°-60°-90°.

Треугольники 45°-90°-45° [ править ]

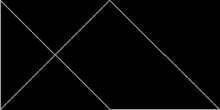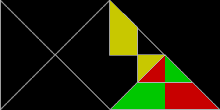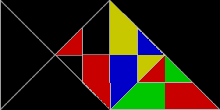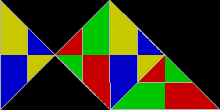
основанные на равнобедренных прямоугольных треугольниках со сторонами в соотношении 1:1: √2 Полиформы , , известны как полиаболы . Бесчисленное множество из них являются рептилиями. Действительно, самая простая из всех реп-плиток — это одиночный равнобедренный прямоугольный треугольник. Это повтор-2, если разделить его одной линией, делящей пополам прямой угол с гипотенузой . Повторные плитки Rep-2 также являются повторами Rep-2. ^н а треугольники повторений-4,8,16+ дают дополнительные плитки-реплики. Их можно найти путем отбрасывания половины подкопий и перестановки остальных до тех пор, пока они не станут зеркально-симметричными внутри прямоугольного треугольника. Другими словами, две копии составят прямоугольный треугольник. Одна из этих новых рептилий напоминает рыбу, состоящую из трех равносторонних треугольников .

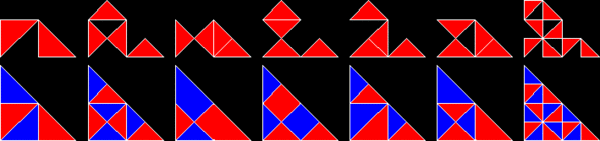
Треугольники 30°-60°-90° [ править ]

Полиформы, основанные на прямоугольных треугольниках 30°-60°-90° со сторонами в соотношении 1: √ 3 :2, известны как полидрафты . Некоторые из них идентичны полиалмазам . ^[4]

Множественные и варианты повторения плиток [ править ]

Многие из распространенных рептилий являются повторяющимися $. 2$ для всех положительных целых значений $n$ . В частности, это справедливо для трех трапеций , в том числе из трех равносторонних треугольников, для трех шестиугольников, параллельных осям (L-тромино, L-тетромино и P-пентамино), и шестиугольника сфинкса. ^[5] Кроме того, многие реп-тайлы, особенно те, у которых более высокое число повторений , могут быть разложены по-разному. Например, L-тетрамино Rep-9 имеет как минимум четырнадцать различных реп-тайлингов. Гексамонд сфинкса Rep-9 также можно облицовать плиткой по-разному.

Реплики с бесконечными сторонами [ править ]

Наиболее распространенными реп-плитами являются многоугольники с конечным числом сторон, но некоторые фигуры с бесконечным числом сторон также могут быть реп-плитами. Например, терагонический треугольник, или рогатый треугольник, — это повтор-4. Это также пример фрактальной реп-плитки .

Пятиугольные повторяющиеся плитки [ править ]

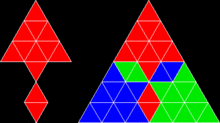
Треугольные и четырехсторонние (четырехсторонние) плитки-реплики распространены, но пятиугольные плитки-реплики встречаются редко. Долгое время , что сфинкс считалось является единственным известным примером, но немецкий / новозеландский математик Карл Шерер и американский математик Джордж Зихерман нашли и другие примеры, в том числе двойную пирамиду и удлиненную версию сфинкса. . Эти пятиугольные рептилии проиллюстрированы на страницах журнала Math Magic, курируемого американским математиком Эрихом Фридманом . ^[6] Однако сфинкс и его расширенные версии — единственные известные пятиугольники, которые можно разложить равными копиями. Кларка См. страницы о рептилиях .

Рептилии и фракталы [ править ]

Реплики как фракталы [ править ]

Реплики можно использовать для создания фракталов фигур или самоподобных во все меньших и меньших масштабах. Фрактал повторяющейся плитки формируется путем разделения повторяющейся плитки, удаления одной или нескольких копий разделенной фигуры и последующего рекурсивного продолжения . Например, ковер Серпинского образуется таким образом путем переплетения квадрата на 27 меньших квадратов, а треугольник Серпинского формируется из переплетения равностороннего треугольника на четыре меньших треугольника. Когда одна подкопия отброшена, L- триомино повтора 4 можно использовать для создания четырех фракталов, два из которых идентичны, за исключением ориентации .

Геометрическое рассечение L-триомино (реп-4)	Фрактал на основе L-тримино (реп-4)
Еще один фрактал на основе L-тримино.	Еще один фрактал на основе L-тримино.

Фракталы как повторяющиеся плитки [ править ]

Поскольку фракталы часто самоподобны в меньших и меньших масштабах, многие из них могут быть разложены на копии самих себя, как рептилия. Однако если фрактал имеет пустую внутреннюю часть , это разложение может не привести к замощению всей плоскости. Например, треугольник Серпинского — это повтор-3, замощенный тремя копиями самого себя, а ковер Серпинского — это повтор-8, замощенный восемью копиями самого себя, но повторение этих разложений не образует замощение. С другой стороны, кривая дракона представляет собой кривую, заполняющую пространство , с непустой внутренней частью; это повтор-4, и он действительно образует мозаику. Точно так же остров Госпера имеет форму Rep-7, образованную из заполняющей пространство кривой Госпера и снова образующей мозаику.

По построению любой фрактал, определяемый итерированной системой функций из n сжимающих отображений одного и того же отношения, является re-n.

Бесконечная мозаика [ править ]

Среди правильных многоугольников только треугольник и квадрат можно разделить на меньшие копии самих себя одинакового размера. Однако правильный шестиугольник можно разрезать на шесть равносторонних треугольников, каждый из которых можно разрезать на правильный шестиугольник и еще три равносторонних треугольника. Это основа бесконечного замощения шестиугольника шестиугольниками. Таким образом, шестиугольник является иррептилией без повтора ∞ или без повторения бесконечности.

Правильный шестиугольник, выложенный бесконечным количеством своих копий.
Фрактальная удлиненная снежинка Коха (сиамская), выложенная бесконечным количеством своих копий. ^[7]

См. также [ править ]

Примечания [ править ]

^ Дюжина Гарднера - истории Мартина на обложке журнала Scientific American
^ Саллоус (2012) .
^ Гарднер (2001) .
^ Полидрафт Иррептилинг
^ Нитис (2003) .
^ Математическая магия, проблема месяца (октябрь 2002 г.)
^ Пьетрокола, Джорджио (2005). «Тартапелаг. Искусство тесселяции» . Маэкла .

Ссылки [ править ]

Гарднер, М. (2001), «Rep-Tiles», Колоссальная книга по математике: классические головоломки, парадоксы и проблемы , Нью-Йорк: WW Norton, стр. 46–58.
Гарднер, М. (1991), «Глава 19: Повторяющиеся плитки, воспроизведение фигур на плоскости», Неожиданное зависание и другие математические развлечения , Чикаго, Иллинойс: Издательство Чикагского университета, стр. 222–233.
Лэнгфорд, CD (1940), «Использование геометрической головоломки», The Mathematical Gazette , 24 (260): 209–211, doi : 10.2307/3605717
Ницица, Виорел (2003), «Возвращение к рептилиям», MASS selecta , Провиденс, Род-Айленд: Американское математическое общество, стр. 205–217, MR 2027179
Саллоус, Ли (2012), «О наборах плиток с самооблицовкой», Mathematics Magazine , 85 (5): 323–333, doi : 10.4169/math.mag.85.5.323 , MR 3007213
Шерер, Карл (1987), Загадочное путешествие к рептилиям и родственным им животным
Уэллс, Д. (1991), Словарь любопытной и интересной геометрии Penguin , Лондон: Penguin, стр. 213–214.

Внешние ссылки [ править ]

Реплики [ править ]

Альбом Математического центра «Сфинкс»: http://mathematicscentre.com/taskcentre/sphinx.htm
Кларк, А.Л. «Рептилии». http://www.recmath.com/PolyPages/PolyPages/Reptiles.htm .
Вайсштейн, Эрик В. «Реп-Плитка» . Математический мир .
http://www.uwgb.edu/dutchs/symmetry/reptile1.htm (1999)
IFStile - программа для поиска реп-тайлов: https://ifstile.com

Irrep-плитки [ править ]

[1] Дюжина Гарднера - истории Мартина на обложке журнала Scientific American

[FOOTNOTESallows2012-2] Саллоус (2012) .

[FOOTNOTEGardner2001-3] Гарднер (2001) .

[polydrafters-4] Полидрафт Иррептилинг

[FOOTNOTENiţică2003-5] Нитис (2003) .

[pentagonal-6] Математическая магия, проблема месяца (октябрь 2002 г.)

[7] Пьетрокола, Джорджио (2005). «Тартапелаг. Искусство тесселяции» . Маэкла .

[1]

[2]

[3]

[4]

[5]

[6]

[7]