Принцип неопределенности

Чтобы узнать о других значениях, см. Принцип неопределенности (значения) .

Каноническое правило коммутации для переменных положения q и импульса p частицы, 1927 г. pq − qp = h /(2 πi ). Принцип неопределенности Гейзенберга, 1927 г.

Принцип неопределенности , также известный как принцип неопределенности Гейзенберга , является фундаментальным понятием квантовой механики . В нем говорится, что существует предел точности, с которой могут быть одновременно известны определенные пары физических свойств, таких как положение и импульс . Другими словами, чем точнее измерено одно свойство, тем менее точно можно узнать другое свойство.

это любое из множества математических неравенств , устанавливающих фундаментальный предел произведения точности определенных связанных пар измерений в квантовой системе, таких как положение x Более формально, принцип неопределенности — и импульс p . Такие парные переменные известны как дополнительные переменные или канонически сопряженные переменные .

Впервые введен в 1927 году немецким физиком Вернером Гейзенбергом . формальное неравенство, связывающее стандартное отклонение положения σ _x и стандартное отклонение импульса σ _p, было получено Эрлом Гессе Кеннардом. позже в том же году и Герман Вейль в 1928 году:

$\sigma _{x}\sigma _{p}\geq {\frac {\hbar }{2}}$

где $\hbar ={\frac {h}{2\pi }}$ – приведенная постоянная Планка .

Квинтэссенция квантовомеханического принципа неопределенности проявляется во многих формах, помимо положения-импульса. Соотношение энергия-время широко используется для связи времени жизни квантового состояния с измеренной шириной энергии, но его формальный вывод чреват запутанными вопросами о природе времени. Основной принцип был расширен во многих направлениях; его необходимо учитывать во многих видах фундаментальных физических измерений.

Позиция-импульс

Основная статья: Введение в квантовую механику

Суперпозиция нескольких плоских волн с образованием волнового пакета. Этот волновой пакет становится все более локализованным с добавлением множества волн. Преобразование Фурье — это математическая операция, которая разделяет волновой пакет на отдельные плоские волны. Показанные здесь волны реальны только для иллюстративных целей; В квантовой механике волновая функция обычно сложна .

Крайне важно проиллюстрировать, как этот принцип применим к относительно понятным физическим ситуациям, поскольку он неразличим на макроскопическом уровне. масштабы, которые испытывают люди. Две альтернативные концепции квантовой физики предлагают разные объяснения принципа неопределенности. Картина принципа неопределенности в волновой механике более визуально интуитивна, но более абстрактная картина матричной механики формулирует его таким образом, что его легче обобщать.

Математически в волновой механике соотношение неопределенности между положением и импульсом возникает потому, что выражения волновой функции в двух соответствующих ортонормированных базисах в гильбертовом пространстве являются преобразованиями Фурье друг друга (т. е. положение и импульс являются сопряженными переменными ). Ненулевая функция и ее преобразование Фурье не могут быть одновременно четко локализованы. Аналогичный компромисс между дисперсиями сопряженных Фурье возникает во всех системах, лежащих в основе анализа Фурье, например, в звуковых волнах: чистый тон представляет собой резкий выброс на одной частоте, в то время как его преобразование Фурье дает форму звуковой волны во времени. домен, который представляет собой полностью делокализованную синусоидальную волну. В квантовой механике два ключевых момента заключаются в том, что положение частицы принимает форму волны материи, а импульс — это ее Фурье-сопряжение, что обеспечивается соотношением де Бройля p = ħk , где k — волновое число .

В матричной механике , математической формулировке квантовой механики , любая пара некоммутирующих самосопряженных операторов, представляющих наблюдаемые, подчиняется аналогичным пределам неопределенности. Собственное состояние наблюдаемой представляет собой состояние волновой функции для определенного значения измерения (собственного значения). Например, если выполняется измерение наблюдаемой A , то система находится в определенном собственном состоянии Ψ этой наблюдаемой. Однако конкретное собственное состояние наблюдаемой A не обязательно должно быть собственным состоянием другой наблюдаемой B : если это так, то оно не имеет для него уникального связанного измерения, поскольку система не находится в собственном состоянии этой наблюдаемой.

Визуализация

Принцип неопределенности можно визуализировать с помощью волновых функций в пространстве положения и импульса для одной бесспиновой частицы с массой в одном измерении.

Чем более локализована волновая функция в пространстве положения, тем больше вероятность того, что частица будет найдена с координатами положения в этой области, и, соответственно, волновая функция в пространстве импульса менее локализована, поэтому возможные компоненты импульса, которые могла бы иметь частица, более широко распространены. И наоборот, чем более локализована волновая функция в пространстве импульса, тем больше вероятность того, что частица будет найдена с такими значениями компонентов импульса в этой области и, соответственно, тем менее локализована волновая функция в пространстве положения, поэтому координаты положения, которые может занять частица, равны более распространено. Эти волновые функции являются преобразованиями Фурье друг друга: математически принцип неопределенности выражает взаимосвязь между сопряженными переменными в преобразовании.

Волновые функции положения x и импульса p, соответствующие квантовым частицам. Непрозрачность цвета частиц соответствует плотности вероятности обнаружения частицы с положением x или компонентой импульса p .
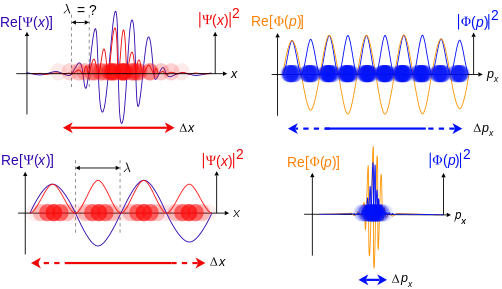
Вверху: если длина волны λ неизвестна, то неизвестны также импульс p , волновой вектор k и энергия E (соотношения де Бройля). Поскольку частица более локализована в позиционном пространстве, Δ x меньше, чем для Δ p _x .
Внизу: если λ известно самое известно и о p , k и E. , то же Поскольку частица более локализована в пространстве импульсов, Δp меньше , чем для Δx .

Интерпретация волновой механики

Плоская волна

Волновой пакет

Распространение волн де Бройля в 1d — действительная часть комплексной амплитуды выделена синим цветом, мнимая часть — зеленым. Вероятность (показанная как непрозрачность цвета ) обнаружения частицы в данной точке x распределена как форма волны, определенного положения частицы не существует. Когда амплитуда увеличивается выше нуля, кривизна меняет знак, поэтому амплитуда снова начинает уменьшаться, и наоборот - в результате получается переменная амплитуда: волна.

Основные статьи: Волновой пакет и уравнение Шрёдингера

Согласно гипотезе де Бройля , каждый объект во Вселенной связан с волной . Таким образом, каждый объект, от элементарной частицы до атомов, молекул и далее, вплоть до планет и за его пределами, подчиняется принципу неопределенности.

Независимая от времени волновая функция одномодовой плоской волны с волновым числом k ₀ или импульсом p ₀ равна $$\psi (x)\propto e^{ik_{0}x}=e^{ip_{0}x/\hbar }~.$$

Правило Борна гласит, что это следует интерпретировать как функцию амплитуды плотности вероятности в том смысле, что вероятность найти частицу между a и b равна $$\operatorname {P} [a\leq X\leq b]=\int _{a}^{b}|\psi (x)|^{2}\,\mathrm {d} x~.$$

В случае одномодовой плоской волны $|\psi (x)|^{2}$ равно 1, если $X=x$ и 0 в противном случае. Другими словами, положение частицы крайне неопределенно в том смысле, что она может находиться практически в любом месте волнового пакета.

С другой стороны, рассмотрим волновую функцию, которая представляет собой сумму многих волн , которую мы можем записать как $$\psi (x)\propto \sum _{n}A_{n}e^{ip_{n}x/\hbar }~,$$где An _p относительный вклад моды n _{представляет} в общую сумму. На рисунках справа показано, как при добавлении множества плоских волн волновой пакет может стать более локализованным. Мы можем сделать еще один шаг вперед к пределу континуума , где волновая функция является интегралом по всем возможным модам. $$\psi (x)={\frac {1}{\sqrt {2\pi \hbar }}}\int _{-\infty }^{\infty }\varphi (p)\cdot e^{ipx/\hbar }\,dp~,$$с $\varphi (p)$ представляющая амплитуду этих мод и называется волновой функцией в импульсном пространстве . В математических терминах мы говорим, что $\varphi (p)$ представляет собой Фурье преобразование $\psi (x)$ и что x и p являются сопряженными переменными . За сложение всех этих плоских волн приходится платить, а именно, импульс стал менее точным, став смесью волн с разными импульсами.

Одним из способов количественной оценки точности положения и импульса является стандартное отклонение   σ . С $|\psi (x)|^{2}$ — функция плотности вероятности позиции, мы вычисляем ее стандартное отклонение.

Точность положения улучшается, т.е. уменьшается σ _x , за счет использования множества плоских волн, тем самым ослабляя точность определения импульса, т.е. увеличивая σ _p . Другой способ выразить это состоит в том, что σ _x и σ _p находятся в обратной зависимости или, по крайней мере, ограничены снизу. Это принцип неопределенности, точным пределом которого является граница Кеннарда.

Доказательство неравенства Кеннарда с помощью волновой механики.

Нас интересуют дисперсии положения и импульса, определяемые как $$\sigma _{x}^{2}=\int _{-\infty }^{\infty }x^{2}\cdot |\psi (x)|^{2}\,dx-\left(\int _{-\infty }^{\infty }x\cdot |\psi (x)|^{2}\,dx\right)^{2}$$$$\sigma _{p}^{2}=\int _{-\infty }^{\infty }p^{2}\cdot |\varphi (p)|^{2}\,dp-\left(\int _{-\infty }^{\infty }p\cdot |\varphi (p)|^{2}\,dp\right)^{2}~.$$

Без ограничения общности будем считать, что средние исчезают, что равнозначно сдвигу начала наших координат. (Более общее доказательство, не делающее этого предположения, приведено ниже.) Это дает нам более простую форму $$\sigma _{x}^{2}=\int _{-\infty }^{\infty }x^{2}\cdot |\psi (x)|^{2}\,dx$$$$\sigma _{p}^{2}=\int _{-\infty }^{\infty }p^{2}\cdot |\varphi (p)|^{2}\,dp~.$$

Функция $f(x)=x\cdot \psi (x)$ можно интерпретировать как вектор в функциональном пространстве . Мы можем определить скалярное произведение для пары функций u ( x ) и v ( x ) в этом векторном пространстве: $$\langle u\mid v\rangle =\int _{-\infty }^{\infty }u^{*}(x)\cdot v(x)\,dx,$$где звездочка обозначает комплексно-сопряженное число .

Определив этот внутренний продукт, отметим, что отклонение позиции можно записать как $$\sigma _{x}^{2}=\int _{-\infty }^{\infty }|f(x)|^{2}\,dx=\langle f\mid f\rangle ~.$$

Мы можем повторить это для импульса, интерпретируя функцию ${\tilde {g}}(p)=p\cdot \varphi (p)$ как вектор, но мы также можем воспользоваться тем фактом, что $\psi (x)$ и $\varphi (p)$ являются преобразованиями Фурье друг друга. Оценим обратное преобразование Фурье путем интегрирования по частям : $${\begin{aligned}g(x)&={\frac {1}{\sqrt {2\pi \hbar }}}\cdot \int _{-\infty }^{\infty }{\tilde {g}}(p)\cdot e^{ipx/\hbar }\,dp\\&={\frac {1}{\sqrt {2\pi \hbar }}}\int _{-\infty }^{\infty }p\cdot \varphi (p)\cdot e^{ipx/\hbar }\,dp\\&={\frac {1}{2\pi \hbar }}\int _{-\infty }^{\infty }\left[p\cdot \int _{-\infty }^{\infty }\psi (\chi )e^{-ip\chi /\hbar }\,d\chi \right]\cdot e^{ipx/\hbar }\,dp\\&={\frac {i}{2\pi }}\int _{-\infty }^{\infty }\left[{\cancel {\left.\psi (\chi )e^{-ip\chi /\hbar }\right|_{-\infty }^{\infty }}}-\int _{-\infty }^{\infty }{\frac {d\psi (\chi )}{d\chi }}e^{-ip\chi /\hbar }\,d\chi \right]\cdot e^{ipx/\hbar }\,dp\\&={\frac {-i}{2\pi }}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }{\frac {d\psi (\chi )}{d\chi }}e^{-ip\chi /\hbar }\,d\chi \,e^{ipx/\hbar }\,dp\\&=-i{\sqrt {\frac {\hbar }{2\pi }}}\int _{-\infty }^{\infty }{\frac {d\psi (\chi )}{d\chi }}e^{-ip\chi /\hbar }\,d\chi \\&=\left(-i\hbar {\frac {d}{dx}}\right)\cdot \psi (x),\end{aligned}}$$где $v={\frac {\hbar }{-ip}}e^{-ip\chi /\hbar }$ при интегрировании по частям отмененный член исчезает, поскольку волновая функция исчезает на бесконечности, а последние два интегрирования вновь подтверждают преобразования Фурье. Часто термин ${\textstyle -i\hbar {\frac {d}{dx}}}$ называется оператором импульса в позиционном пространстве. Применяя теорему Парсеваля , мы видим, что дисперсию импульса можно записать как $$\sigma _{p}^{2}=\int _{-\infty }^{\infty }|{\tilde {g}}(p)|^{2}\,dp=\int _{-\infty }^{\infty }|g(x)|^{2}\,dx=\langle g\mid g\rangle .$$

утверждает Неравенство Коши – Шварца , что $$\sigma _{x}^{2}\sigma _{p}^{2}=\langle f\mid f\rangle \cdot \langle g\mid g\rangle \geq |\langle f\mid g\rangle |^{2}~.$$

любого Квадрат модуля комплексного числа z можно выразить как $$|z|^{2}={\Big (}{\text{Re}}(z){\Big )}^{2}+{\Big (}{\text{Im}}(z){\Big )}^{2}\geq {\Big (}{\text{Im}}(z){\Big )}^{2}=\left({\frac {z-z^{\ast }}{2i}}\right)^{2}.$$мы позволяем $z=\langle f|g\rangle$ и $z^{*}=\langle g\mid f\rangle$ и подставьте их в приведенное выше уравнение, чтобы получить $$|\langle f\mid g\rangle |^{2}\geq \left({\frac {\langle f\mid g\rangle -\langle g\mid f\rangle }{2i}}\right)^{2}~.$$

Остается только оценить эти внутренние продукты.

$${\begin{aligned}\langle f\mid g\rangle -\langle g\mid f\rangle ={}&\int _{-\infty }^{\infty }\psi ^{*}(x)\,x\cdot \left(-i\hbar {\frac {d}{dx}}\right)\,\psi (x)\,dx\\&{}-\int _{-\infty }^{\infty }\psi ^{*}(x)\,\left(-i\hbar {\frac {d}{dx}}\right)\cdot x\,\psi (x)\,dx\\={}&i\hbar \cdot \int _{-\infty }^{\infty }\psi ^{*}(x)\left[\left(-x\cdot {\frac {d\psi (x)}{dx}}\right)+{\frac {d(x\psi (x))}{dx}}\right]\,dx\\={}&i\hbar \cdot \int _{-\infty }^{\infty }\psi ^{*}(x)\left[\left(-x\cdot {\frac {d\psi (x)}{dx}}\right)+\psi (x)+\left(x\cdot {\frac {d\psi (x)}{dx}}\right)\right]\,dx\\={}&i\hbar \cdot \int _{-\infty }^{\infty }\psi ^{*}(x)\psi (x)\,dx\\={}&i\hbar \cdot \int _{-\infty }^{\infty }|\psi (x)|^{2}\,dx\\={}&i\hbar \end{aligned}}$$

Подставляя это в приведенные выше неравенства, мы получаем $$\sigma _{x}^{2}\sigma _{p}^{2}\geq |\langle f\mid g\rangle |^{2}\geq \left({\frac {\langle f\mid g\rangle -\langle g\mid f\rangle }{2i}}\right)^{2}=\left({\frac {i\hbar }{2i}}\right)^{2}={\frac {\hbar ^{2}}{4}}$$или извлечь квадратный корень $$\sigma _{x}\sigma _{p}\geq {\frac {\hbar }{2}}~.$$

с равенством тогда и только тогда, когда p и x линейно зависимы. Обратите внимание, что единственная физика, задействованная в этом доказательстве, заключалась в том, что $\psi (x)$ и $\varphi (p)$ являются волновыми функциями положения и импульса, которые являются преобразованиями Фурье друг друга. Аналогичный результат справедлив для любой пары сопряженных переменных.

Интерпретация матричной механики

(Ссылка )

Основная статья: Матричная механика

В матричной механике такие наблюдаемые величины, как положение и импульс, представлены самосопряженными операторами. При рассмотрении пар наблюдаемых важной величиной является коммутатор . Для пары операторов Â и ${\hat {B}}$, их коммутатор определяется как $$[{\hat {A}},{\hat {B}}]={\hat {A}}{\hat {B}}-{\hat {B}}{\hat {A}}.$$В случае положения и импульса коммутатором является каноническое коммутационное соотношение $$[{\hat {x}},{\hat {p}}]=i\hbar .$$

Физический смысл некоммутативности можно понять, рассмотрев влияние коммутатора на собственные состояния положения и импульса . Позволять $|\psi \rangle$ быть правым собственным состоянием положения с постоянным собственным значением x ₀ . По определению это означает, что ${\hat {x}}|\psi \rangle =x_{0}|\psi \rangle .$ Применение коммутатора к $|\psi \rangle$ урожайность $$[{\hat {x}},{\hat {p}}]|\psi \rangle =({\hat {x}}{\hat {p}}-{\hat {p}}{\hat {x}})|\psi \rangle =({\hat {x}}-x_{0}{\hat {I}}){\hat {p}}\,|\psi \rangle =i\hbar |\psi \rangle ,$$где Î — тождественный оператор .

Предположим, для доказательства от противного , что $|\psi \rangle$ также является правым собственным состоянием импульса с постоянным собственным значением p ₀ . Если бы это было правдой, то можно было бы написать $$({\hat {x}}-x_{0}{\hat {I}}){\hat {p}}\,|\psi \rangle =({\hat {x}}-x_{0}{\hat {I}})p_{0}\,|\psi \rangle =(x_{0}{\hat {I}}-x_{0}{\hat {I}})p_{0}\,|\psi \rangle =0.$$С другой стороны, приведенное выше каноническое коммутационное соотношение требует, чтобы $$[{\hat {x}},{\hat {p}}]|\psi \rangle =i\hbar |\psi \rangle \neq 0.$$Это означает, что ни одно квантовое состояние не может одновременно быть одновременно положением и собственным состоянием импульса.

Когда состояние измеряется, оно проецируется на собственное состояние на основе соответствующей наблюдаемой. Например, если измеряется положение частицы, то состояние представляет собой собственное состояние положения. Однако это означает, что состояние не является собственным состоянием импульса, а скорее может быть представлено как сумма нескольких собственных состояний базиса импульса. Другими словами, импульс должен быть менее точным. Эту точность можно количественно оценить с помощью стандартных отклонений, $$\sigma _{x}={\sqrt {\langle {\hat {x}}^{2}\rangle -\langle {\hat {x}}\rangle ^{2}}}$$$$\sigma _{p}={\sqrt {\langle {\hat {p}}^{2}\rangle -\langle {\hat {p}}\rangle ^{2}}}.$$

Как и в приведенной выше интерпретации волновой механики, можно увидеть компромисс между соответствующими точностью этих двух методов, количественно определяемый принципом неопределенности.

Примеры

(ссылки )

Стационарные состояния квантового гармонического осциллятора

Основные статьи: Квантовый гармонический осциллятор и стационарное состояние

Рассмотрим одномерный квантовый гармонический осциллятор. Операторы положения и импульса можно выразить через операторы рождения и уничтожения : $${\hat {x}}={\sqrt {\frac {\hbar }{2m\omega }}}(a+a^{\dagger })$$$${\hat {p}}=i{\sqrt {\frac {m\omega \hbar }{2}}}(a^{\dagger }-a).$$

Используя стандартные правила для операторов рождения и уничтожения собственных состояний энергии, $$a^{\dagger }|n\rangle ={\sqrt {n+1}}|n+1\rangle$$$$a|n\rangle ={\sqrt {n}}|n-1\rangle ,$$дисперсии могут быть вычислены напрямую, $$\sigma _{x}^{2}={\frac {\hbar }{m\omega }}\left(n+{\frac {1}{2}}\right)$$$$\sigma _{p}^{2}=\hbar m\omega \left(n+{\frac {1}{2}}\right)\,.$$Тогда произведение этих стандартных отклонений равно $$\sigma _{x}\sigma _{p}=\hbar \left(n+{\frac {1}{2}}\right)\geq {\frac {\hbar }{2}}.~$$

В частности, приведенная выше оценка Кеннарда является насыщенным для основного состояния n =0 , для которого плотность вероятности представляет собой просто нормальное распределение .

Квантовые гармонические осцилляторы с гауссовским начальным условием

Плотности вероятности положения (синий) и импульса (красный) для исходного гауссова распределения. Сверху вниз на анимации показаны случаи Ω = ω , Ω = 2 ω и Ω = ω /2 . Обратите внимание на компромисс между шириной распределений.

В квантовом гармоническом генераторе с характеристической угловой частотой ω поместите состояние, которое смещено от дна потенциала на некоторое смещение x ₀ как $$\psi (x)=\left({\frac {m\Omega }{\pi \hbar }}\right)^{1/4}\exp {\left(-{\frac {m\Omega (x-x_{0})^{2}}{2\hbar }}\right)},$$где Ω описывает ширину начального состояния, но не обязательно должна быть такой же, как ω . Благодаря интеграции с распространителем мы можем найти решение, полностью зависящее от времени. После многих сокращений плотности вероятности уменьшаются до $$|\Psi (x,t)|^{2}\sim {\mathcal {N}}\left(x_{0}\cos {(\omega t)},{\frac {\hbar }{2m\Omega }}\left(\cos ^{2}(\omega t)+{\frac {\Omega ^{2}}{\omega ^{2}}}\sin ^{2}{(\omega t)}\right)\right)$$$$|\Phi (p,t)|^{2}\sim {\mathcal {N}}\left(-mx_{0}\omega \sin(\omega t),{\frac {\hbar m\Omega }{2}}\left(\cos ^{2}{(\omega t)}+{\frac {\omega ^{2}}{\Omega ^{2}}}\sin ^{2}{(\omega t)}\right)\right),$$где мы использовали обозначение ${\mathcal {N}}(\mu ,\sigma ^{2})$ для обозначения нормального распределения среднего значения µ и дисперсии σ ² . Копируя приведенные выше отклонения и применяя тригонометрические тождества , мы можем записать произведение стандартных отклонений как $${\begin{aligned}\sigma _{x}\sigma _{p}&={\frac {\hbar }{2}}{\sqrt {\left(\cos ^{2}{(\omega t)}+{\frac {\Omega ^{2}}{\omega ^{2}}}\sin ^{2}{(\omega t)}\right)\left(\cos ^{2}{(\omega t)}+{\frac {\omega ^{2}}{\Omega ^{2}}}\sin ^{2}{(\omega t)}\right)}}\\&={\frac {\hbar }{4}}{\sqrt {3+{\frac {1}{2}}\left({\frac {\Omega ^{2}}{\omega ^{2}}}+{\frac {\omega ^{2}}{\Omega ^{2}}}\right)-\left({\frac {1}{2}}\left({\frac {\Omega ^{2}}{\omega ^{2}}}+{\frac {\omega ^{2}}{\Omega ^{2}}}\right)-1\right)\cos {(4\omega t)}}}\end{aligned}}$$

Из отношений $${\frac {\Omega ^{2}}{\omega ^{2}}}+{\frac {\omega ^{2}}{\Omega ^{2}}}\geq 2,\quad |\cos(4\omega t)|\leq 1,$$мы можем заключить следующее (самое правое равенство имеет место только при Ω = ω ): $$\sigma _{x}\sigma _{p}\geq {\frac {\hbar }{4}}{\sqrt {3+{\frac {1}{2}}\left({\frac {\Omega ^{2}}{\omega ^{2}}}+{\frac {\omega ^{2}}{\Omega ^{2}}}\right)-\left({\frac {1}{2}}\left({\frac {\Omega ^{2}}{\omega ^{2}}}+{\frac {\omega ^{2}}{\Omega ^{2}}}\right)-1\right)}}={\frac {\hbar }{2}}.$$

Когерентные состояния

Основная статья: Когерентное состояние

Когерентное состояние — это правое собственное состояние оператора уничтожения . $${\hat {a}}|\alpha \rangle =\alpha |\alpha \rangle ,$$которое можно представить в терминах состояний Фока как $$|\alpha \rangle =e^{-{|\alpha |^{2} \over 2}}\sum _{n=0}^{\infty }{\alpha ^{n} \over {\sqrt {n!}}}|n\rangle$$

В картине, где когерентное состояние представляет собой массивную частицу в квантовом гармоническом осцилляторе, операторы положения и импульса могут быть выражены через операторы аннигиляции в тех же формулах, приведенных выше, и использоваться для расчета дисперсий: $$\sigma _{x}^{2}={\frac {\hbar }{2m\omega }},$$$$\sigma _{p}^{2}={\frac {\hbar m\omega }{2}}.$$Следовательно, каждое когерентное состояние насыщает границу Кеннарда $$\sigma _{x}\sigma _{p}={\sqrt {\frac {\hbar }{2m\omega }}}\,{\sqrt {\frac {\hbar m\omega }{2}}}={\frac {\hbar }{2}}.$$с позицией и импульсом, каждый из которых вносит определенную сумму ${\textstyle {\sqrt {\hbar /2}}}$ «сбалансированным» образом. Более того, каждое сжатое когерентное состояние также насыщает границу Кеннарда, хотя отдельные вклады позиции и импульса в целом не обязательно должны быть сбалансированы.

Частица в коробке

Основная статья: Частица в коробке

Рассмотрим частицу в одномерном ящике длиной $L$. Собственные функции в пространстве положений и импульсов равны $$\psi _{n}(x,t)={\begin{cases}A\sin(k_{n}x)\mathrm {e} ^{-\mathrm {i} \omega _{n}t},&0<x<L,\\0,&{\text{otherwise,}}\end{cases}}$$и $$\varphi _{n}(p,t)={\sqrt {\frac {\pi L}{\hbar }}}\,\,{\frac {n\left(1-(-1)^{n}e^{-ikL}\right)e^{-i\omega _{n}t}}{\pi ^{2}n^{2}-k^{2}L^{2}}},$$где ${\textstyle \omega _{n}={\frac {\pi ^{2}\hbar n^{2}}{8L^{2}m}}}$ и мы использовали соотношение де Бройля $p=\hbar k$. Отклонения $x$ и $p$ можно вычислить явно: $$\sigma _{x}^{2}={\frac {L^{2}}{12}}\left(1-{\frac {6}{n^{2}\pi ^{2}}}\right)$$$$\sigma _{p}^{2}=\left({\frac {\hbar n\pi }{L}}\right)^{2}.$$

Следовательно, произведение стандартных отклонений равно $$\sigma _{x}\sigma _{p}={\frac {\hbar }{2}}{\sqrt {{\frac {n^{2}\pi ^{2}}{3}}-2}}.$$Для всех $n=1,\,2,\,3,\,\ldots$, количество ${\textstyle {\sqrt {{\frac {n^{2}\pi ^{2}}{3}}-2}}}$ больше 1, поэтому принцип неопределенности никогда не нарушается. Для числовой конкретности наименьшее значение имеет место, когда $n=1$, в этом случае $$\sigma _{x}\sigma _{p}={\frac {\hbar }{2}}{\sqrt {{\frac {\pi ^{2}}{3}}-2}}\approx 0.568\hbar >{\frac {\hbar }{2}}.$$

Они имеют постоянное значение

Основная статья: Волновой пакет

Плотность вероятности в пространстве положений первоначально гауссовского состояния, движущегося с минимально неопределенным постоянным импульсом в свободном пространстве

Предположим, что частица изначально имеет пространственно- волновую функцию импульса, описываемую нормальным распределением вокруг некоторого постоянного импульса p ₀ в соответствии с $$\varphi (p)=\left({\frac {x_{0}}{\hbar {\sqrt {\pi }}}}\right)^{1/2}\exp \left({\frac {-x_{0}^{2}(p-p_{0})^{2}}{2\hbar ^{2}}}\right),$$где мы ввели эталонную шкалу ${\textstyle x_{0}={\sqrt {\hbar /m\omega _{0}}}}$, с $\omega _{0}>0$ характеризующее ширину распределения — ср. безразмерность . Если состоянию разрешено развиваться в свободном пространстве, то зависящие от времени волновые функции импульса и положения будут следующими: $$\Phi (p,t)=\left({\frac {x_{0}}{\hbar {\sqrt {\pi }}}}\right)^{1/2}\exp \left({\frac {-x_{0}^{2}(p-p_{0})^{2}}{2\hbar ^{2}}}-{\frac {ip^{2}t}{2m\hbar }}\right),$$$$\Psi (x,t)=\left({\frac {1}{x_{0}{\sqrt {\pi }}}}\right)^{1/2}{\frac {e^{-x_{0}^{2}p_{0}^{2}/2\hbar ^{2}}}{\sqrt {1+i\omega _{0}t}}}\,\exp \left(-{\frac {(x-ix_{0}^{2}p_{0}/\hbar )^{2}}{2x_{0}^{2}(1+i\omega _{0}t)}}\right).$$

С $\langle p(t)\rangle =p_{0}$ и $\sigma _{p}(t)=\hbar /({\sqrt {2}}x_{0})$, это можно интерпретировать как движение частицы с постоянным импульсом со сколь угодно высокой точностью. С другой стороны, стандартное отклонение позиции равно $$\sigma _{x}={\frac {x_{0}}{\sqrt {2}}}{\sqrt {1+\omega _{0}^{2}t^{2}}}$$так что произведение неопределенности может увеличиваться со временем только как $$\sigma _{x}(t)\sigma _{p}(t)={\frac {\hbar }{2}}{\sqrt {1+\omega _{0}^{2}t^{2}}}$$

Принцип неопределенности энергии и времени

Ширина линии энергетического спектра в зависимости от времени жизни

Соотношение неопределенности энергии и времени, например $$\Delta E\Delta t\gtrsim \hbar /2,$$ имеет долгую и противоречивую историю; смысл $\Delta t$ и $\Delta E$ варьируется, и разные формулировки имеют разные сферы применения. Однако одно известное приложение хорошо зарекомендовало себя и экспериментально проверено: связь между временем жизни резонансного состояния, $\tau _{\sqrt {1/2}}$ и его энергетическая ширина $\Delta E$: $$\tau _{\sqrt {1/2}}\Delta E=\pi \hbar /4.$$В физике элементарных частиц ширины, полученные в результате экспериментальных подгонок к распределению энергии Брейта – Вигнера, используются для характеристики времени жизни квазистабильных или распадающихся состояний.

Неформальный, эвристический смысл принципа следующий: Состояние, существующее лишь короткое время, не может иметь определенной энергии. Чтобы иметь определенную энергию, частота состояния должна быть точно определена, а это требует, чтобы состояние зависало в течение многих циклов, что является обратной величиной требуемой точности. Например, в спектроскопии возбужденные состояния имеют конечное время жизни. По принципу неопределенности время-энергия они не имеют определенной энергии, и каждый раз при распаде выделяемая ими энергия немного отличается. Средняя энергия вылетающего фотона имеет пик при теоретической энергии состояния, но распределение имеет конечную ширину, называемую естественной шириной линии . Быстро затухающие состояния имеют широкую ширину линии, а медленно затухающие состояния имеют узкую ширину линии. Тот же эффект ширины линии также затрудняет определение массы покоя нестабильных, быстро распадающихся частиц в физике элементарных частиц . Чем быстрее распадается частица частицы (чем короче ее время жизни), тем менее определенна ее масса (чем больше ширина ).

Время в квантовой механике

Концепция «времени» в квантовой механике ставит множество проблем. Квантовой теории измерения времени не существует; теория относительности фундаментальна для времени, и ее трудно включить в квантовую механику. Хотя положение и импульс связаны с одной частицей, время является свойством системы: у него нет оператора, необходимого для соотношения Робертсона-Шредингера. Математическая трактовка стабильных и нестабильных квантовых систем различается. В совокупности эти факторы делают принципы неопределенности энергии и времени спорными.

Можно выделить три понятия «времени»: внешний, внутренний и наблюдаемый. Внешнее или лабораторное время видит экспериментатор; внутреннее время определяется изменениями динамических переменных, таких как стрелки часов или движение свободной частицы; наблюдаемое время касается времени как наблюдаемого, измерения событий, разделенных во времени.

Принцип неопределенности энергии и времени во внешнем времени мог бы сказать, что измерение энергии квантовой системы с точностью $\Delta E$ требует временного интервала $\Delta t>h/\Delta E$. Однако Якир Ахаронов и Дэвид Бом показали, что в некоторых квантовых системах энергию можно точно измерить за сколь угодно короткое время: принципы неопределенности внешнего времени не универсальны.

Внутреннее время является основой для нескольких формулировок соотношений неопределенности энергия-время, включая соотношение Мандельштама-Тамма, обсуждаемое в следующем разделе. Физическая система, внутреннее время которой точно соответствует внешнему лабораторному времени, называется «часами».

Наблюдаемое время, измеряющее время между двумя событиями, остается проблемой для квантовых теорий; некоторый прогресс был достигнут в использовании концепций позитивных операторных мер .

Мандельштам–Тамм

В 1945 году Леонид Мандельштам и Игорь Тамм вывели нерелятивистское соотношение неопределенности время-энергия следующим образом. Из механики Гейзенберга — обобщенная теорема Эренфеста для наблюдаемой B без явной зависимости от времени, представленной самосопряженным оператором. ${\hat {B}}$ связывает временную зависимость среднего значения ${\hat {B}}$ к среднему значению его коммутатора с гамильтонианом:

$${\frac {d\langle {\hat {B}}\rangle }{dt}}={\frac {i}{\hbar }}\langle [{\hat {H}},{\hat {B}}]\rangle .$$

Стоимость $\langle [{\hat {H}},{\hat {B}}]\rangle$ затем подставляется в соотношение неопределенности Робертсона для оператора энергии ${\hat {H}}$ и ${\hat {B}}$: $$\sigma _{H}\sigma _{B}\geq \left|{\frac {1}{2i}}\langle [{\hat {H}},{\hat {B}}]\rangle \right|,$$предоставление $$\sigma _{H}{\frac {\sigma _{B}}{\left|{\frac {d\langle {\hat {B}}\rangle }{dt}}\right|}}\geq {\frac {\hbar }{2}}$$(всякий раз, когда знаменатель не равен нулю).Хотя это универсальный результат, он зависит от выбранной наблюдаемой и того, что отклонения $\sigma _{H}$ и $\sigma _{B}$ рассчитываются для конкретного состояния.Идентификация $\Delta E\equiv \sigma _{E}$ и характерное время $$\tau _{B}\equiv {\frac {\sigma _{B}}{\left|{\frac {d\langle {\hat {B}}\rangle }{dt}}\right|}}$$дает соотношение энергии и времени $\Delta E\tau _{B}\geq {\frac {\hbar }{2}}.$Хотя $\tau _{B}$ имеет размерность времени, он отличается от временного параметра t , который входит в уравнение Шрёдингера . Этот $\tau _{B}$ можно интерпретировать как время, в течение которого математическое ожидание наблюдаемой $\langle {\hat {B}}\rangle ,$ изменяется на величину, равную одному стандартному отклонению. Примеры:

• Время прохождения свободной квантовой частицей точки пространства более неопределенно, поскольку энергия состояния контролируется более точно: $\Delta T=\hbar /2\Delta E.$ Поскольку разброс по времени связан с разбросом положения частицы, а разброс по энергии связан с разбросом по импульсу, это соотношение напрямую связано с неопределенностью положения и импульса.
• , Дельта-частица квазистабильная смесь кварков, связанных с протонами и нейтронами, имеет время жизни 10 ⁻²³ с, поэтому его измеренная масса эквивалентна энергии , 1232 МэВ/ с. ² , изменяется на ±120 МэВ/ c ² ; это изменение является внутренним и не вызвано ошибками измерения.
• Два энергетических состояния $\psi _{1,2}$ с энергиями $E_{1,2},$ накладывается для создания составного состояния

$$\Psi (x,t)=a\psi _{1}(x)e^{-iE_{1}t/h}+b\psi _{2}(x)e^{-iE_{2}t/h}.$$

Амплитуда вероятности этого состояния имеет зависящий от времени интерференционный член:

$$|\Psi (x,t)|^{2}=a^{2}|\psi _{1}(x)|^{2}+b^{2}|\psi _{2}(x)|^{2}+2ab\cos({\frac {E_{2}-E_{1}}{\hbar }}t).$$

Период колебаний изменяется обратно пропорционально разности энергий: $\tau =2\pi \hbar /(E_{2}-E_{1})$.

Каждый пример имеет различное значение неопределенности времени в зависимости от используемой наблюдаемой и состояния.

Квантовая теория поля

Некоторые формулировки квантовой теории поля используют в своих расчетах временные пары электрон-позитрон, называемые виртуальными частицами . Масса-энергия и время жизни этих частиц связаны соотношением неопределенности энергия-время. Энергия квантовых систем не известна с достаточной точностью, чтобы ограничить их поведение одной простой историей. Таким образом, влияние всех историй должно быть включено в квантовые расчеты, включая те, энергия которых намного больше или меньше, чем среднее значение измеренного/расчетного распределения энергии.

Принцип неопределенности энергии и времени не нарушает временно сохранения энергии ; это не означает, что энергию можно «заимствовать» у Вселенной, если она «возвращается» в течение короткого промежутка времени. Энергия Вселенной не всегда является точно известным параметром. Когда события происходят через очень короткие промежутки времени, существует неопределенность в энергии этих событий.

Внутренняя квантовая неопределенность

Исторически принцип неопределенности путали с родственным эффектом в физике , называемым эффектом наблюдателя , который отмечает, что измерения определенных систем не могут быть выполнены, не затрагивая систему, то есть, не меняя ничего в системе. Гейзенберг использовал такой эффект наблюдателя на квантовом уровне (см. ниже) как физическое «объяснение» квантовой неопределенности. Однако с тех пор стало яснее, что принцип неопределенности присущ свойствам всех волнообразных систем . и что оно возникает в квантовой механике просто из-за волновой природы материи всех квантовых объектов. Таким образом, принцип неопределенности на самом деле утверждает фундаментальное свойство квантовых систем, а не является утверждением об успехе современных технологий в наблюдениях.

Математический формализм

Начав с вывода Кеннарда неопределенности положения-импульса, Говард Перси Робертсон разработал формулировка для произвольных эрмитовых операторов- операторов ${\hat {\mathcal {O}}}$ выражается через их стандартное отклонение $$\sigma _{\mathcal {O}}={\sqrt {\langle {\hat {\mathcal {O}}}^{2}\rangle -\langle {\hat {\mathcal {O}}}\rangle ^{2}}},$$где скобки $\langle {\mathcal {O}}\rangle$ укажите ожидаемое значение . Для пары операторов ${\hat {A}}$ и ${\hat {B}}$, определим их коммутатор как $$[{\hat {A}},{\hat {B}}]={\hat {A}}{\hat {B}}-{\hat {B}}{\hat {A}},$$

а соотношение неопределенности Робертсона имеет вид $$\sigma _{A}\sigma _{B}\geq \left|{\frac {1}{2i}}\langle [{\hat {A}},{\hat {B}}]\rangle \right|={\frac {1}{2}}\left|\langle [{\hat {A}},{\hat {B}}]\rangle \right|,$$

Эрвин Шрёдингер показал, как учесть корреляцию между операторами, что дает более сильное неравенство, известное как соотношение неопределенностей Робертсона-Шредингера ,

$\sigma _{A}^{2}\sigma _{B}^{2}\geq \left|{\frac {1}{2}}\langle \{{\hat {A}},{\hat {B}}\}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle \right|^{2}+\left|{\frac {1}{2i}}\langle [{\hat {A}},{\hat {B}}]\rangle \right|^{2},$

где антикоммутатор , $\{{\hat {A}},{\hat {B}}\}={\hat {A}}{\hat {B}}+{\hat {B}}{\hat {A}}$ используется.

Доказательство Шрёдингера. соотношения неопределенностей

Показанный здесь вывод включает в себя и основывается на выводах, показанных Робертсоном, Шрёдингер и стандартные учебники, такие как Griffiths. Для любого эрмитова оператора ${\hat {A}}$, основываясь на определении дисперсии , мы имеем $$\sigma _{A}^{2}=\langle ({\hat {A}}-\langle {\hat {A}}\rangle )\Psi |({\hat {A}}-\langle {\hat {A}}\rangle )\Psi \rangle .$$мы позволяем $|f\rangle =|({\hat {A}}-\langle {\hat {A}}\rangle )\Psi \rangle$ и таким образом $$\sigma _{A}^{2}=\langle f\mid f\rangle \,.$$

Аналогично для любого другого эрмитова оператора ${\hat {B}}$ в том же состоянии $$\sigma _{B}^{2}=\langle ({\hat {B}}-\langle {\hat {B}}\rangle )\Psi |({\hat {B}}-\langle {\hat {B}}\rangle )\Psi \rangle =\langle g\mid g\rangle$$для $|g\rangle =|({\hat {B}}-\langle {\hat {B}}\rangle )\Psi \rangle .$

Таким образом, произведение двух отклонений можно выразить как

$\sigma _{A}^{2}\sigma _{B}^{2}=\langle f\mid f\rangle \langle g\mid g\rangle .$ ( 1 )

Чтобы связать два вектора $|f\rangle$ и $|g\rangle$, воспользуемся неравенством Коши–Шварца который определяется как $$\langle f\mid f\rangle \langle g\mid g\rangle \geq |\langle f\mid g\rangle |^{2},$$и, таким образом, уравнение ( 1 ) можно записать как

$\sigma _{A}^{2}\sigma _{B}^{2}\geq |\langle f\mid g\rangle |^{2}.$ ( 2 )

С $\langle f\mid g\rangle$ вообще говоря, это комплексное число, мы используем тот факт, что квадрат модуля любого комплексного числа $z$ определяется как $|z|^{2}=zz^{*}$, где $z^{*}$ представляет собой комплексное сопряжение $z$. Квадрат модуля также можно выразить как

$|z|^{2}={\Big (}\operatorname {Re} (z){\Big )}^{2}+{\Big (}\operatorname {Im} (z){\Big )}^{2}={\Big (}{\frac {z+z^{\ast }}{2}}{\Big )}^{2}+{\Big (}{\frac {z-z^{\ast }}{2i}}{\Big )}^{2}.$ ( 3 )

мы позволяем $z=\langle f\mid g\rangle$ и $z^{*}=\langle g\mid f\rangle$ и подставьте их в приведенное выше уравнение, чтобы получить

$|\langle f\mid g\rangle |^{2}={\bigg (}{\frac {\langle f\mid g\rangle +\langle g\mid f\rangle }{2}}{\bigg )}^{2}+{\bigg (}{\frac {\langle f\mid g\rangle -\langle g\mid f\rangle }{2i}}{\bigg )}^{2}$ ( 4 )

Внутренний продукт $\langle f\mid g\rangle$ записывается явно как $$\langle f\mid g\rangle =\langle ({\hat {A}}-\langle {\hat {A}}\rangle )\Psi |({\hat {B}}-\langle {\hat {B}}\rangle )\Psi \rangle ,$$и используя тот факт, что ${\hat {A}}$ и ${\hat {B}}$ являются эрмитовыми операторами, находим $${\begin{aligned}\langle f\mid g\rangle &=\langle \Psi |({\hat {A}}-\langle {\hat {A}}\rangle )({\hat {B}}-\langle {\hat {B}}\rangle )\Psi \rangle \\[4pt]&=\langle \Psi \mid ({\hat {A}}{\hat {B}}-{\hat {A}}\langle {\hat {B}}\rangle -{\hat {B}}\langle {\hat {A}}\rangle +\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle )\Psi \rangle \\[4pt]&=\langle \Psi \mid {\hat {A}}{\hat {B}}\Psi \rangle -\langle \Psi \mid {\hat {A}}\langle {\hat {B}}\rangle \Psi \rangle -\langle \Psi \mid {\hat {B}}\langle {\hat {A}}\rangle \Psi \rangle +\langle \Psi \mid \langle {\hat {A}}\rangle \langle {\hat {B}}\rangle \Psi \rangle \\[4pt]&=\langle {\hat {A}}{\hat {B}}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle +\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle \\[4pt]&=\langle {\hat {A}}{\hat {B}}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle .\end{aligned}}$$

Аналогично можно показать, что $\langle g\mid f\rangle =\langle {\hat {B}}{\hat {A}}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle .$

Таким образом, мы имеем $$\langle f\mid g\rangle -\langle g\mid f\rangle =\langle {\hat {A}}{\hat {B}}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle -\langle {\hat {B}}{\hat {A}}\rangle +\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle =\langle [{\hat {A}},{\hat {B}}]\rangle$$и $$\langle f\mid g\rangle +\langle g\mid f\rangle =\langle {\hat {A}}{\hat {B}}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle +\langle {\hat {B}}{\hat {A}}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle =\langle \{{\hat {A}},{\hat {B}}\}\rangle -2\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle .$$

Теперь мы подставим два приведенных выше уравнения обратно в уравнение. ( 4 ) и получим $$|\langle f\mid g\rangle |^{2}={\Big (}{\frac {1}{2}}\langle \{{\hat {A}},{\hat {B}}\}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle {\Big )}^{2}+{\Big (}{\frac {1}{2i}}\langle [{\hat {A}},{\hat {B}}]\rangle {\Big )}^{2}\,.$$

Подставив приведенное выше в уравнение ( 2 ), мы получаем соотношение неопределенностей Шредингера $$\sigma _{A}\sigma _{B}\geq {\sqrt {{\Big (}{\frac {1}{2}}\langle \{{\hat {A}},{\hat {B}}\}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle {\Big )}^{2}+{\Big (}{\frac {1}{2i}}\langle [{\hat {A}},{\hat {B}}]\rangle {\Big )}^{2}}}.$$

Это доказательство имеет проблему связанных с доменами задействованных операторов. Чтобы доказательство имело смысл, вектор ${\hat {B}}|\Psi \rangle$ должен находиться в области определения неограниченного оператора ${\hat {A}}$, что не всегда так. Фактически соотношение неопределенности Робертсона неверно, если ${\hat {A}}$ является угловой переменной и ${\hat {B}}$ является производной по этой переменной. В этом примере коммутатор представляет собой ненулевую константу — как и в соотношении неопределенностей Гейзенберга — и тем не менее существуют состояния, в которых произведение неопределенностей равно нулю. (См. раздел «Противопримеры» ниже.) Эту проблему можно решить, используя вариационный метод : для доказательства или работая с возведенной в степень версией канонических коммутационных соотношений.

Заметим, что в общей форме соотношения неопределенностей Робертсона–Шредингера нет необходимости предполагать, что операторы ${\hat {A}}$ и ${\hat {B}}$ являются самосопряженными операторами . Достаточно предположить, что это просто симметричные операторы . (Различие между этими двумя понятиями обычно замалчивается в физической литературе, где термин «эрмитиан» используется для одного или обоих классов операторов. См. главу 9 книги Холла. для подробного обсуждения этого важного, но технического различия.)

Смешанные состояния

Соотношение неопределенностей Робертсона-Шредингера можно легко обобщить для описания смешанных состояний . $$\sigma _{A}^{2}\sigma _{B}^{2}\geq \left|{\frac {1}{2}}\operatorname {tr} (\rho \{A,B\})-\operatorname {tr} (\rho A)\operatorname {tr} (\rho B)\right|^{2}+\left|{\frac {1}{2i}}\operatorname {tr} (\rho [A,B])\right|^{2}.$$

Соотношения неопределенности Макконе – Пати.

Соотношение неопределенностей Робертсона-Шредингера может быть тривиальным, если состояние системы выбрано как собственное состояние одной из наблюдаемых. Более сильные соотношения неопределенности, доказанные Лоренцо Макконе и Аруном К. Пати, дают нетривиальные оценки суммы дисперсий для двух несовместимых наблюдаемых. (Более ранние работы по соотношениям неопределенностей, сформулированным как сумма дисперсий, включают, например, работу благодаря Ичену Хуану.) Для двух некоммутирующих наблюдаемых $A$ и $B$ первое более сильное соотношение неопределенностей имеет вид $$\sigma _{A}^{2}+\sigma _{B}^{2}\geq \pm i\langle \Psi \mid [A,B]|\Psi \rangle +\mid \langle \Psi \mid (A\pm iB)\mid {\bar {\Psi }}\rangle |^{2},$$где $\sigma _{A}^{2}=\langle \Psi |A^{2}|\Psi \rangle -\langle \Psi \mid A\mid \Psi \rangle ^{2}$, $\sigma _{B}^{2}=\langle \Psi |B^{2}|\Psi \rangle -\langle \Psi \mid B\mid \Psi \rangle ^{2}$, $|{\bar {\Psi }}\rangle$ - нормированный вектор, ортогональный состоянию системы $|\Psi \rangle$ и следует выбрать знак $\pm i\langle \Psi \mid [A,B]\mid \Psi \rangle$ чтобы сделать эту действительную величину положительным числом.

Второе более сильное соотношение неопределенностей имеет вид $$\sigma _{A}^{2}+\sigma _{B}^{2}\geq {\frac {1}{2}}|\langle {\bar {\Psi }}_{A+B}\mid (A+B)\mid \Psi \rangle |^{2}$$где $|{\bar {\Psi }}_{A+B}\rangle$ это состояние, ортогональное $|\Psi \rangle$.Форма $|{\bar {\Psi }}_{A+B}\rangle$ подразумевает, что правая часть нового соотношения неопределенности отлична от нуля, если только $|\Psi \rangle$ является собственным состоянием $(A+B)$. Можно отметить, что $|\Psi \rangle$ может быть собственным состоянием $(A+B)$ не являясь собственным состоянием ни того, ни другого $A$ или $B$. Однако, когда $|\Psi \rangle$ является собственным состоянием одной из двух наблюдаемых, соотношение неопределенностей Гейзенберга-Шредингера становится тривиальным. Но нижняя граница в новом соотношении отлична от нуля, если только $|\Psi \rangle$ является собственным состоянием обоих.

Улучшение соотношения неопределенностей Робертсона–Шредингера на основе разложения матрицы плотности

Неопределенность Робертсона-Шредингера можно улучшить, отметив, что она должна соблюдаться для всех компонентов. $\varrho _{k}$ в любом разложении матрицы плотности, заданной как $$\varrho =\sum _{k}p_{k}\varrho _{k}.$$Здесь для вероятностей $p_{k}\geq 0$ и $\sum _{k}p_{k}=1$ держать. Тогда, используя соотношение $$\sum _{k}a_{k}\sum _{k}b_{k}\geq \left(\sum _{k}{\sqrt {a_{k}b_{k}}}\right)^{2}$$для $a_{k},b_{k}\geq 0$,отсюда следует, что $$\sigma _{A}^{2}\sigma _{B}^{2}\geq \left[\sum _{k}p_{k}L(\varrho _{k})\right]^{2},$$где функция в границе определена $$L(\varrho )={\sqrt {\left|{\frac {1}{2}}\operatorname {tr} (\rho \{A,B\})-\operatorname {tr} (\rho A)\operatorname {tr} (\rho B)\right|^{2}+\left|{\frac {1}{2i}}\operatorname {tr} (\rho [A,B])\right|^{2}}}.$$Вышеупомянутое соотношение очень часто имеет более высокую оценку, чем исходное соотношение неопределенности Робертсона-Шредингера. Таким образом, нам нужно вычислить границу неопределенности Робертсона-Шредингера для смешанных компонентов квантового состояния, а не для квантового состояния, и вычислить среднее значение их квадратных корней. Следующее выражение сильнее, чем соотношение неопределенностей Робертсона – Шредингера. $$\sigma _{A}^{2}\sigma _{B}^{2}\geq \left[\max _{p_{k},\varrho _{k}}\sum _{k}p_{k}L(\varrho _{k})\right]^{2},$$где справа имеется вогнутая крыша над разложениями матрицы плотности.Усовершенствованное соотношение, приведенное выше, насыщается всеми однокубитными квантовыми состояниями.

Аналогичными рассуждениями можно вывести соотношение с выпуклой крышей в правой части $$\sigma _{A}^{2}F_{Q}[\varrho ,B]\geq 4\left[\min _{p_{k},\Psi _{k}}\sum _{k}p_{k}L(\vert \Psi _{k}\rangle \langle \Psi _{k}\vert )\right]^{2}$$где $F_{Q}[\varrho ,B]$ обозначает квантовую информацию Фишера , а матрица плотности разлагается на чистые состояния как $$\varrho =\sum _{k}p_{k}\vert \Psi _{k}\rangle \langle \Psi _{k}\vert .$$При выводе используется тот факт, что квантовая информация Фишера представляет собой выпуклую крышу дисперсии, умноженной на четыре.

Более простое неравенство следует без выпуклой крыши. $$\sigma _{A}^{2}F_{Q}[\varrho ,B]\geq \vert \langle i[A,B]\rangle \vert ^{2},$$что сильнее, чем соотношение неопределенностей Гейзенберга, поскольку для квантовой информации Фишера мы имеем $$F_{Q}[\varrho ,B]\leq 4\sigma _{B},$$тогда как для чистых состояний равенство имеет место.

Фазовое пространство

В формулировке квантовой механики в фазовом пространстве соотношение Робертсона-Шредингера следует из условия положительности действительной функции «звезда-квадрат». Учитывая функцию Вигнера $W(x,p)$ со звездным продуктом ★ и функцией f обычно справедливо следующее: $$\langle f^{*}\star f\rangle =\int (f^{*}\star f)\,W(x,p)\,dx\,dp\geq 0~.$$

Выбор $f=a+bx+cp$, мы приходим к $$\langle f^{*}\star f\rangle ={\begin{bmatrix}a^{*}&b^{*}&c^{*}\end{bmatrix}}{\begin{bmatrix}1&\langle x\rangle &\langle p\rangle \\\langle x\rangle &\langle x\star x\rangle &\langle x\star p\rangle \\\langle p\rangle &\langle p\star x\rangle &\langle p\star p\rangle \end{bmatrix}}{\begin{bmatrix}a\\b\\c\end{bmatrix}}\geq 0~.$$

Поскольку это условие положительности верно для всех a , b и c , отсюда следует, что все собственные значения матрицы неотрицательны.

Тогда неотрицательные собственные значения влекут за собой соответствующее условие неотрицательности определителя , $$\det {\begin{bmatrix}1&\langle x\rangle &\langle p\rangle \\\langle x\rangle &\langle x\star x\rangle &\langle x\star p\rangle \\\langle p\rangle &\langle p\star x\rangle &\langle p\star p\rangle \end{bmatrix}}=\det {\begin{bmatrix}1&\langle x\rangle &\langle p\rangle \\\langle x\rangle &\langle x^{2}\rangle &\left\langle xp+{\frac {i\hbar }{2}}\right\rangle \\\langle p\rangle &\left\langle xp-{\frac {i\hbar }{2}}\right\rangle &\langle p^{2}\rangle \end{bmatrix}}\geq 0~,$$или, явно, после алгебраических манипуляций, $$\sigma _{x}^{2}\sigma _{p}^{2}=\left(\langle x^{2}\rangle -\langle x\rangle ^{2}\right)\left(\langle p^{2}\rangle -\langle p\rangle ^{2}\right)\geq \left(\langle xp\rangle -\langle x\rangle \langle p\rangle \right)^{2}+{\frac {\hbar ^{2}}{4}}~.$$

Примеры

Поскольку соотношения Робертсона и Шредингера предназначены для общих операторов, эти соотношения можно применять к любым двум наблюдаемым для получения конкретных соотношений неопределенности. Ниже приведены некоторые из наиболее распространенных отношений, встречающихся в литературе.

• Соотношение неопределенности положения и линейного импульса : для операторов положения и линейного импульса каноническое коммутационное соотношение $[{\hat {x}},{\hat {p}}]=i\hbar$ следует неравенство Кеннарда сверху: $$\sigma _{x}\sigma _{p}\geq {\frac {\hbar }{2}}.$$
• Соотношение неопределенности углового момента : для двух ортогональных компонентов оператора полного углового момента объекта: $$\sigma _{J_{i}}\sigma _{J_{j}}\geq {\frac {\hbar }{2}}{\big |}\langle J_{k}\rangle {\big |},$$ где i , j , k различны, а J _i обозначает угловой момент вдоль оси x _i . Это соотношение подразумевает, что, если все три компонента не исчезают вместе, только один компонент углового момента системы может быть определен с произвольной точностью, обычно компонент, параллельный внешнему (магнитному или электрическому) полю. Более того, для $[J_{x},J_{y}]=i\hbar \varepsilon _{xyz}J_{z}$, выбор ${\hat {A}}=J_{x}$, ${\hat {B}}=J_{y}$, в мультиплетах углового момента, ψ = | j , m ⟩, ограничивает инвариант Казимира (квадрат углового момента, $\langle J_{x}^{2}+J_{y}^{2}+J_{z}^{2}\rangle$) снизу и, таким образом, дает полезные ограничения, такие как j ( j + 1) ≥ m ( m + 1) и, следовательно, j ≥ m , среди других.

• О числе электронов в сверхпроводнике и фазе его параметра порядка Гинзбурга–Ландау $$\Delta N\,\Delta \varphi \geq 1.$$

Ограничения

Вывод неравенства Робертсона для операторов ${\hat {A}}$ и ${\hat {B}}$ требует ${\hat {A}}{\hat {B}}\psi$ и ${\hat {B}}{\hat {A}}\psi$ быть определены. Существуют квантовые системы, где эти условия не выполняются. Одним из примеров является квантовая частица на кольце , волновая функция которой зависит от угловой переменной. $\theta$ в интервале $[0,2\pi ]$. Определить операторы «положение» и «импульс». ${\hat {A}}$ и ${\hat {B}}$ к $${\hat {A}}\psi (\theta )=\theta \psi (\theta ),\quad \theta \in [0,2\pi ],$$и $${\hat {B}}\psi =-i\hbar {\frac {d\psi }{d\theta }},$$с периодическими граничными условиями на ${\hat {B}}$. Определение ${\hat {A}}$ зависит от $\theta$ диапазон от 0 до $2\pi$. Эти операторы удовлетворяют обычным коммутационным соотношениям для операторов положения и импульса: $[{\hat {A}},{\hat {B}}]=i\hbar$. Точнее, ${\hat {A}}{\hat {B}}\psi -{\hat {B}}{\hat {A}}\psi =i\hbar \psi$ всякий раз, когда оба ${\hat {A}}{\hat {B}}\psi$ и ${\hat {B}}{\hat {A}}\psi$ определены, и пространство таких $\psi$ является плотным подпространством квантового гильбертова пространства.

Теперь позвольте $\psi$ быть любым из собственных состояний ${\hat {B}}$, которые даны $\psi (\theta )=e^{2\pi in\theta }$. Эти состояния нормируемы, в отличие от собственных состояний оператора импульса на прямой. Также оператор ${\hat {A}}$ ограничено, поскольку $\theta$ колеблется в ограниченном интервале. Таким образом, в государстве $\psi$, неопределенность $B$ равна нулю, а неопределенность $A$ конечно, так что $$\sigma _{A}\sigma _{B}=0.$$Принцип неопределенности Робертсона в этом случае не применяется: $\psi$ не находится в домене оператора ${\hat {B}}{\hat {A}}$, поскольку умножение на $\theta$ нарушает периодические граничные условия, наложенные на ${\hat {B}}$.

Для обычных операторов положения и импульса ${\hat {X}}$ и ${\hat {P}}$ в действительности никаких подобных контрпримеров возникнуть не может. Пока $\sigma _{x}$ и $\sigma _{p}$ определены в штате $\psi$, принцип неопределенности Гейзенберга справедлив, даже если $\psi$ не находится в области ${\hat {X}}{\hat {P}}$ или из ${\hat {P}}{\hat {X}}$.

Дополнительные соотношения неопределенности

Предел Гейзенберга

В квантовой метрологии , и особенно в интерферометрии , предел Гейзенберга — это оптимальная скорость, при которой точность измерения может масштабироваться в зависимости от энергии, используемой в измерении. Обычно это измерение фазы (применительно к одному плечу светоделителя ) , а энергия определяется количеством фотонов, используемых в интерферометре . Хотя некоторые утверждают, что преодолели предел Гейзенберга, это отражает разногласия по поводу определения ресурса масштабирования. При правильном определении предел Гейзенберга является следствием основных принципов квантовой механики и не может быть превзойден, хотя слабый предел Гейзенберга можно превзойти.

Систематические и статистические ошибки

Приведенные выше неравенства сосредоточены на статистической неточности наблюдаемых величин, количественно выраженной стандартным отклонением. $\sigma$. Однако первоначальная версия Гейзенберга имела дело с систематической ошибкой , возмущением квантовой системы, производимым измерительным прибором, то есть эффектом наблюдателя.

Если мы позволим $\varepsilon _{A}$ представляют ошибку (т. е. неточность ) измерения наблюдаемой A и $\eta _{B}$ возмущение, возникающее при последующем измерении сопряженной переменной B в результате предыдущего измерения A , то неравенство, предложенное Одзавой, включающее как систематические, так и статистические ошибки, имеет место:

$\varepsilon _{A}\,\eta _{B}+\varepsilon _{A}\,\sigma _{B}+\sigma _{A}\,\eta _{B}\,\geq \,{\frac {1}{2}}\,\left|{\Bigl \langle }{\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|$

Принцип неопределенности Гейзенберга, первоначально описанный в формулировке 1927 года, упоминает только первый член неравенства Одзавы, касающийся систематической ошибки . Используя приведенные выше обозначения для описания ошибки/помехи эффекта последовательных измерений (сначала A , затем B ), это можно записать как

$\varepsilon _{A}\,\eta _{B}\,\geq \,{\frac {1}{2}}\,\left|{\Bigl \langle }{\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|$

Формальный вывод соотношения Гейзенберга возможен, но далеко не интуитивен. Она не была предложена Гейзенбергом, но математически последовательно сформулирована лишь в последние годы. Также следует подчеркнуть, что формулировка Гейзенберга не учитывает внутренние статистические ошибки. $\sigma _{A}$ и $\sigma _{B}$. Появляется все больше экспериментальных данных что полная квантовая неопределенность не может быть описана одним членом Гейзенберга, а требует присутствия всех трех членов неравенства Одзавы.

Используя тот же формализм, можно также ввести другой вид физической ситуации, которую часто путают с предыдущей, а именно случай одновременных измерений ( A и B одновременно):

$\varepsilon _{A}\,\varepsilon _{B}\,\geq \,{\frac {1}{2}}\,\left|{\Bigl \langle }{\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|$

Два одновременных измерения на A и B обязательно нерезкий или слабый .

Также возможно вывести соотношение неопределенности, которое, как и соотношение Одзавы, сочетает в себе как статистическую, так и систематическую составляющие ошибки, но сохраняет форму, очень близкую к исходному неравенству Гейзенберга. Добавив Робертсона

$\sigma _{A}\,\sigma _{B}\,\geq \,{\frac {1}{2}}\,\left|{\Bigl \langle }{\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|$

и отношения Одзавы, мы получаем $$\varepsilon _{A}\eta _{B}+\varepsilon _{A}\,\sigma _{B}+\sigma _{A}\,\eta _{B}+\sigma _{A}\sigma _{B}\geq \left|{\Bigl \langle }{\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|.$$Четыре термина можно записать так: $$(\varepsilon _{A}+\sigma _{A})\,(\eta _{B}+\sigma _{B})\,\geq \,\left|{\Bigl \langle }{\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|.$$Определение: $${\bar {\varepsilon }}_{A}\,\equiv \,(\varepsilon _{A}+\sigma _{A})$$как погрешность измеренных значений переменной А и $${\bar {\eta }}_{B}\,\equiv \,(\eta _{B}+\sigma _{B})$$как результирующее колебание сопряженной переменной B , Кадзуо Фудзикава установил соотношение неопределенности, аналогичное исходному соотношению Гейзенберга, но справедливое как для систематических, так и для статистических ошибок :

${\bar {\varepsilon }}_{A}\,{\bar {\eta }}_{B}\,\geq \,\left|{\Bigl \langle }{\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|$

Принцип квантовой энтропийной неопределенности

Для многих распределений стандартное отклонение не является особенно естественным способом количественной оценки структуры. Например, соотношения неопределенностей, в которых одной из наблюдаемых является угол, имеют мало физического смысла для флуктуаций, превышающих один период. Другие примеры включают сильно бимодальные распределения или унимодальные распределения с расходящейся дисперсией.

Решением, позволяющим преодолеть эти проблемы, является неопределенность, основанная на энтропийной неопределенности, а не на продукте дисперсий. Формулируя многомировую интерпретацию квантовой механики в 1957 году, Хью Эверетт III предположил более сильное расширение принципа неопределенности, основанное на энтропийной уверенности. Эта гипотеза, также изученная И.И. Хиршманом и доказано в 1975 году В. Бекнером и Иво Бялиницкий-Бирула и Ежи Мицельский. заключается в том, что для двух нормализованных безразмерных пар преобразований Фурье f ( a ) и g ( b ) , где

$f(a)=\int _{-\infty }^{\infty }g(b)\ e^{2\pi iab}\,db$    и     $\,\,\,g(b)=\int _{-\infty }^{\infty }f(a)\ e^{-2\pi iab}\,da$

Шеннона информационная энтропия $$H_{a}=\int _{-\infty }^{\infty }f(a)\log(f(a))\,da,$$и $$H_{b}=\int _{-\infty }^{\infty }g(b)\log(g(b))\,db$$подчиняются следующему ограничению:

$H_{a}+H_{b}\geq \log(e/2)$

где логарифмы могут быть в любом основании.

Функции распределения вероятностей, связанные с волновой функцией положения ψ ( x ) и волновой функцией импульса φ ( x ), имеют размеры, обратные длине и импульсу соответственно, но энтропию можно сделать безразмерной с помощью $$H_{x}=-\int |\psi (x)|^{2}\ln \left(x_{0}\,|\psi (x)|^{2}\right)dx=-\left\langle \ln \left(x_{0}\,\left|\psi (x)\right|^{2}\right)\right\rangle$$$$H_{p}=-\int |\varphi (p)|^{2}\ln(p_{0}\,|\varphi (p)|^{2})\,dp=-\left\langle \ln(p_{0}\left|\varphi (p)\right|^{2})\right\rangle$$где x ₀ и p ₀ — некоторые произвольно выбранные длина и импульс соответственно, которые делают аргументы логарифмов безразмерными. Обратите внимание, что энтропия будет функцией этих выбранных параметров. Из-за соотношения преобразования Фурье между волновой функцией положения ψ ( x ) и волновой функцией импульса φ ( p ) вышеуказанное ограничение может быть записано для соответствующих энтропий как

$H_{x}+H_{p}\geq \log \left({\frac {e\,h}{2\,x_{0}\,p_{0}}}\right)$

где h — постоянная Планка .

В зависимости от выбора произведения x ₀ p ₀ выражение можно записать разными способами. Если x ₀ p ₀ выбрано равным h , то $$H_{x}+H_{p}\geq \log \left({\frac {e}{2}}\right)$$

Если вместо этого x ₀ p ₀ выбрано равным ħ , то $$H_{x}+H_{p}\geq \log(e\,\pi )$$

Если x ₀ и p ₀ выбраны равными единице в любой используемой системе единиц, то $$H_{x}+H_{p}\geq \log \left({\frac {e\,h}{2}}\right)$$где h интерпретируется как безразмерное число, равное значению постоянной Планка в выбранной системе единиц. Обратите внимание, что эти неравенства можно распространить на многомодовые квантовые состояния или волновые функции более чем в одном пространственном измерении.

Квантово-энтропийный принцип неопределенности является более ограничительным, чем принцип неопределенности Гейзенберга. Из обратных логарифмических неравенств Соболева $$H_{x}\leq {\frac {1}{2}}\log(2e\pi \sigma _{x}^{2}/x_{0}^{2})~,$$$$H_{p}\leq {\frac {1}{2}}\log(2e\pi \sigma _{p}^{2}/p_{0}^{2})~,$$(эквивалентно, из того факта, что нормальные распределения максимизируют энтропию всех таких с заданной дисперсией), из этого легко следует, что этот принцип энтропийной неопределенности сильнее, чем принцип, основанный на стандартных отклонениях , потому что $$\sigma _{x}\sigma _{p}\geq {\frac {\hbar }{2}}\exp \left(H_{x}+H_{p}-\log \left({\frac {e\,h}{2\,x_{0}\,p_{0}}}\right)\right)\geq {\frac {\hbar }{2}}~.$$

Другими словами, принцип неопределенности Гейзенберга является следствием квантово-энтропийного принципа неопределенности, а не наоборот. Несколько замечаний по поводу этих неравенств. Во-первых, выбор основания e является общепринятым в физике. Альтернативно логарифм может быть в любом основании, при условии, что он непротиворечив с обеих сторон неравенства. Во-вторых, вспомните, энтропия Шеннона что использовалась , а не квантовая энтропия фон Неймана . Наконец, нормальное распределение насыщает неравенство, и это единственное распределение с этим свойством, поскольку это распределение вероятностей с максимальной энтропией среди распределений с фиксированной дисперсией ( см. здесь доказательство ).

showЭнтропийная неопределенность нормального распределения

We demonstrate this method on the ground state of the QHO, which as discussed above saturates the usual uncertainty based on standard deviations. The length scale can be set to whatever is convenient, so we assign $$x_{0}={\sqrt {\frac {\hbar }{2m\omega }}}$$$${\begin{aligned}\psi (x)&=\left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}\exp {\left(-{\frac {m\omega x^{2}}{2\hbar }}\right)}\\&=\left({\frac {1}{2\pi x_{0}^{2}}}\right)^{1/4}\exp {\left(-{\frac {x^{2}}{4x_{0}^{2}}}\right)}\end{aligned}}$$ The probability distribution is the normal distribution$$|\psi (x)|^{2}={\frac {1}{x_{0}{\sqrt {2\pi }}}}\exp {\left(-{\frac {x^{2}}{2x_{0}^{2}}}\right)}$$with Shannon entropy$${\begin{aligned}H_{x}&=-\int |\psi (x)|^{2}\ln(|\psi (x)|^{2}\cdot x_{0})\,dx\\&=-{\frac {1}{x_{0}{\sqrt {2\pi }}}}\int _{-\infty }^{\infty }\exp {\left(-{\frac {x^{2}}{2x_{0}^{2}}}\right)}\ln \left[{\frac {1}{\sqrt {2\pi }}}\exp {\left(-{\frac {x^{2}}{2x_{0}^{2}}}\right)}\right]\,dx\\&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\exp {\left(-{\frac {u^{2}}{2}}\right)}\left[\ln({\sqrt {2\pi }})+{\frac {u^{2}}{2}}\right]\,du\\&=\ln({\sqrt {2\pi }})+{\frac {1}{2}}.\end{aligned}}$$ A completely analogous calculation proceeds for the momentum distribution. Choosing a standard momentum of $p_{0}=\hbar /x_{0}$:$$\varphi (p)=\left({\frac {2x_{0}^{2}}{\pi \hbar ^{2}}}\right)^{1/4}\exp {\left(-{\frac {x_{0}^{2}p^{2}}{\hbar ^{2}}}\right)}$$$$|\varphi (p)|^{2}={\sqrt {\frac {2x_{0}^{2}}{\pi \hbar ^{2}}}}\exp {\left(-{\frac {2x_{0}^{2}p^{2}}{\hbar ^{2}}}\right)}$$$${\begin{aligned}H_{p}&=-\int |\varphi (p)|^{2}\ln(|\varphi (p)|^{2}\cdot \hbar /x_{0})\,dp\\&=-{\sqrt {\frac {2x_{0}^{2}}{\pi \hbar ^{2}}}}\int _{-\infty }^{\infty }\exp {\left(-{\frac {2x_{0}^{2}p^{2}}{\hbar ^{2}}}\right)}\ln \left[{\sqrt {\frac {2}{\pi }}}\exp {\left(-{\frac {2x_{0}^{2}p^{2}}{\hbar ^{2}}}\right)}\right]\,dp\\&={\sqrt {\frac {2}{\pi }}}\int _{-\infty }^{\infty }\exp {\left(-2v^{2}\right)}\left[\ln \left({\sqrt {\frac {\pi }{2}}}\right)+2v^{2}\right]\,dv\\&=\ln \left({\sqrt {\frac {\pi }{2}}}\right)+{\frac {1}{2}}.\end{aligned}}$$ The entropic uncertainty is therefore the limiting value$${\begin{aligned}H_{x}+H_{p}&=\ln({\sqrt {2\pi }})+{\frac {1}{2}}+\ln \left({\sqrt {\frac {\pi }{2}}}\right)+{\frac {1}{2}}\\&=1+\ln \pi =\ln(e\pi ).\end{aligned}}$$

Измерительное устройство будет иметь конечное разрешение, устанавливаемое путем дискретизации его возможных выходных сигналов по элементам разрешения с вероятностью попадания в один из элементов разрешения, заданной правилом Борна. Мы рассмотрим наиболее распространенную экспериментальную ситуацию, в которой контейнеры имеют одинаковый размер. Пусть δx — мера пространственного разрешения. Мы принимаем нулевой интервал по центру вблизи начала координат, возможно, с небольшим постоянным смещением c . Вероятность попадания в j-й интервал ширины δx равна $$\operatorname {P} [x_{j}]=\int _{(j-1/2)\delta x-c}^{(j+1/2)\delta x-c}|\psi (x)|^{2}\,dx$$

Чтобы учесть эту дискретизацию, мы можем определить энтропию Шеннона волновой функции для данного измерительного устройства как $$H_{x}=-\sum _{j=-\infty }^{\infty }\operatorname {P} [x_{j}]\ln \operatorname {P} [x_{j}].$$

Согласно приведенному выше определению, энтропийное соотношение неопределенности имеет вид $$H_{x}+H_{p}>\ln \left({\frac {e}{2}}\right)-\ln \left({\frac {\delta x\delta p}{h}}\right).$$

Здесь отметим, что δx δp / h — типичный бесконечно малый объем фазового пространства, используемый при вычислении статистической суммы . Неравенство также является строгим и ненасыщенным. Попытки улучшить эту границу являются активной областью исследований.

showПример нормального распределения

We demonstrate this method first on the ground state of the QHO, which as discussed above saturates the usual uncertainty based on standard deviations. $$\psi (x)=\left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}\exp {\left(-{\frac {m\omega x^{2}}{2\hbar }}\right)}$$ The probability of lying within one of these bins can be expressed in terms of the error function. $${\begin{aligned}\operatorname {P} [x_{j}]&={\sqrt {\frac {m\omega }{\pi \hbar }}}\int _{(j-1/2)\delta x}^{(j+1/2)\delta x}\exp \left(-{\frac {m\omega x^{2}}{\hbar }}\right)\,dx\\&={\sqrt {\frac {1}{\pi }}}\int _{(j-1/2)\delta x{\sqrt {m\omega /\hbar }}}^{(j+1/2)\delta x{\sqrt {m\omega /\hbar }}}e^{u^{2}}\,du\\&={\frac {1}{2}}\left[\operatorname {erf} \left(\left(j+{\frac {1}{2}}\right)\delta x\cdot {\sqrt {\frac {m\omega }{\hbar }}}\right)-\operatorname {erf} \left(\left(j-{\frac {1}{2}}\right)\delta x\cdot {\sqrt {\frac {m\omega }{\hbar }}}\right)\right]\end{aligned}}$$ The momentum probabilities are completely analogous. $$\operatorname {P} [p_{j}]={\frac {1}{2}}\left[\operatorname {erf} \left(\left(j+{\frac {1}{2}}\right)\delta p\cdot {\frac {1}{\sqrt {\hbar m\omega }}}\right)-\operatorname {erf} \left(\left(j-{\frac {1}{2}}\right)\delta x\cdot {\frac {1}{\sqrt {\hbar m\omega }}}\right)\right]$$ For simplicity, we will set the resolutions to$$\delta x={\sqrt {\frac {h}{m\omega }}}$$$$\delta p={\sqrt {hm\omega }}$$so that the probabilities reduce to$$\operatorname {P} [x_{j}]=\operatorname {P} [p_{j}]={\frac {1}{2}}\left[\operatorname {erf} \left(\left(j+{\frac {1}{2}}\right){\sqrt {2\pi }}\right)-\operatorname {erf} \left(\left(j-{\frac {1}{2}}\right){\sqrt {2\pi }}\right)\right]$$ The Shannon entropy can be evaluated numerically.$${\begin{aligned}H_{x}=H_{p}&=-\sum _{j=-\infty }^{\infty }\operatorname {P} [x_{j}]\ln \operatorname {P} [x_{j}]\\&=-\sum _{j=-\infty }^{\infty }{\frac {1}{2}}\left[\operatorname {erf} \left(\left(j+{\frac {1}{2}}\right){\sqrt {2\pi }}\right)-\operatorname {erf} \left(\left(j-{\frac {1}{2}}\right){\sqrt {2\pi }}\right)\right]\ln {\frac {1}{2}}\left[\operatorname {erf} \left(\left(j+{\frac {1}{2}}\right){\sqrt {2\pi }}\right)-\operatorname {erf} \left(\left(j-{\frac {1}{2}}\right){\sqrt {2\pi }}\right)\right]\\&\approx 0.3226\end{aligned}}$$ The entropic uncertainty is indeed larger than the limiting value.$$H_{x}+H_{p}\approx 0.3226+0.3226=0.6452>\ln \left({\frac {e}{2}}\right)-\ln 1\approx 0.3069$$ Note that despite being in the optimal case, the inequality is not saturated.

showПример функции Sinc

An example of a unimodal distribution with infinite variance is the sinc function. If the wave function is the correctly normalized uniform distribution, $$\psi (x)={\begin{cases}{1}/{\sqrt {2a}}&{\text{for }}|x|\leq a,\\[8pt]0&{\text{for }}|x|>a\end{cases}}$$then its Fourier transform is the sinc function,$$\varphi (p)={\sqrt {\frac {a}{\pi \hbar }}}\cdot \operatorname {sinc} \left({\frac {ap}{\hbar }}\right)$$which yields infinite momentum variance despite having a centralized shape. The entropic uncertainty, on the other hand, is finite. Suppose for simplicity that the spatial resolution is just a two-bin measurement, δx = a, and that the momentum resolution is δp = h/a. Partitioning the uniform spatial distribution into two equal bins is straightforward. We set the offset c = 1/2 so that the two bins span the distribution.$$\operatorname {P} [x_{0}]=\int _{-a}^{0}{\frac {1}{2a}}\,dx={\frac {1}{2}}$$$$\operatorname {P} [x_{1}]=\int _{0}^{a}{\frac {1}{2a}}\,dx={\frac {1}{2}}$$$$H_{x}=-\sum _{j=0}^{1}\operatorname {P} [x_{j}]\ln \operatorname {P} [x_{j}]=-{\frac {1}{2}}\ln {\frac {1}{2}}-{\frac {1}{2}}\ln {\frac {1}{2}}=\ln 2$$ The bins for momentum must cover the entire real line. As done with the spatial distribution, we could apply an offset. It turns out, however, that the Shannon entropy is minimized when the zeroth bin for momentum is centered at the origin. (The reader is encouraged to try adding an offset.) The probability of lying within an arbitrary momentum bin can be expressed in terms of the sine integral. $${\begin{aligned}\operatorname {P} [p_{j}]&={\frac {a}{\pi \hbar }}\int _{(j-1/2)\delta p}^{(j+1/2)\delta p}\operatorname {sinc} ^{2}\left({\frac {ap}{\hbar }}\right)\,dp\\&={\frac {1}{\pi }}\int _{2\pi (j-1/2)}^{2\pi (j+1/2)}\operatorname {sinc} ^{2}(u)\,du\\&={\frac {1}{\pi }}\left[\operatorname {Si} ((4j+2)\pi )-\operatorname {Si} ((4j-2)\pi )\right]\end{aligned}}$$ The Shannon entropy can be evaluated numerically.$$H_{p}=-\sum _{j=-\infty }^{\infty }\operatorname {P} [p_{j}]\ln \operatorname {P} [p_{j}]=-\operatorname {P} [p_{0}]\ln \operatorname {P} [p_{0}]-2\cdot \sum _{j=1}^{\infty }\operatorname {P} [p_{j}]\ln \operatorname {P} [p_{j}]\approx 0.53$$ The entropic uncertainty is indeed larger than the limiting value.$$H_{x}+H_{p}\approx 0.69+0.53=1.22>\ln \left({\frac {e}{2}}\right)-\ln 1\approx 0.31$$

Соотношение неопределенности с тремя компонентами углового момента

Для частицы спин- $j$ имеет место следующее соотношение неопределенностей $$\sigma _{J_{x}}^{2}+\sigma _{J_{y}}^{2}+\sigma _{J_{z}}^{2}\geq j,$$где $J_{l}$ являются компонентами углового момента. Отношение может быть получено из $$\langle J_{x}^{2}+J_{y}^{2}+J_{z}^{2}\rangle =j(j+1),$$и $$\langle J_{x}\rangle ^{2}+\langle J_{y}\rangle ^{2}+\langle J_{z}\rangle ^{2}\leq j.$$Отношения можно усилить, если $$\sigma _{J_{x}}^{2}+\sigma _{J_{y}}^{2}+F_{Q}[\varrho ,J_{z}]/4\geq j,$$где $F_{Q}[\varrho ,J_{z}]$ – это квантовая информация Фишера.

Гармонический анализ

Основная статья: преобразование Фурье § Принцип неопределенности

В контексте гармонического анализа , раздела математики, принцип неопределенности подразумевает, что нельзя одновременно локализовать значение функции и ее преобразование Фурье. А именно, имеет место неравенство $$\left(\int _{-\infty }^{\infty }x^{2}|f(x)|^{2}\,dx\right)\left(\int _{-\infty }^{\infty }\xi ^{2}|{\hat {f}}(\xi )|^{2}\,d\xi \right)\geq {\frac {\|f\|_{2}^{4}}{16\pi ^{2}}}.$$

Дальнейшие математические неравенства неопределенности, включая вышеупомянутую энтропийную неопределенность , справедливы между функцией f и ее преобразованием Фурье ƒ̂ : $$H_{x}+H_{\xi }\geq \log(e/2)$$

Обработка сигналов

В контексте обработки сигналов и, в частности, частотно-временного анализа , принципы неопределенности называются пределом Габора , в честь Денниса Габора , или иногда пределом Гейзенберга-Габора . Основной результат, который следует из приведенной ниже «теоремы Бенедикса», заключается в том, что функция не может быть одновременно ограниченной по времени и по полосе (функция и ее преобразование Фурье не могут одновременно иметь ограниченную область определения) - см. « Ограниченная полоса» и « ограниченная по времени» . Точнее, произведение временной полосы или продолжительности полосы пропускания удовлетворяет $$\sigma _{{\text{energy}},t}\cdot \sigma _{{\text{energy}},f}\geq {\frac {1}{4\pi }}\approx 0.08{\text{ cycles}},$$где $\sigma _{{\text{energy}},t}$ и $\sigma _{{\text{energy}},f}$ являются стандартными отклонениями представления энергии или мощности (т.е. квадрата) времени и частоты соответственно. Минимум достигается для импульса гауссовой формы ( вейвлет Габора ). $\sigma _{t}\sigma _{f}=1/2\pi$; возведение в квадрат уменьшает каждую $\sigma$ по фактору ${\sqrt {2}}$.] Другой распространенной мерой является произведение полной ширины времени и частоты на половине максимума (мощности/энергии), что для гауссовой функции равно $2\ln 2/\pi \approx 0.44$ (см . импульс с ограниченной полосой пропускания ).

Альтернативно можно сказать: «Нельзя одновременно точно локализовать сигнал (функцию f ) как во временной, так и в частотной области ( ƒ̂ , его преобразование Фурье)».

Применительно к фильтрам результат означает, что нельзя одновременно достичь высокого временного и частотного разрешения; Конкретным примером являются проблемы разрешения кратковременного преобразования Фурье : если использовать широкое окно, можно достичь хорошего разрешения по частоте за счет временного разрешения, в то время как узкое окно имеет противоположный компромисс.

Альтернативные теоремы дают более точные количественные результаты, и в частотно-временном анализе вместо того, чтобы интерпретировать (1-мерную) временную и частотную области отдельно, вместо этого предел интерпретируется как нижний предел носителя функции в (2 -мерная) плоскость время-частота. На практике предел Габора ограничивает одновременное частотно-временное разрешение, которого можно достичь без помех; можно добиться более высокого разрешения, но за счет того, что разные компоненты сигнала мешают друг другу.

В результате для анализа сигналов, в которых переходные процессы важны вейвлет-преобразование , вместо преобразования Фурье часто используется .

Дискретное преобразование Фурье

Позволять $\left\{\mathbf {x_{n}} \right\}:=x_{0},x_{1},\ldots ,x_{N-1}$ быть последовательностью N комплексных чисел и $\left\{\mathbf {X_{k}} \right\}:=X_{0},X_{1},\ldots ,X_{N-1},$ — его дискретное преобразование Фурье .

Обозначим через $\|x\|_{0}$ количество ненулевых элементов во временной последовательности $x_{0},x_{1},\ldots ,x_{N-1}$ и по $\|X\|_{0}$ количество ненулевых элементов в частотной последовательности $X_{0},X_{1},\ldots ,X_{N-1}$. Затем, $$\|x\|_{0}\cdot \|X\|_{0}\geq N.$$

Это неравенство является точным : равенство достигается, когда x или X является массой Дирака или, в более общем смысле, когда x является ненулевым кратным гребенки Дирака, поддерживаемой подгруппой целых чисел по модулю N (в этом случае X также является гребенкой Дирака, поддерживаемой на дополнительную подгруппу и наоборот).

В более общем смысле, если T и W являются подмножествами целых чисел по модулю N , пусть $L_{T},R_{W}:\ell ^{2}(\mathbb {Z} /N\mathbb {Z} )\to \ell ^{2}(\mathbb {Z} /N\mathbb {Z} )$ обозначают оператор ограничения времени и оператор ограничения полосы соответственно. Затем $$\|L_{T}R_{W}\|^{2}\leq {\frac {|T||W|}{|G|}}$$где норма — это операторная норма операторов в гильбертовом пространстве. $\ell ^{2}(\mathbb {Z} /N\mathbb {Z} )$ функций над целыми числами по N. модулю Это неравенство имеет значение для восстановления сигнала .

Когда N — простое число , справедливо более сильное неравенство: $$\|x\|_{0}+\|X\|_{0}\geq N+1.$$ Это неравенство, открытое Теренсом Тао , также является резким.

Теорема Бенедикса

Амрейн-Бертье и теорема Бенедикса интуитивно говорит, что набор точек, где f не равно нулю, и набор точек, где ƒ̂ не равно нулю, не могут быть одновременно малыми.

В частности, невозможно, чтобы функция f из L ² ( R ) и его преобразование Фурье ƒ̂ поддерживаются меры на множествах конечной Лебега . Более количественная версия $$\|f\|_{L^{2}(\mathbf {R} ^{d})}\leq Ce^{C|S||\Sigma |}{\bigl (}\|f\|_{L^{2}(S^{c})}+\|{\hat {f}}\|_{L^{2}(\Sigma ^{c})}{\bigr )}~.$$

Ожидается, что фактор Ce ^{С | С || С |} может быть заменен на Ce ^{С (| С || С |) 1/ д} , что известно только в том случае, если S или Σ выпуклы.

Принцип неопределенности Харди

Математик Г.Х. Харди сформулировал следующий принцип неопределенности: невозможно, чтобы f и ƒ̂ были «очень быстро убывающими». В частности, если f в $L^{2}(\mathbb {R} )$ таков, что $$|f(x)|\leq C(1+|x|)^{N}e^{-a\pi x^{2}}$$и $$|{\hat {f}}(\xi )|\leq C(1+|\xi |)^{N}e^{-b\pi \xi ^{2}}$$ ( $C>0,N$ целое число),тогда, если ab > 1, f = 0 , а если ab = 1 , то существует многочлен P степени ≤ N такой, что $$f(x)=P(x)e^{-a\pi x^{2}}.$$

Позже это было улучшено следующим образом: если $f\in L^{2}(\mathbb {R} ^{d})$ таков, что $$\int _{\mathbb {R} ^{d}}\int _{\mathbb {R} ^{d}}|f(x)||{\hat {f}}(\xi )|{\frac {e^{\pi |\langle x,\xi \rangle |}}{(1+|x|+|\xi |)^{N}}}\,dx\,d\xi <+\infty ~,$$затем $$f(x)=P(x)e^{-\pi \langle Ax,x\rangle }~,$$где P — многочлен степени ( N − d )/2 , а A — действительная положительно определенная матрица размера d × d .

Этот результат был сформулирован в полном собрании сочинений Бёрлинга без доказательства и доказан Хёрмандером. (дело $d=1,N=0$) и Бонами, Деманж и Джеминг для общего случая. Обратите внимание, что версия Хёрмандера-Берлинга подразумевает случай ab > 1 в теореме Харди, в то время как версия Бонами-Деманжа-Джейминга охватывает всю силу теоремы Харди. Другое доказательство теоремы Берлинга, основанное на теореме Лиувилля, появилось в работе.

Полное описание случая ab <1 , а также следующее расширение распределений классов Шварца можно найти в ссылке.

Теорема . Если умеренное распределение $f\in {\mathcal {S}}'(\mathbb {R} ^{d})$ таков, что $$e^{\pi |x|^{2}}f\in {\mathcal {S}}'(\mathbb {R} ^{d})$$и $$e^{\pi |\xi |^{2}}{\hat {f}}\in {\mathcal {S}}'(\mathbb {R} ^{d})~,$$затем $$f(x)=P(x)e^{-\pi \langle Ax,x\rangle }~,$$для некоторого удобного многочлена P и вещественной положительно определенной матрицы A типа d × d .

История

Смотрите также: История квантовой механики.

В 1925 году Гейзенберг опубликовал статью «Umdeutung» (переинтерпретация) , в которой показал, что центральным аспектом квантовой теории является некоммутативность : теория подразумевала, что относительный порядок измерения положения и импульса важен. Работая с Максом Борном и Паскуалем Джорданом , он продолжал развивать матричную механику , которая стала первой современной формулировкой квантовой механики.

Вернер Гейзенберг и Нильс Бор

В марте 1926 года, работая в институте Бора, Гейзенберг понял, что из некоммутативности следует принцип неопределенности. В письме Вольфгангу Паули в феврале 1927 года он разработал основные концепции.

В своей знаменитой статье 1927 года « Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik » («О перцептивном содержании квантовой теоретической кинематики и механики») Гейзенберг установил это выражение как минимальную величину неизбежного возмущения импульса, вызванного любым измерением положения: но он не дал точного определения неопределенностей Δx и Δp . Вместо этого он дал некоторые правдоподобные оценки для каждого случая отдельно. В его статье был дан анализ с использованием микроскопа, который, как показал Бор, был неверным; Гейзенберг включил в публикацию дополнение.

В своей лекции в Чикаго в 1930 г. он усовершенствовал свой принцип:

$\Delta x\,\Delta p\gtrsim h$ ( А1 )

Более поздние работы расширили эту концепцию. Любые две переменные, которые не коммутируют, не могут быть измерены одновременно: чем точнее известна одна, тем менее точно может быть известна другая. Гейзенберг писал:

В простейшей форме ее можно выразить следующим образом: никогда нельзя знать с совершенной точностью оба этих важных фактора, определяющих движение одной из мельчайших частиц, — ее положение и ее скорость. Невозможно точно определить положение , направление и скорость частицы одновременно .

Кеннард в 1927 году впервые доказал современное неравенство:

$\sigma _{x}\sigma _{p}\geq {\frac {\hbar }{2}}$ ( А2 )

где ħ = ⁠ h / 2 π ⁠ и σ _x , σ _p — стандартные отклонения положения и импульса. (Гейзенберг доказал соотношение ( A2 ) только для частного случая гауссовских состояний. ) В 1929 году Робертсон обобщил неравенство на все наблюдаемые, а в 1930 году Шредингер расширил форму, чтобы обеспечить ненулевую ковариацию операторов; этот результат называется неравенством Робертсона-Шредингера.

Терминология и перевод

В основной части своей оригинальной статьи 1927 года, написанной на немецком языке, Гейзенберг использовал слово «Ungenauigkeit». описать основной теоретический принцип. Лишь в примечании он перешел на слово «Unsicherheit». Позже он всегда использовал «Unbestimmtheit». Однако, когда в 1930 году была опубликована англоязычная версия учебника Гейзенберга « Физические принципы квантовой теории », использовалось только английское слово «неопределенность», и оно стало термином в английском языке.

Микроскоп Гейзенберга

Гамма-микроскоп Гейзенберга для обнаружения электрона (показан синим цветом). Входящий гамма-луч (показан зеленым) рассеивается электроном вверх под углом апертуры микроскопа θ . Рассеянное гамма-излучение показано красным. Классическая оптика показывает, что положение электрона можно определить только с точностью до неопределенности Δ x , которая зависит от θ и длины волны λ падающего света.

Основная статья: микроскоп Гейзенберга

Этот принцип совершенно нелогичен, поэтому первых исследователей квантовой теории нужно было убедить в том, что наивные измерения, нарушающие этот принцип, всегда будут неработоспособными. Один из способов, с помощью которого Гейзенберг первоначально проиллюстрировал внутреннюю невозможность нарушения принципа неопределенности, — это использование эффекта наблюдателя воображаемого микроскопа в качестве измерительного устройства.

Он представляет себе экспериментатора, пытающегося измерить положение и импульс электрона , стреляя в него фотоном .

• Проблема 1. Если у фотона короткая длина волны и, следовательно, большой импульс, положение можно точно измерить. Но фотон рассеивается в случайном направлении, передавая электрону большое и неопределенное количество импульса. Если фотон имеет большую длину волны и малый импульс, столкновение не сильно нарушит импульс электрона, но рассеяние лишь смутно выявит его положение.
• Проблема 2. Если в микроскопе используется большая апертура , местоположение электрона можно хорошо определить (см. Критерий Рэлея ); но согласно принципу сохранения импульса поперечный импульс падающего фотона влияет на импульс линии луча электрона, и, следовательно, новый импульс электрона плохо разрешается. Если используется маленькая апертура, точность обоих разрешений обратная.

Сочетание этих компромиссов означает, что независимо от того, какая длина волны фотона и размер апертуры используются, произведение неопределенности в измеренном положении и измеренном импульсе больше или равно нижнему пределу, который (с точностью до небольшого числового коэффициента) ) равна постоянной Планка . Гейзенберг не позаботился сформулировать принцип неопределенности как точный предел и предпочел вместо этого использовать его как эвристическое количественное утверждение с поправкой до малых числовых коэффициентов, что делает неизбежной радикально новую некоммутативность квантовой механики.

Критические реакции

Основная статья: Дебаты Бора и Эйнштейна

Копенгагенская интерпретация квантовой механики и принцип неопределенности Гейзенберга изначально рассматривались недоброжелателями как две мишени. Согласно копенгагенской интерпретации квантовой механики, не существует фундаментальной реальности, которую описывает квантовое состояние , а есть лишь предписание для расчета экспериментальных результатов. Невозможно сказать, каково фундаментальное состояние системы, можно только сказать, каким может быть результат наблюдений.

Альберт Эйнштейн считал, что случайность — это отражение нашего незнания некоторых фундаментальных свойств реальности, а Нильс Бор считал, что распределения вероятностей фундаментальны и неприводимы и зависят от того, какие измерения мы решаем выполнить. Эйнштейн и Бор обсуждали принцип неопределенности на протяжении многих лет.

Идеальный сторонний наблюдатель

Вольфганг Паули назвал фундаментальное возражение Эйнштейна против принципа неопределенности «идеалом стороннего наблюдателя» (фраза в переводе с немецкого):

«Подобно тому, как Луна имеет определенное положение, — сказал мне прошлой зимой Эйнштейн, — независимо от того, смотрим мы на Луну или нет, то же самое должно справедливо и для атомных объектов, поскольку не существует резкого различия между ними и макроскопическими объектами. Наблюдение не может создать такой элемент реальности, как позиция, в полном описании физической реальности должно содержаться что-то, что соответствует возможности наблюдения позиции, еще до того, как наблюдение действительно было произведено». Надеюсь, я правильно процитировал Эйнштейна; всегда трудно процитировать по памяти кого-то, с кем не согласен. Именно такой постулат я называю идеалом стороннего наблюдателя.

- Письмо Паули Нильсу Бору, 15 февраля 1955 г.

щель Эйнштейна

Эйнштейна, Первый из мысленных экспериментов бросающих вызов принципу неопределенности, заключался в следующем:

Рассмотрим частицу, проходящую через щель шириной d . Щель вносит неопределенность в импульс примерно ⁠ h / d ⁠ потому что частица проходит сквозь стену. Но давайте определим импульс частицы, измерив отдачу стенки. При этом мы находим импульс частицы с произвольной точностью по закону сохранения импульса.

Ответ Бора заключался в том, что стена также является квантовомеханической и что для измерения отдачи с точностью Δ p необходимо знать импульс стены с этой точностью до того, как частица пройдет через нее. Это вносит неопределенность в положение стенки и, следовательно, положение щели, равную ⁠ h / Δ p ⁠ , и если импульс стены известен достаточно точно, чтобы измерить отдачу, положение щели достаточно неопределенно, чтобы исключить измерение положения.

Похожий анализ частиц, дифрагирующих через несколько щелей, дан Ричардом Фейнманом .

ящик Эйнштейна

Бор присутствовал, когда Эйнштейн предложил мысленный эксперимент, который стал известен как ящик Эйнштейна . Эйнштейн утверждал, что «уравнение неопределенности Гейзенберга подразумевало, что неопределенность во времени связана с неопределенностью в энергии, а произведение этих двух величин связано с постоянной Планка». Рассмотрим, сказал он, идеальную коробку, облицованную зеркалами, так что она может бесконечно содержать свет. Коробку можно было взвесить, прежде чем часовой механизм в выбранный момент открыл идеальную заслонку, позволяющую вылететь одному-единственному фотону. «Теперь мы знаем, — объяснил Эйнштейн, — точное время, когда фотон покинул ящик». «Теперь взвесьте ящик еще раз. Изменение массы отражает энергию излучаемого света. Таким образом, — говорил Эйнштейн, — можно измерить излучаемую энергию и время, когда она была высвобождена, с любой желаемой точностью, что противоречит принципу неопределенности». ."

Бор провел бессонную ночь, обдумывая этот аргумент, и в конце концов понял, что он ошибочен. Он указывал, что если бы ящик взвешивался, скажем, с помощью пружины и указателя на весах, «поскольку ящик должен двигаться вертикально с изменением его веса, возникнет неопределенность в его вертикальной скорости и, следовательно, неопределенность в его высота над столом... Кроме того, неопределенность относительно высоты над поверхностью Земли приведет к неопределенности хода часов». из-за собственной теории Эйнштейна о влиянии гравитации на время .«С помощью этой цепочки неопределенностей Бор показал, что эксперимент Эйнштейна со световым ящиком не может одновременно точно измерить как энергию фотона, так и время его выхода».

Парадокс ЭПР для запутанных частиц

Основная статья: парадокс ЭПР

В 1935 году Эйнштейн, Борис Подольский и Натан Розен опубликовали анализ пространственно разделенных запутанных частиц (парадокс ЭПР). Согласно ЭПР, можно измерить положение одной из запутанных частиц и импульс второй частицы и на основе этих измерений вывести положение и импульс обеих частиц с любой точностью, нарушая принцип неопределенности. Чтобы избежать такой возможности, измерение одной частицы должно мгновенно изменить распределение вероятностей другой частицы, что может привести к нарушению принципа локальности .

В 1964 году Джон Стюарт Белл показал, что это предположение можно опровергнуть, поскольку оно подразумевало бы определенное неравенство между вероятностями различных экспериментов. Экспериментальные результаты подтверждают предсказания квантовой механики, исключая основное предположение ЭПР о локальных скрытых переменных .

Критика Поппера

Основная статья: Эксперимент Поппера

Философ науки Карл Поппер подошел к проблеме неопределенности как логик и метафизический реалист . Он не согласился с применением соотношений неопределенности к отдельным частицам, а не к ансамблям одинаково приготовленных частиц, назвав их «статистическими соотношениями рассеяния». В этой статистической интерпретации конкретное измерение может быть произведено с произвольной точностью, не опровергая квантовую теорию.

В 1934 году Поппер опубликовал «Критику науках» отношений неопределенности в естественных . и в том же году Logik der Forschung (переведенная и обновленная автором как «Логика научного открытия» в 1959 г.). ), изложив свои аргументы в пользу статистической интерпретации. В 1982 году он развил свою теорию квантовой теории и раскола в физике , написав:

Формулы [Гейзенберга], вне всякого сомнения, являются выводными статистическими формулами квантовой теории. Но они обычно неправильно интерпретировались теми квантовыми теоретиками, которые говорили, что эти формулы можно интерпретировать как определяющие некий верхний предел точности наших измерений . [оригинальный акцент]

Поппер предложил эксперимент по фальсификации соотношений неопределенности, хотя позже он отказался от своей первоначальной версии после обсуждений с Карлом Фридрихом фон Вайцзеккером , Гейзенбергом и Эйнштейном; Поппер отправил свою статью Эйнштейну, и она, возможно, повлияла на формулировку парадокса ЭПР.

Свободная воля

Некоторые ученые, включая Артура Комптона и Мартин Гейзенберг предположили, что принцип неопределенности или, по крайней мере, общая вероятностная природа квантовой механики может служить доказательством двухэтапной модели свободы воли. Однако одна критика заключается в том, что, помимо основной роли квантовой механики как основы химии, нетривиальные биологические механизмы, требующие квантовой механики , маловероятны из-за быстрого времени декогеренции квантовых систем при комнатной температуре. Сторонники этой теории обычно говорят, что эта декогеренция преодолевается как экранирующими, так и свободными от декогеренции подпространствами, обнаруженными в биологических клетках.

Термодинамика

Есть основания полагать, что нарушение принципа неопределенности также в значительной степени влечет за собой нарушение второго закона термодинамики . См. Парадокс Гиббса .

Отказ от принципа

Принципы неопределенности связывают квантовые частицы – например, электроны – с классическими понятиями – положением и импульсом. Это предполагает, что квантовые частицы имеют положение и импульс. Эдвин К. Кембл отметил в 1937 г. такие свойства не могут быть проверены экспериментально и предположение о их существовании порождает множество противоречий; аналогичным образом Рудольф Хааг отмечает, что положение в квантовой механике является атрибутом взаимодействия, скажем, между электроном и детектором, а не внутренним свойством. С этой точки зрения принцип неопределенности — это не фундаментальное квантовое свойство, а концепция, «перенесенная из языка наших предков», как говорит Кембл.

Приложения

Поскольку принцип неопределенности является фундаментальным результатом квантовой механики, в типичных экспериментах по квантовой механике обычно наблюдаются его аспекты. Все формы спектроскопии , включая физику элементарных частиц, используют это соотношение, чтобы связать измеренную ширину энергетической линии со временем жизни квантовых состояний. Однако некоторые эксперименты могут намеренно проверять определенную форму принципа неопределенности в рамках своей основной исследовательской программы. К ним относятся, например, испытания соотношений неопределенности число-фаза в сверхпроводниках. или квантовая оптика системы. Приложения, работа которых зависит от принципа неопределенности, включают в себя технологии с чрезвычайно низким уровнем шума, например, необходимые в интерферометрах гравитационных волн .

См. также

• Принцип соответствия
• Введение в квантовую механику
• Принцип неопределенности Купфмюллера.
• Квантовая неопределенность
• Квантовое туннелирование
• Физика и не только (воспоминания Гейзенберга)
• Более сильные отношения неопределенности

Внешние ссылки

• «Принцип неопределенности» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Статья в Стэнфордской энциклопедии философии