Геометрическая алгебра

Для общей алгебраической структуры см. «Алгебра Клиффорда» . Чтобы узнать о других значениях, см. Геометрическую алгебру (значения) .

Не путать с алгебраической геометрией .

В математике геометрическая алгебра (также известная как алгебра Клиффорда ) является расширением элементарной алгебры для работы с геометрическими объектами, такими как векторы . Геометрическая алгебра построена из двух фундаментальных операций: сложения и геометрического произведения. Умножение векторов приводит к созданию объектов более высокой размерности, называемых мультивекторами . По сравнению с другими формализмами манипулирования геометрическими объектами геометрическая алгебра примечательна тем, что поддерживает деление векторов (хотя, как правило, не для всех элементов) и добавление объектов разных размерностей.

Впервые о геометрическом произведении кратко упомянул Герман Грассман . который был главным образом заинтересован в развитии близкородственной внешней алгебры . В 1878 году Уильям Кингдон Клиффорд значительно расширил работу Грассмана, сформировав то, что сейчас обычно называют алгебрами Клиффорда в его честь (хотя сам Клиффорд предпочитал называть их «геометрическими алгебрами»). Клиффорд определил алгебру Клиффорда и ее произведение как объединение алгебры Грассмана Гамильтона и алгебры кватернионов . Добавление двойственного внешнего произведения Грассмана («встречи») позволяет использовать алгебру Грассмана – Кэли , а конформная версия последней вместе с конформной алгеброй Клиффорда дает конформную геометрическую алгебру (CGA), обеспечивающую основу для классической геометрии . На практике эти и некоторые производные операции позволяют сопоставить элементы, подпространства и операции алгебры с геометрическими интерпретациями. В течение нескольких десятилетий геометрические алгебры несколько игнорировались, их сильно затмило векторное исчисление , недавно разработанное для описания электромагнетизма. Термин «геометрическая алгебра» был повторно популяризирован в 1960-х годах Хестеном , который отстаивал его важность для релятивистской физики.

Скаляры и векторы имеют свою обычную интерпретацию и составляют отдельные подпространства геометрической алгебры. Бивекторы обеспечивают более естественное представление псевдовекторных величин векторного исчисления, которые получаются как векторное произведение , таких как ориентированная площадь, ориентированный угол поворота, крутящий момент, угловой момент и магнитное поле . Тривектор . может представлять собой ориентированный объем и так далее Элемент, называемый лезвием, может использоваться для представления подпространства ⁠. $V$⁠ и ортогональные проекции на это подпространство. Вращения и отражения представлены как элементы. В отличие от векторной алгебры, геометрическая алгебра естественным образом допускает любое количество измерений и любую квадратичную форму, например, в теории относительности .

Примеры геометрических алгебр, применяемых в физике, включают алгебру пространства-времени (и менее распространенную алгебру физического пространства ) и конформную геометрическую алгебру . Геометрическое исчисление , расширение ГА, включающее дифференцирование и интегрирование , может использоваться для формулирования других теорий, таких как комплексный анализ и дифференциальная геометрия , например, используя алгебру Клиффорда вместо дифференциальных форм . Геометрическую алгебру защищал, в первую очередь Дэвид Хестенс. и Крис Доран , как предпочтительная математическая основа физики . Сторонники утверждают, что он обеспечивает компактные и интуитивно понятные описания во многих областях, включая классическую и квантовую механику , теорию электромагнетизма и теорию относительности . GA также нашел применение в качестве вычислительного инструмента в компьютерной графике. и робототехника .

Определение и обозначения

Существует несколько различных способов определения геометрической алгебры. Первоначальный подход Гестенеса был аксиоматическим: «полный геометрической значимости» и эквивалентный универсальному Алгебра Клиффорда. Учитывая конечномерное векторное пространство ⁠ $V$⁠ над полем ⁠ $F$⁠ с симметричной билинейной формой ( скалярное произведение , например, евклидова или лоренцева метрика ) ⁠ $g:V\times V\to F$⁠ , геометрическая алгебра квадратичного пространства ⁠ $(V,g)$⁠ — алгебра Клиффорда ⁠ $\operatorname {Cl} (V,g)$⁠ , элемент которого называется мультивектором. Алгебра Клиффорда обычно определяется как факторалгебра тензорной алгебры , хотя это определение является абстрактным, поэтому следующее определение представлено без требования абстрактной алгебры .

Определение

Ассоциативная алгебра с единицей ⁠ $\operatorname {Cl} (V,g)$⁠ с невырожденной симметричной билинейной формой ⁠ $g:V\times V\to F$⁠ — алгебра Клиффорда квадратичного пространства ⁠ $(V,g)$⁠ если

• он содержит ⁠ $F$⁠ и ⁠ $V$⁠ как отдельные подпространства
• ⁠ $a^{2}=g(a,a)1$⁠ для ⁠ $a\in V$⁠
• ⁠ $V$⁠ генерирует ⁠ $\operatorname {Cl} (V,g)$⁠ как алгебра
• ⁠ $\operatorname {Cl} (V,g)$⁠ не порождается никаким собственным подпространством ⁠ $V$⁠ .

Чтобы охватить вырожденные симметричные билинейные формы, последнее условие необходимо изменить. Можно показать, что эти условия однозначно характеризуют геометрическое произведение.

В оставшейся части статьи рассматривается только реальный случай: ⁠ $F=\mathbb {R}$⁠ , будет рассмотрено. Обозначение ⁠ ${\mathcal {G}}(p,q)$⁠ (соответственно ⁠ ${\mathcal {G}}(p,q,r)$⁠ ) ​​будет использоваться для обозначения геометрической алгебры, для которой билинейная форма ⁠ $g$⁠ есть подпись ⁠ $(p,q)$⁠ (соответственно ⁠ $(p,q,r)$⁠ ).

Произведение в алгебре называется геометрическим произведением , а произведение в содержащейся внешней алгебре называется внешним произведением (часто называемым клиновым произведением и реже внешним произведением) . ). Обычно их обозначают сопоставлением (т. е. подавлением любого явного символа умножения) и символом ⁠. $\wedge$⁠ .

Приведенное выше определение геометрической алгебры все еще несколько абстрактно, поэтому мы суммируем здесь свойства геометрического произведения. Для мультивекторов ⁠ $A,B,C\in {\mathcal {G}}(p,q)$⁠ :

• ⁠ $AB\in {\mathcal {G}}(p,q)$⁠ ( закрытие )
• ⁠ $1A=A1=A$⁠ , где ⁠ $1$⁠ — элемент идентичности (существование элемента идентичности )
• ⁠ $A(BC)=(AB)C$⁠ ( ассоциативность )
• ⁠ $A(B+C)=AB+AC$⁠ и ⁠ $(B+C)A=BA+CA$⁠ ( дистрибутивность )
• ⁠ $a^{2}=g(a,a)1$⁠ для ⁠ $a\in V$⁠ .

Внешний продукт имеет те же свойства, за исключением того, что последнее свойство, указанное выше, заменено на ⁠. $a\wedge a=0$⁠ для ⁠ $a\in V$⁠ .

Обратите внимание, что в последнем свойстве выше действительное число ⁠ $g(a,a)$⁠ не обязательно должен быть неотрицательным, если ⁠ $g$⁠ не является положительно-определенным. Важным свойством геометрического произведения является существование элементов, имеющих мультипликативный обратный. Для вектора ⁠ $a$⁠ , если $a^{2}\neq 0$ затем $a^{-1}$ существует и равен ⁠ $g(a,a)^{-1}a$⁠ . Ненулевой элемент алгебры не обязательно имеет мультипликативный обратный. Например, если $u$ является вектором в $V$ такой, что ⁠ $u^{2}=1$⁠ , элемент $\textstyle {\frac {1}{2}}(1+u)$ является одновременно нетривиальным идемпотентным элементом и ненулевым делителем нуля и, следовательно, не имеет обратного.

Обычно определяют $\mathbb {R}$ и $V$ со своими изображениями под естественными вложениями $\mathbb {R} \to {\mathcal {G}}(p,q)$ и ⁠ $V\to {\mathcal {G}}(p,q)$⁠ . В данной статье предполагается такая идентификация. Везде термины скаляр и вектор относятся к элементам $\mathbb {R}$ и $V$ соответственно (и их изображений под этим вложением).

Геометрическое произведение

Смотрите также: Симметричная билинейная форма и Внешняя алгебра.

Учитывая два вектора $a$ и ⁠ $b$⁠ , если геометрическое произведение $ab$ является антикоммутативный; они перпендикулярны (вверху), потому что ⁠ $a\cdot b=0$⁠ , если он коммутативен; они параллельны (внизу), потому что ⁠ $a\wedge b=0$⁠ .

Ориентация определяется упорядоченным набором векторов.

Обратная ориентация соответствует отрицанию внешнего продукта.

Геометрическая интерпретация сорта- $n$ элементы реальной внешней алгебры для $n=0$ (подписанная точка), $1$ (направленный отрезок или вектор), $2$ (ориентированный плоский элемент), $3$ (ориентированный объем). Внешний вид продукта $n$ векторы можно визуализировать как любые ⁠ $n$⁠ -мерная форма (например , ⁠ $n$⁠ - параллелоэдр , ⁠ $n$⁠ — эллипсоид ); с величиной ( гиперобъемом ) и ориентацией, определяемой этим на его ⁠ $(n-1)$⁠ -мерная граница и на какой стороне находится внутренность.

Для векторов ⁠ $a$⁠ и ⁠ $b$⁠ , мы можем записать геометрическое произведение любых двух векторов ⁠ $a$⁠ и ⁠ $b$⁠ как сумма симметричного и антисимметричного произведений:

$ab={\frac {1}{2}}(ab+ba)+{\frac {1}{2}}(ab-ba).$

Таким образом, мы можем определить внутренний продукт векторов как

$a\cdot b:=g(a,b),$

так что симметричное произведение можно записать как

${\frac {1}{2}}(ab+ba)={\frac {1}{2}}\left((a+b)^{2}-a^{2}-b^{2}\right)=a\cdot b.$

И наоборот, ⁠ $g$⁠ полностью определяется алгеброй. Антисимметричная часть — это внешнее произведение двух векторов, произведение содержащейся внешней алгебры :

$a\wedge b:={\frac {1}{2}}(ab-ba)=-(b\wedge a).$

Затем простым сложением:

$ab=a\cdot b+a\wedge b$ необобщенная или векторная форма геометрического произведения.

Внутренние и внешние продукты связаны со знакомыми понятиями стандартной векторной алгебры. Геометрически, $a$ и $b$ параллельны , если их геометрическое произведение равно их внутреннему произведению, тогда как $a$ и $b$ перпендикулярны , если их геометрическое произведение равно внешнему произведению. В геометрической алгебре, для которой квадрат любого ненулевого вектора положителен, скалярное произведение двух векторов можно отождествить со скалярным произведением стандартной векторной алгебры. Внешнее произведение двух векторов можно идентифицировать по области со знаком, заключенной в параллелограмм, стороны которого являются векторами. Перекрестное произведение двух векторов в $3$ измерения с положительно определенной квадратичной формой тесно связаны с их внешним произведением.

Большинство представляющих интерес примеров геометрических алгебр имеют невырожденную квадратичную форму. Если квадратичная форма полностью вырождена , скалярное произведение любых двух векторов всегда равно нулю, и тогда геометрическая алгебра является просто внешней алгеброй. Если не указано иное, в этой статье будут рассматриваться только невырожденные геометрические алгебры.

Внешний продукт естественным образом расширяется как ассоциативный билинейный бинарный оператор между любыми двумя элементами алгебры, удовлетворяющий тождествам

${\begin{aligned}1\wedge a_{i}&=a_{i}\wedge 1=a_{i}\\a_{1}\wedge a_{2}\wedge \cdots \wedge a_{r}&={\frac {1}{r!}}\sum _{\sigma \in {\mathfrak {S}}_{r}}\operatorname {sgn} (\sigma )a_{\sigma (1)}a_{\sigma (2)}\cdots a_{\sigma (r)},\end{aligned}}$

где сумма ведется по всем перестановкам индексов, причем $\operatorname {sgn} (\sigma )$ знак перестановки и $a_{i}$ являются векторами (не общими элементами алгебры). Поскольку каждый элемент алгебры может быть выражен как сумма произведений этого вида, это определяет внешний продукт для каждой пары элементов алгебры. Из определения следует, что внешнее произведение образует знакопеременную алгебру .

Эквивалентное структурное уравнение для алгебры Клиффорда:

$a_{1}a_{2}a_{3}\dots a_{n}=\sum _{i=0}^{[{\frac {n}{2}}]}\sum _{\mu \in {}{\mathcal {C}}}(-1)^{k}\operatorname {Pf} (a_{\mu _{1}}\cdot a_{\mu _{2}},\dots ,a_{\mu _{2i-1}}\cdot a_{\mu _{2i}})a_{\mu _{2i+1}}\land \dots \land a_{\mu _{n}}$

где $\operatorname {Pf} (A)$ является пфаффианом ⁠ ​ $A$⁠ и ${\textstyle {\mathcal {C}}={\binom {n}{2i}}}$ предоставляет комбинации , ⁠ $\mu$⁠ , из ⁠ $n$⁠ индексы разделены на ⁠ $2i$⁠ и ⁠ $n-2i$⁠ части и ⁠ $k$⁠ — четность комбинации ​ .

Пфаффиан обеспечивает метрику внешней алгебры, и, как отметил Клод Шевалле, алгебра Клиффорда сводится к внешней алгебре с нулевой квадратичной формой. Роль, которую играет пфаффиан, можно понять с геометрической точки зрения, разработав алгебру Клиффорда на основе симплексов . Этот вывод обеспечивает лучшую связь между треугольником Паскаля и симплексами , поскольку он дает интерпретацию первого столбца единиц.

Лезвия, сорта и основа

Мультивектор, являющийся внешним произведением $r$ линейно независимых векторов называется лезвием и имеет степень ⁠ $r$⁠ . Мультивектор, представляющий собой сумму лопастей класса $r$ называется (однородным) мультивектором степени ⁠ $r$⁠ . Из аксиом с замыканием каждый мультивектор геометрической алгебры представляет собой сумму лопастей.

Рассмотрим набор $r$ линейно независимые векторы $\{a_{1},\ldots ,a_{r}\}$ охватывающий ⁠ $r$⁠ -мерное подпространство векторного пространства. С их помощью мы можем определить действительную симметричную матрицу (так же, как матрица Грама )

$[\mathbf {A} ]_{ij}=a_{i}\cdot a_{j}$

По теореме спектральной $\mathbf {A}$ можно диагонализировать до диагональной матрицы $\mathbf {D}$ ортогональной матрицей $\mathbf {O}$ с помощью

$\sum _{k,l}[\mathbf {O} ]_{ik}[\mathbf {A} ]_{kl}[\mathbf {O} ^{\mathrm {T} }]_{lj}=\sum _{k,l}[\mathbf {O} ]_{ik}[\mathbf {O} ]_{jl}[\mathbf {A} ]_{kl}=[\mathbf {D} ]_{ij}$

Определите новый набор векторов ⁠ $\{e_{1},\ldots ,e_{r}\}$⁠ , известные как ортогональные базисные векторы, которые преобразуются ортогональной матрицей:

$e_{i}=\sum _{j}[\mathbf {O} ]_{ij}a_{j}$

Поскольку ортогональные преобразования сохраняют скалярные произведения, отсюда следует, что $e_{i}\cdot e_{j}=[\mathbf {D} ]_{ij}$ и таким образом $\{e_{1},\ldots ,e_{r}\}$ перпендикулярны. Другими словами, геометрическое произведение двух различных векторов $e_{i}\neq e_{j}$ полностью определяется их внешним продуктом или, в более общем смысле,

${\begin{array}{rl}e_{1}e_{2}\cdots e_{r}&=e_{1}\wedge e_{2}\wedge \cdots \wedge e_{r}\\&=\left(\sum _{j}[\mathbf {O} ]_{1j}a_{j}\right)\wedge \left(\sum _{j}[\mathbf {O} ]_{2j}a_{j}\right)\wedge \cdots \wedge \left(\sum _{j}[\mathbf {O} ]_{rj}a_{j}\right)\\&=(\det \mathbf {O} )a_{1}\wedge a_{2}\wedge \cdots \wedge a_{r}\end{array}}$

Поэтому каждое лезвие сорта $r$ можно записать как внешний продукт $r$ векторы. В более общем смысле, если разрешена вырожденная геометрическая алгебра, то ортогональная матрица заменяется блочной матрицей , ортогональной в невырожденном блоке, а диагональная матрица имеет нулевые элементы вдоль вырожденных измерений. Если новые векторы невырожденного подпространства нормализованы согласно

${\hat {e}}_{i}={\frac {1}{\sqrt {|e_{i}\cdot e_{i}|}}}e_{i},$

тогда эти нормализованные векторы должны быть квадратными $+1$ или ⁠ $-1$⁠ . По закону инерции Сильвестра общее количество ⁠ $+1$⁠ и общее количество ⁠ $-1$⁠ s вдоль диагональной матрицы инвариантен. В более широком смысле общее число $p$ этих векторов, которые квадратичны $+1$ и общее количество $q$ этот квадрат к $-1$ является инвариантным. (Общее количество базисных векторов, обращающихся в ноль, также инвариантно и может быть отличным от нуля, если разрешен вырожденный случай.) Обозначим эту алгебру ⁠ ${\mathcal {G}}(p,q)$⁠ . Например, ${\mathcal {G}}(3,0)$ моделирует трехмерное евклидово пространство , ${\mathcal {G}}(1,3)$ релятивистское пространство-время и ${\mathcal {G}}(4,1)$ конформная геометрическая алгебра трехмерного пространства.

Набор всех возможных продуктов $n$ ортогональные базисные векторы с индексами в порядке возрастания, в том числе $1$ как пустое произведение образует основу всей геометрической алгебры (аналог теоремы PBW ). Например, следующее является основой геометрической алгебры ⁠ ${\mathcal {G}}(3,0)$⁠ :

$\{1,e_{1},e_{2},e_{3},e_{1}e_{2},e_{2}e_{3},e_{3}e_{1},e_{1}e_{2}e_{3}\}$

Базис, сформированный таким образом, называется стандартным базисом геометрической алгебры, а любой другой ортогональный базис геометрической алгебры. $V$ создаст еще одну стандартную основу. Каждая стандартная основа состоит из $2^{n}$ элементы. Каждый мультивектор геометрической алгебры можно выразить как линейную комбинацию стандартных базисных элементов. Если стандартные базисные элементы $\{B_{i}\mid i\in S\}$ с $S$ будучи набором индексов, то геометрическое произведение любых двух мультивекторов равно

$\left(\sum _{i}\alpha _{i}B_{i}\right)\left(\sum _{j}\beta _{j}B_{j}\right)=\sum _{i,j}\alpha _{i}\beta _{j}B_{i}B_{j}.$

Терминология» $k$-вектор» часто встречается для описания мультивекторов, содержащих элементы только одного сорта. В пространстве более высоких измерений некоторые такие мультивекторы не являются лопастями (не могут быть учтены во внешнем произведении $k$ векторы). В качестве примера, $e_{1}\wedge e_{2}+e_{3}\wedge e_{4}$ в ${\mathcal {G}}(4,0)$ не может быть факторизован; однако обычно такие элементы алгебры не поддаются геометрической интерпретации как объекты, хотя они могут представлять геометрические величины, такие как вращения. Только ⁠ $0$⁠ -, ⁠ $1$⁠ -, ⁠ $(n-1)$⁠ - и ⁠ $n$⁠ -векторы всегда являются лезвиями в ⁠ $n$⁠ -пространство.

Я поворачиваюсь

А ⁠ $k$⁠ -версор — это мультивектор, который можно выразить как геометрическое произведение $k$ обратимые векторы. Единичные кватернионы (первоначально названные Гамильтоном версорами) могут быть отождествлены с роторами в трехмерном пространстве почти так же, как реальные двумерные роторы включают в себя комплексные числа; за подробностями обращайтесь в Дорст.

Некоторые авторы используют термин «версорный продукт» для обозначения часто встречающегося случая, когда операнд «зажат» между операторами. Описания вращений и отражений, включая их внешние морфизмы, являются примерами такого сэндвичинга. Эти внешние морфизмы имеют особенно простую алгебраическую форму. В частности, отображение векторов вида

$V\to V:a\mapsto RaR^{-1}$ продолжается до внешнего морфизма ${\mathcal {G}}(V)\to {\mathcal {G}}(V):A\mapsto RAR^{-1}.$

Поскольку и операторы, и операнды являются версорами, существует потенциал для альтернативных примеров, таких как вращение ротора или отражение спинора, всегда при условии, что таким операциям можно придать некоторый геометрический или физический смысл.

По теореме Картана-Дьедонне мы получаем, что каждая изометрия может быть задана как отражения в гиперплоскостях, а поскольку составные отражения обеспечивают вращения, то ортогональные преобразования являются версорами.

В групповом смысле для реального, невырожденного ⁠ ${\mathcal {G}}(p,q)$⁠ , определив группу ${\mathcal {G}}^{\times }$ как группа всех обратимых элементов ⁠ ${\mathcal {G}}$⁠ Лундхольм доказывает, что «группа версора» $\{v_{1}v_{2}\cdots v_{k}\in {\mathcal {G}}\mid v_{i}\in V^{\times }\}$ (множество обратимых версоров) равно группе Липшица $\Gamma$ ( также известная как группа Клиффорда, хотя Лундхольм не одобряет такое использование).

Подгруппы группы Липшица

Обозначим инволюцию степени как ⁠ ${\hat {X}}$⁠ и реверсия как ⁠ ${\tilde {X}}$⁠ .

Хотя группа Липшица (определяемая как ⁠ $\{X\in {\mathcal {G}}^{\times }\mid {\hat {X}}VX^{-1}\subseteq V\}$⁠ ) ​​и группа версоров (определяемая как ⁠ $\textstyle \{\prod _{i=0}^{k}v_{i}\mid v_{i}\in V^{\times },k\in \mathbb {N} \}$⁠ ) имеют разные определения, это одна и та же группа. Лундхольм определяет ⁠ $\operatorname {Pin}$⁠ , ⁠ $\operatorname {Spin}$⁠ и ⁠ $\operatorname {Spin} ^{+}$⁠ подгруппы группы Липшица.

Подгруппа	Определение	срок общего пользования
$\Gamma$	$\{X\in {\mathcal {G}}^{\times }\mid {\hat {X}}VX^{-1}\subseteq V\}$	поставлять
$\operatorname {Pin}$	$\{X\in \Gamma \mid X{\tilde {X}}=\pm 1\}$	поставка единицы
$\operatorname {Spin}$	${\operatorname {Pin} }\cap {\mathcal {G}}^{[0]}$	даже единицы поставок
$\operatorname {Spin} ^{+}$	$\{X\in \operatorname {Spin} \mid X{\tilde {X}}=1\}$	роторы

Множественный анализ спиноров использует GA в качестве представления.

Прогноз оценки

А ⁠ $\mathbb {Z}$⁠ - структура градуированного векторного пространства может быть установлена ​​в геометрической алгебре с помощью внешнего произведения, которое естественным образом индуцируется геометрическим произведением.

Поскольку геометрическое произведение и внешнее произведение равны на ортогональных векторах, эту градуировку удобно построить с использованием ортогонального базиса ⁠ $\{e_{1},\ldots ,e_{n}\}$⁠ .

Элементы геометрической алгебры, скалярно кратные $1$ имеют класс $0$ и называются скалярами . Элементы, находящиеся в диапазоне $\{e_{1},\ldots ,e_{n}\}$ имеют сорт ⁠ $1$⁠ и — обычные векторы. Элементы в диапазоне $\{e_{i}e_{j}\mid 1\leq i<j\leq n\}$ имеют класс $2$ и являются бивекторами. Эта терминология сохраняется до последнего класса ⁠. $n$⁠- векторы. Альтернативно, ⁠ $n$⁠ -векторы называются псевдоскалярами , ⁠ $(n-1)$⁠ -векторы называются псевдовекторами и т. д. Многие элементы алгебры не классифицируются по этой схеме, поскольку они представляют собой суммы элементов разной степени. Такие элементы называются смешанными . Градация мультивекторов не зависит от изначально выбранного базиса.

Это градуировка векторного пространства, но не алгебры. Потому что произведение ⁠ $r$⁠ -лезвие и ⁠ $s$⁠ -лезвие содержится в промежутке $0$ через ⁠ $r+s$⁠ -лопасти, геометрическая алгебра является фильтрованной алгеброй .

Многовекторный $A$ можно разложить с помощью оператора проекции оценок ⁠ $\langle A\rangle _{r}$⁠ , который выводит оценку- ⁠ $r$⁠ часть ⁠ $A$⁠ . Как результат:

$A=\sum _{r=0}^{n}\langle A\rangle _{r}$

Например, геометрическое произведение двух векторов $ab=a\cdot b+a\wedge b=\langle ab\rangle _{0}+\langle ab\rangle _{2}$ с $\langle ab\rangle _{0}=a\cdot b$ и $\langle ab\rangle _{2}=a\wedge b$ и ⁠ $\langle ab\rangle _{i}=0$⁠ , для $i$ кроме $0$ и ⁠ $2$⁠ .

Многовекторный $A$ также могут быть разложены на четные и нечетные компоненты, которые соответственно могут быть выражены как сумма четных и нечетных компонентов оценки, указанных выше:

$A^{[0]}=\langle A\rangle _{0}+\langle A\rangle _{2}+\langle A\rangle _{4}+\cdots$

$A^{[1]}=\langle A\rangle _{1}+\langle A\rangle _{3}+\langle A\rangle _{5}+\cdots$

Это результат забывания структуры из ⁠ $\mathrm {Z}$⁠ - градуированное векторное пространство в ⁠ $\mathrm {Z} _{2}$⁠ — градуированное векторное пространство . Геометрическое произведение учитывает эту более грубую градацию. Таким образом, помимо того, что это ⁠ $\mathrm {Z} _{2}$⁠ — градуированное векторное пространство , геометрическая алгебра — это ⁠ $\mathrm {Z} _{2}$⁠ - градуированная алгебра , же супералгебра она .

Ограничиваясь четной частью, произведение двух четных элементов также является четным. Это означает, что четные мультивекторы определяют четную подалгебру . Четная подалгебра ⁠ $n$⁠ -мерная геометрическая алгебра алгебра-изоморфна (без сохранения ни фильтрации, ни градуировки) полной геометрической алгебре $(n-1)$ размеры. Примеры включают в себя ${\mathcal {G}}^{[0]}(2,0)\cong {\mathcal {G}}(0,1)$ и ⁠ ${\mathcal {G}}^{[0]}(1,3)\cong {\mathcal {G}}(3,0)$⁠ .

Представление подпространств

Смотрите также: Грассманиан

Геометрическая алгебра представляет подпространства $V$ как лезвия, и поэтому они сосуществуют в одной алгебре с векторами из ⁠ $V$⁠ . А ⁠ $k$⁠ -мерное подпространство $W$ из $V$ представляется путем взятия ортогонального базиса $\{b_{1},b_{2},\ldots ,b_{k}\}$ и используя геометрическое произведение для формирования лезвия ⁠ $D=b_{1}b_{2}\cdots b_{k}$⁠ . Есть несколько лезвий, обозначающих ⁠ $W$⁠ ; все те, кто представляет $W$ являются скалярными кратными ⁠ $D$⁠ . Эти лезвия можно разделить на два набора: положительные кратные $D$ и отрицательные кратные ⁠ $D$⁠ . Положительные кратные $D$ Говорят, что они имеют ту же ориентацию , что и ⁠ $D$⁠ , а отрицательное кратно противоположной ориентации .

Лезвия важны, поскольку геометрические операции, такие как проекции, вращения и отражения, зависят от факторизуемости через внешний продукт, который (ограниченный класс) ⁠ $n$⁠ -лезвия обеспечивают, но этот (обобщенный класс) класс- ⁠ $n$⁠ мультивекторы этого не делают, когда ⁠ $n\geq 4$⁠ .

Единичные псевдоскаляры

Единичные псевдоскаляры — это лезвия, которые играют важную роль в GA. Единичный псевдоскаляр для невырожденного подпространства $W$ из $V$ - это лезвие, являющееся произведением членов ортонормированного базиса для ⁠ $W$⁠ . Можно показать, что если $I$ и $I'$ оба являются единичными псевдоскалярами для ⁠ $W$⁠ , тогда $I=\pm I'$ и ⁠ $I^{2}=\pm 1$⁠ . Если не выбрать ортонормированный базис для ⁠ $W$⁠ , то вложение Плюкера дает вектор во внешней алгебре, но только с точностью до масштабирования. Используя изоморфизм векторного пространства между геометрической алгеброй и внешней алгеброй, это дает класс эквивалентности $\alpha I$ для всех ⁠ $\alpha \neq 0$⁠ . Ортонормальность избавляет от этой двусмысленности, за исключением признаков, указанных выше.

Предположим, что геометрическая алгебра ${\mathcal {G}}(n,0)$ со знакомым положительно определенным внутренним продуктом на $\mathbb {R} ^{n}$ формируется. Учитывая плоскость (двумерное подпространство) ⁠ $\mathbb {R} ^{n}$⁠ можно найти ортонормированный базис $\{b_{1},b_{2}\}$ охватывающую плоскость, и таким образом найти единичный псевдоскаляр $I=b_{1}b_{2}$ представляющий этот самолет. Геометрическое произведение любых двух векторов в диапазоне $b_{1}$ и $b_{2}$ лежит в ⁠ $\{\alpha _{0}+\alpha _{1}I\mid \alpha _{i}\in \mathbb {R} \}$⁠ , то есть это сумма ⁠ $0$⁠ -вектор и ⁠ $2$⁠- вектор.

По свойствам геометрического произведения ⁠ $I^{2}=b_{1}b_{2}b_{1}b_{2}=-b_{1}b_{2}b_{2}b_{1}=-1$⁠ . Сходство с воображаемой единицей не случайно: подпространство $\{\alpha _{0}+\alpha _{1}I\mid \alpha _{i}\in \mathbb {R} \}$ это ⁠ $\mathbb {R}$⁠- алгебра, изоморфная комплексным числам . Таким образом, копия комплексных чисел встраивается в геометрическую алгебру для каждого двумерного подпространства. $V$ на котором квадратичная форма определена.

Иногда можно определить наличие мнимой единицы в физическом уравнении. Такие единицы возникают из одной из многих величин в реальной алгебре, которые возводятся в квадрат ⁠ $-1$⁠ , и они имеют геометрическое значение из-за свойств алгебры и взаимодействия ее различных подпространств.

В ⁠ ${\mathcal {G}}(3,0)$⁠ , имеет место еще один знакомый случай. Дан стандартный базис, состоящий из ортонормированных векторов. $e_{i}$ из ⁠ $V$⁠ , множество всех ⁠ $2$⁠ -векторы охватываются

$\{e_{3}e_{2},e_{1}e_{3},e_{2}e_{1}\}.$

Маркировка этих ⁠ $i$⁠ , $j$ и $k$ (на мгновение отклоняясь от нашего соглашения о верхнем регистре), подпространство, порожденное ⁠ $0$⁠ -векторы и ⁠ $2$⁠ -векторы — это ровно ⁠ $\{\alpha _{0}+i\alpha _{1}+j\alpha _{2}+k\alpha _{3}\mid \alpha _{i}\in \mathbb {R} \}$⁠ . Это множество рассматривается как четная подалгебра ⁠ ${\mathcal {G}}(3,0)$⁠ , и, кроме того, изоморфен ⁠ $\mathbb {R}$⁠ -алгебра кватернионов , еще одна важная алгебраическая система.

Расширения внутренних и внешних продуктов

Обычной практикой является расширение внешнего произведения векторов на всю алгебру. Это можно сделать с помощью вышеупомянутого оператора проекции уклона :

$C\wedge D:=\sum _{r,s}\langle \langle C\rangle _{r}\langle D\rangle _{s}\rangle _{r+s}$ ( внешний продукт )

Это обобщение согласуется с приведенным выше определением антисимметризации. Другое обобщение, связанное с внешним произведением, - это коммутаторное произведение:

$C\times D:={\tfrac {1}{2}}(CD-DC)$ ( коммутаторное произведение )

Регрессивный продукт является двойником внешнего продукта (соответственно соответствующему «встрече» и «объединению» в этом контексте). Двойная спецификация элементов позволяет для лезвий ⁠ $C$⁠ и ⁠ $D$⁠ , пересечение (или встреча), где следует принять двойственность относительно лезвия a, содержащего оба ⁠ $C$⁠ и ⁠ $D$⁠ (самое маленькое из таких лезвий — соединение).

$C\vee D:=((CI^{-1})\wedge (DI^{-1}))I$

с ⁠ $I$⁠ единичный псевдоскаляр алгебры. Регрессивный продукт, как и внешний продукт, ассоциативен.

Внутреннее произведение векторов также можно обобщить, но более чем одним неэквивалентным способом. В статье ( Дорст 2002 ) дается полное описание нескольких различных внутренних продуктов, разработанных для геометрических алгебр и их взаимосвязей, и обозначения взяты оттуда. Многие авторы используют тот же символ, что и для внутреннего произведения векторов выбранного ими расширения (например, Гестен и Первасс). Никаких последовательных обозначений не появилось.

Среди этих нескольких различных обобщений скалярного произведения векторов:

$C\;\rfloor \;D:=\sum _{r,s}\langle \langle C\rangle _{r}\langle D\rangle _{s}\rangle _{s-r}$ ( левое сокращение )

$C\;\lfloor \;D:=\sum _{r,s}\langle \langle C\rangle _{r}\langle D\rangle _{s}\rangle _{r-s}$ ( правое сокращение )

$C*D:=\sum _{r,s}\langle \langle C\rangle _{r}\langle D\rangle _{s}\rangle _{0}$ ( скалярное произведение )

$C\bullet D:=\sum _{r,s}\langle \langle C\rangle _{r}\langle D\rangle _{s}\rangle _{|s-r|}$ (продукт «(жирная) точка»)

Дорст (2002) приводит доводы в пользу использования сокращений вместо внутреннего продукта Гестенеса; они алгебраически более регулярны и имеют более чистую геометрическую интерпретацию. Ряд тождеств, включающих сокращения, действительны без ограничения их входных данных.Например,

$C\;\rfloor \;D=(C\wedge (DI^{-1}))I$

$C\;\lfloor \;D=I((I^{-1}C)\wedge D)$

$(A\wedge B)*C=A*(B\;\rfloor \;C)$

$C*(B\wedge A)=(C\;\lfloor \;B)*A$

$A\;\rfloor \;(B\;\rfloor \;C)=(A\wedge B)\;\rfloor \;C$

$(A\;\rfloor \;B)\;\lfloor \;C=A\;\rfloor \;(B\;\lfloor \;C).$

Преимущества использования левого сокращения в качестве расширения внутреннего произведения векторов включают в себя то, что тождество $ab=a\cdot b+a\wedge b$ распространяется на $aB=a\;\rfloor \;B+a\wedge B$ для любого вектора $a$ и многовекторный ⁠ $B$⁠ и что проецирования операция ${\mathcal {P}}_{b}(a)=(a\cdot b^{-1})b$ распространяется на ${\mathcal {P}}_{B}(A)=(A\;\rfloor \;B^{-1})\;\rfloor \;B$ для любого лезвия $B$ и любой многовектор $A$ (с небольшой модификацией для размещения нуля ⁠ $B$⁠ , приведено ниже ).

Двойной базис

Позволять $\{e_{1},\ldots ,e_{n}\}$ быть основой ⁠ $V$⁠ , то есть набор $n$ линейно независимые векторы, охватывающие ⁠ $n$⁠ -мерное векторное пространство ⁠ $V$⁠ . Базис, двойственный $\{e_{1},\ldots ,e_{n}\}$ — множество элементов двойственного векторного пространства $V^{*}$ который образует биортогональную систему с этим базисом, таким образом, являясь элементами, обозначаемыми $\{e^{1},\ldots ,e^{n}\}$ удовлетворяющий

$e^{i}\cdot e_{j}=\delta ^{i}{}_{j},$

где $\delta$ это дельта Кронекера .

Учитывая невырожденную квадратичную форму на ⁠ $V$⁠ , $V^{*}$ естественным образом отождествляется с ⁠ $V$⁠ , а двойственный базис можно рассматривать как элементы ⁠ $V$⁠ , но в целом не являются тем же набором, что и исходный базис.

Учитывая далее GA ⁠ $V$⁠ , пусть

$I=e_{1}\wedge \cdots \wedge e_{n}$

быть псевдоскаляром (который не обязательно квадрат к ⁠ $\pm 1$⁠ ) ​​образовано из основы ⁠ $\{e_{1},\ldots ,e_{n}\}$⁠ . Двойственные базисные векторы могут быть построены как

$e^{i}=(-1)^{i-1}(e_{1}\wedge \cdots \wedge {\check {e}}_{i}\wedge \cdots \wedge e_{n})I^{-1},$

где ${\check {e}}_{i}$ означает, что ⁠ $i$⁠ -й базисный вектор исключен из произведения.

Двойной базис также известен как взаимный базис или обратная основа.

Основное использование двойного базиса — разделение векторов на компоненты. Учитывая вектор ⁠ $a$⁠ , скалярные компоненты $a^{i}$ может быть определен как

$a^{i}=a\cdot e^{i}\ ,$

с точки зрения чего $a$ можно разделить на векторные компоненты как

$a=\sum _{i}a^{i}e_{i}\ .$

Мы также можем определить скалярные компоненты $a_{i}$ как

$a_{i}=a\cdot e_{i}\ ,$

с точки зрения чего $a$ можно разделить на векторные компоненты в терминах двойственного базиса как

$a=\sum _{i}a_{i}e^{i}\ .$

Двойственный базис, определенный выше для векторного подпространства геометрической алгебры, может быть расширен до покрытия всей алгебры. Для компактности мы будем использовать одну заглавную букву для обозначения упорядоченного набора векторных индексов. Тоесть, написание

$J=(j_{1},\dots ,j_{n})\ ,$

где ⁠ $j_{1}<j_{2}<\dots <j_{n}$⁠ ,мы можем написать базовый клинок как

$e_{J}=e_{j_{1}}\wedge e_{j_{2}}\wedge \cdots \wedge e_{j_{n}}\ .$

Соответствующая ответная лопасть имеет индексы в обратном порядке:

$e^{J}=e^{j_{n}}\wedge \cdots \wedge e^{j_{2}}\wedge e^{j_{1}}\ .$

Аналогично приведенному выше случаю с векторами, можно показать, что

$e^{J}*e_{K}=\delta _{K}^{J}\ ,$

где $*$ скалярное произведение.

С $A$ мультивектор, мы можем определить скалярные компоненты как

$A^{ij\cdots k}=(e^{k}\wedge \cdots \wedge e^{j}\wedge e^{i})*A\ ,$

с точки зрения чего $A$ могут быть разделены на компоненты лезвий, как

$A=\sum _{i<j<\cdots <k}A^{ij\cdots k}e_{i}\wedge e_{j}\wedge \cdots \wedge e_{k}\ .$

Альтернативно мы можем определить скалярные компоненты

$A_{ij\cdots k}=(e_{k}\wedge \cdots \wedge e_{j}\wedge e_{i})*A\ ,$

с точки зрения чего $A$ могут быть разделены на компоненты лезвий, как

$A=\sum _{i<j<\cdots <k}A_{ij\cdots k}e^{i}\wedge e^{j}\wedge \cdots \wedge e^{k}\ .$

Линейные функции

Хотя с версором проще работать, поскольку его можно непосредственно представить в алгебре как мультивектор, версоры представляют собой подгруппу линейных функций на мультивекторах, которые все равно можно использовать при необходимости. Геометрическая алгебра ⁠ $n$⁠ -мерное векторное пространство натянуто на базис $2^{n}$ элементы. Если мультивектор представлен $2^{n}\times 1$ вещественной матрицы-столбца коэффициентов базиса алгебры, то все линейные преобразования мультивектора можно выразить как умножение матрицы на $2^{n}\times 2^{n}$ настоящая матрица. Однако такое общее линейное преобразование допускает произвольный обмен между оценками, например «поворот» скаляра в вектор, который не имеет очевидной геометрической интерпретации.

Представляет интерес общее линейное преобразование векторов в векторы. С естественным ограничением на сохранение индуцированной внешней алгебры внешний морфизм линейного преобразования является единственным расширение версора. Если $f$ — линейная функция, отображающая векторы в векторы, то ее внешний морфизм — это функция, подчиняющаяся правилу

${\underline {\mathsf {f}}}(a_{1}\wedge a_{2}\wedge \cdots \wedge a_{r})=f(a_{1})\wedge f(a_{2})\wedge \cdots \wedge f(a_{r})$

для лезвия, распространенного на всю алгебру за счет линейности.

Моделирование геометрии

Хотя CGA было уделено много внимания, следует отметить, что GA — это не просто одна алгебра, а одно из семейств алгебр с одинаковой существенной структурой.

Векторная космическая модель

Основная статья: Сравнение векторной алгебры и геометрической алгебры

Чётная подалгебра ​ ${\mathcal {G}}(2,0)$ изоморфен комплексным числам , в чем можно убедиться, написав вектор $P$ через его компоненты в ортонормированном базисе и умножении слева на базисный вектор ⁠ $e_{1}$⁠ , уступая

$Z=e_{1}P=e_{1}(xe_{1}+ye_{2})=x(1)+y(e_{1}e_{2}),$

где мы определяем $i\mapsto e_{1}e_{2}$ с

$(e_{1}e_{2})^{2}=e_{1}e_{2}e_{1}e_{2}=-e_{1}e_{1}e_{2}e_{2}=-1.$

Аналогично, четная подалгебра ${\mathcal {G}}(3,0)$ с основой $\{1,e_{2}e_{3},e_{3}e_{1},e_{1}e_{2}\}$ изоморфен кватернионам , как можно увидеть, отождествив ⁠ $i\mapsto -e_{2}e_{3}$⁠ , $j\mapsto -e_{3}e_{1}$ и ⁠ $k\mapsto -e_{1}e_{2}$⁠ .

Каждая ассоциативная алгебра имеет матричное представление; замена трех декартовых базисных векторов матрицами Паули дает представление ⁠ ${\mathcal {G}}(3,0)$⁠ :

${\begin{aligned}e_{1}=\sigma _{1}=\sigma _{x}&={\begin{pmatrix}0&1\\1&0\end{pmatrix}}\\e_{2}=\sigma _{2}=\sigma _{y}&={\begin{pmatrix}0&-i\\i&0\end{pmatrix}}\\e_{3}=\sigma _{3}=\sigma _{z}&={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}\,.\end{aligned}}$

Расстановка точек на « векторе Паули » ( диаде ):

$\sigma =\sigma _{1}e_{1}+\sigma _{2}e_{2}+\sigma _{3}e_{3}$ с произвольными векторами $a$ и $b$ и умножение через дает:

$(\sigma \cdot a)(\sigma \cdot b)=a\cdot b+a\wedge b$ (Эквивалентно, при осмотре, ⁠ $a\cdot b+i\sigma \cdot (a\times b)$⁠ )

Модель пространства-времени

В физике основными приложениями являются геометрическая алгебра пространства-времени Минковского 3+1 , ⁠ ${\mathcal {G}}(1,3)$⁠ , называемая алгеброй пространства-времени (STA), или реже, ⁠ ${\mathcal {G}}(3,0)$⁠ , интерпретировал алгебру физического пространства (АФП).

Если в STA точки пространства-времени представлены просто векторами, то в APS — точками ⁠ $(3+1)$⁠ -мерное пространство-время вместо этого представлено паравекторами , трехмерным вектором (пространством) плюс одномерным скаляром (временем).

В алгебре пространства-времени тензор электромагнитного поля имеет бивекторное представление ⁠ ${F}=({E}+ic{B})\gamma _{0}$⁠ . Здесь $i=\gamma _{0}\gamma _{1}\gamma _{2}\gamma _{3}$ — единичный псевдоскаляр (или элемент четырехмерного объема), $\gamma _{0}$ - единичный вектор во времени, а $E$ и $B$ – классические векторы электрического и магнитного полей (с нулевой временной составляющей). Используя четырехток ⁠ ${J}$⁠ , уравнения Максвелла тогда примут вид

Формулировка	Однородные уравнения	Неоднородные уравнения
Поля	$DF=\mu _{0}J$
	$D\wedge F=0$	$D~\rfloor ~F=\mu _{0}J$
Потенциалы (любая калибра)	$F=D\wedge A$	$D~\rfloor ~(D\wedge A)=\mu _{0}J$
Потенциалы (калибровка Лоренца)	$F=DA$ $D~\rfloor ~A=0$	$D^{2}A=\mu _{0}J$

В геометрическом исчислении сопоставление векторов, например, в $DF$ обозначают геометрическое произведение и могут быть разложены на части как ⁠ $DF=D~\rfloor ~F+D\wedge F$⁠ . Здесь $D$ является производной ковектора в любом пространстве-времени и сводится к $\nabla$ в плоском пространстве-времени. Где $\bigtriangledown$ играет роль в Минковском ⁠ $4$⁠ -пространство-время, которое является синонимом роли $\nabla$ в евклидовом ⁠ $3$⁠ -пространство и связано с даламберианом соотношением ⁠ $\Box =\bigtriangledown ^{2}$⁠ . Действительно, если наблюдатель представлен будущим указывающим времениподобным вектором $\gamma _{0}$ у нас есть

$\gamma _{0}\cdot \bigtriangledown ={\frac {1}{c}}{\frac {\partial }{\partial t}}$

$\gamma _{0}\wedge \bigtriangledown =\nabla$

Повышение в этом лоренцевом метрическом пространстве имеет то же выражение $e^{\beta }$ как вращение в евклидовом пространстве, где ${\beta }$ - это бивектор, порожденный временем и задействованными направлениями пространства, тогда как в евклидовом случае это бивектор, порожденный двумя направлениями пространства, что усиливает «аналогию» почти до идентичности.

Матрицы Дирака представляют собой ⁠ ${\mathcal {G}}(1,3)$⁠ , показывающая эквивалентность матричным представлениям, используемым физиками.

Однородные модели

Однородные модели обычно относятся к проективному представлению, в котором элементы одномерных подпространств векторного пространства представляют точки геометрии.

В геометрической алгебре пространства $n$ размеров, роторы представляют собой совокупность преобразований с $n(n-1)/2$ степени свободы, соответствующие вращениям – например, $3$ когда $n=3$ и $6$ когда ⁠ $n=4$⁠ . Геометрическая алгебра часто используется для моделирования проективного пространства , т.е. как однородная модель : точка, линия, плоскость и т. д. представляется классом эквивалентности элементов алгебры, отличающихся обратимым скалярным множителем.

Роторы в пространстве измерений $n+1$ иметь $n(n-1)/2+n$ степени свободы, такие же, как количество степеней свободы при вращениях и перемещениях, объединенных для ⁠ $n$⁠ -мерное пространство.

Именно так обстоит дело в проективной геометрической алгебре (PGA), которая используется для представления евклидовых изометрий в евклидовой геометрии (тем самым охватывая подавляющее большинство инженерных приложений геометрии). В этой модели к трем евклидовым измерениям добавляется вырожденное измерение, чтобы сформировать алгебру ⁠. ${\mathcal {G}}(3,0,1)$⁠ . При подходящей идентификации подпространств для представления точек, линий и плоскостей версоры этой алгебры представляют все собственные евклидовы изометрии, которые всегда представляют собой винтовые движения в трехмерном пространстве, а также все неправильные евклидовы изометрии, которые включают отражения, роторные отражения, трансфлексии. , и точечные отражения.

PGA объединяет ${\mathcal {G}}(3,0,1)$ с двойным оператором для получения формул пересечения, соединения, расстояния и угла. В зависимости от автора, это может означать звезду Ходжа или проективную двойственность , хотя оба приводят к получению идентичных уравнений, хотя и с разными обозначениями. По сути, двойственные переключатели базисных векторов присутствуют и отсутствуют в выражении каждого члена алгебраического представления. Например, в PGA или трехмерном пространстве двойственная линия ${\boldsymbol {e}}_{12}$ это линия ⁠ ${\boldsymbol {e}}_{03}$⁠ , потому что ${\boldsymbol {e}}_{0}$ и ${\boldsymbol {e}}_{3}$ являются базовыми элементами, которые не содержатся в ${\boldsymbol {e}}_{12}$ но содержатся в ⁠ ${\boldsymbol {e}}_{03}$⁠ . В PGA двумерного пространства двойственный ${\boldsymbol {e}}_{12}$ это ⁠ ${\boldsymbol {e}}_{0}$⁠ , поскольку нет ${\boldsymbol {e}}_{3}$ элемент.

PGA — широко используемая система, сочетающая геометрическую алгебру с однородными представлениями в геометрии, но существует несколько других подобных систем. Конформная модель, обсуждаемая ниже, является однородной, как и «Коническая геометрическая алгебра». и см. Геометрическую алгебру на основе плоскостей для обсуждения однородных моделей эллиптической и гиперболической геометрии по сравнению с евклидовой геометрией, полученной из PGA.

Конформная модель

Основная статья: Конформная геометрическая алгебра

Работа в ГА, евклидовом пространстве ${\mathcal {E}}^{3}$ (вместе с конформной точкой на бесконечности) проективно вложен в CGA ${\mathcal {G}}(4,1)$ посредством идентификации евклидовых точек с 1D-подпространствами в 4D-нулевом конусе 5D-векторного подпространства CGA. Это позволяет выполнять все конформные преобразования как вращения и отражения и является ковариантным , расширяя отношения инцидентности проективной геометрии на круги и сферы.

В частности, мы добавляем ортогональные базисные векторы $e_{+}$ и $e_{-}$ такой, что $e_{+}^{2}=+1$ и $e_{-}^{2}=-1$ к основе векторного пространства, которое порождает ${\mathcal {G}}(3,0)$ и идентифицировать нулевые векторы

$n_{\infty }=e_{-}+e_{+}$ как конформная точка на бесконечности (см. Компактификация ) и

$n_{\text{o}}={\tfrac {1}{2}}(e_{-}-e_{+})$ как точка начала координат, давая

$n_{\infty }\cdot n_{\text{o}}=-1.$

Эта процедура имеет некоторое сходство с процедурой работы с однородными координатами в проективной геометрии и в этом случае позволяет моделировать евклидовы преобразования $\mathbf {R} ^{3}$ как ортогональные преобразования подмножества ⁠ $\mathbf {R} ^{4,1}$⁠ .

Быстро меняющаяся и изменчивая область ГА, CGA также исследуется на предмет применения в релятивистской физике.

Таблица моделей

Обратите внимание в этом списке, что ⁠ $p$⁠ и ⁠ $q$⁠ можно поменять местами, применяется то же имя; например, при относительно небольших изменениях см. соглашение о знаках . Например, ${\mathcal {G}}(3,1,0)$ и ${\mathcal {G}}(1,3,0)$ называются оба алгеброй пространства-времени.

Имя	Подпись	Лезвия, например, ориентированные геометрические объекты, которые может представлять алгебра.	Роторы, например, преобразования, сохраняющие ориентацию , которые может представлять алгебра.	Примечания
Векторпространство GA, VGA Алгебра физического пространства , АПС	${\mathcal {G}}(3,0,0)$	Плоскости и прямые, проходящие через начало координат	Ротации, например $\mathrm {SO} (3)$	Первый обнаруженный ГА
Плоский ГА , Проективный ГА, PGA	${\mathcal {G}}(3,0,1)$	Плоскости, линии и точки в любой точке пространства.	Вращения и перемещения, например, жесткие движения , $\mathrm {SE} (3)$ он же $\mathrm {SO} (3,0,1)$	Небольшие изменения в сигнатуре позволяют моделировать гиперболическое и эллиптическое пространство, см. основную статью. Невозможно смоделировать всю «проективную» группу.
Алгебра пространства-времени , STA	${\mathcal {G}}(3,1,0)$	Объемы, плоскости и линии, проходящие через начало координат в пространстве-времени.	Вращения и ускорения пространства-времени, например ⁠ $\mathrm {SO} (3,1)$⁠ , группа Лоренца	Основы калибровочной теории гравитации .
Проективизированная алгебра пространства-времени, ШАГ	${\mathcal {G}}(3,1,1)$	Объемы, плоскости, линии и точки (события) в пространстве-времени.	Вращения, перемещения и ускорение пространства-времени ( группа Пуанкаре )
Конформный ГА , КГА	${\mathcal {G}}(4,1,0)$	Сферы, круги, пары точек, линии и плоскости в любой точке пространства.	Преобразования пространства, сохраняющие углы ( Конформная группа ⁠ $\mathrm {SO} (4,1)$⁠ )
Конформная алгебра пространства-времени, CSTA	${\mathcal {G}}(4,2,0)$	Сферы, круги, плоскости, линии, световые конусы, траектории объектов с постоянным ускорением — все в пространстве-времени.	Конформные преобразования пространства-времени, например преобразования, сохраняющие скорость по длине дуги в пространстве-времени.	Относится к теории твисторов .
Мать Алгебра	${\mathcal {G}}(3,3,0)$	Неизвестный	Проективная группа
GA для Conics, GAC Квадрикичный конформный 2D GA QC2GA	${\mathcal {G}}(5,3,0)$	Очки, пара/тройка/четверка, Коника, Карандаш до 6 независимых коник.	Отражения, переводы, вращения, расширения и т. д.	Коники можно создавать из контрольных точек и карандашей коник.
Квадричный конформный ГА, ККГА	${\mathcal {G}}(9,6,0)$	Точки, кортежи до 8 точек, квадратичные поверхности, коники, коники на квадратичных поверхностях (например, сферическая коника ), пучки до 9 квадратичных поверхностей.	Отражения, переводы, вращения, расширения и т. д.	Квадрикические поверхности можно создавать из контрольных точек и определять нормали к их поверхностям.
Двойная конформная геометрическая алгебра (DCGA)	${\mathcal {G}}(8,2,0)$	Точки, циклиды Дарбу, поверхности квадрик.	Отражения, переводы, вращения, расширения и т. д.	Использует бивекторы двух независимых базисов CGA для представления симметричных «матриц» 5x5 из 15 уникальных коэффициентов. Это ценой возможности выполнения пересечений и построения по точкам.

Геометрическая интерпретация в модели векторного пространства

Проекция и отвержение

В трехмерном пространстве бивектор $a\land b$ определяет подпространство двумерной плоскости (голубой, простирается бесконечно в указанных направлениях). Любой вектор $c$ в 3D пространстве можно разложить на свою проекцию $c_{\Vert }$ на плоскость и ее отказ $c_{\perp }$ с этого самолета.

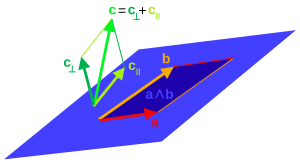
Для любого вектора $a$ и любой обратимый вектор ⁠ $m$⁠ ,

$a=amm^{-1}=(a\cdot m+a\wedge m)m^{-1}=a_{\|m}+a_{\perp m},$

где проекция ​ $a$ на $m$ (или параллельная часть)

$a_{\|m}=(a\cdot m)m^{-1}$

и отказ от $a$ от $m$ (или ортогональная часть) равна

$a_{\perp m}=a-a_{\|m}=(a\wedge m)m^{-1}.$

Используя концепцию ⁠ $k$⁠ -лезвие ⁠ $B$⁠ как представление подпространства ⁠ $V$⁠ и каждый мультивектор, в конечном счете, выражается через векторы, это обобщается до проекции общего мультивектора на любой обратимый ⁠ $k$⁠ -лезвие ⁠ $B$⁠ как

${\mathcal {P}}_{B}(A)=(A\;\rfloor \;B)\;\rfloor \;B^{-1},$

при этом отказ определяется как

${\mathcal {P}}_{B}^{\perp }(A)=A-{\mathcal {P}}_{B}(A).$

Проекция и отклонение обобщаются для нулевых лезвий. $B$ путем замены обратного $B^{-1}$ с псевдообратным $B^{+}$ относительно сжимающего произведения. Результат проекции совпадает в обоих случаях для ненулевых лопастей. Для нулевых лезвий ⁠ $B$⁠ следует использовать определение проекции, данное здесь, с первым сокращением, а не со вторым, являющимся псевдообратным, поскольку только тогда результат обязательно будет в подпространстве, представленном ⁠ $B$⁠ . Проекция посредством линейности обобщается на общие мультивекторы ⁠ $A$⁠ . Проекция нелинейна в ⁠ $B$⁠ и не распространяется на объекты ⁠ $B$⁠ это не лезвия.

Отражение

Простые отражения в гиперплоскости легко выражаются в алгебре через сопряжение с одним вектором. Они служат для создания группы общих роторных отражений и вращений .

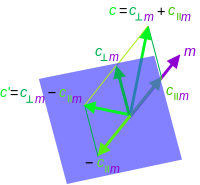
Отражение вектора $c$ вдоль вектора ⁠ $m$⁠ . Только компонент $c$ параллельно $m$ отрицается.

Отражение $c'$ вектора $c$ вдоль вектора ⁠ $m$⁠ или, что то же самое, в гиперплоскости, ортогональной ⁠ $m$⁠ , то же самое, что отрицание компонента вектора, параллельного ⁠ $m$⁠ . Результатом отражения будет

$c'={-c_{\|m}+c_{\perp m}}={-(c\cdot m)m^{-1}+(c\wedge m)m^{-1}}={(-m\cdot c-m\wedge c)m^{-1}}=-mcm^{-1}$

Это не самая общая операция, которую можно рассматривать как отражение, когда размерность ⁠ $n\geq 4$⁠ . Общее отражение может быть выражено как совокупность любого нечетного числа одноосных отражений. Таким образом, общее размышление $a'$ вектора $a$ может быть написано

$a\mapsto a'=-MaM^{-1},$

где

$M=pq\cdots r$ и $M^{-1}=(pq\cdots r)^{-1}=r^{-1}\cdots q^{-1}p^{-1}.$

Если мы определим отражение вдоль ненулевого вектора $m$ произведения векторов как отражения каждого вектора в произведении вдоль того же вектора, мы получаем для любого произведения нечетного числа векторов, что, например,

$(abc)'=a'b'c'=(-mam^{-1})(-mbm^{-1})(-mcm^{-1})=-ma(m^{-1}m)b(m^{-1}m)cm^{-1}=-mabcm^{-1}\,$

и для произведения четного числа векторов, которое

$(abcd)'=a'b'c'd'=(-mam^{-1})(-mbm^{-1})(-mcm^{-1})(-mdm^{-1})=mabcdm^{-1}.$

Используя концепцию каждого мультивектора, в конечном итоге выражаемую через векторы, отражение общего мультивектора $A$ использование любого средства отражения $M$ может быть написано

$A\mapsto M\alpha (A)M^{-1},$

где $\alpha$ — автоморфизм отражения через начало векторного пространства ( ⁠ $v\mapsto -v$⁠ ) распространяется за счет линейности на всю алгебру.

Ротации

Ротор, вращающий векторы в плоскости, вращает векторы на угол ⁠. $\theta$⁠ , то есть $x\mapsto R_{\theta }x{\tilde {R}}_{\theta }$ представляет собой вращение $x$ сквозной угол ⁠ $\theta$⁠ . Угол между $u$ и $v$ это ⁠ $\theta /2$⁠ . Аналогичные интерпретации справедливы и для общей многовекторности. $X$ вместо вектора ⁠ $x$⁠ .

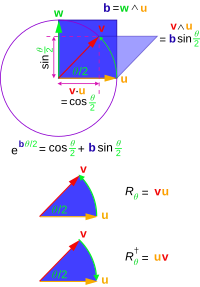
Если у нас есть произведение векторов $R=a_{1}a_{2}\cdots a_{r}$ то мы обозначим обратное как

${\tilde {R}}=a_{r}\cdots a_{2}a_{1}.$

В качестве примера предположим, что $R=ab$ мы получаем

$R{\tilde {R}}=abba=ab^{2}a=a^{2}b^{2}=ba^{2}b=baab={\tilde {R}}R.$

Масштабирование $R$ так что $R{\tilde {R}}=1$ затем

$(Rv{\tilde {R}})^{2}=Rv^{2}{\tilde {R}}=v^{2}R{\tilde {R}}=v^{2}$

так $Rv{\tilde {R}}$ оставляет длину $v$ без изменений. Мы также можем показать, что

$(Rv_{1}{\tilde {R}})\cdot (Rv_{2}{\tilde {R}})=v_{1}\cdot v_{2}$

итак трансформация $Rv{\tilde {R}}$ сохраняет длину и угол. Поэтому его можно определить как вращение или роторное отражение; $R$ называется ротором, если это правильное вращение (как если бы его можно было выразить как произведение четного числа векторов) и является примером того, что известно в GA как версор .

Существует общий метод вращения вектора, заключающийся в формировании мультивектора вида $R=e^{-B\theta /2}$ который производит вращение $\theta$ в плоскости и с ориентацией, определяемой ⁠ $2$⁠ -лезвие ⁠ $B$⁠ .

Роторы - это обобщение кватернионов на ⁠ $n$⁠ -мерные пространства.

Примеры и приложения

Гиперобъем параллелоэдра, натянутого векторами

Для векторов ⁠ $a$⁠ и ⁠ $b$⁠ охватывая параллелограмм, мы имеем

$a\wedge b=((a\wedge b)b^{-1})b=a_{\perp b}b$

в результате чего ⁠ $a\wedge b$⁠ линеен по произведению «высоты» и «основания» параллелограмма, то есть его площади.

Подобные интерпретации верны для любого количества векторов, охватывающих ⁠ $n$⁠ -мерный параллелоэдр ; внешнее произведение векторов ⁠ $a_{1},a_{2},\ldots ,a_{n}$⁠ , то есть ⁠ $\textstyle \bigwedge _{i=1}^{n}a_{i}$⁠ , имеет величину, равную объёму ⁠ $n$⁠ -параллелотоп. Ан ⁠ $n$⁠ -вектор не обязательно имеет форму параллелоэдра – это удобная визуализация. Форма может быть любой, но объем равен объему параллелоэдра.

Пересечение прямой и плоскости

Линия L, определяемая точками T и P (которые мы ищем), и плоскость, определяемая бивектором B, содержащим точки P и Q.

Мы можем параметрически определить линию с помощью ⁠ $p=t+\alpha \ v$⁠ , где ⁠ $p$⁠ и ⁠ $t$⁠ — векторы положения точек P и T и ⁠ $v$⁠ — вектор направления линии.

Затем

$B\wedge (p-q)=0$ и $B\wedge (t+\alpha v-q)=0$

так

$\alpha ={\frac {B\wedge (q-t)}{B\wedge v}}$

и

$p=t+\left({\frac {B\wedge (q-t)}{B\wedge v}}\right)v.$

Вращающиеся системы

Величина вращения, такая как крутящий момент или угловой момент, описывается в геометрической алгебре как бивектор. Предположим, что круговой путь в произвольной плоскости содержит ортонормированные векторы ⁠ ${\hat {u}}$⁠ и ⁠ ${\hat {v}}$⁠ параметризуется углом.

$\mathbf {r} =r({\hat {u}}\cos \theta +{\hat {v}}\sin \theta )=r{\hat {u}}(\cos \theta +{\hat {u}}{\hat {v}}\sin \theta )$

Обозначив единичный бивектор этой плоскости мнимым числом

${i}={\hat {u}}{\hat {v}}={\hat {u}}\wedge {\hat {v}}$

$i^{2}=-1$

этот вектор пути удобно записать в комплексной экспоненциальной форме

$\mathbf {r} =r{\hat {u}}e^{i\theta }$

а производная по углу равна

${\frac {d\mathbf {r} }{d\theta }}=r{\hat {u}}ie^{i\theta }=\mathbf {r} i.$

Перекрестное произведение по отношению к внешнему произведению. Красным обозначены единичный вектор нормали и «параллельный» единичный бивектор.

Например, крутящий момент обычно определяется как величина перпендикулярной составляющей силы, умноженная на расстояние, или работа на единицу угла. Таким образом, крутящий момент, скорость изменения работы ⁠ $W$⁠ по углу, из-за силы ⁠ $F$⁠ , это

$\tau ={\frac {dW}{d\theta }}=F\cdot {\frac {dr}{d\theta }}=F\cdot (\mathbf {r} i).$

Вращательные величины представлены в векторном исчислении в трех измерениях с использованием векторного произведения . Вместе с выбором ориентированной формы объёма ⁠ $I$⁠ их можно связать с внешним произведением с его более естественной геометрической интерпретацией таких величин как бивекторы, используя двойственное соотношение

$a\times b=-I(a\wedge b).$

В отличие от описания крутящего момента в виде перекрестного произведения, ⁠ $\tau =\mathbf {r} \times F$⁠ описание геометрической алгебры не вводит вектор в нормальном направлении; вектор, который не существует в двух измерениях и не уникален более чем в трех измерениях. Единичный бивектор описывает плоскость и ориентацию вращения, а направление вращения определяется углом между векторами ⁠ ${\hat {u}}$⁠ и ⁠ ${\hat {v}}$⁠ .

Геометрическое исчисление

Основная статья: Геометрическое исчисление

Геометрическое исчисление расширяет формализм, включив в него дифференцирование и интегрирование, включая дифференциальную геометрию и дифференциальные формы .

По сути, векторная производная определяется так, чтобы версия теоремы Грина верна GA:

$\int _{A}dA\,\nabla f=\oint _{\partial A}dx\,f$

и тогда можно будет написать

$\nabla f=\nabla \cdot f+\nabla \wedge f$

как геометрическое произведение, эффективно обобщающее теорему Стокса (включая ее версию в дифференциальной форме).

В 1D, когда ⁠ $A$⁠ — кривая с концами ⁠ $a$⁠ и ⁠ $b$⁠ , тогда

$\int _{A}dA\,\nabla f=\oint _{\partial A}dx\,f$

сводится к

$\int _{a}^{b}dx\,\nabla f=\int _{a}^{b}dx\cdot \nabla f=\int _{a}^{b}df=f(b)-f(a)$

или фундаментальная теорема интегрального исчисления.

Развиваются также понятие векторного многообразия и геометрическая теория интегрирования (обобщающая дифференциальные формы).

История

До 20 века

Хотя связь геометрии с алгеброй восходит, по крайней мере, к в » Евклида «Началам третьем веке до нашей эры (см. Греческая геометрическая алгебра ), ГА в том смысле, который используется в этой статье, не получил развития до 1844 года, когда он был использован в систематический способ описания геометрических свойств и преобразований пространства. В этом году Герман Грассман ввел идею геометрической алгебры в полной общности как некое исчисление (аналог исчисления высказываний ), кодирующее всю геометрическую информацию пространства. Алгебраическая система Грассмана может быть применена к ряду различных типов пространств, главными из которых являются евклидово пространство , аффинное пространство и проективное пространство . Вслед за Грассманом в 1878 году Уильям Кингдон Клиффорд исследовал алгебраическую систему Грассмана вместе с кватернионами Уильяма Роуэна Гамильтона в ( Clifford 1878 ). С его точки зрения, кватернионы описывали определенные преобразования (которые он назвал роторами ), тогда как алгебра Грассмана описывала определенные свойства (или Стрекена, такие как длина, площадь и объем). Его вклад заключался в том, чтобы определить новый продукт – геометрический продукт – на существующей алгебре Грассмана, который реализовал кватернионы как живущие внутри этой алгебры. Впоследствии Рудольф Липшиц в 1886 году обобщил интерпретацию кватернионов Клиффорда и применил ее к геометрии вращений в ⁠. $n$⁠ размеры. Позже эти разработки побудили других математиков 20-го века формализовать и изучить свойства алгебры Клиффорда.

Тем не менее, другое революционное развитие 19-го века полностью затмило геометрические алгебры: векторный анализ , разработанный независимо Джозайей Уиллардом Гиббсом и Оливером Хевисайдом . Векторный анализ был мотивирован исследованиями Джеймса Клерка Максвелла по электромагнетизму и, в частности, необходимостью удобно выражать и манипулировать некоторыми дифференциальными уравнениями . Векторный анализ имел определенную интуитивную привлекательность по сравнению со строгостью новых алгебр. Физики и математики с готовностью приняли его в качестве своего любимого геометрического инструментария, особенно после влиятельного учебника 1901 года «Векторный анализ» Эдвина Бидуэлла Уилсона , последовавшего за лекциями Гиббса.

Более подробно, существовало три подхода к геометрической алгебре: кватернионный анализ, начатый Гамильтоном в 1843 году и геометризированный как роторы Клиффордом в 1878 году; геометрическая алгебра, начатая Грассманом в 1844 году; и векторный анализ, разработанный на основе кватернионного анализа в конце 19 века Гиббсом и Хевисайдом. Наследие кватернионного анализа в векторном анализе можно увидеть в использовании ⁠ $i$⁠ , ⁠ $j$⁠ , ⁠ $k$⁠ для обозначения базисных векторов ⁠ $\mathbf {R} ^{3}$⁠ : его рассматривают как чисто мнимые кватернионы. С точки зрения геометрической алгебры четная подалгебра алгебры пространства-времени изоморфна GA трехмерного евклидова пространства, а кватернионы изоморфны четной подалгебре GA трехмерного евклидова пространства, что объединяет три подхода.

20 век и настоящее время

Прогресс в изучении алгебр Клиффорда спокойно продвигался на протяжении двадцатого века, хотя во многом благодаря работам абстрактных алгебраистов, таких как Эли Картан , Герман Вейль и Клод Шевалле . Геометрический подход к геометрическим алгебрам пережил ряд возрождений в 20-м веке. В математике » Эмиля Артина . «Геометрическая алгебра обсуждает алгебру, связанную с каждой из множества геометрий, включая аффинную геометрию , проективную геометрию , симплектическую геометрию и ортогональную геометрию . В физике геометрические алгебры были возрождены как «новый» способ изучения классической механики и электромагнетизма, а также более сложных тем, таких как квантовая механика и калибровочная теория. Дэвид Хестенс переосмыслил матрицы Паули и Дирака как векторы в обычном пространстве и пространстве-времени соответственно и был основным современным сторонником использования геометрической алгебры.

В компьютерной графике и робототехнике геометрические алгебры были возрождены для эффективного представления вращений и других преобразований. О применении ГА в робототехнике ( теория винтов , кинематика и динамика с использованием версоров), компьютерном зрении, управлении и нейронных вычислениях (геометрическое обучение) см. Bayro (2010).

См. также

• Сравнение векторной алгебры и геометрической алгебры
• Алгебра Клиффорда
• Алгебра Грассмана – Кэли
• Алгебра пространства-времени
• Спинор
• Кватернион
• Алгебра физического пространства
• Универсальная геометрическая алгебра

Ссылки и дальнейшее чтение

Расположено в хронологическом порядке

• Грассман, Герман (1844), Теория линейного расширения - новая отрасль математики: представлена ​​и объяснена посредством приложений к другим разделам математики, а также к статике, механике, теории магнетизма и кристаллономии , Лейпциг: О. Виганд, ОСЛК   20521674
• Клиффорд, профессор (1878), «Приложения обширной алгебры Грассмана», Американский журнал математики , 1 (4): 350–358, doi : 10.2307/2369379 , JSTOR   2369379
• Артин, Эмиль (1988) [1957], Геометрическая алгебра , Библиотека классиков Уайли, Уайли, doi : 10.1002/9781118164518 , ISBN  978-0-471-60839-4 , МР   1009557
• Хестенес, Дэвид (1966), Алгебра пространства-времени , Гордон и Брич, ISBN  978-0-677-01390-9 , OCLC   996371
• Уиллер, Дж.А.; Миснер, К.; Торн, KS (1973), Гравитация , WH Freeman, ISBN  978-0-7167-0344-0
• Бурбаки, Николя (1980), «Глава 9 «Алгебры Клиффорда» », Элементы математики. Алгебра , Герман, ISBN  9782225655166
• Хестенес, Дэвид ; Собчик, Гаррет (1984), от алгебры Клиффорда до геометрического исчисления, единого языка математики и физики , Springer Нидерланды, ISBN  978-90-277-1673-6
• Хестенес, Дэвид (1986), «Единый язык математики и физики», в JSR Chisholm; AK Commons (ред.), Алгебры Клиффорда и их приложения в математической физике , Серия NATO ASI (серия C), том. 183, Springer, стр. 1–23, номер документа : 10.1007/978-94-009-4728-3_1 , ISBN.  978-94-009-4728-3
• Уилмот, Г. П. (1988a), Структура алгебры Клиффорда. Журнал математической физики , вып. 29, стр. 2338–2345.
• Уилмот, Г. П. (1988b), «Алгебра Клиффорда и расширение Пфаффа», Журнал математической физики , 29 : 2346–2350, doi : 10.1063/1.528118
• Шевалле, Клод (1991), Алгебраическая теория спиноров и алгебр Клиффорда, Собрание сочинений , том. 2, Спрингер, ISBN  3-540-57063-2
• Доран, Крис Дж.Л. (1994), Геометрическая алгебра и ее применение к математической физике (докторская диссертация), Кембриджский университет , doi : 10.17863/CAM.16148 , hdl : 1810/251691 , OCLC   53604228
• Бейлис, МЫ, изд. (2011) [1996], Клиффордская (геометрическая) алгебра с приложениями к физике, математике и технике , Биркхойзер , ISBN  9781461241058
• Арагон, Г.; Арагон, JL; Родригес, Массачусетс (1997), «Алгебры Клиффорда и геометрическая алгебра», Достижения в области прикладных алгебр Клиффорда , 7 (2): 91–102, doi : 10.1007/BF03041220 , S2CID   120860757
• Хестенес, Дэвид (1999), Новые основы классической механики (2-е изд.), Springer Verlag, ISBN  978-0-7923-5302-7
• Ласенби, Джоан; Ласенби, Энтони Н.; Доран, Крис Дж.Л. (2000), «Единый математический язык физики и техники в 21 веке» (PDF) , Philosophical Transactions of the Royal Society A , 358 (1765): 21–39, Bibcode : 2000RSPTA.358.. .21L , doi : 10.1098/rsta.2000.0517 , S2CID   91884543 , заархивировано (PDF) из оригинала 19 марта 2015 г.
• Лунесто, Пертти (2001), Клиффордские алгебры и спиноры (2-е изд.), Cambridge University Press , ISBN  978-0-521-00551-7
• Бейлис, МЫ (2002), Электродинамика: современный геометрический подход (2-е изд.), Биркхойзер , ISBN  978-0-8176-4025-5
• Дорст, Лео (2002), «Внутренние произведения геометрической алгебры», Дорст, Л.; Доран, К.; Ласенби, Дж. (ред.), Приложения геометрической алгебры в информатике и технике , Биркхойзер , стр. 35–46, doi : 10.1007/978-1-4612-0089-5_2 , ISBN  978-1-4612-0089-5
• Доран, Крис Дж.Л .; Ласенби, Энтони Н. (2003), Геометрическая алгебра для физиков (PDF) , Cambridge University Press, ISBN  978-0-521-71595-9 , заархивировано (PDF) из оригинала 6 января 2009 г.
• Хестенес, Дэвид (2003), «Лекция по медали Эрстеда 2002: Реформирование математического языка физики» (PDF) , Am. Дж. Физ. , 71 (2): 104–121, Bibcode : 2003AmJPh..71..104H , CiteSeerX   10.1.1.649.7506 , doi : 10.1119/1.1522700 {{citation}}: CS1 maint: статус URL ( ссылка )
• Хильденбранд, Дитмар; Фонтейн, Дэниел; Первасс, Кристиан; Дорст, Лео (2004), «Геометрическая алгебра и ее применение к компьютерной графике» (PDF) , Proceedings of Eurographics 2004 , doi : 10.2312/egt.20041032 , заархивировано (PDF) из оригинала 6 сентября 2015 г.
• Ласенби, Энтони (2004), «Конформные модели пространства де Ситтера, начальные условия инфляции и CMB», Материалы конференции AIP , том. 736, стр. 53–70, arXiv : astro-ph/0411579 , doi : 10.1063/1.1835174 , S2CID   18034896
• Хестенес, Дэвид (2005), Введение в учебник для начинающих по геометрической алгебре
• Селиг, Дж. М. (2005). Геометрические основы робототехники . Монографии по информатике. Нью-Йорк, штат Нью-Йорк: Springer New York. дои : 10.1007/b138859 . ISBN  978-0-387-20874-9 .
• Бэйн, Дж. (2006), «Структурализм пространства-времени: §5 Многообразия против геометрической алгебры», в Деннисе Диксе (редактор), Онтология пространства-времени , Elsevier, стр. 54 и далее , ISBN  978-0-444-52768-4
• Дорст, Лео; Фонтейн, Дэниел; Манн, Стивен (2007), Геометрическая алгебра для информатики: объектно-ориентированный подход к геометрии , Elsevier, ISBN  978-0-12-369465-2 , OCLC   132691969
• Пенроуз, Роджер (2007), Дорога к реальности , Винтажные книги, ISBN  978-0-679-77631-4
• Фрэнсис, Мэтью Р.; Косовский, Артур (2008), «Построение спиноров в геометрической алгебре», Annals of Physics , 317 (2): 383–409, arXiv : math-ph/0403040v2 , Bibcode : 2005AnPhy.317..383F , doi : 10.1016 /j.aop.2004.11.008 , S2CID   119632876
• Ли, Хунбо (2008), Инвариантные алгебры и геометрические рассуждения , World Scientific, ISBN  9789812770110 . Глава 1 в формате PDF
• Винс, Джон А. (2008), Геометрическая алгебра для компьютерной графики , Springer, ISBN  978-1-84628-996-5
• Лундхольм, Дуглас; Свенссон, Ларс (2009), «Алгебра Клиффорда, геометрическая алгебра и приложения», arXiv : 0907.5356v1 [ math-ph ]
• Первасс, Кристиан (2009), Геометрическая алгебра с приложениями в технике , геометрии и вычислениях, том. 4, Бибкод : 2009gaae.book.....P , doi : 10.1007/978-3-540-89068-3 , ISBN  978-3-540-89067-6
• Селиг, Дж. М. (2000), «Алгебра Клиффорда точек, линий и плоскостей» (PDF) , Robotica , 18 (5): 545–556, doi : 10.1017/S0263574799002568 , S2CID   28929170
• Байро-Коррочано, Эдуардо (2010), Геометрические вычисления для вейвлет-преобразований, зрение роботов, обучение, управление и действие , Springer Verlag, ISBN  9781848829299
• Байро-Коррошано, Э.; Шойерманн, Герик, ред. (2010), Геометрические алгебраические вычисления в технике и информатике , Springer, ISBN  9781849961080 Отрывок из Интернета по адресу https://davidhestenes.net/geocalc/html/UAFCG.html № 5. Новые инструменты для вычислительной геометрии и возрождения теории винтов.
• Гольдман, Рон (2010), «Переосмысление кватернионов: теория и вычисления» , Морган и Клейпул, Часть III. Переосмысление кватернионов и алгебр Клиффорда, ISBN  978-1-60845-420-4
• Дорст, Лео .; Ласенби, Джоан (2011), Руководство по геометрической алгебре на практике , Springer, ISBN  9780857298119
• Макдональд, Алан (2011), Линейная и геометрическая алгебра , CreateSpace, ISBN  9781453854938 , OCLC   704377582
• Снигг, Джон (2011), Новый подход к дифференциальной геометрии с использованием геометрической алгебры Клиффорда , Springer, ISBN  978-0-8176-8282-8
• Хильденбранд, Дитмар (2012), «Основы вычислений геометрической алгебры», Численный анализ и прикладная математика Icnaam 2012: Международная конференция по численному анализу и прикладной математике , Материалы конференции AIP, 1479 (1): 27–30, Bibcode : 2012AIPC.1479 ...27H , doi : 10.1063/1.4756054
• Соколов, Андрей (2013), Алгебра Клиффорда и проективная модель пространств Минковского (псевдоевклидовы) , arXiv : 1307.4179
• Бромборский, Алан (2014), Введение в геометрическую алгебру и исчисление (PDF) , заархивировано (PDF) из оригинала 15 октября 2019 г.
• Клавиттер, Дэниел (2015), Алгебра Клиффорда , номер документа : 10.1007/978-3-658-07618-4 , ISBN  978-3-658-07617-7
• Канатани, Кеничи (2015), Понимание геометрической алгебры: Гамильтон, Грассманн и Клиффорд для компьютерного зрения и графики , CRC Press, ISBN  978-1-4822-5951-3
• Ли, Хунбо; Хуан, Лей; Шао, Чанпэн; Донг, Лей (2015), «Трехмерная проективная геометрия с геометрической алгеброй», arXiv : 1507.06634v1 [ math.MG ]
• Хестенес, Дэвид (2017), «Происхождение геометрической алгебры: личная ретроспектива», « Достижения в области прикладных алгебр Клиффорда» , 27 : 351–379, doi : 10.1007/s00006-016-0664-z , S2CID   253592888
• Дорст, Лео (2016), «3D-ориентированная проективная геометрия через версоры ⁠ $\mathbb {R} ^{3,3}$⁠ ", Успехи в прикладной алгебре Клиффорда , 26 (4): 1137–1172, doi : 10.1007/s00006-015-0625-y
• Лендьел, Эрик (2016). Основы разработки игровых движков . Математика. Том. 1. Линкольн, Калифорния: Terathon Software LLC. ISBN  978-0-9858117-4-7 .
• Ваз, Джейме; да Роша, Ролдан (2016), Введение в алгебры и спиноры Клиффорда , Oxford University Press, Bibcode : 2016icas.book.....V , ISBN  978-0-19-878292-6
• Пасха, Роберт Бенджамин; Хитцер, Экхард (2017), «Двойная конформная геометрическая алгебра», Достижения в области прикладных алгебр Клиффорда , 27 (3): 2175–2199, doi : 10.1007/s00006-017-0784-0 , S2CID   253600526
• Ду, Хуан; Голдман, Рон; Манн, Стивен (2017), «Моделирование трехмерной геометрии в алгебре Клиффорда R(4, 4)», « Достижения в области прикладных алгебр Клиффорда» , 27 (4): 3039–3062, doi : 10.1007/s00006-017-0798-7 , S2CID   253587390
• Байро-Коррошано, Эдуардо (2018). Компьютерное зрение, графика и нейрокомпьютеры . Приложения геометрической алгебры. Том. И. Спрингер. ISBN  978-3-319-74830-6 .
• Брейль, Стефан (2018). Алгоритмическая структура операторов геометрической алгебры и ее применение к квадратичным поверхностям (PDF) (PHD). университет-Париж-EST. Архивировано (PDF) из оригинала 14 июля 2019 г.
• Лавор, Карлайл; Ксамбо-Декамп, Себастья; Заплана, Исайя (2018). Геометрическая алгебра: приглашение к физике пространства-времени, робототехнике и молекулярной геометрии . Спрингер. стр. 1–. ISBN  978-3-319-90665-2 .
• Герой, Ярослав; Вернись, Алесь; Вашик, Петр (2018), «Геометрическая алгебра для коник», Достижения в области прикладных алгебр Клиффорда , 28 (3), doi : 10.1007/s00006-018-0879-2 , S2CID   125649450
• Брейльс, Стефан; Фукс, Лоран; Хитцер, Экхард; Нозик, Винсент; Сугимото, Акихиро (2019), «Трехмерные квадрики в расширенных конформных геометрических алгебрах более высоких размерностей из контрольных точек, неявных уравнений и выравнивания осей» (PDF) , Достижения в области прикладных алгебр Клиффорда , 29 (3), doi : 10.1007/s00006 -019-0974-з , S2CID   253597480
• Йосипович, Мирослав (2019). Геометрическое умножение векторов: введение в геометрическую алгебру в физике . Springer International Publishing; Биркхойзер. п. 256. ИСБН  978-3-030-01756-9 .
• Хэдфилд, Хьюго; Ласенби, Джоан (2020), «Динамика с ограничениями в конформной и проективной геометрической алгебре» , Достижения в компьютерной графике , Конспекты лекций по информатике, том. 12221, стр. 459–471, номер doi : 10.1007/978-3-030-61864-3_39 , ISBN.  978-3-030-61863-6 , S2CID   224820480
• Ву, Бофэн (2022), «Сигнатурная инвариантная геометрическая алгебра для физики пространства-времени и ее применения в релятивистской динамике массивных частиц и гироскопической прецессии», Scientific Reports , 12 (1): 3981, arXiv : 2111.07353 , Bibcode : 2022NatSR. .12.3981W , doi : 10.1038/s41598-022-06895-0 , PMC   8901677 , PMID   35256628
• Уилмот, врач общей практики (2023). «Алгебра геометрии» . Гитхаб .

Внешние ссылки

• Обзор геометрической алгебры и геометрического исчисления Алан Макдональд , Колледж Лютера, Айова.
• Мнимые числа нереальны – Геометрическая алгебра пространства-времени . Введение (Кембриджская группа Джорджии).
• Геометрическая алгебра 2015, магистерский курс по научным вычислениям , от доктора Криса Дорана (Кембридж).
• Математика для программистов (игр): 5 – Многовекторные методы . Комплексное введение и справочник для программистов от Яна Белла .
• Летняя школа IMPA 2010 Фернандес Оливейра. Вступление и слайды.
• Публикации Университета Фукуи ESM Hitzer и Japan GA.
• Группа Google для Google Analytics
• Учебник по геометрической алгебре. Введение в ГА, Яап Сутер.
• Вики-сайт «Ресурсы геометрической алгебры» , куратор Пабло Блейер.
• Прикладные геометрические алгебры в информатике и инженерии, ранние труды 2018 г.
• bivector.net Веб-сайт сообщества «Геометрическая алгебра для компьютерной графики, видения и инженерии»
• Видео AGACSE 2021

Английские переводы ранних книг и статей

• Г. Комбебиак, «Исчисление трикватернионов» (Докторская диссертация)
• М. Маркич, «Трансформанты: новый математический аппарат. Синтез трикватернионов Комбебиака и геометрической системы Грассмана. Исчисление квадрикватернионов»
• К. Бурали-Форти, «Метод Грассмана в проективной геометрии». Сборник трех заметок о применении внешней алгебры к проективной геометрии.
• К. Бурали-Форти, «Введение в дифференциальную геометрию по методу Х. Грассмана». Ранняя книга по применению алгебры Грассмана.
• Г. Грассман, «Механика в соответствии с принципами теории расширения». Одна из его работ о приложениях внешней алгебры.

Исследовательские группы

• Международное геометрическое исчисление . Ссылки на исследовательские группы, программное обеспечение и конференции по всему миру.
• Группа Кембриджской геометрической алгебры . Полнотекстовые интернет-издания и другие материалы.
• Группа Университета Амстердама
• Исследования и разработки в области геометрического исчисления (архив веб-сайта Хестенса в Университете штата Аризона).
• Блог GA-Net и архив информационных бюллетеней . Новости развития геометрической алгебры/алгебры Клиффорда.
• Геометрическая алгебра для систем восприятия действия. Группа геометрической кибернетики (CINVESTAV, кампус Гвадалахара, Мексика).