Евклидова геометрия

«Плоская геометрия» перенаправляется сюда. Чтобы узнать о других значениях, см. Плоскую геометрию (значения) .

Фрагмент из Рафаэля «Афинской школы» , изображающий греческого математика, возможно, олицетворяющего Евклида или Архимеда , использующего компас для рисования геометрической конструкции.

Евклидова геометрия — математическая система, приписываемая древнегреческому математику Евклиду , которую он описал в своем учебнике по геометрии « » Начала . Подход Евклида состоит в том, чтобы принять небольшой набор интуитивно привлекательных аксиом (постулатов) и вывести из них множество других предложений ( теорем ). Хотя многие результаты Евклида были сформулированы ранее, Евклид был первым, кто организовал эти предложения в логическую систему , в которой каждый результат доказывается на основе аксиом и ранее доказанных теорем.

« Начала » начинаются с плоской геометрии , которую до сих пор преподают в средней школе (старшей школе) как первая аксиоматическая система и первые примеры математических доказательств . Это переходит к твердой геометрии трех измерений . Большая часть « Элементов» содержит результаты того, что сейчас называется алгеброй и теорией чисел , объясненные на геометрическом языке.

For more than two thousand years, the adjective "Euclidean" was unnecessary becauseEuclid's axioms seemed so intuitively obvious (with the possible exception of the parallel postulate) that theorems proved from them were deemed absolutely true, and thus no other sorts of geometry were possible. Today, however, many other self-consistent non-Euclidean geometries are known, the first ones having been discovered in the early 19th century. An implication of Albert Einstein's theory of general relativity is that physical space itself is not Euclidean, and Euclidean space is a good approximation for it only over short distances (relative to the strength of the gravitational field).

Euclidean geometry is an example of synthetic geometry, in that it proceeds logically from axioms describing basic properties of geometric objects such as points and lines, to propositions about those objects. This is in contrast to analytic geometry, introduced almost 2,000 years later by René Descartes, which uses coordinates to express geometric properties by means of algebraic formulas.

The Elements

Main article: Euclid's Elements

The Elements is mainly a systematization of earlier knowledge of geometry. Its improvement over earlier treatments was rapidly recognized, with the result that there was little interest in preserving the earlier ones, and they are now nearly all lost.

There are 13 books in the Elements:

Books I–IV and VI discuss plane geometry. Many results about plane figures are proved, for example, "In any triangle, two angles taken together in any manner are less than two right angles." (Book I proposition 17) and the Pythagorean theorem "In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle." (Book I, proposition 47)

Books V and VII–X deal with number theory, with numbers treated geometrically as lengths of line segments or areas of surface regions. Notions such as prime numbers and rational and irrational numbers are introduced. It is proved that there are infinitely many prime numbers.

Books XI–XIII concern solid geometry. A typical result is the 1:3 ratio between the volume of a cone and a cylinder with the same height and base. The platonic solids are constructed.

Axioms

The parallel postulate (Postulate 5): If two lines intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough.

Euclidean geometry is an axiomatic system, in which all theorems ("true statements") are derived from a small number of simple axioms. Until the advent of non-Euclidean geometry, these axioms were considered to be obviously true in the physical world, so that all the theorems would be equally true. However, Euclid's reasoning from assumptions to conclusions remains valid independently from the physical reality.

Near the beginning of the first book of the Elements, Euclid gives five postulates (axioms) for plane geometry, stated in terms of constructions (as translated by Thomas Heath):

Let the following be postulated:

1. To draw a straight line from any point to any point.
2. To produce (extend) a finite straight line continuously in a straight line.
3. To describe a circle with any centre and distance (radius).
4. That all right angles are equal to one another.
5. [The parallel postulate]: That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which the angles are less than two right angles.

Although Euclid explicitly only asserts the existence of the constructed objects, in his reasoning he also implicitly assumes them to be unique.

The Elements also include the following five "common notions":

1. Things that are equal to the same thing are also equal to one another (the transitive property of a Euclidean relation).
2. If equals are added to equals, then the wholes are equal (Addition property of equality).
3. If equals are subtracted from equals, then the differences are equal (subtraction property of equality).
4. Things that coincide with one another are equal to one another (reflexive property).
5. The whole is greater than the part.

Modern scholars agree that Euclid's postulates do not provide the complete logical foundation that Euclid required for his presentation. Modern treatments use more extensive and complete sets of axioms.

Parallel postulate

Main article: Parallel postulate

To the ancients, the parallel postulate seemed less obvious than the others. They aspired to create a system of absolutely certain propositions, and to them, it seemed as if the parallel line postulate required proof from simpler statements. It is now known that such a proof is impossible since one can construct consistent systems of geometry (obeying the other axioms) in which the parallel postulate is true, and others in which it is false. Euclid himself seems to have considered it as being qualitatively different from the others, as evidenced by the organization of the Elements: his first 28 propositions are those that can be proved without it.

Many alternative axioms can be formulated which are logically equivalent to the parallel postulate (in the context of the other axioms). For example, Playfair's axiom states:

In a plane, through a point not on a given straight line, at most one line can be drawn that never meets the given line.

The "at most" clause is all that is needed since it can be proved from the remaining axioms that at least one parallel line exists.

A proof from Euclid's Elements that, given a line segment, one may construct an equilateral triangle that includes the segment as one of its sides: an equilateral triangle ΑΒΓ is made by drawing circles Δ and Ε centered on the points Α and Β, and taking one intersection of the circles as the third vertex of the triangle.

Methods of proof

Euclidean Geometry is constructive. Postulates 1, 2, 3, and 5 assert the existence and uniqueness of certain geometric figures, and these assertions are of a constructive nature: that is, we are not only told that certain things exist, but are also given methods for creating them with no more than a compass and an unmarked straightedge. In this sense, Euclidean geometry is more concrete than many modern axiomatic systems such as set theory, which often assert the existence of objects without saying how to construct them, or even assert the existence of objects that cannot be constructed within the theory. Strictly speaking, the lines on paper are models of the objects defined within the formal system, rather than instances of those objects. For example, a Euclidean straight line has no width, but any real drawn line will have. Though nearly all modern mathematicians consider nonconstructive methods just as sound as constructive ones, Euclid's constructive proofs often supplanted fallacious nonconstructive ones—e.g., some of the Pythagoreans' proofs that involved irrational numbers, which usually required a statement such as "Find the greatest common measure of ..."

Euclid often used proof by contradiction. Euclidean geometry also allows the method of superposition, in which a figure is transferred to another point in space. For example, proposition I.4, side–angle–side congruence of triangles, is proved by moving one of the two triangles so that one of its sides coincides with the other triangle's equal side, and then proving that the other sides coincide as well. Some modern treatments add a sixth postulate, the rigidity of the triangle, which can be used as an alternative to superposition.

Notation and terminology

Naming of points and figures

Points are customarily named using capital letters of the alphabet. Other figures, such as lines, triangles, or circles, are named by listing a sufficient number of points to pick them out unambiguously from the relevant figure, e.g., triangle ABC would typically be a triangle with vertices at points A, B, and C.

Complementary and supplementary angles

Angles whose sum is a right angle are called complementary. Complementary angles are formed when a ray shares the same vertex and is pointed in a direction that is in between the two original rays that form the right angle. The number of rays in between the two original rays is infinite.

Angles whose sum is a straight angle are supplementary. Supplementary angles are formed when a ray shares the same vertex and is pointed in a direction that is in between the two original rays that form the straight angle (180 degree angle). The number of rays in between the two original rays is infinite.

Modern versions of Euclid's notation

In modern terminology, angles would normally be measured in degrees or radians.

Modern school textbooks often define separate figures called lines (infinite), rays (semi-infinite), and line segments (of finite length). Euclid, rather than discussing a ray as an object that extends to infinity in one direction, would normally use locutions such as "if the line is extended to a sufficient length", although he occasionally referred to "infinite lines". A "line" in Euclid could be either straight or curved, and he used the more specific term "straight line" when necessary.

Some important or well known results

• 
  The pons asinorum or bridge of asses theorem states that in an isosceles triangle, α = β and γ = δ.
• 
  The triangle angle sum theorem states that the sum of the three angles of any triangle, in this case angles α, β, and γ, will always equal 180 degrees.
• 
  The Pythagorean theorem states that the sum of the areas of the two squares on the legs (a and b) of a right triangle equals the area of the square on the hypotenuse (c).
• 
  Thales' theorem states that if AC is a diameter, then the angle at B is a right angle.

Pons asinorum

The pons asinorum (bridge of asses) states that in isosceles triangles the angles at the base equal one another, and, if the equal straight lines are produced further, then the angles under the base equal one another. Its name may be attributed to its frequent role as the first real test in the Elements of the intelligence of the reader and as a bridge to the harder propositions that followed. It might also be so named because of the geometrical figure's resemblance to a steep bridge that only a sure-footed donkey could cross.

Congruence of triangles

Congruence of triangles is determined by specifying two sides and the angle between them (SAS), two angles and the side between them (ASA) or two angles and a corresponding adjacent side (AAS). Specifying two sides and an adjacent angle (SSA), however, can yield two distinct possible triangles unless the angle specified is a right angle.

Triangles are congruent if they have all three sides equal (SSS), two sides and the angle between them equal (SAS), or two angles and a side equal (ASA) (Book I, propositions 4, 8, and 26). Triangles with three equal angles (AAA) are similar, but not necessarily congruent. Also, triangles with two equal sides and an adjacent angle are not necessarily equal or congruent.

Triangle angle sum

The sum of the angles of a triangle is equal to a straight angle (180 degrees). This causes an equilateral triangle to have three interior angles of 60 degrees. Also, it causes every triangle to have at least two acute angles and up to one obtuse or right angle.

Pythagorean theorem

The celebrated Pythagorean theorem (book I, proposition 47) states that in any right triangle, the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angle).

Thales' theorem

Thales' theorem, named after Thales of Miletus states that if A, B, and C are points on a circle where the line AC is a diameter of the circle, then the angle ABC is a right angle. Cantor supposed that Thales proved his theorem by means of Euclid Book I, Prop. 32 after the manner of Euclid Book III, Prop. 31.

Scaling of area and volume

In modern terminology, the area of a plane figure is proportional to the square of any of its linear dimensions, $A\propto L^{2}$, and the volume of a solid to the cube, $V\propto L^{3}$. Euclid proved these results in various special cases such as the area of a circle and the volume of a parallelepipedal solid. Euclid determined some, but not all, of the relevant constants of proportionality. E.g., it was his successor Archimedes who proved that a sphere has 2/3 the volume of the circumscribing cylinder.

System of measurement and arithmetic

Euclidean geometry has two fundamental types of measurements: angle and distance. The angle scale is absolute, and Euclid uses the right angle as his basic unit, so that, for example, a 45-degree angle would be referred to as half of a right angle. The distance scale is relative; one arbitrarily picks a line segment with a certain nonzero length as the unit, and other distances are expressed in relation to it. Addition of distances is represented by a construction in which one line segment is copied onto the end of another line segment to extend its length, and similarly for subtraction.

Measurements of area and volume are derived from distances. For example, a rectangle with a width of 3 and a length of 4 has an area that represents the product, 12. Because this geometrical interpretation of multiplication was limited to three dimensions, there was no direct way of interpreting the product of four or more numbers, and Euclid avoided such products, although they are implied, for example in the proof of book IX, proposition 20.

An example of congruence. The two figures on the left are congruent, while the third is similar to them. The last figure is neither. Congruences alter some properties, such as location and orientation, but leave others unchanged, like distance and angles. The latter sort of properties are called invariants and studying them is the essence of geometry.

Euclid refers to a pair of lines, or a pair of planar or solid figures, as "equal" (ἴσος) if their lengths, areas, or volumes are equal respectively, and similarly for angles. The stronger term "congruent" refers to the idea that an entire figure is the same size and shape as another figure. Alternatively, two figures are congruent if one can be moved on top of the other so that it matches up with it exactly. (Flipping it over is allowed.) Thus, for example, a 2x6 rectangle and a 3x4 rectangle are equal but not congruent, and the letter R is congruent to its mirror image. Figures that would be congruent except for their differing sizes are referred to as similar. Corresponding angles in a pair of similar shapes are equal and corresponding sides are in proportion to each other.

In engineering

Design and Analysis

• Stress Analysis: Stress Analysis - Euclidean geometry is pivotal in determining stress distribution in mechanical components, which is essential for ensuring structural integrity and durability.

Механический стресс

• Gear Design: Gear - The design of gears, a crucial element in many mechanical systems, relies heavily on Euclidean geometry to ensure proper tooth shape and engagement for efficient power transmission.

Механизм

• Проектирование теплообменника : Теплообменник . В теплотехнике евклидова геометрия используется для проектирования теплообменников , где геометрическая конфигурация сильно влияет на тепловой КПД . см. в разделе «Кожухотрубные теплообменники» и «Пластинчатые теплообменники» . Более подробную информацию

U-Tube Shell and Tube Heat Exchanger

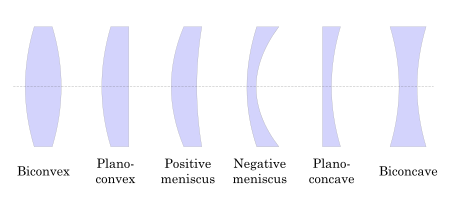
• Конструкция линзы : Линза . В оптической технике евклидова геометрия имеет решающее значение при проектировании линз, где точные геометрические формы определяют свойства фокусировки . Геометрическая оптика фокусировку света линзами анализирует и зеркалами .

Типы линз

Динамика

• Анализ вибрации : Вибрация . Евклидова геометрия важна для анализа и понимания вибраций в механических системах , помогая в разработке систем, которые могут противостоять или эффективно использовать эти вибрации .

Вибрация – колебания

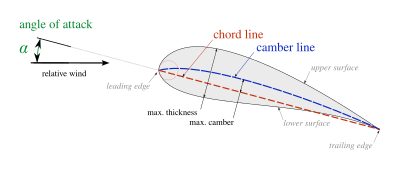
• Конструкция крыла : Конструкция крыла самолета . Применение евклидовой геометрии в аэродинамике очевидно в самолетов конструкции крыльев , аэродинамических профилях и подводных крыльях , где геометрическая форма напрямую влияет на характеристики подъемной силы и сопротивления .

Номенклатура профиля крыла

• Орбиты спутников , что важно для успешных : Орбиты спутников. Евклидова геометрия помогает в расчете и прогнозировании орбит спутников космических миссий и со спутниками операций . См. также астродинамику , небесную механику и эллиптическую орбиту .

Анимация орбиты по эксцентриситету

САПР-системы

• 3D-моделирование . В системах САПР (системы автоматизированного проектирования) евклидова геометрия имеет основополагающее значение для создания точных 3D-моделей механических деталей. Эти модели имеют решающее значение для визуализации и тестирования конструкций перед производством .

• Проектирование и производство : Большая часть CAM (компьютерного производства) опирается на евклидову геометрию. Геометрия конструкции в CAD/CAM обычно состоит из фигур, ограниченных плоскостями , цилиндрами , конусами , торами и другими подобными евклидовыми формами. Сегодня CAD/CAM играет важную роль в проектировании широкого спектра продуктов: от автомобилей и самолетов до кораблей и смартфонов .

• Эволюция практик черчения : Исторически продвинутая евклидова геометрия, включая такие теоремы, как теорема Паскаля и теорема Брианшона , была неотъемлемой частью практики черчения. Однако с появлением современных САПР такое глубокое знание этих теорем становится менее необходимым в современных процессах проектирования и производства.

См. Также: История программного обеспечения САПР.

3D CAD Model

Схемотехника

• Компоновка печатных плат : При проектировании печатных плат (PCB) используется евклидова геометрия для эффективного размещения и маршрутизации компонентов, обеспечивая функциональность и оптимизируя пространство . Эффективное расположение электронных компонентов на печатных платах имеет решающее значение для минимизации помех сигналов и оптимизации производительности схемы .

Печатная плата DVD-плеера

Электромагнитные поля и поля потока жидкости

• Проектирование антенны : Проектирование антенны . Евклидова геометрия антенн помогает в проектировании антенн, где пространственное расположение и размеры напрямую влияют на характеристики антенны и решетки при передаче и приеме электромагнитных волн .

НАСА Кассегрен , Чрезвычайно высокий коэффициент усиления ~70 дБи.

• Теория поля : сложный потенциальный поток . При изучении полей невязкого потока и электромагнитных полей евклидова геометрия помогает визуализировать и решать потенциального потока проблемы . Это важно для понимания взаимодействия поля скорости жидкости и электромагнитного поля в трехмерном пространстве. Связь которых характеризуется безвихревым соленоидальным полем или консервативным векторным полем .

Потенциальный поток вокруг источника без циркуляции

Элементы управления

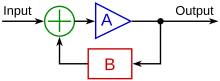
• Анализ систем управления : Системы управления . Применение евклидовой геометрии в теории управления помогает в анализе и проектировании систем управления , особенно в понимании и оптимизации системы устойчивости и реакции .

Базовый цикл обратной связи.

• Инструменты расчета : Якобиан -евклидова геометрия является неотъемлемой частью использования матриц Якобиана для преобразований и систем управления как в области механики , так и в области электротехники , обеспечивая понимание поведения и свойств системы. Якобиан служит линеаризованной матрицей плана в статистической регрессии и подборе кривой ; см. нелинейный метод наименьших квадратов . Якобиан также используется в случайных матрицах , моментах , статистике и диагностике .

Другие общие приложения

Из-за фундаментального статуса евклидовой геометрии в математике непрактично приводить здесь более чем репрезентативную выборку приложений.

• 
  Геодезист использует уровень
• 
  Упаковка сферы применяется к стопке апельсинов .
• 
  Параболическое зеркало фокусирует параллельные лучи света.

Как следует из этимологии этого слова, одной из самых ранних причин интереса, а также одним из наиболее распространенных в настоящее время применений геометрии является геодезия . Кроме того, он использовался в когнитивных и вычислительных подходах к зрительному восприятию объектов . Некоторые практические результаты евклидовой геометрии (такие как свойство прямоугольного треугольника 3-4-5) использовались задолго до того, как они были доказаны формально. Основными типами измерений в евклидовой геометрии являются расстояния и углы, оба из которых могут быть измерены непосредственно геодезистом. Исторически расстояния часто измерялись цепями, такими как цепь Гюнтера , а углы — с помощью градуированных кругов, а позже — теодолита .

Применением евклидовой твердотельной геометрии является определение способов упаковки , например, проблема поиска наиболее эффективной упаковки сфер в n измерениях. Эта проблема имеет применение в обнаружении и исправлении ошибок .

• 
  Геометрия используется в искусстве и архитектуре.
• 
  Водонапорная башня состоит из конуса, цилиндра и полусферы. Его объем можно рассчитать, используя твердотельную геометрию.
• 
  Геометрию можно использовать для создания оригами.

Геометрия широко используется в архитектуре .

Геометрию можно использовать для создания оригами . Некоторые классические задачи построения геометрии невозможно решить с помощью циркуля и линейки , но можно решить с помощью оригами .

Более поздняя история

Смотрите также: История геометрии и неевклидова геометрия § История

Архимед и Аполлоний

Сфера имеет 2/3 объема и площади поверхности окружающего ее цилиндра. На могилу Архимеда по его просьбе были помещены сфера и цилиндр.

Архимед ( ок. 287 г. до н. э. – ок. 212 г. до н. э. ), яркая фигура, о которой записано множество исторических анекдотов, помнят наряду с Евклидом как одного из величайших древних математиков. Хотя основы его работы были заложены Евклидом, его работа, в отличие от работы Евклида, считается полностью оригинальной. Он доказал уравнения объемов и площадей различных фигур в двух и трех измерениях и сформулировал архимедово свойство конечных чисел.

Аполлоний Пергский ( ок. 240 г. до н. э. – ок. 190 г. до н. э. ) в основном известен своими исследованиями конических сечений.

Рене Декарт. Портрет по мотивам Франса Хальса , 1648 год.

17 век: Декарт

Рене Декарт (1596–1650) разработал аналитическую геометрию — альтернативный метод формализации геометрии, направленный на превращение геометрии в алгебру.

В этом подходе точка на плоскости представлена ​​ее декартовыми координатами ( x , y ), линия представлена ​​ее уравнением и так далее.

В оригинальном подходе Евклида теорема Пифагора следует из аксиом Евклида. В картезианском подходе аксиомы являются аксиомами алгебры, а уравнение, выражающее теорему Пифагора, является тогда определением одного из терминов аксиом Евклида, которые теперь считаются теоремами.

Уравнение

$|PQ|={\sqrt {(p_{x}-q_{x})^{2}+(p_{y}-q_{y})^{2}}}\,$

определение расстояния между двумя точками P = ( p _x , p _y ) и Q = ( q _x , q _y ) тогда известно как евклидова метрика , а другие метрики определяют неевклидову геометрию .

С точки зрения аналитической геометрии ограничение классической геометрии конструкциями циркуля и линейки означает ограничение на уравнения первого и второго порядка, например, y = 2 x + 1 (линия) или x ² + и ² = 7 (круг).

Также в 17 веке Жирар Дезарг , руководствуясь теорией перспективы , ввел концепцию идеализированных точек, линий и плоскостей на бесконечности. Результат можно рассматривать как разновидность обобщенной геометрии, проективной геометрии , но его также можно использовать для получения доказательств в обычной евклидовой геометрии, в которой количество частных случаев уменьшено.

Квадратирование круга: площади этого квадрата и этого круга равны. В 1882 году было доказано, что эту фигуру невозможно построить за конечное число шагов с помощью идеализированного циркуля и линейки .

18 век

Геометры XVIII века изо всех сил пытались определить границы евклидовой системы. Многие тщетно пытались доказать пятый постулат из первых четырёх. К 1763 году было опубликовано как минимум 28 различных доказательств, но все они были признаны неверными.

В преддверии этого периода геометры также пытались определить, какие конструкции можно реализовать в евклидовой геометрии. Например, проблема разделения угла на три части с помощью циркуля и линейки естественным образом возникает в теории, поскольку аксиомы относятся к конструктивным операциям, которые можно выполнить с помощью этих инструментов. Однако столетия усилий не смогли найти решение этой проблемы, пока в 1837 году Пьер Ванцель не опубликовал доказательство невозможности такой конструкции. Другие конструкции, которые оказались невозможными, включают удвоение куба и квадратуру круга . В случае удвоения куба невозможность построения связана с тем, что в методе циркуля и линейки используются уравнения, порядок которых есть целая степень двойки: а удвоение куба требует решения уравнения третьего порядка.

Эйлер обсуждал обобщение евклидовой геометрии, называемое аффинной геометрией , которая сохраняет пятый постулат неизмененным, одновременно ослабляя постулаты третий и четвертый таким образом, что устраняются понятия угла (откуда прямоугольные треугольники становятся бессмысленными) и равенства длин отрезков прямой в целом ( откуда круги становятся бессмысленными), сохраняя при этом понятия параллельности как отношения эквивалентности между линиями и равенства длин параллельных отрезков линий (поэтому отрезки линий продолжают иметь среднюю точку).

19 век

Сравнение эллиптической, евклидовой и гиперболической геометрии в двух измерениях.

В начале 19 века Карно и Мёбиус систематически разработали использование знаковых углов и отрезков линий как способ упрощения и унификации результатов.

Высшие измерения

В 1840-х годах Уильям Роуэн Гамильтон разработал кватернионы , а Джон Т. Грейвс и Артур Кэли октонионы — . Это нормированные алгебры , расширяющие комплексные числа . Позже стало понятно, что кватернионы также представляют собой евклидову геометрическую систему с четырьмя действительными декартовыми координатами. Кэли использовал кватернионы для изучения вращений в 4-мерном евклидовом пространстве .

В середине века Людвиг Шлефли разработал общую концепцию евклидова пространства , расширив евклидову геометрию до более высоких измерений . определил многосхемы , позже названные многогранниками , которые являются многомерными аналогами многоугольников Он и многогранников . Он развил их теорию и открыл все правильные многогранники, т.е. $n$-мерные аналоги правильных многоугольников и Платоновых тел . Он обнаружил, что существует шесть правильных выпуклых многогранников в четвертом измерении и три во всех высших измерениях.

показывать Правильные выпуклые 4-многогранники
Symmetry group	A4	B4		F4	H4
Name	5-cell Hyper-tetrahedron 5-point	16-cell Hyper-octahedron 8-point	8-cell Hyper-cube 16-point	24-cell 24-point	600-cell Hyper-icosahedron 120-point	120-cell Hyper-dodecahedron 600-point
Schläfli symbol	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Coxeter mirrors
Mirror dihedrals	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/4⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/4⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/4⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/5⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/5⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠
Graph
Vertices	5 tetrahedral	8 octahedral	16 tetrahedral	24 cubical	120 icosahedral	600 tetrahedral
Edges	10 triangular	24 square	32 triangular	96 triangular	720 pentagonal	1200 triangular
Faces	10 triangles	32 triangles	24 squares	96 triangles	1200 triangles	720 pentagons
Cells	5 tetrahedra	16 tetrahedra	8 cubes	24 octahedra	600 tetrahedra	120 dodecahedra
Tori	1 5-tetrahedron	2 8-tetrahedron	2 4-cube	4 6-octahedron	20 30-tetrahedron	12 10-dodecahedron
Inscribed	120 in 120-cell	675 in 120-cell	2 16-cells	3 8-cells	25 24-cells	10 600-cells
Great polygons		2 squares x 3	4 rectangles x 4	4 hexagons x 4	12 decagons x 6	100 irregular hexagons x 4
Petrie polygons	1 pentagon x 2	1 octagon x 3	2 octagons x 4	2 dodecagons x 4	4 30-gons x 6	20 30-gons x 4
Long radius	$1$	$1$	$1$	$1$	$1$	$1$
Edge length	${\sqrt {\tfrac {5}{2}}}\approx 1.581$	${\sqrt {2}}\approx 1.414$	$1$	$1$	${\tfrac {1}{\phi }}\approx 0.618$	${\tfrac {1}{\phi ^{2}{\sqrt {2}}}}\approx 0.270$
Short radius	${\tfrac {1}{4}}$	${\tfrac {1}{2}}$	${\tfrac {1}{2}}$	${\sqrt {\tfrac {1}{2}}}\approx 0.707$	${\sqrt {\tfrac {\phi ^{4}}{8}}}\approx 0.926$	${\sqrt {\tfrac {\phi ^{4}}{8}}}\approx 0.926$
Area	$10\left({\tfrac {5{\sqrt {3}}}{8}}\right)\approx 10.825$	$32\left({\sqrt {\tfrac {3}{4}}}\right)\approx 27.713$	$24$	$96\left({\sqrt {\tfrac {3}{16}}}\right)\approx 41.569$	$1200\left({\tfrac {\sqrt {3}}{4\phi ^{2}}}\right)\approx 198.48$	$720\left({\tfrac {\sqrt {25+10{\sqrt {5}}}}{8\phi ^{4}}}\right)\approx 90.366$
Volume	$5\left({\tfrac {5{\sqrt {5}}}{24}}\right)\approx 2.329$	$16\left({\tfrac {1}{3}}\right)\approx 5.333$	$8$	$24\left({\tfrac {\sqrt {2}}{3}}\right)\approx 11.314$	$600\left({\tfrac {\sqrt {2}}{12\phi ^{3}}}\right)\approx 16.693$	$120\left({\tfrac {15+7{\sqrt {5}}}{4\phi ^{6}{\sqrt {8}}}}\right)\approx 18.118$
4-Content	${\tfrac {\sqrt {5}}{24}}\left({\tfrac {\sqrt {5}}{2}}\right)^{4}\approx 0.146$	${\tfrac {2}{3}}\approx 0.667$	$1$	$2$	${\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 3.863$	${\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 4.193$

Шлефли выполнил эту работу в относительной безвестности, и она была опубликована полностью только посмертно в 1901 году. Она не имела большого влияния, пока не была заново открыта и полностью задокументирована в 1948 году Коксетером Х.С.М. .

В 1878 году Уильям Кингдон Клиффорд представил то, что сейчас называется геометрической алгеброй , объединив кватернионы Гамильтона с алгеброй Германа Грассмана и раскрыв геометрическую природу этих систем, особенно в четырех измерениях. Операции геометрической алгебры приводят к зеркальному отображению, вращению, перемещению и отображению моделируемых геометрических объектов в новые положения. на Тор Клиффорда поверхности 3-сферы — это простейшее и наиболее симметричное плоское вложение декартова произведения двух окружностей (в том же смысле, в каком «плоская» поверхность цилиндра).

Неевклидова геометрия

Основная статья: Неевклидова геометрия

Наиболее влиятельное развитие геометрии в столетии произошло, когда около 1830 года Янош Бойяи и Николай Иванович Лобачевский по отдельности опубликовали работу по неевклидовой геометрии , в которой постулат о параллельности недействителен. Поскольку неевклидова геометрия доказуемо относительно согласуется с евклидовой геометрией, постулат о параллельности не может быть доказан на основе других постулатов.

В XIX веке также стало понятно, что десяти аксиом и общих понятий Евклида недостаточно для доказательства всех теорем, изложенных в « Началах» . Например, Евклид неявно предполагал, что любая прямая содержит по крайней мере две точки, но это предположение не может быть доказано из других аксиом и, следовательно, само должно быть аксиомой. Самое первое геометрическое доказательство в « Элементах», показанное на рисунке выше, состоит в том, что любой отрезок прямой является частью треугольника; Евклид строит это обычным способом, рисуя круги вокруг обеих конечных точек и принимая их пересечение в качестве третьей вершины . Однако его аксиомы не гарантируют, что круги действительно пересекаются, поскольку они не утверждают геометрическое свойство непрерывности, которое в декартовых терминах эквивалентно свойству полноты действительных чисел. Начиная с Морица Паша в 1882 году, было предложено множество улучшенных аксиоматических систем геометрии, наиболее известными из которых являются системы Гильберта . Джордж Биркгоф , и Тарский .

20 век и теория относительности

Опровержение евклидовой геометрии как описания физического пространства. В ходе проверки общей теории относительности в 1919 году звезды (отмеченные короткими горизонтальными линиями) были сфотографированы во время солнечного затмения . Лучи звездного света преломлялись гравитацией Солнца на пути к Земле. Это интерпретируется как свидетельство в пользу предсказания Эйнштейна о том, что гравитация будет вызывать отклонения от евклидовой геометрии.

Эйнштейна Специальная теория относительности предполагает четырехмерное пространство-время , пространство Минковского , которое не является евклидовым . Это показывает, что неевклидовы геометрии, которые были введены несколькими годами ранее для демонстрации невозможности доказательства постулата параллельности , также полезны для описания физического мира.

Однако трехмерная «пространственная часть» пространства Минковского остается пространством евклидовой геометрии. Это не относится к общей теории относительности , для которой геометрия пространственной части пространства-времени не является евклидовой геометрией. Например, если треугольник построен из трех лучей света, то в целом сумма внутренних углов не составит 180 градусов из-за силы тяжести. Относительно слабое гравитационное поле, такое как земное или солнечное, представлено метрикой, которая приблизительно, но не совсем, евклидова. До 20 века не существовало технологии, способной обнаружить эти отклонения лучей света от евклидовой геометрии, но Эйнштейн предсказал, что такие отклонения будут существовать. Позже они были подтверждены такими наблюдениями, как небольшое отклонение звездного света Солнцем во время солнечного затмения в 1919 году, и такие соображения теперь являются неотъемлемой частью программного обеспечения, которое управляет системой GPS .

Как описание строения пространства

Евклид считал, что его аксиомы являются самоочевидными утверждениями о физической реальности. Доказательства Евклида основаны на предположениях, возможно, неочевидных в основных аксиомах Евклида. в частности, что определенные движения фигур не меняют их геометрических свойств, таких как длины сторон и внутренних углов, так называемые евклидовы движения , которые включают перемещения, отражения и вращения фигур. Постулат 2 (продолжение линии), рассматриваемый как физическое описание пространства, утверждает, что пространство не имеет дыр или границ; постулат 4 (равенство прямых углов) гласит, что пространство изотропно и фигуры можно перемещать в любое место, сохраняя конгруэнтность ; и постулат 5 ( постулат параллельности ) о том, что пространство плоское (не имеет внутренней кривизны ).

Как обсуждалось выше, Альберта Эйнштейна существенно теория относительности модифицирует эту точку зрения.

Неоднозначный характер аксиом, первоначально сформулированных Евклидом, позволяет различным комментаторам расходиться во мнениях по поводу некоторых других их последствий для структуры пространства, например, о том, бесконечно оно или нет. (см. ниже) и какова его топология . Современные, более строгие переформулировки системы обычно стремятся к более четкому разделению этих вопросов. Интерпретируя аксиомы Евклида в духе этого более современного подхода, аксиомы 1–4 согласуются либо с бесконечным, либо с конечным пространством (как в эллиптической геометрии ), а все пять аксиом согласуются с различными топологиями (например, плоскость, цилиндр , или тор для двумерной евклидовой геометрии).

Лечение бесконечности

Бесконечные объекты

Евклид иногда явно различал «конечные линии» (например, Постулат 2) и « бесконечные линии» (книга I, предложение 12). Однако он обычно не делал таких различий, если в них не было необходимости. Постулаты не относятся явно к бесконечным линиям, хотя, например, некоторые комментаторы интерпретируют постулат 3 (существование круга любого радиуса) как предполагающий, что пространство бесконечно.

Понятие бесконечно малых величин ранее широко обсуждалось в Элейской школе , но никто не смог поставить их на прочную логическую основу, при этом возникали такие парадоксы, как парадокс Зенона , которые не были решены к всеобщему удовлетворению. Евклид использовал метод исчерпания, а не бесконечно малых.

Более поздние древние комментаторы, такие как Прокл (410–485 гг. н.э.), рассматривали многие вопросы о бесконечности как вопросы, требующие доказательства, и, например, Прокл утверждал, что доказал бесконечную делимость прямой, основываясь на доказательстве от противного, в котором он рассматривал случаи четного и нечетного числа составляющих его точек.

На рубеже 20-го века Отто Штольц , Поль дю Буа-Реймон , Джузеппе Веронезе и другие создали противоречивые работы по неархимедовым моделям евклидовой геометрии, в которых расстояние между двумя точками может быть бесконечным или бесконечно малым, в книге Ньютона. – смысл Лейбница . Пятьдесят лет спустя Авраам Робинсон предоставил строгое логическое обоснование работе Веронезе.

Бесконечные процессы

Древние геометры, возможно, считали постулат о параллельности (что две параллельные линии никогда не пересекаются) менее достоверным, чем другие, поскольку он утверждает о бесконечно удаленных областях пространства и поэтому не может быть физически проверен.

Современная формулировка доказательства по индукции не была разработана до 17 века, но некоторые более поздние комментаторы считают ее неявной в некоторых доказательствах Евклида, например, в доказательстве бесконечности простых чисел.

Предполагаемые парадоксы, включающие бесконечные ряды, такие как парадокс Зенона , возникли еще до Евклида. Евклид избегал таких обсуждений, приведя, например, выражение для частных сумм геометрической прогрессии в IX.35, не комментируя возможность допустить, чтобы число членов стало бесконечным.

Логическая основа

См. также: аксиомы Гильберта , аксиоматическая система и действительное замкнутое поле.

Классическая логика

Евклид часто использовал метод доказательства от противного , и поэтому традиционное изложение евклидовой геометрии предполагает классическую логику , в которой каждое предложение либо истинно, либо ложно, т. е. для любого предложения P предложение «P или не P» автоматически истинно. .

Современные стандарты строгости

Помещение евклидовой геометрии на прочную аксиоматическую основу было заботой математиков на протяжении веков. Роль примитивных понятий или неопределенных концепций была четко выдвинута Алессандро Падоа из делегации Пеано на Парижской конференции 1900 года:

... когда мы начинаем формулировать теорию, мы можем представить, что неопределенные символы полностью лишены значения и что недоказанные утверждения являются просто условиями, наложенными на неопределенные символы.

Тогда система идей , которую мы изначально выбрали, — это просто одна из интерпретаций неопределенных символов; но... эта интерпретация может быть проигнорирована читателем, который волен заменить ее в своем уме другой интерпретацией ... которая удовлетворяет условиям...

Таким образом, логические вопросы становятся совершенно независимыми от эмпирических или психологических вопросов...

Тогда систему неопределенных символов можно рассматривать как абстракцию, полученную из специализированных теорий , которые возникают, когда... система неопределенных символов последовательно заменяется каждой из интерпретаций...

- Падоа, Очерк алгебраической теории целых чисел с логическим введением в любую дедуктивную теорию.

То есть математика — это контекстно-независимые знания в иерархической структуре. Как сказал Бертран Рассел :

Если наша гипотеза касается чего угодно , а не какой-то одной или нескольких конкретных вещей, то наши выводы составляют математику. Таким образом, математику можно определить как предмет, в котором мы никогда не знаем, о чем говорим, и истинно ли то, что мы говорим.

- Бертран Рассел, Математика и метафизики

Такие основополагающие подходы варьируются между фундаментализмом и формализмом .

Аксиоматические формулировки

Геометрия – это наука о правильном рассуждении о неправильных фигурах.

- Джордж Полиа , Как решить эту проблему , с. 208

• Аксиомы Евклида: В своей диссертации в Тринити-колледже в Кембридже Бертран Рассел резюмировал меняющуюся роль геометрии Евклида в умах философов того времени. Это был конфликт между определенным знанием, независимым от эксперимента, и эмпиризмом, требующим экспериментального ввода. Эта проблема стала ясна, когда было обнаружено, что постулат о параллельности не обязательно был действительным, и его применимость была эмпирическим вопросом, решающим, была ли применимая геометрия евклидовой или неевклидовой .
• Аксиомы Гильберта : Целью аксиом Гильберта было определение простого и полного набора независимых аксиом, из которых можно было бы вывести наиболее важные геометрические теоремы. Выдающиеся цели заключались в том, чтобы сделать евклидову геометрию строгой (избегая скрытых предположений) и прояснить последствия постулата параллельности.
• Аксиомы Биркгофа : Биркгоф предложил четыре постулата евклидовой геометрии, которые можно подтвердить экспериментально с помощью масштаба и транспортира. Эта система во многом опирается на свойства действительных чисел . Понятия угла и расстояния становятся примитивными понятиями.
• Аксиомы Тарского : Альфред Тарский (1902–1983) и его ученики определили элементарную евклидову геометрию как геометрию, которая может быть выражена в логике первого порядка и не зависит от теории множеств в качестве своей логической основы. в отличие от аксиом Гильберта, которые включают множества точек. непротиворечива и полна Тарский доказал, что его аксиоматическая формулировка элементарной евклидовой геометрии в определенном смысле : существует алгоритм, который для каждого предложения может быть показан либо истинным, либо ложным. (Это не нарушает теорему Гёделя , поскольку евклидова геометрия не может описать достаточное количество арифметики для применения этой теоремы. ) Это эквивалентно разрешимости реальных замкнутых полей , моделью которых является элементарная евклидова геометрия.

См. также

• Абсолютная геометрия
• Аналитическая геометрия
• Аксиомы Биркгофа
• Декартова система координат
• Аксиомы Гильберта
• Геометрия падения
• Список программного обеспечения для интерактивной геометрии
• Метрическое пространство
• Неевклидова геометрия
• Упорядоченная геометрия
• Постулат параллельности
• Теория типов

Классические теоремы

• Теорема о биссектрисе угла
• Теорема о бабочке
• Теорема Чевы
• Формула Герона
• Теорема Менелая
• Девятиточечный круг
• Теорема Пифагора

Ссылки

• Болл, У. В. Роуз (1960). Краткий отчет об истории математики (4-е изд. [Перепечатка. Оригинальная публикация: Лондон: Macmillan & Co., 1908] изд.). Нью-Йорк: Dover Publications. стр. 50–62 . ISBN  0-486-20630-0 .
• Коксетер, HSM (1961). Введение в геометрию . Нью-Йорк: Уайли.
• Ивс, Ховард (1963). Обзор геометрии (том первый) . Аллин и Бэкон.
• Хит, Томас Л. (1956). Тринадцать книг «Элементов Евклида» (2-е изд. [Факсимиле. Оригинальная публикация: Cambridge University Press, 1925] изд.). Нью-Йорк: Dover Publications. В 3-х т.: т. 1 ISBN   0-486-60088-2 , том. 2 ISBN   0-486-60089-0 , том. 3 ISBN   0-486-60090-4 . Авторитетный перевод «Начал» Евклида, сделанный Хитом, а также его обширные исторические исследования и подробные комментарии по всему тексту.
• Миснер, Чарльз В .; Торн, Кип С .; Уилер, Джон Арчибальд (1973). Гравитация . У. Х. Фриман.
• Млодинов (2001). Окно Евклида . Свободная пресса. ISBN  9780684865232 .
• Нагель, Э.; Ньюман, младший (1958). Доказательство Гёделя . Издательство Нью-Йоркского университета.
• Тарский, Альфред (1951). Метод принятия решений для элементарной алгебры и геометрии . унив. из Калифорнии Пресс.
• Стиллвелл, Джон (январь 2001 г.). «История 120 ячеек» (PDF) . Уведомления АМС . 48 (1): 17–25.
• Перес-Грасиа, Альба; Томас, Федерико (2017). «О факторизации Кэли четырехмерных вращений и приложениях» (PDF) . Адв. Прил. Алгебры Клиффорда . 27 : 523–538. дои : 10.1007/s00006-016-0683-9 . hdl : 2117/113067 . S2CID   12350382 .

Внешние ссылки

• «Евклидова геометрия» , Математическая энциклопедия , EMS Press , 2001 [1994]
• «Плоская тригонометрия» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Киран Кедлайя, Geometry Unbound. Архивировано 26 октября 2011 г. в Wayback Machine (обработка с использованием аналитической геометрии; формат PDF, лицензия GFDL).