Ограниченная вариация

В математическом анализе функция ограниченной вариации , также известная как BV функция , представляет собой вещественнозначную обладающей этим свойством , функцию которой , полная вариация ограничена (конечна): график функции, ведет себя хорошо в точном смысле. Для непрерывной функции одной переменной наличие ограниченной вариации означает, что y , пренебрегая вкладом движения расстояние вдоль направления оси вдоль x оси , пройденное точкой, движущейся по графику, имеет конечное значение. Для непрерывной функции нескольких переменных смысл определения тот же, за исключением того, что рассматриваемый непрерывный путь не может быть всем графиком данной функции (который является гиперповерхностью в данном случае ), а может быть каждое пересечение самого графика с гиперплоскостью (в случае функций двух переменных — плоскостью ), параллельной фиксированной оси x и оси y .

Функции ограниченной вариации — это именно те функции, по отношению к которым можно найти интегралы Римана–Стилтьеса от всех непрерывных функций.

Другая характеристика утверждает, что функции ограниченной вариации на компактном интервале — это в точности те функции f , которые можно записать как разность g − h , где и g , и h ограничены монотонно . В частности, функция BV может иметь разрывы, но их не более счетного числа.

В случае нескольких переменных функция f , определенная на открытом подмножестве Ω множества $\mathbb {R} ^{n}$ Говорят, что она имеет ограниченную вариацию, если ее распределительная производная является векторной конечной мерой Радона .

Одним из наиболее важных аспектов функций ограниченной вариации является то, что они образуют алгебру разрывных функций , первая производная которых существует почти всюду : благодаря этому они могут и часто используются для определения обобщенных решений нелинейных задач, включающих функционалы , обычные и уравнения в частных производных в математике , физике и технике .

Имеются следующие цепочки включений для непрерывных функций на замкнутом ограниченном интервале вещественной прямой:

Непрерывно дифференцируемая ⊆ Липшицева непрерывная ⊆ абсолютно непрерывная ⊆ непрерывная и ограниченная вариация ⊆ дифференцируемая почти всюду

История

По словам Бориса Голубова, БВ-функции одной переменной были впервые введены Камиллой Жорданом в статье ( Жордан, 1881 г. ), посвященной сходимости рядов Фурье . Первый успешный шаг в обобщении этой концепции на функции многих переменных был сделан Леонидой Тонелли , который ввел класс непрерывных функций BV в 1926 году ( Cesari 1986 , стр. 47–48), чтобы расширить свой прямой метод поиска решений задач вариационного исчисления более чем одной переменной. Десять лет спустя, в ( Cesari 1936 ), Ламберто Чезари изменил требование непрерывности в определении Тонелли на менее ограничительное интегрируемости требование , впервые получив класс функций ограниченной вариации нескольких переменных в его полной общности: как это сделал ранее Джордан ему он применил эту концепцию для решения проблемы сходимости рядов Фурье, но для функций двух переменных . После него несколько авторов применили функции БВ для изучения рядов Фурье от нескольких переменных, геометрической теории меры , вариационного исчисления и математической физики . Ренато Каччиопполи и Эннио Де Джорджи использовали их для определения меры негладких ( границ множеств см . в статье « Набор Каччиопполи дополнительную информацию »). Ольга Арсеньевна Олейник изложила свой взгляд на обобщенные решения задачи. нелинейные уравнения в частных производных как функции из пространства BV в статье ( Олейник 1957 ), и смог построить обобщенное решение ограниченной вариации уравнения в частных производных первого порядка в статье ( Олейник 1959 ): несколько лет спустя Эдвард Д. Конвей и Джоэл А. Смоллер применили BV-функции к исследованию одного нелинейного гиперболического уравнения в частных производных первого порядка в статье ( Conway & Smoller 1966 ), доказав, что решение задачи Коши для таких уравнений является функцией. ограниченная вариация при условии, что начальное значение принадлежит тому же классу. Айзик Исаакович Вольперт широко разработал исчисление для БВ-функций: в статье ( Вольперт, 1967 ) он доказал цепное правило для БВ-функций , а в книге ( Худжаев, Вольперт, 1985 ) совместно со своим учеником Сергеем Ивановичем Худжаев широко исследовал свойства БВ-функций и их применение. Его формула цепного правила позже была расширена Луиджи Амбросио и Джанни Даль Масо. в статье ( Амбросио и Даль Масо, 1990 ).

Формальное определение

БВ-функции одной переменной

Определение 1.1. Полное изменение вещественной f (или, в более общем смысле, функции комплексной) , определенной на интервале $[a,b]\subset \mathbb {R}$ это количество

$V_{a}^{b}(f)=\sup _{P\in {\mathcal {P}}}\sum _{i=0}^{n_{P}-1}|f(x_{i+1})-f(x_{i})|.\,$

где верхняя грань берется по множеству ${\textstyle {\mathcal {P}}=\left\{P=\{x_{0},\dots ,x_{n_{P}}\}\mid P{\text{ is a partition of }}[a,b]{\text{ satisfying }}x_{i}\leq x_{i+1}{\text{ for }}0\leq i\leq n_{P}-1\right\}}$ всех разбиений рассматриваемого интервала.

Если f дифференцируема длины и ее производная интегрируема по Риману, ее полная вариация представляет собой вертикальную составляющую дуги ее графика, то есть:

$V_{a}^{b}(f)=\int _{a}^{b}|f'(x)|\,\mathrm {d} x.$

Определение 1.2. Действительнозначная функция $f$ на действительной прямой называется ограниченной вариацией ( функция BV ) на выбранном интервале $[a,b]\subset \mathbb {R}$ если его полная вариация конечна, т.е.

$f\in \operatorname {BV} ([a,b])\iff V_{a}^{b}(f)<+\infty$

Можно доказать, что действительная функция $f$ имеет ограниченную вариацию $[a,b]$ тогда и только тогда, когда это можно записать как разность $f=f_{1}-f_{2}$ двух неубывающих функций $f_{1}$ и $f_{2}$ на $[a,b]$: этот результат известен как жордановое разложение функции и связан с жордановым разложением меры .

Через интеграл Стилтьеса любая функция ограниченной вариации на замкнутом интервале $[a,b]$ определяет ограниченный линейный функционал на $C([a,b])$. В этом особом случае Теорема о представлении Рисса –Маркова–Какутани утверждает, что каждый ограниченный линейный функционал возникает таким образом единственным образом. Нормированные положительные функционалы или вероятностные меры соответствуют положительным неубывающим полунепрерывным снизу функциям . Эта точка зрения сыграла важную роль в спектральная теория , в частности, в его применении к обыкновенным дифференциальным уравнениям .

БВ-функции нескольких переменных

Функции ограниченной вариации, функции BV , — это функции, производная распределения которых является конечной Радоновая мера . Точнее:

Определение 2.1. Позволять $\Omega$ быть открытым подмножеством $\mathbb {R} ^{n}$. Функция $u$ принадлежащий $L^{1}(\Omega )$ говорят об ограниченной вариации ( функция BV ) и пишут

$u\in \operatorname {\operatorname {BV} } (\Omega )$

если существует конечная векторная мера Радона $Du\in {\mathcal {M}}(\Omega ,\mathbb {R} ^{n})$ такая, что имеет место равенство

$\int _{\Omega }u(x)\operatorname {div} {\boldsymbol {\phi }}(x)\,\mathrm {d} x=-\int _{\Omega }\langle {\boldsymbol {\phi }},Du(x)\rangle \qquad \forall {\boldsymbol {\phi }}\in C_{c}^{1}(\Omega ,\mathbb {R} ^{n})$

то есть, $u$ определяет линейный функционал в пространстве $C_{c}^{1}(\Omega ,\mathbb {R} ^{n})$ непрерывно дифференцируемых векторных функций ${\boldsymbol {\phi }}$ компактной поддержки, содержащейся в $\Omega$: векторная мера $Du$ следовательно, распределительный или слабый градиент представляет собой , $u$.

BV можно определить эквивалентно следующим образом.

Определение 2.2. Дана функция $u$ принадлежащий $L^{1}(\Omega )$, общее изменение $u$ в $\Omega$ определяется как

$V(u,\Omega ):=\sup \left\{\int _{\Omega }u(x)\operatorname {div} {\boldsymbol {\phi }}(x)\,\mathrm {d} x:{\boldsymbol {\phi }}\in C_{c}^{1}(\Omega ,\mathbb {R} ^{n}),\ \Vert {\boldsymbol {\phi }}\Vert _{L^{\infty }(\Omega )}\leq 1\right\}$

где $\Vert \;\Vert _{L^{\infty }(\Omega )}$ является основной высшей нормой . Иногда, особенно в теории множеств Каччиопполи , используются следующие обозначения

$\int _{\Omega }\vert Du\vert =V(u,\Omega )$

чтобы подчеркнуть это $V(u,\Omega )$ — это общее распределения / слабого градиента изменение $u$. Это обозначение напоминает также, что если $u$ имеет класс $C^{1}$ (т.е. непрерывная и дифференцируемая функция , имеющая непрерывные производные ), то ее изменение в точности равно интегралу абсолютного значения ее градиента .

Тогда пространство функций ограниченной вариации ( функций BV ) можно определить как

$\operatorname {\operatorname {BV} } (\Omega )=\{u\in L^{1}(\Omega )\colon V(u,\Omega )<+\infty \}$

Оба определения эквивалентны, поскольку если $V(u,\Omega )<+\infty$ затем

$\left|\int _{\Omega }u(x)\operatorname {div} {\boldsymbol {\phi }}(x)\,\mathrm {d} x\right|\leq V(u,\Omega )\Vert {\boldsymbol {\phi }}\Vert _{L^{\infty }(\Omega )}\qquad \forall {\boldsymbol {\phi }}\in C_{c}^{1}(\Omega ,\mathbb {R} ^{n})$

поэтому ${\textstyle \displaystyle {\boldsymbol {\phi }}\mapsto \,\int _{\Omega }u(x)\operatorname {div} {\boldsymbol {\phi }}(x)\,dx}$ определяет непрерывный линейный функционал в пространстве $C_{c}^{1}(\Omega ,\mathbb {R} ^{n})$. С $C_{c}^{1}(\Omega ,\mathbb {R} ^{n})\subset C^{0}(\Omega ,\mathbb {R} ^{n})$ как линейное подпространство , этот непрерывный линейный функционал можно непрерывно и линейно продолжить на все $C^{0}(\Omega ,\mathbb {R} ^{n})$ по теореме Хана-Банаха . Следовательно, непрерывный линейный функционал определяет меру Радона по теореме о представлении Рисса–Маркова–Какутани .

Локальные функции BV

Если функциональное пространство , локально интегрируемых функций т.е. функций, принадлежащих $L_{\text{loc}}^{1}(\Omega )$, рассматривается в предыдущих определениях 1.2 , 2.1 и 2.2 вместо пространства глобально интегрируемых функций , то определенное функциональное пространство является пространством функций локально ограниченной вариации . Точнее, развивая эту идею для определения 2.2 , локальная вариация определяется следующим образом:

$V(u,U):=\sup \left\{\int _{\Omega }u(x)\operatorname {div} {\boldsymbol {\phi }}(x)\,\mathrm {d} x:{\boldsymbol {\phi }}\in C_{c}^{1}(U,\mathbb {R} ^{n}),\ \Vert {\boldsymbol {\phi }}\Vert _{L^{\infty }(\Omega )}\leq 1\right\}$

для каждого набора $U\in {\mathcal {O}}_{c}(\Omega )$, определив ${\mathcal {O}}_{c}(\Omega )$ как множество всех предкомпактных открытых подмножеств $\Omega$ относительно стандартной топологии конечномерных и соответственно векторных пространств класс функций локально ограниченной вариации определяется как

$\operatorname {BV} _{\text{loc}}(\Omega )=\{u\in L_{\text{loc}}^{1}(\Omega )\colon \,(\forall U\in {\mathcal {O}}_{c}(\Omega ))\,V(u,U)<+\infty \}$

Обозначения

По сути, существуют два различных соглашения для обозначения пространств функций локально или глобально ограниченной вариации, и, к сожалению, они очень похожи: первое, принятое в этой статье, используется, например, в ссылках Джусти (1984). (частично), Худжаев и Вольперт (1985) (частично), Джаквинта, Модика и Соучек (1998) и следующий:

• $\operatorname {\operatorname {BV} } (\Omega )$ определяет пространство функций глобально ограниченной вариации
• $\operatorname {\operatorname {BV} } _{\text{loc}}(\Omega )$ идентифицирует пространство функций локально ограниченной вариации

Второе, принятое в работах Вольперта (1967) и Мазья (1985) (частично), следующее:

• ${\overline {\operatorname {\operatorname {BV} } }}(\Omega )$ определяет пространство функций глобально ограниченной вариации
• $\operatorname {\operatorname {BV} } (\Omega )$ идентифицирует пространство функций локально ограниченной вариации

Основные свойства

только свойства, общие для функций одной переменной и функций В дальнейшем будут рассматриваться нескольких переменных, а доказательства будут проводиться только для функций нескольких переменных, так как доказательство для случая одной переменной представляет собой непосредственную адаптацию нескольких переменных. Случай переменных: также в каждом разделе будет указано, является ли свойство общим и для функций локально ограниченной вариации или нет. ссылки ( Giusti 1984 , стр. 7–9), ( Hudjaev & Vol'pert 1985 ) и ( Màlek et al. 1996 Широко используются ).

BV-функции имеют только скачкообразные или устранимые разрывы.

В случае одной переменной утверждение ясно: для каждой точки $x_{0}$ в интервале $[a,b]\subset \mathbb {R}$ определения функции $u$, верно любое из следующих двух утверждений

$\lim _{x\rightarrow x_{0^{-}}}\!\!\!u(x)=\!\!\!\lim _{x\rightarrow x_{0^{+}}}\!\!\!u(x)$

$\lim _{x\rightarrow x_{0^{-}}}\!\!\!u(x)\neq \!\!\!\lim _{x\rightarrow x_{0^{+}}}\!\!\!u(x)$

при этом оба предела существуют и конечны. В случае функций нескольких переменных необходимо понять некоторые предпосылки: прежде всего, существует континуум направлений , по которым можно приблизиться к данной точке. $x_{0}$ принадлежность к домену $\Omega$⊂ $\mathbb {R} ^{n}$. Необходимо уточнить подходящее понятие предела : выбор единичного вектора. ${\boldsymbol {\hat {a}}}\in \mathbb {R} ^{n}$ можно разделить $\Omega$ в двух комплектах

$\Omega _{({\boldsymbol {\hat {a}}},{\boldsymbol {x}}_{0})}=\Omega \cap \{{\boldsymbol {x}}\in \mathbb {R} ^{n}|\langle {\boldsymbol {x}}-{\boldsymbol {x}}_{0},{\boldsymbol {\hat {a}}}\rangle >0\}\qquad \Omega _{(-{\boldsymbol {\hat {a}}},{\boldsymbol {x}}_{0})}=\Omega \cap \{{\boldsymbol {x}}\in \mathbb {R} ^{n}|\langle {\boldsymbol {x}}-{\boldsymbol {x}}_{0},-{\boldsymbol {\hat {a}}}\rangle >0\}$

Тогда для каждой точки $x_{0}$ принадлежность к домену $\Omega \in \mathbb {R} ^{n}$ функции BV $u$, только одно из следующих двух утверждений верно

$\lim _{\overset {{\boldsymbol {x}}\rightarrow {\boldsymbol {x}}_{0}}{{\boldsymbol {x}}\in \Omega _{({\boldsymbol {\hat {a}}},{\boldsymbol {x}}_{0})}}}\!\!\!\!\!\!u({\boldsymbol {x}})=\!\!\!\!\!\!\!\lim _{\overset {{\boldsymbol {x}}\rightarrow {\boldsymbol {x}}_{0}}{{\boldsymbol {x}}\in \Omega _{(-{\boldsymbol {\hat {a}}},{\boldsymbol {x}}_{0})}}}\!\!\!\!\!\!\!u({\boldsymbol {x}})$

$\lim _{\overset {{\boldsymbol {x}}\rightarrow {\boldsymbol {x}}_{0}}{{\boldsymbol {x}}\in \Omega _{({\boldsymbol {\hat {a}}},{\boldsymbol {x}}_{0})}}}\!\!\!\!\!\!u({\boldsymbol {x}})\neq \!\!\!\!\!\!\!\lim _{\overset {{\boldsymbol {x}}\rightarrow {\boldsymbol {x}}_{0}}{{\boldsymbol {x}}\in \Omega _{(-{\boldsymbol {\hat {a}}},{\boldsymbol {x}}_{0})}}}\!\!\!\!\!\!\!u({\boldsymbol {x}})$

или $x_{0}$ к подмножеству принадлежит $\Omega$ имея ноль $n-1$-мерная мера Хаусдорфа . Количества

$\lim _{\overset {{\boldsymbol {x}}\rightarrow {\boldsymbol {x}}_{0}}{{\boldsymbol {x}}\in \Omega _{({\boldsymbol {\hat {a}}},{\boldsymbol {x}}_{0})}}}\!\!\!\!\!\!u({\boldsymbol {x}})=u_{\boldsymbol {\hat {a}}}({\boldsymbol {x}}_{0})\qquad \lim _{\overset {{\boldsymbol {x}}\rightarrow {\boldsymbol {x}}_{0}}{{\boldsymbol {x}}\in \Omega _{(-{\boldsymbol {\hat {a}}},{\boldsymbol {x}}_{0})}}}\!\!\!\!\!\!\!u({\boldsymbol {x}})=u_{-{\boldsymbol {\hat {a}}}}({\boldsymbol {x}}_{0})$

называются приближенными пределами функции BV $u$ в точку $x_{0}$.

V (⋅, Ω) полунепрерывен снизу на L ¹ (Ой)

Функционал ​ $V(\cdot ,\Omega ):\operatorname {\operatorname {BV} } (\Omega )\rightarrow \mathbb {R} ^{+}$ является полунепрерывным снизу : чтобы убедиться в этом, выберите последовательность Коши BV-функций $\{u_{n}\}_{n\in \mathbb {N} }$ сходящиеся к $u\in L_{\text{loc}}^{1}(\Omega )$. Тогда, поскольку все функции последовательности и их предельная функция интегрируемы и по определению нижнего предела

${\begin{aligned}\liminf _{n\rightarrow \infty }V(u_{n},\Omega )&\geq \liminf _{n\rightarrow \infty }\int _{\Omega }u_{n}(x)\operatorname {div} \,{\boldsymbol {\phi }}\,\mathrm {d} x\\&\geq \int _{\Omega }\lim _{n\rightarrow \infty }u_{n}(x)\operatorname {div} \,{\boldsymbol {\phi }}\,\mathrm {d} x\\&=\int _{\Omega }u(x)\operatorname {div} {\boldsymbol {\phi }}\,\mathrm {d} x\qquad \forall {\boldsymbol {\phi }}\in C_{c}^{1}(\Omega ,\mathbb {R} ^{n}),\quad \Vert {\boldsymbol {\phi }}\Vert _{L^{\infty }(\Omega )}\leq 1\end{aligned}}$

Теперь рассмотрим верхнюю грань на множестве функций ${\boldsymbol {\phi }}\in C_{c}^{1}(\Omega ,\mathbb {R} ^{n})$ такой, что $\Vert {\boldsymbol {\phi }}\Vert _{L^{\infty }(\Omega )}\leq 1$ то справедливо следующее неравенство

$\liminf _{n\rightarrow \infty }V(u_{n},\Omega )\geq V(u,\Omega )$

что и есть определение полунепрерывности снизу .

BV(Ω) — банахово пространство.

По определению $\operatorname {\operatorname {BV} } (\Omega )$ является подмножеством ​ $L^{1}(\Omega )$, а линейность следует из свойств линейности определяющего интеграла , т.е.

${\begin{aligned}\int _{\Omega }[u(x)+v(x)]\operatorname {div} {\boldsymbol {\phi }}(x)\,\mathrm {d} x&=\int _{\Omega }u(x)\operatorname {div} {\boldsymbol {\phi }}(x)\,\mathrm {d} x+\int _{\Omega }v(x)\operatorname {div} {\boldsymbol {\phi }}(x)\,\mathrm {d} x=\\&=-\int _{\Omega }\langle {\boldsymbol {\phi }}(x),Du(x)\rangle -\int _{\Omega }\langle {\boldsymbol {\phi }}(x),Dv(x)\rangle =-\int _{\Omega }\langle {\boldsymbol {\phi }}(x),[Du(x)+Dv(x)]\rangle \end{aligned}}$

для всех $\phi \in C_{c}^{1}(\Omega ,\mathbb {R} ^{n})$ поэтому $u+v\in \operatorname {\operatorname {BV} } (\Omega )$для всех $u,v\in \operatorname {\operatorname {BV} } (\Omega )$, и

$\int _{\Omega }c\cdot u(x)\operatorname {div} {\boldsymbol {\phi }}(x)\,\mathrm {d} x=c\int _{\Omega }u(x)\operatorname {div} {\boldsymbol {\phi }}(x)\,\mathrm {d} x=-c\int _{\Omega }\langle {\boldsymbol {\phi }}(x),Du(x)\rangle$

для всех $c\in \mathbb {R}$, поэтому $cu\in \operatorname {\operatorname {BV} } (\Omega )$ для всех $u\in \operatorname {\operatorname {BV} } (\Omega )$, и все $c\in \mathbb {R}$. Из доказанных свойств векторного пространства следует, что $\operatorname {\operatorname {BV} } (\Omega )$ является векторным подпространством $L^{1}(\Omega )$. Рассмотрим теперь функцию $\|\;\|_{\operatorname {BV} }:\operatorname {\operatorname {BV} } (\Omega )\rightarrow \mathbb {R} ^{+}$ определяется как

$\|u\|_{\operatorname {BV} }:=\|u\|_{L^{1}}+V(u,\Omega )$

где $\|\;\|_{L^{1}}$ это обычный $L^{1}(\Omega )$ норма : легко доказать, что это норма на $\operatorname {\operatorname {BV} } (\Omega )$. Чтобы увидеть это $\operatorname {\operatorname {BV} } (\Omega )$ является полным относительно него, т. е. является банаховым пространством , рассмотрим последовательность Коши $\{u_{n}\}_{n\in \mathbb {N} }$ в $\operatorname {\operatorname {BV} } (\Omega )$. По определению это также последовательность Коши в $L^{1}(\Omega )$ и поэтому имеет предел $u$ в $L^{1}(\Omega )$: с $u_{n}$ ограничен $\operatorname {\operatorname {BV} } (\Omega )$ для каждого $n$, затем $\Vert u\Vert _{\operatorname {BV} }<+\infty$ снизу полунепрерывностью вариации $V(\cdot ,\Omega )$, поэтому $u$ является функцией BV. Наконец, снова в силу полунепрерывности снизу, выбрав произвольно малое положительное число $\varepsilon$

$\Vert u_{j}-u_{k}\Vert _{\operatorname {BV} }<\varepsilon \quad \forall j,k\geq N\in \mathbb {N} \quad \Rightarrow \quad V(u_{k}-u,\Omega )\leq \liminf _{j\rightarrow +\infty }V(u_{k}-u_{j},\Omega )\leq \varepsilon$

Из этого мы делаем вывод, что $V(\cdot ,\Omega )$ является непрерывным, потому что это норма.

BV(Ω) не сепарабельна

Чтобы убедиться в этом, достаточно рассмотреть следующий пример, принадлежащий пространству $\operatorname {\operatorname {BV} } ([0,1])$: для каждого 0 < α < 1 определим

$\chi _{\alpha }=\chi _{[\alpha ,1]}={\begin{cases}0&{\mbox{if }}x\notin \;[\alpha ,1]\\1&{\mbox{if }}x\in [\alpha ,1]\end{cases}}$

как характеристическая функция левозамкнутого интервала $[\alpha ,1]$. Затем, выбрав $\alpha ,\beta \in [0,1]$ такой, что $\alpha \neq \beta$ справедливо следующее соотношение:

$\Vert \chi _{\alpha }-\chi _{\beta }\Vert _{\operatorname {BV} }=2$

Теперь, чтобы доказать, что каждое плотное подмножество $\operatorname {\operatorname {BV} } (]0,1[)$ не может быть счетным , достаточно убедиться, что для любого $\alpha \in [0,1]$ можно построить шары

$B_{\alpha }=\left\{\psi \in \operatorname {\operatorname {BV} } ([0,1]);\Vert \chi _{\alpha }-\psi \Vert _{\operatorname {BV} }\leq 1\right\}$

Очевидно, что эти шары попарно не пересекаются , а также представляют собой семейство множеств индексированное которого , индексный набор равен $[0,1]$. Это означает, что это семейство имеет мощность континуума : теперь, поскольку каждое плотное подмножество $\operatorname {\operatorname {BV} } ([0,1])$ должно иметь хотя бы одну точку внутри каждого члена этого семейства, его мощность не ниже мощности континуума и, следовательно, не может быть счетным подмножеством. Этот пример, очевидно, можно распространить на более высокие измерения, и, поскольку он затрагивает только локальные свойства , из него следует, что то же самое свойство верно и для $\operatorname {BV} _{loc}$.

Цепное правило для функций BV

Цепные правила для негладких функций очень важны в математике и математической физике, поскольку существует несколько важных физических моделей , поведение которых описывается функциями или функционалами с очень ограниченной степенью гладкости . В работе доказано следующее цепное правило ( Вольперт, 1967 , с. 248). Обратите внимание, что все частные производные следует интерпретировать в обобщенном смысле, т. е. как обобщенные производные .

Теорема . Позволять $f:\mathbb {R} ^{p}\rightarrow \mathbb {R}$ быть функцией класса $C^{1}$ (т.е. непрерывная и дифференцируемая функция , имеющая непрерывные производные ) и пусть ${\boldsymbol {u}}({\boldsymbol {x}})=(u_{1}({\boldsymbol {x}}),\ldots ,u_{p}({\boldsymbol {x}}))$ быть функцией в $\operatorname {\operatorname {BV} } (\Omega )$ с $\Omega$ являясь открытым подмножеством $\mathbb {R} ^{n}$. Затем $f\circ {\boldsymbol {u}}({\boldsymbol {x}})=f({\boldsymbol {u}}({\boldsymbol {x}}))\in \operatorname {\operatorname {BV} } (\Omega )$ и

${\frac {\partial f({\boldsymbol {u}}({\boldsymbol {x}}))}{\partial x_{i}}}=\sum _{k=1}^{p}{\frac {\partial {\bar {f}}({\boldsymbol {u}}({\boldsymbol {x}}))}{\partial u_{k}}}{\frac {\partial {u_{k}({\boldsymbol {x}})}}{\partial x_{i}}}\qquad \forall i=1,\ldots ,n$

где ${\bar {f}}({\boldsymbol {u}}({\boldsymbol {x}}))$ — среднее значение функции в точке $x\in \Omega$, определяемый как

${\bar {f}}({\boldsymbol {u}}({\boldsymbol {x}}))=\int _{0}^{1}f\left({\boldsymbol {u}}_{\boldsymbol {\hat {a}}}({\boldsymbol {x}})t+{\boldsymbol {u}}_{-{\boldsymbol {\hat {a}}}}({\boldsymbol {x}})(1-t)\right)\,dt$

Более общая цепного правила формула для липшицевых непрерывных функций $f:\mathbb {R} ^{p}\rightarrow \mathbb {R} ^{s}$ был найден Луиджи Амбросио и Джанни Даль Масо и опубликован в статье ( Амбросио и Даль Масо 1990 ). Однако даже эта формула имеет очень важные прямые следствия: использование $(u({\boldsymbol {x}}),v({\boldsymbol {x}}))$ вместо ${\boldsymbol {u}}({\boldsymbol {x}})$, где $v({\boldsymbol {x}})$ также является функцией «BV», и выбор $f((u,v))=uv$, предыдущая формула дает правило Лейбница для функций «BV»

${\frac {\partial v({\boldsymbol {x}})u({\boldsymbol {x}})}{\partial x_{i}}}={{\bar {u}}({\boldsymbol {x}})}{\frac {\partial v({\boldsymbol {x}})}{\partial x_{i}}}+{{\bar {v}}({\boldsymbol {x}})}{\frac {\partial u({\boldsymbol {x}})}{\partial x_{i}}}$

Это означает, что произведение двух функций ограниченной вариации снова является функцией ограниченной вариации , поэтому $\operatorname {\operatorname {BV} } (\Omega )$ является алгеброй .

BV(Ω) — банахова алгебра

Это свойство непосредственно следует из того, что $\operatorname {\operatorname {BV} } (\Omega )$ является банаховым пространством , а также ассоциативной алгеброй : это означает, что если $\{v_{n}\}$ и $\{u_{n}\}$ являются последовательностями Коши функций БВ, сходящимися соответственно к функциям $v$ и $u$ в $\operatorname {\operatorname {BV} } (\Omega )$, затем

${\begin{matrix}vu_{n}{\xrightarrow[{n\to \infty }]{}}vu\\v_{n}u{\xrightarrow[{n\to \infty }]{}}vu\end{matrix}}\quad \Longleftrightarrow \quad vu\in \operatorname {\operatorname {BV} } (\Omega )$

обычное произведение функций непрерывно по поэтому $\operatorname {\operatorname {BV} } (\Omega )$ относительно каждого аргумента, что делает это функциональное пространство банаховой алгеброй .

Обобщения и расширения

Взвешенные функции BV

можно обобщить Вышеупомянутое понятие общей вариации так, чтобы разные вариации имели разный вес. Точнее, пусть $\varphi :[0,+\infty )\longrightarrow [0,+\infty )$ — любая возрастающая функция такая, что $\varphi (0)=\varphi (0+)=\lim _{x\rightarrow 0_{+}}\varphi (x)=0$ ( весовая функция ) и пусть $f:[0,T]\longrightarrow X$ быть функцией из интервала $[0,T]$$\subset \mathbb {R}$ принятие значений в нормированном векторном пространстве $X$. Тогда ${\boldsymbol {\varphi }}$-вариация ​ $f$ над $[0,T]$ определяется как

$\mathop {\varphi {\text{-}}\operatorname {Var} } _{[0,T]}(f):=\sup \sum _{j=0}^{k}\varphi \left(|f(t_{j+1})-f(t_{j})|_{X}\right),$

где, как обычно, верхняя грань берется по всем конечным разбиениям интервала $[0,T]$, т.е. все конечные множества чисел действительных $t_{i}$ такой, что

$0=t_{0}<t_{1}<\cdots <t_{k}=T.$

Исходное понятие вариации, рассмотренное выше, представляет собой частный случай $\varphi$-вариант, для которого весовая функция является тождественной функцией : следовательно, интегрируемая функция $f$ называется взвешенной функцией BV (веса $\varphi$) тогда и только тогда, когда $\varphi$-вариация конечна.

$f\in \operatorname {BV} _{\varphi }([0,T];X)\iff \mathop {\varphi {\text{-}}\operatorname {Var} } _{[0,T]}(f)<+\infty$

Пространство $\operatorname {BV} _{\varphi }([0,T];X)$ является топологическим векторным пространством по норме

$\|f\|_{\operatorname {BV} _{\varphi }}:=\|f\|_{\infty }+\mathop {\varphi {\text{-}}\operatorname {Var} } _{[0,T]}(f),$

где $\|f\|_{\infty }$ обозначает обычную верхнюю норму $f$. Взвешенные функции BV были введены и изучены в полной мере Владиславом Орличем и Юлианом Муселяком в статье Musielak & Orlicz 1959 : Лоуренс Чисхолм Янг ранее изучал этот случай. $\varphi (x)=x^{p}$ где $p$ является положительным целым числом.

Функции СБВ

Функции SBV , т.е. специальные функции ограниченной вариации, были введены Луиджи Амбросио и Эннио Де Джорджи в статье ( Амбросио и Де Джорджи 1988 ), посвященной вариационным проблемам со свободным разрывом : с учетом открытого подмножества $\Omega$ из $\mathbb {R} ^{n}$, пространство $\operatorname {SBV} (\Omega )$ является собственным линейным подпространством $\operatorname {\operatorname {BV} } (\Omega )$, поскольку слабый градиент каждой принадлежащей ему функции состоит именно суммы из $n$- размеров поддержка и $n-1$- измерений поддержки мера и отсутствие терминов промежуточных измерений , как видно из следующего определения.

Определение . Дана локально интегрируемая функция $u$, затем $u\in \operatorname {SBV} (\Omega )$ тогда и только тогда, когда

1. Существуют две борелевские функции $f$ и $g$ домена ​ $\Omega$ и кодомен $\mathbb {R} ^{n}$ такой, что

$\int _{\Omega }\vert f\vert \,dH^{n}+\int _{\Omega }\vert g\vert \,dH^{n-1}<+\infty .$

2. Для всех непрерывно дифференцируемых вектор-функций $\phi$ компактной поддержки, содержащейся в $\Omega$, то есть для всех $\phi \in C_{c}^{1}(\Omega ,\mathbb {R} ^{n})$ верна следующая формула:

$\int _{\Omega }u\operatorname {div} \phi \,dH^{n}=\int _{\Omega }\langle \phi ,f\rangle \,dH^{n}+\int _{\Omega }\langle \phi ,g\rangle \,dH^{n-1}.$

где $H^{\alpha }$ это $\alpha$- мерная мера Хаусдорфа .

Подробности о свойствах функций SBV можно найти в работах, цитируемых в разделе библиографии: в частности, статья ( De Giorgi 1992 ) содержит полезную библиографию .

BV-последовательности

В качестве конкретных примеров пространств банаховых Данфорд и Шварц (1958 , глава IV) рассматривают пространства последовательностей ограниченной вариации в дополнение к пространствам функций ограниченной вариации. Полная вариация последовательности x = ( x _i ) действительных или комплексных чисел определяется формулой

$\operatorname {TV} (x)=\sum _{i=1}^{\infty }|x_{i+1}-x_{i}|.$

Пространство всех последовательностей конечной полной вариации обозначается BV. Норма БВ определяется выражением

$\|x\|_{\operatorname {BV} }=|x_{1}|+\operatorname {TV} (x)=|x_{1}|+\sum _{i=1}^{\infty }|x_{i+1}-x_{i}|.$

С этой нормой пространство BV является банаховым пространством, изоморфным $\ell _{1}$.

Сама полная вариация определяет норму на некотором подпространстве BV, обозначаемом BV ₀ , состоящем из последовательностей x = ( x _i ), для которых

$\lim _{n\to \infty }x_{n}=0.$

Норму на BV ₀ обозначим

$\|x\|_{\operatorname {BV} _{0}}=\operatorname {TV} (x)=\sum _{i=1}^{\infty }|x_{i+1}-x_{i}|.$

По отношению к этой норме BV ₀ также становится банаховым пространством, изоморфным и изометричным пространству $\ell _{1}$ (хотя и не естественным путем).

Меры ограниченной вариации

Знаковая комплексная или ( ) мера $\mu$ на измеримом пространстве $(X,\Sigma )$ называется ограниченной вариацией, если ее полная вариация $\Vert \mu \Vert =|\mu |(X)$ ограничен: см. Халмош (1950 , стр. 123), Колмогоров и Фомин (1969 , стр. 346) или статью « Полная вариация » для получения более подробной информации.

Примеры

Функция f ( x ) = sin(1/ x ) не имеет ограниченной вариации на интервале $[0,2/\pi ]$.

Как упоминалось во введении, два больших класса примеров функций BV — это монотонные функции и абсолютно непрерывные функции. Для отрицательного примера: функция

$f(x)={\begin{cases}0,&{\mbox{if }}x=0\\\sin(1/x),&{\mbox{if }}x\neq 0\end{cases}}$

имеет не ограниченной вариации на интервале $[0,2/\pi ]$

Функция f ( x ) = x sin(1/ x ) не имеет ограниченной вариации на интервале $[0,2/\pi ]$.

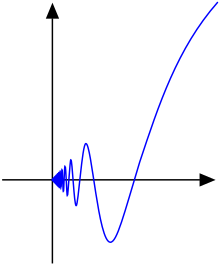
Хотя это труднее увидеть, непрерывная функция

$f(x)={\begin{cases}0,&{\mbox{if }}x=0\\x\sin(1/x),&{\mbox{if }}x\neq 0\end{cases}}$

имеет не ограниченной вариации на интервале $[0,2/\pi ]$ или.

Функция f ( x ) = x ² sin(1/ x ) имеет ограниченную вариацию на интервале $[0,2/\pi ]$.

В то же время функция

$f(x)={\begin{cases}0,&{\mbox{if }}x=0\\x^{2}\sin(1/x),&{\mbox{if }}x\neq 0\end{cases}}$

имеет ограниченную вариацию на интервале $[0,2/\pi ]$. Однако все три функции имеют ограниченную вариацию на каждом интервале. $[a,b]$ с $a>0$.

Каждая монотонная ограниченная функция имеет ограниченную вариацию. Для такой функции $f$ на интервале $[a,b]$ и любой раздел $P=\{x_{0},\ldots ,x_{n_{P}}\}$ этого интервала видно, что

$\sum _{i=0}^{n_{P}-1}|f(x_{i+1})-f(x_{i})|=|f(b)-f(a)|$

от того, что сумма слева телескопическая . Отсюда следует, что для такого $f$,

$V_{a}^{b}(f)=|f(b)-f(a)|.$

В частности, монотонная функция Кантора является хорошо известным примером функции ограниченной вариации, которая не является абсолютно непрерывной .

The Sobolev space $W^{1,1}(\Omega )$ является правильным подмножеством $\operatorname {\operatorname {BV} } (\Omega )$. Фактически для каждого $u$ в $W^{1,1}(\Omega )$ можно выбрать меру $\mu :=\nabla u{\mathcal {L}}$ (где ${\mathcal {L}}$ является мерой Лебега на $\Omega$) такой, что выполняется равенство

$\int u\operatorname {div} \phi =-\int \phi \,d\mu =-\int \phi \,\nabla u\qquad \forall \phi \in C_{c}^{1}$

верно, поскольку это не что иное, как определение слабой производной , и, следовательно, оно верно. Можно легко найти пример функции BV, которая не является $W^{1,1}$: в размерности один подойдет любая ступенчатая функция с нетривиальным скачком.

Приложения

Математика

Функции ограниченной вариации изучались в связи с множеством разрывов функций и дифференцируемостью вещественных функций, и хорошо известны следующие результаты. Если $f$ является вещественной функцией ограниченной вариации на интервале $[a,b]$ затем

• $f$ является непрерывным, за исключением не более чем счетного множества ;
• $f$ везде имеет односторонние пределы (всюду пределы слева $(a,b]$, и справа повсюду в $[a,b)$ ;
• производная ​ $f'(x)$ существует почти всюду (т.е. за исключением множества меры нуль ).

Для вещественных функций нескольких действительных переменных

• характеристическая функция множества Каччиопполи - это функция BV: функции BV лежат в основе современной теории периметров.
• Минимальные поверхности представляют собой графики функций BV: в этом контексте см. ссылку ( Giusti 1984 ).

Физика и инженерия

Способность БВ-функций справляться с разрывами сделала их широкое использование в прикладных науках: решения задач механики, физики, химической кинетики очень часто представляются функциями ограниченной вариации. В книге ( Худжаев и Вольперт, 1985 ) подробно описан очень обширный набор приложений BV-функций в математической физике. Также есть несколько современных приложений, заслуживающих краткого описания.

• Функционал Мамфорда – Шаха : проблема сегментации двумерного изображения, т.е. проблема точного воспроизведения контуров и шкал серого, эквивалентна минимизации такого функционала .
• Полное шумоподавление вариаций

См. также

• Ренато Каччиопполи
• Набор Каччиопполи
• Ламберто Чезари
• Эннио Де Джорджи
• Теорема выбора Хелли
• Локально интегрируемая функция
• л ^п (Ом) пространство
• Интеграл Лебега – Стилтьеса
• Радоновая мера
• Приведенная производная
• Интеграл Римана – Стилтьеса
• Общая вариация
• Квадратичная вариация
• p-вариация
• Айзик Исакович Вольперт
• Полное шумоподавление вариаций
• Общая вариация уменьшается

Ссылки

Исследовательские работы

• Амбросио, Луиджи ; Фуско, Никола ; Паллара, Диего (2000), Функции ограниченной вариации и проблемы свободного разрыва , Oxford Mathematical Monographys, Oxford: The Clarendon Press / Oxford University Press, стр. xviii+434, ISBN  978-0-19-850245-6 , МР   1857292 , Збл   0957.49001 .
• Брудный, Юрий (2007), «Многомерные функции ограниченной ( k , p ) –вариации» , в Рандриантоанина, Беата; Рандриантоанина, Нарцисс (ред.), Банаховы пространства и их приложения в анализе. Материалы международной конференции, Университет Майами, Оксфорд, Огайо, США, 22–27 мая 2006 г. В честь 60-летия Найджела Калтона , Берлин – Бостон: Уолтер Де Грюйтер, стр. 37–58, doi : 10.1515/9783110918298.37 , ISBN  978-3-11-019449-4 , МР   2374699 , Збл   1138.46019
• Данфорд, Нельсон ; Шварц, Джейкоб Т. (1958), Линейные операторы. Часть I: Общая теория , Чистая и прикладная математика, вып. VII, Нью-Йорк – Лондон – Сидней: Wiley-Interscience, ISBN  0-471-60848-3 , Збл   0084.10402 . Включает обсуждение функционально-аналитических свойств пространств функций ограниченной вариации.
• Джаквинта, Мариано ; Модика, Джузеппе; Соучек, Иржи (1998), Декартовы течения в вариационном исчислении I , Результаты математики и ее границы . 3-й эпизод. Серия современных обзоров по математике, том. 37, Берлин-Гейдельберг-Нью-Йорк: Springer Verlag, ISBN  3-540-64009-6 , Збл   0914.49001 .
• Джусти, Энрико (1984), Минимальные поверхности и функции ограниченных вариаций , Монографии по математике, том. 80, Базель – Бостон – Штутгарт: Birkhäuser Verlag, стр. XII + 240, ISBN.  978-0-8176-3153-6 , MR   0775682 , Zbl   0545.49018 , в частности часть I, глава 1 « Функции ограниченной вариации и множества Каччиопполи ». Хороший справочник по теории множеств Каччиопполи и их применению к проблеме минимальной поверхности .
• Халмос, Пол (1950), Теория меры , Ван Ностранд и компания, ISBN  978-0-387-90088-9 , Збл   0040.16802 . Ссылка ведет на предварительный просмотр более позднего переиздания Springer-Verlag.
• Худжаев Сергей Иванович; Вольперт, Айзик Исаакович (1985), Анализ в классах разрывных функций и уравнениях математической физики , Механика: анализ, вып. 8, Дордрехт – Бостон – Ланкастер: Издательство Мартинуса Нийхоффа, ISBN  90-247-3109-7 , МР   0785938 , Збл   0564.46025 . Вся книга посвящена теории БВ -функций и их приложениям к задачам математической физики, связанным с разрывными функциями и геометрическими объектами с негладкими границами .
• Каннан, Рангачари; Крюгер, Кэрол Кинг (1996), Расширенный анализ реальной линии , Universitext, Берлин – Гейдельберг – Нью-Йорк: Springer Verlag, стр. x + 259, ISBN  978-0-387-94642-9 , МР   1390758 , Збл   0855.26001 . Пожалуй, самый полный справочник по теории БВ -функций одной переменной: классические результаты и продвинутые результаты собраны в главе 6 « Ограниченная вариация » вместе с несколькими упражнениями. Первым автором был сотрудник Ламберто Чезари .
• Колмогоров Андрей Н .; Фомин, Сергей В. (1969), Вводный реальный анализ , Нью-Йорк: Dover Publications, стр. xii+403, ISBN  0-486-61226-0 , МР   0377445 , Збл   0213.07305 .
• Леони, Джованни (2017), Первый курс по пространствам Соболева , Аспирантура по математике (второе изд.), Американское математическое общество, стр. xxii+734, ISBN  978-1-4704-2921-8 .
• Малек, Йозеф; Нечас, Йиндржих; Рокита, Мирко; Ружичка, Майкл (1996), Слабые и мерозначные решения эволюционных уравнений в частных уравнениях , Прикладная математика и математические вычисления, том. 13, Лондон – Вайнхайм – Нью-Йорк – Токио – Мельбурн – Мадрас: Chapman & Hall CRC Press, стр. xi + 331, ISBN  0-412-57750-Х , МР   1409366 , Збл   0851.35002 . Одна из наиболее полных монографий по теории мер Юнга , сильно ориентированная на приложения в механике сплошных сред жидкостей.
• Maz'ya, Vladimir G. (1985), Sobolev Spaces , Berlin–Heidelberg–New York: Springer-Verlag, ISBN  0-387-13589-8 , Збл   0692.46023 ; особенно главу 6 «О функциях в пространстве BV(Ω) ». Одна из лучших монографий по теории пространств Соболева .
• Моро, Жан Жак (1988), «Ограниченное изменение во времени», Моро, Дж. Дж.; Панагиотопулос, доктор медицинских наук; Странг, Г. (ред.), Темы негладкой механики , Базель-Бостон-Штутгарт: Birkhäuser Verlag, стр. 1–74, ISBN.  3-7643-1907-0 , Збл   0657.28008
• Мусилак, Джулиан; Орлич, Владислав (1959), «Об обобщенных вариациях (I)» (PDF) , Studia Mathematica , 18 , Варшава – Вроцлав: 13–41, doi : 10.4064/sm-18-1-11-41 , Zbl   0088.26901 . В этой статье Мусиелак и Орлич развили концепцию взвешенных функций BV , введенную Лоуренсом Чизхолмом Янгом, до ее полной общности.
• Рисс, Фредерик ; Секефальви-Надь, Бела (1990), Функциональный анализ , Нью-Йорк: Dover Publications, ISBN  0-486-66289-6 , Збл   0732.47001
• Вольперт, Айзик Исаакович (1967), "Пространства БВ и квазилинейные уравнения" , Математический сборник , (НС) (на русском), 73 (115) (2): 255–302, МР   0216338 , Збл   0168.07402 . Фундаментальная статья, в которой тщательно изучаются множества Каччиопполи и функции БВ , а также вводится понятие функциональной суперпозиции , которое применяется к теории уравнений в частных производных : она также была переведена на английский язык как ВольПерт, А.И. (1967), "Пространства БВ и квазилинейные уравнения", Математика СССР-Сборник , 2 (2): 225–267, Бибкод : 1967SbMat...2..225V , doi : 10.1070/ SM1967v002n02ABEH002340 , hdl : 10338.dmlcz/102500 , MR   0216338 , Zbl   0168.07402 .

Исторические справки

• Адамс, К. Рэймонд ; Кларксон, Джеймс А. (1933), «Об определениях ограниченной вариации функций двух переменных», Transactions of the American Mathematical Society , 35 (4): 824–854, doi : 10.1090/S0002-9947-1933-1501718- 2 , МР   1501718 , Збл   0008.00602 .
• Альберти, Джованни; Мантегацца, Карло (1997), «Заметки по теории функций SBV», Bollettino dell'Unione Matematica Italiana , IV Serie, 11 (2): 375–382, MR   1459286 , Zbl   0877.49001 . В данной работе авторы доказывают компактность пространства SBV-функций.
• Амбросио, Луиджи ; Дал Масо, Джанни (1990), «Общее правило цепочки для производных распределения», Труды Американского математического общества , 108 (3): 691, doi : 10.1090/S0002-9939-1990-0969514-3 , MR   0969514 , Zbl   0685.49027 . Статья, содержащая очень общую формулу цепного правила для композиции функций BV.
• Амбросио, Луиджи ; Де Джорджи, Эннио (1988), «Новый вид функционала в вариационном исчислении» , Труды Национальной академии Линчеи, Отчеты класса физических, математических и естественных наук , VIII (на итальянском языке), LXXXII (2 ): 199–210, МР   1152641 , Збл   0715.49014 . Первая статья о функциях SBV и связанных с ними вариационных задачах.
• Чезари, Ламберто (1936), «Sulle funzioni a variazione limitata» , Annali della Scuola Normale Superiore , Serie II (на итальянском языке), 5 (3–4): 299–313, MR   1556778 , Zbl   0014.29605 . Доступно в Намдаме . В статье « О функциях ограниченной вариации » (английский перевод названия) Чезари он расширяет концепцию плоской вариации Тонелли , включив в определение подкласс класса интегрируемых функций.
• Чезари, Ламберто (1986), «Работы Леониды Тонелли и его влияние на научную мысль века», в Монталенти, Г.; Америо, Л .; Аккуаро, Г.; Байада, Э.; и др. (ред.), Конференция, посвященная столетию со дня рождения Мауро Пиконе и Леониды Тонелли (6–9 мая 1985 г.) , Proceedings of the Lincei Conferences (на итальянском языке), vol. 77, Рим: Национальная академия Линчеи , стр. 41–73, заархивировано из оригинала 23 февраля 2011 года . « Работа Леониды Тонелли и его влияние на научную мысль в этом столетии » (английский перевод названия) представляет собой обширную памятную статью, в которой излагаются воспоминания Автора об учителях и коллегах, а также подробный обзор его и их научной деятельности. представлен на Международном конгрессе по случаю празднования столетия со дня рождения Мауро Пиконе и Леониды Тонелли (проходил в Риме 6–9 мая 1985 г.).
• Конвей, Эдвард Д.; Смоллер, Джоэл А. (1966), «Глобальные решения задачи Коши для квазилинейных уравнений первого порядка с несколькими пространственными переменными», Communications on Pure and Applied Mathematics , 19 (1): 95–105, doi : 10.1002/ спа.3160190107 , МР   0192161 , Збл   0138.34701 . Важная статья, в которой свойства БВ-функций были применены для получения глобальной во времени существования одиночных теоремы гиперболических уравнений первого порядка от любого числа переменных .
• Де Джорджи, Эннио (1992), «Вариационные задачи со свободными разрывами», Амальди, Э .; Америо, Л .; Фичера, Г .; Грегори, Т.; Гриоли, Г .; Мартинелли, Э .; Монталенти, Г.; Пиньедоли, А. ; Сальвини, Джорджо ; Скорца Драгони, Джузеппе (ред.), Международная конференция памяти Вито Вольтерры (8–11 октября 1990 г.) , Труды конференций Линчеи (на итальянском языке), том. 92, Рим: Национальная академия Линчеи , стр. 39–76, ISSN   0391-805X , MR   1783032 , Zbl   1039.49507 , заархивировано из оригинала 7 января 2017 г. Обзорный доклад по вариационным проблемам со свободным разрывом , включающий некоторые подробности теории SBV -функций, их приложений и богатую библиографию.
• Фалескини, Бруно (1956a), «Все определения и свойства функций, ограниченные вариациями из-за переменных. Примечание I». [Об определениях и свойствах функций ограниченной вариации двух переменных. Примечание I], Bollettino dell'Unione Matematica Italiana , Serie III (на итальянском языке), 11 (1): 80–92, MR   0080169 , Zbl   0071.27901 . Первая часть обзора множества различных определений « полной вариации » и связанных с ней функций ограниченной вариации.
• Фалескини, Бруно (1956b), «Об определениях и свойствах функций с ограниченным изменением двух переменных. Примечание II». [Об определениях и свойствах функций ограниченной вариации двух переменных. Примечания I], Бюллетень Итальянского математического союза , серия III (на итальянском языке), 11 (2): 260–75, MR   0080169 , Zbl   0073.04501 . Вторая часть обзора множества различных определений « полной вариации » и связанных с ней функций ограниченной вариации.
• Джордан, Камилла (1881), «О ряде Фурье», еженедельные отчеты о сессиях Академии наук , 92 : 228–230 (в Галлике ). По словам Бориса Голубова, это первая статья о функциях ограниченной вариации.
• Олейник, Ольга Александровна (1957), "Разрывные решения нелинейных дифференциальных уравнений" , Успехи математических наук , 12 (3(75)): 3–73, Збл   0080.07701 ( на русском языке) . Важная статья, в которой автор описывает обобщенные решения нелинейных уравнений в частных производных как БВ . функции
• Олейник, Ольга Александровна (1959), "Построение обобщенного решения задачи Коши для квазилинейного уравнения первого порядка путем введения "исчезающей вязкости" " , Успехи математических наук , 14 (2(86)): 159–164, Збл   0096.06603 ( (на русском языке) ). Важная статья, в которой автор строит слабое решение в BV нелинейного уравнения в частных производных методом исчезающей вязкости .
• Тони Ф. Чан и Цзяньхун (Джеки) Шен (2005), Обработка и анализ изображений — вариационные, PDE, вейвлет-методы и стохастические методы , SIAM Publisher, ISBN   0-89871-589-X (с подробным описанием и обширным применением ограниченных вариаций в современной обработке изображений, начатых Рудином, Ошером и Фатеми).

Внешние ссылки

Теория

• Голубов Борис И.; Витушкин, Анатолий Григорьевич (2001) [1994], «Вариация функции» , Энциклопедия Математики , EMS Press
• «Функция БВ» . ПланетаМатематика . .
• Роуленд, Тодд и Вайсштейн, Эрик В. «Ограниченная вариация» . Математический мир .
• Функция ограниченной вариации в математической энциклопедии

Другой

• Луиджи Амбросио Домашняя страница в Scuola Normale Superiore di Pisa . Академическая домашняя страница (с препринтами и публикациями) одного из авторов теории и приложений функций BV.
• Исследовательская группа по вариационному исчислению и геометрической теории меры , Scuola Normale Superiore di Pisa .

Эта статья включает в себя материал из функции BV на PlanetMath , которая распространяется по лицензии Creative Commons Attribution/Share-Alike License .