Молекулярная динамика

Пример моделирования молекулярной динамики в простой системе: осаждение одного меди (Cu) атома на холодный кристалл меди ( с индексом Миллера (001) поверхность ). Каждый круг представляет положение одного атома. Кинетическая энергия атома, приближающегося сверху, перераспределяется между другими атомами, поэтому вместо того, чтобы отскакивать, он остается прикрепленным за счет сил притяжения между атомами.

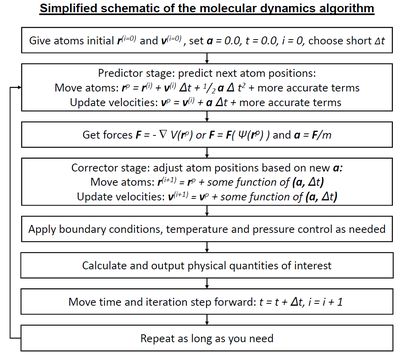
Молекулярная динамика ( МД ) – это метод компьютерного моделирования анализа физических движений атомов молекул и для . Атомам и молекулам разрешено взаимодействовать в течение фиксированного периода времени, что дает представление о динамической «эволюции» системы. В наиболее распространенной версии траектории атомов и молекул определяются путем численного решения уравнений движения Ньютона для системы взаимодействующих частиц, где силы между частицами и их потенциальные энергии часто рассчитываются с использованием межатомных потенциалов или молекулярных механических силовых полей . Метод применяется главным образом в химической физике , материаловедении и биофизике .

невозможно определить свойства таких сложных систем Поскольку молекулярные системы обычно состоят из огромного количества частиц, аналитически ; МД-моделирование позволяет обойти эту проблему, используя численные методы. Однако длительное МД-моделирование математически плохо обусловлено , генерируя совокупные ошибки численного интегрирования, которые можно минимизировать при правильном выборе алгоритмов и параметров, но не устранить.

Для систем, которые подчиняются эргодической гипотезе , эволюция одного моделирования молекулярной динамики может быть использована для определения макроскопических термодинамических свойств системы: средние значения по времени эргодической системы соответствуют средним значениям микроканонического ансамбля . MD также называют « статистической механикой в числах» и « ньютоновской видением Лапласа механики », предсказывающей будущее путем оживления сил природы. ^{[ 1 ]} и позволяет понять молекулярное движение в атомном масштабе.

История

Первоначально МД была разработана в начале 1950-х годов после более ранних успехов моделирования Монте-Карло , которые сами по себе относятся к восемнадцатому веку, в задаче Бюффона об игле например, , но была популяризирована для статистической механики в Национальной лаборатории Лос-Аламоса Маршаллом Розенблютом и Николасом. Метрополис в том, что сегодня известно как алгоритм Метрополиса-Гастингса . Интерес к временной эволюции систем N тел возник гораздо раньше, в семнадцатом веке, начиная с Исаака Ньютона , и продолжался в следующем столетии, в основном с акцентом на небесную механику и такие вопросы, как стабильность Солнечной системы . Многие из численных методов, используемых сегодня, были разработаны в этот период времени, до использования компьютеров; например, наиболее распространенный алгоритм интегрирования, используемый сегодня, алгоритм интегрирования Верле , был использован еще в 1791 году Жаном Батистом Жозефом Деламбром . Численные расчеты с использованием этих алгоритмов можно считать MD, выполняемыми «вручную».

Еще в 1941 году интегрирование уравнений движения многих тел было выполнено с помощью аналоговых компьютеров . Некоторые взялись за трудоемкую работу по моделированию движения атомов путем построения физических моделей, например, с использованием макроскопических сфер. Целью было расположить их таким образом, чтобы воспроизвести структуру жидкости и использовать ее для изучения ее поведения. Дж. Д. Бернал описал этот процесс в 1962 году, написав: ^{[ 2 ]}

... Я взял несколько резиновых шариков и склеил их стержнями разной длины от 2,75 до 4 дюймов. Во-первых, я старался делать это как можно более непринужденно, работая в своем кабинете, меня прерывали примерно каждые пять минут и я не помнил, что я делал до того, как меня прервали.

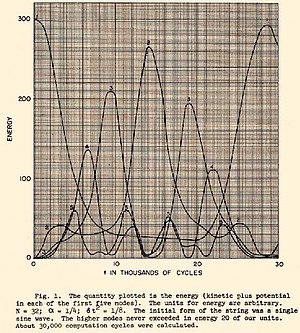
После открытия микроскопических частиц и развития компьютеров интерес расширился за пределы испытательного полигона гравитационных систем к статистическим свойствам материи. Пытаясь понять происхождение необратимости , Энрико Ферми в 1953 году предложил и опубликовал в 1955 году: ^{[ 3 ]} использование раннего компьютера MANIAC I , также находящегося в Национальной лаборатории Лос-Аламоса , для решения временной эволюции уравнений движения системы многих тел, подчиняющихся нескольким выборам силовых законов. Сегодня эта плодотворная работа известна как проблема Ферми-Пасты-Улама-Цингу . Эволюция энергии исходной работы во времени показана на рисунке справа.

В 1957 году Берни Алдер и Томас Уэйнрайт использовали компьютер IBM 704 для моделирования идеально упругих столкновений между твердыми сферами . ^{[ 4 ]} В 1960 году, возможно, в первой реалистичной модели материи, Дж. Б. Гибсон и др . смоделировал радиационное повреждение твердой меди , используя Борна-Майера отталкивающее взаимодействие типа вместе с поверхностной силой сцепления . ^{[ 5 ]} В 1964 году Анисур Рахман опубликовал моделирование жидкого аргона , в котором использовался потенциал Леннарда-Джонса ; расчеты свойств системы, таких как коэффициент самодиффузии , хорошо сравниваются с экспериментальными данными. ^{[ 6 ]} Сегодня потенциал Леннарда-Джонса по-прежнему остается одним из наиболее часто используемых межмолекулярных потенциалов . ^{[ 7 ]}^{[ 8 ]} Он используется для описания простых веществ (он же Леннард-Джонезий ^{[ 9 ]}^{[ 10 ]}^{[ 11 ]}) для концептуальных и модельных исследований, а также в качестве строительного блока во многих силовых полях реальных веществ. ^{[ 12 ]}^{[ 13 ]}

Области применения и ограничения

Впервые использованный в теоретической физике , метод молекулярной динамики вскоре приобрел популярность в материаловедении , а с 1970-х годов он также широко используется в биохимии и биофизике . MD часто используется для уточнения трехмерных структур белков и других макромолекул на основе экспериментальных ограничений, полученных из рентгеновской кристаллографии или ЯМР-спектроскопии . В физике МД используется для изучения динамики явлений атомного уровня, которые невозможно наблюдать напрямую, таких как рост тонких пленок и ионная субплантация, а также для изучения физических свойств нанотехнологических устройств, которые еще не созданы или еще не могут быть созданы. В биофизике и структурной биологии этот метод часто применяется для изучения движений макромолекул, таких как белки и нуклеиновые кислоты , что может быть полезно для интерпретации результатов определенных биофизических экспериментов и для моделирования взаимодействий с другими молекулами, например, при стыковке лигандов . В принципе, МД можно использовать для ab прогнозирования initio структуру белка путем моделирования сворачивания полипептидной цепи из случайного клубка .

Результаты МД-моделирования можно проверить путем сравнения с экспериментами по измерению молекулярной динамики, популярным методом которых является ЯМР-спектроскопия. Прогнозы структуры, полученные с помощью MD, можно проверить с помощью экспериментов в масштабах всего сообщества по критической оценке прогнозирования структуры белка ( CASP ), хотя исторически этот метод имел ограниченный успех в этой области. Майкл Левитт , получивший Нобелевскую премию частично за применение МД к белкам, писал в 1999 году, что участники CASP обычно не использовали этот метод из-за «... центрального затруднения молекулярной механики , а именно того, что минимизация энергии или молекулярная динамика в целом приводит к модели, которая меньше похожа на экспериментальную структуру». ^{[ 14 ]} Улучшения в вычислительных ресурсах, позволяющие использовать все более и более длинные траектории МД, в сочетании с современными улучшениями качества параметров силового поля привели к некоторым улучшениям как в прогнозировании структуры, так и в уточнении модели гомологии , не достигая точки практической полезности в этих областях; многие считают параметры силового поля ключевой областью для дальнейшего развития. ^{[ 15 ]}^{[ 16 ]}^{[ 17 ]}

Сообщалось о применении МД-моделирования при разработке фармакофоров и дизайне лекарств . ^{[ 18 ]} Например, Пинто и др . реализовали MD-моделирование комплексов Bcl-xL для расчета средних положений критических аминокислот, участвующих в связывании лигандов. ^{[ 19 ]} Карлсон и др . реализовали моделирование молекулярной динамики для идентификации соединений, которые дополняют рецептор , вызывая при этом минимальное нарушение конформации и гибкости активного сайта. Снимки белка через постоянные интервалы времени во время моделирования накладывались для идентификации консервативных областей связывания (консервативных как минимум в трех из одиннадцати кадров) для разработки фармакофора. Спиракис и др . полагались на рабочий процесс MD-моделирования, отпечатков пальцев для лигандов и белков (FLAP) и линейного дискриминантного анализа (LDA) для определения лучших конформаций лиганд-белок, которые будут действовать в качестве шаблонов фармакофоров, на основе ретроспективного ROC- анализа полученных фармакофоров. В попытке улучшить моделирование открытия лекарств на основе структуры, учитывая необходимость во многих смоделированных соединениях, Hatmal et al . предложили комбинацию МД-моделирования и анализа межмолекулярных контактов лиганд-рецептор, чтобы отличить критические межмолекулярные контакты (связывающие взаимодействия) от избыточных в одном лиганд-белковом комплексе. Критические контакты затем могут быть преобразованы в модели фармакофора, которые можно использовать для виртуального скрининга. ^{[ 20 ]}

Важным фактором являются внутримолекулярные водородные связи , ^{[ 21 ]} которые явно не включены в современные силовые поля, но описываются как кулоновские взаимодействия атомных точечных зарядов . ^{[ нужна ссылка ]} Это грубое приближение, поскольку водородные связи имеют частично квантово-механическую и химическую природу. Кроме того, электростатические взаимодействия обычно рассчитываются с использованием диэлектрической проницаемости вакуума , хотя окружающий водный раствор имеет гораздо более высокую диэлектрическую проницаемость. Таким образом, использование макроскопической диэлектрической проницаемости на малых межатомных расстояниях сомнительно. Наконец, ван-дер-ваальсовые взаимодействия в МД обычно описываются потенциалами Леннарда-Джонса. ^{[ 22 ]}^{[ 23 ]} основан на теории Фрица Лондона , которая применима только в вакууме. ^{[ нужна ссылка ]} Однако все виды сил Ван-дер-Ваальса в конечном счете имеют электростатическое происхождение и поэтому зависят от диэлектрических свойств среды . ^{[ 24 ]} Прямое измерение сил притяжения между различными материалами (как константа Гамакера ) показывает, что «взаимодействие между углеводородами в воде составляет около 10% от взаимодействия в вакууме». ^{[ 24 ]} Зависимость сил Ван-дер-Ваальса от окружающей среды не учитывается в стандартном моделировании, но может быть учтена путем разработки поляризуемых силовых полей.

Ограничения дизайна

При разработке моделирования молекулярной динамики следует учитывать доступную вычислительную мощность. Размер моделирования ( n = количество частиц), временной шаг и общая продолжительность времени должны быть выбраны так, чтобы расчет мог завершиться в течение разумного периода времени. Однако моделирование должно быть достаточно продолжительным, чтобы соответствовать временным масштабам изучаемых природных процессов. Чтобы сделать статистически обоснованные выводы из моделирования, моделируемый промежуток времени должен соответствовать кинетике естественного процесса. В противном случае это аналогично выводу о том, как человек ходит, глядя только на один шаг. Большинство научных публикаций о динамике белков и ДНК ^{[ 25 ]}^{[ 26 ]} использовать данные моделирования, охватывающие наносекунды (10 ⁻⁹ с) до микросекунд (10 ⁻⁶ с). Для получения таких симуляций от нескольких ЦП-дней требуется до ЦП-лет. Параллельные алгоритмы позволяют распределять нагрузку между процессорами ; примером является алгоритм пространственной или силовой декомпозиции. ^{[ 27 ]}

Во время классического МД-моделирования наиболее ресурсоемкой задачей ЦП является оценка потенциала как функции внутренних координат частиц. В рамках этой энергетической оценки самой дорогой является несвязанная или нековалентная часть. В обозначении «большое О» общие симуляции молекулярной динамики масштабируются на $O(n^{2})$ если все парные электростатические и ван-дер-ваальсовые взаимодействия должны быть учтены явно. Эти вычислительные затраты можно уменьшить, используя методы электростатики, такие как суммирование Эвальда на сетке частиц ( $O(n\log(n))$ ), сетка частица-частица-частица ( P ³M ) или хорошие методы сферического отсечения ( $O(n)$ ). ^{[ нужна ссылка ]}

Еще одним фактором, влияющим на общее время процессора, необходимое для моделирования, является размер временного шага интегрирования. Это промежуток времени между оценками потенциала. Временной шаг должен быть выбран достаточно малым, чтобы избежать ошибок дискретизации (т. е. меньшим, чем период, относящийся к самой высокой частоте колебаний в системе). Типичные временные шаги для классической МД составляют порядка 1 фемтосекунды (10 ⁻¹⁵ с). Это значение может быть увеличено с помощью таких алгоритмов, как алгоритм ограничения SHAKE , который фиксирует колебания самых быстрых атомов (например, водородов) на месте. Также были разработаны методы с несколькими временными шкалами, которые позволяют увеличить время между обновлениями более медленных сил дальнего действия. ^{[ 28 ]}^{[ 29 ]}^{[ 30 ]}

Для моделирования молекул в растворителе необходимо сделать выбор между явным и неявным растворителем . Частицы явного растворителя (такие как модели воды TIP3P , SPC/E и SPC-f ) должны рассчитываться с помощью силового поля, в то время как неявные растворители используют подход среднего поля . Использование явного растворителя требует больших вычислительных затрат и требует включения в моделирование примерно в десять раз больше частиц. Но зернистость и вязкость явного растворителя необходимы для воспроизведения определенных свойств молекул растворенного вещества. Это особенно важно для воспроизведения химической кинетики .

Во всех видах моделирования молекулярной динамики размер окна моделирования должен быть достаточно большим, чтобы избежать артефактов граничных условий . Граничные условия часто обрабатываются путем выбора фиксированных значений на краях (что может вызвать артефакты) или использования периодических граничных условий , при которых одна сторона моделирования возвращается к противоположной стороне, имитируя объемную фазу (что также может вызывать артефакты). .

Микроканонический ансамбль (НВЭ)

В микроканоническом ансамбле система изолирована от изменений молей (N), объема (V) и энергии (E). Это соответствует адиабатическому процессу без теплообмена. Траекторию микроканонической молекулярной динамики можно рассматривать как обмен потенциальной и кинетической энергией с сохранением полной энергии. Для системы N частиц с координатами $X$ и скорости $V$ , следующую пару дифференциальных уравнений первого порядка можно записать в обозначениях Ньютона как

F(X)=-\nabla U(X)=M{\dot {V}}(t)

V(t)={\dot {X}}(t).

Функция потенциальной энергии $U(X)$ системы является функцией координат частицы $X$ . Его называют просто потенциалом в физике или силовым полем в химии. Первое уравнение происходит из законов движения Ньютона ; сила $F$ действующее на каждую частицу в системе, можно рассчитать как отрицательный градиент $U(X)$ .

Для каждого временного шага положение каждой частицы $X$ и скорость $V$ может быть интегрирован с помощью метода симплектического интегратора, такого как интеграция Верле . Временная эволюция $X$ и $V$ называется траекторией. Учитывая начальные позиции (например, из теоретических знаний) и скорости (например, рандомизированную гауссову ), мы можем вычислить все будущие (или прошлые) позиции и скорости.

Одним из частых источников путаницы является значение температуры в MD. Обычно у нас есть опыт работы с макроскопическими температурами, в которых участвует огромное количество частиц, но температура — это статистическая величина. Если число атомов достаточно большое, статистическую температуру можно оценить по мгновенной температуре , которая находится путем приравнивания кинетической энергии системы к nk _B T /2, где n — число степеней свободы системы. .

Явление, связанное с температурой, возникает из-за небольшого количества атомов, которые используются в МД-моделировании. Например, рассмотрим моделирование роста медной пленки, начиная с подложки, содержащей 500 атомов и энергии осаждения 100 эВ . В реальном мире энергия 100 эВ от осажденного атома быстро переносится и распределяется между большим количеством атомов ( $10^{10}$ или более) без больших изменений температуры. Однако когда атомов всего 500, подложка почти сразу испаряется при осаждении. Нечто подобное происходит и в биофизическом моделировании. Температура системы при NVE естественным образом повышается, когда макромолекулы, такие как белки, подвергаются экзотермическим конформационным изменениям и связыванию.

Канонический ансамбль (НВТ)

В каноническом ансамбле сохраняются количество вещества (N), объём (V) и температура (Т). Его также иногда называют молекулярной динамикой при постоянной температуре (CTMD). В НВТ происходит обмен энергией эндо- и экзотермических процессов с термостатом .

Доступны различные алгоритмы термостата для более или менее реалистичного добавления и удаления энергии за границы МД-моделирования, аппроксимируя канонический ансамбль . Популярные методы контроля температуры включают изменение масштаба скорости, термостат Нозе-Гувера , цепи Нозе-Гувера, термостат Берендсена , термостат Андерсена и динамику Ланжевена . Термостат Берендсена может вызвать эффект летающего кубика льда , который приводит к нефизическим перемещениям и вращениям моделируемой системы.

С помощью этих алгоритмов получить каноническое ансамблевое распределение конформаций и скоростей непросто. Как это зависит от размера системы, выбора термостата, параметров термостата, временного шага и интегратора, является предметом многих статей в этой области.

Изотермально-изобарический (NPT) ансамбль

В изотермо-изобарном ансамбле сохраняются количество вещества (N), давление (Р) и температура (Т). Помимо термостата баростат необходим . Он наиболее точно соответствует лабораторным условиям с колбой, открытой при температуре и давлении окружающей среды.

При моделировании мембран биологических изотропное управление давлением нецелесообразно. Для липидных бислоев контроль давления происходит при постоянной площади мембраны (NPAT) или постоянном поверхностном натяжении «гамма» (NPγT).

Обобщенные ансамбли

Метод обмена репликами представляет собой обобщенный ансамбль. Первоначально он был создан для изучения медленной динамики неупорядоченных спиновых систем. Его еще называют параллельным отпуском. Формулировка репликационного обмена MD (REMD) ^{[ 31 ]} пытается преодолеть проблему нескольких минимумов, меняя температуру невзаимодействующих реплик системы, работающей при нескольких температурах.

Возможности моделирования МД

Моделирование молекулярной динамики требует определения потенциальной функции или описания условий, с помощью которых частицы в моделировании будут взаимодействовать. В химии и биологии это обычно называют силовым полем , а в физике материалов — межатомным потенциалом . Потенциалы могут быть определены на многих уровнях физической точности; те, которые наиболее часто используются в химии, основаны на молекулярной механике и воплощают классическую механическую трактовку взаимодействий между частицами, которая может воспроизводить структурные и конформационные изменения , но обычно не может воспроизводить химические реакции .

Сведение от полностью квантового описания к классическому потенциалу предполагает два основных приближения. Первое — это приближение Борна-Оппенгеймера , которое утверждает, что динамика электронов настолько быстра, что можно считать, что они мгновенно реагируют на движение своих ядер. В результате их можно рассматривать отдельно. Второй рассматривает ядра, которые намного тяжелее электронов, как точечные частицы, подчиняющиеся классической ньютоновской динамике. В классической молекулярной динамике влияние электронов аппроксимируется как одна поверхность потенциальной энергии, обычно представляющая основное состояние.

Когда необходимы более тонкие уровни детализации, потенциалы, основанные на квантовой механике используются ; некоторые методы пытаются создать гибридные классические/квантовые потенциалы, где основная часть системы рассматривается классически, но небольшая область рассматривается как квантовая система, обычно подвергающаяся химическому превращению.

Эмпирические потенциалы

Эмпирические потенциалы, используемые в химии, часто называют силовыми полями , а в физике материалов — межатомными потенциалами .

Большинство силовых полей в химии являются эмпирическими и состоят из суммы связанных сил, связанных с химическими связями , валентными углами и двугранниками связей , а также несвязанных сил, связанных с силами Ван-дер-Ваальса и электростатическим зарядом . ^{[ 32 ]} Эмпирические потенциалы представляют квантово-механические эффекты ограниченным образом посредством специальных функциональных приближений. Эти потенциалы содержат свободные параметры, такие как заряд атома , параметры Ван-дер-Ваальса, отражающие оценки атомного радиуса , а также равновесную длину связи , угол и двугранник; они получены путем сопоставления подробных электронных расчетов (квантово-химическое моделирование) или экспериментальных физических свойств, таких как упругие константы , параметры решетки и спектроскопические измерения.

Из-за нелокальной природы несвязанных взаимодействий они включают, по крайней мере, слабые взаимодействия между всеми частицами в системе. Его расчет обычно является узким местом в скорости моделирования МД. Чтобы снизить вычислительные затраты, силовые поля используют численные аппроксимации, такие как смещенные радиусы отсечки, алгоритмы поля реакции сетки частиц , суммирование Эвальда или более новая сетка частица-частица-частица-сетка ( P3M ).

В химических силовых полях обычно используются заранее заданные схемы связей (исключение составляет динамика ab initio ), и поэтому они не могут явно моделировать процесс разрыва химических связей и реакции. С другой стороны, многие из потенциалов, используемых в физике, например, основанные на формализме порядка связей, могут описывать несколько различных координаций системы и разрыва связей. ^{[ 33 ]}^{[ 34 ]} Примеры таких потенциалов включают потенциал Бреннера. ^{[ 35 ]} по углеводородам и их дальнейшие разработки для C-Si-H ^{[ 36 ]} и COH ^{[ 37 ]} системы. Потенциал ReaxFF ^{[ 38 ]} можно рассматривать как полностью реактивный гибрид между потенциалами порядка связей и химическими силовыми полями.

Парные потенциалы против многочастичных потенциалов

Потенциальные функции, представляющие несвязанную энергию, формулируются как сумма по взаимодействиям между частицами системы. Самый простой выбор, используемый во многих популярных силовых полях , - это «парный потенциал», в котором полная потенциальная энергия может быть рассчитана из суммы энергетических вкладов между парами атомов. Поэтому эти силовые поля также называют «аддитивными силовыми полями». Примером такого парного потенциала является несвязанный потенциал Леннарда-Джонса (также называемый потенциалом 6–12), используемый для расчета сил Ван-дер-Ваальса.

U(r)=4\varepsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]

Другой пример — борновская (ионная) модель ионной решетки. Первый член в следующем уравнении представляет собой закон Кулона для пары ионов, второй член — это короткодействующее отталкивание, объясняемое принципом запрета Паули, а последний член — это член дисперсионного взаимодействия. Обычно моделирование включает только диполярный член, хотя иногда включается и квадрупольный член. ^{[ 39 ]}^{[ 40 ]} При n _l = 6 этот потенциал также называют потенциалом Кулона–Букингема .

U_{ij}(r_{ij})={\frac {z_{i}z_{j}}{4\pi \epsilon _{0}}}{\frac {1}{r_{ij}}}+A_{l}\exp {\frac {-r_{ij}}{p_{l}}}+C_{l}r_{ij}^{-n_{l}}+\cdots

В потенциалах многих тел потенциальная энергия включает в себя эффекты трех или более частиц, взаимодействующих друг с другом. ^{[ 41 ]} В симуляциях с парными потенциалами глобальные взаимодействия в системе также существуют, но они происходят только через парные члены. В потенциалах многих тел потенциальная энергия не может быть найдена путем суммы по парам атомов, поскольку эти взаимодействия рассчитываются явно как комбинация членов более высокого порядка. С статистической точки зрения зависимость между переменными вообще не может быть выражена с использованием только попарных произведений степеней свободы. Например, Терсоффа потенциал ^{[ 42 ]} который первоначально использовался для моделирования углерода , кремния и германия и с тех пор использовался для широкого спектра других материалов, включает в себя суммирование по группам из трех атомов, при этом углы между атомами являются важным фактором потенциала. Другими примерами являются метод встроенного атома (EAM), ^{[ 43 ]} ЭДИП, ^{[ 41 ]} и потенциалы Приближения второго момента сильной связи (TBSMA), ^{[ 44 ]} где плотность электронных состояний в области атома рассчитывается из суммы вкладов окружающих атомов, а вклад потенциальной энергии является функцией этой суммы.

Полуэмпирические потенциалы

Полуэмпирические потенциалы используют матричное представление квантовой механики. Однако значения матричных элементов находятся с помощью эмпирических формул, оценивающих степень перекрытия конкретных атомных орбиталей. Затем матрица диагонализируется для определения занятости различных атомных орбиталей, а эмпирические формулы снова используются для определения энергетических вкладов орбиталей.

Существует большое разнообразие полуэмпирических потенциалов, называемых потенциалами сильной связи , которые варьируются в зависимости от моделируемых атомов.

Поляризуемые потенциалы

Большинство классических силовых полей неявно включают эффект поляризуемости , например, путем увеличения парциальных зарядов, полученных в результате квантово-химических расчетов. Эти частичные заряды стационарны по отношению к массе атома. Но моделирование молекулярной динамики может явно моделировать поляризуемость с помощью индуцированных диполей с помощью различных методов, таких как частицы Друде или флуктуирующие заряды. Это позволяет осуществлять динамическое перераспределение заряда между атомами, которое реагирует на локальную химическую среду.

В течение многих лет поляризуемые модели МД рекламировались как следующее поколение. Для однородных жидкостей, таких как вода, повышенная точность была достигнута за счет учета поляризуемости. ^{[ 45 ]}^{[ 46 ]}^{[ 47 ]} Некоторые многообещающие результаты были достигнуты и в отношении белков. ^{[ 48 ]}^{[ 49 ]} Однако до сих пор неясно, как лучше всего аппроксимировать поляризуемость в моделировании. ^{[ нужна ссылка ]} Этот вопрос становится более важным, когда частица испытывает различные условия окружающей среды во время своей траектории моделирования, например, транслокация лекарства через клеточную мембрану. ^{[ 50 ]}

Возможности ab initio методов

В классической молекулярной динамике в силовом поле представлена одна поверхность потенциальной энергии (обычно основное состояние). Это следствие приближения Борна-Оппенгеймера . В возбужденных состояниях, химических реакциях или когда необходимо более точное представление, поведение электрона можно получить из первых принципов с использованием квантово-механического метода, такого как теория функционала плотности . Это называется Ab Initio Molecular Dynamics (AIMD). Из-за стоимости обработки электронных степеней свободы вычислительная нагрузка этого моделирования намного выше, чем в классической молекулярной динамике. По этой причине AIMD обычно ограничивается меньшими системами и более коротким временем.

методы ab initio Квантово-механические и химические могут использоваться для расчета потенциальной энергии системы на лету, что необходимо для конформаций на траектории. Этот расчет обычно производится в непосредственной близости от координаты реакции . Хотя могут использоваться различные приближения, они основаны на теоретических соображениях, а не на эмпирических данных. Расчеты ab initio дают огромное количество информации, недоступной с помощью эмпирических методов, таких как плотность электронных состояний или другие электронные свойства. Существенным преимуществом использования методов ab initio является возможность изучения реакций, связанных с разрывом или образованием ковалентных связей, соответствующих множественным электронным состояниям. Более того, методы ab initio также позволяют восстанавливать эффекты, выходящие за рамки приближения Борна-Оппенгеймера, используя такие подходы, как смешанная квантово-классическая динамика .

Гибридный QM/MM

КМ (квантово-механические) методы очень эффективны. Однако они являются дорогостоящими в вычислительном отношении, в то время как методы ММ (классической или молекулярной механики) быстры, но имеют несколько ограничений (требуют обширной параметризации; полученные оценки энергии не очень точны; не могут использоваться для моделирования реакций, в которых ковалентные связи разрываются/образуются). и ограничены в своих возможностях предоставления точных сведений о химической среде). Появился новый класс методов, сочетающий в себе преимущества расчетов QM (точность) и MM (скорость). Эти методы называются смешанными или гибридными методами квантовой механики и молекулярной механики (гибридными КМ/ММ). ^{[ 51 ]}

Самым важным преимуществом гибридного метода QM/MM является скорость. Стоимость проведения классической молекулярной динамики (ММ) в наиболее простом случае масштабируется O(n ²), где n — количество атомов в системе. В основном это связано с термином электростатических взаимодействий (каждая частица взаимодействует с каждой другой частицей). Однако использование радиуса отсечки, периодические обновления списков пар и, в последнее время, вариации метода Эвальда (PME) сетки частиц сократили это значение до уровня от O (n) до O (n). ²). Другими словами, если смоделировать систему с вдвое большим количеством атомов, то потребуется в два-четыре раза больше вычислительной мощности. С другой стороны, простейшие расчеты ab initio обычно масштабируются O(n ³) или хуже ( Хартри – Фока для масштабирования ~O(n было предложено ограничиться расчетами ^2.7)). Чтобы преодолеть ограничение, небольшая часть системы обрабатывается квантово-механически (обычно активный центр фермента), а оставшаяся система обрабатывается классически.

В более сложных реализациях методы КМ/ММ существуют для обработки как легких ядер, чувствительных к квантовым эффектам (таких как водороды), так и электронных состояний. Это позволяет генерировать волновые функции водорода (аналогичные волновым функциям электронов). Эта методология оказалась полезной при исследовании таких явлений, как туннелирование водорода. Одним из примеров, когда методы КМ/ММ привели к новым открытиям, является расчет переноса гидрида в ферменте алкогольдегидрогеназы печени . В этом случае квантовое туннелирование важно для водорода, поскольку оно определяет скорость реакции. ^{[ 52 ]}

Грубозернистые и уменьшенные представления

На другом конце шкалы детализации находятся крупнозернистые и решетчатые модели. Вместо явного представления каждого атома системы для обозначения групп атомов используются «псевдоатомы». МД-моделирование в очень больших системах может потребовать таких больших компьютерных ресурсов, что их невозможно легко изучить традиционными полноатомными методами. Точно так же моделирование процессов в длительных временных масштабах (более 1 микросекунды) является непомерно дорогим, поскольку требует очень большого количества временных шагов. В этих случаях иногда можно решить проблему, используя сокращенные представления, которые также называются крупнозернистыми моделями . ^{[ 53 ]}

Примерами методов грубого измельчения (CG) являются разрывная молекулярная динамика (CG-DMD). ^{[ 54 ]}^{[ 55 ]} и Go-модели. ^{[ 56 ]} Иногда выполняется грубое измельчение с использованием псевдоатомов большего размера. Такие приближения объединенного атома использовались при МД-моделировании биологических мембран. Реализация такого подхода в системах, где электрические свойства представляют интерес, может быть сложной задачей из-за сложности использования правильного распределения заряда на псевдоатомах. ^{[ 57 ]} Алифатические хвосты липидов представлены несколькими псевдоатомами, в каждом псевдоатоме собрано от 2 до 4 метиленовых групп.

Параметризация этих очень грубых моделей должна осуществляться эмпирически, путем сопоставления поведения модели с соответствующими экспериментальными данными или полноатомным моделированием. учитывать как энтальпийный , так и энтропийный вклад в свободную энергию. В идеале эти параметры должны неявным образом ^{[ 58 ]} Когда грубая обработка выполняется на более высоких уровнях, точность динамического описания может быть менее надежной. Но очень грубые модели успешно использовались для изучения широкого круга вопросов структурной биологии, организации жидких кристаллов и полимерных стекол.

Примеры применения крупнозернистости:

исследования сворачивания белков и прогнозирования структуры белков часто проводятся с использованием одного или нескольких псевдоатомов на аминокислоту; ^{[ 53 ]}
Фазовые переходы жидких кристаллов исследовались в ограниченной геометрии и/или во время течения с использованием потенциала Гей-Берна , который описывает анизотропные виды;
Полимерные стекла при деформации изучались с использованием простых гармонических или FENE- пружин для соединения сфер, описываемых потенциалом Леннарда-Джонса ;
Сверхспирализация ДНК исследовалась с использованием 1–3 псевдоатомов на пару оснований и с еще более низким разрешением;
Упаковка двухспиральной ДНК в бактериофаг была исследована с помощью моделей, в которых один псевдоатом представляет один виток (около 10 пар оснований) двойной спирали;
Структура РНК в рибосоме и других крупных системах моделировалась с использованием одного псевдоатома на нуклеотид.

Самая простая форма грубого анализа — это объединенный атом (иногда называемый расширенным атомом ), который использовался в большинстве ранних моделей МД белков, липидов и нуклеиновых кислот. Например, вместо того, чтобы явно рассматривать все четыре атома метильной группы CH ₃ (или все три атома метиленовой группы CH ₂ ), представляют всю группу с одним псевдоатомом. Разумеется, она должна быть правильно параметризована, чтобы ее взаимодействия Ван-дер-Ваальса с другими группами имели правильную зависимость от расстояния. Аналогичные соображения применимы и к связям, углам и кручениям, в которых участвует псевдоатом. В этом виде представления объединенного атома обычно исключаются все явные атомы водорода, за исключением тех, которые способны участвовать в водородных связях ( полярные водороды ). Примером этого является CHARMM силовое поле 19.

Полярные водороды обычно сохраняются в модели, поскольку правильное рассмотрение водородных связей требует достаточно точного описания направленности и электростатических взаимодействий между донорными и акцепторными группами. Например, гидроксильная группа может быть как донором, так и акцептором водородной связи, и обработать ее одним псевдоатомом ОН было бы невозможно. Около половины атомов белка или нуклеиновой кислоты представляют собой неполярные атомы водорода, поэтому использование объединенных атомов может обеспечить существенную экономию компьютерного времени.

Включение эффектов растворителя

Во многих симуляциях системы растворенное вещество-растворитель основное внимание уделяется поведению растворенного вещества, при этом поведение растворителя мало интересует, особенно в тех молекулах растворителя, которые находятся в областях, далеких от молекулы растворенного вещества. ^{[ 59 ]} Растворители могут влиять на динамическое поведение растворенных веществ посредством случайных столкновений и создания сопротивления трения при движении растворенного вещества через растворитель. Использование непрямоугольных периодических граничных условий, стохастических границ и оболочек растворителя может помочь уменьшить количество требуемых молекул растворителя и позволить вместо этого тратить большую часть вычислительного времени на моделирование растворенного вещества. Также возможно включить эффекты растворителя без необходимости присутствия каких-либо явных молекул растворителя. Одним из примеров этого подхода является использование потенциальной средней силы (PMF), которая описывает, как изменяется свободная энергия при изменении конкретной координаты. Изменение свободной энергии, описываемое PMF, содержит усредненные эффекты растворителя.

Без учета эффектов растворителя моделирование макромолекул (таких как белки) может привести к нереалистичному поведению, и даже небольшие молекулы могут принять более компактные конформации из-за благоприятных сил Ван-дер-Ваальса и электростатических взаимодействий, которые будут ослабляться в присутствии растворителя. ^{[ 60 ]}

Силы дальнего действия

Дальнодействующее взаимодействие — это взаимодействие, при котором пространственное взаимодействие спадает не быстрее, чем $r^{-d}$ где $d$ – размерность системы. Примеры включают взаимодействия заряд-заряд между ионами и диполь-дипольные взаимодействия между молекулами. Моделирование этих сил представляет собой довольно сложную задачу, поскольку они значительны на расстоянии, которое может превышать половину длины ящика при моделировании многих тысяч частиц. Хотя одним из решений могло бы стать значительное увеличение длины блока, этот подход грубой силы не идеален, поскольку моделирование стало бы очень дорогостоящим в вычислительном отношении. О сферическом усечении потенциала также не может быть и речи, поскольку может наблюдаться нереалистичное поведение, когда расстояние близко к предельному расстоянию. ^{[ 61 ]}

Управляемая молекулярная динамика (SMD)

Моделирование управляемой молекулярной динамики (SMD), или моделирование силового зонда, применяет силы к белку, чтобы манипулировать его структурой, перемещая его по желаемым степеням свободы. Эти эксперименты можно использовать для выявления структурных изменений в белке на атомном уровне. SMD часто используется для моделирования таких событий, как механическое разворачивание или растяжение. ^{[ 62 ]}

Существует два типичных протокола SMD: один, в котором скорость вытягивания поддерживается постоянной, и другой, в котором приложенная сила постоянна. Обычно часть изучаемой системы (например, атом белка) удерживается гармоническим потенциалом. Затем к конкретным атомам прикладывают силы либо с постоянной скоростью, либо с постоянной силой. Зонтичная выборка используется для перемещения системы вдоль желаемой координаты реакции путем изменения, например, сил, расстояний и углов, которыми манипулируют при моделировании. Посредством зонтичного отбора проб все конфигурации системы – как высокоэнергетические, так и низкоэнергетические – подвергаются адекватной выборке. Затем изменение свободной энергии каждой конфигурации можно рассчитать как потенциал средней силы . ^{[ 63 ]} Популярным методом расчета PMF является метод анализа взвешенных гистограмм (WHAM), который анализирует серию моделей зонтичной выборки. ^{[ 64 ]}^{[ 65 ]}

Многие важные применения SMD находятся в области открытия лекарств и биомолекулярных наук. Например, SMD использовался для исследования стабильности протофибрилл болезни Альцгеймера. ^{[ 66 ]} изучить взаимодействие белка-лиганда в циклин-зависимой киназе 5 ^{[ 67 ]} и даже показать влияние электрического поля на комплекс тромбина (белка) и аптамера (нуклеотида). ^{[ 68 ]} среди многих других интересных исследований.

Примеры приложений

Молекулярная динамика используется во многих областях науки.

Первое МД-моделирование упрощенного процесса биологического сворачивания было опубликовано в 1975 году. Его моделирование, опубликованное в журнале Nature, проложило путь к обширной области современного вычислительного процесса сворачивания белков. ^{[ 70 ]}
Первое МД-моделирование биологического процесса было опубликовано в 1976 году. Его моделирование, опубликованное в журнале Nature, проложило путь к пониманию движения белка как важного функционального элемента, а не просто вспомогательного. ^{[ 71 ]}
МД является стандартным методом лечения каскадов столкновений в режиме тепловых пиков, т.е. эффектов, которые облучение энергичными нейтронами и ионами оказывает на твердые тела и твердые поверхности. ^{[ 72 ]}

Следующие биофизические примеры иллюстрируют заметные усилия по созданию моделирования систем очень большого размера (полный вирус) или очень длительного времени моделирования (до 1,112 миллисекунды):

MD-моделирование вируса полной спутниковой табачной мозаики (STMV) (2006 г., Размер: 1 миллион атомов, Время моделирования: 50 нс, программа: NAMD ). Этот вирус представляет собой небольшой икосаэдрический вирус растений, который ухудшает симптомы заражения вирусом табачной мозаики. (ТМВ). Моделирование молекулярной динамики использовалось для исследования механизмов сборки вируса . Вся частица STMV состоит из 60 идентичных копий одного белка, составляющих вирусный капсид одноцепочечной РНК из 1063 нуклеотидов (оболочку), и генома . Одним из ключевых открытий является то, что капсид очень нестабильен, когда внутри нет РНК. На моделирование одного настольного компьютера 2006 года ушло около 35 лет. Таким образом, это делалось во многих процессорах параллельно с постоянной связью между ними. ^{[ 73 ]}
Моделирование складывания головного убора злодея во всех атомных деталях (2006 г., размер: 20 000 атомов; время моделирования: 500 мкс = 500 000 нс, программа: Folding@home ). Это моделирование было запущено на 200 000 процессорах участвующих персональных компьютеров по всему миру. На этих компьютерах была установлена программа Folding@home — крупномасштабная программа распределенных вычислений, координируемая Виджаем Панде из Стэнфордского университета. Кинетические свойства белка Villin Headpiece были исследованы с использованием множества независимых коротких траекторий, управляемых процессорами без непрерывной связи в реальном времени. Одним из использованных методов был анализ значения Pfold, который измеряет вероятность сворачивания до разворачивания конкретной исходной конформации. Pfold дает информацию о структурах переходного состояния и упорядочении конформаций по пути сворачивания . Каждая траектория в расчете Pfold может быть относительно короткой, но необходимо много независимых траекторий. ^{[ 74 ]}
Моделирование длительных непрерывных траекторий было выполнено на Антоне , суперкомпьютере с массовым параллелизмом, спроектированном и построенном на основе специализированных интегральных схем (ASIC) и межсоединений, разработанных DE Shaw Research . Самый длинный опубликованный результат моделирования, выполненного с использованием Anton, — это моделирование NTL9 за 1,112 миллисекунды при 355 К; Также было выполнено второе независимое моделирование этой конфигурации за 1,073 миллисекунды (и многие другие моделирования с непрерывным химическим временем более 250 мкс). ^{[ 75 ]} В книге « Как сворачиваются быстро сворачивающиеся белки » исследователи Крестен Линдорф-Ларсен, Стефано Пиана, Рон О. Дрор и Дэвид Э. Шоу обсуждают «результаты моделирования молекулярной динамики на атомном уровне в течение периодов от 100 мкс до 1 мс, которые раскрыть набор общих принципов, лежащих в основе сворачивания 12 структурно различных белков». Изучение этих разнообразных длинных траекторий с помощью специализированного оборудования позволило им прийти к выводу, что «в большинстве случаев сворачивание следует одному доминирующему маршруту, в котором элементы естественной структуры появляются в порядке, сильно коррелирующем с их склонностью к формированию в развернутое состояние». ^{[ 75 ]} В отдельном исследовании Антон использовался для проведения 1,013-миллисекундного моделирования динамики динамики бычьего ингибитора трипсина поджелудочной железы (BPTI) в нативном состоянии при 300 К. ^{[ 76 ]}

Еще одно важное применение метода МД заключается в его способности трехмерной характеристики и анализа микроструктурной эволюции на атомном уровне.

МД-моделирование используется для характеристики изменения размера зерна, например, при описании износа и трения нанокристаллических материалов Al и Al(Zr). ^{[ 77 ]} В этом моделировании в процессе трения анализируется эволюция дислокаций и эволюция размера зерен. Поскольку метод МД предоставил полную информацию о микроструктуре, эволюция размера зерен была рассчитана в 3D с использованием сопоставления многогранных шаблонов. ^{[ 78 ]} Сегментация зерна, ^{[ 79 ]} и кластеризация графов ^{[ 80 ]} методы. При таком моделировании метод МД обеспечил точное измерение размера зерна. Используя эту информацию, были извлечены, измерены и представлены реальные зернистые структуры. По сравнению с традиционным методом использования СЭМ с одним двумерным срезом материала, МД обеспечивает трехмерный и точный способ охарактеризовать микроструктурную эволюцию на атомном уровне.

Алгоритмы молекулярной динамики

Модель неявного растворителя экранированных кулоновских потенциалов

Интеграторы

Симплектический интегратор
Интеграция Верле-Штермера
Интеграция Рунге – Кутты
Алгоритм Бимана
Алгоритмы ограничений (для систем с ограничениями)

Алгоритмы ближнего взаимодействия

Списки ячеек
Список Верле
Связанные взаимодействия

Алгоритмы дальнего взаимодействия

Суммирование Эвальда
сетки частиц Суммирование по Эвальду (PME)
Частица–частица-частица–сетка ( П3М )
Метод смещенной силы

Стратегии распараллеливания

Метод декомпозиции предметной области (Распределение системных данных для параллельных вычислений )

Молекулярная динамика ab-initio

Молекулярная динамика Кар – Парринелло

Специализированное оборудование для моделирования МД

Антон - специализированный суперкомпьютер с массовым параллелизмом, предназначенный для выполнения MD-моделирования.
MDGRAPE - система специального назначения, созданная для молекулярно-динамического моделирования, особенно для прогнозирования структуры белков.

Видеокарта как оборудование для моделирования МД

Моделирование ионной жидкости на графическом процессоре ( Abalone )

Молекулярное моделирование на графическом процессоре — это метод использования графического процессора (GPU) для молекулярного моделирования. ^{[ 81 ]}

В 2007 году компания NVIDIA представила видеокарты, которые можно было использовать не только для отображения графики, но и для научных расчетов. Эти карточки содержат множество арифметических единиц (по состоянию на 2016 год). , до 3584 в Tesla P100), работающих параллельно. Задолго до этого события вычислительные мощности видеокарт использовались исключительно для ускорения графических вычислений. Новым было то, что NVIDIA позволила разрабатывать параллельные программы с помощью высокоуровневого интерфейса прикладного программирования (API) под названием CUDA . Эта технология существенно упростила программирование, позволив писать программы на C / C++ . Совсем недавно OpenCL позволил обеспечить кроссплатформенное ускорение графического процессора.

См. также

Ссылки

^ Шлик Т. (1996). «Реализация видения Лапласа в отношении современных компьютеров». Математические подходы к биомолекулярной структуре и динамике . Тома IMA по математике и ее приложениям. Том. 82. стр. 219–247. дои : 10.1007/978-1-4612-4066-2_13 . ISBN 978-0-387-94838-6 .
^ Бернал Дж.Д. (январь 1997 г.). «Бейкеровская лекция, 1962 г. Структура жидкостей». Труды Лондонского королевского общества. Серия А. Математические и физические науки . 280 (1382): 299–322. Бибкод : 1964RSPSA.280..299B . дои : 10.1098/rspa.1964.0147 . S2CID 178710030 .
^ Ферми Э., Паста Дж., Улам С., Лос-Аламосский отчет LA-1940 (1955).
^ Олдер Б.Дж., Уэйнрайт Т. (август 1959 г.). «Исследования по молекулярной динамике. I. Общий метод». Журнал химической физики . 31 (2): 459–466. Бибкод : 1959ЖЧФ..31..459А . дои : 10.1063/1.1730376 .
^ Гибсон Дж. Б., Голанд А. Н., Милгрэм М., Виньярд Дж. (1960). «Динамика радиационного поражения». Физ. Преподобный . 120 (4): 1229–1253. Бибкод : 1960PhRv..120.1229G . дои : 10.1103/PhysRev.120.1229 .
^ Рахман А. (19 октября 1964 г.). «Корреляции в движении атомов в жидком аргоне». Физический обзор . 136 (2А): А405–А411. Бибкод : 1964PhRv..136..405R . дои : 10.1103/PhysRev.136.A405 .
^ Стефан С., Тол М., Врабец Дж., Хассе Х. (октябрь 2019 г.). «Теплофизические свойства жидкости Леннарда-Джонса: база данных и оценка данных» . Журнал химической информации и моделирования . 59 (10): 4248–4265. doi : 10.1021/acs.jcim.9b00620 . ПМИД 31609113 . S2CID 204545481 .
^ Ван X, Рамирес-Хинестроса С, Добникар Дж, Френкель Д (май 2020 г.). «Потенциал Леннарда-Джонса: когда (не) его использовать». Физическая химия Химическая физика . 22 (19): 10624–10633. arXiv : 1910.05746 . Бибкод : 2020PCCP...2210624W . дои : 10.1039/C9CP05445F . ПМИД 31681941 . S2CID 204512243 .
^ Мик Дж., Хайлат Э., Руссо В., Рушайдат К., Швиберт Л., Потофф Дж. (декабрь 2013 г.). «Моделирование Леннарда-Джонсиума в ансамбле Гиббса с использованием графического процессора». Компьютерная физика. Коммуникации . 184 (12): 2662–2669. Бибкод : 2013CoPhC.184.2662M . дои : 10.1016/j.cpc.2013.06.020 .
^ Чапела Г.А., Скривен Л.Е., Дэвис Х.Т. (октябрь 1989 г.). «Молекулярная динамика разрывного потенциала. IV. Леннард-Джонезиум» . Журнал химической физики . 91 (7): 4307–4313. Бибкод : 1989JChPh..91.4307C . дои : 10.1063/1.456811 . ISSN 0021-9606 .
^ Ленхард, Йоханнес; Стефан, Саймон; Хассе, Ганс (февраль 2024 г.). «Дитя предсказания. Об истории, онтологии и вычислениях Леннарда-Джонезиума». Исследования по истории и философии науки . 103 : 105–113. дои : 10.1016/j.shpsa.2023.11.007 . ПМИД 38128443 . S2CID 266440296 .
^ Эггиманн Б.Л., Суннарборг А.Дж., Стерн Х.Д., Блисс А.П., Зипманн Дж.И. (24 декабря 2013 г.). «Онлайн-база данных параметров и свойств силового поля TraPPE». Молекулярное моделирование . 40 (1–3): 101–105. дои : 10.1080/08927022.2013.842994 . ISSN 0892-7022 . S2CID 95716947 .
^ Стефан С., Хорш М.Т., Врабец Дж., Хассе Х. (03.07.2019). «MolMod – база данных силовых полей с открытым доступом для молекулярного моделирования жидкостей» . Молекулярное моделирование . 45 (10): 806–814. arXiv : 1904.05206 . дои : 10.1080/08927022.2019.1601191 . ISSN 0892-7022 . S2CID 119199372 .
^ Кёль П., Левитт М. (февраль 1999 г.). «Светлое будущее предсказания структуры белка». Структурная биология природы . 6 (2): 108–111. дои : 10.1038/5794 . ПМИД 10048917 . S2CID 3162636 .
^ Раваль А., Пиана С., член парламента Иствуда, Дрор Р.О., Шоу Д.Е. (август 2012 г.). «Уточнение моделей гомологии структуры белков с помощью длительного полноатомного молекулярно-динамического моделирования». Белки . 80 (8): 2071–2079. дои : 10.1002/прот.24098 . ПМИД 22513870 . S2CID 10613106 .
^ Бошам К.А., Лин Ю.С., Дас Р., Панде В.С. (апрель 2012 г.). «Улучшаются ли силовые поля белков? Систематический тест на основе 524 разнообразных измерений ЯМР» . Журнал химической теории и вычислений . 8 (4): 1409–1414. дои : 10.1021/ct2007814 . ПМЦ 3383641 . ПМИД 22754404 .
^ Пиана С., Клепейс Дж.Л., Шоу Д.Е. (февраль 2014 г.). «Оценка точности физических моделей, используемых при моделировании сворачивания белков: количественные данные, полученные в результате длительного моделирования молекулярной динамики» . Современное мнение в области структурной биологии . 24 : 98–105. дои : 10.1016/j.sbi.2013.12.006 . ПМИД 24463371 .
^ Чоудхури С., Приякумар У.Д., Састри Г.Н. (апрель 2015 г.). «Динамические фармакофорные модели для скрининга потенциальных ингибиторов микобактериальной циклопропансинтазы». Журнал химической информации и моделирования . 55 (4): 848–60. дои : 10.1021/ci500737b . ПМИД 25751016 .
^ Пинто М., Перес Дж. Дж., Рубио-Мартинес Дж. (январь 2004 г.). «Исследование молекулярной динамики пептидных сегментов домена BH3 проапоптотических белков Bak, Bax, Bid и Hrk, связанных с белками Bcl-xL и Bcl-2». Журнал компьютерного молекулярного дизайна . 18 (1): 13–22. Бибкод : 2004JCAMD..18...13P . doi : 10.1023/b:jcam.0000022559.72848.1c . ПМИД 15143800 . S2CID 11339000 .
^ Хатмал М.М., Джабер С., Таха М.О. (декабрь 2016 г.). «Сочетание молекулярно-динамического моделирования и анализа контактов лиганд-рецептор как новый подход к моделированию фармакофоров: бета-секретаза 1 и киназа контрольной точки 1 в качестве тематических исследований». Журнал компьютерного молекулярного дизайна . 30 (12): 1149–1163. Бибкод : 2016JCAMD..30.1149H . дои : 10.1007/s10822-016-9984-2 . ПМИД 27722817 . S2CID 11561853 .
^ Майерс Дж. К., Пейс CN (октябрь 1996 г.). «Водородная связь стабилизирует глобулярные белки» . Биофизический журнал . 71 (4): 2033–2039. Бибкод : 1996BpJ....71.2033M . дои : 10.1016/s0006-3495(96)79401-8 . ПМЦ 1233669 . ПМИД 8889177 .
^ Ленхард, Йоханнес; Стефан, Саймон; Хассе, Ганс (июнь 2024 г.). «К истории потенциала Леннарда-Джонса» . Аннален дер Физик . 536 (6). дои : 10.1002/andp.202400115 . ISSN 0003-3804 .
^ Фишер, Иоганн; Вендланд, Мартин (октябрь 2023 г.). «К истории ключевых эмпирических межмолекулярных потенциалов» . Жидкостно-фазовые равновесия . 573 : 113876. Бибкод : 2023FlPEq.57313876F . дои : 10.1016/j.fluid.2023.113876 .
^ Jump up to: ^а ^б Исраэлачвили Дж (1992). Межмолекулярные и поверхностные силы . Сан-Диего: Академическая пресса.
^ Круз Ф.Дж., де Пабло Дж.Дж., Мота Дж.П. (июнь 2014 г.). «Эндоэдральное удержание додекамера ДНК на чистых углеродных нанотрубках и стабильность канонической формы B». Журнал химической физики . 140 (22): 225103. arXiv : 1605.01317 . Бибкод : 2014JChPh.140v5103C . дои : 10.1063/1.4881422 . ПМИД 24929415 . S2CID 15149133 .
^ Круз Ф.Дж., Мота Дж.П. (2016). «Конформационная термодинамика цепей ДНК в гидрофильных нанопорах». Дж. Физ. хим. С. 120 (36): 20357–20367. дои : 10.1021/acs.jpcc.6b06234 .
^ Плимптон С. «Молекулярная динамика — параллельные алгоритмы» . Sandia.gov .
^ Стритт В.Б., Тилдесли DJ, Сэвилл Дж. (1978). «Многошаговые методы в молекулярной динамике». Мол Физ . 35 (3): 639–648. Бибкод : 1978МолФ..35..639С . дои : 10.1080/00268977800100471 .
^ Такерман М.Э., Берн Б.Дж., Мартина Г.Дж. (1991). «Алгоритм молекулярной динамики для нескольких временных масштабов: системы с дальнодействующими силами». J Chem Phys . 94 (10): 6811–6815. Бибкод : 1991ЖЧФ..94.6811Т . дои : 10.1063/1.460259 .
^ Такерман М.Э., Берн Б.Дж., Мартина Г.Дж. (1992). «Обратимая молекулярная динамика во многих временных масштабах». J Chem Phys . 97 (3): 1990–2001. Бибкод : 1992ЖЧФ..97.1990Т . дои : 10.1063/1.463137 . S2CID 488073 .
^ Сугита Ю., Окамото Ю. (ноябрь 1999 г.). «Метод репликано-обменной молекулярной динамики сворачивания белков». Письма по химической физике . 314 (1–2): 141–151. Бибкод : 1999CPL...314..141S . дои : 10.1016/S0009-2614(99)01123-9 .
^ Риццути Б (2022). «Молекулярное моделирование белков: от упрощенных физических взаимодействий к сложным биологическим явлениям». Biochimica et Biophysical Acta (BBA) - Белки и протеомика . 1870 (3): 140757. doi : 10.1016/j.bbapap.2022.140757 . ПМИД 35051666 . S2CID 263455009 .
^ Синнотт С.Б. , Бреннер Д.В. (2012). «Три десятилетия многочастичных потенциалов в исследовании материалов» . Вестник МРС . 37 (5): 469–473. Бибкод : 2012MRSBu..37..469S . дои : 10.1557/mrs.2012.88 .
^ Альбе К., Нордлунд К., Авербак Р.С. (2002). «Моделирование взаимодействия металл-полупроводник: аналитический потенциал порядка связи платина-углерод». Физ. Преподобный Б. 65 (19): 195124. Бибкод : 2002PhRvB..65s5124A . дои : 10.1103/physrevb.65.195124 .
^ Бреннер Д.В. (ноябрь 1990 г.). «Эмпирический потенциал углеводородов для использования при моделировании химического осаждения алмазных пленок из паровой фазы» (PDF) . Физический обзор B . 42 (15): 9458–9471. Бибкод : 1990PhRvB..42.9458B . дои : 10.1103/physrevb.42.9458 . ПМИД 9995183 . Архивировано из оригинала 22 сентября 2017 года.
^ Бердмор К., Смит Р. (1996). «Эмпирические потенциалы систем C-Si-H с применением к взаимодействиям C ₆₀ с поверхностями кристаллов Si». Философский журнал А. 74 (6): 1439–1466. Бибкод : 1996PMagA..74.1439B . дои : 10.1080/01418619608240734 .
^ Ни Б., Ли К.Х., Синнотт С.Б. (2004). «Реактивный эмпирический потенциал порядка связи (ребо) для взаимодействий углеводородов с кислородом». Физический журнал: конденсированное вещество . 16 (41): 7261–7275. Бибкод : 2004JPCM...16.7261N . дои : 10.1088/0953-8984/16/41/008 . S2CID 250760409 .
^ Ван Дуин А.С., Дасгупта С., Лорант Ф., Годдард В.А. (октябрь 2001 г.). «ReaxFF: Поле реактивной силы для углеводородов». Журнал физической химии А. 105 (41): 9396–9409. Бибкод : 2001JPCA..105.9396V . CiteSeerX 10.1.1.507.6992 . дои : 10.1021/jp004368u .
^ Круз Ф.Дж., Лопес Х.Н., Каладо Х.К., Минас да Пьедаде М.Э. (декабрь 2005 г.). «Молекулярно-динамическое исследование термодинамических свойств апатитов кальция. 1. Гексагональные фазы». Журнал физической химии Б. 109 (51): 24473–24479. дои : 10.1021/jp054304p . ПМИД 16375450 .
^ Круз Ф.Дж., Лопес Х.Н., Каладо Х.К. (март 2006 г.). «Молекулярно-динамическое моделирование расплавленного гидроксиапатита кальция». Жидкостно-фазовые равновесия . 241 (1–2): 51–58. Бибкод : 2006FlPEq.241...51C . doi : 10.1016/j.fluid.2005.12.021 .
^ Jump up to: ^а ^б Хусто Дж.Ф., Базант М.З., Каширас Э., Булатов В.В., Йип С. (1998). «Межатомный потенциал дефектов кремния и неупорядоченных фаз». Физ. Преподобный Б. 58 (5): 2539–2550. arXiv : cond-mat/9712058 . Бибкод : 1998PhRvB..58.2539J . дои : 10.1103/PhysRevB.58.2539 . S2CID 14585375 .
^ Терсофф Дж. (март 1989 г.). «Моделирование химии твердого тела: межатомные потенциалы для многокомпонентных систем». Физический обзор B . 39 (8): 5566–5568. Бибкод : 1989PhRvB..39.5566T . дои : 10.1103/physrevb.39.5566 . ПМИД 9948964 .
^ Доу М.С. , Фойлес С.М. , Баскес М.И. (март 1993 г.). «Метод встроенного атома: обзор теории и приложений» . Отчеты по материаловедению . 9 (7–8): 251–310. дои : 10.1016/0920-2307(93)90001-У .
^ Клери Ф, Розато В (июль 1993 г.). «Потенциалы сильной связи переходных металлов и сплавов». Физический обзор B . 48 (1): 22–33. Бибкод : 1993PhRvB..48...22C . дои : 10.1103/physrevb.48.22 . ПМИД 10006745 .
^ Ламуре Г., Хардер Э., Воробьев И.В., Ру Б., МакКерелл А.Д. (2006). «Поляризуемая модель воды для молекулярно-динамического моделирования биомолекул». Chem Phys Lett . 418 (1): 245–249. Бибкод : 2006CPL...418..245L . дои : 10.1016/j.cplett.2005.10.135 .
^ Сохан В.П., Джонс А.П., Чипсиган Ф.С., Крэйн Дж., Мартина Дж.Дж. (май 2015 г.). «Особенные свойства воды: их молекулярно-электронное происхождение» . Труды Национальной академии наук Соединенных Штатов Америки . 112 (20): 6341–6346. Бибкод : 2015PNAS..112.6341S . дои : 10.1073/pnas.1418982112 . ПМЦ 4443379 . ПМИД 25941394 .
^ Чипсиган Ф.С., Сохан В.П., Джонс А.П., Крейн Дж., Мартина Дж.Дж. (апрель 2015 г.). «Водородная связь и ориентация молекул на границе раздела жидкость-пар воды» . Физическая химия Химическая физика . 17 (14): 8660–8669. Бибкод : 2015PCCP...17.8660C . дои : 10.1039/C4CP05506C . hdl : 20.500.11820/0bd0cd1a-94f1-4053-809c-9fb68bbec1c9 . ПМИД 25715668 .
^ Махмуди М., Линч И., Эджтехади М.Р., член парламента от Монополи, Бомбелли Ф.Б., Лоран С. (сентябрь 2011 г.). «Взаимодействия белка и наночастиц: возможности и проблемы». Химические обзоры . 111 (9): 5610–5637. дои : 10.1021/cr100440g . ПМИД 21688848 .
^ Патель С., Маккерелл А.Д., Брукс К.Л. (сентябрь 2004 г.). «Поле флуктуирующих сил заряда CHARMM для белков: II свойства белка/растворителя на основе молекулярно-динамического моделирования с использованием неаддитивной электростатической модели» . Журнал вычислительной химии . 25 (12): 1504–1514. дои : 10.1002/jcc.20077 . ПМИД 15224394 . S2CID 16741310 .
^ Наджла Хоссейни А., Лунд М., Эйтехади М.Р. (май 2022 г.). «Влияние электронной поляризации на мембранную транслокацию противораковых препаратов». Физическая химия Химическая физика . 24 (20): 12281–12292. Бибкод : 2022PCCP...2412281N . дои : 10.1039/D2CP00056C . ПМИД 35543365 . S2CID 248696332 .
^ Методология таких методов была представлена Уоршелом и его коллегами. В последние годы пионерами выступили несколько групп, в том числе: Арье Варшел ( Университет Южной Калифорнии ), Вейтао Ян ( Университет Дьюка ), Шэрон Хаммес-Шиффер ( Университет штата Пенсильвания ), Дональд Трулар и Цзяли Гао ( Университет Миннесоты ) и Кеннет Мерц ( Университет Флориды ).
^ Биллетер С.Р., Уэбб С.П., Агарвал П.К., Иорданов Т., Хаммес-Шиффер С. (ноябрь 2001 г.). «Перенос гидрида в алкогольдегидрогеназе печени: квантовая динамика, кинетические изотопные эффекты и роль движения фермента». Журнал Американского химического общества . 123 (45): 11262–11272. дои : 10.1021/ja011384b . ПМИД 11697969 .
^ Jump up to: ^а ^б Кмиецик С., Гронт Д., Колински М., Витеска Л., Давид А.Е., Колински А. (июль 2016 г.). «Крупнозернистые белковые модели и их применение» . Химические обзоры . 116 (14): 7898–7936. doi : 10.1021/acs.chemrev.6b00163 . ПМИД 27333362 .
^ Фоглер Смит А., Холл С.К. (август 2001 г.). «Формирование альфа-спирали: прерывистая молекулярная динамика на модели белка промежуточного разрешения». Белки . 44 (3): 344–360. дои : 10.1002/прот.1100 . ПМИД 11455608 . S2CID 21774752 .
^ Дин Ф., Боррегеро Дж.М., Булдырей С.В., Стэнли Х.Э., Дохолян Н.В. (ноябрь 2003 г.). «Механизм перехода альфа-спирали в бета-шпильку». Белки . 53 (2): 220–228. дои : 10.1002/прот.10468 . ПМИД 14517973 . S2CID 17254380 .
^ Пачи Э., Вендруколо М., Карплюс М. (декабрь 2002 г.). «Достоверность моделей Го: сравнение с эмпирическим энергетическим разложением, защищенным растворителем» . Биофизический журнал . 83 (6): 3032–3038. Бибкод : 2002BpJ....83.3032P . дои : 10.1016/S0006-3495(02)75308-3 . ПМК 1302383 . ПМИД 12496075 .
^ Чакрабарти А., Кейгин Т. (май 2010 г.). «Крупнозернистое моделирование полиимидных сополимеров». Полимер . 51 (12): 2786–2794. doi : 10.1016/j.polymer.2010.03.060 .
^ Фоли Т.Т., Shell MS, Noid WG (декабрь 2015 г.). «Влияние разрешения на энтропию и информацию в крупнозернистых моделях». Журнал химической физики . 143 (24): 243104. Бибкод : 2015JChPh.143x3104F . дои : 10.1063/1.4929836 . ПМИД 26723589 .
^ Лич А (30 января 2001 г.). Молекулярное моделирование: принципы и приложения (2-е изд.). Харлоу: Прентис Холл. ISBN 9780582382107 . АСИН 0582382106 .
^ Лич А.Р. (2001). Молекулярное моделирование: принципы и приложения (2-е изд.). Харлоу, Англия: Прентис Холл. п. 320. ИСБН 0-582-38210-6 . OCLC 45008511 .
^ Аллен, член парламента, Тилдесли, диджей (22 августа 2017 г.). Компьютерное моделирование жидкостей (2-е изд.). Издательство Оксфордского университета. п. 216. ИСБН 9780198803201 . АСИН 0198803206 .
^ Ниенхаус ГУ (2005). Белково-лигандные взаимодействия: методы и приложения . Хумана Пресс. стр. 54–56 . ISBN 978-1-61737-525-5 .
^ Лещинский Ю (2005). Вычислительная химия: обзоры современных тенденций, Том 9 . Всемирная научная. стр. 54–56. ISBN 978-981-256-742-0 .
^ Кумар С., Розенберг Дж. М., Бузида Д., Свендсен Р. Х., Коллман П. А. (октябрь 1992 г.). «Метод анализа взвешенных гистограмм для расчета свободной энергии биомолекул. I. Метод». Журнал вычислительной химии . 13 (8): 1011–1021. дои : 10.1002/jcc.540130812 . S2CID 8571486 .
^ Бартельс С. (декабрь 2000 г.). «Анализ предвзятого моделирования Монте-Карло и молекулярной динамики». Письма по химической физике . 331 (5–6): 446–454. Бибкод : 2000CPL...331..446B . дои : 10.1016/S0009-2614(00)01215-X .
^ Лемкул Дж.А., Беван Д.Р. (февраль 2010 г.). «Оценка стабильности амилоидных протофибрилл болезни Альцгеймера с использованием молекулярной динамики». Журнал физической химии Б. 114 (4): 1652–1660. дои : 10.1021/jp9110794 . ПМИД 20055378 .
^ Патель Дж.С., Бертеотти А., Ронсисвалле С., Роккиа В., Кавалли А. (февраль 2014 г.). «Управляемое молекулярно-динамическое моделирование для изучения взаимодействия белок-лиганд в циклин-зависимой киназе 5». Журнал химической информации и моделирования . 54 (2): 470–480. дои : 10.1021/ci4003574 . ПМИД 24437446 .
^ Госай А., Ма Х, Баласубраманян Г, Шротрия П (ноябрь 2016 г.). «Связывание/рассвязывание комплекса тромбин-аптамер человека, контролируемое электрическим стимулом» . Научные отчеты . 6 (1): 37449. Бибкод : 2016НатСР...637449Г . дои : 10.1038/srep37449 . ПМК 5118750 . ПМИД 27874042 .
^ Пальма, Калифорния; Бьорк, Дж.; Рао, Ф.; Кюне, Д.; Клаппенбергер, Ф.; Барт, СП (2014). «Топологическая динамика в супрамолекулярных роторах». Нано-буквы . 148 (8): 4461–4468. Бибкод : 2014NanoL..14.4461P . дои : 10.1021/nl5014162 . ПМИД 25078022 .
^ Левитт М., Варшел А. (февраль 1975 г.). «Компьютерное моделирование сворачивания белка». Природа . 253 (5494): 694–698. Бибкод : 1975Natur.253..694L . дои : 10.1038/253694a0 . ПМИД 1167625 . S2CID 4211714 .
^ Варшел А. (апрель 1976 г.). «Модель велосипеда с педалями для первого шага в процессе видения». Природа . 260 (5553): 679–683. Бибкод : 1976Natur.260..679W . дои : 10.1038/260679a0 . ПМИД 1264239 . S2CID 4161081 .
^ Смит, Р., изд. (1997). Столкновения атомов и ионов в твердых телах и на поверхностях: теория, моделирование и приложения . Кембридж, Великобритания: Издательство Кембриджского университета. ^{[ нужна страница ]}
^ Фреддолино П., Архипов А., Ларсон С.Б., Макферсон А., Шультен К. «Моделирование молекулярной динамики спутникового вируса табачной мозаики (STMV)» . Группа теоретической и вычислительной биофизики . Университет Иллинойса в Урбана Шампейн.
^ Джаячандран Г., Вишал В., Панде В.С. (апрель 2006 г.). «Использование массово-параллельного моделирования и марковских моделей для изучения сворачивания белка: изучение динамики головного убора злодея» . Журнал химической физики . 124 (16): 164902. Бибкод : 2006JChPh.124p4902J . дои : 10.1063/1.2186317 . ПМИД 16674165 .
^ Jump up to: ^а ^б Линдорф-Ларсен К., Пиана С., Дрор Р.О., Шоу Д.Е. (октябрь 2011 г.). «Как быстро сворачиваются белки». Наука . 334 (6055): 517–520. Бибкод : 2011Sci...334..517L . CiteSeerX 10.1.1.1013.9290 . дои : 10.1126/science.1208351 . ПМИД 22034434 . S2CID 27988268 .
^ Шоу Д.Е., Марагакис П., Линдорф-Ларсен К., Пиана С., Дрор Р.О., Иствуд М.П. и др. (октябрь 2010 г.). «Характеристика структурной динамики белков на атомном уровне». Наука . 330 (6002): 341–346. Бибкод : 2010Sci...330..341S . дои : 10.1126/science.1187409 . ПМИД 20947758 . S2CID 3495023 .
^ Ши Ю, Шлуфарска I (ноябрь 2020 г.). «Микроструктурная эволюция нанокристаллического алюминия, вызванная износом, и роль легирующих добавок циркония» . Акта Материалия . 200 : 432–441. Бибкод : 2020AcMat.200..432S . doi : 10.1016/j.actamat.2020.09.005 . S2CID 224954349 .
^ Ларсен П.М., Шмидт С., Шиотц Дж. (1 июня 2016 г.). «Надежная структурная идентификация посредством сопоставления многогранных шаблонов». Моделирование и симуляция в материаловедении и инженерии . 24 (5): 055007. arXiv : 1603.05143 . Бибкод : 2016MSMSE..24e5007M . дои : 10.1088/0965-0393/24/5/055007 . S2CID 53980652 .
^ Хоффрогге П.В., Барралес-Мора, Лос-Анджелес (февраль 2017 г.). «Кинетика и вращение с разрешением зерен во время роста зерен нанокристаллического алюминия методом молекулярной динамики». Вычислительное материаловедение . 128 : 207–222. arXiv : 1608.07615 . дои : 10.1016/j.commatsci.2016.11.027 . S2CID 118371554 .
^ Бональд Т., Шарпантье Б., Галланд А., Холлоку А. (22 июня 2018 г.). «Кластеризация иерархических графов с использованием выборки пар узлов». arXiv : 1806.01664 [ cs.SI ].
^ Стоун Дж.Э., Филлипс Дж.К., Фреддолино П.Л., Харди DJ, Трабуко Л.Г., Шультен К. (декабрь 2007 г.). «Ускорение приложений молекулярного моделирования с помощью графических процессоров». Журнал вычислительной химии . 28 (16): 2618–2640. CiteSeerX 10.1.1.466.3823 . дои : 10.1002/jcc.20829 . ПМИД 17894371 . S2CID 15313533 .

Общие ссылки

Аллен, член парламента, диджей Тилдесли (1989). Компьютерное моделирование жидкостей . Издательство Оксфордского университета. ISBN 0-19-855645-4 .
Маккаммон Дж. А., Харви СК (1987). Динамика белков и нуклеиновых кислот . Издательство Кембриджского университета. ISBN 0-521-30750-3 .
Рапапорт, округ Колумбия (1996). Искусство молекулярно-динамического моделирования . ISBN 0-521-44561-2 .
Грибель М. , Кнапек С., Зумбуш Г. (2007). Численное моделирование в молекулярной динамике . Берлин, Гейдельберг: Springer. ISBN 978-3-540-68094-9 .
Френкель Д. , Смит Б. (2002) [2001]. Понимание молекулярного моделирования: от алгоритмов к приложениям . Сан-Диего: Академическая пресса. ISBN 978-0-12-267351-1 .
Хайле Дж. М. (2001). Молекулярно-динамическое моделирование: элементарные методы . Уайли. ISBN 0-471-18439-Х .
Садус Р.Дж. (2002). Молекулярное моделирование жидкостей: теория, алгоритмы и объектная ориентация . Эльзевир. ISBN 0-444-51082-6 .
Беккер О.М., Маккерелл-младший А.Д., Ру Б., Ватанабэ М. (2001). Вычислительная биохимия и биофизика . Марсель Деккер. ISBN 0-8247-0455-Х .
Лич А (2001). Молекулярное моделирование: принципы и приложения (2-е изд.). Прентис Холл. ISBN 978-0-582-38210-7 .
Шлик Т. (2002). Молекулярное моделирование и симуляция . Спрингер. ISBN 0-387-95404-Х .
Гувер ВБ (1991). Вычислительная статистическая механика . Эльзевир. ISBN 0-444-88192-1 .
Эванс DJ, Моррис Джи (2008). Статистическая механика неравновесных жидкостей (Второе изд.). Издательство Кембриджского университета. ISBN 978-0-521-85791-8 .

Внешние ссылки

[1] Шлик Т. (1996). «Реализация видения Лапласа в отношении современных компьютеров». Математические подходы к биомолекулярной структуре и динамике . Тома IMA по математике и ее приложениям. Том. 82. стр. 219–247. дои : 10.1007/978-1-4612-4066-2_13 . ISBN 978-0-387-94838-6 .

[2] Бернал Дж.Д. (январь 1997 г.). «Бейкеровская лекция, 1962 г. Структура жидкостей». Труды Лондонского королевского общества. Серия А. Математические и физические науки . 280 (1382): 299–322. Бибкод : 1964RSPSA.280..299B . дои : 10.1098/rspa.1964.0147 . S2CID 178710030 .

[fput-3] Ферми Э., Паста Дж., Улам С., Лос-Аламосский отчет LA-1940 (1955).

[a&w-4] Олдер Б.Дж., Уэйнрайт Т. (август 1959 г.). «Исследования по молекулярной динамике. I. Общий метод». Журнал химической физики . 31 (2): 459–466. Бибкод : 1959ЖЧФ..31..459А . дои : 10.1063/1.1730376 .

[5] Гибсон Дж. Б., Голанд А. Н., Милгрэм М., Виньярд Дж. (1960). «Динамика радиационного поражения». Физ. Преподобный . 120 (4): 1229–1253. Бибкод : 1960PhRv..120.1229G . дои : 10.1103/PhysRev.120.1229 .

[a.rahman-6] Рахман А. (19 октября 1964 г.). «Корреляции в движении атомов в жидком аргоне». Физический обзор . 136 (2А): А405–А411. Бибкод : 1964PhRv..136..405R . дои : 10.1103/PhysRev.136.A405 .

[7] Стефан С., Тол М., Врабец Дж., Хассе Х. (октябрь 2019 г.). «Теплофизические свойства жидкости Леннарда-Джонса: база данных и оценка данных» . Журнал химической информации и моделирования . 59 (10): 4248–4265. doi : 10.1021/acs.jcim.9b00620 . ПМИД 31609113 . S2CID 204545481 .

[8] Ван X, Рамирес-Хинестроса С, Добникар Дж, Френкель Д (май 2020 г.). «Потенциал Леннарда-Джонса: когда (не) его использовать». Физическая химия Химическая физика . 22 (19): 10624–10633. arXiv : 1910.05746 . Бибкод : 2020PCCP...2210624W . дои : 10.1039/C9CP05445F . ПМИД 31681941 . S2CID 204512243 .

[9] Мик Дж., Хайлат Э., Руссо В., Рушайдат К., Швиберт Л., Потофф Дж. (декабрь 2013 г.). «Моделирование Леннарда-Джонсиума в ансамбле Гиббса с использованием графического процессора». Компьютерная физика. Коммуникации . 184 (12): 2662–2669. Бибкод : 2013CoPhC.184.2662M . дои : 10.1016/j.cpc.2013.06.020 .

[10] Чапела Г.А., Скривен Л.Е., Дэвис Х.Т. (октябрь 1989 г.). «Молекулярная динамика разрывного потенциала. IV. Леннард-Джонезиум» . Журнал химической физики . 91 (7): 4307–4313. Бибкод : 1989JChPh..91.4307C . дои : 10.1063/1.456811 . ISSN 0021-9606 .

[11] Ленхард, Йоханнес; Стефан, Саймон; Хассе, Ганс (февраль 2024 г.). «Дитя предсказания. Об истории, онтологии и вычислениях Леннарда-Джонезиума». Исследования по истории и философии науки . 103 : 105–113. дои : 10.1016/j.shpsa.2023.11.007 . ПМИД 38128443 . S2CID 266440296 .

[12] Эггиманн Б.Л., Суннарборг А.Дж., Стерн Х.Д., Блисс А.П., Зипманн Дж.И. (24 декабря 2013 г.). «Онлайн-база данных параметров и свойств силового поля TraPPE». Молекулярное моделирование . 40 (1–3): 101–105. дои : 10.1080/08927022.2013.842994 . ISSN 0892-7022 . S2CID 95716947 .

[13] Стефан С., Хорш М.Т., Врабец Дж., Хассе Х. (03.07.2019). «MolMod – база данных силовых полей с открытым доступом для молекулярного моделирования жидкостей» . Молекулярное моделирование . 45 (10): 806–814. arXiv : 1904.05206 . дои : 10.1080/08927022.2019.1601191 . ISSN 0892-7022 . S2CID 119199372 .

[Koehl-14] Кёль П., Левитт М. (февраль 1999 г.). «Светлое будущее предсказания структуры белка». Структурная биология природы . 6 (2): 108–111. дои : 10.1038/5794 . ПМИД 10048917 . S2CID 3162636 .

[15] Раваль А., Пиана С., член парламента Иствуда, Дрор Р.О., Шоу Д.Е. (август 2012 г.). «Уточнение моделей гомологии структуры белков с помощью длительного полноатомного молекулярно-динамического моделирования». Белки . 80 (8): 2071–2079. дои : 10.1002/прот.24098 . ПМИД 22513870 . S2CID 10613106 .

[16] Бошам К.А., Лин Ю.С., Дас Р., Панде В.С. (апрель 2012 г.). «Улучшаются ли силовые поля белков? Систематический тест на основе 524 разнообразных измерений ЯМР» . Журнал химической теории и вычислений . 8 (4): 1409–1414. дои : 10.1021/ct2007814 . ПМЦ 3383641 . ПМИД 22754404 .

[17] Пиана С., Клепейс Дж.Л., Шоу Д.Е. (февраль 2014 г.). «Оценка точности физических моделей, используемых при моделировании сворачивания белков: количественные данные, полученные в результате длительного моделирования молекулярной динамики» . Современное мнение в области структурной биологии . 24 : 98–105. дои : 10.1016/j.sbi.2013.12.006 . ПМИД 24463371 .

[pmid25751016-18] Чоудхури С., Приякумар У.Д., Састри Г.Н. (апрель 2015 г.). «Динамические фармакофорные модели для скрининга потенциальных ингибиторов микобактериальной циклопропансинтазы». Журнал химической информации и моделирования . 55 (4): 848–60. дои : 10.1021/ci500737b . ПМИД 25751016 .

[pmid15143800-19] Пинто М., Перес Дж. Дж., Рубио-Мартинес Дж. (январь 2004 г.). «Исследование молекулярной динамики пептидных сегментов домена BH3 проапоптотических белков Bak, Bax, Bid и Hrk, связанных с белками Bcl-xL и Bcl-2». Журнал компьютерного молекулярного дизайна . 18 (1): 13–22. Бибкод : 2004JCAMD..18...13P . doi : 10.1023/b:jcam.0000022559.72848.1c . ПМИД 15143800 . S2CID 11339000 .

[pmid27722817-20] Хатмал М.М., Джабер С., Таха М.О. (декабрь 2016 г.). «Сочетание молекулярно-динамического моделирования и анализа контактов лиганд-рецептор как новый подход к моделированию фармакофоров: бета-секретаза 1 и киназа контрольной точки 1 в качестве тематических исследований». Журнал компьютерного молекулярного дизайна . 30 (12): 1149–1163. Бибкод : 2016JCAMD..30.1149H . дои : 10.1007/s10822-016-9984-2 . ПМИД 27722817 . S2CID 11561853 .

[Myers-21] Майерс Дж. К., Пейс CN (октябрь 1996 г.). «Водородная связь стабилизирует глобулярные белки» . Биофизический журнал . 71 (4): 2033–2039. Бибкод : 1996BpJ....71.2033M . дои : 10.1016/s0006-3495(96)79401-8 . ПМЦ 1233669 . ПМИД 8889177 .

[22] Ленхард, Йоханнес; Стефан, Саймон; Хассе, Ганс (июнь 2024 г.). «К истории потенциала Леннарда-Джонса» . Аннален дер Физик . 536 (6). дои : 10.1002/andp.202400115 . ISSN 0003-3804 .

[23] Фишер, Иоганн; Вендланд, Мартин (октябрь 2023 г.). «К истории ключевых эмпирических межмолекулярных потенциалов» . Жидкостно-фазовые равновесия . 573 : 113876. Бибкод : 2023FlPEq.57313876F . дои : 10.1016/j.fluid.2023.113876 .

[Israelachvili-24] Jump up to: ^а ^б Исраэлачвили Дж (1992). Межмолекулярные и поверхностные силы . Сан-Диего: Академическая пресса.

[ReferenceB-25] Круз Ф.Дж., де Пабло Дж.Дж., Мота Дж.П. (июнь 2014 г.). «Эндоэдральное удержание додекамера ДНК на чистых углеродных нанотрубках и стабильность канонической формы B». Журнал химической физики . 140 (22): 225103. arXiv : 1605.01317 . Бибкод : 2014JChPh.140v5103C . дои : 10.1063/1.4881422 . ПМИД 24929415 . S2CID 15149133 .

[ReferenceC-26] Круз Ф.Дж., Мота Дж.П. (2016). «Конформационная термодинамика цепей ДНК в гидрофильных нанопорах». Дж. Физ. хим. С. 120 (36): 20357–20367. дои : 10.1021/acs.jpcc.6b06234 .

[27] Плимптон С. «Молекулярная динамика — параллельные алгоритмы» . Sandia.gov .

[Streett-28] Стритт В.Б., Тилдесли DJ, Сэвилл Дж. (1978). «Многошаговые методы в молекулярной динамике». Мол Физ . 35 (3): 639–648. Бибкод : 1978МолФ..35..639С . дои : 10.1080/00268977800100471 .

[Tuckerman1991-29] Такерман М.Э., Берн Б.Дж., Мартина Г.Дж. (1991). «Алгоритм молекулярной динамики для нескольких временных масштабов: системы с дальнодействующими силами». J Chem Phys . 94 (10): 6811–6815. Бибкод : 1991ЖЧФ..94.6811Т . дои : 10.1063/1.460259 .

[Tuckerman1992-30] Такерман М.Э., Берн Б.Дж., Мартина Г.Дж. (1992). «Обратимая молекулярная динамика во многих временных масштабах». J Chem Phys . 97 (3): 1990–2001. Бибкод : 1992ЖЧФ..97.1990Т . дои : 10.1063/1.463137 . S2CID 488073 .

[31] Сугита Ю., Окамото Ю. (ноябрь 1999 г.). «Метод репликано-обменной молекулярной динамики сворачивания белков». Письма по химической физике . 314 (1–2): 141–151. Бибкод : 1999CPL...314..141S . дои : 10.1016/S0009-2614(99)01123-9 .

[32] Риццути Б (2022). «Молекулярное моделирование белков: от упрощенных физических взаимодействий к сложным биологическим явлениям». Biochimica et Biophysical Acta (BBA) - Белки и протеомика . 1870 (3): 140757. doi : 10.1016/j.bbapap.2022.140757 . ПМИД 35051666 . S2CID 263455009 .

[33] Синнотт С.Б. , Бреннер Д.В. (2012). «Три десятилетия многочастичных потенциалов в исследовании материалов» . Вестник МРС . 37 (5): 469–473. Бибкод : 2012MRSBu..37..469S . дои : 10.1557/mrs.2012.88 .

[34] Альбе К., Нордлунд К., Авербак Р.С. (2002). «Моделирование взаимодействия металл-полупроводник: аналитический потенциал порядка связи платина-углерод». Физ. Преподобный Б. 65 (19): 195124. Бибкод : 2002PhRvB..65s5124A . дои : 10.1103/physrevb.65.195124 .

[35] Бреннер Д.В. (ноябрь 1990 г.). «Эмпирический потенциал углеводородов для использования при моделировании химического осаждения алмазных пленок из паровой фазы» (PDF) . Физический обзор B . 42 (15): 9458–9471. Бибкод : 1990PhRvB..42.9458B . дои : 10.1103/physrevb.42.9458 . ПМИД 9995183 . Архивировано из оригинала 22 сентября 2017 года.

[36] Бердмор К., Смит Р. (1996). «Эмпирические потенциалы систем C-Si-H с применением к взаимодействиям C ₆₀ с поверхностями кристаллов Si». Философский журнал А. 74 (6): 1439–1466. Бибкод : 1996PMagA..74.1439B . дои : 10.1080/01418619608240734 .

[37] Ни Б., Ли К.Х., Синнотт С.Б. (2004). «Реактивный эмпирический потенциал порядка связи (ребо) для взаимодействий углеводородов с кислородом». Физический журнал: конденсированное вещество . 16 (41): 7261–7275. Бибкод : 2004JPCM...16.7261N . дои : 10.1088/0953-8984/16/41/008 . S2CID 250760409 .

[38] Ван Дуин А.С., Дасгупта С., Лорант Ф., Годдард В.А. (октябрь 2001 г.). «ReaxFF: Поле реактивной силы для углеводородов». Журнал физической химии А. 105 (41): 9396–9409. Бибкод : 2001JPCA..105.9396V . CiteSeerX 10.1.1.507.6992 . дои : 10.1021/jp004368u .

[39] Круз Ф.Дж., Лопес Х.Н., Каладо Х.К., Минас да Пьедаде М.Э. (декабрь 2005 г.). «Молекулярно-динамическое исследование термодинамических свойств апатитов кальция. 1. Гексагональные фазы». Журнал физической химии Б. 109 (51): 24473–24479. дои : 10.1021/jp054304p . ПМИД 16375450 .

[40] Круз Ф.Дж., Лопес Х.Н., Каладо Х.К. (март 2006 г.). «Молекулярно-динамическое моделирование расплавленного гидроксиапатита кальция». Жидкостно-фазовые равновесия . 241 (1–2): 51–58. Бибкод : 2006FlPEq.241...51C . doi : 10.1016/j.fluid.2005.12.021 .

[ReferenceA-41] Jump up to: ^а ^б Хусто Дж.Ф., Базант М.З., Каширас Э., Булатов В.В., Йип С. (1998). «Межатомный потенциал дефектов кремния и неупорядоченных фаз». Физ. Преподобный Б. 58 (5): 2539–2550. arXiv : cond-mat/9712058 . Бибкод : 1998PhRvB..58.2539J . дои : 10.1103/PhysRevB.58.2539 . S2CID 14585375 .

[42] Терсофф Дж. (март 1989 г.). «Моделирование химии твердого тела: межатомные потенциалы для многокомпонентных систем». Физический обзор B . 39 (8): 5566–5568. Бибкод : 1989PhRvB..39.5566T . дои : 10.1103/physrevb.39.5566 . ПМИД 9948964 .

[43] Доу М.С. , Фойлес С.М. , Баскес М.И. (март 1993 г.). «Метод встроенного атома: обзор теории и приложений» . Отчеты по материаловедению . 9 (7–8): 251–310. дои : 10.1016/0920-2307(93)90001-У .

[44] Клери Ф, Розато В (июль 1993 г.). «Потенциалы сильной связи переходных металлов и сплавов». Физический обзор B . 48 (1): 22–33. Бибкод : 1993PhRvB..48...22C . дои : 10.1103/physrevb.48.22 . ПМИД 10006745 .

[Lamoureux3-45] Ламуре Г., Хардер Э., Воробьев И.В., Ру Б., МакКерелл А.Д. (2006). «Поляризуемая модель воды для молекулярно-динамического моделирования биомолекул». Chem Phys Lett . 418 (1): 245–249. Бибкод : 2006CPL...418..245L . дои : 10.1016/j.cplett.2005.10.135 .

[Sokhan2015-46] Сохан В.П., Джонс А.П., Чипсиган Ф.С., Крэйн Дж., Мартина Дж.Дж. (май 2015 г.). «Особенные свойства воды: их молекулярно-электронное происхождение» . Труды Национальной академии наук Соединенных Штатов Америки . 112 (20): 6341–6346. Бибкод : 2015PNAS..112.6341S . дои : 10.1073/pnas.1418982112 . ПМЦ 4443379 . ПМИД 25941394 .

[Cipcigan-47] Чипсиган Ф.С., Сохан В.П., Джонс А.П., Крейн Дж., Мартина Дж.Дж. (апрель 2015 г.). «Водородная связь и ориентация молекул на границе раздела жидкость-пар воды» . Физическая химия Химическая физика . 17 (14): 8660–8669. Бибкод : 2015PCCP...17.8660C . дои : 10.1039/C4CP05506C . hdl : 20.500.11820/0bd0cd1a-94f1-4053-809c-9fb68bbec1c9 . ПМИД 25715668 .

[48] Махмуди М., Линч И., Эджтехади М.Р., член парламента от Монополи, Бомбелли Ф.Б., Лоран С. (сентябрь 2011 г.). «Взаимодействия белка и наночастиц: возможности и проблемы». Химические обзоры . 111 (9): 5610–5637. дои : 10.1021/cr100440g . ПМИД 21688848 .

[Patel2004b-49] Патель С., Маккерелл А.Д., Брукс К.Л. (сентябрь 2004 г.). «Поле флуктуирующих сил заряда CHARMM для белков: II свойства белка/растворителя на основе молекулярно-динамического моделирования с использованием неаддитивной электростатической модели» . Журнал вычислительной химии . 25 (12): 1504–1514. дои : 10.1002/jcc.20077 . ПМИД 15224394 . S2CID 16741310 .

[50] Наджла Хоссейни А., Лунд М., Эйтехади М.Р. (май 2022 г.). «Влияние электронной поляризации на мембранную транслокацию противораковых препаратов». Физическая химия Химическая физика . 24 (20): 12281–12292. Бибкод : 2022PCCP...2412281N . дои : 10.1039/D2CP00056C . ПМИД 35543365 . S2CID 248696332 .

[51] Методология таких методов была представлена Уоршелом и его коллегами. В последние годы пионерами выступили несколько групп, в том числе: Арье Варшел ( Университет Южной Калифорнии ), Вейтао Ян ( Университет Дьюка ), Шэрон Хаммес-Шиффер ( Университет штата Пенсильвания ), Дональд Трулар и Цзяли Гао ( Университет Миннесоты ) и Кеннет Мерц ( Университет Флориды ).

[52] Биллетер С.Р., Уэбб С.П., Агарвал П.К., Иорданов Т., Хаммес-Шиффер С. (ноябрь 2001 г.). «Перенос гидрида в алкогольдегидрогеназе печени: квантовая динамика, кинетические изотопные эффекты и роль движения фермента». Журнал Американского химического общества . 123 (45): 11262–11272. дои : 10.1021/ja011384b . ПМИД 11697969 .

[:0-53] Jump up to: ^а ^б Кмиецик С., Гронт Д., Колински М., Витеска Л., Давид А.Е., Колински А. (июль 2016 г.). «Крупнозернистые белковые модели и их применение» . Химические обзоры . 116 (14): 7898–7936. doi : 10.1021/acs.chemrev.6b00163 . ПМИД 27333362 .

[54] Фоглер Смит А., Холл С.К. (август 2001 г.). «Формирование альфа-спирали: прерывистая молекулярная динамика на модели белка промежуточного разрешения». Белки . 44 (3): 344–360. дои : 10.1002/прот.1100 . ПМИД 11455608 . S2CID 21774752 .

[55] Дин Ф., Боррегеро Дж.М., Булдырей С.В., Стэнли Х.Э., Дохолян Н.В. (ноябрь 2003 г.). «Механизм перехода альфа-спирали в бета-шпильку». Белки . 53 (2): 220–228. дои : 10.1002/прот.10468 . ПМИД 14517973 . S2CID 17254380 .

[56] Пачи Э., Вендруколо М., Карплюс М. (декабрь 2002 г.). «Достоверность моделей Го: сравнение с эмпирическим энергетическим разложением, защищенным растворителем» . Биофизический журнал . 83 (6): 3032–3038. Бибкод : 2002BpJ....83.3032P . дои : 10.1016/S0006-3495(02)75308-3 . ПМК 1302383 . ПМИД 12496075 .

[57] Чакрабарти А., Кейгин Т. (май 2010 г.). «Крупнозернистое моделирование полиимидных сополимеров». Полимер . 51 (12): 2786–2794. doi : 10.1016/j.polymer.2010.03.060 .

[58] Фоли Т.Т., Shell MS, Noid WG (декабрь 2015 г.). «Влияние разрешения на энтропию и информацию в крупнозернистых моделях». Журнал химической физики . 143 (24): 243104. Бибкод : 2015JChPh.143x3104F . дои : 10.1063/1.4929836 . ПМИД 26723589 .

[59] Лич А (30 января 2001 г.). Молекулярное моделирование: принципы и приложения (2-е изд.). Харлоу: Прентис Холл. ISBN 9780582382107 . АСИН 0582382106 .

[60] Лич А.Р. (2001). Молекулярное моделирование: принципы и приложения (2-е изд.). Харлоу, Англия: Прентис Холл. п. 320. ИСБН 0-582-38210-6 . OCLC 45008511 .

[61] Аллен, член парламента, Тилдесли, диджей (22 августа 2017 г.). Компьютерное моделирование жидкостей (2-е изд.). Издательство Оксфордского университета. п. 216. ИСБН 9780198803201 . АСИН 0198803206 .

[Nienhaus-62] Ниенхаус ГУ (2005). Белково-лигандные взаимодействия: методы и приложения . Хумана Пресс. стр. 54–56 . ISBN 978-1-61737-525-5 .

[Leszczyński-63] Лещинский Ю (2005). Вычислительная химия: обзоры современных тенденций, Том 9 . Всемирная научная. стр. 54–56. ISBN 978-981-256-742-0 .

[64] Кумар С., Розенберг Дж. М., Бузида Д., Свендсен Р. Х., Коллман П. А. (октябрь 1992 г.). «Метод анализа взвешенных гистограмм для расчета свободной энергии биомолекул. I. Метод». Журнал вычислительной химии . 13 (8): 1011–1021. дои : 10.1002/jcc.540130812 . S2CID 8571486 .

[65] Бартельс С. (декабрь 2000 г.). «Анализ предвзятого моделирования Монте-Карло и молекулярной динамики». Письма по химической физике . 331 (5–6): 446–454. Бибкод : 2000CPL...331..446B . дои : 10.1016/S0009-2614(00)01215-X .

[66] Лемкул Дж.А., Беван Д.Р. (февраль 2010 г.). «Оценка стабильности амилоидных протофибрилл болезни Альцгеймера с использованием молекулярной динамики». Журнал физической химии Б. 114 (4): 1652–1660. дои : 10.1021/jp9110794 . ПМИД 20055378 .

[67] Патель Дж.С., Бертеотти А., Ронсисвалле С., Роккиа В., Кавалли А. (февраль 2014 г.). «Управляемое молекулярно-динамическое моделирование для изучения взаимодействия белок-лиганд в циклин-зависимой киназе 5». Журнал химической информации и моделирования . 54 (2): 470–480. дои : 10.1021/ci4003574 . ПМИД 24437446 .

[68] Госай А., Ма Х, Баласубраманян Г, Шротрия П (ноябрь 2016 г.). «Связывание/рассвязывание комплекса тромбин-аптамер человека, контролируемое электрическим стимулом» . Научные отчеты . 6 (1): 37449. Бибкод : 2016НатСР...637449Г . дои : 10.1038/srep37449 . ПМК 5118750 . ПМИД 27874042 .

[69] Пальма, Калифорния; Бьорк, Дж.; Рао, Ф.; Кюне, Д.; Клаппенбергер, Ф.; Барт, СП (2014). «Топологическая динамика в супрамолекулярных роторах». Нано-буквы . 148 (8): 4461–4468. Бибкод : 2014NanoL..14.4461P . дои : 10.1021/nl5014162 . ПМИД 25078022 .

[70] Левитт М., Варшел А. (февраль 1975 г.). «Компьютерное моделирование сворачивания белка». Природа . 253 (5494): 694–698. Бибкод : 1975Natur.253..694L . дои : 10.1038/253694a0 . ПМИД 1167625 . S2CID 4211714 .

[71] Варшел А. (апрель 1976 г.). «Модель велосипеда с педалями для первого шага в процессе видения». Природа . 260 (5553): 679–683. Бибкод : 1976Natur.260..679W . дои : 10.1038/260679a0 . ПМИД 1264239 . S2CID 4161081 .

[Smith-72] Смит, Р., изд. (1997). Столкновения атомов и ионов в твердых телах и на поверхностях: теория, моделирование и приложения . Кембридж, Великобритания: Издательство Кембриджского университета. ^{[ нужна страница ]}

[73] Фреддолино П., Архипов А., Ларсон С.Б., Макферсон А., Шультен К. «Моделирование молекулярной динамики спутникового вируса табачной мозаики (STMV)» . Группа теоретической и вычислительной биофизики . Университет Иллинойса в Урбана Шампейн.

[74] Джаячандран Г., Вишал В., Панде В.С. (апрель 2006 г.). «Использование массово-параллельного моделирования и марковских моделей для изучения сворачивания белка: изучение динамики головного убора злодея» . Журнал химической физики . 124 (16): 164902. Бибкод : 2006JChPh.124p4902J . дои : 10.1063/1.2186317 . ПМИД 16674165 .

[DESRES-Science2011-75] Jump up to: ^а ^б Линдорф-Ларсен К., Пиана С., Дрор Р.О., Шоу Д.Е. (октябрь 2011 г.). «Как быстро сворачиваются белки». Наука . 334 (6055): 517–520. Бибкод : 2011Sci...334..517L . CiteSeerX 10.1.1.1013.9290 . дои : 10.1126/science.1208351 . ПМИД 22034434 . S2CID 27988268 .

[76] Шоу Д.Е., Марагакис П., Линдорф-Ларсен К., Пиана С., Дрор Р.О., Иствуд М.П. и др. (октябрь 2010 г.). «Характеристика структурной динамики белков на атомном уровне». Наука . 330 (6002): 341–346. Бибкод : 2010Sci...330..341S . дои : 10.1126/science.1187409 . ПМИД 20947758 . S2CID 3495023 .

[77] Ши Ю, Шлуфарска I (ноябрь 2020 г.). «Микроструктурная эволюция нанокристаллического алюминия, вызванная износом, и роль легирующих добавок циркония» . Акта Материалия . 200 : 432–441. Бибкод : 2020AcMat.200..432S . doi : 10.1016/j.actamat.2020.09.005 . S2CID 224954349 .

[78] Ларсен П.М., Шмидт С., Шиотц Дж. (1 июня 2016 г.). «Надежная структурная идентификация посредством сопоставления многогранных шаблонов». Моделирование и симуляция в материаловедении и инженерии . 24 (5): 055007. arXiv : 1603.05143 . Бибкод : 2016MSMSE..24e5007M . дои : 10.1088/0965-0393/24/5/055007 . S2CID 53980652 .

[79] Хоффрогге П.В., Барралес-Мора, Лос-Анджелес (февраль 2017 г.). «Кинетика и вращение с разрешением зерен во время роста зерен нанокристаллического алюминия методом молекулярной динамики». Вычислительное материаловедение . 128 : 207–222. arXiv : 1608.07615 . дои : 10.1016/j.commatsci.2016.11.027 . S2CID 118371554 .

[80] Бональд Т., Шарпантье Б., Галланд А., Холлоку А. (22 июня 2018 г.). «Кластеризация иерархических графов с использованием выборки пар узлов». arXiv : 1806.01664 [ cs.SI ].

[81] Стоун Дж.Э., Филлипс Дж.К., Фреддолино П.Л., Харди DJ, Трабуко Л.Г., Шультен К. (декабрь 2007 г.). «Ускорение приложений молекулярного моделирования с помощью графических процессоров». Журнал вычислительной химии . 28 (16): 2618–2640. CiteSeerX 10.1.1.466.3823 . дои : 10.1002/jcc.20829 . ПМИД 17894371 . S2CID 15313533 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

[ 26 ]

[ 27 ]

[ 28 ]

[ 29 ]

[ 30 ]

[ 31 ]

[ 32 ]

[ 33 ]

[ 34 ]

[ 35 ]

[ 36 ]

[ 37 ]

[ 38 ]

[ 39 ]

[ 40 ]

[ 41 ]

[ 42 ]

[ 43 ]

[ 44 ]

[ 45 ]

[ 46 ]

[ 47 ]

[ 48 ]

[ 49 ]

[ 50 ]

[ 51 ]

[ 52 ]

[ 53 ]

[ 54 ]

[ 55 ]

[ 56 ]

[ 57 ]

[ 58 ]

[ 59 ]

[ 60 ]

[ 61 ]

[ 62 ]

[ 63 ]

[ 64 ]

[ 65 ]

[ 66 ]

[ 67 ]

[ 68 ]

[ 69 ]

[ 70 ]

[ 71 ]

[ 72 ]

[ 73 ]

[ 74 ]

[ 75 ]

[ 76 ]

[ 77 ]

[ 78 ]

[ 79 ]

[ 80 ]

[ 81 ]

v т и Отрасли химии
Словарь химических формул Список биомолекул Список неорганических соединений Периодическая таблица
Аналитический	Инструментальная химия Электроаналитические методы Спектроскопия И Рамановский УФ-Вид ЯМР Масс-спектрометрия НЕТ ПМС МАЛЬДИ Процесс разделения Хроматография ГК ВЭЖХ Кристаллография Характеристика Титрование Мокрая химия Калориметрия Элементный анализ
Теоретический	Квантовая химия Вычислительная химия Математическая химия Молекулярное моделирование Молекулярная механика Молекулярная динамика Молекулярная геометрия Теория ВСЕПР
Физический	Электрохимия Спектроэлектрохимия Фотоэлектрохимия Термохимия Химическая термодинамика Наука о поверхности Интерфейс и коллоидная наука Микромеритика Криохимия Сонохимия Структурная химия Химическая физика Молекулярная физика Фемтохимия Химическая кинетика Спектроскопия Фотохимия Спиновая химия Микроволновая химия Равновесная химия Механохимия
Неорганический	Координационная химия Магнитохимия Металлоорганическая химия Лантанидорганическая химия Кластерная химия Химия твердого тела Керамическая химия
Органический	Стереохимия Стереохимия алканов Физическая органическая химия Органические реакции Органический синтез Ретросинтетический анализ Энантиоселективный синтез Полный синтез / Полусинтез Фуллереновая химия Полимерная химия Нефтехимия Динамическая ковалентная химия
Биологический	Биохимия Молекулярная биология Клеточная биология Химическая биология Биоортогональная химия Медицинская химия Фармакология Клиническая химия Нейрохимия Биоорганическая химия Биоорганометаллическая химия Бионеорганическая химия Биофизическая химия
Междисциплинарность	Ядерная химия Радиохимия Радиационная химия Актинидная химия Космохимия / Астрохимия / Звездная химия Геохимия Биогеохимия Фотогеохимия Экологическая химия Химия атмосферы Химия океана Глиняная химия Карбохимия Пищевая химия Углеводная химия Пищевая физическая химия Агрохимия Химия почвы Химическое образование Любительская химия Общая химия Тайная химия Судебная химия Судебная токсикология Посмертная химия Nanochemistry Супрамолекулярная химия Химический синтез Зеленая химия Нажмите химия Комбинаторная химия Биосинтез Химическая инженерия Стехиометрия Материаловедение Металлургия Керамическая инженерия Полимерная наука
См. также	История химии Нобелевская премия по химии Хронология химии открытий элементов « Центральная наука » Химическая реакция Катализ Химический элемент Химическое соединение Атом Молекула Ион Химическое вещество Химическая связь Алхимия Квантовая механика
Категория Коммонс Портал ВикиПроект