Набор (математика)

Эта статья о том, что математики называют «интуитивной» или «наивной» теорией множеств. Более подробную информацию см. в разделе Наивная теория множеств . Строгую современную аксиоматическую трактовку множеств см. в Теории множеств .

Набор многоугольников на диаграмме Эйлера

Этот набор аналогичен изображенному выше, поскольку оба состоят из одних и тех же элементов.

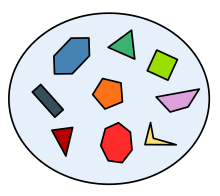
В математике множество – это совокупность различных вещи; эти вещи называются элементами или членами множества и обычно представляют собой математические объекты любого типа: числа, символы, точки в пространстве, линии, другие геометрические фигуры, переменные или даже другие множества. Множество может иметь конечное число элементов или быть бесконечным . Существует уникальный набор без элементов, называемый пустым набором ; набор с одним элементом является синглтоном .

Наборы уникально характеризуются своими элементами; это означает, что два множества, состоящие из одних и тех же элементов, равны (это один и тот же набор). Это свойство называется экстенсиональностью . В частности, это означает, что существует только одно пустое множество.

Множества широко распространены в современной математике. Действительно, теория множеств , а точнее теория множеств Цермело-Френкеля , была стандартным способом обеспечения строгих основ для всех областей математики с первой половины 20-го века.

Определение и обозначения

В математических текстах множества обычно обозначаются заглавными буквами. курсивом ​ например A , B , C. , Набор также можно называть коллекцией или семейством , особенно если его элементы сами являются наборами.

Обозначение реестра

Нотация реестра или перечисления определяет набор путем перечисления его элементов в фигурных скобках , разделенных запятыми:

А = {4, 2, 1, 3}

B = {синий, белый, красный} .

Это обозначение было введено Эрнстом Цермело в 1908 году. В наборе все, что имеет значение, это то, находится ли в нем каждый элемент или нет, поэтому порядок элементов в записи списка не имеет значения (напротив, в последовательности , кортеже или перестановке набора порядок элементов в наборе не имеет значения). условия имеют значение). Например, {2, 4, 6} и {4, 6, 4, 2} представляют один и тот же набор.

Для наборов со многими элементами, особенно тех, которые следуют неявному шаблону, список членов можно сократить с помощью многоточия ' ... ' . Например, набор из первой тысячи положительных целых чисел может быть указан в записи реестра как

{1, 2, 3, ..., 1000} .

Бесконечные множества в реестровых обозначениях

Бесконечное множество — это множество с бесконечным списком элементов. Чтобы описать бесконечное множество в записи списка, в конце списка или на обоих концах ставится многоточие, чтобы указать, что список продолжается вечно. Например, набор неотрицательных целых чисел равен

{0, 1, 2, 3, 4, ...} ,

и набор всех целых чисел равен

{..., −3, −2, −1, 0, 1, 2, 3, ...} .

Семантическое определение

Другой способ определить набор — использовать правило для определения элементов:

Пусть A — множество, членами которого являются первые четыре положительных целых числа .

Пусть B — набор цветов французского флага .

Такое определение называется семантическим описанием .

Обозначение построителя множеств

Основная статья: Обозначение построителя множеств

Обозначение построителя множеств определяет набор как выборку из большего набора, определяемого условием элементов. Например, набор F можно определить следующим образом:

$$F=\{n\mid n{\text{ is an integer, and }}0\leq n\leq 19\}.$$

В этом обозначении вертикальная черта "|" означает «такой, что», а описание можно интерпретировать как « F — множество всех чисел n таких, что n — целое число в диапазоне от 0 до 19 включительно». используют двоеточие «:». Некоторые авторы вместо вертикальной черты

Классификация методов определения

Философия использует конкретные термины для классификации типов определений:

• Интенсиональное определение использует правило для определения членства. Примерами являются семантические определения и определения, использующие нотацию построителя множеств.
• Экстенсиональное определение описывает множество, перечисляя все его элементы . Такие определения еще называют перечислительными .
• Указательное определение — это определение, которое описывает множество, приводя примеры элементов; Примером может служить список с многоточием.

Членство

Основная статья: Элемент (математика)

Если B — множество, а x — элемент B , это сокращенно записывается как x ∈ B , что также можно прочитать как « x принадлежит B » или « x находится в B ». Утверждение « y не является элементом B » записывается как y ∉ B , что также можно прочитать как « y не является элементом B ».

Например, относительно множеств A = {1, 2, 3, 4} , B = {blue, white, red} и F = { n | n — целое число и 0 ≤ n ≤ 19} ,

4 € А и 12 € F ; и

20 ∉ F и зеленый B. ∉

Пустой набор

Основная статья: Пустой набор

Пустой набор (или нулевой набор ) — это уникальный набор, не имеющий членов. Обозначается ∅ , $\emptyset$, { }, φ , или φ .

Наборы синглтонов

Основная статья: Синглтон (математика)

Одноэлементный набор — это набор, состоящий ровно из одного элемента; такой набор также можно назвать единичным набором . Любой такой набор можно записать как { x }, где x — элемент.Набор { x } и элемент x означают разные вещи; Халмош проводит аналогию с тем, что коробка со шляпой — это не то же самое, что шляпа.

Подмножества

Основная статья: Подмножество

Если каждый элемент множества A также находится в B , то A описывается как подмножество B или содержится в B , записывая A ⊆ B , или Б ⊇ А. ​ Последнее обозначение может быть прочитано как B содержит A , B включает A или B является расширенным набором A . Отношения между множествами , установленные ⊆, называются включением или включением . Два множества равны, если они содержат друг друга: A ⊆ B и B ⊆ A эквивалентно A = B .

Если A является подмножеством B , но не равно B , то A называется подмножеством B. собственным A Это можно записать A ⊊ B . Аналогично, B ⊋ A означает, что является собственным надмножеством A , т. е. B содержит A и не равно A. B

Третья пара операторов ⊂ и ⊃ используется разными авторами по-разному: некоторые авторы используют A ⊂ B и B ⊃ A, подразумевая, что A является любым подмножеством B (и не обязательно собственным подмножеством), в то время как другие резервируют A ⊂ B и B ⊃ A для случаев, когда A является собственным подмножеством B .

Примеры:

• Совокупность всех людей является подмножеством совокупности всех млекопитающих.
• {1, 3} ⊂ {1, 2, 3, 4} .
• {1, 2, 3, 4} ⊆ {1, 2, 3, 4} .

Пустое множество является подмножеством каждого множества, и каждое множество является подмножеством самого себя:

• ∅ ⊆ А .
• А ⊆ А. ​

Диаграммы Эйлера и Венна

A подмножеством B. является
B надмножеством A. является

Диаграмма Эйлера — это графическое представление набора множеств; каждый набор изображается как плоская область, заключенная в петлю, с элементами внутри. Если A является подмножеством B , то область, представляющая , полностью находится внутри области, представляющей B. A Если два набора не имеют общих элементов, регионы не перекрываются.

Диаграмма Венна , напротив, представляет собой графическое представление n множеств, в которых n петель делят плоскость на 2 части. ^н зоны такие, что для каждого способа выбора некоторых из n наборов (возможно, всех или ни одного) существует зона для элементов, принадлежащих всем выбранным наборам и ни одному из других. Например, если множествами являются A , B и C , должна быть зона для элементов, находящихся внутри A и C и снаружи B (даже если такие элементы не существуют).

Специальные наборы чисел в математике

Натуральные числа $\mathbb {N}$ содержатся в целых числах $\mathbb {Z}$, которые содержатся в рациональных числах $\mathbb {Q}$, которые содержатся в действительных числах $\mathbb {R}$, которые содержатся в комплексных числах $\mathbb {C}$

Существуют множества такой математической важности, к которым математики так часто обращаются, что они получили специальные названия и обозначения для их идентификации.

Многие из этих важных наборов представлены в математических текстах жирным шрифтом (например, $\mathbf {Z}$) или жирным шрифтом на доске (например, $\mathbb {Z}$) шрифт. К ним относятся

• $\mathbf {N}$ или $\mathbb {N}$, набор всех натуральных чисел : $\mathbf {N} =\{0,1,2,3,...\}$ (часто авторы исключают 0 );
• $\mathbf {Z}$ или $\mathbb {Z}$, набор всех целых чисел (положительных, отрицательных или нулевых): $\mathbf {Z} =\{...,-2,-1,0,1,2,3,...\}$;
• $\mathbf {Q}$ или $\mathbb {Q}$, набор всех рациональных чисел (то есть набор всех правильных и неправильных дробей ): $\mathbf {Q} =\left\{{\frac {a}{b}}\mid a,b\in \mathbf {Z} ,b\neq 0\right\}$. Например, — ⁠ 7/4 ​ 5 ⁠ ∈ Q и = ⁠ 5 / 1 ⁠ ∈ Q ;
• $\mathbf {R}$ или $\mathbb {R}$, набор всех действительных чисел , включая все рациональные числа и все иррациональные числа (в том числе алгебраические числа, такие как ${\sqrt {2}}$ которые невозможно переписать в виде дробей, а также трансцендентных чисел, таких как π и e );
• $\mathbf {C}$ или $\mathbb {C}$, множество всех комплексных чисел : C = { a + bi | a , b ∈ R } например, 1 + 2 i ∈ C. ,

Каждый из приведенных выше наборов чисел имеет бесконечное количество элементов. Каждый из них представляет собой подмножество наборов, перечисленных под ним.

Наборы положительных или отрицательных чисел иногда обозначаются надстрочными знаками плюс и минус соответственно. Например, $\mathbf {Q} ^{+}$ представляет собой набор положительных рациональных чисел.

Функции

Функция — это (или отображение ) множества A в множество B правило, которое присваивает каждому «входному» элементу A «выходной элемент», который является элементом B ; более формально, функция — это особый вид отношения , которое связывает каждый элемент A с одним элементом B. ровно Функция называется

• инъективен (или взаимно однозначен), если он отображает любые два разных элемента A в разные элементы B ,
• сюръективен (или на), если для каждого элемента B существует хотя бы один элемент A , который отображается в него, и
• биективное (или взаимно однозначное соответствие), если функция одновременно инъективна и сюръективна - в этом случае каждый элемент A соединен с уникальным элементом B , а каждый элемент B соединен с уникальным элементом A , чтобы не было непарных элементов.

Инъективная функция называется инъекцией , сюръективная функция называется сюръекцией , а биективная функция называется биекцией или взаимно однозначным соответствием .

Мощность

Основная статья: Кардинальность

Мощность множества S , обозначаемая | С | , число членов S . Например, если B = {синий, белый, красный} , то | Б | = 3 . Повторные участники в записи реестра не учитываются, так | {синий, белый, красный, синий, белый} | = 3 тоже.

Более формально, два множества имеют одинаковую мощность, если между ними существует биекция.

Мощность пустого множества равна нулю.

Бесконечные множества и бесконечная мощность

Список элементов некоторых множеств бесконечен или бесконечен . Например, набор $\mathbb {N}$ натуральных чисел бесконечно. Фактически, все специальные наборы чисел, упомянутые в разделе выше, бесконечны. Бесконечные множества имеют бесконечную мощность .

Некоторые бесконечные мощности больше других. Возможно, один из наиболее важных результатов теории множеств заключается в том, что набор действительных чисел имеет большую мощность, чем набор натуральных чисел. Наборы с мощностью меньше или равной $\mathbb {N}$ называются счетными множествами ; это либо конечные множества, либо счетно бесконечные множества (множества той же мощности, что и $\mathbb {N}$); некоторые авторы используют слово «счетный» для обозначения «счетной бесконечности». Множества с мощностью строго большей, чем у $\mathbb {N}$ называются несчетными множествами .

Однако можно показать, что мощность прямой линии (т. е. количество точек на прямой) такая же, как мощность любого отрезка этой линии, всей плоскости и даже любого конечномерного евклидова космос .

Гипотеза континуума

Основная статья: Гипотеза континуума

Гипотеза континуума, сформулированная Георгом Кантором в 1878 году, представляет собой утверждение о том, что не существует множества с мощностью строго между мощностью натуральных чисел и мощностью прямой линии. В 1963 году Пол Коэн доказал, что гипотеза континуума не зависит от системы аксиом ZFC, состоящей из теории множеств Цермело – Френкеля с аксиомой выбора . (ZFC — наиболее широко изученная версия аксиоматической теории множеств.)

Силовые наборы

Основная статья: Набор мощности

Набор мощности набора S - это набор всех подмножеств S . Пустое множество и само S являются элементами набора мощности S , поскольку оба они являются S. подмножествами Например, набор степеней {1, 2, 3} равен {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1 , 2, 3}} . Набор мощности набора S обычно записывается как P ( S ) или 2. ^С .

Если S имеет n элементов, то P ( S ) имеет 2 ^н элементы. Например, {1, 2, 3} состоит из трех элементов, а его набор мощности имеет 2 элемента. ³ = 8 элементов, как показано выше.

Если S бесконечно (неважно, счетно или несчетно ), то P ( S ) несчетно. Более того, набор степеней всегда строго «больше», чем исходный набор, в том смысле, что любая попытка объединить элементы S с элементами P ( S ) оставит некоторые элементы P ( S ) неспаренными. не существует биекции S P на S ( ( Никогда ) .)

Перегородки

Основная статья: Раздел набора

Раздел множества S — это набор непустых подмножеств S , такой, что каждый элемент x в S находится ровно в одном из этих подмножеств. То есть подмножества попарно не пересекаются (это означает, что любые два множества раздела не содержат общих элементов), а объединение всех подмножеств раздела равно S .

Основные операции

Основная статья: Алгебра множеств

Дополнение ​ A ​ в U

Предположим, что универсальное множество U (множество, содержащее все обсуждаемые элементы) фиксировано и что A является подмножеством U .

• Дополнением A не , является множество всех элементов U которые принадлежат A. ) ( Его можно обозначить А ^с или А ' . В обозначениях построителя множеств, $A^{\text{c}}=\{a\in U:a\notin A\}$. Дополнение также можно назвать абсолютным дополнением, чтобы отличить его от относительного дополнения, приведенного ниже. Пример: Если универсальный набор считается набором целых чисел, то дополнением набора четных целых чисел является набор нечетных целых чисел.

Объединение ​ A B и B , A ∪ обозначаемое

Пересечение ​ A B и B , A ∩ обозначаемое

Установленная разница А \ В

Симметричная разность A ​ и B

Учитывая любые два множества A и B ,

• их объединение A ∪ B представляет собой множество всех вещей, которые являются членами A или B, или того и другого.
• их пересечение A ∩ B представляет собой множество всех вещей, которые являются членами как A , так и B . Если A ∩ B = ∅ , то A и B называются непересекающимися .
• разность множеств A \ B (также обозначаемая как A − B ) — это набор всех вещей, которые принадлежат A , но не принадлежат B . Особенно когда B подмножеством A , его также называют дополнением B A. в является относительным С Б ^с как абсолютное дополнение к B (в универсальном множестве U ), A \ B = A ∩ B ^с .
• их симметричная разность A Δ B представляет собой совокупность всех вещей, принадлежащих A или B , но не обоим одновременно. У одного есть $A\,\Delta \,B=(A\setminus B)\cup (B\setminus A)$.
• их декартово произведение A × B — это набор всех упорядоченных пар ( a , b ) таких, что — элемент A , а b — элемент B. a

Примеры:

• {1, 2, 3} ∪ {3, 4, 5} = {1, 2, 3, 4, 5 }.
• {1, 2, 3} ∩ {3, 4, 5} = {3 }.
• {1, 2, 3} − {3, 4, 5} = {1, 2 }.
• {1, 2, 3} D {3, 4, 5} = {1, 2, 4, 5 }.
• { а , б } × {1, 2, 3} = {( а ,1), ( а ,2), ( а ,3), ( б ,1), ( б ,2), ( б ,3) }.

Вышеописанные операции удовлетворяют многим тождествам. Например, один из законов Де Моргана гласит, что ( A ∪ B )′ = A ′ ∩ B ′ (то есть элементы вне объединения A и B — это элементы, находящиеся вне A и вне B ).

Мощность A × B является произведением мощностей A и B .(Это элементарный факт, когда A и B конечны. Когда одно или оба бесконечны, для того чтобы это было верным, определено умножение кардинальных чисел.)

Набор степеней любого набора становится булевым кольцом с симметричной разницей как сложение кольца и пересечением как умножение кольца.

Приложения

Множества широко распространены в современной математике. Например, структуры в абстрактной алгебре , такие как группы , поля и кольца , представляют собой множества, замкнутые относительно одной или нескольких операций.

Одним из основных применений наивной теории множеств является построение отношений . Отношение области A к кодомену B является подмножеством декартова произведения A × B . Например, если рассматривать набор S = {камень, бумага, ножницы} фигур игре в одноименной , то отношение «бьется» от S к S — это набор B = {(ножницы, бумага), (бумага, камень ), (камень, ножницы)} ; таким образом, побеждает y в игре, если пара ( x , y ) является членом B. x Другим примером является множество F всех пар ( x , x ² ) , где x вещественный. Это отношение является подмножеством R × R , поскольку множество всех квадратов является подмножеством множества всех действительных чисел. Поскольку для каждого x в R одна и только одна пара ( x ,...) находится в F , она называется функцией . В функциональной записи это соотношение можно записать как F ( x ) = x ² .

Принцип включения и исключения

Основная статья: Принцип включения-исключения

Принцип включения-исключения для двух конечных множеств гласит, что размер их объединения равен сумме размеров множеств минус размер их пересечения.

Принцип включения-исключения — это метод подсчета элементов в объединении двух конечных множеств с точки зрения размеров двух множеств и их пересечения. Символически это можно выразить как $$|A\cup B|=|A|+|B|-|A\cap B|.$$

Более общая форма принципа дает мощность любого конечного объединения конечных множеств: $${\begin{aligned}\left|A_{1}\cup A_{2}\cup A_{3}\cup \ldots \cup A_{n}\right|=&\left(\left|A_{1}\right|+\left|A_{2}\right|+\left|A_{3}\right|+\ldots \left|A_{n}\right|\right)\\&{}-\left(\left|A_{1}\cap A_{2}\right|+\left|A_{1}\cap A_{3}\right|+\ldots \left|A_{n-1}\cap A_{n}\right|\right)\\&{}+\ldots \\&{}+\left(-1\right)^{n-1}\left(\left|A_{1}\cap A_{2}\cap A_{3}\cap \ldots \cap A_{n}\right|\right).\end{aligned}}$$

История

Основная статья: Теория множеств

Понятие множества возникло в математике в конце XIX века. Немецкое слово Menge , обозначающее множество , было придумано Бернаром Больцано в его работе «Парадоксы бесконечности» .

Отрывок с переводом оригинального определения Георга Кантора. Немецкое слово Menge, означающее «множество», здесь переводится словом «агрегат» .

Георг Кантор , один из основателей теории множеств, дал следующее определение в начале своего вклада в создание трансфинитной теории множеств :

Набор — это совокупность в целое определенных, различных объектов нашего восприятия или нашего мышления, которые называются элементами набора.

Бертран Рассел ввел различие между множеством и классом (множество — это класс, но некоторые классы, например класс всех множеств, не являются множествами; см. парадокс Рассела ):

Когда математики имеют дело с тем, что они называют многообразием, агрегатом, Менге , ансамблем или каким-либо эквивалентным именем, обычно, особенно когда число задействованных терминов конечно, рассматривают рассматриваемый объект (который на самом деле является классом) как определяется перечислением его терминов и состоит, возможно, из одного термина, которым в данном случае является класс.

Наивная теория множеств

Основная статья: Наивная теория множеств

Главным свойством множества является то, что оно может иметь элементы, также называемые членами . Два множества равны, если они содержат одинаковые элементы. Точнее, множества A и B равны, если каждый элемент A является элементом B , а каждый элемент B является элементом A ; это свойство называется экстенсиональностью множеств . Как следствие, например, {2, 4, 6} и {4, 6, 4, 2} представляют один и тот же набор. В отличие от наборов, мультимножества можно отличить по количеству вхождений элемента; например, [2, 4, 6] и [4, 6, 4, 2] представляют разные мультимножества, а [2, 4, 6] и [6, 4, 2] равны. Кортежи можно различать даже по порядку элементов; например (2, 4, 6) и (6, 4, 2) представляют разные кортежи.

Простое понятие множества оказалось чрезвычайно полезным в математике, но возникают парадоксы , если не накладывать никаких ограничений на то, как могут быть построены множества:

• Парадокс Рассела показывает, что «множество всех множеств, которые не содержат самих себя », т. е. { x | x — множество и x ∉ x } не может существовать.
• Парадокс Кантора показывает, что «множество всех множеств» не может существовать.

Наивная теория множеств определяет множество как любую четко определенную совокупность различных элементов, но проблемы возникают из-за расплывчатости термина « четко определенный» .

Аксиоматическая теория множеств

В последующих попытках разрешить эти парадоксы со времени первоначальной формулировки наивной теории множеств свойства множеств определялись с помощью аксиом . Аксиоматическая теория множеств принимает понятие множества как примитивное понятие . Цель аксиом — предоставить базовую основу, из которой можно вывести истинность или ложность конкретных математических утверждений (утверждений) о множествах, используя логику первого порядка . Однако, согласно теоремам Гёделя о неполноте , невозможно использовать логику первого порядка, чтобы доказать, что любая такая конкретная аксиоматическая теория множеств свободна от парадоксов.

См. также

• Алгебра множеств
• Альтернативная теория множеств
• Категория наборов
• Класс (теория множеств)
• Семейство наборов
• Нечеткий набор
• Мереология
• Принципы математики

Ссылки

• Добен, Джозеф В. (1979). Георг Кантор: Его математика и философия бесконечного . Бостон: Издательство Гарвардского университета . ISBN  0-691-02447-2 .
• Халмос, Пол Р. (1960). Наивная теория множеств . Принстон, Нью-Джерси: Ван Ностранд. ISBN  0-387-90092-6 .
• Столл, Роберт Р. (1979). Теория множеств и логика . Минеола, Нью-Йорк: Dover Publications . ISBN  0-486-63829-4 .
• Веллеман, Дэниел (2006). Как это доказать: структурированный подход . Издательство Кембриджского университета . ISBN  0-521-67599-5 .

Внешние ссылки

• Словарное определение множества в Викисловаре
• «Вклад Кантора в обоснование теории трансфинитных множеств» (на немецком языке)