Стереографическая проекция

Информацию о картографической проекции см. в разделе Стереографическая картографическая проекция .

3D-иллюстрация стереографической проекции северного полюса на плоскость под сферой

В математике стереографическая проекция — это перспективная проекция сферы , через определенную точку сферы ( полюс или центр проекции ) на плоскость ( плоскость проекции ) , перпендикулярную диаметру проходящему через точку. Это гладкая . биективная функция всей сферы, кроме центра проекции на всю плоскость Он отображает круги на сфере в круги или линии на плоскости и является конформным , что означает, что он сохраняет углы, под которыми пересекаются кривые, и, таким образом, локально приблизительно сохраняет формы . Он не является ни изометрическим (с сохранением расстояния), ни равноплощадным (с сохранением площади).

Стереографическая проекция позволяет представить сферу плоскостью. Метрика , индуцированная обратной стереографической проекцией плоскости на сферу, определяет геодезическое расстояние между точками на плоскости, равное сферическому расстоянию между сферическими точками, которые они представляют. Двумерная система координат на стереографической плоскости является альтернативой сферической аналитической геометрии вместо сферических полярных координат или трехмерных декартовых координат . Это сферический аналог модели диска Пуанкаре гиперболической плоскости .

Интуитивно, стереографическая проекция — это способ изображения сферы как плоскости с некоторыми неизбежными компромиссами. Поскольку сфера и плоскость появляются во многих областях математики и ее приложений, то же самое можно сказать и о стереографической проекции; он находит применение в различных областях, включая комплексный анализ , картографию , геологию и фотографию . Иногда стереографические вычисления выполняются графически с использованием специального вида миллиметровой бумаги, называемого стереографической сетью , сокращенно стереосетью , или сетью Вульфа .

История

Смотрите также: Астролябия § История

Иллюстрация Рубенса к книге Франсуа д'Агилона «Opticorum libri sex philosophis juxta ac mathematicis utiles» . Он демонстрирует принцип общей перспективной проекции, частным случаем которой является стереографическая проекция.

Происхождение стереографической проекции неизвестно, но считается, что она была открыта древнегреческими астрономами и использовалась для проецирования небесной сферы на плоскость, чтобы можно было анализировать движения звезд и планет с использованием плоской геометрии . Его самое раннее дошедшее до нас описание находится в ( » Птолемея «Планисфере ) неоднозначно приписал его Гиппарху (2 век 2 век нашей эры), но Синезий ( около 400 года нашей эры до нашей эры ). а Аполлония » « Коники ( около 200 г. до н. э. ) содержат теорему , которая имеет решающее значение для доказательства того свойства, что стереографическая проекция отображает круги в круги. Гиппарху, Аполлонию, Архимеду и даже Евдоксу (4 век до н.э.) иногда предположительно приписывали изобретение или знание стереографической проекции. но некоторые эксперты считают эти приписывания неоправданными. Птолемей ссылается на использование стереографической проекции в «гороскопическом инструменте», возможно, в анафорических часах описано Витрувием (I век до н. э.).

Ко времени Теона Александрийского (4 век) планисфера была объединена с диоптрой , образуя планисферическую астролябию («звездоприемник»). мощное портативное устройство, которое можно было использовать для измерения положения звезд и выполнения широкого спектра астрономических расчетов. Астролябия постоянно использовалась византийскими астрономами и была значительно развита средневековыми исламскими астрономами . Он был передан в Западную Европу в XI–XII веках, а арабские тексты были переведены на латынь.

В 16 и 17 веках экваториальный аспект стереографической проекции широко использовался для карт Восточного и Западного полушарий . Считается, что уже карта, созданная в 1507 году Гвальтериусом Лудом была в стереографической проекции, как и позже карты Жана Роза (1542 г.), Румольда Меркатора (1595 г.) и многих других. В звездных картах даже этот экваториальный аспект уже использовался древними астрономами, такими как Птолемей .

Франсуа д'Агилон дал стереографической проекции ее нынешнее название в своей работе 1613 года Opticorum libri sex philosophis juxta ac mathematicis utiles (Шесть книг по оптике, полезных как философам, так и математикам).

В конце 16 века Томас Хэрриот доказал, что стереографическая проекция конформна ; однако это доказательство так и не было опубликовано и пролежало среди его бумаг в ящике более трех столетий. В 1695 году Эдмон Галлей , движимый интересом к звездным картам , первым опубликовал доказательство. Он использовал недавно появившиеся инструменты исчисления , изобретенные его другом Исааком Ньютоном .

Определение

Первая формулировка

Стереографическая проекция единичной сферы от северного полюса на плоскость z = 0 , показанная здесь в поперечном сечении.

Единичная сфера S ² в трехмерном пространстве R ³ — это набор точек ( x , y , z ) таких, что x ² + и ² + я ² = 1 . Пусть N = (0, 0, 1) — «северный полюс», а M — остальная часть сферы. Плоскость z = 0 проходит через центр сферы; «экватор» — это пересечение сферы с этой плоскостью.

Для любой точки P на M существует единственная линия, проходящая через N и P эта линия пересекает плоскость z = 0 ровно в одной точке P ′ , известной как стереографическая проекция P , и на плоскость.

В декартовых координатах ( x , y , z ) на сфере и ( X , Y ) на плоскости проекция и обратная ей задаются формулами

${\begin{aligned}(X,Y)&=\left({\frac {x}{1-z}},{\frac {y}{1-z}}\right),\\(x,y,z)&=\left({\frac {2X}{1+X^{2}+Y^{2}}},{\frac {2Y}{1+X^{2}+Y^{2}}},{\frac {-1+X^{2}+Y^{2}}{1+X^{2}+Y^{2}}}\right).\end{aligned}}$

В сферических координатах ( φ , θ ) на сфере (где φ — зенитный угол , 0 ≤ φ ≤ π , и θ — , азимут 0 ≤ θ ≤ 2π ) и полярных координатах ( R , Θ ) на плоскости, проекция и его обратные значения

${\begin{aligned}(R,\Theta )&=\left({\frac {\sin \varphi }{1-\cos \varphi }},\theta \right)=\left(\cot {\frac {\varphi }{2}},\theta \right),\\(\varphi ,\theta )&=\left(2\arctan {\frac {1}{R}},\Theta \right).\end{aligned}}$

Здесь , что φ понимается имеет значение π, когда R = 0. Кроме того, существует множество способов переписать эти формулы, используя тригонометрические тождества . В цилиндрических координатах ( r , θ , z ) на сфере и полярных координатах ( R , Θ ) на плоскости проекция и ее обратная сторона равны

${\begin{aligned}(R,\Theta )&=\left({\frac {r}{1-z}},\theta \right),\\(r,\theta ,z)&=\left({\frac {2R}{1+R^{2}}},\Theta ,{\frac {R^{2}-1}{R^{2}+1}}\right).\end{aligned}}$

Другие конвенции

Стереографическая проекция единичной сферы от северного полюса на плоскость z = −1 , показанная здесь в поперечном сечении.

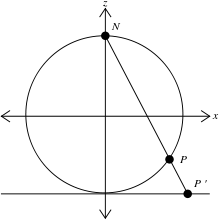
Некоторые авторы определим стереографическую проекцию северного полюса (0, 0, 1) на плоскость z = −1 , которая касается единичной сферы на южном полюсе (0, 0, −1). Это можно описать как композицию описанной выше проекции на экваториальную плоскость и гомотетии от нее к полярной плоскости. Гомотетия масштабирует изображение в 2 раза (отношение диаметра к радиусу сферы), следовательно, значения X и Y , создаваемые этой проекцией, ровно в два раза превышают значения, полученные экваториальной проекцией, описанной в предыдущем разделе. Например, эта проекция отправляет экватор в круг радиуса 2 с центром в начале координат. В то время как экваториальная проекция не создает бесконечно малых искажений площади вдоль экватора, эта проекция, касательная к полюсу, вместо этого не создает бесконечно малых искажений площади на южном полюсе.

Другие авторы используйте сферу радиуса ⁠ 1/2 ⁠ = z плоскость и − ⁠ 1/2 ​ ⁠ ​ . В этом случае формулы примут вид

${\begin{aligned}(x,y,z)\rightarrow (\xi ,\eta )&=\left({\frac {x}{{\frac {1}{2}}-z}},{\frac {y}{{\frac {1}{2}}-z}}\right),\\(\xi ,\eta )\rightarrow (x,y,z)&=\left({\frac {\xi }{1+\xi ^{2}+\eta ^{2}}},{\frac {\eta }{1+\xi ^{2}+\eta ^{2}}},{\frac {-1+\xi ^{2}+\eta ^{2}}{2+2\xi ^{2}+2\eta ^{2}}}\right).\end{aligned}}$

Стереографическая проекция сферы из точки Q на плоскость E , показанная здесь в поперечном сечении.

В общем, можно определить стереографическую проекцию любой точки Q на сфере на любую плоскость E такую, что

• E перпендикулярен диаметру, проходящему через Q , и
• E не Q. содержит

Пока E удовлетворяет этим условиям, тогда для любой точки P, кроме Q, линия, проходящая через P и Q , пересекает E ровно в одной точке P ′ , которая определяется как стереографическая проекция P на E .

Обобщения

В более общем смысле, стереографическая проекция может быть применена к единице n -сферы S. ^н в ( n + 1 )-мерном евклидовом пространстве E ^{п +1} . Если Q — точка S ^н и E гиперплоскость — в E ^{п +1} , то стереографическая проекция точки P ∈ S ^н − { Q } — точка P ′ пересечения прямой QP с E . В декартовых координатах ( x _i , i от 0 до n ) на S ^н и ( X _i , i от 1 до n ) на E проекция из Q = (1, 0, 0, ..., 0) ∈ S ^н дается $$X_{i}={\frac {x_{i}}{1-x_{0}}}\quad (i=1,\dots ,n).$$Определение $$s^{2}=\sum _{j=1}^{n}X_{j}^{2}={\frac {1+x_{0}}{1-x_{0}}},$$обратное выражение определяется выражением $$x_{0}={\frac {s^{2}-1}{s^{2}+1}}\quad {\text{and}}\quad x_{i}={\frac {2X_{i}}{s^{2}+1}}\quad (i=1,\dots ,n).$$

В еще более общем смысле предположим, что S — (неособая) квадричная гиперповерхность в проективном пространстве P ^{п +1} . Другими словами, S — это место нулей неособой квадратичной формы f ( x ₀ , ..., x _{n +1} ) в однородных координатах x _i . Зафиксируем любую точку Q на S и гиперплоскость E в P. ^{п +1} не Q. содержащий Тогда стереографическая проекция точки P в S − { Q } является единственной точкой пересечения QP с E . Как и раньше, стереографическая проекция конформна и обратима на непустом открытом множестве Зарисского. Стереографическая проекция представляет квадратичную гиперповерхность как рациональную гиперповерхность . Эта конструкция играет роль в алгебраической геометрии и конформной геометрии .

Характеристики

Первая стереографическая проекция, определенная в предыдущем разделе, отправляет «южный полюс» (0, 0, −1) единичной сферы в (0, 0), экватор в единичный круг , южное полушарие в область внутри круга. , а северное полушарие — в область за пределами круга.

Проекция не определена в точке проекции N = (0, 0, 1). Малые окрестности этой точки отправляются в подмножества плоскости, далекие от (0, 0). Чем ближе P к (0, 0, 1), тем дальше его изображение от (0, 0) на плоскости. По этой причине принято говорить о (0, 0, 1) как об отображении на «бесконечность» на плоскости, а о сфере как о дополнении плоскости добавлением точки на бесконечности . Это понятие находит применение в проективной геометрии и комплексном анализе. На чисто топологическом уровне это иллюстрирует, как сфера гомеоморфна одноточечной компактификации плоскости.

В декартовых координатах точка P ( x , y , z ) на сфере и ее образ P ′ ( X , Y ) на плоскости либо обе являются рациональными точками , либо ни одна из них:

$P\in \mathbb {Q} ^{3}\iff P'\in \mathbb {Q} ^{2}$

Декартова сетка на плоскости на сфере выглядит искаженной. Линии сетки по-прежнему перпендикулярны, но площади квадратов сетки уменьшаются по мере приближения к северному полюсу.

Полярная сетка на плоскости на сфере выглядит искаженной. Кривые сетки по-прежнему перпендикулярны, но площади секторов сетки сужаются по мере приближения к северному полюсу.

Стереографическая проекция конформна, то есть сохраняет углы, под которыми кривые пересекают друг друга (см. рисунки). С другой стороны, стереографическая проекция не сохраняет площадь; вообще говоря, площадь области сферы не равна площади ее проекции на плоскость. Элемент площади задается в ( X , Y ) координатах следующим образом:

$dA={\frac {4}{(1+X^{2}+Y^{2})^{2}}}\;dX\;dY.$

По единичной окружности, где X ² + И ² = 1 , в пределе нет увеличения площади, что дает масштабный коэффициент 1. Области, близкие к (0, 0), увеличиваются в 4 раза, а области, близкие к бесконечности, увеличиваются в сколь угодно малых коэффициентах.

Метрика задается в ( X , Y ) координатах следующим образом:

${\frac {4}{(1+X^{2}+Y^{2})^{2}}}\;(dX^{2}+dY^{2}),$

и представляет собой уникальную формулу, найденную в Бернхарда Римана по докторской диссертации основам геометрии, произнесенной в Геттингене в 1854 году и озаглавленной «О гипотезах, лежащих в основе геометрии» .

Никакая карта сферы на плоскость не может быть одновременно конформной и сохраняющей площадь. Если бы это было так, то это была бы локальная изометрия и сохраняла бы гауссову кривизну . Сфера и плоскость имеют разную гауссову кривизну, поэтому это невозможно.

Окружности на сфере , не проходящие через точку проекции, проецируются на окружности на плоскости. Круги на сфере, проходящие через точку проекции, проецируются на прямые линии на плоскости. Эти линии иногда представляют собой круги, проходящие через бесконечную точку, или круги бесконечного радиуса. Эти свойства можно проверить, используя выражения $x,y,z$ с точки зрения $X,Y,Z,$ приведено в § Первая формулировка : использование этих выражений для замены в уравнении $ax+by+cz-d=0$ плоскости, содержащей окружность на сфере, и очищая знаменатели, получаем уравнение окружности, т. е. уравнение второй степени с $(c-d)(X^{2}+Y^{2})$ как его квадратичная часть. Уравнение становится линейным, если $c=d,$ то есть, если плоскость проходит через точку проекции.

Все линии на плоскости, преобразованные в круги на сфере посредством обратной стереографической проекции, встречаются в точке проекции. Параллельные прямые, не пересекающиеся в плоскости, преобразуются в окружности, касающиеся точки проекции. Пересекающиеся линии преобразуются в окружности, пересекающиеся трансверсально в двух точках сферы, одна из которых является точкой проекции. (Аналогичные замечания справедливы и относительно реальной проективной плоскости , но отношения пересечения там другие.)

Сфера с различными локсодромами , показанными разными цветами.

Локсодромы . сферы отображаются в кривые на плоскости формы

$R=e^{\Theta /a},\,$

где параметр а измеряет «герметичность» локсодрома. Таким образом, локсодромы соответствуют логарифмическим спиралям . Эти спирали пересекают радиальные линии на плоскости под равными углами, так же как локсодромы пересекают меридианы на сфере под равными углами.

Стереографическая проекция просто связана с инверсией плоскости. Пусть P и Q — две точки на сфере с проекциями P ′ и Q ′ на плоскость. Тогда P ' и Q ' являются прообразами друг друга в образе экваториальной окружности тогда и только тогда, когда P и Q являются отражениями друг друга в экваториальной плоскости.

Другими словами, если:

• P — точка на сфере, но не «северный полюс» N и не ее антипод , «южный полюс» S ,
• P ′ — изображение P в стереографической проекции с точкой проекции N и
• P″ — изображение P в стереографической проекции с точкой проекции S ,

тогда P ′ и P″ являются прообразами друг друга в единичном круге.

$\triangle NOP^{\prime }\sim \triangle P^{\prime \prime }OS\implies OP^{\prime }:ON=OS:OP^{\prime \prime }\implies OP^{\prime }\cdot OP^{\prime \prime }=r^{2}$

Вульф нет

Сеть Вульфа или стереосеть, используемая для построения графиков стереографической проекции вручную.

Создание сети Вульфа (круговая сеть внутри красного круга) с помощью стереографической проекции с центром C и плоскостью проекции. $\pi$

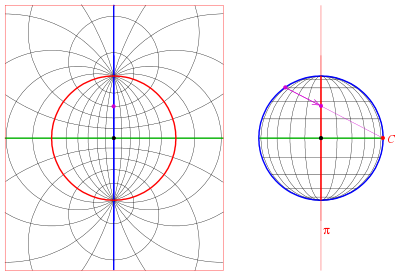
Графики стереографической проекции могут быть построены с помощью компьютера с использованием явных формул, приведенных выше. Однако для построения графиков вручную эти формулы громоздки. Вместо этого обычно используют миллиметровую бумагу, разработанную специально для этой задачи. Эта специальная миллиметровая бумага называется стереосеткой или сетью Вульфа , по имени российского минералога Георгия (Юрия Викторовича) Вульфа .

Показанная здесь сеть Вульфа представляет собой стереографическую проекцию сетки параллелей и меридианов полушария с центром в точке на экваторе (например, в восточном или западном полушарии планеты).

На рисунке свойство стереографической проекции искажать площадь можно увидеть, сравнив сектор сетки рядом с центром сети с сектором, расположенным крайним справа или слева. Оба сектора имеют равные площади на сфере. На диске площадь последнего почти в четыре раза превышает площадь первого. Если сетку сделать более мелкой, это соотношение приближается ровно к 4.

На сети Вульфа изображения параллелей и меридианов пересекаются под прямым углом. Это свойство ортогональности является следствием свойства стереографической проекции сохранять угол. (Однако свойство сохранения угла сильнее этого свойства. Не все проекции, сохраняющие ортогональность параллелей и меридианов, сохраняют угол.)

Иллюстрация шагов 1–4 построения точки на сети Вульфа.

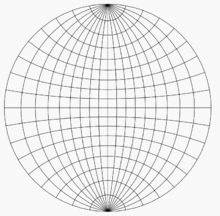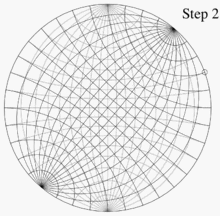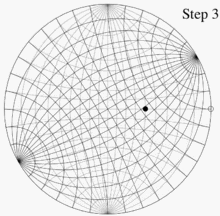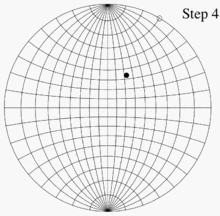
В качестве примера использования сети Вульфа представьте себе две ее копии на тонкой бумаге, расположенные одна поверх другой, выровненные и скрепленные по взаимному центру. Пусть P — точка в нижнем полушарии, сферические координаты которой равны (140°, 60°), а декартовы координаты — (0,321, 0,557, −0,766). Эта точка лежит на линии, ориентированной на 60° против часовой стрелки от положительной оси x (или на 30° по часовой стрелке от положительной оси y ) и на 50° ниже горизонтальной плоскости z = 0 . Как только эти углы известны, для построения графика P необходимо выполнить четыре шага :

1. Используя линии сетки, которые на рисунках расположены на расстоянии 10° друг от друга, отметьте точку на краю сетки, которая находится на расстоянии 60° против часовой стрелки от точки (1, 0) (или 30° по часовой стрелке от точки (0, 1). )).
2. Поворачивайте верхнюю сеть, пока эта точка не совпадет с (1, 0) нижней сети.
3. Используя линии сетки на нижней сетке, отметьте точку, расположенную под углом 50° к центру от этой точки.
4. Поверните верхнюю сетку в направлении, противоположном тому, как она была ориентирована раньше, чтобы выровнять ее с нижней сеткой. Точка, отмеченная на шаге 3, является той проекцией, которую мы хотели.

Для построения других точек, углы которых не являются такими круглыми числами, как 60° и 50°, необходимо визуально интерполировать между ближайшими линиями сетки. Полезно иметь сетку с меньшим шагом, чем 10°. Расстояния в 2° являются обычными.

Чтобы найти центральный угол между двумя точками на сфере на основе их стереографического графика, наложите график на сеть Вульфа и вращайте график вокруг центра до тех пор, пока две точки не окажутся на меридиане или рядом с ним. Затем измерьте угол между ними, посчитав линии сетки вдоль этого меридиана.

• 
  точки P1 _{На прозрачном листе ,} и P2 . _две прикрепленном к началу сетки Вульфа, нарисованы
• 
  Прозрачный лист поворачивают и определяют центральный угол вдоль общего меридиана к обеим точкам P ₁ и P ₂ .

Приложения в математике

Комплексный анализ

Стереографическая проекция северного полюса сферы на ее экваториальную плоскость устанавливает взаимно однозначное соответствие между сферой и экваториальной плоскостью, расширенной с точкой на бесконечности, обозначаемой ∞ . Когда экваториальная плоскость является комплексной плоскостью , это обеспечивает визуализацию сферы Римана.

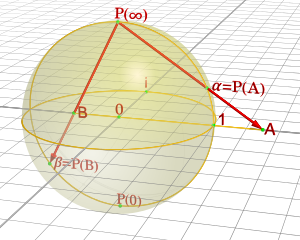
Хотя в любой стереографической проекции не хватает одной точки сферы (точки проекции), всю сферу можно отобразить с помощью двух проекций из разных точек проекции. Другими словами, сферу можно покрыть двумя стереографическими параметризациями (инверсиями проекций) с плоскости. Параметризации могут быть выбраны так, чтобы обеспечить одинаковую ориентацию на сфере. Вместе они описывают сферу как ориентированную поверхность (или двумерное многообразие ).

Эта конструкция имеет особое значение в комплексном анализе. Точку ( X , Y ) на вещественной плоскости можно отождествить с числом ζ = X + i Y. комплексным Тогда будет стереографическая проекция северного полюса на экваториальную плоскость.

${\begin{aligned}\zeta &={\frac {x+iy}{1-z}},\\\\(x,y,z)&=\left({\frac {2\operatorname {Re} \zeta }{1+{\bar {\zeta }}\zeta }},{\frac {2\operatorname {Im} \zeta }{1+{\bar {\zeta }}\zeta }},{\frac {-1+{\bar {\zeta }}\zeta }{1+{\bar {\zeta }}\zeta }}\right).\end{aligned}}$

Аналогично, если ξ = X − i Y — еще одна комплексная координата, функции

${\begin{aligned}\xi &={\frac {x-iy}{1+z}},\\(x,y,z)&=\left({\frac {2\operatorname {Re} \xi }{1+{\bar {\xi }}\xi }},{\frac {-2\operatorname {Im} \xi }{1+{\bar {\xi }}\xi }},{\frac {1-{\bar {\xi }}\xi }{1+{\bar {\xi }}\xi }}\right)\end{aligned}}$

определить стереографическую проекцию южного полюса на экваториальную плоскость. Тогда карты перехода между ζ- и ξ -координатами будут ζ = ⁠ 1 / ξ ⁠ и ξ = ⁠ 1 / ζ ⁠ , где ζ приближается к 0, когда ξ стремится к бесконечности, и наоборот . Это облегчает элегантное и полезное понятие бесконечности для комплексных чисел и даже целую теорию мероморфных функций, отображающихся на сферу Римана . Стандартная метрика на единичной сфере согласуется с метрикой Фубини – Студи на сфере Римана.

Визуализация линий и плоскостей

Анимация линий Кикучи четырех из восьми зон <111> в ГЦК-кристалле. Плоскости, видимые с ребра (полосчатые линии), пересекаются под фиксированными углами.

Совокупность всех прямых, проходящих через начало координат в трехмерном пространстве, образует пространство, называемое реальной проективной плоскостью . Эту плоскость сложно визуализировать, поскольку ее нельзя встроить в трехмерное пространство.

Однако можно представить его в виде диска следующим образом. Любая линия, проходящая через начало координат, пересекает южное полушарие z ≤ 0 в точке, которую затем можно стереографически спроецировать на точку на диске в плоскости XY. Горизонтальные линии, проходящие через начало координат, пересекают южное полушарие в двух противоположных точках вдоль экватора, которые выступают на границу диска. Любую из двух проецируемых точек можно считать частью диска; подразумевается, что противоположные точки на экваторе представляют собой одну линию в трехмерном пространстве и одну точку на границе проецируемого диска (см . фактортопологию ). Таким образом, любой набор линий, проходящих через начало координат, можно представить как набор точек на проецируемом диске. Но граничные точки ведут себя иначе, чем граничные точки обычного двумерного диска, поскольку любая из них одновременно находится близко к внутренним точкам на противоположных сторонах диска (так же, как две почти горизонтальные линии, проходящие через начало координат, могут проектироваться в точки на противоположных сторонах диска).

Кроме того, каждая плоскость, проходящая через начало координат, пересекает единичную сферу по большому кругу, называемому следом плоскости. Этот круг отображается в круг в стереографической проекции. Таким образом, проекция позволяет нам визуализировать плоскости как дуги окружности на диске. До появления компьютеров стереографические проекции с большими кругами часто включали рисование дуг большого радиуса, что требовало использования лучевого компаса . Компьютеры теперь значительно облегчают эту задачу.

плоскости Кроме того, с каждой плоскостью связана уникальная линия, называемая полюсом , которая проходит через начало координат и перпендикулярна плоскости. Эту линию можно нарисовать как точку на диске, как и любую линию, проходящую через начало координат. Таким образом, стереографическая проекция также позволяет нам визуализировать плоскости как точки на диске. Для графиков, включающих множество плоскостей, отображение их полюсов дает менее загроможденную картину, чем отображение их трасс.

Эта конструкция используется для визуализации данных о направлении в кристаллографии и геологии, как описано ниже.

Другая визуализация

Стереографическая проекция также применяется для визуализации многогранников . В диаграмме Шлегеля -мерный многогранник n в R ^{п +1} проецируется на n -мерную сферу, которая затем стереографически проецируется на R ^н . Сокращение от R ^{п +1} в Р ^н может облегчить визуализацию и понимание многогранника.

Арифметическая геометрия

Рациональные точки окружности в стереографической проекции соответствуют рациональным точкам прямой.

В элементарной арифметической геометрии стереографическая проекция единичного круга позволяет описать все примитивные пифагоровы тройки . В частности, стереографическая проекция северного полюса (0,1) на ось x дает взаимно однозначное соответствие между рационального числа точками ( x , y ) на единичном круге (при y ≠ 1 ) и рациональными точками. оси x . Если ( ⁠ m / n ⁠ , 0) — рациональная точка на оси x , то ее обратная стереографическая проекция — это точка

$\left({\frac {2mn}{m^{2}+n^{2}}},{\frac {m^{2}-n^{2}}{m^{2}+n^{2}}}\right)$

что дает формулу Евклида для пифагоровой тройки.

Замена касательной полуугла

Основная статья: Замена касательной полуугла

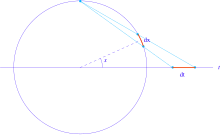
Пару тригонометрических функций (sin x , cos x ) можно рассматривать как параметризацию единичного круга. Стереографическая проекция дает альтернативную параметризацию единичного круга:

$\cos x={\frac {1-t^{2}}{1+t^{2}}},\quad \sin x={\frac {2t}{t^{2}+1}}.$

При такой перепараметризации элемент длины dx единичной окружности переходит в

$dx={\frac {2\,dt}{t^{2}+1}}.$

Эта замена иногда может упростить интегралы, включающие тригонометрические функции.

Приложения к другим дисциплинам

Картография

Основная статья: Стереографическая картографическая проекция

Фундаментальная проблема картографии заключается в том, что ни одна карта сферы на плоскости не может точно отображать одновременно углы и площади. с сохранением площади В целом, картографические проекции предпочтительнее для статистических приложений, тогда как картографические проекции с сохранением угла (конформные) предпочтительнее для навигации .

Стереографическая проекция попадает во вторую категорию. Когда проекция центрируется на северном или южном полюсе Земли, она обладает дополнительными полезными свойствами: она направляет меридианы к лучам, исходящим из начала координат, и параллели к кругам с центром в начале координат.

• 
  Стереографическая проекция мира к северу от 30°ю.ш. сетка 15°.
• 
  Стереографическая проекция с Тиссо . индикатрисой деформации

Планетарная наука

Стереографическая проекция Луны , показывающая регионы к полюсу от 60° северной широты. Кратеры, представляющие собой круги на сфере, в этой проекции кажутся круглыми, независимо от того, расположены ли они близко к полюсу или краю карты.

Стереографическая проекция — единственная проекция, которая отображает все круги на сфере в круги на плоскости . Это свойство ценно при картографировании планет, где типичными особенностями являются кратеры. Множество окружностей, проходящих через точку проекции, имеют неограниченный радиус и поэтому вырождаются в прямые.

Кристаллография

Кристаллографическая полюсная фигура решетки алмаза в направлении [111].

Основная статья: Полюсная фигура

В кристаллографии ориентация осей и граней кристаллов в трехмерном пространстве является центральной геометрической проблемой, например, при интерпретации картин дифракции рентгеновских лучей и электронов . Эти ориентации можно визуализировать, как описано в разделе «Визуализация линий и плоскостей» выше. То есть оси кристалла и полюса кристаллических плоскостей пересекаются с северным полушарием, а затем наносятся на график с использованием стереографической проекции. Участок полюсов называется полюсной фигурой .

При дифракции электронов пары линий Кикучи выглядят как полосы, украшающие пересечение следов плоскости решетки и сферы Эвальда , что обеспечивает экспериментальный доступ к стереографической проекции кристалла. Модельные карты Кикучи в обратном пространстве, и карты видимости границ для использования с контурами изгибов в прямом пространстве, таким образом, они служат дорожными картами для исследования ориентационного пространства с помощью кристаллов в просвечивающем электронном микроскопе .

Геология

Использование стереографической проекции нижнего полушария для построения плоских и линейных данных в структурной геологии на примере плоскости разлома с линией скольжения.

Исследователей структурной геологии беспокоит ориентация плоскостей и линий по ряду причин. Слоистость называемую камня — это плоская особенность, которая часто содержит линейную особенность, линеацией . Аналогичным образом, плоскость разлома — это плоский объект, который может содержать линейные элементы, такие как стенки скольжения .

Эти ориентации линий и плоскостей в различных масштабах можно отобразить с помощью методов, описанных выше в разделе «Визуализация линий и плоскостей» . Как и в кристаллографии, плоскости обычно изображаются по полюсам. В отличие от кристаллографии, вместо северного используется южное полушарие (поскольку рассматриваемые геологические объекты лежат ниже поверхности Земли). В этом контексте стереографическую проекцию часто называют равноугольной проекцией нижнего полушария . Также используется равновеликая проекция нижнего полушария, определяемая азимутальной равновеликой проекцией Ламберта , особенно когда график подлежит последующему статистическому анализу, например, контурированию плотности .

Фотография

Стереографическая проекция сферической панорамы скульптуры «Тайная вечеря» Микеле Ведани в Эсино Ларио , Ломбардия, Италия, во время Wikimania 2016.

«Круговой вид на горы, который мы открываем с вершины ледника Буэ», Орас-Бенедикт де Соссюр, « Путешествие в Альпы», которому предшествует очерк естественной истории окрестностей Женевы . Невшатель, 1779–96, пл. 8.

Некоторые объективы типа «рыбий глаз» используют стереографическую проекцию для захвата широкоугольного изображения. По сравнению с более традиционными линзами типа «рыбий глаз», в которых используется проекция равной площади, области, расположенные вблизи края, сохраняют свою форму, а прямые линии менее изогнуты. Однако стереографические линзы типа «рыбий глаз» обычно дороже в производстве. Программное обеспечение для переназначения изображений, такое как Panotools , позволяет автоматически переназначать фотографии из «рыбий глаз» равной площади в стереографическую проекцию.

Стереографическая проекция использовалась для картографирования сферических панорам , начиная с панорамы Горация Бенедикта де Соссюра в 1779 году. Это приводит к эффектам, известным как маленькая планета (когда центром проекции является надир ) и трубка (когда центр проекции это зенит ).

Популярность использования стереографических проекций для отображения панорам по сравнению с другими азимутальными проекциями объясняется сохранением формы, которое является результатом конформности проекции.

См. также

• Список картографических проекций
• Астролябия
• Астрономические часы
• Модель диска Пуанкаре , аналогичное отображение гиперболической плоскости
• Стереографическая проекция в картографии
• Криволинейная перспектива
• Объектив «рыбий глаз»

Ссылки

Источники

• Апостол, Том (1974). Математический анализ (2-е изд.). Аддисон-Уэсли. ISBN  0-201-00288-4 .
• Браун, Джеймс и Черчилль, Руэл (1989). Комплексные переменные и приложения . Нью-Йорк: МакГроу-Хилл. ISBN  0-07-010905-2 .
• Кассельман, Билл (2014), Тематическая колонка, февраль 2014 г.: Стереографическая проекция , AMS , получено 12 декабря 2014 г.
• Герман, Даниэль; Берчилль, Л.; Дюре-Луц, А.; Перес-Дуарте, С.; Перес-Дуарте, Э.; Соммерс, Дж. (июнь 2007 г.). «Сглаживание видимой сферы». Труды по вычислительной эстетике 2007 . Банф: Еврографика. стр. 23–28.
• Гельфанд, ИМ ; Минлос, РА ; Шапиро, З.Я. (1963), Представления групп вращения и Лоренца и их приложения , Нью-Йорк: Pergamon Press.
• Ду Карму ; Манфредо П. (1976). Дифференциальная геометрия кривых и поверхностей . Энглвуд Клиффс, Нью-Джерси: Прентис Холл. ISBN  0-13-212589-7 .
• Элкинс, Джеймс (1988). «Разработал ли Леонардо теорию криволинейной перспективы?: Вместе с некоторыми замечаниями об аксиомах« угла »и« расстояния »». Журнал институтов Варбурга и Курто . 51 . Институт Варбурга: 190–196. дои : 10.2307/751275 . JSTOR   751275 . S2CID   193430645 .
• Опрея, Джон (2003). Дифференциальная геометрия и приложения . Энглвуд Клиффс, Нью-Джерси: Прентис Холл. ISBN  0-13-065246-6 .
• Педо, Дэн (1988). Геометрия . Дувр. ISBN  0-486-65812-0 .
• Шафаревич, Игорь (1995). Основная алгебраическая геометрия I . Спрингер. ISBN  0-387-54812-2 .
• Снайдер, Джон П. (1987). Картографические проекции. Рабочее руководство, Профессиональный документ 1395 . Геологическая служба США.
• Снайдер, Джон П. (1989). Альбом картографических проекций, профессиональная статья 1453 . Геологическая служба США.
• Снайдер, Джон П. (1993). Уплощение Земли . Чикагский университет. ISBN  0-226-76746-9 .
• Спивак, Михаил (1999). Всестороннее введение в дифференциальную геометрию, том IV . Хьюстон, Техас: Опубликуй или погибни. ISBN  0-914098-73-Х .

Внешние ссылки

• Стереографическая проекция и инверсия от Cut-the-Knot
• Пакет преподавания и обучения DoITPoMS - «Стереографическая проекция»

Видео

• Доказательство стереографической проекции, переводящей круги на сфере в круги на плоскости.
• Стереографическая проекция замедленного действия on Vimeo

Программное обеспечение

• Stereonet , программный инструмент для структурной геологии, разработанный Риком Аллмендингером .
• PTCLab , лаборатория кристаллографии фазовых превращений
• Sphaerica , программный инструмент для построения линейки и циркуля на сфере, включая опцию отображения стереографической проекции.
• Estereografica Web — веб-приложение для стереографической проекции в структурной геологии и кинематике разломов, созданное Эрнесто Кристаллини.