Распределение Накагами

Накагами

Функция плотности вероятности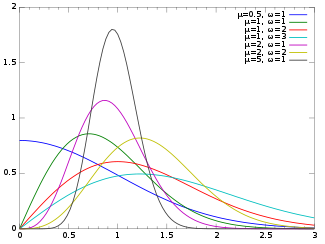
Кумулятивная функция распределения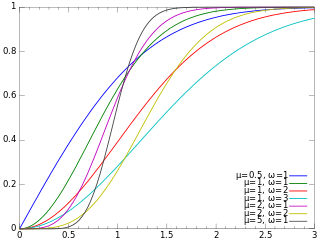
Параметры	$m{\text{ or }}\mu \geq 0.5$ форма ( настоящая ) $\Omega {\text{ or }}\omega >0$ распространение (реальное)
Поддерживать	$x>0\!$
PDF	${\frac {2m^{m}}{\Gamma (m)\Omega ^{m}}}x^{2m-1}\exp \left(-{\frac {m}{\Omega }}x^{2}\right)$
CDF	${\frac {\gamma \left(m,{\frac {m}{\Omega }}x^{2}\right)}{\Gamma (m)}}$
Иметь в виду	${\frac {\Gamma (m+{\frac {1}{2}})}{\Gamma (m)}}\left({\frac {\Omega }{m}}\right)^{1/2}$
медиана	Нет простой закрытой формы
Режим	$\left({\frac {(2m-1)\Omega }{2m}}\right)^{1/2}$
Дисперсия	$\Omega \left(1-{\frac {1}{m}}\left({\frac {\Gamma (m+{\frac {1}{2}})}{\Gamma (m)}}\right)^{2}\right)$

Распределение Накагами или Накагами -m распределение представляет собой распределение вероятностей, связанное с гамма-распределением. Он используется для моделирования физических явлений, например, тех, которые встречаются в медицинской ультразвуковой визуализации, технике связи, метеорологии, гидрологии, мультимедиа и сейсмологии.

Семейство распределений Накагами имеет два параметра: параметр формы $m\geq 1/2$ и второй параметр, управляющий распространением $\Omega >0$.

Характеристика

Его функция плотности вероятности (pdf) равна

$f(x;\,m,\Omega )={\frac {2m^{m}}{\Gamma (m)\Omega ^{m}}}x^{2m-1}\exp \left(-{\frac {m}{\Omega }}x^{2}\right){\text{ for }}x\geq 0.$

где $m\geq 1/2$ и $\Omega >0$.

Его кумулятивная функция распределения (CDF) равна

$F(x;\,m,\Omega )={\frac {\gamma \left(m,{\frac {m}{\Omega }}x^{2}\right)}{\Gamma (m)}}=P\left(m,{\frac {m}{\Omega }}x^{2}\right)$

где P — регуляризованная (нижняя) неполная гамма-функция .

Параметризация

Параметры $m$ и $\Omega$ являются

$m={\frac {\left(\operatorname {E} [X^{2}]\right)^{2}}{\operatorname {Var} [X^{2}]}},$

и

$\Omega =\operatorname {E} [X^{2}].$

этого распределения не существует решения в замкнутой форме Для медианы , хотя существуют особые случаи, такие как ${\sqrt {\Omega \ln(2)}}$ когда m = 1. Для практических целей медиану следует рассчитывать как 50-й процентиль наблюдений.

Оценка параметров

Альтернативным способом подбора распределения является повторная параметризация $\Omega$ как σ знак равно Ω/ м .

Учитывая независимые наблюдения ${\textstyle X_{1}=x_{1},\ldots ,X_{n}=x_{n}}$ из распределения Накагами функция правдоподобия равна

$L(\sigma ,m)=\left({\frac {2}{\Gamma (m)\sigma ^{m}}}\right)^{n}\left(\prod _{i=1}^{n}x_{i}\right)^{2m-1}\exp \left(-{\frac {\sum _{i=1}^{n}x_{i}^{2}}{\sigma }}\right).$

Его логарифм

$\ell (\sigma ,m)=\log L(\sigma ,m)=-n\log \Gamma (m)-nm\log \sigma +(2m-1)\sum _{i=1}^{n}\log x_{i}-{\frac {\sum _{i=1}^{n}x_{i}^{2}}{\sigma }}.$

Поэтому

${\begin{aligned}{\frac {\partial \ell }{\partial \sigma }}={\frac {-nm\sigma +\sum _{i=1}^{n}x_{i}^{2}}{\sigma ^{2}}}\quad {\text{and}}\quad {\frac {\partial \ell }{\partial m}}=-n{\frac {\Gamma '(m)}{\Gamma (m)}}-n\log \sigma +2\sum _{i=1}^{n}\log x_{i}.\end{aligned}}$

Эти производные исчезают только тогда, когда

$\sigma ={\frac {\sum _{i=1}^{n}x_{i}^{2}}{nm}}$

а значение m, при котором производная по m обращается в нуль, находится численными методами, в том числе методом Ньютона–Рафсона .

Можно показать, что в критической точке достигается глобальный максимум, поэтому критическая точка является оценкой максимального правдоподобия ( m , σ ). Из-за эквивариантности оценки максимального правдоподобия также получается оценка максимального правдоподобия для Ω.

Генерация случайной переменной

Распределение Накагами связано с гамма-распределением .В частности, учитывая случайную величину $Y\,\sim {\textrm {Gamma}}(k,\theta )$, можно получить случайную величину $X\,\sim {\textrm {Nakagami}}(m,\Omega )$, установив $k=m$, $\theta =\Omega /m$и извлекая квадратный корень из $Y$:

$X={\sqrt {Y}}.\,$

Альтернативно, распределение Накагами $f(y;\,m,\Omega )$ может быть сгенерировано из распределения хи с параметром $k$ установлен на $2m$ а затем следует масштабное преобразование случайных величин. То есть случайная величина Накагами $X$ генерируется путем простого масштабного преобразования случайной величины с распределением хи $Y\sim \chi (2m)$ как показано ниже.

$X={\sqrt {(\Omega /2m)Y}}.$

Для хи-распределения степени свободы $2m$ должно быть целым числом, но для Накагами $m$ может быть любым действительным числом, большим 1/2. Это критическая разница, и, соответственно, Накагами-м рассматривается как обобщение распределения хи, аналогично гамма-распределению, рассматриваемому как обобщение распределений хи-квадрат.

История и приложения

Распределение Накагами является относительно новым: оно было впервые предложено в 1960 году Минору Накагами в качестве математической модели мелкомасштабных замираний при распространении высокочастотных радиоволн на большие расстояния. Он использовался для моделирования затухания беспроводных сигналов, проходящих по нескольким путям. и изучить влияние замирания каналов на беспроводную связь.

Связанные дистрибутивы

• Ограничение m единичным интервалом ( q = m ; 0 < q < 1) определяет распределение Накагами - q , также известное как Хойта Распределение , впервые изученное Р. С. Хойтом в 1940-х годах. В частности, радиус вокруг истинного среднего значения двумерной нормальной случайной величины, переписанной в полярных координатах (радиус и угол), соответствует распределению Хойта. Точно так же действует и модуль комплексной нормальной случайной величины.
• При 2 m = k распределение Накагами дает масштабированное распределение ци .
• С $m={\tfrac {1}{2}}$, распределение Накагами дает масштабированное полунормальное распределение .
• Распределение Накагами — это особая форма обобщенного гамма-распределения с p = 2 и d = 2 м .

См. также

• Гамма-распределение
• Модифицированное полунормальное распределение
• Субгауссово распределение