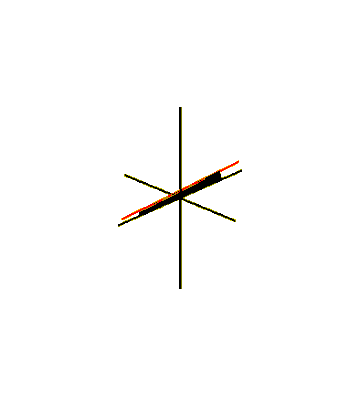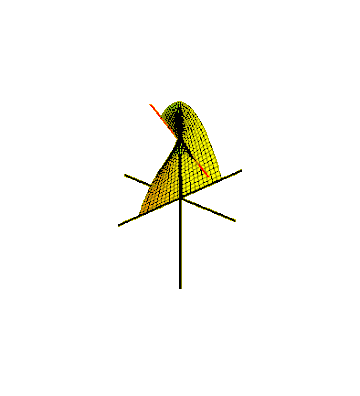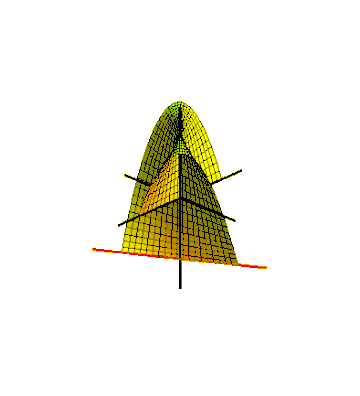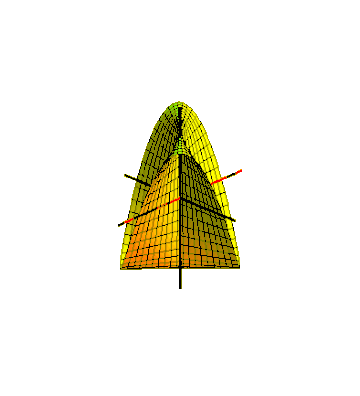Мёбиус Стрип

В математике , Möbius Strip , Möbius Band или Möbius Loop ^{[ А ]} это поверхность , которая может быть сформирована, прикрепляя концы полосы бумаги вместе с полупроблемой. Как математический объект, он был обнаружен Листингом Иоганна Бенедикта и Августом Фердинандом Мёбиусом в 1858 году, но он уже появился в римских мозаиках с третьего века нашей эры . Полоса Möbius-это неэлементная поверхность, а это означает, что внутри него нельзя последовательно различать по часовой стрелке от поворотов против часовой стрелки. Каждая неэлементная поверхность содержит полосу Möbius.

Как абстрактное топологическое пространство , полоска Möbius может быть встроена в трехмерное евклидовое пространство разными способами: пол-мошенника по часовой стрелке отличается от полупроблемы против часовой стрелки, и он также может быть встроен с нечетным количеством поворотов больше, чем больше, чем один, или с завязанной центральной линией. Любые два встроения с одним и тем же узлом для центральной линии и одинаковое число и направление поворотов, топологически эквивалентны . Все эти встраивания имеют только одну сторону, но при встроении в другие пространства полоса Мёбиуса может иметь две стороны. У этого есть только одна кривая границы .

Несколько геометрических конструкций полосы Möbius обеспечивают ее дополнительную конструкцию. Он может быть охвачен в виде управляемой поверхности линейным сегментом, вращающимся в вращающейся плоскости, с самостоятельными или без самостоятельных перекрестков. Тонкая бумажная полоса с соединением концов, чтобы сформировать полосу Möbius, может плавно сгибаться в качестве развивающейся поверхности или быть сложенной плоской ; Сплюснутые полоски Möbius включают трихексафлексагон . Суданская полоса Möbius-это минимальная поверхность в гиперсен , а полоса Möbius Möbius Meeks-это минимальная поверхность в обычном евклидовом пространстве. Как суданская полоса Мёбиуса, так и еще одна самоуверенная полоса Мёбиуса, перекрестная капитализация, имеют круговую границу. Полоса Möbius без границы, называемая открытой полосой Möbius, может образовывать поверхности постоянной кривизны . Определенные очень симметричные пространства, точки которых представляют линии в плоскости, имеют форму полосы Мёбиуса.

Многие применения полосок Möbius включают механические ремни , которые равномерно носят с обеих сторон, ролик с двумя дорожками , чьи вагоны чередуются между двумя треками, и карты мира, напечатанные так, что антиподы кажутся друг напротив. Полосы Möbius появляются в молекулах и устройствах с новыми электрическими и электромеханическими свойствами и использовались для доказывания невозможных результатов в теории социального выбора . В популярной культуре Möbius полосы появляются в произведении искусства MC Escher , Max Bill и других, а также в дизайне символа утилизации . Многие архитектурные концепции были вдохновлены полосой Möbius, включая дизайн здания для Зала славы NASCAR . Исполнители, в том числе Гарри Блэкстоун -старший и Томас Нельсон Даунс, основали магические уловки сценических магистралей на свойствах полосы Мёбиуса. Каноны . JS Bach были проанализированы с использованием полос Möbius Многие произведения спекулятивной фантастики функции Möbius полосы; В более общем плане, структура сюжета, основанная на полосе Möbius, событий, которые повторяются с поворотом, распространена в художественной литературе.

История

Мозаика из древнего Стражи, изображая Айон, держащий полоску Мёбиуса

Цепный насос с приводной цепью Мёбиуса, Исмаил аль-Джазари (1206)

Открытие полосы Мёбиуса как математического объекта приписывается независимо от листинга немецких математиков Иоганна Бенедикта и Августа Фердинанда Мёбиуса в 1858 году. ^{[ 2 ]} Однако это было известно задолго до этого, как как физический объект, так и в художественных изображениях; В частности, это можно увидеть в нескольких римских мозаиках с третьего века н.э.. ^{[ 3 ]}^{[ 4 ]} Во многих случаях они просто изображают спиральные ленты как границы. Когда количество катушек нечетное, эти ленты являются полосками Möbius, но для равномерного количества катушек они топологически эквивалентны расколанным кольцам . Следовательно, может ли ленточная полоса Möbius, может быть случайной, а не преднамеренным выбором. По крайней мере, в одном случае была нарисована лента с разными цветами с разных сторон, заставляя своего художника сделать неуклюжие исправление в точке, где цвета не совпадают. ^{[ 3 ]} Другая мозаика из города Стражинум ( изображена) показывает зодиак , удерживаемый Богом Айоном , как группа с лишь одним поворотом. Нет четких доказательств того, что односторонность этого визуального представления небесного времени была преднамеренной; Это могло быть выбрано просто как способ сделать все признаки зодиака на видимой стороне полосы. некоторые другие древние изображения ошобоуросов или украшений в восьмой фигуре Предполагается, что изображают, но неясно, были ли они предназначены для изображения плоских полос любого типа. ^{[ 4 ]}

Независимо от математической традиции, машинисты давно известны, что механические ремни изношат вдвое же наполовину, когда они образуют полоски Мёбиуса, потому что они используют всю поверхность ремня, а не только внутреннюю поверхность врезанного пояса. ^{[ 3 ]} Кроме того, такой ремень может быть менее склонным к керлингу из стороны в сторону. Раннее письменное описание этой техники датируется 1871 году, которое после первых математических публикаций, касающихся полосы Мёбиуса. Гораздо раньше изображение цепного насоса в работе Исмаила аль-Джазари из 1206 изображает конфигурацию полоски Möbius для своей цепочки привода. ^{[ 4 ]} Другое использование этой поверхности было сделано швея в Париже (на неопределенную дату): они инициировали новичков, потребовав от них, чтобы сшивать полоску Мёбиуса в качестве воротника на одежду. ^{[ 3 ]}

Характеристики

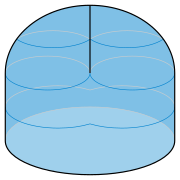
В полосе Мёбиуса есть несколько любопытных свойств. Это неэлементная поверхность : если асимметричный двумерный объект скользит один раз по полосе, он возвращается к своему исходному положению в качестве зеркального изображения. В частности, изогнутая стрелка, указывающая по часовой стрелке (↻), будет возвращаться в виде стрелки, указывающей против часовой стрелки (↺), подразумевая, что в полосе Мёбиуса невозможно последовательно определить, что значит быть по часовой стрелке или против часовой стрелки. Это самая простая неэлементная поверхность: любая другая поверхность не ориентирована, тогда как и только тогда, когда у нее есть полоска Möbius в качестве подмножества. ^{[ 5 ]} В связи с тем, что при включении в евклидовое пространство полоса Мёбиуса имеет только одну сторону. Трехмерный объект, который скользит один раз по поверхности полосы, не зернут, а вместо этого возвращается к одной и той же точке полосы на то, что кажется локально, чтобы быть ее другой стороной, показывая, что обе позиции действительно являются частью одной стороны Полем Такое поведение отличается от знакомых ориентированных поверхностей в трех измерениях, таких как те, которые смоделированы плоскими листами бумаги, цилиндрическими питьевыми соломинками или полыми шариками, для которых одна сторона поверхности не связана с другой. ^{[ 6 ]} Тем не менее, это свойство внедрения в космос, а не внутреннее свойство самой полосы Мёбиуса: существуют другие топологические пространства, в которые может быть встроена полоса Мёбиуса, чтобы у нее было две стороны. ^{[ 7 ]} Например, если передние и задние грани куба приклеены друг к другу с отражением зеркала левого вправо, результатом является трехмерное топологическое пространство ( декартовое произведение полосы Möbius с интервалом), в котором верхний и нижние половины куба могут быть отделены друг от друга двухсторонней полосой Мёбиуса. ^{[ B ]} от дисков, сферов и цилиндров, для которых можно одновременно встроить необоснованный набор непересекающихся В отличие копий в трехмерное пространство, может быть одновременно встроено только исчисляемое количество полос Möbius. ^{[ 9 ]}^{[ 10 ]}^{[ 11 ]}

Путь вдоль края полосы Мёбиуса, прослеженная до возвращения к своей отправной точке на краю, включает в себя все граничные точки полосы Мёбиуса в одной непрерывной кривой. Для полосы Möbius, образованной приклеиванием и скручиванием прямоугольника, она имеет в два раза больше центральной линии полосы. В этом смысле полоса Möbius отличается от раскрученного кольца и, как круговой диск, имея только одну границу. ^{[ 6 ]} Полоса Мёбиуса в евклидовом пространстве не может быть перемещена или растянута в зеркальное изображение; Это хиральный объект с правой или левшей. ^{[ 12 ]} Мёбий полоски со странным числом полусушителей больше одного, или которые завязаны перед склеиванием, отличаются как встроенные подмножества трехмерного пространства, даже если все они эквивалентны в виде двумерных топологических поверхностей. ^{[ 13 ]} Точнее, две полосы Möbius эквивалентно встроены в трехмерное пространство, когда их центральные линии определяют один и тот же узел, и они имеют одинаковое количество поворотов, что и друг друга. ^{[ 14 ]} Однако с ровным количеством поворотов получает другую топологическую поверхность, называемую кольцом . ^{[ 15 ]}

Полоса Möbius может быть непрерывно трансформироваться в свою центральную линию, делая ее более узкой, зафиксируя точки на центральной линии. Это преобразование является примером ретракции деформации , и ее существование означает, что полоска Мёбиуса обладает многими из тех же свойств, что и ее центральная линия, что является топологически кругом. В частности, его фундаментальная группа совпадает с фундаментальной группой круга, бесконечной циклической группой . Следовательно, пути на полосе Мёбиуса, которые начинаются и заканчиваются в той же точке, можно отличить топологически (вплоть до гомотопии ) только по количеству раз, когда они плывут вокруг полосы. ^{[ 16 ]}

Резка центральная линия создает двухстороннюю (не-Мёбий) полосу

Один разрез за пределами центра создает полосу Möbius (фиолетовый), связанная с двусторонней полосой с двойной длиной

Нарезание полосы Möbius вдоль центральной линии с парой ножниц дает одну длинную полосу с четырьмя полупроблеками в ней (по сравнению с раскрученным кольцом или цилиндром), а не с двумя отдельными полосками. Двое из полувистов исходят из-за того, что эта более тонкая полоса проходит два раза через полупробранную в оригинальной полосе Möbius, а два других исходят от того, как две половинки более тонкой полосы обернуты друг на друга. Результатом является не полоса Мёбиуса, а топологически эквивалент цилиндра. Нарезание этой двойной полосы снова вдоль его центральной линии создает две связанные двойные полоски. Если вместо этого полоса Möbius вырезана вдоль, треть пути по ширине, она производит две связанные полосы. Один из них-центральная, более тонкая, Möbius Strip, в то время как у другой есть два полувиста. ^{[ 6 ]} Эти взаимосвязанные фигуры, образованные продольными срезами полос Möbius с различной шириной, иногда называют парадромными кольцами . ^{[ 17 ]}^{[ 18 ]}

Подразделение в шесть взаимовыгодных областей, ограниченных графиком Титце

Решение проблемы трех коммунальных услуг на полосе Möbius

Полоса Мёбиуса может быть разрезана на шесть взаимовыгодных областей, показывая, что карты на поверхности полосы Мёбиуса иногда могут потребовать шесть цветов, в отличие от четырех цветной теоремы для плоскости. ^{[ 19 ]} Шести цветов всегда достаточно. Этот результат является частью теоремы Рингеля -Море , в которой говорится, сколько цветов нужно каждой топологической поверхности. ^{[ 20 ]} Край и вершины этих шести регионов образуют график Титце , который представляет собой двойной график с шестью веретками на этой поверхности для полного графика , но не может быть нарисована без пересечений на плоскости . Другая семья графиков, которые могут быть встроены на полосу Мёбиуса, но не на плоскости,-это лестницы Мёбиуса , границы подразделений полосы Мёбиуса в прямоугольники, встречающие сквозные. ^{[ 21 ]} Они включают в себя утилитный график, шестивертекс, полное двухпартное график , встроенный в полосу Möbius показывает, что, в отличие от плоскости, проблема трех утилит может быть решена на прозрачной полосе Möbius. ^{[ 22 ]} Эйлера , характерная для полосы Мёбиуса, равна нулю , что означает, что для любого подразделения полосы вершинами и ребрами в области, числа $V$ , $E$ , и $F$ вершин, краев и регионов удовлетворяют $V-E+F=0$ Полем Например, график Титце $12$ Вершины, $18$ края и $6$ регионы; $12-18+6=0$ . ^{[ 19 ]}

Конструкции

Существует много разных способов определения геометрических поверхностей с топологией полосы Мёбиуса, что дает реализации с дополнительными геометрическими свойствами.

Подметать сегмент линии

Полоса Мёбиуса вылетала сегментом вращающейся линии в вращающейся плоскости

Коноид Плюкера вылетал другим движением сегмента линии

Одним из способов встроить полосу Möbius в трехмерное евклидовое пространство, является ее смести линейным сегментом, вращающимся в плоскости, которая, в свою очередь, вращается вокруг одной из ее линий. ^{[ 23 ]} Для того, чтобы заместительная поверхность встретилась с собой после полупробрика, сегмент линии должен вращаться вокруг своего центра в половине угловой скорости вращения плоскости. Это может быть описано как параметрическая поверхность , определяемая уравнениями для картезианских координат его точек, ${\begin{aligned}x(u,v)&=\left(1+{\frac {v}{2}}\cos {\frac {u}{2}}\right)\cos u\\y(u,v)&=\left(1+{\frac {v}{2}}\cos {\frac {u}{2}}\right)\sin u\\z(u,v)&={\frac {v}{2}}\sin {\frac {u}{2}}\\\end{aligned}}$ для $0\leq u<2\pi$ и $-1\leq v\leq 1$ В где один параметр $u$ Описывает угол вращения плоскости вокруг его центральной оси и другого параметра $v$ Описывает положение точки вдоль сегмента вращающейся линии. Это производит полоску ширины 1, центральный круг, в центре чьего -либо радиус 1, лежит в $xy$ -Полете и сосредоточен на $(0,0,0)$ . ^{[ 24 ]} Тот же метод может создавать полоски Möbius с любым нечетным количеством полупробрикатов, когда быстрее вращались сегмент в своей плоскости. Вращающийся сегмент сметает круглый диск в плоскости, который он вращается, и полоса Мёбиуса, которую генерирует он Из-за односторонности этого срезов нарезанный торус остается подключенным. ^{[ 25 ]}

Линейный или линейный сегмент промежуток в другом движении, вращающемся в горизонтальной плоскости вокруг начала координат, когда он движется вверх и вниз, образует коноид или цилиндроид Плакера алгебраичкой , правилую в форме самокничивающейся полосы Möbius. ^{[ 26 ]} Он имеет приложения в проектировании передач . ^{[ 27 ]}

Многогранные поверхности и плоские складывания

Полоса бумаги может образовывать сплющенную полоску Möbius в плоскости, сложив ее на $60^{\circ }$ углы, так что его центральная линия лежит вдоль равностороннего треугольника и прикрепляя концы. Самая короткая полоса, для которой это возможно, состоит из трех равносторонних треугольников, сложенных по краям, где встречаются два треугольника. Его соотношение сторон - соотношение длины полосы ^{[ C ]} к его ширине - ${\sqrt {3}}\approx 1.73$ и тот же метод складывания работает для любого большего соотношения сторон. ^{[ 28 ]}^{[ 29 ]} Для полосы из девяти равносторонних треугольников результатом является трихексафлексагон , который может быть согнут, чтобы выявить различные части ее поверхности. ^{[ 30 ]} Для слишком коротких полос, чтобы напрямую применить этот метод, можно сначала «аккордеон сгибать» полосу в его широком направлении вперед и назад, используя равномерное количество сгиб. Например, с двумя сгибами $1\times 1$ полоса станет $1\times {\tfrac {1}{3}}$ Складная полоса, поперечное сечение которой находится в форме «n» и останется «n» после полупробрика. Более узкая аккордеонная полоса может затем быть сложена и соединена так же, как и более длинная полоса . ^{[ 28 ]}^{[ 29 ]}

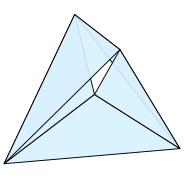
Пяти-вертекс многогранные и плоские полоски Möbius

Полоса Möbius также может быть встроена в качестве многогранной поверхности в пространстве или плоскосленной в плоскости, и только пять треугольных граней, разделяющих пять вершин. В этом смысле он проще, чем цилиндр , который требует шести треугольников и шесть вершин, даже если представлена более абстрактно как упрощенный комплекс . ^{[ 31 ]}^{[ D ]} Полоса Möbius из пяти треугольников может быть представлена наиболее симметрично пятью из десяти равносторонних треугольников четырехмерного регулярного простого . Эта четырехмерная многогранная полоса Мёбиуса является единственной плотной полосой Мёбиуса, которая полностью четырехмерная и для которой все разрезают гиперплоины, разделяют ее на две части, которые топологически эквивалентны дискам или кругам. ^{[ 32 ]}

Другие многогранные встраивания полос Möbius включают в себя один с четырьмя выпуклыми четырехсторонними в качестве грани, другой с тремя невыпульными четырехугольниками . ^{[ 33 ]} и один использует вершины и центральную точку обычного октаэдрона , с треугольной границей. ^{[ 34 ]} Каждая абстрактная триангуляция проективной плоскости может быть включена в 3D в качестве многогранной полосы Мёбия с треугольной границей после удаления одного из его грани; ^{[ 35 ]} Примером является шесть-версийная проективная плоскость, полученная путем добавления одной вершины к пятиверовой полосе Möbius, соединенной треугольниками, к каждому из его граничных краев. ^{[ 31 ]} Однако не каждая абстрактная триангуляция полосы Möbius может быть представлена геометрически, как многогранная поверхность. ^{[ 36 ]} Чтобы быть реализованным, необходимо и достаточное, чтобы в триангуляции не было двух непересекаемых 3-циклов . ^{[ 37 ]}

Плавно встроенные прямоугольники

Прямоугольная полоса Möbius, изготовленная путем прикрепления концов прямоугольника бумаги, может быть плавно встроена в трехмерное пространство, когда его соотношение сторон больше, чем ${\sqrt {3}}\approx 1.73$ , то же соотношение, что и для плоской равенственной версии Möbius Strip. ^{[ 38 ]} Это плоское треугольное встраивание может подняться до гладкого ^{[ E ]} встраивая в три измерения, в которых полоса находится в трех параллельных плоскостях между тремя цилиндрическими роликами, каждая касаясь двух плоскостей . ^{[ 38 ]} Математически, плавно встроенный лист бумаги может быть смоделирован как развивающаяся поверхность , которая может сгибаться, но не может растянуться. ^{[ 39 ]}^{[ 40 ]} По мере того, как его соотношение уменьшается в сторону ${\sqrt {3}}$ Все гладкие встраивания, кажется, приближаются к одной и той же треугольной форме. ^{[ 41 ]}

Продольные складки плоской полосы Möbius с аккордеоном, предотвращающей его образование трехмерного встраивания, в которое слои отделяются друг от друга и плавно сгибаются без смят или растягивания от складок. ^{[ 29 ]} Вместо этого, в отличие от плоского случая, существует нижний предел к соотношению сторон плавных прямоугольных полос Möbius. Их соотношение сторон не может быть меньше, чем $\pi /2\approx 1.57$ , даже если самостоятельные превзойти разрешены. Самоуверенные гладкие полосы Möbius существуют для любого соотношения сторон выше этого границы. ^{[ 29 ]}^{[ 42 ]} Без межотраслевых соотношений должно быть, по крайней мере, ^{[ 43 ]} ${\frac {2}{3}}{\sqrt {3+2{\sqrt {3}}}}\approx 1.695.$

Нерешенная проблема в математике :

Может а

12\times 7

Прямоугольник бумаги склеивается, чтобы сформировать гладкую полосу Möbius, встроенная в пространство? ^{[ f ]}

(Более нерешенные проблемы в математике)

Для соотношений сторон между этим связанным и ${\sqrt {3}}$ себе Это была открытая проблема, существуют ли плавные встраиваемые встроения, без участия в . ^{[ 29 ]}^{[ 42 ]}^{[ 43 ]} В 2023 году Ричард Шварц объявил о том, что их не существует, но этот результат все еще ожидает рассмотрения и публикации. ^{[ 44 ]}^{[ 45 ]} Если потребность в гладкости расслаблена, чтобы обеспечить постоянно дифференцируемые поверхности, теорема Нэш -Куйпер подразумевает, что любые два противоположных края любого прямоугольника могут быть приклеены для формирования встроенной полосы Мёбия, независимо от того, насколько маленьким ни является соотношение сторон. ^{[ G ]} Ограничивающий корпус, поверхность, полученная из бесконечной полосы плоскости между двумя параллельными линиями, приклеенной противоположной ориентацией друг к другу, называется неограниченной полосой Мёбиуса или реальной тавтологической линии . ^{[ 46 ]} Хотя он не имеет плавного закрытого встраивания в трехмерное пространство, его можно плавно встроить в виде закрытого подмножества четырехмерного евклидового пространства. ^{[ 47 ]}

Минимальная энергия форма гладкой полосы Möbius, приклеенной из прямоугольника, не имеет известного аналитического описания, но может быть рассчитана численно и является предметом большого исследования теории пластин с момента первоначальной работы по этому вопросу в 1930 году Михаилом Садовский . ^{[ 39 ]}^{[ 40 ]} Также можно найти алгебраические поверхности Möbius . , которые содержат прямоугольные разработанные полоски ^{[ 48 ]}^{[ 49 ]}

Создание граничного кругового

Приклеивая две полоски Möbius, чтобы сформировать бутылку Klein

Проекция суданской полосы Мёбиуса

Край, или полосы Мёбиуса топологически эквивалентен кругу . граница В общих формах полосы Möbius он имеет отличную форму от круга, но она не подчеркивается , и поэтому вся полоса может быть растянута без пересечения, чтобы сделать край идеально круглым. ^{[ 50 ]} Один из таких примеров основан на топологии бутылки Klein , односторонней поверхности без границы, которая не может быть включена в трехмерное пространство, но может быть погружена (позволяя поверхности пересекать себя определенными ограниченными способами). Бутылка Klein-это поверхность, которая возникает, когда две полосы Möbius приклеены вместе с краем до края, и-реверсирование этого процесса-бутылку Klein можно нарезать вдоль тщательно выбранного разреза, чтобы произвести две полосы Möbius. ^{[ 51 ]} Для формы бутылки Klein, известной как бутылка Klein's Lawson, кривая, вдоль которой она нарезана, может быть сделана круглой, что приводит к полоскам Möbius с круглыми краями. ^{[ 52 ]}

Бутылка Klein's Klein-это минимальная поверхность перекрестной самостоятельной поверхности . $(\cos \theta \cos \phi ,\sin \theta \cos \phi ,\cos 2\theta \sin \phi ,\sin 2\theta \sin \phi )$ для $0\leq \theta <\pi ,0\leq \phi <2\pi$ . ^{[ 53 ]} Половина этой бутылки Klein, подмножество с $0\leq \phi <\pi$ , дает полоску Möbius, встроенная в гиперсфере как минимальную поверхность с большим кругом в качестве границы. ^{[ 54 ]} Это вкладывание иногда называют «суданской полосой Мёбиуса» после того, как топологи Сью Гудман и Даниэль Асимова, которые обнаружили ее в 1970 -х годах. ^{[ 55 ]} Геометрически бутылка Кляна Лоусона может быть построена путем промежутка большого круга через великое циркулярное движение в 3-х сфер, а суданская полоса Мёбиуса получается путем подметания полукруга вместо круга или эквивалентно, нарезав бутылку Кляйна вдоль круга вместо круга или эквивалентно, нарезав бутылку Кляйна вдоль круга вместо круга или эквивалентно, нарезав бутылку Кляйна вдоль круга. Это перпендикулярно всем застреленным кругам. ^{[ 52 ]}^{[ 56 ]} Стереографическая проекция превращает эту форму из трехмерного сферического пространства в трехмерное евклидовое пространство, сохраняя круговую границу . ^{[ 52 ]} Наиболее симметричная проекция получается с использованием точки проекции, которая лежит на этом большом круге, который проходит через середину каждого из полукруг, но создает неограниченное встрадание с точкой проекции, удаленной из его центральной линии. ^{[ 54 ]} Вместо этого, оставив суданскую полоску Мёбиуса бездействующей, в 3-х сфере оставляет его с бесконечной группой симметрий изоморфной для ортогональной группы $\mathrm {O} (2)$ , группа симметрий круга . ^{[ 53 ]}

Суданская полоса Мёбиуса простирается на всех сторонах своего пограничного круга, неизбежно, если поверхность должна избежать пересечения. Другая форма полосы Möbius, называемая поперечной капитализацией или перекрестной колпачкой , также имеет круговую границу, но в противном случае остается только на одной стороне плоскости этого круга, ^{[ 57 ]} Сделать его более удобным для прикрепления к круглым отверстиям на других поверхностях. Для этого он пересекает себя. Это может быть сформировано путем удаления четырехстороннего с вершины полушария, ориентируя края четырехугольника в чередующихся направлениях, а затем склеивая противоположные пары этих краев, последовательно с этой ориентацией. ^{[ 58 ]} Две части поверхности, образованные двумя приклеенными парами краев, пересекают друг друга с точкой щепотки, подобной тем, что у зонтника Уитни на каждом конце сегмента пересечения, ^{[ 59 ]} Та же самая топологическая структура, наблюдаемая в коноиде Плюкера . ^{[ 26 ]}

Поверхности постоянной кривизны

Открытая полоса Möbius является относительной внутренней частью стандартной полосы Möbius, образованной путем пропущения точек на границе. Ему может быть дана римановая геометрия постоянной положительной, негативной или нулевой гауссовой кривизны . Случаи негативной и нулевой кривизны образуют геодезически полные поверхности, что означает, что все геодезики («прямые линии» на поверхности) могут быть расширены на неопределенный срок в любом направлении.

Нулевая кривизна: Открытая полоса с нулевой кривизны может быть построена путем склеивания противоположных сторон плоской полосы между двумя параллельными линиями, описанными выше как тавтологическая линейная пучка. ^{[ 46 ]} Полученная метрика превращает открытую полосу Möbius в (геодезически) полную плоскую поверхность (то есть, имеющую нулевую гауссовую кривизну повсюду). Это уникальная метрика на полосе Möbius, вплоть до равномерного масштабирования, которое является одновременно плоским и полным. Это однозначное пространство плоскости с помощью скользящего отражения , и (вместе с плоскостью, цилиндром , торусом и бутылкой Klein ) является одним из пяти двумерных полных плоских коллекторов . ^{[ 60 ]}
Негативная кривизна: Открытая полоса Möbius также допускает полные показатели постоянной негативной кривизны. Один из способов увидеть это - начать с модели верхней половины плоскости (пуанкаре) гиперболической плоскости , геометрии постоянной кривизны, линии которой представлены в модели полукругами, которые соответствуют $x$ -Ка по прямым углам. Возьмите подмножество верхней половины плоскости между любыми двумя вложенными полукругами и определите внешний полукруг с обращением влево-правой внутренней полукруга. Результатом является топологически полная и некомпактная полоса Möbius с постоянной негативной кривизны. Это «нестандартная» полная гиперболическая поверхность в том смысле, что она содержит полную гиперболическую полплости (на самом деле две, на противоположных сторонах оси, скользящей рефлексии), и является одной из 13 нестандартных поверхностей. ^{[ 61 ]} Опять же, это можно понимать как коэффициент гиперболической плоскости с помощью скользящего отражения. ^{[ 62 ]}
Положительная кривизна: Полоса постоянной положительной кривизны Möbius не может быть завершена, поскольку известно, что единственными полными поверхностями постоянной положительной кривизны являются сфера и проективная плоскость . ^{[ 60 ]} Тем не менее, в некотором смысле это всего лишь одна точка от полной поверхности, так как открытая полоса Möbius является гомеоморфной для некогда закрепленной проективной плоскости, поверхности, полученной путем удаления любой точки из проективной плоскости. ^{[ 63 ]}

Минимальные поверхности описываются как имеющие постоянную среднюю кривизну вместо постоянной гауссовой кривизны. Суданская полоса Мёбиуса была построена как минимальная поверхность, ограниченная большим кругом в 3-х сфере, но в евклидовом пространстве также есть уникальная полная (безграничная) поверхность, погруженная в евклидовое пространство. Это называется Meeks Möbius Strip, ^{[ 64 ]} После его описания 1982 года Уильяма Гамильтона Микс, iii . ^{[ 65 ]} Несмотря на то, что глобально нестабильна в виде минимальной поверхности, ее небольшие пятна, ограниченные неконтролируемыми кривыми внутри поверхности, могут образовывать стабильные встроенные полоски Möbius в виде минимальных поверхностей. ^{[ 66 ]} И полоска Möbius Möbius Meeks, и каждая более высокая минимальная поверхность с топологией полосы Möbius может быть построена с использованием решений проблемы Björling , которая определяет минимальную поверхность уникально из ее пограничной кривой и касательных плоскостей вдоль этой кривой. ^{[ 67 ]}

Пространства линий

Семейству линий в плоскости может быть предоставлена структура гладкого пространства, причем каждая линия представлена в качестве точки в этом пространстве. Полученное пространство линий топологически эквивалентно открытой полосе Möbius. ^{[ 68 ]} Один из способов увидеть это - расширить евклидовую плоскость до реальной проективной плоскости, добавив еще одну линию, линию в бесконечности . Проективной двойственностью пространство линий в проективной плоскости эквивалентно ее пространству точек, самой проективной плоскости. Удаление линии в бесконечности, чтобы произвести пространство евклидовых линий, пробивает это пространство проективных линий. ^{[ 69 ]} Следовательно, пространство евклидовых линий представляет собой проколотую проективную плоскость, которая является одной из форм открытой полосы Möbius. ^{[ 63 ]} Пространство линий в гиперболической плоскости может быть параметризовано непопопомопочными парами различных точек на круге, пары точек в бесконечности каждой линии. Это пространство, опять же, имеет топологию открытой полосы Möbius. ^{[ 70 ]}

Эти пространства линий очень симметричны. Симметрия евклидовых линий включают аффинные преобразования , а симметрия гиперболических линий включают преобразования Мёбиуса . ^{[ 71 ]} Аффинные преобразования и преобразования Möbius Обе образуют 6-мерные группы LIE , топологические пространства, имеющие совместимую алгебраическую структуру, описывающую состав симметрии. ^{[ 72 ]}^{[ 73 ]} Поскольку каждая линия в плоскости симметрична для любой другой линии, открытая полоса Möbius представляет собой однородное пространство , пространство с симметриями, которое переносит каждую точку для каждой другой точки. Гомогенные пространства групп лжи называются solvmanifolds , а полоса Möbius может использоваться в качестве контр -образца что не каждый сольвманифорт - это Nilmanifold , и что не каждый сольвманифорт может быть включен в прямой продукт компактного , показывая , solvmanifold с $\mathbb {R} ^{n}$ Полем Эти симметрии также обеспечивают еще один способ построить саму полоску Мёбиуса, как групповая модель этих групп. Групповая модель состоит из группы лжи и подгруппы стабилизатора своей действия; Сокращение косета подгруппы с точками создает пространство с той же топологией, что и базовое однородное пространство. В случае симметрии евклидовых линий стабилизатор $x$ Ось состоит из всех симметрий, которые приносят ось к себе. Каждая строка $\ell$ соответствует косо, набор симметрий, которые карту $\ell$ в $x$ -ось. Следовательно, коэффициент пространства , пространство, которое имеет одну точку на космос и наследует свою топологию от пространства симметрий, такое же, как пространство линий, и снова является открытой полосой Мёбиуса. ^{[ 74 ]}

Приложения

Помимо уже обсуждаемых применений полос Möbius к проектированию механических ремней, которые равномерно изношены на всей их поверхности, и из Plücker Conoid к конструкции передач, другие применения полос Möbius включают в себя:

Графеновые ленты, скрученные, образуя полоски Möbius с новыми электронными характеристиками, включая спиральный магнетизм ^{[ 75 ]}
Ароматичность Möbius , свойство органических химических веществ , молекулярная структура которых образует цикл, с молекулярными орбиталями, выровненными вдоль цикла в рисунке полосы Möbius ^{[ 76 ]}^{[ 77 ]}
Резистор Мёбиуса , полоса проводящего материала, покрывающего единую сторону диэлектрической полосы Мёбиуса, таким образом, что отменяет его собственную самоуверенность ^{[ 78 ]}^{[ 79 ]}
Резонаторы с компактной конструкцией и резонансной частотой, которая вдвое меньше, чем у одинаково сконструированных линейных катушек ^{[ 80 ]}^{[ 81 ]}
Паттерны поляризации в свете, появляющихся из q -пластин ^{[ 82 ]}
Доказательство невозможности непрерывного, анонимного и единодушного двухпартийного агрегации правил в теории социального выбора ^{[ 83 ]}
Möbius Loop Roller Roller Roller , форма американских горных горных горных сумасшедших ^{[ 84 ]}^{[ 85 ]}
Мировые карты, проецируемые на полоску Мёбиуса с удобными свойствами, которые нет в восточном и западном западе, и что антипода любой точки на карте может быть найдена на другой печатной стороне поверхности в той же точке полосы Мёбия ^{[ 86 ]}^{[ 87 ]}

Ученые также изучали энергетику мыльных фильмов, формируемых как полоски Möbius, ^{[ 88 ]}^{[ 89 ]} Химический синтез молекул с формой полосы Мёбиуса, ^{[ 90 ]}^{[ 91 ]} и образование более крупных наноразмерных полос Möbius с использованием ДНК оригами . ^{[ 92 ]}

В популярной культуре

Двумерные произведения искусства с участием Мёбиус Стрип включают безумную картину 1947 года Коррадо Кагли (увековеченная в стихотворении Чарльза Олсона ), ^{[ 93 ]}^{[ 94 ]} и два отпечатка MC Escher : Möbius Band I (1961), изображающие три сложенные плоды , кусающие хвосты друг друга; и Möbius Band II (1963), изображающие муравьев, ползающих вокруг полосы Möbius в форме Lemniscate . ^{[ 95 ]}^{[ 96 ]} Это также популярный предмет математической скульптуры , в том числе работы Макса Билла ( бесконечная лента , 1953), Хосе де Ривера ( Infinity , 1967) и Себастьян . ^{[ 93 ]} Полоса подписанную на Trefoil, использовалась в Джона Робинсона ( бессмертии Möbius , 1982). ^{[ 97 ]} (1976) Чарльза О. Перри - Continuum одна из нескольких произведений Perry, исследующей вариации полосы Möbius. ^{[ 98 ]}

Символ утилизации

Логотип Google Drive (2012–2014)

Логотип Impa на марок

Из -за их легко узнаваемой формы полосы Möbius являются общим элементом графического дизайна . ^{[ 97 ]} Знакомый логотип с тремя воротами для переработки , разработанный в 1970 году, основан на гладкой треугольной форме полосы Möbius, ^{[ 99 ]} как был логотип для экологической экспозиции 74 года . ^{[ 100 ]} Некоторые вариации символа утилизации используют другое встраивание с тремя полусушителями вместо одного, ^{[ 99 ]} А в оригинальной версии логотипа Google Drive использовалась плоская тройка Möbius Strip, как и другие подобные дизайны. ^{[ 101 ]} Бразильский институт Nacional de Matemática Pura E Aplicada (IMPA) использует стилизованную гладкую полоску Möbius в качестве логотипа и имеет соответствующую большую скульптуру полосы Möbius, выставленную в их здании. ^{[ 102 ]} Möbius Strip также показала в произведении искусства для почтовых марков из стран, в том числе Бразилии, Бельгии, Нидерландов и Швейцарии. ^{[ 103 ]}^{[ 104 ]}

Полосы Möbius были частым вдохновением для архитектурного дизайна зданий и мостов. Тем не менее, многие из них являются проектами или концептуальными проектами, а не построенными объектами, или растягивают их интерпретацию полосы Мёбия за пределами его узнаваемости как математическую форму или функциональную часть архитектуры. ^{[ 105 ]}^{[ 106 ]} Примером является Национальная библиотека Казахстана , для которой здание было запланировано в форме утолщенной полосы Мёбиуса, но восстановилось другим дизайном после того, как оригинальные архитекторы вышли из проекта. ^{[ 107 ]} Одним из заметных зданий, включающих полосу Möbius, является Зал славы NASCAR , который окружен большой скрученной лентой из нержавеющей стали, действующей в качестве фасада и навеса, и вызывает изогнутые формы гоночных треков. ^{[ 108 ]} В меньшем масштабе Moebius Chair (2006) от Педро Рейеса - это ухаживающая скамья , у которой и боковые стороны есть форма полосы Möbius. ^{[ 109 ]} В качестве формы математики и волоконного искусства шарфы были вязаны в полоски Мёбиуса после работы Элизабет Циммерманн в начале 1980 -х годов. ^{[ 110 ]} В стиле пищи , полосы Möbius использовались для нарезки бубликов , ^{[ 111 ]} Сделать петли из бекона , ^{[ 112 ]} и создание новых форм для макарон . ^{[ 113 ]}

Хотя математически полоска Мёбиуса и четвертое измерение являются чисто пространственными понятиями, их часто вызывают в спекулятивной художественной литературе в качестве основы для цикла времени , в которую неосторожные жертвы могут оказаться в ловушке. Примеры этой тропы включают Мартина Гарднера ( «безстороннего профессора» 1946), Армин Джозеф Дойш « Метро по имени Мобиус » (1950) и фильм «Мобиус» (1996), основанный на нем. Целый мир в форме полосы Мёбиуса - это обстановка Артура Кларка «Стена тьмы» (1946), в то время как обычные полосы Мёбиуса используются в качестве умных изобретений в нескольких историях Уильяма Хазлетта Апсона из 1940 -х годов. ^{[ 114 ]} Другие художественные произведения были проанализированы как имеющиеся в виде полосы Мёбиуса, в которой элементы сюжета повторяются с поворотом; К ним относятся Марсель Пруст в поисках потерянного времени (1913–1927), Луиджи Пиранделло шесть персонажей в поисках автора (1921), Фрэнк Капра - это замечательная жизнь (1946), потерян Джона Барта в Funhouse (1968), Сэмюэля Р. Делани ( (1975 ) Dhalgren 1975) и фильм «Донни Дарко» (2001). ^{[ 115 ]}

Один из музыкальных канонов , Дж. С. Баха пятый из 14 канонов ( BWV 1087 ), обнаруженный в 1974 году в копии Баха вариациях Голдберга , показывает симметрию , рефлекторную скольжение , в которой каждый голос в каноне повторяется, с перевернутыми нотами , одинаковые Мотив из двух мер ранее. Из -за этой симметрии этот канон можно считать, что его счет написал на полосе Мёбиуса. ^{[ 116 ]}^{[ H ]} В теории музыки тоны, которые различаются в результатом октавы, обычно считаются эквивалентными нотами, а пространство возможных нот образует круг, хроматический круг . Поскольку полоса Мёбиуса-это пространство конфигурации двух неупорядоченных точек на круге, пространство всех аккордов с двумя нотами принимает форму полосы Мёбиуса. Эта концепция и обобщения к большему количеству пунктов являются значительным применением орбифолдов к теории музыки . ^{[ 117 ]}^{[ 118 ]} Современные музыкальные группы взяли свое название от Möbius Strip включают American Electronic Rock Trio Band Band ^{[ 119 ]} и норвежская прогрессивная рок -группа Ring Van Möbius . ^{[ 120 ]}

Möbius Strips и их свойства использовались в дизайне сценической магии . Один из таких трюков, известный как афганские полосы, использует тот факт, что полоска Möbius остается одной полосой при вырезании вдоль. Он возник в 1880 -х годах и был очень популярен в первой половине двадцатого века. Многие версии этого трюка существуют и были выполнены известными иллюзионистами, такими как Гарри Блэкстоун -старший и Томас Нельсон Даунс . ^{[ 121 ]}^{[ 122 ]}

Смотрите также

Счетчик Möbius , реестр смены, выходной бит которого дополняется, прежде чем подавать обратно в входной бит
Пенроуз -треугольник , невозможная фигура, граница которой, кажется, обернулась вокруг него в полоску Мёбиуса
Теория лент , математическая теория бесконечно -мадово тонких полос, которые следуют за узлыми космическими кривыми
- William Аттрактор Smale
Пупочный торус

Примечания

^ Произносится США : / M Oʊ / B I S , MAY M - Eɪ MOH , -BEE- - AS -BEE Великобритания : / ˈ M ɜː B I ə s / ; ^{[ 1 ]} Немецкий: [ˈmøːbi̯ʊs] . Как обычное дело для слов, содержащих умлаут , это также часто пишет Mobius или Moebius .
^ По сути, этот пример, но для бутылки Кляйна, а не полоска Мёбиуса, приведен Блэттом (1982) . ^{[ 8 ]}
^ Длина полосы может быть измерена на его центральной линии или путем разрезания полученной полосы Möbius перпендикулярно его границе, так что она образует прямоугольник
^ Плоскомолетная полоса Möbius, образованная из трех равносторонних треугольников, не поступает из абстрактного упрощенного комплекса , потому что все три треугольника имеют одни и те же три вершины, в то время как абстрактные упрощенные комплексы требуют, чтобы каждый треугольник имел различный набор вершин.
^ Это кусочно -планарное и цилиндрическое встроение имеет плавности класс $C^{2}$ , и может быть точно точно аппроксимировано бесконечно дифференцируемым (класс $C^{\infty }$ ) внедрения. ^{[ 39 ]}
^ 12/7 является самым простым рациональным числом в диапазоне соотношений сторон, между 1,695 и 1,73, для которого существование плавного встраивания неизвестно.
^ Эти поверхности имеют класс плавности $C^{1}$ Полем Для более мелкозернистого анализа предположений о плавности, которые заставляют внедрять внедрение, по сравнению с допущениями, при которых теорема Нэш-Куйпер допускает произвольно гибкие встраивания, см. Замечания Bartels & Hornung (2015) , с. 116, после теоремы 2.2. ^{[ 39 ]}
^ Мёбийские полосы также использовались для анализа многих других канонов Бахом и другими, но в большинстве из этих случаев другие петлевые поверхности, такие как цилиндр, могли использоваться одинаково хорошо. ^{[ 116 ]}

Ссылки

^ Уэллс, Джон С. (2008). Лонгман Словарь произношения (3 -е изд.). Лонгман. ISBN 978-1-4058-8118-0 .
^ Пиковер, Клиффорд А. (2005). Полоса Мёбиуса: изумительная группа доктора Августа Мёбиуса по математике, играм, литературе, искусству, технологиям и космологии . Громовой жим. С. 28–29. ISBN 978-1-56025-826-1 .
^ Подпрыгнуть до: ^а ^{беременный} ^в ^{дюймовый} Ларисон, Лорейн Л. (1973). «Группа Möbius в римской мозаике». Американский ученый . 61 (5): 544–547. Bibcode : 1973AMSCI..61..544L . JSTOR 27843983 .
^ Подпрыгнуть до: ^а ^{беременный} ^в Картрайт, июль он ; Гонсалес, Диего Л. (2016). «Мёбий полоски перед Мёбиусом: топологические намеки в древних представлениях». Математический интеллект . 38 (2): 69–76. Arxiv : 1609.07779 . BIBCODE : 2016ARXIV160907779C . doi : 10.1007/s00283-016-9631-8 . MR 3507121 . S2CID 119587191 .
^ Falan, Erica (2000). Когда топология встречается с химией: топологический взгляд на молекулярную хиральность . Перспективы. Вашингтон, округ Колумбия: Математическая ассоциация Америки. С. 82–83 . doi : 10.1017/cbo9780511626272 . ISBN 0-521-66254-0 Полем Мистер 1781912 .
^ Подпрыгнуть до: ^а ^{беременный} ^в Pickoker (2005) , стр. 8–9.
^ Волл, Джон В. младший (весна 1971). «Односторонние поверхности и ориентировочность». Двухлетний журнал по математике колледжа . 2 (1): 5–18. doi : 10.2307/3026946 . JSTOR 3026946 .
^ Блэкетт, Дональд В. (1982). Элементарная топология: комбинаторный и алгебраический подход . Академическая пресса. п. 195. ISBN 9781483262536 .
^ Frolkina, Olga D. (2018). «Пара разбивает группы Мобиуса в космосе». Журнал теории узлов и его последствий . 27 (9): 1842005, 9. Arxiv : 2212.02983 . doi : 10.1142/s0218216518420051 . MR 3848635 . S2CID 126421578 .
^ Лэмб, Эвелин (20 февраля 2019 г.). «Мёбиус полосы бросают вызов связи с бесконечностью» . Quanta Magazine .
^ Мелихов, Сергей А. (2019). «Примечание о бумаге О. Фолкина« Пара не пересекает группы Мобиуса в космосе » . Журнал теории узлов и его последствий . 28 (7): 1971001, 3. Arxiv : 1810.04089 . doi : 10.1142/s0218216519710019 . MR 3975576 . S2CID 119179202 .
^ Пиковер (2005) , с. 52
^ Пиковер (2005) , с. 12
^ Кайл, RH (1955). «Встроения групп Möbius в трехмерном пространстве». Труды Королевской ирландской академии, раздел а . 57 : 131–136. JSTOR 20488581 . MR 0091480 .
^ Пиковер (2005) , с. 11
^ Massey, William S. (1991). Основной курс по алгебраической топологии . Выпускники текстов по математике. Тол. 127. Нью-Йорк: Springer-Verlag. п. 49. ISBN 0-387-97430-X Полем MR 1095046 .
^ Rouse Ball, WW (1892). «Парадромные кольца». Математические воссоздания и проблемы прошлого и настоящего времени (2 -е изд.). Лондон и Нью -Йорк: Macmillan и Co. С. 53–54. ISBN 9780608377803 .
^ Беннетт, GT (июнь 1923 г.). «Парадромные кольца» . Природа . 111 (2800): 882. Bibcode : 1923nater.111r.882b . doi : 10.1038/111882b0 . S2CID 4099647 .
^ Подпрыгнуть до: ^а ^{беременный} Титце, Генрих (1910). «Некоторые комментарии по вопросу окрашивания карт на одной областях» (PDF) . Годовой отчет немецкой математической ассоциации . 19 : 155–159.
^ Рингель, Г .; Янг, JWT (1968). «Решение проблемы расцвета карты Heawood» . Труды Национальной академии наук Соединенных Штатов Америки . 60 (2): 438–445. Bibcode : 1968pnas ... 60..438r . doi : 10.1073/pnas.60.2.438 . MR 0228378 . PMC 225066 . PMID 16591648 .
^ Джаблан, Славик; Радович, Лжильджана; Sazdanović, Radmila (2011). «Непланарные графики, полученные из кодов виртуальных узлов и ссылок Гаусса». Журнал математической химии . 49 (10): 2250–2267. doi : 10.1007/S10910-011-9884-6 . MR 2846715 . S2CID 121332704 .
^ Ларсен, Могенс Эсром (1994). «Непонимание моих лабиринтов может сделать меня несчастным». В парне Ричард К . ; Вудроу, Роберт Э. (ред.). Материалы Мемориальной конференции Eugène Strens по рекреационной математике и ее истории, состоявшейся в Университете Калгари, Калгари, Альберта, август 1986 года . MAA Spectrum. Вашингтон, округ Колумбия: Математическая ассоциация Америки. С. 289–293. ISBN 0-88385-516-х Полем MR 1303141 . Полем См. Рисунок 7, с. 292
^ Машке, Генрих (1900). «Примечание на односторонней поверхности Мобиуса» . Труды Американского математического общества . 1 (1): 39. doi : 10.2307/1986401 . JSTOR 1986401 . MR 1500522 .
^ Junghenn, Hugo D. (2015). Курс в реальном анализе . Бока Ратон, Флорида: CRC Press. п. 430. ISBN 978-1-4822-1927-2 Полем MR 3309241 .
^ Séquin, Carlo H. (2005). «Разделение Тори, узлов и групп Мобиуса» . В Сарханги, Реза; Муди, Роберт В. (ред.). Ренессанс Банф: математика, музыка, искусство, культура . Юго -западный колледж, Уинфилд, Канзас: Конференция Бриджес. С. 211–218. ISBN 0-9665201-6-5 .
^ Подпрыгнуть до: ^а ^{беременный} Фрэнсис, Джордж К. (1987). "Plücker Conoid". Топологическая книжка с картинками . Springer-Verlag, Нью-Йорк. С. 81–83. ISBN 0-387-96426-6 Полем MR 0880519 .
^ Дунер, Дэвид Б.; Сейрег, Али (1995). «3.4.2 Цилиндроид» . Кинематическая геометрия передачи: одновременный инженерный подход . Серия Wiley в области дизайна. Тол. 3. Джон Вили и сыновья. С. 135–137. ISBN 9780471045977 .
^ Подпрыгнуть до: ^а ^{беременный} Барр, Стивен (1964). Эксперименты в топологии . Нью -Йорк: Компания Томаса Й. Кроуэлл. С. 40–49, 200–201. ISBN 9780690278620 .
^ Подпрыгнуть до: ^а ^{беременный} ^в ^{дюймовый} ^и Фукс, Дмитрий ; Табачников, Серж (2007). «Лекция 14: Paper Möbius Band». Математический омнибус: тридцать лекций по классической математике (PDF) . Провиденс, Род -Айленд: Американское математическое общество. С. 199–206. doi : 10.1090/mbk/046 . ISBN 978-0-8218-4316-1 Полем Мистер 2350979 . Архивировано из оригинала (PDF) 2016-04-24.
^ Пук, Лес (2003). «4.2: Trihexaflexagon Revisited» . Flexagons наизнанку . Кембридж, Великобритания: издательство Кембриджского университета. С. 33–36. doi : 10.1017/cbo9780511543302 . ISBN 0-521-81970-9 Полем MR 2008500 .
^ Подпрыгнуть до: ^а ^{беременный} Kühnel, W.; Banchoff, TF (1983). «9-вертексная проективная плоскость» (PDF) . Математический интеллект . 5 (3): 11–22. doi : 10.1007/bf03026567 . MR 0737686 . S2CID 120926324 .
^ Kuiper, Nicolaas H. (1972). «Тяжелые топологические встраивания группы Moebius» . Журнал дифференциальной геометрии . 6 (3): 271–283. doi : 10.4310/jdg/1214430493 . MR 0314057 .
^ Szilassi, Lajos (2008). «Полигранная модель в евклидовом 3-пространстве карты шестикратного продюса проективной плоскости» . Дискретная и вычислительная геометрия . 40 (3): 395–400. doi : 10.1007/s00454-007-9033-y . MR 2443291 . S2CID 38606607 .
^ Такерман, Брайант (1948). «Непочечная многогранная группа Мёбиуса, граница которой-треугольник». Американский математический ежемесячный . 55 (5): 309–311. doi : 10.2307/2305482 . JSTOR 2305482 . MR 0024138 .
^ Боннингтон, С. Пол; Nakamoto, Atsuhiro (2008). «Геометрическая реализация триангуляции на проективной плоскости с удаленным лицом» . Дискретная и вычислительная геометрия . 40 (1): 141–157. doi : 10.1007/s00454-007-9035-9 . MR 2429652 . S2CID 10887519 .
^ Брем, Ульрих (1983). «Неполихедральная триангулированная Метбиус Стрип». Труды Американского математического общества . 89 (3): 519–522. doi : 10.2307/2045508 . JSTOR 2045508 . MR 0715878 .
^ Накамото, Атсухиро; Цучия, Шоичи (2012). «О геометрически реализуемых триангуляциях Мёбия» . Дискретная математика . 312 (14): 2135–2139. doi : 10.1016/j.disc.2011.06.007 . MR 2921579 .
^ Подпрыгнуть до: ^а ^{беременный} Хинц, Денис Ф.; Фрид, Элиот (2015). «Перевод статьи Майкла Садоуского» элементарное доказательство существования развивающейся группы Möbius и приписывание геометрической проблемы к вариационной проблеме » . Журнал эластичности . 119 (1–2): 3–6. Arxiv : 1408.3034 . doi : 10.1007/s10659-014-9490-5 . MR 3326180 . S2CID 119733903 . Перепечатано в Фосдик, Роджер; Фрид, Элиот (2016). Механика лент и полос Möbius (PDF) . Спрингер, Дордрехт. С. 3–6. doi : 10.1007/978-94-017-7300-3 . ISBN 978-94-017-7299-0 Полем MR 3381564 .
^ Подпрыгнуть до: ^а ^{беременный} ^в ^{дюймовый} Bartels, Sören; Хорнунг, Питер (2015). «Изгибающая бумага и полоска Мёбиуса». Журнал эластичности . 119 (1–2): 113–136. doi : 10.1007/s10659-014-9501-6 . MR 3326187 . S2CID 119782792 . Перепечатано в Fosdick & Fried (2016) , с. 113–136. См. В частности, раздел 5.2, с. 129–130.
^ Подпрыгнуть до: ^а ^{беременный} Starostin, El; Ван дер Хейджен, GHM (2015). «Равновесные формы с локализацией стресса для нестабильной эластичной Мёбиуса и других полос» . Журнал эластичности . 119 (1–2): 67–112. doi : 10.1007/s10659-014-9495-0 . MR 3326186 . S2CID 53462568 . Перепечатано в Fosdick & Fried (2016) , с. 67–112.
^ Schwarz, Gideon E. (1990). «Темная сторона полосы Мобиуса». Американский математический ежемесячный . 97 (10): 890–897. doi : 10.1080/00029890.1990.11995680 . JSTOR 2324325 . MR 1079975 .
^ Подпрыгнуть до: ^а ^{беременный} Halpern, B.; Weaver, C. (1977). «Инвертирование цилиндра через изометрические погружения и изометрические встраивания» . Труды Американского математического общества . 230 : 41–70. doi : 10.2307/1997711 . JSTOR 1997711 . MR 0474388 .
^ Подпрыгнуть до: ^а ^{беременный} Шварц, Ричард Эван (2021). «Улучшенная граница на оптимальной бумаге Band Moebius». Geometriae Dedicata . 215 : 255–267. Arxiv : 2008.11610 . doi : 10.1007/s10711-021-00648-5 . MR 4330341 . S2CID 220279013 .
^ Шварц, Ричард (2023). «Оптимальная бумага Moebius Band». arxiv : 2308.12641 [ math.mg ].
^ Кроуэлл, Рэйчел (12 сентября 2023 г.). «Математики решают 50-летнюю головоломку Метбиуса» . Scientific American .
^ Подпрыгнуть до: ^а ^{беременный} Dundas, Bjørn Ian (2018). «Пример 5.1.3: неограниченная группа Möbius». Короткий курс по дифференциальной топологии . Кембриджские математические учебники. Издательство Кембриджского университета, Кембридж. п. https://books.google.com/books?id=7a1edwaaqbaj&pg=pa101 . doi : 10.1017/9781108349130 . ISBN 978-1-108-42579-7 Полем MR 3793640 . S2CID 125997451 .
^ Блануша, Данило (1954). «Изометрическое погружение бесконечно широкой евклидовой группы Möbius в сферическом, параболическом или гиперболическом пространстве с четырьмя измерениями». Международный бюллетень Югославской академии наук и изобразительных искусств . 12 : 19–23. MR 0071060 .
^ Wunderlich, W. (1962). «О ручной мебельной группе». Ежемесячные буклеты для математики . 66 (3): 276–289. Doi : 10.1007/bf01299052 . MR 0143115 . S2CID 122215321 .
^ Schwarz, Gideon (1990). «Претендент к названию« Каноническая моубиусская полоса » . Тихоокеанский журнал по математике . 143 (1): 195–200. doi : 10.2140/pjm.1990.143.195 . MR 1047406 .
^ Хилберт, Дэвид ; COHN-VOSSEN, Стефан (1952). Геометрия и воображение (2 -е изд.). Челси. С. 315–316. ISBN 978-0-8284-1087-8 .
^ Спивак, Майкл (1979). Комплексное введение в дифференциальную геометрию, том I (2 -е изд.). Уилмингтон, штат Делавэр: публикуйте или погибнет. п. 591.
^ Подпрыгнуть до: ^а ^{беременный} ^в Knöppel, Felix (лето 2019). «Учебное пособие 3: Минимальные поверхности Лоусона и суданская группа Möbius» . DDG2019: курс визуализации в Ту Берлин .
^ Подпрыгнуть до: ^а ^{беременный} Лоусон, Х. Блейн -младший (1970). "Полные минимальные поверхности в $S^{3}$ ". математики . Вторая серия. 92 (3): 335–374 : 10.2307 1970625 . JSTOR 1970625 . DOI . / Анналы $\tau _{1,2}$ .
^ Подпрыгнуть до: ^а ^{беременный} Шлеймер, Саул; Сегерман, Генри (2012). «Скульптуры в $с 3$ " В Босхе, Роберт; МакКенна, Дуглас; Сарханги, Реза (ред.). Труды мостов 2012: Математика, музыка, искусство, архитектура, культура . С. 103–110 Феникс, Аризона: Тесселлации. Публикация . . . ISBN 978-1-938664-00-7 .
^ Ганн, Чарльз (23 августа 2018 г.). "Суданская группа Möbius" . Vimeo . Получено 2022-03-17 .
^ Франзони, Грегорио (2012). «Бутылка Klein: вариации на тему» . Уведомления об американском математическом обществе . 59 (8): 1076–1082. doi : 10.1090/noti880 . Мистер 2985809 .
^ Хуггетт, Стивен; Джордан, Дэвид (2009). Топологический аперитиф (пересмотренный изд.). Springr-Publisher. п. 57. ISBN 978-1-84800-912-7 Полем MR 2483686 .
^ Falan, Erica (2016). Узлы, молекулы и вселенная: введение в топологию . Провиденс, Род -Айленд: Американское математическое общество. С. 99–100. doi : 10.1090/mbk/096 . ISBN 978-1-4704-2535-7 Полем MR 3443369 .
^ Ричесон, Дэвид С. (2008). Драгоценный камень Эйлера: формула многогранника и рождение топологии . Принстон, Нью -Джерси: издательство Принстонского университета. п. 171 . ISBN 978-0-691-12677-7 Полем MR 2440945 .
^ Подпрыгнуть до: ^а ^{беременный} Годиньо, Леонор; Натарио, Хосе (2014). Введение в геометрию римана: с применениями к механике и относительности . Universitext. Springer, Cham. С. 152–153. doi : 10.1007/978-3-319-08666-8 . ISBN 978-3-319-08665-1 Полем MR 3289090 .
^ Кантвелл, Джон; Конлон, Лоуренс (2015). «Гиперболическая геометрия и гомотопические гомеоморфизмы поверхностей». Geometriae Dedicata . 177 : 27–42. Arxiv : 1305.1379 . doi : 10.1007/s10711-014-9975-1 . MR 3370020 . S2CID 119640200 .
^ Стиллвелл, Джон (1992). «4.6 Классификация изометрии». Геометрия поверхностей . Universitext. Чам: Спрингер. С. 96–98. doi : 10.1007/978-1-4612-0929-4 . ISBN 0-387-97743-0 Полем MR 1171453 .
^ Подпрыгнуть до: ^а ^{беременный} Сейферт, Герберт ; Therelfall, William (1980). Учебник топологии . Чистая и прикладная математика. Тол. 89. Перевод Goldman, Michael A. New York & London: Academic Press. п. 12. ISBN 0-12-634850-2 Полем MR 0575168 .
^ Лопес, Франциско Дж.; Мартин, Франциско (1997). «Полные неориентированные минимальные поверхности с самой высокой группой симметрии». Американский журнал математики . 119 (1): 55–81. doi : 10.1353/ajm.1997.0004 . MR 1428058 . S2CID 121366986 .
^ Микс, Уильям Х. III (1981). "Классификация полных минимальных поверхностей в $\mathbb {R} ^{3}$ с полной кривизны, превышающей, чем $-8\pi$ ". Математический журнал герцога . 48 (3): 523–535. DOI : 10.1215/S0012-7094-81-04829-8 . MR 0630583 .
^ Пески, Адриана I .; Гольдштейн, Рэймонд Э .; Александр, Гарет П.; Моффат, Х. Кит (2015). «Нестабильность минимальной поверхности Möbius Strip и связь с систолической геометрией» (PDF) . Письма о физическом обзоре . 114 (12): 127801. Bibcode : 2015phrvl.114l7801p . doi : 10.1103/physrevlett.114.127801 . MR 3447638 . PMID 25860771 .
^ Мира, Пабло (2006). "Полный минимальный мобиус полоски в $\mathbb {R} ^{n}$ и проблема Björling ». Журнал геометрии и физики . 56 (9): 1506–1515. Bibcode : 2006jgp .... 56.1506m . DOI : 10.1016/j.geomphys.2005.08.001 . MR 2240407 .
^ Паркер, Филип Э. (1993). "Пространства гостезика " В Deleego, L. (ed.). Geanaato, 1992) . Aptacies Mat. Нотатас Исследование. Тол. 8. Soc. Матт Мексика, мексико. стр. 67–79. MR 1304924 . Архивировано из оригинальности 2016-03-1 2022-03-2 {{cite book}}: CS1 Maint: Bot: исходный статус URL неизвестен ( ссылка )
^ Бикель, Холгер (1999). «Двойственность в стабильных плоскостях и связанных с ними закрытия и операций ядра». Журнал геометрии . 64 (1–2): 8–15. doi : 10.1007/bf01229209 . Мистер 1675956 . S2CID 122209943 .
^ Мангахас, Джоанна (июль 2017 г.). «Офисный час пятый: пинг-понг лемма». В глине, Мэтт; Маргалит, Дэн (ред.). Рабочее время с геометрическим теоретиком группы . ПРИЗНАЯ УНИВЕРСИТЕТА ПРИСЕТА. С. 85–105. doi : 10.1515/9781400885398 . ISBN 9781400885398 Полем См. В частности, проект 7, с. 104–105.
^ Ана Ирен; Seade, Хосе (2007). Классическая геометрия Базель: Birkhäuser Verlag. стр. 83–88, 157–163. ISBN 978-3-7643-7517-1 Полем MR 2305055 .
^ Fomenko, Anatolij T . ; Kunii, Tosiyasu L. (2013). Топологическое моделирование для визуализации . Спрингер. п. 269. ISBN 9784431669562 .
^ Ишам, Крис Дж. (1999). Современная дифференциальная геометрия для физиков . Всемирные научные лекции заметки в физике. Тол. 61 (2 -е изд.). Мировой научный. п. 269. ISBN 981-02-3555-0 Полем Мистер 1698234 .
^ Gorbatsevich, VV; Оннишхик, Ал; Винберг, è. Б. (1993). Ложи группы и алгебры Lie I: основы теории лжи; Группы трансформации лжи . Энциклопедия математических наук. Тол. 20. Springer-Verlag, Берлин. С. 164–166. doi : 10.1007/978-3-642-57999-8 . ISBN 3-540-18697-2 Полем MR 1306737 .
^ Ямаширо, Ацуши; Shimoi, Юкихиро; Харигая, Кикуо; Wakabayashi, Katsunori (2004). «Новые электронные состояния в графенских лентах: компетентные заказы на спин и заряд» » Физика e 22 (1–3): 688–6 Arxiv : cond-mat/ 0309636 Bibcode : 2004 Phye ... 22..688y Doi : 10.1016/ j.physe.2003.12.1 17102453S2CID
^ Рзепа, Генри С. (сентябрь 2005 г.). «Ароматичность и делокализация Мёбиуса». Химические обзоры . 105 (10): 3697–3715. doi : 10.1021/cr030092l . PMID 16218564 .
^ Юн, Зин Сок; Осука, Атсухиро; Ким, Донхо (май 2009 г.). «Ароматичность и антиаромальность Möbius в расширенных порфиринах». Природная химия . 1 (2): 113–122. Bibcode : 2009natch ... 1..113y . doi : 10.1038/nchem.172 . PMID 21378823 .
^ «Создание резисторов с математикой» . Время . Тол. 84, нет. 13. 25 сентября 1964 года.
^ Pickover (2005) , стр. 45–46.
^ Понд, JM (2000). «Мобиус двойные резонаторы и полосы фильтров». IEEE транзакции по микроволновой теории и методам . 48 (12): 2465–2471. Bibcode : 2000itmtt..48.2465p . doi : 10.1109/22.898999 .
^ Rohde, Ulrich L.; Поддар, Аджай; Сундарараджан, Д. (ноябрь 2013). «Печатные резонаторы: теория и приложения Метбиуса» (PDF) . Микроволновый журнал . 56 (11).
^ Бауэр, Томас; Банзер, Питер; Карими, Эбрагим; Орлов, Сержж; Рубано, Андреа; Marrucci, Lorenzo; Сантамато, Энрико; Бойд, Роберт В.; Leuchs, GERD (февраль 2015 г.). «Наблюдение за оптической поляризацией полос Möbius». Наука . 347 (6225): 964–966. Bibcode : 2015sci ... 347..964b . doi : 10.1126/science.1260635 . PMID 25636796 . S2CID 206562350 .
^ Сфера, Хуан Карлос; Индурайн, Стивен 1994). «Полоса Мобиуса и парадокс социального выбора» Экономические письма 45 (3): 407–412. doi : 10.1016/0165-1765 (94) 045-0
^ Easdown, Martin (2012). Поездки парка развлечений . Bloomsbury Publishing. п. 43. ISBN 9781782001522 .
^ Хук, Патрик (2019). Билет на поездку: основное руководство по величайшим в мире американским гостям и аттракционов . Книги Чартвелла. п. 20. ISBN 9780785835776 .
^ Tobler, Waldo R. (1961). «Карта мира на полосе Мёбиуса» . Ссылка и картирование . 21 : 486.
^ Камлер, Марк П .; Tobler, Waldo R. (январь 1991 г.). «Три карты мира на полосе Мобиуса». Картография и географические информационные системы . 18 (4): 275–276. doi : 10.1559/152304091783786781 .
^ Курант, Ричард (1940). «Эксперименты с мыльной пленкой с минимальными поверхностями». Американский математический ежемесячный . 47 (3): 167–174. doi : 10.1080/00029890.1940.11990957 . JSTOR 2304225 . MR 0001622 .
^ Гольдштейн, Рэймонд Э .; Моффат, Х. Кит ; Пески, Адриана I .; Рикка, Ренцо Л. (декабрь 2010 г.). «Мыльная пленка Möbius Strip меняет топологию с изюминкой синтулярности» . Труды Национальной академии наук . 107 (51): 21979–21984. BIBCODE : 2010PNAS..10721979G . doi : 10.1073/pnas.1015997107 . PMC 3009808 .
^ Walba, David M.; Ричардс, Родни М.; Haltiwanger, R. Curtis (июнь 1982 г.). «Полный синтез первой молекулярной полосы Мобиуса». Журнал Американского химического общества . 104 (11): 3219–3221. doi : 10.1021/ja00375a051 .
^ Pickover (2005) , стр. 52–58.
^ Гитиг, Диана (18 октября 2010 г.). «Химические оригами, используемые для создания полосы ДНК Мёбиуса» . Ars Technica . Получено 2022-03-28 .
^ Подпрыгнуть до: ^а ^{беременный} Эммер, Мишель (весна 1980). «Визуальное искусство и математика: группа Moebius» . Леонардо . 13 (2): 108–111. doi : 10.2307/1577979 . JSTOR 1577979 . S2CID 123908555 .
^ Байерс, Марк (2018). Чарльз Олсон и американский модернизм: практика себя . Издательство Оксфордского университета. С. 77–78. ISBN 9780198813255 .
^ Crato, Nuno (2010). «Эшер и Мёбиус Стрип». Выяснить это: развлекательные встречи с повседневной математикой . Спрингер. С. 123–126. doi : 10.1007/978-3-642-04833-3_29 .
^ Керстен, Эрик (13 марта 2017 г.). "Мёбий Стрип I" . Эшер во дворце . Получено 2022-04-17 .
^ Подпрыгнуть до: ^а ^{беременный} Пикер (2005) , с. 13
^ Брехер, Кеннет (2017). «Искусство бесконечности» . В Сварте, Дэвид; Séquin, Carlo H.; Фенивеси, Кристоф (ред.). Труды мостов 2017: математика, искусство, музыка, архитектура, образование, культура . Феникс, Аризона: Tessellations Publishing. С. 153–158. ISBN 978-1-938664-22-9 .
^ Подпрыгнуть до: ^а ^{беременный} Петерсон, Иварс (2002). «Топология утилизации» . Математические походы: от сюрреалистических чисел до волшебных кругов . MAA Spectrum. Математическая ассоциация Америки, Вашингтон, округ Колумбия. С. 31–35. ISBN 0-88385-537-2 Полем Мистер 1874198 .
^ «Выбранный символ Expo '74» . Пресс-секретарь . 12 марта 1972 г. с. 1
^ Миллвард, Стивен (30 апреля 2012 г.). "Google Drive скопировал свой значок из китайского приложения?" Полем Технология в Азии . Получено 2022-03-27 -через Yahoo! Новости.
^ "Impa Symbol" . Для тех, кто является поклонником Impa, десять курьезов в отношении института . Имп. 7 мая 2020 года . Получено 2022-03-27 .
^ Pickover (2005) , стр. 156–157.
^ Декер, Хайнц; Старк, Эберхард (1983). «Мёбиус связки: ... и, конечно же, также на марках». Практика математики . 25 (7): 207–215. MR 0720681 .
^ Thulaseedas, Jolly; Krawzyk, Robert J. (2003). "Концепции Мёбиуса в архитектуре " в Баралло, Хавьер; Фридман, Натаниэль; Мальдод, Хуан Антонио; Mart \ Iz-Aroza, Хосе; Сарханги, Реза; Séquin, Carlo (Eds.). с Альгамброй, Исама-мосты. Встреча Граната, Испания: Университет Гранады. Стр. 353–3 ISBN 84-930669-1-5 .
^ Séquin, Carlo H. (январь 2018 г.). "Мобиус мосты" Искусство и искусство 12 (2–3): 181–1 doi : 10.1080/ 17513472.2017.141933 S2CID 216116708 .
^ Уэйнрайт, Оливер (17 октября 2017 г.). « Норман сказал, что президент хочет пирамиду»: как строили звездочки » . Хранитель .
^ Мурет, Дон (17 мая 2010 г.). «Зал славы NASCAR» выглядит быстро сидя на месте » . Спортивный бизнес -журнал .
^ Гопник, Блейк (17 октября 2014 г.). «Педро Рейес делает бесконечное место для любви» . Artnet News .
^ Томас, Нэнси Дж. (4 октября 1998 г.). «Сделать Мобиуса вопросом математики» . The Times (Трентон) . п. AA3 - через Newsbank .
^ Пашман, Дэн (6 августа 2015 г.). «Разрежьте бублик по -математически правильный путь» . Соль . ЭНЕРГЕТИЧЕСКИЙ ЯДЕРНЫЙ РЕАКТОР.
^ Миллер, Росс (5 сентября 2014 г.). «Как сделать математическую полосу бекона» . Грава .
^ Чанг, Кеннет (9 января 2012 г.). «Паста выпускники от алфавитного супа до продвинутой геометрии» . New York Times .
^ Pickover (2005) , стр. 174–177.
^ Pickover (2005) , стр. 179–187.
^ Подпрыгнуть до: ^а ^{беременный} Филлипс, Тони (25 ноября 2016 г.). «Бах и музыкальная полоса Мёбиуса» . Плюс журнал . Перепечатано из колонки Американского математического общества.
^ Московиц, Клара (6 мая 2008 г.). «Музыка сводится к красивой математике» . Живая наука . Получено 2022-03-21 .
^ Tymoczko, Dmitri (7 июля 2006 г.). «Геометрия музыкальных аккордов» (PDF) . Наука . 313 (5783): 72–4. Bibcode : 2006sci ... 313 ... 72t . doi : 10.1126/science.1126287 . JSTOR 3846592 . PMID 16825563 . S2CID 2877171 .
^ Паркс, Эндрю (30 августа 2007 г.). "Mobius Band: Friendly Fire" . Магнит .
^ Лоусон, Дом (9 февраля 2021 г.). "Кольцо Ван Мёбиус" . Прогик
^ Prevos, Peter (2018). Полоса Мёбиуса в магии: трактат на афганских группах . Кенгуру квартира: третье полушарие.
^ Гарднер, Мартин (1956). "Афганские группы" . Математика, магия и тайна . Нью -Йорк: Dover Books. С. 70–73.

Внешние ссылки

СМИ, связанные с Moebius Strip в Wikimedia Commons
Вейсштейн, Эрик У. "Мёбиус Стрип" . MathWorld .

[2] Произносится США : / M Oʊ / B I S , MAY M - Eɪ MOH , -BEE- - AS -BEE Великобритания : / ˈ M ɜː B I ə s / ; ^{[ 1 ]} Немецкий: [ˈmøːbi̯ʊs] . Как обычное дело для слов, содержащих умлаут , это также часто пишет Mobius или Moebius .

[10] По сути, этот пример, но для бутылки Кляйна, а не полоска Мёбиуса, приведен Блэттом (1982) . ^{[ 8 ]}

[30] Длина полосы может быть измерена на его центральной линии или путем разрезания полученной полосы Möbius перпендикулярно его границе, так что она образует прямоугольник

[35] Плоскомолетная полоса Möbius, образованная из трех равносторонних треугольников, не поступает из абстрактного упрощенного комплекса , потому что все три треугольника имеют одни и те же три вершины, в то время как абстрактные упрощенные комплексы требуют, чтобы каждый треугольник имел различный набор вершин.

[44] Это кусочно -планарное и цилиндрическое встроение имеет плавности класс $C^{2}$ , и может быть точно точно аппроксимировано бесконечно дифференцируемым (класс $C^{\infty }$ ) внедрения. ^{[ 39 ]}

[49] 12/7 является самым простым рациональным числом в диапазоне соотношений сторон, между 1,695 и 1,73, для которого существование плавного встраивания неизвестно.

[52] Эти поверхности имеют класс плавности $C^{1}$ Полем Для более мелкозернистого анализа предположений о плавности, которые заставляют внедрять внедрение, по сравнению с допущениями, при которых теорема Нэш-Куйпер допускает произвольно гибкие встраивания, см. Замечания Bartels & Hornung (2015) , с. 116, после теоремы 2.2. ^{[ 39 ]}

[124] Мёбийские полосы также использовались для анализа многих других канонов Бахом и другими, но в большинстве из этих случаев другие петлевые поверхности, такие как цилиндр, могли использоваться одинаково хорошо. ^{[ 116 ]}

[1] Уэллс, Джон С. (2008). Лонгман Словарь произношения (3 -е изд.). Лонгман. ISBN 978-1-4058-8118-0 .

[pickover-3] Пиковер, Клиффорд А. (2005). Полоса Мёбиуса: изумительная группа доктора Августа Мёбиуса по математике, играм, литературе, искусству, технологиям и космологии . Громовой жим. С. 28–29. ISBN 978-1-56025-826-1 .

[roman-4] Подпрыгнуть до: ^а ^{беременный} ^в ^{дюймовый} Ларисон, Лорейн Л. (1973). «Группа Möbius в римской мозаике». Американский ученый . 61 (5): 544–547. Bibcode : 1973AMSCI..61..544L . JSTOR 27843983 .

[ancient-5] Подпрыгнуть до: ^а ^{беременный} ^в Картрайт, июль он ; Гонсалес, Диего Л. (2016). «Мёбий полоски перед Мёбиусом: топологические намеки в древних представлениях». Математический интеллект . 38 (2): 69–76. Arxiv : 1609.07779 . BIBCODE : 2016ARXIV160907779C . doi : 10.1007/s00283-016-9631-8 . MR 3507121 . S2CID 119587191 .

[chirality-6] Falan, Erica (2000). Когда топология встречается с химией: топологический взгляд на молекулярную хиральность . Перспективы. Вашингтон, округ Колумбия: Математическая ассоциация Америки. С. 82–83 . doi : 10.1017/cbo9780511626272 . ISBN 0-521-66254-0 Полем Мистер 1781912 .

[FOOTNOTEPickover20058–9-7] Подпрыгнуть до: ^а ^{беременный} ^в Pickoker (2005) , стр. 8–9.

[woll-8] Волл, Джон В. младший (весна 1971). «Односторонние поверхности и ориентировочность». Двухлетний журнал по математике колледжа . 2 (1): 5–18. doi : 10.2307/3026946 . JSTOR 3026946 .

[blackett-9] Блэкетт, Дональд В. (1982). Элементарная топология: комбинаторный и алгебраический подход . Академическая пресса. п. 195. ISBN 9781483262536 .

[frolkina-11] Frolkina, Olga D. (2018). «Пара разбивает группы Мобиуса в космосе». Журнал теории узлов и его последствий . 27 (9): 1842005, 9. Arxiv : 2212.02983 . doi : 10.1142/s0218216518420051 . MR 3848635 . S2CID 126421578 .

[defy-12] Лэмб, Эвелин (20 февраля 2019 г.). «Мёбиус полосы бросают вызов связи с бесконечностью» . Quanta Magazine .

[melikhov-13] Мелихов, Сергей А. (2019). «Примечание о бумаге О. Фолкина« Пара не пересекает группы Мобиуса в космосе » . Журнал теории узлов и его последствий . 28 (7): 1971001, 3. Arxiv : 1810.04089 . doi : 10.1142/s0218216519710019 . MR 3975576 . S2CID 119179202 .

[FOOTNOTEPickover200552-14] Пиковер (2005) , с. 52

[FOOTNOTEPickover200512-15] Пиковер (2005) , с. 12

[kyle-16] Кайл, RH (1955). «Встроения групп Möbius в трехмерном пространстве». Труды Королевской ирландской академии, раздел а . 57 : 131–136. JSTOR 20488581 . MR 0091480 .

[FOOTNOTEPickover200511-17] Пиковер (2005) , с. 11

[massey-18] Massey, William S. (1991). Основной курс по алгебраической топологии . Выпускники текстов по математике. Тол. 127. Нью-Йорк: Springer-Verlag. п. 49. ISBN 0-387-97430-X Полем MR 1095046 .

[rouseball-19] Rouse Ball, WW (1892). «Парадромные кольца». Математические воссоздания и проблемы прошлого и настоящего времени (2 -е изд.). Лондон и Нью -Йорк: Macmillan и Co. С. 53–54. ISBN 9780608377803 .

[paradromic-20] Беннетт, GT (июнь 1923 г.). «Парадромные кольца» . Природа . 111 (2800): 882. Bibcode : 1923nater.111r.882b . doi : 10.1038/111882b0 . S2CID 4099647 .

[tietze-21] Подпрыгнуть до: ^а ^{беременный} Титце, Генрих (1910). «Некоторые комментарии по вопросу окрашивания карт на одной областях» (PDF) . Годовой отчет немецкой математической ассоциации . 19 : 155–159.

[ringel-youngs-22] Рингель, Г .; Янг, JWT (1968). «Решение проблемы расцвета карты Heawood» . Труды Национальной академии наук Соединенных Штатов Америки . 60 (2): 438–445. Bibcode : 1968pnas ... 60..438r . doi : 10.1073/pnas.60.2.438 . MR 0228378 . PMC 225066 . PMID 16591648 .

[jab-rad-saz-23] Джаблан, Славик; Радович, Лжильджана; Sazdanović, Radmila (2011). «Непланарные графики, полученные из кодов виртуальных узлов и ссылок Гаусса». Журнал математической химии . 49 (10): 2250–2267. doi : 10.1007/S10910-011-9884-6 . MR 2846715 . S2CID 121332704 .

[larsen-24] Ларсен, Могенс Эсром (1994). «Непонимание моих лабиринтов может сделать меня несчастным». В парне Ричард К . ; Вудроу, Роберт Э. (ред.). Материалы Мемориальной конференции Eugène Strens по рекреационной математике и ее истории, состоявшейся в Университете Калгари, Калгари, Альберта, август 1986 года . MAA Spectrum. Вашингтон, округ Колумбия: Математическая ассоциация Америки. С. 289–293. ISBN 0-88385-516-х Полем MR 1303141 . Полем См. Рисунок 7, с. 292

[maschke-25] Машке, Генрих (1900). «Примечание на односторонней поверхности Мобиуса» . Труды Американского математического общества . 1 (1): 39. doi : 10.2307/1986401 . JSTOR 1986401 . MR 1500522 .

[parameterization-26] Junghenn, Hugo D. (2015). Курс в реальном анализе . Бока Ратон, Флорида: CRC Press. п. 430. ISBN 978-1-4822-1927-2 Полем MR 3309241 .

[split-tori-27] Séquin, Carlo H. (2005). «Разделение Тори, узлов и групп Мобиуса» . В Сарханги, Реза; Муди, Роберт В. (ред.). Ренессанс Банф: математика, музыка, искусство, культура . Юго -западный колледж, Уинфилд, Канзас: Конференция Бриджес. С. 211–218. ISBN 0-9665201-6-5 .

[francis-28] Подпрыгнуть до: ^а ^{беременный} Фрэнсис, Джордж К. (1987). "Plücker Conoid". Топологическая книжка с картинками . Springer-Verlag, Нью-Йорк. С. 81–83. ISBN 0-387-96426-6 Полем MR 0880519 .

[dooner-seirig-29] Дунер, Дэвид Б.; Сейрег, Али (1995). «3.4.2 Цилиндроид» . Кинематическая геометрия передачи: одновременный инженерный подход . Серия Wiley в области дизайна. Тол. 3. Джон Вили и сыновья. С. 135–137. ISBN 9780471045977 .

[barr-31] Подпрыгнуть до: ^а ^{беременный} Барр, Стивен (1964). Эксперименты в топологии . Нью -Йорк: Компания Томаса Й. Кроуэлл. С. 40–49, 200–201. ISBN 9780690278620 .

[fuchs-tabachnikov-32] Подпрыгнуть до: ^а ^{беременный} ^в ^{дюймовый} ^и Фукс, Дмитрий ; Табачников, Серж (2007). «Лекция 14: Paper Möbius Band». Математический омнибус: тридцать лекций по классической математике (PDF) . Провиденс, Род -Айленд: Американское математическое общество. С. 199–206. doi : 10.1090/mbk/046 . ISBN 978-0-8218-4316-1 Полем Мистер 2350979 . Архивировано из оригинала (PDF) 2016-04-24.

[pook-33] Пук, Лес (2003). «4.2: Trihexaflexagon Revisited» . Flexagons наизнанку . Кембридж, Великобритания: издательство Кембриджского университета. С. 33–36. doi : 10.1017/cbo9780511543302 . ISBN 0-521-81970-9 Полем MR 2008500 .

[9vertex-34] Подпрыгнуть до: ^а ^{беременный} Kühnel, W.; Banchoff, TF (1983). «9-вертексная проективная плоскость» (PDF) . Математический интеллект . 5 (3): 11–22. doi : 10.1007/bf03026567 . MR 0737686 . S2CID 120926324 .

[kuiper-36] Kuiper, Nicolaas H. (1972). «Тяжелые топологические встраивания группы Moebius» . Журнал дифференциальной геометрии . 6 (3): 271–283. doi : 10.4310/jdg/1214430493 . MR 0314057 .

[szilassi-37] Szilassi, Lajos (2008). «Полигранная модель в евклидовом 3-пространстве карты шестикратного продюса проективной плоскости» . Дискретная и вычислительная геометрия . 40 (3): 395–400. doi : 10.1007/s00454-007-9033-y . MR 2443291 . S2CID 38606607 .

[tuckerman-38] Такерман, Брайант (1948). «Непочечная многогранная группа Мёбиуса, граница которой-треугольник». Американский математический ежемесячный . 55 (5): 309–311. doi : 10.2307/2305482 . JSTOR 2305482 . MR 0024138 .

[bon-nak-39] Боннингтон, С. Пол; Nakamoto, Atsuhiro (2008). «Геометрическая реализация триангуляции на проективной плоскости с удаленным лицом» . Дискретная и вычислительная геометрия . 40 (1): 141–157. doi : 10.1007/s00454-007-9035-9 . MR 2429652 . S2CID 10887519 .

[brehm-40] Брем, Ульрих (1983). «Неполихедральная триангулированная Метбиус Стрип». Труды Американского математического общества . 89 (3): 519–522. doi : 10.2307/2045508 . JSTOR 2045508 . MR 0715878 .

[nak-tsu-41] Накамото, Атсухиро; Цучия, Шоичи (2012). «О геометрически реализуемых триангуляциях Мёбия» . Дискретная математика . 312 (14): 2135–2139. doi : 10.1016/j.disc.2011.06.007 . MR 2921579 .

[sadowsky-translation-42] Подпрыгнуть до: ^а ^{беременный} Хинц, Денис Ф.; Фрид, Элиот (2015). «Перевод статьи Майкла Садоуского» элементарное доказательство существования развивающейся группы Möbius и приписывание геометрической проблемы к вариационной проблеме » . Журнал эластичности . 119 (1–2): 3–6. Arxiv : 1408.3034 . doi : 10.1007/s10659-014-9490-5 . MR 3326180 . S2CID 119733903 . Перепечатано в Фосдик, Роджер; Фрид, Элиот (2016). Механика лент и полос Möbius (PDF) . Спрингер, Дордрехт. С. 3–6. doi : 10.1007/978-94-017-7300-3 . ISBN 978-94-017-7299-0 Полем MR 3381564 .

[bartels-hornung-43] Подпрыгнуть до: ^а ^{беременный} ^в ^{дюймовый} Bartels, Sören; Хорнунг, Питер (2015). «Изгибающая бумага и полоска Мёбиуса». Журнал эластичности . 119 (1–2): 113–136. doi : 10.1007/s10659-014-9501-6 . MR 3326187 . S2CID 119782792 . Перепечатано в Fosdick & Fried (2016) , с. 113–136. См. В частности, раздел 5.2, с. 129–130.

[starostin-vdh-45] Подпрыгнуть до: ^а ^{беременный} Starostin, El; Ван дер Хейджен, GHM (2015). «Равновесные формы с локализацией стресса для нестабильной эластичной Мёбиуса и других полос» . Журнал эластичности . 119 (1–2): 67–112. doi : 10.1007/s10659-014-9495-0 . MR 3326186 . S2CID 53462568 . Перепечатано в Fosdick & Fried (2016) , с. 67–112.

[darkside-46] Schwarz, Gideon E. (1990). «Темная сторона полосы Мобиуса». Американский математический ежемесячный . 97 (10): 890–897. doi : 10.1080/00029890.1990.11995680 . JSTOR 2324325 . MR 1079975 .

[halpern-weaver-47] Подпрыгнуть до: ^а ^{беременный} Halpern, B.; Weaver, C. (1977). «Инвертирование цилиндра через изометрические погружения и изометрические встраивания» . Труды Американского математического общества . 230 : 41–70. doi : 10.2307/1997711 . JSTOR 1997711 . MR 0474388 .

[schwartz-48] Подпрыгнуть до: ^а ^{беременный} Шварц, Ричард Эван (2021). «Улучшенная граница на оптимальной бумаге Band Moebius». Geometriae Dedicata . 215 : 255–267. Arxiv : 2008.11610 . doi : 10.1007/s10711-021-00648-5 . MR 4330341 . S2CID 220279013 .

[optimal-50] Шварц, Ричард (2023). «Оптимальная бумага Moebius Band». arxiv : 2308.12641 [ math.mg ].

[crowell-51] Кроуэлл, Рэйчел (12 сентября 2023 г.). «Математики решают 50-летнюю головоломку Метбиуса» . Scientific American .

[dundas-53] Подпрыгнуть до: ^а ^{беременный} Dundas, Bjørn Ian (2018). «Пример 5.1.3: неограниченная группа Möbius». Короткий курс по дифференциальной топологии . Кембриджские математические учебники. Издательство Кембриджского университета, Кембридж. п. https://books.google.com/books?id=7a1edwaaqbaj&pg=pa101 . doi : 10.1017/9781108349130 . ISBN 978-1-108-42579-7 Полем MR 3793640 . S2CID 125997451 .

[blanusa-54] Блануша, Данило (1954). «Изометрическое погружение бесконечно широкой евклидовой группы Möbius в сферическом, параболическом или гиперболическом пространстве с четырьмя измерениями». Международный бюллетень Югославской академии наук и изобразительных искусств . 12 : 19–23. MR 0071060 .

[wunderlich-55] Wunderlich, W. (1962). «О ручной мебельной группе». Ежемесячные буклеты для математики . 66 (3): 276–289. Doi : 10.1007/bf01299052 . MR 0143115 . S2CID 122215321 .

[schwarz-56] Schwarz, Gideon (1990). «Претендент к названию« Каноническая моубиусская полоса » . Тихоокеанский журнал по математике . 143 (1): 195–200. doi : 10.2140/pjm.1990.143.195 . MR 1047406 .

[hilbert-cohn-vossen-57] Хилберт, Дэвид ; COHN-VOSSEN, Стефан (1952). Геометрия и воображение (2 -е изд.). Челси. С. 315–316. ISBN 978-0-8284-1087-8 .

[spivak-58] Спивак, Майкл (1979). Комплексное введение в дифференциальную геометрию, том I (2 -е изд.). Уилмингтон, штат Делавэр: публикуйте или погибнет. п. 591.

[ddg-59] Подпрыгнуть до: ^а ^{беременный} ^в Knöppel, Felix (лето 2019). «Учебное пособие 3: Минимальные поверхности Лоусона и суданская группа Möbius» . DDG2019: курс визуализации в Ту Берлин .

[lawson-60] Подпрыгнуть до: ^а ^{беременный} Лоусон, Х. Блейн -младший (1970). "Полные минимальные поверхности в $S^{3}$ ". математики . Вторая серия. 92 (3): 335–374 : 10.2307 1970625 . JSTOR 1970625 . DOI . / Анналы $\tau _{1,2}$ .

[schleimer-segerman-61] Подпрыгнуть до: ^а ^{беременный} Шлеймер, Саул; Сегерман, Генри (2012). «Скульптуры в $с 3$ " В Босхе, Роберт; МакКенна, Дуглас; Сарханги, Реза (ред.). Труды мостов 2012: Математика, музыка, искусство, архитектура, культура . С. 103–110 Феникс, Аризона: Тесселлации. Публикация . . . ISBN 978-1-938664-00-7 .

[sudanese-62] Ганн, Чарльз (23 августа 2018 г.). "Суданская группа Möbius" . Vimeo . Получено 2022-03-17 .

[franzoni-63] Франзони, Грегорио (2012). «Бутылка Klein: вариации на тему» . Уведомления об американском математическом обществе . 59 (8): 1076–1082. doi : 10.1090/noti880 . Мистер 2985809 .

[huggett-jordan-64] Хуггетт, Стивен; Джордан, Дэвид (2009). Топологический аперитиф (пересмотренный изд.). Springr-Publisher. п. 57. ISBN 978-1-84800-912-7 Полем MR 2483686 .

[flapan-65] Falan, Erica (2016). Узлы, молекулы и вселенная: введение в топологию . Провиденс, Род -Айленд: Американское математическое общество. С. 99–100. doi : 10.1090/mbk/096 . ISBN 978-1-4704-2535-7 Полем MR 3443369 .

[richeson-66] Ричесон, Дэвид С. (2008). Драгоценный камень Эйлера: формула многогранника и рождение топологии . Принстон, Нью -Джерси: издательство Принстонского университета. п. 171 . ISBN 978-0-691-12677-7 Полем MR 2440945 .

[godinho-natario-67] Подпрыгнуть до: ^а ^{беременный} Годиньо, Леонор; Натарио, Хосе (2014). Введение в геометрию римана: с применениями к механике и относительности . Universitext. Springer, Cham. С. 152–153. doi : 10.1007/978-3-319-08666-8 . ISBN 978-3-319-08665-1 Полем MR 3289090 .

[cantwell-conlon-68] Кантвелл, Джон; Конлон, Лоуренс (2015). «Гиперболическая геометрия и гомотопические гомеоморфизмы поверхностей». Geometriae Dedicata . 177 : 27–42. Arxiv : 1305.1379 . doi : 10.1007/s10711-014-9975-1 . MR 3370020 . S2CID 119640200 .

[stillwell-69] Стиллвелл, Джон (1992). «4.6 Классификация изометрии». Геометрия поверхностей . Universitext. Чам: Спрингер. С. 96–98. doi : 10.1007/978-1-4612-0929-4 . ISBN 0-387-97743-0 Полем MR 1171453 .

[seifert-threlfall-70] Подпрыгнуть до: ^а ^{беременный} Сейферт, Герберт ; Therelfall, William (1980). Учебник топологии . Чистая и прикладная математика. Тол. 89. Перевод Goldman, Michael A. New York & London: Academic Press. п. 12. ISBN 0-12-634850-2 Полем MR 0575168 .

[lopez-martin-71] Лопес, Франциско Дж.; Мартин, Франциско (1997). «Полные неориентированные минимальные поверхности с самой высокой группой симметрии». Американский журнал математики . 119 (1): 55–81. doi : 10.1353/ajm.1997.0004 . MR 1428058 . S2CID 121366986 .

[meeks-72] Микс, Уильям Х. III (1981). "Классификация полных минимальных поверхностей в $\mathbb {R} ^{3}$ с полной кривизны, превышающей, чем $-8\pi$ ". Математический журнал герцога . 48 (3): 523–535. DOI : 10.1215/S0012-7094-81-04829-8 . MR 0630583 .

[systolic-73] Пески, Адриана I .; Гольдштейн, Рэймонд Э .; Александр, Гарет П.; Моффат, Х. Кит (2015). «Нестабильность минимальной поверхности Möbius Strip и связь с систолической геометрией» (PDF) . Письма о физическом обзоре . 114 (12): 127801. Bibcode : 2015phrvl.114l7801p . doi : 10.1103/physrevlett.114.127801 . MR 3447638 . PMID 25860771 .

[bjorling-74] Мира, Пабло (2006). "Полный минимальный мобиус полоски в $\mathbb {R} ^{n}$ и проблема Björling ». Журнал геометрии и физики . 56 (9): 1506–1515. Bibcode : 2006jgp .... 56.1506m . DOI : 10.1016/j.geomphys.2005.08.001 . MR 2240407 .

[parker-75] Паркер, Филип Э. (1993). "Пространства гостезика " В Deleego, L. (ed.). Geanaato, 1992) . Aptacies Mat. Нотатас Исследование. Тол. 8. Soc. Матт Мексика, мексико. стр. 67–79. MR 1304924 . Архивировано из оригинальности 2016-03-1 2022-03-2 {{cite book}}: CS1 Maint: Bot: исходный статус URL неизвестен ( ссылка )

[bickel-76] Бикель, Холгер (1999). «Двойственность в стабильных плоскостях и связанных с ними закрытия и операций ядра». Журнал геометрии . 64 (1–2): 8–15. doi : 10.1007/bf01229209 . Мистер 1675956 . S2CID 122209943 .

[mangahas-77] Мангахас, Джоанна (июль 2017 г.). «Офисный час пятый: пинг-понг лемма». В глине, Мэтт; Маргалит, Дэн (ред.). Рабочее время с геометрическим теоретиком группы . ПРИЗНАЯ УНИВЕРСИТЕТА ПРИСЕТА. С. 85–105. doi : 10.1515/9781400885398 . ISBN 9781400885398 Полем См. В частности, проект 7, с. 104–105.

[ramirez-seade-78] Ана Ирен; Seade, Хосе (2007). Классическая геометрия Базель: Birkhäuser Verlag. стр. 83–88, 157–163. ISBN 978-3-7643-7517-1 Полем MR 2305055 .

[fomenko-kunii-79] Fomenko, Anatolij T . ; Kunii, Tosiyasu L. (2013). Топологическое моделирование для визуализации . Спрингер. п. 269. ISBN 9784431669562 .

[isham-80] Ишам, Крис Дж. (1999). Современная дифференциальная геометрия для физиков . Всемирные научные лекции заметки в физике. Тол. 61 (2 -е изд.). Мировой научный. п. 269. ISBN 981-02-3555-0 Полем Мистер 1698234 .

[gor-oni-vin-81] Gorbatsevich, VV; Оннишхик, Ал; Винберг, è. Б. (1993). Ложи группы и алгебры Lie I: основы теории лжи; Группы трансформации лжи . Энциклопедия математических наук. Тол. 20. Springer-Verlag, Берлин. С. 164–166. doi : 10.1007/978-3-642-57999-8 . ISBN 3-540-18697-2 Полем MR 1306737 .

[graphene-82] Ямаширо, Ацуши; Shimoi, Юкихиро; Харигая, Кикуо; Wakabayashi, Katsunori (2004). «Новые электронные состояния в графенских лентах: компетентные заказы на спин и заряд» » Физика e 22 (1–3): 688–6 Arxiv : cond-mat/ 0309636 Bibcode : 2004 Phye ... 22..688y Doi : 10.1016/ j.physe.2003.12.1 17102453S2CID

[aromaticity1-83] Рзепа, Генри С. (сентябрь 2005 г.). «Ароматичность и делокализация Мёбиуса». Химические обзоры . 105 (10): 3697–3715. doi : 10.1021/cr030092l . PMID 16218564 .

[aromaticity2-84] Юн, Зин Сок; Осука, Атсухиро; Ким, Донхо (май 2009 г.). «Ароматичность и антиаромальность Möbius в расширенных порфиринах». Природная химия . 1 (2): 113–122. Bibcode : 2009natch ... 1..113y . doi : 10.1038/nchem.172 . PMID 21378823 .

[resistor-85] «Создание резисторов с математикой» . Время . Тол. 84, нет. 13. 25 сентября 1964 года.

[FOOTNOTEPickover200545–46-86] Pickover (2005) , стр. 45–46.

[resonator-87] Понд, JM (2000). «Мобиус двойные резонаторы и полосы фильтров». IEEE транзакции по микроволновой теории и методам . 48 (12): 2465–2471. Bibcode : 2000itmtt..48.2465p . doi : 10.1109/22.898999 .

[resonator2-88] Rohde, Ulrich L.; Поддар, Аджай; Сундарараджан, Д. (ноябрь 2013). «Печатные резонаторы: теория и приложения Метбиуса» (PDF) . Микроволновый журнал . 56 (11).

[polarization-89] Бауэр, Томас; Банзер, Питер; Карими, Эбрагим; Орлов, Сержж; Рубано, Андреа; Marrucci, Lorenzo; Сантамато, Энрико; Бойд, Роберт В.; Leuchs, GERD (февраль 2015 г.). «Наблюдение за оптической поляризацией полос Möbius». Наука . 347 (6225): 964–966. Bibcode : 2015sci ... 347..964b . doi : 10.1126/science.1260635 . PMID 25636796 . S2CID 206562350 .

[can-ind-90] Сфера, Хуан Карлос; Индурайн, Стивен 1994). «Полоса Мобиуса и парадокс социального выбора» Экономические письма 45 (3): 407–412. doi : 10.1016/0165-1765 (94) 045-0

[coaster1-91] Easdown, Martin (2012). Поездки парка развлечений . Bloomsbury Publishing. п. 43. ISBN 9781782001522 .

[coaster2-92] Хук, Патрик (2019). Билет на поездку: основное руководство по величайшим в мире американским гостям и аттракционов . Книги Чартвелла. п. 20. ISBN 9780785835776 .

[maps1-93] Tobler, Waldo R. (1961). «Карта мира на полосе Мёбиуса» . Ссылка и картирование . 21 : 486.

[maps2-94] Камлер, Марк П .; Tobler, Waldo R. (январь 1991 г.). «Три карты мира на полосе Мобиуса». Картография и географические информационные системы . 18 (4): 275–276. doi : 10.1559/152304091783786781 .

[courant-95] Курант, Ричард (1940). «Эксперименты с мыльной пленкой с минимальными поверхностями». Американский математический ежемесячный . 47 (3): 167–174. doi : 10.1080/00029890.1940.11990957 . JSTOR 2304225 . MR 0001622 .

[soap-96] Гольдштейн, Рэймонд Э .; Моффат, Х. Кит ; Пески, Адриана I .; Рикка, Ренцо Л. (декабрь 2010 г.). «Мыльная пленка Möbius Strip меняет топологию с изюминкой синтулярности» . Труды Национальной академии наук . 107 (51): 21979–21984. BIBCODE : 2010PNAS..10721979G . doi : 10.1073/pnas.1015997107 . PMC 3009808 .

[synthesis-97] Walba, David M.; Ричардс, Родни М.; Haltiwanger, R. Curtis (июнь 1982 г.). «Полный синтез первой молекулярной полосы Мобиуса». Журнал Американского химического общества . 104 (11): 3219–3221. doi : 10.1021/ja00375a051 .

[FOOTNOTEPickover200552–58-98] Pickover (2005) , стр. 52–58.

[dna-99] Гитиг, Диана (18 октября 2010 г.). «Химические оригами, используемые для создания полосы ДНК Мёбиуса» . Ars Technica . Получено 2022-03-28 .

[emmer-100] Подпрыгнуть до: ^а ^{беременный} Эммер, Мишель (весна 1980). «Визуальное искусство и математика: группа Moebius» . Леонардо . 13 (2): 108–111. doi : 10.2307/1577979 . JSTOR 1577979 . S2CID 123908555 .

[olson-101] Байерс, Марк (2018). Чарльз Олсон и американский модернизм: практика себя . Издательство Оксфордского университета. С. 77–78. ISBN 9780198813255 .

[escher1-102] Crato, Nuno (2010). «Эшер и Мёбиус Стрип». Выяснить это: развлекательные встречи с повседневной математикой . Спрингер. С. 123–126. doi : 10.1007/978-3-642-04833-3_29 .

[escher2-103] Керстен, Эрик (13 марта 2017 г.). "Мёбий Стрип I" . Эшер во дворце . Получено 2022-04-17 .

[FOOTNOTEPickover200513-104] Подпрыгнуть до: ^а ^{беременный} Пикер (2005) , с. 13

[brecher-105] Брехер, Кеннет (2017). «Искусство бесконечности» . В Сварте, Дэвид; Séquin, Carlo H.; Фенивеси, Кристоф (ред.). Труды мостов 2017: математика, искусство, музыка, архитектура, образование, культура . Феникс, Аризона: Tessellations Publishing. С. 153–158. ISBN 978-1-938664-22-9 .

[peterson-106] Подпрыгнуть до: ^а ^{беременный} Петерсон, Иварс (2002). «Топология утилизации» . Математические походы: от сюрреалистических чисел до волшебных кругов . MAA Spectrum. Математическая ассоциация Америки, Вашингтон, округ Колумбия. С. 31–35. ISBN 0-88385-537-2 Полем Мистер 1874198 .

[expo74-107] «Выбранный символ Expo '74» . Пресс-секретарь . 12 марта 1972 г. с. 1

[gdrive-108] Миллвард, Стивен (30 апреля 2012 г.). "Google Drive скопировал свой значок из китайского приложения?" Полем Технология в Азии . Получено 2022-03-27 -через Yahoo! Новости.

[impa-109] "Impa Symbol" . Для тех, кто является поклонником Impa, десять курьезов в отношении института . Имп. 7 мая 2020 года . Получено 2022-03-27 .

[FOOTNOTEPickover2005156–157-110] Pickover (2005) , стр. 156–157.

[briefmarken-111] Декер, Хайнц; Старк, Эберхард (1983). «Мёбиус связки: ... и, конечно же, также на марках». Практика математики . 25 (7): 207–215. MR 0720681 .

[architecture-112] Thulaseedas, Jolly; Krawzyk, Robert J. (2003). "Концепции Мёбиуса в архитектуре " в Баралло, Хавьер; Фридман, Натаниэль; Мальдод, Хуан Антонио; Mart \ Iz-Aroza, Хосе; Сарханги, Реза; Séquin, Carlo (Eds.). с Альгамброй, Исама-мосты. Встреча Граната, Испания: Университет Гранады. Стр. 353–3 ISBN 84-930669-1-5 .

[bridges-113] Séquin, Carlo H. (январь 2018 г.). "Мобиус мосты" Искусство и искусство 12 (2–3): 181–1 doi : 10.1080/ 17513472.2017.141933 S2CID 216116708 .

[kazakh-114] Уэйнрайт, Оливер (17 октября 2017 г.). « Норман сказал, что президент хочет пирамиду»: как строили звездочки » . Хранитель .

[nascar-115] Мурет, Дон (17 мая 2010 г.). «Зал славы NASCAR» выглядит быстро сидя на месте » . Спортивный бизнес -журнал .

[reyes-116] Гопник, Блейк (17 октября 2014 г.). «Педро Рейес делает бесконечное место для любви» . Artnet News .

[zimmermann-117] Томас, Нэнси Дж. (4 октября 1998 г.). «Сделать Мобиуса вопросом математики» . The Times (Трентон) . п. AA3 - через Newsbank .

[bagel-118] Пашман, Дэн (6 августа 2015 г.). «Разрежьте бублик по -математически правильный путь» . Соль . ЭНЕРГЕТИЧЕСКИЙ ЯДЕРНЫЙ РЕАКТОР.

[bacon-119] Миллер, Росс (5 сентября 2014 г.). «Как сделать математическую полосу бекона» . Грава .

[pasta-120] Чанг, Кеннет (9 января 2012 г.). «Паста выпускники от алфавитного супа до продвинутой геометрии» . New York Times .

[FOOTNOTEPickover2005174–177-121] Pickover (2005) , стр. 174–177.

[FOOTNOTEPickover2005179–187-122] Pickover (2005) , стр. 179–187.

[phillips-123] Подпрыгнуть до: ^а ^{беременный} Филлипс, Тони (25 ноября 2016 г.). «Бах и музыкальная полоса Мёбиуса» . Плюс журнал . Перепечатано из колонки Американского математического общества.

[music-125] Московиц, Клара (6 мая 2008 г.). «Музыка сводится к красивой математике» . Живая наука . Получено 2022-03-21 .

[chords-126] Tymoczko, Dmitri (7 июля 2006 г.). «Геометрия музыкальных аккордов» (PDF) . Наука . 313 (5783): 72–4. Bibcode : 2006sci ... 313 ... 72t . doi : 10.1126/science.1126287 . JSTOR 3846592 . PMID 16825563 . S2CID 2877171 .

[bandband-127] Паркс, Эндрю (30 августа 2007 г.). "Mobius Band: Friendly Fire" . Магнит .

[ringvan-128] Лоусон, Дом (9 февраля 2021 г.). "Кольцо Ван Мёбиус" . Прогик

[magic-129] Prevos, Peter (2018). Полоса Мёбиуса в магии: трактат на афганских группах . Кенгуру квартира: третье полушарие.

[gardner-130] Гарднер, Мартин (1956). "Афганские группы" . Математика, магия и тайна . Нью -Йорк: Dover Books. С. 70–73.

[ А ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ B ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

[ 26 ]

[ 27 ]

[ C ]

[ 28 ]

[ 29 ]

[ 30 ]

[ 31 ]

[ D ]

[ 32 ]

[ 33 ]

[ 34 ]

[ 35 ]

[ 36 ]

[ 37 ]

[ 38 ]

[ E ]

[ 39 ]

[ 40 ]

[ 41 ]

[ 42 ]

[ 43 ]

[ f ]

[ 44 ]

[ 45 ]

[ G ]

[ 46 ]

[ 47 ]

[ 48 ]

[ 49 ]

[ 50 ]

[ 51 ]

[ 52 ]

[ 53 ]

[ 54 ]

[ 55 ]

[ 56 ]

[ 57 ]

[ 58 ]

[ 59 ]

[ 60 ]

[ 61 ]

[ 62 ]

[ 63 ]

[ 64 ]

[ 65 ]

[ 66 ]

[ 67 ]

[ 68 ]

[ 69 ]

[ 70 ]

[ 71 ]

[ 72 ]

[ 73 ]

[ 74 ]

[ 75 ]

[ 76 ]

[ 77 ]

[ 78 ]

[ 79 ]

[ 80 ]

[ 81 ]

[ 82 ]

[ 83 ]

[ 84 ]

[ 85 ]

[ 86 ]

[ 87 ]

[ 88 ]

[ 89 ]

[ 90 ]

[ 91 ]

[ 92 ]

[ 93 ]

[ 94 ]

[ 95 ]

v Т и Математика складывания бумаги
Flat folding	Big-little-big lemma Crease pattern Huzita–Hatori axioms Kawasaki's theorem Maekawa's theorem Map folding Napkin folding problem Pureland origami Yoshizawa–Randlett system
Strip folding	Dragon curve Flexagon Möbius strip Regular paperfolding sequence
3d structures	Miura fold Modular origami Paper bag problem Rigid origami Schwarz lantern Sonobe Yoshimura buckling
Polyhedra	Alexandrov's uniqueness theorem Flexible polyhedron (Bricard octahedron, Steffen's polyhedron) Net Blooming Common net Source unfolding Star unfolding
Miscellaneous	Fold-and-cut theorem Lill's method
Publications	Geometric Exercises in Paper Folding Geometric Folding Algorithms Geometric Origami A History of Folding in Mathematics Origami Polyhedra Design Origamics
People	Roger C. Alperin Margherita Piazzola Beloch Yan Chen Robert Connelly Erik Demaine Martin Demaine Rona Gurkewitz David A. Huffman Tom Hull Kôdi Husimi Humiaki Huzita Toshikazu Kawasaki Robert J. Lang Anna Lubiw Jun Maekawa Kōryō Miura Joseph O'Rourke Tomohiro Tachi Eve Torrence