Переписка AdS/CFT
| Теория струн |
|---|
 |
| Фундаментальные объекты |
| Пертурбативная теория |
|
| Непертурбативные результаты |
| Феноменология |
| Математика |
В теоретической физике соответствие антиде Ситтера/конформной теории поля (часто сокращенно AdS/CFT) представляет собой предполагаемую связь между двумя видами физических теорий. С одной стороны — антидеситтеровские пространства (AdS), которые используются в теориях квантовой гравитации , сформулированных в терминах теории струн или М-теории . По другую сторону соответствия находятся конформные теории поля (КТП), которые являются квантовыми теориями поля , включая теории, подобные теориям Янга-Миллса , которые описывают элементарные частицы.
Дуальность представляет собой крупный прогресс в понимании теории струн и квантовой гравитации. [1] Это потому, что она обеспечивает непертурбативную формулировку теории струн с определенными граничными условиями и потому, что это наиболее успешная реализация голографического принципа , идеи в квантовой гравитации, первоначально предложенной Джерардом 'т Хоофтом и продвигаемой Леонардом Зюскиндом .
Он также предоставляет мощный инструментарий для изучения сильно связанных квантовых теорий поля. [2] Большая часть полезности дуальности проистекает из того факта, что это дуальность сильная-слабая: когда поля квантовой теории поля сильно взаимодействуют, поля гравитационной теории взаимодействуют слабо и, следовательно, более математически понятны. Этот факт использовался для изучения многих аспектов физики ядра и конденсированного состояния путем перевода проблем по этим предметам в более математически решаемые задачи теории струн.
Соответствие AdS/CFT было впервые предложено Хуаном Малдасеной в конце 1997 года. [3] Важные аспекты переписки вскоре были подробно описаны в двух статьях: одна Стивена Губсера , Игоря Клебанова и Александра Полякова , а другая Эдварда Виттена . К 2015 году статья Малдасены имела более 10 000 цитирований, став самой цитируемой статьей в области физики высоких энергий . [4]
Одним из наиболее ярких примеров соответствия AdS/CFT было соответствие AdS5/CFT4: связь между N = 4 суперсимметричной теорией Янга – Миллса в измерениях 3+1 и теорией суперструн типа IIB на AdS 5 × S. 5 . [5]
Фон
[ редактировать ]Квантовая гравитация и струны
[ редактировать ]Современное понимание гравитации основано на Альберта Эйнштейна общей теории относительности . [6] Сформулированная в 1915 году общая теория относительности объясняет гравитацию с точки зрения геометрии пространства и времени, или пространства-времени . Она сформулирована на языке классической физики. [7] который был разработан такими физиками, как Исаак Ньютон и Джеймс Клерк Максвелл . Остальные негравитационные силы объясняются в рамках квантовой механики . Квантовая механика, разработанная в первой половине двадцатого века рядом различных физиков, предлагает радикально иной способ описания физических явлений, основанный на вероятности. [8]
Квантовая гравитация — это раздел физики, который пытается описать гравитацию, используя принципы квантовой механики. В настоящее время популярным подходом к квантовой гравитации является теория струн . [9] которая моделирует элементарные частицы не как нульмерные точки, а как одномерные объекты, называемые струнами . В переписке AdS/CFT обычно рассматриваются теории квантовой гравитации, полученные из теории струн или ее современного расширения, М-теории . [10]
В повседневной жизни есть три привычных измерения пространства (вверх/вниз, влево/вправо и вперед/назад) и одно измерение времени. Таким образом, на языке современной физики говорят, что пространство-время четырехмерно. [11] Одной из особенностей теории струн и М-теории является то, что эти теории требуют дополнительных измерений пространства-времени для своей математической непротиворечивости: в теории струн пространство-время десятимерно, а в М-теории — одиннадцатимерно. [12] Теории квантовой гравитации, возникающие в соответствии AdS/CFT, обычно получаются из теории струн и М-теории с помощью процесса, известного как компактификация . Это порождает теорию, в которой пространство-время фактически имеет меньшее количество измерений, а дополнительные измерения «свернуты» в круги. [13]
Стандартная аналогия компактификации — рассмотреть многомерный объект, например садовый шланг. Если смотреть на шланг с достаточного расстояния, кажется, что он имеет только одно измерение — длину, но, приближаясь к шлангу, обнаруживаешь, что он содержит второе измерение — его окружность. Таким образом, муравей, ползающий внутри него, будет двигаться в двух измерениях. [14]
Квантовая теория поля
[ редактировать ]Применение квантовой механики к физическим объектам, таким как электромагнитное поле , которые простираются в пространстве и времени, известно как квантовая теория поля . [15] В физике элементарных частиц квантовые теории поля составляют основу нашего понимания элементарных частиц, которые моделируются как возбуждения в фундаментальных полях. Квантовые теории поля также используются в физике конденсированного состояния для моделирования частицоподобных объектов, называемых квазичастицами . [16]
В переписке AdS/CFT, помимо теории квантовой гравитации, рассматривается определенный вид квантовой теории поля, называемый конформной теорией поля . Это особенно симметричный и математически хорошо продуманный тип квантовой теории поля. [17] Такие теории часто изучаются в контексте теории струн, где они связаны с поверхностью , охваченной струной, распространяющейся в пространстве-времени, и в статистической механике , где они моделируют системы в термодинамической критической точке . [18]
Обзор переписки
[ редактировать ]
Геометрия антидеситтеровского пространства
[ редактировать ]В переписке AdS/CFT теория струн или М-теория рассматривается на фоне анти-де Ситтера . Это означает, что геометрия пространства-времени описывается в терминах некоего вакуумного решения уравнения Эйнштейна, называемого антиде-ситтеровским пространством . [19]
Проще говоря, антидеситтеровское пространство — это математическая модель пространства-времени, в которой понятие расстояния между точками (метрика ) отличается от понятия расстояния в обычной евклидовой геометрии . Оно тесно связано с гиперболическим пространством , которое можно рассматривать как диск , как показано справа. [20] На этом изображении показано мозаика диска треугольниками и квадратами. Расстояние между точками этого диска можно определить так, чтобы все треугольники и квадраты были одинакового размера, а внешняя граница круга находилась бесконечно далеко от любой точки внутри. [21]
Теперь представьте себе стопку гиперболических дисков, каждый из которых представляет состояние Вселенной в данный момент времени. Полученный геометрический объект представляет собой трехмерное антидеситтеровское пространство. [20] Он выглядит как сплошной цилиндр , у которого любое сечение является копией гиперболического диска. На этой картинке время течет по вертикали. Поверхность этого цилиндра играет важную роль в соответствии AdS/CFT. Как и в случае с гиперболической плоскостью, антидеситтеровское пространство искривлено таким образом, что любая точка внутри него фактически находится бесконечно далеко от этой граничной поверхности. [22]

Эта конструкция описывает гипотетическую вселенную только с двумя пространственными и одним временным измерениями, но ее можно обобщить на любое количество измерений. Действительно, гиперболическое пространство может иметь более двух измерений, и можно «складывать» копии гиперболического пространства, чтобы получить многомерные модели антидеситтеровского пространства. [20]
Идея AdS/CFT
[ редактировать ]Важной особенностью антидеситтеровского пространства является его граница (которая в случае трехмерного антидеситтеровского пространства выглядит как цилиндр). Одним из свойств этой границы является то, что локально вокруг любой точки она выглядит точно так же, как пространство Минковского — модель пространства-времени, используемая в негравитационной физике. [23]
Поэтому можно рассмотреть вспомогательную теорию, в которой «пространство-время» задается границей антидеситтеровского пространства. Это наблюдение является отправной точкой для соответствия AdS/CFT, в котором говорится, что границу антидеситтеровского пространства можно рассматривать как «пространство-время» для конформной теории поля. Утверждается, что эта конформная теория поля эквивалентна теории гравитации в объемном антидеситтеровском пространстве в том смысле, что существует «словарь» для перевода вычислений в одной теории в вычисления в другой. Каждая сущность в одной теории имеет аналог в другой теории. Например, отдельная частица в теории гравитации может соответствовать некоторому набору частиц в теории границ. Кроме того, предсказания двух теорий количественно идентичны: если две частицы имеют 40-процентную вероятность столкновения в теории гравитации, то соответствующие совокупности в теории границ также будут иметь 40-процентную вероятность столкновения. [24]

Обратите внимание, что граница антидеситтеровского пространства имеет меньше измерений, чем само антидеситтеровское пространство. Например, в трехмерном примере, показанном выше, граница представляет собой двумерную поверхность. Соответствие AdS/CFT часто описывается как «голографическая двойственность», поскольку эти отношения между двумя теориями аналогичны отношениям между трехмерным объектом и его изображением в виде голограммы . [25] Хотя голограмма двумерна, она кодирует информацию обо всех трех измерениях объекта, который она представляет. Точно так же теории, связанные соответствием AdS/CFT, считаются абсолютно эквивалентными, несмотря на то, что они существуют в разном количестве измерений. Конформная теория поля подобна голограмме, которая фиксирует информацию о многомерной квантовой теории гравитации. [21]
Примеры переписки
[ редактировать ]Следуя открытиям Малдасены в 1997 году, теоретики обнаружили множество различных реализаций соответствия AdS/CFT. Они связывают различные конформные теории поля с компактификациями теории струн и М-теории в различном числе измерений. Используемые теории, как правило, не являются жизнеспособными моделями реального мира, но у них есть определенные особенности, такие как содержание частиц или высокая степень симметрии, которые делают их полезными для решения проблем квантовой теории поля и квантовой гравитации. [26]
Самый известный пример соответствия AdS/CFT гласит, что теория струн типа IIB в пространстве продуктов AdS 5 × S 5 эквивалентно N = 4 суперсимметричной теории Янга–Миллса на четырехмерной границе. [27] В этом примере пространство-время, в котором живет теория гравитации, фактически является пятимерным (отсюда и обозначение AdS 5 ), и существует пять дополнительных компактных измерений (закодированных S 5 фактор). В реальном мире пространство-время четырехмерно, по крайней мере, макроскопически, поэтому эта версия соответствия не дает реалистичной модели гравитации. Точно так же дуальная теория не является жизнеспособной моделью какой-либо реальной системы, поскольку она предполагает большое количество суперсимметрии . Тем не менее, как объясняется ниже, эта теория границ имеет некоторые общие черты с квантовой хромодинамикой , фундаментальной теорией сильного взаимодействия . Оно описывает частицы, подобные глюонам квантовой хромодинамики, вместе с некоторыми фермионами . [9] В результате он нашел применение в ядерной физике , в частности при изучении кварк-глюонной плазмы . [28] [29]
Другая реализация соответствия утверждает, что М-теория на AdS 7 × S 4 эквивалентна так называемой (2,0)-теории в шести измерениях. [3] В этом примере пространство-время теории гравитации фактически семимерно. Существование (2,0)-теории, возникающей по одну сторону двойственности, предсказывает классификация суперконформных теорий поля . Она до сих пор плохо понята, поскольку представляет собой квантовомеханическую теорию без классического предела . [30] Несмотря на присущие трудности изучения этой теории, она считается интересным объектом по ряду причин, как физических, так и математических. [31]
Еще одна реализация соответствия утверждает, что М-теория на AdS 4 × S 7 эквивалентна суперконформной теории поля ABJM в трех измерениях. [32] Здесь теория гравитации имеет четыре некомпактных измерения, поэтому эта версия соответствия дает несколько более реалистичное описание гравитации. [33]
Приложения к квантовой гравитации
[ редактировать ]Непертурбативная формулировка теории струн
[ редактировать ]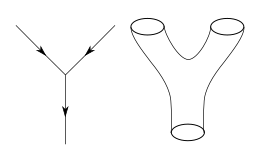
В квантовой теории поля обычно вычисляются вероятности различных физических событий, используя методы теории возмущений . Пертурбативная квантовая теория поля, разработанная Ричардом Фейнманом и другими в первой половине двадцатого века, использует специальные диаграммы, называемые диаграммами Фейнмана для организации вычислений . Думается, что эти диаграммы изображают пути точечных частиц и их взаимодействия. [34] Хотя этот формализм чрезвычайно полезен для предсказаний, эти предсказания возможны только тогда, когда сила взаимодействий, константа связи , достаточно мала, чтобы надежно описать теорию как близкую к теории без взаимодействий . [35]
Отправной точкой теории струн является идея о том, что точечные частицы квантовой теории поля также можно моделировать как одномерные объекты, называемые струнами. Взаимодействие струн проще всего определить путем обобщения теории возмущений, используемой в обычной квантовой теории поля. На уровне диаграмм Фейнмана это означает замену одномерной диаграммы, изображающей путь точечной частицы, двумерной поверхностью, изображающей движение струны. В отличие от квантовой теории поля, теория струн пока не имеет полного непертурбативного определения, поэтому многие теоретические вопросы, на которые физики хотели бы ответить, остаются вне досягаемости. [36]
Проблема разработки непертурбативной формулировки теории струн была одной из первоначальных мотиваций для изучения соответствия AdS/CFT. [37] Как объяснялось выше, переписка дает несколько примеров квантовых теорий поля, которые эквивалентны теории струн в антидеситтеровском пространстве. Альтернативно можно рассматривать это соответствие как определение теории струн в особом случае, когда гравитационное поле является асимптотически анти-де Ситтером (то есть, когда гравитационное поле напоминает поле анти-де Ситтера на пространственной бесконечности). Физически интересные величины в теории струн определяются в терминах величин дуальной квантовой теории поля. [21]
Информационный парадокс черной дыры
[ редактировать ]В 1975 году Стивен Хокинг опубликовал расчет, который предположил, что черные дыры не являются полностью черными, а испускают тусклое излучение из-за квантовых эффектов вблизи горизонта событий . [38] Поначалу результат Хокинга представлял проблему для теоретиков, поскольку предполагал, что черные дыры уничтожают информацию. Точнее, расчет Хокинга, казалось, противоречил одному из основных постулатов квантовой механики , который утверждает, что физические системы развиваются во времени согласно уравнению Шредингера . Это свойство обычно называют унитарностью временной эволюции. Очевидное противоречие между расчетами Хокинга и постулатом унитарности квантовой механики стало известно как информационный парадокс черной дыры . [39]
Соответствие AdS/CFT разрешает информационный парадокс черной дыры, по крайней мере в некоторой степени, поскольку оно показывает, как черная дыра может развиваться в соответствии с квантовой механикой в некоторых контекстах. Действительно, можно рассматривать черные дыры в контексте соответствия AdS/CFT, и любая такая черная дыра соответствует конфигурации частиц на границе антидеситтеровского пространства. [40] Эти частицы подчиняются обычным правилам квантовой механики и, в частности, развиваются унитарным образом, поэтому черная дыра также должна развиваться унитарным образом, соблюдая принципы квантовой механики. [41] В 2005 году Хокинг объявил, что парадокс был решен в пользу сохранения информации посредством переписки AdS/CFT, и предложил конкретный механизм, с помощью которого черные дыры могут сохранять информацию. [42]
Приложения к квантовой теории поля
[ редактировать ]Ядерная физика
[ редактировать ]Одной из физических систем , которая изучалась с использованием соответствия AdS/CFT, является кварк-глюонная плазма, экзотическое состояние материи, создаваемое в ускорителях частиц . Это состояние вещества возникает на короткие мгновения, когда тяжелые ионы, такие как золота или свинца, ядра сталкиваются при высоких энергиях. Такие столкновения заставляют кварки , составляющие атомные ядра, разграничиваться при температурах примерно два триллиона Кельвинов , условиях, аналогичных тем, которые существуют при температуре около 10 градусов. −11 секунд после Большого взрыва . [43]
Физика кварк-глюонной плазмы определяется квантовой хромодинамикой, но эта теория математически неразрешима в задачах, связанных с кварк-глюонной плазмой. [44] В статье, появившейся в 2005 году, Дам Тхань Сон и его сотрудники показали, что соответствие AdS/CFT можно использовать для понимания некоторых аспектов кварк-глюонной плазмы, описывая ее на языке теории струн. [28] [29] Применяя соответствие AdS/CFT, Сан и его коллеги смогли описать кварк-глюонную плазму в терминах черных дыр в пятимерном пространстве-времени. Расчет показал, что соотношение двух величин, связанных с кварк-глюонной плазмой, сдвиговой вязкости η и объемной плотности энтропии s , должно быть примерно равно некоторой универсальной константе :
где ħ обозначает приведенную постоянную Планка , а k — постоянную Больцмана . [45] [29] Кроме того, авторы предположили, что эта универсальная константа дает нижнюю оценку η / s в большом классе систем. В эксперименте, проведенном на релятивистском коллайдере тяжелых ионов в Брукхейвенской национальной лаборатории , экспериментальный результат в одной модели был близок к этой универсальной константе, но в другой модели это было не так. [46]
Еще одним важным свойством кварк-глюонной плазмы является то, что кварки очень высоких энергий, движущиеся через плазму, останавливаются или «гасятся» после прохождения всего лишь нескольких фемтометров . Это явление характеризуется числом называемым параметром тушения струи , которое связывает потерю энергии такого кварка с квадратом расстояния, пройденного через плазму. Расчеты на основе соответствия AdS/CFT дают оценочную величину ≈ 4 ГэВ. 2 /fm , а экспериментальное значение лежит в диапазоне 5–15 ГэВ. 2 /фм . [45]
Физика конденсированного состояния
[ редактировать ]
За десятилетия физики- экспериментаторы конденсированного состояния открыли ряд экзотических состояний материи, включая сверхпроводники и сверхтекучие жидкости . Эти состояния описываются с использованием формализма квантовой теории поля, но некоторые явления трудно объяснить с помощью стандартных методов теории поля. Некоторые теоретики конденсированного состояния, в том числе Субир Сачдев, надеются, что соответствие AdS/CFT позволит описать эти системы на языке теории струн и узнать больше об их поведении. [28]
К настоящему времени достигнуты определенные успехи в использовании методов теории струн для описания перехода сверхтекучей жидкости в изолятор . Сверхтекучая жидкость — это система электрически нейтральных атомов , которая течет без всякого трения . Такие системы часто производятся в лаборатории с использованием жидкого гелия , но в последнее время [ когда? ] Экспериментаторы разработали новые способы создания искусственных сверхтекучих жидкостей путем заливки триллионов холодных атомов в решетку перекрещивающихся лазеров . Эти атомы изначально ведут себя как сверхтекучие, но по мере того, как экспериментаторы увеличивают интенсивность лазеров, они становятся менее подвижными, а затем внезапно переходят в изолирующее состояние. Во время перехода атомы ведут себя необычным образом. Например, атомы замедляются до остановки со скоростью, которая зависит от температуры и постоянной Планка, фундаментального параметра квантовой механики, который не входит в описание других фаз . Это поведение недавно было понято путем рассмотрения двойного описания, в котором свойства жидкости описываются в терминах черной дыры более высокого измерения. [48]
Критика
[ редактировать ]Поскольку многие физики обращаются к струнным методам для решения проблем ядерной физики и физики конденсированного состояния, некоторые теоретики, работающие в этих областях, выразили сомнения относительно того, может ли соответствие AdS/CFT предоставить инструменты, необходимые для реалистичного моделирования систем реального мира. В своем выступлении на конференции Quark Matter в 2006 году [49] Американский физик Ларри Маклерран отметил, что теория супер Янга – Миллса N = 4 , которая появляется в соответствии AdS/CFT, существенно отличается от квантовой хромодинамики, что затрудняет применение этих методов к ядерной физике. По словам Маклеррана,
N = 4 суперсимметричный Янга – Миллса не является КХД ... Он не имеет масштаба масс и конформно инвариантен. Он не имеет ограничения и постоянной константы связи. Он суперсимметричен. Он не имеет нарушения киральной симметрии или образования массы. В присоединенном представлении он имеет шесть скаляров и фермионов... Возможно, удастся исправить некоторые или все вышеперечисленные проблемы, или, для различных физических проблем, некоторые возражения могут оказаться неактуальными. Пока еще не существует ни консенсуса, ни убедительных аргументов в пользу предполагаемых исправлений или явлений, которые гарантировали бы, что суперсимметричные результаты Янга Миллса N = 4 будут надежно отражать КХД. [49]
В письме в журнал Physics Today нобелевский лауреат Филип Андерсон выразил аналогичные опасения по поводу применения AdS/CFT в физике конденсированного состояния, заявив, что
В качестве очень общей проблемы подхода AdS/CFT в теории конденсированного состояния мы можем указать на эти характерные инициалы «CFT» — конформную теорию поля. Проблемы конденсированного состояния, вообще говоря, не являются ни релятивистскими, ни конформными. Вблизи квантовой критической точки и время, и пространство могут масштабироваться, но даже там у нас все еще есть предпочтительная система координат и, обычно, решетка. Есть некоторые свидетельства существования других фаз с линейной Т-фазой слева от странного металла, о которых они могут размышлять, но опять же в этом случае проблема конденсированного состояния переопределена экспериментальными фактами. [50]
История и развитие
[ редактировать ]
Теория струн и ядерная физика
[ редактировать ]Открытие соответствия AdS/CFT в конце 1997 года стало кульминацией долгой истории попыток связать теорию струн с ядерной физикой. [51] Фактически, теория струн была первоначально разработана в конце 1960-х и начале 1970-х годов как теория адронов , субатомных частиц, таких как протон и нейтрон , которые удерживаются вместе сильными ядерными силами . Идея заключалась в том, что каждую из этих частиц можно рассматривать как отдельный режим колебаний струны. В конце 1960-х годов экспериментаторы обнаружили, что адроны делятся на семейства, называемые траекториями Редже, с квадратом энергии, пропорциональным угловому моменту , а теоретики показали, что эта связь естественным образом возникает из физики вращающейся релятивистской струны. [52]
С другой стороны, попытки смоделировать адроны как струны столкнулись с серьезными проблемами. Одна из проблем заключалась в том, что теория струн включает безмассовую частицу со спином 2, тогда как в физике адронов такая частица не встречается. [51] Такая частица будет передавать силу со свойствами гравитации. В 1974 году Джоэл Шерк и Джон Шварц предположили, что теория струн, таким образом, является не теорией ядерной физики, как думали многие теоретики, а теорией квантовой гравитации. [53] В то же время стало понятно, что адроны на самом деле состоят из кварков, и от подхода теории струн отказались в пользу квантовой хромодинамики. [51]
В квантовой хромодинамике кварки обладают своего рода зарядом , который бывает трех разновидностей, называемых цветами . В статье 1974 года Джерард 'т Хоофт изучал взаимосвязь между теорией струн и ядерной физикой с другой точки зрения, рассматривая теории, подобные квантовой хромодинамике, где количество цветов равно некоторому произвольному числу N , а не трем. В этой статье 'т Хофт рассмотрел некий предел, при котором N стремится к бесконечности, и утверждал, что в этом пределе некоторые вычисления в квантовой теории поля напоминают вычисления в теории струн. [54]
Черные дыры и голография
[ редактировать ]
В 1975 году Стивен Хокинг опубликовал расчет, который показал, что черные дыры не являются полностью черными, а испускают тусклое излучение из-за квантовых эффектов вблизи горизонта событий. [38] Эта работа расширила предыдущие результаты Джейкоба Бекенштейна , который предположил, что черные дыры имеют четко определенную энтропию. [55] Поначалу казалось, что результат Хокинга противоречит одному из основных постулатов квантовой механики, а именно унитарности эволюции во времени. Интуитивно постулат унитарности говорит о том, что квантово-механические системы не уничтожают информацию при переходе из одного состояния в другое. По этой причине кажущееся противоречие стало известно как информационный парадокс черной дыры. [56]

Позже, в 1993 году, Джерард 'т Хоофт написал спекулятивную статью о квантовой гравитации, в которой он вновь обратился к работе Хокинга по термодинамике черной дыры , заключив, что общее число степеней свободы в области пространства-времени, окружающей черную дыру, пропорционально поверхности . область горизонта. [57] Эта идея была выдвинута Леонардом Зюскиндом и теперь известна как голографический принцип . [58] Голографический принцип и его реализация в теории струн посредством соответствия AdS/CFT помогли пролить свет на тайны черных дыр, предложенные в работе Хокинга, и, как полагают, обеспечивают разрешение информационного парадокса черной дыры. [41] В 2004 году Хокинг признал, что черные дыры не нарушают квантовую механику. [59] и он предложил конкретный механизм, с помощью которого они могли бы сохранять информацию. [42]
Статья Малдасены
[ редактировать ]
1 января 1998 года Хуан Малдасена опубликовал знаковую статью, положившую начало изучению AdS/CFT. [3] По словам Александра Марковича Полякова , «работа [Малдасены] открыла шлюзы». [60] Гипотеза сразу же вызвала большой интерес в сообществе теоретиков струн. [41] и рассматривалось в статье Стивена Габсера , Игоря Клебанова и Полякова, [61] и еще одна статья Эдварда Виттена . [62] Эти работы уточнили гипотезу Малдасены и показали, что фигурирующая в переписке конформная теория поля существует на границе антидеситтеровского пространства. [60]
В одном частном случае предложения Малдасены говорится, что N = 4 супертеория Янга – Миллса, калибровочная теория , в некотором смысле похожая на квантовую хромодинамику, эквивалентна теории струн в пятимерном антиде Ситтеровском пространстве. [32] Этот результат помог прояснить более раннюю работу 'т Хофта о взаимосвязи между теорией струн и квантовой хромодинамикой, вернув теорию струн к ее истокам как теории ядерной физики. [52] Результаты Малдасены также обеспечили конкретную реализацию голографического принципа, что имело важные последствия для квантовой гравитации и физики черных дыр. [1] К 2015 году статья Малдасены стала самой цитируемой статьей в области физики высоких энергий с более чем 10 000 цитирований. [4] Эти последующие статьи предоставили значительные доказательства того, что соответствие верно, хотя до сих пор это не было строго доказано . [41] [63]
Обобщения
[ редактировать ]Трехмерная гравитация
[ редактировать ]Чтобы лучше понять квантовые аспекты гравитации в нашей четырехмерной Вселенной, некоторые физики рассмотрели низкомерную математическую модель , в которой пространство-время имеет только два пространственных измерения и одно временное измерение. [64] В этом случае математика, описывающая гравитационное поле, радикально упрощается, и можно изучать квантовую гравитацию, используя знакомые методы квантовой теории поля, устраняя необходимость в теории струн или других более радикальных подходах к квантовой гравитации в четырех измерениях. [65]
Начиная с работы Дж. Дэвида Брауна и Марка Хенно в 1986 г. [66] физики заметили, что квантовая гравитация в трехмерном пространстве-времени тесно связана с двумерной конформной теорией поля. В 1995 году Энно и его коллеги исследовали эту взаимосвязь более подробно, предположив, что трехмерная гравитация в анти-де Ситтеровском пространстве эквивалентна конформной теории поля, известной как теория поля Лиувилля . [67] Другая гипотеза, сформулированная Эдвардом Виттеном, утверждает, что трехмерная гравитация в антидеситтеровском пространстве эквивалентна конформной теории поля с симметрией группы монстров . [68] Эти гипотезы предоставляют примеры соответствия AdS/CFT, которые не требуют полного аппарата струны или М-теории. [69]
переписка dS/CFT
[ редактировать ]В отличие от нашей Вселенной, которая, как теперь известно, расширяется с возрастающей скоростью, пространство антиде Ситтера не расширяется и не сжимается. Вместо этого он всегда выглядит одинаково. [20] Говоря более техническим языком, можно сказать, что пространство антиде Ситтера соответствует Вселенной с отрицательной космологической постоянной , тогда как реальная Вселенная имеет небольшую положительную космологическую постоянную. [70]
Хотя свойства гравитации на малых расстояниях должны быть несколько независимыми от значения космологической постоянной, [71] желательно иметь версию соответствия AdS/CFT для положительной космологической постоянной. В 2001 году Эндрю Строминджер представил версию двойственности, названную соответствием dS/CFT . [72] Эта двойственность включает в себя модель пространства-времени, называемую пространством де Ситтера, с положительной космологической постоянной. Такая двойственность интересна с точки зрения космологии, поскольку многие космологи полагают, что самая ранняя Вселенная была близка к пространству де Ситтера. [20]
Переписка Керра и CFT
[ редактировать ]Хотя соответствие AdS/CFT часто полезно для изучения свойств черных дыр, [73] большинство черных дыр, рассматриваемых в контексте AdS/CFT, физически нереалистичны. Действительно, как объяснялось выше, большинство версий соответствия AdS/CFT включают модели пространства-времени более высокой размерности с нефизической суперсимметрией.
В 2009 году Моника Гуика, Томас Хартман, Вэй Сун и Эндрю Строминджер показали, что идеи AdS/CFT, тем не менее, можно использовать для понимания некоторых астрофизических черных дыр. Точнее, их результаты применимы к черным дырам, которые аппроксимируются экстремальными черными дырами Керра , имеющими максимально возможный угловой момент, совместимый с данной массой. [74] Они показали, что такие черные дыры имеют эквивалентное описание в терминах конформной теории поля. Позднее соответствие Керра/CFT было распространено на черные дыры с меньшим угловым моментом. [75]
Высшие спиновые калибровочные теории
[ редактировать ]Соответствие AdS/CFT тесно связано с другой двойственностью, выдвинутой Игорем Клебановым и Александром Марковичем Поляковым в 2002 году. [76] Эта двойственность утверждает, что некоторые «теории с более высокой спиновой калибровкой» в антидеситтеровском пространстве эквивалентны конформным теориям поля с симметрией O (N) . Здесь теория в объеме представляет собой разновидность калибровочной теории, описывающей частицы сколь угодно высокого спина. Это похоже на теорию струн, где возбужденные моды колеблющихся струн соответствуют частицам с более высоким спином, и это может помочь лучше понять теоретико-струнные версии AdS/CFT и, возможно, даже доказать соответствие. [77] В 2010 году Симоне Джомби и Си Инь получили дополнительные доказательства этой двойственности, вычислив величины, называемые трехточечными функциями . [78]
См. также
[ редактировать ]Примечания
[ редактировать ]- ^ Перейти обратно: а б де Аро и др. 2013 , с. 2
- ^ Клебанов и Малдасена, 2009 г.
- ^ Перейти обратно: а б с Maldacena 1998. Препринт был представлен в 1997 году и опубликован 1 января 1998 года.
- ^ Перейти обратно: а б «Самые цитируемые статьи всех времен (издание 2014 г.)» . INSPIRE-HEP . Архивировано из оригинала 6 сентября 2015 года . Проверено 26 декабря 2015 г.
- ^ Аммон и Эрдменгер, 2015 г.
- ^ Стандартный учебник по общей теории относительности — Wald 1984 .
- ^ Малдасена 2005 , с. 58
- ^ Гриффитс 2004
- ^ Перейти обратно: а б Малдасена 2005 , с. 62.
- ^ См. подраздел § Примеры переписки . Примеры, не связанные с теорией струн или М-теорией, см. в разделе § Обобщения .
- ^ Уолд 1984 , с. 4
- ^ Цвибах 2009 , стр. 8.
- ^ Zwiebach 2009 , стр. 7–8.
- ^ Эта аналогия используется, например, в Greene 2000 , p. 186.
- ^ Стандартный текст — Peskin & Schroeder 1995 .
- ^ Введение в приложения квантовой теории поля к физике конденсированного состояния см. Zee 2010 .
- ^ Конформные теории поля характеризуются своей инвариантностью относительно конформных преобразований .
- ^ Введение в конформную теорию поля с акцентом на ее приложения к теории пертурбативных струн см. в томе II книги Делиня и др. 1999.
- ^ Клебанов и Малдасена 2009 , с. 28.
- ^ Перейти обратно: а б с д и Малдасена 2005 , с. 60.
- ^ Перейти обратно: а б с Малдасена 2005 , с. 61
- ^ Математическая взаимосвязь между внутренней частью и границей антидеситтеровского пространства связана с конструкцией окружающей среды Чарльза Феффермана и Робина Грэма . Подробности см. в Fefferman & Graham 1985 , Fefferman & Graham 2011 .
- ^ Цвибах 2009 , стр. 552.
- ^ Мальдасена 2005 , стр. 61–62.
- ^ Малдасена 2005 , с. 57
- ^ Известные реализации AdS/CFT обычно включают нефизические числа измерений пространства-времени и нефизические суперсимметрии.
- ^ Этот пример является основной темой трех новаторских статей об AdS/CFT: Maldacena 1998 ; Губсер, Клебанов и Поляков 1998 ; и Виттен 1998 .
- ^ Перейти обратно: а б с Они измерили 2011 год , с. 303
- ^ Перейти обратно: а б с Ковтун, Сын и Старинец 2005 г.
- ^ Обзор (2,0)-теории см. в Moore 2012 .
- ^ См. Мур 2012 и Алдай, Гайотто и Тачикава 2010 .
- ^ Перейти обратно: а б Ахарони и др. 2008 год
- ^ Ахарони и др. 2008 г. , с. 1
- ^ Стандартный учебник, знакомящий с формализмом диаграмм Фейнмана, - Peskin & Schroeder 1995 .
- ^ Зи 2010 , с. 43
- ^ Цвибах 2009 , стр. 12.
- ^ Мальдасена 1998 , сек. 6
- ^ Перейти обратно: а б Хокинг 1975 г.
- ^ Доступное введение в информационный парадокс черной дыры и связанный с ним научный спор между Хокингом и Леонардом Сасскиндом см. Susskind 2008 .
- ^ Цвибах 2009 , стр. 554.
- ^ Перейти обратно: а б с д Малдасена 2005 , с. 63
- ^ Перейти обратно: а б Хокинг 2005 г.
- ^ Цвибах 2009 , стр. 559.
- ^ Точнее, нельзя применять методы пертурбативной квантовой теории поля.
- ^ Перейти обратно: а б Цвибах 2009 , стр. 561.
- ^ Лузум и Роматшке 2008 , Часть IV. С
- ^ Измерено в 2011 году.
- ^ Сачдев 2013 , с. 51
- ^ Перейти обратно: а б МакЛерран 2007 г.
- ^ Андерсон 2013
- ^ Перейти обратно: а б с Цвибах 2009 , стр. 525.
- ^ Перейти обратно: а б Ахарони и др. 2008 г. , с. 1.1
- ^ Шерк и Шварц, 1974 г.
- ^ 'т Хофт 1974
- ^ Бекенштейн 1973
- ^ Сасскинд 2008
- ^ 'т Хоофт 1993
- ^ Сасскинд 1995
- ^ Сасскинд 2008 , с. 444
- ^ Перейти обратно: а б Polyakov 2008 , p. 6
- ^ Gubser, Klebanov & Polyakov 1998
- ^ Виттен 1998 г.
- ^ Коуэн 2013
- ^ Обзор см. в Carlip 2003 .
- ^ Согласно результатам Виттена 1988 , трехмерную квантовую гравитацию можно понять, связав ее с теорией Черна-Саймонса .
- ^ Браун и Хенно, 1986 г.
- ^ Куссер, Хенно и ван Дрил, 1995 г.
- ^ Виттен 2007
- ^ Гуика и др. 2009 , с. 1
- ^ Перлмуттер 2003
- ^ Бикард 2005 , с. 33
- ^ Строминджер 2001
- ^ См. подраздел § Информационный парадокс черной дыры .
- ^ Гуика и др. 2009 год
- ^ Кастро, Мэлони и Строминджер, 2010 г.
- ^ Klebanov & Polyakov 2002
- ^ См. введение в книге Клебанов и Поляков, 2002 .
- ^ Джомби и Инь, 2010 г.
Ссылки
[ редактировать ]- Ахарони, Офер; Бергман, Орен; Джафферис, Дэниел Луи; Мальдасена, Хуан (2008). « N = 6 суперконформных теорий Черна – Саймонса-материи, M2-браны и их гравитационные двойники». Журнал физики высоких энергий . 2008 (10): 091. arXiv : 0806.1218 . Бибкод : 2008JHEP...10..091A . дои : 10.1088/1126-6708/2008/10/091 . S2CID 16987793 .
- Ахарони, Офер; Губсер, Стивен; Мальдасена, Хуан; Оогури, Хироси; Оз, Ярон (2000). «Теории больших N-полей, теория струн и гравитация». Физ. Представитель . 323 (3–4): 183–386. arXiv : hep-th/9905111 . Бибкод : 2000PhR...323..183A . дои : 10.1016/S0370-1573(99)00083-6 . S2CID 119101855 .
- Алдай, Луис; Гайотто, Давиде; Тачикава, Юдзи (2010). «Корреляционные функции Лиувилля из четырехмерных калибровочных теорий». Письма по математической физике . 91 (2): 167–197. arXiv : 0906.3219 . Бибкод : 2010LMaPh..91..167A . дои : 10.1007/s11005-010-0369-5 . S2CID 15459761 .
- Аммон, Мартин; Эрдменгер, Йоханна (2015). Калибровочная/гравитационная дуальность: основы и приложения (1-е изд.). Издательство Кембриджского университета. п. 180. ИСБН 978-1-107-01034-5 .
- Андерсон, Филип (2013). «Странные связи со странными металлами» . Физика сегодня . 66 (4): 9. Бибкод : 2013ФТ....66д...9А . дои : 10.1063/PT.3.1929 .
- Бекенштейн, Джейкоб (1973). «Черные дыры и энтропия». Физический обзор D . 7 (8): 2333–2346. Бибкод : 1973PhRvD...7.2333B . дои : 10.1103/PhysRevD.7.2333 . S2CID 122636624 .
- Бикард, Оливье (2005). Соответствие AdS/CFT: метрики Эйнштейна и их конформные границы . Европейское математическое общество. ISBN 978-3-03719-013-5 .
- Браун, Дж. Дэвид; Хенно, Марк (1986). «Центральные заряды в канонической реализации асимптотических симметрий: пример трехмерной гравитации» . Связь в математической физике . 104 (2): 207–226. Бибкод : 1986CMaPh.104..207B . дои : 10.1007/BF01211590 . S2CID 55421933 .
- Карлип, Стивен (2003). Квантовая гравитация в измерениях 2+1 . Кембриджские монографии по математической физике. ISBN 978-0-521-54588-4 .
- Кастро, Алехандра; Мэлони, Александр; Строминджер, Эндрю (2010). «Скрытая конформная симметрия черной дыры Керра». Физический обзор D . 82 (2): 024008. arXiv : 1004.0996 . Бибкод : 2010PhRvD..82b4008C . дои : 10.1103/PhysRevD.82.024008 . S2CID 118600898 .
- Куссер, Оливер; Энно, Марк; ван Дрил, Питер (1995). «Асимптотическая динамика трехмерной гравитации Эйнштейна с отрицательной космологической постоянной». Классическая и квантовая гравитация . 12 (12): 2961–2966. arXiv : gr-qc/9506019 . Бибкод : 1995CQGra..12.2961C . дои : 10.1088/0264-9381/12/12/012 . S2CID 14161636 .
- Коуэн, Рон (2013). «Моделирование подтверждает теорию о том, что Вселенная — это голограмма» . Новости природы и комментарии . дои : 10.1038/nature.2013.14328 . S2CID 124928147 . Проверено 21 декабря 2013 г.
- де Аро, Себастьян; Дикс, Деннис; 'т Хофт, Джерард; Верлинде, Эрик (2013). «Сорок лет теории струн в размышлениях об ее основах» . Основы физики . 43 (1): 1–7. Бибкод : 2013FoPh...43....1D . дои : 10.1007/s10701-012-9691-3 .
- Делинь, Пьер; Этингоф, Павел; Фрид, Дэниел; Джеффри, Лиза; Каждан, Дэвид; Морган, Джон; Моррисон, Дэвид; Виттен, Эдвард, ред. (1999). Квантовые поля и струны: курс для математиков . Американское математическое общество. ISBN 978-0-8218-2014-8 .
- Фефферман, Чарльз; Грэм, Робин (1985). «Конформные инварианты». Астериск : 95–116.
- Фефферман, Чарльз; Грэм, Робин (2011). Окружающая метрика . Издательство Принстонского университета. ISBN 978-1-4008-4058-8 .
- Джомби, Симона; Инь, Си (2010). «Высшая спиновая калибровочная теория и голография: трехточечные функции». Журнал физики высоких энергий . 2010 (9): 1–80. arXiv : 0912.3462 . Бибкод : 2010JHEP...09..115G . дои : 10.1007/JHEP09(2010)115 . S2CID 119117545 .
- Грин, Брайан (2000). Элегантная Вселенная: суперструны, скрытые измерения и поиск окончательной теории . Случайный дом. ISBN 978-0-9650888-0-0 .
- Гриффитс, Дэвид (2004). Введение в квантовую механику . Пирсон Прентис Холл. ISBN 978-0-13-111892-8 .
- Губсер, Стивен; Клебанов Игорь; Поляков, Александр (1998). «Корреляторы калибровочной теории из некритической теории струн». Буквы по физике Б. 428 (1–2): 105–114. arXiv : hep-th/9802109 . Бибкод : 1998PhLB..428..105G . дои : 10.1016/S0370-2693(98)00377-3 . S2CID 15693064 .
- Гуика, Моника; Хартман, Томас; Сун, Вэй; Строминджер, Эндрю (2009). «Переписка Керра и CFT». Физический обзор D . 80 (12): 124008. arXiv : 0809.4266 . Бибкод : 2009PhRvD..80l4008G . дои : 10.1103/PhysRevD.80.124008 . S2CID 15010088 .
- Хокинг, Стивен (1975). «Рождение частиц черными дырами» . Связь в математической физике . 43 (3): 199–220. Бибкод : 1975CMaPh..43..199H . дои : 10.1007/BF02345020 . S2CID 55539246 .
- Хокинг, Стивен (2005). «Потеря информации в черных дырах». Физический обзор D . 72 (8): 084013. arXiv : hep-th/0507171 . Бибкод : 2005PhRvD..72h4013H . дои : 10.1103/PhysRevD.72.084013 . S2CID 118893360 .
- Клебанов Игорь; Мальдасена, Хуан (2009). «Решение квантовых теорий поля с помощью искривленного пространства-времени» . Физика сегодня . 62 (1): 28–33. Бибкод : 2009ФТ....62а..28К . дои : 10.1063/1.3074260 .
- Клебанов Игорь; Поляков, Александр (2002). «AdS-двойник критической векторной модели O (N)». Буквы по физике Б. 550 (3–4): 213–219. arXiv : hep-th/0210114 . Бибкод : 2002PhLB..550..213K . дои : 10.1016/S0370-2693(02)02980-5 . S2CID 14628213 .
- Ковтун, ПК; Сын, Дам Т.; Старинец, АО (2005). «Вязкость в сильно взаимодействующих квантовых теориях поля из физики черных дыр». Письма о физических отзывах . 94 (11): 111601. arXiv : hep-th/0405231 . Бибкод : 2005PhRvL..94k1601K . doi : 10.1103/PhysRevLett.94.111601 . ПМИД 15903845 . S2CID 119476733 .
- Лузум, Мэтью; Ромачке, Пол (2008). «Конформная релятивистская вязкая гидродинамика: приложения к результатам RHIC в = 200 ГэВ». Physical Review C. 78 ( 3): 034915. arXiv : 0804.4015 . Bibcode : 2008PhRvC..78c4915L . doi : 10.1103/PhysRevC.78.034915 .
- Мальдасена, Хуан (1998). «Большой предел N суперконформных теорий поля и супергравитации». Успехи теоретической и математической физики . 2 (4): 231–252. arXiv : hep-th/9711200 . Бибкод : 1998AdTMP...2..231M . дои : 10.4310/ATMP.1998.V2.N2.A1 .
- Мальдасена, Хуан (2005). «Иллюзия гравитации» (PDF) . Научный американец . 293 (5): 56–63. Бибкод : 2005SciAm.293e..56M . doi : 10.1038/scientificamerican1105-56 . ПМИД 16318027 . Архивировано из оригинала (PDF) 10 ноября 2013 г.
- Маклерран, Ларри (2007). «Краткий обзор теории: кварковая материя 2006». Журнал физики G: Ядерная физика и физика элементарных частиц . 34 (8): С583–С592. arXiv : hep-ph/0702004 . Бибкод : 2007JPhG...34S.583M . дои : 10.1088/0954-3899/34/8/S50 . S2CID 16238211 .
- Мерали, Зия (2011). «Коллаборативная физика: теория струн находит помощника» . Природа . 478 (7369): 302–304. Бибкод : 2011Natur.478..302M . дои : 10.1038/478302a . ПМИД 22012369 .
- Мур, Грегори (2012). «Конспекты лекций Феликса Кляйна» (PDF) . Проверено 14 августа 2013 г.
- Перлмуттер, Сол (2003). «Сверхновые, темная энергия и ускоряющаяся Вселенная». Физика сегодня . 56 (4): 53–62. Бибкод : 2003ФТ....56д..53П . CiteSeerX 10.1.1.77.7990 . дои : 10.1063/1.1580050 .
- Пескин, Майкл; Шредер, Дэниел (1995). Введение в квантовую теорию поля . Вествью Пресс. ISBN 978-0-201-50397-5 .
- Поляков, Александр (2008). «От кварков к струнам». arXiv : 0812.0183 [ шестнадцатый ].
- Рангамани, Мукунд (2009). «Гравитация и гидродинамика: Лекции о соответствии жидкости и гравитации». Классическая и квантовая гравитация . 26 (22): 4003. arXiv : 0905.4352 . Бибкод : 2009CQGra..26v4003R . дои : 10.1088/0264-9381/26/22/224003 . S2CID 1517118 .
- Сачдев, Субир (2013). «Странный и вязкий». Научный американец . 308 (44): 44–51. Бибкод : 2012SciAm.308a..44S . doi : 10.1038/scientificamerican0113-44 . ПМИД 23342451 .
- Шерк, Джоэл; Шварц, Джон (1974). «Двойные модели для неадронов». Ядерная физика Б . 81 (1): 118–144. Бибкод : 1974НуФБ..81..118С . дои : 10.1016/0550-3213(74)90010-8 .
- Строминджер, Эндрю (2001). «Переписка dS/CFT». Журнал физики высоких энергий . 2001 (10): 034. arXiv : hep-th/0106113 . Бибкод : 2001JHEP...10..034S . дои : 10.1088/1126-6708/2001/10/034 . S2CID 17490361 .
- Сасскинд, Леонард (1995). «Мир как голограмма». Журнал математической физики . 36 (11): 6377–6396. arXiv : hep-th/9409089 . Бибкод : 1995JMP....36.6377S . дои : 10.1063/1.531249 . S2CID 17316840 .
- Сасскинд, Леонард (2008). Война черных дыр: моя битва со Стивеном Хокингом за то, чтобы сделать мир безопасным для квантовой механики . Литтл, Браун и компания. ISBN 978-0-316-01641-4 .
- 'т Хоофт, Джерард (1974). «Теория плоских диаграмм сильных взаимодействий» . Ядерная физика Б . 72 (3): 461–473. Бибкод : 1974НуФБ..72..461Т . дои : 10.1016/0550-3213(74)90154-0 .
- 'т Хоофт, Джерард (1993). «Размерное уменьшение квантовой гравитации». arXiv : gr-qc/9310026 .
- Уолд, Роберт (1984). Общая теория относительности . Издательство Чикагского университета. ISBN 978-0-226-87033-5 .
- Виттен, Эдвард (1988). «2+1-мерная гравитация как точно разрешимая система». Ядерная физика Б . 311 (1): 46–78. Бибкод : 1988НуФБ.311...46Вт . дои : 10.1016/0550-3213(88)90143-5 . hdl : 10338.dmlcz/143077 .
- Виттен, Эдвард (1998). «Анти-де Ситтеровское пространство и голография». Успехи теоретической и математической физики . 2 (2): 253–291. arXiv : hep-th/9802150 . Бибкод : 1998AdTMP...2..253W . дои : 10.4310/ATMP.1998.v2.n2.a2 . S2CID 10882387 .
- Виттен, Эдвард (2007). «Возвращение к трехмерной гравитации». arXiv : 0706.3359 [ hep-th ].
- Зи, Энтони (2010). Квантовая теория поля в двух словах (2-е изд.). Издательство Принстонского университета. ISBN 978-0-691-14034-6 .
- Цвибах, Бартон (2009). Первый курс теории струн . Издательство Кембриджского университета. ISBN 978-0-521-88032-9 .

