Масса
| Масса | |
|---|---|
 Чугунная гиря массой 2 кг (4,4 фунта), используемая для весов. | |
Общие символы | м |
| И объединились | килограмм |
| Обширный ? | да |
| Сохранено ? | да |
| Часть серии о |
| Классическая механика |
|---|
Масса – это свойство тела внутреннее . Традиционно считалось, что это связано с в теле количеством материи до открытия атома и физики элементарных частиц . Было обнаружено, что разные атомы и разные элементарные частицы , теоретически содержащие одно и то же количество вещества, имеют, тем не менее, разные массы. Масса в современной физике имеет несколько определений , которые концептуально различны, но физически эквивалентны. Массу можно экспериментально определить как меру тела инерции , то есть сопротивления ускорению (изменению скорости ) при чистой силы . приложении [1] Масса объекта также определяет силу его гравитационного притяжения к другим телам.
Базовая единица массы в системе СИ — килограмм (кг). В физике масса — это не то же самое , что вес , хотя масса часто определяется путем измерения веса объекта с помощью пружинных весов , а не весов, сравнивающих его напрямую с известными массами. Объект на Луне будет весить меньше, чем на Земле, из-за меньшей гравитации, но его масса останется той же. Это потому, что вес — это сила, а масса — это свойство, которое (наряду с гравитацией) определяет силу этой силы.
В Стандартной модели физики считается, что масса элементарных частиц является результатом их взаимодействия с бозоном Хиггса в так называемом механизме Браута-Энглерта-Хиггса . [2]
Явления
Есть несколько различных явлений, которые можно использовать для измерения массы. Хотя некоторые теоретики предполагают, что некоторые из этих явлений могут быть независимыми друг от друга, [3] текущие эксперименты не обнаружили разницы в результатах независимо от того, как они измеряются:
- Инертная масса измеряет сопротивление объекта ускорению силой (представленной соотношением F = ma ).
- Активная гравитационная масса определяет силу гравитационного поля, создаваемого объектом.
- Пассивная гравитационная масса измеряет гравитационную силу, действующую на объект в известном гравитационном поле.
Масса объекта определяет его ускорение при наличии приложенной силы. Инерция и инертная масса описывают это свойство физических тел на качественном и количественном уровне соответственно. Согласно второму закону движения Ньютона , если на тело фиксированной массы m действует единственная сила F , его ускорение a определяется выражением F / m . Масса тела также определяет степень, в которой оно генерирует и подвергается воздействию гравитационного поля . Если первое тело массы m A помещено на расстоянии r (от центра масс до центра масс) от второго тела массы m B , на каждое тело действует сила притяжения F g = Gm A m B / r. 2 , где G = 6,67 × 10 −11 N⋅kg −2 ⋅m 2 это «универсальная гравитационная постоянная ». Иногда ее называют гравитационной массой. [примечание 1] Неоднократные эксперименты, начиная с 17 века, показали, что инерционная и гравитационная массы идентичны; было включено с 1915 года это наблюдение априори в принцип эквивалентности общей теории относительности .
Единицы массы

килограмм ( Единицей массы Международной системы единиц (СИ) является кг ). Килограмм равен 1000 граммам (г) и впервые был определен в 1795 году как масса одного кубического дециметра воды при температуре таяния льда. Однако, поскольку точное измерение кубического дециметра воды при заданных температуре и давлении было затруднено, в 1889 году килограмм был переопределен как масса металлического предмета и, таким образом, стал независимым от метра и свойств воды, поскольку это медный прототип могилы в 1793 году, платиновый килограмм архивов в 1799 году и платино-иридиевый международный прототип килограмма (IPK) в 1889 году.
Однако было обнаружено, что масса ИПК и его национальных копий со временем меняется. Новое определение килограмма и некоторых других единиц вступило в силу 20 мая 2019 года после окончательного голосования CGPM в ноябре 2018 года. [4] В новом определении используются только инвариантные величины природы: скорость света , сверхтонкая частота цезия , постоянная Планка и элементарный заряд . [5]
Единицы, не входящие в систему СИ, принятые для использования с единицами СИ, включают:
- тонна (т) (или «метрическая тонна »), равная 1000 кг.
- электронвольт ( эВ ), единица энергии , используемая для выражения массы в единицах эВ/ с. 2 через эквивалентность массы и энергии
- дальтон атома (Да), равный 1/12 массы свободного углерода-12 , примерно 1,66 × 10 −27 кг . [примечание 2]
Вне системы СИ к другим единицам массы относятся:
- слизень . (сл), британская единица массы (около 14,6 кг)
- фунт . (фунт), единица массы (около 0,45 кг), которая используется наряду с одноименным фунтом (силой) (около 4,5 Н), единицей силы [примечание 3]
- планковская масса (около 2,18 × 10 −8 кг ), величина, полученная из фундаментальных констант
- солнечная масса ( M ☉ ), определяемая как масса Солнца , в основном используется в астрономии для сравнения больших масс, таких как звезды или галактики (≈ 1,99 × 10 30 кг )
- масса частицы, определяемая ее обратной комптоновской длиной волны ( 1 см −1 ≘ 3.52 × 10 −41 кг )
- масса звезды или черной дыры , определяемая ее радиусом Шварцшильда ( 1 см ≘ 6,73 × 10 24 кг ).
Определения
В физической науке можно концептуально различать по крайней мере семь различных аспектов массы или семь физических понятий, которые включают в себя концепцию массы . [6] Каждый эксперимент на сегодняшний день показал, что эти семь величин пропорциональны , а в некоторых случаях равны, и эта пропорциональность порождает абстрактное понятие массы. Существует несколько способов измерения или оперативного определения массы :
- Инертная масса — это мера сопротивления объекта ускорению при силы приложении . Оно определяется путем приложения силы к объекту и измерения ускорения, возникающего в результате этой силы. Объект с малой инерционной массой будет ускоряться быстрее, чем объект с большой инерционной массой, под действием той же силы. Говорят, что тело большей массы обладает большей инерцией .
- Активная гравитационная масса [примечание 4] объекта является мерой силы гравитационного потока (гравитационный поток равен поверхностному интегралу гравитационного поля по окружающей поверхности). Гравитационное поле можно измерить, позволив небольшому «испытуемому объекту» свободно падать и измерив его ускорение свободного падения . Например, объект, находящийся в свободном падении вблизи Луны , подвергается меньшему гравитационному полю и, следовательно, ускоряется медленнее, чем тот же объект, если бы он находился в свободном падении вблизи Земли. Гравитационное поле вблизи Луны слабее, поскольку Луна имеет менее активную гравитационную массу.
- Пассивная гравитационная масса — это мера силы взаимодействия объекта с гравитационным полем . Пассивная гравитационная масса определяется путем деления веса объекта на его ускорение свободного падения. Два объекта в одном и том же гравитационном поле будут испытывать одинаковое ускорение; однако объект с меньшей пассивной гравитационной массой будет испытывать меньшую силу (меньший вес), чем объект с большей пассивной гравитационной массой.
- Согласно теории относительности , масса — это не что иное, как энергия покоя системы частиц, то есть энергия этой системы в системе отсчета , где она имеет нулевой импульс . Масса может быть преобразована в другие формы энергии в соответствии с принципом эквивалентности массы и энергии . Эта эквивалентность иллюстрируется большим количеством физических процессов, включая образование пар , бета-распад и ядерный синтез . Образование пар и ядерный синтез — это процессы, в которых измеримые количества массы преобразуются в кинетическую энергию или наоборот.
- Искривление пространства-времени — релятивистское проявление существования массы. Такая кривизна чрезвычайно слаба и ее трудно измерить. По этой причине кривизна была открыта только после того, как она была предсказана общей теорией относительности Эйнштейна. Например, обнаружено, что чрезвычайно точные атомные часы на поверхности Земли измеряют меньше времени (идут медленнее) по сравнению с аналогичными часами в космосе. Эта разница в прошедшем времени является формой искривления, называемой гравитационным замедлением времени . Другие формы кривизны были измерены с помощью Gravity Probe B. спутника
- объекта Квантовая масса проявляется как разница между квантовой частотой и его волновым числом . Квантовая масса частицы пропорциональна обратной комптоновской длине волны и может быть определена с помощью различных методов спектроскопии . В релятивистской квантовой механике масса является одной из меток неприводимого представления группы Пуанкаре.
Вес против массы

В повседневном использовании массы и « вес » часто используются как синонимы. Например, вес человека может быть указан как 75 кг. В постоянном гравитационном поле вес объекта пропорционален его массе, и для обоих понятий нетрудно использовать одну и ту же единицу измерения. Но из-за небольших различий в силе гравитационного поля Земли в разных местах это различие становится важным для измерений с точностью лучше нескольких процентов, а также для мест, удаленных от поверхности Земли, например, в космосе или на других объектах. планеты. Концептуально «масса» (измеренная в килограммах ) относится к внутреннему свойству объекта, тогда как «вес» (измеренный в ньютонах ) измеряет сопротивление объекта отклонению от его текущего курса свободного падения , на которое может влиять близлежащая гравитация. поле. Каким бы сильным ни было гравитационное поле, объекты в свободном падении невесомы , хотя и имеют массу. [7]
Сила, известная как «вес», пропорциональна массе и ускорению во всех ситуациях, когда масса ускоряется от свободного падения. Например, когда тело покоится в гравитационном поле (а не в свободном падении), оно должно быть ускорено силой масштаба или поверхности планетарного тела, такого как Земля или Луна . Эта сила удерживает объект от свободного падения. В таких обстоятельствах вес является противодействующей силой и, таким образом, определяется ускорением свободного падения. На поверхности Земли, например, объект массой 50 килограммов весит 491 ньютон, а это значит, что 491 ньютон приложен для того, чтобы удержать объект от перехода в свободное падение. Напротив, на поверхности Луны тот же объект все еще имеет массу 50 килограммов, но весит всего 81,5 ньютона, потому что всего 81,5 ньютона требуется, чтобы удержать этот объект от свободного падения на Луну. Выражаясь математическими терминами, на поверхности Земли вес W объекта связан с его массой. м на W = mg , где g = 9,80665 м/с. 2 — ускорение гравитационного поля Земли (выраженное как ускорение, испытываемое свободно падающим объектом).
В других ситуациях, например, когда объекты подвергаются механическому ускорению от сил, отличных от сопротивления поверхности планеты, сила веса пропорциональна массе объекта, умноженной на общее ускорение от свободного падения, которое называется правильным ускорение . Благодаря таким механизмам объекты в лифтах, транспортных средствах, центрифугах и т.п. могут испытывать силы веса, во много раз превышающие силы, вызванные сопротивлением воздействию силы тяжести на объекты, возникающие на поверхностях планет. В таких случаях обобщенное уравнение веса W объекта связано с его массой m уравнением W = – ma , где a – собственное ускорение объекта, вызванное всеми воздействиями, кроме гравитации. (Опять же, если единственным влиянием является гравитация, например, когда объект свободно падает, его вес будет равен нулю).
Инерционная и гравитационная масса
Хотя инертная масса, пассивная гравитационная масса и активная гравитационная масса концептуально различны, ни один эксперимент никогда однозначно не продемонстрировал никакой разницы между ними. В классической механике третий закон Ньютона подразумевает, что активная и пассивная гравитационные массы всегда должны быть одинаковыми (или, по крайней мере, пропорциональными), но классическая теория не предлагает убедительных причин, почему гравитационная масса должна равняться инертной массе. То, что это так, является просто эмпирическим фактом.
Альберт Эйнштейн разработал свою общую теорию относительности, исходя из предположения, что инерционная и пассивная гравитационные массы одинаковы. Это известно как принцип эквивалентности .
Особая эквивалентность, часто называемая «принципом эквивалентности Галилея» или « принципом слабой эквивалентности », имеет наиболее важные последствия для свободно падающих объектов. Предположим, что объект имеет инерционную и гравитационную массы m и M соответственно. Если единственная сила, действующая на объект, исходит от гравитационного поля g , сила, действующая на объект, равна:
Учитывая эту силу, ускорение объекта можно определить по второму закону Ньютона:
Если сложить все это вместе, гравитационное ускорение определяется выражением:
Это говорит о том, что отношение гравитационной массы к инертной массе любого объекта равно некоторой постоянной K тогда и только тогда, когда все объекты падают с одинаковой скоростью в данном гравитационном поле. Это явление называется «универсальностью свободного падения». Кроме того, константу K можно принять равной 1, если правильно определить наши единицы измерения.
Первые эксперименты, демонстрирующие универсальность свободного падения, согласно научному «фольклору», были проведены Галилеем и получены путем сбрасывания предметов с Пизанской башни . Скорее всего, это апокриф: свои эксперименты он, скорее всего, проводил с шариками, катящимися по наклонным плоскостям, почти не имеющим трения , чтобы замедлить движение и повысить точность измерения времени. Проводятся все более точные эксперименты, например, проведенные Лорандом Этвосом . [8] с использованием торсионного маятника в 1889 году. По состоянию на 2008 год. [update], никаких отклонений от универсальности и, следовательно, от галилеевой эквивалентности, никогда не было обнаружено, по крайней мере, с точностью 10 −6 . Более точные экспериментальные усилия все еще проводятся. [9]
Универсальность свободного падения применима только к системам, в которых гравитация является единственной действующей силой. Все остальные силы, особенно трение и сопротивление воздуха , должны отсутствовать или, по крайней мере, быть незначительными. Например, если молоток и перо уронить с одной и той же высоты в воздух на Земле, перу потребуется гораздо больше времени, чтобы достичь земли; перо на самом деле не находится в свободном падении, потому что сила сопротивления воздуха, направленного вверх против пера, сравнима с силой тяжести, направленной вниз. С другой стороны, если опыт производить в вакууме , в котором нет сопротивления воздуха, молоток и перо должны удариться о землю точно в одно и то же время (при условии ускорения обоих объектов друг к другу, а также ускорения земля по отношению к обоим объектам, в свою очередь, незначительна). Это можно легко сделать в лаборатории средней школы, поместив предметы в прозрачные трубки, из которых воздух удален с помощью вакуумного насоса. Это становится еще более драматичным, если делать это в среде, в которой естественным образом присутствует вакуум. Дэвид Скотт сделал это на поверхности Луны во время миссии «Аполлон-15» .
Более сильная версия принципа эквивалентности, известная как принцип эквивалентности Эйнштейна или сильный принцип эквивалентности , лежит в основе общей теории относительности . Принцип эквивалентности Эйнштейна гласит, что в достаточно малых областях пространства-времени невозможно отличить однородное ускорение от однородного гравитационного поля. Таким образом, теория постулирует, что сила, действующая на массивный объект, вызванная гравитационным полем, является результатом тенденции объекта двигаться по прямой (другими словами, его инерции) и, следовательно, должна быть функцией его инерционной массы и силы тяжести. сила гравитационного поля.
Источник
В теоретической физике механизм образования массы — это теория, которая пытается объяснить происхождение массы на основе самых фундаментальных законов физики . На сегодняшний день предложен ряд различных моделей, отстаивающих разные взгляды на происхождение массы. Проблема осложняется тем фактом, что понятие массы тесно связано с гравитационным взаимодействием , но теория последнего еще не согласована с популярной в настоящее время моделью физики элементарных частиц , известной как Стандартная модель .
Доньютоновские концепции
Вес как сумма
Понятие суммы очень старо и появилось еще до письменной истории . Понятие «вес» будет включать в себя «количество» и приобретет двойное значение, которое не было четко признано как таковое. [10]
То, что мы теперь знаем как массу, до времен Ньютона называлось «весом». ... Ювелир считал, что унция золота — это количество золота. ... Но древние верили, что весы также измеряют «тяжесть», которую они распознавали посредством своих мышечных чувств. ... Считалось, что масса и связанная с ней нисходящая сила — это одно и то же.
- К.М. Браун, Доньютоновское значение слова «вес».
В какой-то ранний период люди поняли, что вес коллекции похожих объектов прямо пропорционален количеству объектов в коллекции:
где W — вес коллекции похожих объектов, а n — количество объектов в коллекции. Пропорциональность по определению подразумевает, что две величины имеют постоянное соотношение :
- или эквивалентно
Одним из первых вариантов использования этого соотношения являются весы баланса , которые уравновешивают силу веса одного объекта с силой веса другого объекта. Две стороны шкалы весов расположены достаточно близко, поэтому объекты испытывают одинаковые гравитационные поля. Следовательно, если они имеют одинаковую массу, то их веса также будут одинаковыми. Это позволяет весам, сравнивая веса, также сравнивать массы.
Следовательно, исторические стандарты веса часто определялись в количествах. Римляне, например, использовали семена рожкового дерева ( карат или кремнезем ) в качестве эталона. Если вес объекта был эквивалентен 1728 семенам рожкового дерева , то считалось, что объект весил один римский фунт. С другой стороны, если вес объекта был эквивалентен 144 семенам рожкового дерева , тогда считалось, что объект весил одну римскую унцию (унцию). Римский фунт и унция определялись как наборы разных размеров одного и того же общего стандарта массы — семян рожкового дерева. Отношение римской унции (144 семян рожкового дерева) к римскому фунту (1728 семян рожкового дерева) было:
Планетарное движение
В 1600 году нашей эры Иоганн Кеплер искал работу у Тихо Браге , который располагал одними из самых точных астрономических данных. Используя точные наблюдения Браге за планетой Марс, Кеплер провел следующие пять лет, разрабатывая свой собственный метод описания движения планет. В 1609 году Иоганн Кеплер опубликовал свои три закона движения планет, объясняющие, как планеты вращаются вокруг Солнца. находится Солнце В последней планетарной модели Кеплера он описал планетарные орбиты как следующие по эллиптическим траекториям, в центре которых . что квадрат каждой периода обращения планеты прямо пропорционален кубу Кеплер обнаружил , большой полуоси ее орбиты или, что то же самое, что соотношение этих двух величин постоянно для всех планет Солнечной системы . [примечание 5]
25 августа 1609 года Галилео Галилей продемонстрировал свой первый телескоп группе венецианских купцов, а в начале января 1610 года Галилей наблюдал вблизи Юпитера четыре тусклых объекта, которые он принял за звезды. Однако после нескольких дней наблюдений Галилей понял, что эти «звезды» на самом деле вращаются вокруг Юпитера. Эти четыре объекта (позже названные галилеевыми спутниками в честь их первооткрывателя) были первыми небесными телами, обращавшимися вокруг чего-то кроме Земли или Солнца. Галилей продолжал наблюдать эти спутники в течение следующих восемнадцати месяцев и к середине 1611 года получил удивительно точные оценки их периодов.
Галилейское свободное падение


Незадолго до 1638 года Галилей обратил внимание на явление свободного падения объектов, пытаясь охарактеризовать эти движения. Галилей не был первым, кто исследовал гравитационное поле Земли, и не был первым, кто точно описал его фундаментальные характеристики. Однако использование Галилеем научных экспериментов для установления физических принципов окажет глубокое влияние на будущие поколения ученых. Неясно, были ли это просто гипотетические эксперименты, использованные для иллюстрации концепции, или это были реальные эксперименты, проведенные Галилеем. [11] но результаты, полученные в результате этих экспериментов, были одновременно реалистичными и убедительными. В биографии ученика Галилея Винченцо Вивиани говорится, что Галилей сбрасывал шары из одного и того же материала, но разной массы, с Пизанской башни чтобы продемонстрировать, что время их падения не зависит от их массы. [примечание 6] В поддержку этого вывода Галилей выдвинул следующий теоретический аргумент: он спросил, связаны ли веревкой два тела с разной массой и разной скоростью падения, падает ли объединенная система быстрее, потому что она теперь более массивна, или более легкое тело падает быстрее? тело в своем более медленном падении удерживает более тяжелое тело? Единственное убедительное решение этого вопроса состоит в том, что все тела должны падать с одинаковой скоростью. [12]
Более поздний эксперимент был описан в «Двух новых науках» Галилея , опубликованных в 1638 году. Один из вымышленных персонажей Галилея, Сальвиати, описывает эксперимент с использованием бронзового шара и деревянного пандуса. Деревянный пандус имел «длину 12 локтей, ширину поллоктя и толщину в три пальца» с прямым, гладким, полированным пазом . Канавка была выложена « пергаментом , также гладким и отполированным, насколько это возможно». И в эту канавку помещался «твердый, гладкий и очень круглый бронзовый шарик». Рампа была наклонена под разными углами , чтобы замедлить ускорение настолько, чтобы можно было измерить прошедшее время. Мячу давали возможность скатиться по рампе на известное расстояние и измеряли время, необходимое мячу для перемещения на известное расстояние. Время измерялось с помощью водяных часов, описанных следующим образом:
- большой сосуд с водой, поставленный на возвышенность; ко дну этого сосуда была припаяна трубка небольшого диаметра, дающая тонкую струю воды, которую мы собирали в небольшой стакан во время каждого спуска, будь то по всей длине канала или на части его длины; собранную таким образом воду после каждого спуска взвешивали на очень точных весах; разности и отношения этих весов дали нам разности и отношения времен, причем с такой точностью, что хотя операцию повторяли много-много раз, заметного расхождения в результатах не было. [13]
Галилей обнаружил, что для объекта, находящегося в свободном падении, расстояние, на которое упал объект, всегда пропорционально квадрату прошедшего времени:
Галилей показал, что объекты, находящиеся в свободном падении под действием гравитационного поля Земли, имеют постоянное ускорение, а современник Галилея Иоганн Кеплер показал, что планеты следуют по эллиптическим траекториям под действием гравитационной массы Солнца. Однако движения свободного падения Галилея и движения планет Кеплера оставались разными при жизни Галилея.
Масса в отличие от веса
По словам К.М. Брауна: «Кеплер сформировал [отчётливое] понятие массы («количества материи» ( copia materiae )), но назвал его «весом», как и все в то время». [10] Наконец, в 1686 году Ньютон дал этому отдельному понятию собственное имя. В первом абзаце « Начал » Ньютон определил количество материи как «плотность и объём одновременно», а массу как количество материи. [14]
Количество материи есть мера ее, возникающая из ее плотности и объема одновременно. ... Именно эту величину я в дальнейшем везде имею в виду под именем тела или массы. И то же самое известно по весу каждого тела; ибо оно пропорционально весу.
- Исаак Ньютон, Математические принципы натуральной философии, Определение I.
Ньютоновская масса
| Луна Земли | Масса Земли | |
|---|---|---|
| Большая полуось | Сидерический орбитальный период | |
| 0,002 569 а.е. | 0,074 802 сидерического года | |
| Гравитация Земли | Радиус Земли | |
| 9,806 65 м/с 2 | 6 375 км | |

Роберт Гук опубликовал свою концепцию гравитационных сил в 1674 году, заявив, что все небесные тела обладают притяжением или силой тяготения к своим собственным центрам, а также притягивают все другие небесные тела, находящиеся в сфере их деятельности. Далее он заявил, что гравитационное притяжение увеличивается по мере того, насколько ближе тело, на которое воздействует, находится к его собственному центру. [15] В переписке с Исааком Ньютоном в 1679 и 1680 годах Гук предположил, что гравитационные силы могут уменьшаться пропорционально удвоению расстояния между двумя телами. [16] Гук призвал Ньютона, который был пионером в развитии исчисления , изучить математические детали кеплеровских орбит, чтобы определить, верна ли гипотеза Гука. Собственные расследования Ньютона подтвердили, что Гук был прав, но из-за личных разногласий между двумя мужчинами Ньютон решил не раскрывать это Гуку. Исаак Ньютон хранил молчание о своих открытиях до 1684 года, когда он рассказал своему другу Эдмонду Галлею , что решил проблему гравитационных орбит, но потерял решение в своем кабинете. [17] Получив поддержку от Галлея, Ньютон решил развить свои идеи о гравитации и опубликовать все свои открытия. В ноябре 1684 года Исаак Ньютон отправил Эдмунду Галлею документ, ныне утерянный, но предположительно озаглавленный De motu corporum in gyrum (лат. «О движении тел по орбите»). [18] Галлей представил открытия Ньютона Лондонскому королевскому обществу , пообещав, что последует более полная презентация. Позже Ньютон записал свои идеи в сборнике из трех книг под названием Philosophiæ Naturalis Principia Mathematica (английский: «Математические принципы естественной философии »). Первый был получен Королевским обществом 28 апреля 1685–1686 гг.; второй - 2 марта 1686–87; и третий - 6 апреля 1686–87. Королевское общество опубликовало всю коллекцию Ньютона за свой счет в мае 1686–87 гг. [19] : 31
Исаак Ньютон преодолел разрыв между гравитационной массой Кеплера и гравитационным ускорением Галилея, что привело к открытию следующей зависимости, которая управляла обоими из них:
где g — кажущееся ускорение тела при прохождении через область пространства, где существуют гравитационные поля, μ — гравитационная масса ( стандартный гравитационный параметр ) тела, вызывающего гравитационные поля, а R — радиальная координата (расстояние между центры двух тел).
Обнаружив точную связь между гравитационной массой тела и его гравитационным полем, Ньютон предложил второй метод измерения гравитационной массы. Массу Земли можно определить с помощью метода Кеплера (по орбите земной Луны) или ее можно определить путем измерения ускорения свободного падения на поверхности Земли и умножения его на квадрат радиуса Земли. Масса Земли составляет примерно три миллионные массы Солнца. На сегодняшний день не обнаружено другого точного метода измерения гравитационной массы. [20]
Пушечное ядро Ньютона

Пушечное ядро Ньютона было мысленным экспериментом, использованным для преодоления разрыва между гравитационным ускорением Галилея и эллиптическими орбитами Кеплера. Оно появилось в книге Ньютона 1728 года «Трактат о системе мира» . Согласно концепции гравитации Галилея, упавший камень с постоянным ускорением падает вниз по направлению к Земле. Однако Ньютон объясняет, что когда камень бросают горизонтально (то есть вбок или перпендикулярно силе тяжести Земли), он следует по изогнутой траектории. «Ибо брошенный камень под давлением собственного веса вытесняется с прямолинейного пути, по которому он должен был идти только с помощью этого проецирования, и заставляет его описывать кривую линию в воздухе; и по этому кривому пути, наконец, он переносится вниз к земле. И чем больше скорость, с которой он летит, тем дальше он проходит, прежде чем упадет на Землю». [19] : 513 Ньютон далее рассуждает, что если бы объект «спроецировался в горизонтальном направлении с вершины высокой горы» с достаточной скоростью, «он, наконец, вышел бы за пределы окружности Земли и вернулся бы на гору, с которой он был спроецирован. ." [21]
Универсальная гравитационная масса
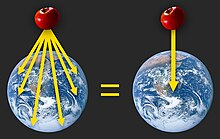
В отличие от более ранних теорий (например, о небесных сферах ), которые утверждали, что небеса состоят из совершенно другого материала, теория массы Ньютона была новаторской отчасти потому, что она вводила универсальную гравитационную массу : каждый объект имеет гравитационную массу, и, следовательно, каждый объект порождает гравитационную массу. поле. Ньютон далее предположил, что сила гравитационного поля каждого объекта будет уменьшаться пропорционально квадрату расстояния до этого объекта. Если бы из большой совокупности мелких объектов образовалось гигантское сферическое тело, такое как Земля или Солнце, Ньютон подсчитал, что эта совокупность создала бы гравитационное поле, пропорциональное общей массе тела. [19] : 397 и обратно пропорциональна квадрату расстояния до центра тела. [19] : 221 [примечание 7]
Например, согласно теории всемирного тяготения Ньютона, каждое семя рожкового дерева создает гравитационное поле. Следовательно, если собрать огромное количество семян рожкового дерева и сформировать из них огромную сферу, то гравитационное поле сферы будет пропорционально количеству семян рожкового дерева в сфере. Следовательно, теоретически возможно определить точное количество семян рожкового дерева, которое потребуется для создания гравитационного поля, подобного земному или солнечному. Фактически, путем преобразования единиц измерения можно просто абстрагироваться, чтобы понять, что любая традиционная единица массы теоретически может использоваться для измерения гравитационной массы.
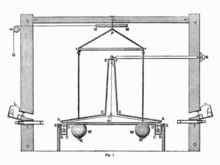
Измерение гравитационной массы в традиционных единицах массы в принципе просто, но на практике чрезвычайно сложно. Согласно теории Ньютона, все объекты создают гравитационные поля, и теоретически возможно собрать огромное количество мелких объектов и сформировать из них огромную гравитационную сферу. Однако с практической точки зрения гравитационные поля небольших объектов чрезвычайно слабы и их трудно измерить. Книги Ньютона о вселенском тяготении были опубликованы в 1680-х годах, но первое успешное измерение массы Земли в традиционных единицах массы — эксперимент Кавендиша — произошло только в 1797 году, более ста лет спустя. Генри Кавендиш обнаружил, что плотность Земли в 5,448 ± 0,033 раза превышает плотность воды. По состоянию на 2009 год масса Земли в килограммах известна только с точностью до пяти цифр, тогда как ее гравитационная масса известна с точностью до более девяти значащих цифр. [ нужны разъяснения ]
Учитывая два объекта A и B масс MA закон гравитации Ньютона гласит , и MB что , разделенные смещением R AB , каждый объект оказывает на другой гравитационную силу величиной
- ,
где G — универсальная гравитационная постоянная . Приведенное выше утверждение можно переформулировать следующим образом: если g — величина в данном месте гравитационного поля, то гравитационная сила, действующая на объект с гравитационной массой M, равна
- .
Это основа определения массы путем взвешивания . В простых пружинных весах , например, сила F пропорциональна смещению пружины под чашкой весов в соответствии с законом Гука , и весы откалиброваны с учетом g массу M. , что позволяет считывать Предполагая, что гравитационное поле одинаково по обе стороны весов, весы измеряют относительный вес, определяя относительную гравитационную массу каждого объекта.
Инерционная масса
Традиционно считалось, что масса является мерой количества материи в физическом теле, равной «количеству материи» в объекте. Например, Барре де Сен-Венан в 1851 году утверждал, что каждый объект содержит ряд «точек» (по сути, взаимозаменяемых элементарных частиц) и что масса пропорциональна количеству точек, содержащихся в объекте. [22] (На практике это определение «количества материи» адекватно большинству классической механики и иногда продолжает использоваться в базовом образовании, если приоритетом является обучение различию между массой и весом.) [23] Это традиционное убеждение о «количестве материи» противоречило тому факту, что разные атомы (а позже и разные элементарные частицы) могут иметь разные массы, а также противоречило теории относительности Эйнштейна (1905 г.), которая показала, что измеримая масса объект увеличивается, когда к нему добавляется энергия (например, путем увеличения его температуры или принуждения его к объекту, который электрически отталкивает его). Это мотивирует поиск другого определения массы, которое было бы более точным, чем традиционное определение «массы». количество материи в объекте». [24]

Инертная масса — это масса объекта, измеряемая его сопротивлением ускорению. Это определение было предложено Эрнстом Махом. [25] [26] развил его в понятие операционализма и с тех пор Перси В. Бриджмен . [27] [28] Простое определение массы в классической механике немного отличается от определения в специальной теории относительности , но основной смысл тот же.
В классической механике согласно второму закону Ньютона мы говорим, что тело имеет массу m , если в любой момент времени оно подчиняется уравнению движения
где F — равнодействующая сила , действующая на тело, а — ускорение центра масс тела. [примечание 8] На данный момент мы оставим в стороне вопрос о том, что на самом деле означает «сила, действующая на тело».
Это уравнение показывает, как масса связана с инерцией тела. Рассмотрим два объекта разной массы. Если мы приложим к каждому из них одинаковую силу, объект с большей массой будет испытывать меньшее ускорение, а объект с меньшей массой будет испытывать большее ускорение. Мы могли бы сказать, что большая масса оказывает большее «сопротивление» изменению своего состояния движения в ответ на силу.
Однако идея приложения «идентичных» сил к разным объектам возвращает нас к тому факту, что мы на самом деле не определили, что такое сила. Мы можем обойти эту трудность с помощью третьего закона Ньютона , который гласит, что если один объект прикладывает силу к другому объекту, он будет испытывать равную и противоположную силу. Точнее, предположим, что у нас есть два объекта с постоянными инерционными массами m 1 и m 2 . Мы изолируем два объекта от всех других физических воздействий, так что единственными присутствующими силами являются сила, действующая на m 1 через m 2 , которую мы обозначаем F 12 , и сила, действующая на m 2 через m 1 , которую мы обозначаем F 21 . . Второй закон Ньютона гласит, что
где a 1 и a 2 — ускорения m 1 и m 2 соответственно. Предположим, что эти ускорения отличны от нуля, так что силы между двумя объектами отличны от нуля. Это происходит, например, если два объекта находятся в процессе столкновения друг с другом. Третий закон Ньютона тогда гласит, что
и таким образом
Если | 1 | не равна нулю, дробь четко определена, что позволяет измерить инерционную массу m 1 . В данном случае m 2 — это наш «эталонный» объект, и мы можем определить его массу m как, скажем, 1 килограмм. Тогда мы сможем измерить массу любого другого объекта во Вселенной, столкнув его с эталонным объектом и измерив ускорения.
тела Кроме того, масса связывает импульс p с его линейной скоростью v :
тела и кинетическую энергию K к его скорости:
Основная трудность с определением массы Маха состоит в том, что оно не учитывает потенциальную энергию (или энергию связи ), необходимую для того, чтобы привести две массы достаточно близко друг к другу, чтобы выполнить измерение массы. [26] Наиболее ярко это демонстрирует сравнение массы протона в ядре дейтерия с массой протона в свободном пространстве (которая больше примерно на 0,239% — это связано с энергией связи дейтерия). Так, например, если за эталонную массу m 2 принять массу нейтрона в свободном пространстве и вычислить относительные ускорения протона и нейтрона в дейтерии, то приведенная выше формула завысит оценку массы m 1 ( на 0,239%) для протона в дейтерии. В лучшем случае формулу Маха можно использовать только для получения отношений масс, то есть как m 1 / m 2 = | 2 | / | а 1 |. указал на дополнительную трудность Анри Пуанкаре , заключающуюся в том, что измерение мгновенного ускорения невозможно: в отличие от измерения времени или расстояния, нет способа измерить ускорение с помощью одного измерения; необходимо выполнить несколько измерений (положения, времени и т. д.) и выполнить вычисления, чтобы получить ускорение. Пуанкаре назвал это «непреодолимым недостатком» в определении массы Маха. [29]
Атомные массы
Обычно массу объектов измеряют в килограммах, которые с 2019 года определяются с точки зрения фундаментальных констант природы. Массу атома или другой частицы можно точнее и удобнее сравнивать с массой другого атома, и поэтому ученые разработали дальтон ( также известный как единая атомная единица массы). По определению, 1 Да (один дальтон ) составляет ровно одну двенадцатую массы атома углерода-12 , и, таким образом, атом углерода-12 имеет массу ровно 12 Да.
В теории относительности
Специальная теория относительности
В некоторых рамках специальной теории относительности физики использовали разные определения этого термина. В этих рамках определяются два вида массы: масса покоя (инвариантная масса), [примечание 9] и релятивистская масса (которая увеличивается со скоростью). Масса покоя — это ньютоновская масса, измеренная наблюдателем, движущимся вместе с объектом. Релятивистская масса — это общее количество энергии в теле или системе, разделенное на c. 2 . Они связаны следующим уравнением:
где – фактор Лоренца :
Инвариантная масса систем одинакова для наблюдателей во всех инерциальных системах отсчета, тогда как релятивистская масса зависит от системы отсчета наблюдателя . Чтобы сформулировать уравнения физики так, чтобы значения массы не менялись между наблюдателями, удобно использовать массу покоя. Масса покоя тела также связана с его энергией E и величиной его импульса p релятивистским уравнением энергии-импульса :
Пока система замкнута по отношению к массе и энергии, оба вида массы сохраняются в любой данной системе отсчета. Сохранение массы сохраняется даже тогда, когда одни типы частиц превращаются в другие. Частицы материи (например, атомы) могут быть преобразованы в нематериальные частицы (например, фотоны света), но это не влияет на общее количество массы или энергии. Хотя такие вещи, как тепло, возможно, и не являются материей, все виды энергии по-прежнему обладают массой. [примечание 10] [30] Таким образом, масса и энергия не переходят друг в друга в теории относительности; скорее, оба являются названиями одного и того же, и ни масса, ни энергия не появляются без другого.
И массу покоя, и релятивистскую массу можно выразить как энергию, применив известное соотношение E = mc. 2 , что дает энергию покоя и «релятивистскую энергию» (полную энергию системы) соответственно:
«Релятивистские» концепции массы и энергии связаны со своими аналогами «покоя», но они не имеют той же ценности, что и их аналоги покоя в системах, где существует чистый импульс. Поскольку релятивистская масса пропорциональна энергии , она постепенно вышла из употребления среди физиков. [31] Существуют разногласия по поводу того, остается ли эта концепция полезной с педагогической точки зрения . [32] [33] [34]
В связанных системах энергию связи часто необходимо вычитать из массы несвязанной системы, поскольку энергия связи обычно покидает систему в момент ее связывания. Масса системы изменяется в этом процессе просто потому, что система не была закрыта во время процесса связывания, поэтому энергия ушла. Например, энергия связи атомных ядер часто теряется в виде гамма-лучей при образовании ядер, в результате чего остаются нуклиды , имеющие меньшую массу, чем свободные частицы ( нуклоны ), из которых они состоят.
Эквивалентность массы и энергии сохраняется и в макроскопических системах. [35] Например, если взять ровно один килограмм льда и приложить тепло, масса полученной талой воды будет больше килограмма: она будет включать массу тепловой энергии ( скрытой теплоты ), использованной для растапливания льда; это следует из закона сохранения энергии . [36] Это число небольшое, но немаловажное: около 3,7 нанограммов. Оно определяется скрытой теплотой тающего льда (334 кДж/кг), деленной на квадрат скорости света ( c 2 ≈ 9 × 10 16 м 2 /с 2 ).
Общая теория относительности
В общей теории относительности принцип эквивалентности представляет собой эквивалентность гравитационной и инертной масс . В основе этого утверждения лежит идея Альберта Эйнштейна о том, что гравитационная сила, испытываемая локально, когда он стоит на массивном теле (таком, как Земля), аналогична псевдосиле, испытываемой наблюдателем в неинерциальном ( т.е. ускоренном) теле. система отсчета.
Однако оказывается, что невозможно найти объективное общее определение понятия инвариантной массы в общей теории относительности. В основе проблемы лежит нелинейность уравнений поля Эйнштейна , из-за которой невозможно записать энергию гравитационного поля как часть тензора энергии-импульса способом, инвариантным для всех наблюдателей. Для данного наблюдателя это может быть достигнуто с помощью псевдотензора напряжения-энергии-импульса . [37]
В квантовой физике
В классической механике инертная масса частицы появляется в уравнении Эйлера–Лагранжа как параметр m :
После квантования, заменяя вектор положения x , волновой функцией появляется параметр m в операторе кинетической энергии :
В якобы ковариантном (релятивистски инвариантном) уравнении Дирака и в натуральных единицах это становится:
где параметр « массы » m теперь является просто константой, связанной с квантом, описываемым волновой функцией ψ.
В Стандартной модели физики элементарных частиц , разработанной в 1960-х годах, этот термин возникает из-за связи поля ψ с дополнительным полем Φ, полем Хиггса . В случае фермионов механизм Хиггса приводит к замене члена m ψ в лагранжиане на . Это сдвигает объяснение значения массы каждой элементарной частицы к значению неизвестной константы связи G ψ .
Тахионные частицы и мнимая (комплексная) масса
, Тахионное поле или просто тахион , — это квантовое поле с мнимой массой. [38] Хотя тахионы ( частицы , которые движутся быстрее света ) — это чисто гипотетическая концепция, в существование которой обычно не верят, [38] [39] поля с мнимой массой стали играть важную роль в современной физике. [40] [41] [42] и обсуждаются в популярных книгах по физике. [38] [43] Ни при каких обстоятельствах в таких теориях никакие возбуждения не распространяются быстрее света — наличие или отсутствие тахионной массы никак не влияет на максимальную скорость сигналов (при этом нет нарушения причинности ) . [44] Хотя поле может иметь мнимую массу, никакие физические частицы ее не имеют; «мнимая масса» показывает, что система становится нестабильной и избавляется от нестабильности, подвергаясь фазовому переходу, называемому тахионной конденсацией (тесно связанному с фазовыми переходами второго рода), который приводит к нарушению симметрии в современных моделях физики элементарных частиц .
Термин « тахион » был введен Джеральдом Фейнбергом в статье 1967 года. [45] но вскоре стало понятно, что модель Фейнберга на самом деле не допускает сверхсветовых скоростей. [44] Вместо этого воображаемая масса создает нестабильность конфигурации: любая конфигурация, в которой одно или несколько возбуждений поля являются тахионными, спонтанно распадается, и полученная конфигурация не содержит физических тахионов. Этот процесс известен как тахионная конденсация. Хорошо известные примеры включают конденсацию в бозона Хиггса физике элементарных частиц и ферромагнетизм в физике конденсированного состояния .
Хотя идея тахионной мнимой массы может показаться тревожной, поскольку не существует классической интерпретации мнимой массы, масса не квантуется. Скорее, это скалярное поле ; даже для тахионных квантовых полей операторы поля в пространственноподобных разделенных точках по-прежнему коммутируют (или антикоммутируют) , таким образом сохраняя причинность. Следовательно, информация все еще не распространяется быстрее света. [45] нет и решения растут экспоненциально, но не сверхсветово (нарушения причинности ). Конденсация тахионов переводит физическую систему, которая достигла локального предела и от которой можно было бы наивно ожидать, что она будет производить физические тахионы, в альтернативное стабильное состояние, в котором физические тахионы не существуют. Как только тахионное поле достигает минимума потенциала, его кванты уже не являются тахионами, а представляют собой обычные частицы с положительным квадратом массы. [46]
Это частный случай общего правила, когда нестабильные массивные частицы формально описываются как имеющие комплексную массу, причем действительная часть — это их масса в обычном понимании, а мнимая часть — скорость распада в натуральных единицах . [46] Однако в квантовой теории поля частица («одночастичное состояние») грубо определяется как состояние, постоянное во времени; е. собственное значение гамильтониана . т . — Нестабильная частица это состояние, которое остается лишь приблизительно постоянным во времени; Если он существует достаточно долго, чтобы его можно было измерить, его можно формально описать как имеющий комплексную массу, при этом действительная часть массы больше, чем ее мнимая часть. Если обе части имеют одинаковую величину, это интерпретируется как резонанс, возникающий в процессе рассеяния, а не в частице, поскольку считается, что он не существует достаточно долго, чтобы его можно было измерить независимо от процесса рассеяния. В случае тахиона действительная часть массы равна нулю, и, следовательно, ему нельзя приписать никакого понятия о частице.
В лоренц-инвариантной теории те же формулы, которые применимы к обычным частицам, движущимся медленнее света (иногда называемым « брадионами » при обсуждении тахионов), также должны применяться и к тахионам. В частности, соотношение энергии и импульса :
(где p — релятивистский импульс брадиона, а m — его масса покоя ) по-прежнему должна применяться вместе с формулой для полной энергии частицы:
Это уравнение показывает, что полная энергия частицы (брадиона или тахиона) содержит вклад от ее массы покоя («масса-энергия покоя») и вклад от ее движения, кинетическую энергию.Когда v больше c , знаменатель в уравнении энергии является «мнимым» , поскольку значение под радикалом отрицательное. Поскольку полная энергия должна быть действительной , числитель также должен быть мнимым: т.е. масса покоя m должна быть мнимой, поскольку чисто мнимое число, разделенное на другое чисто мнимое число, является действительным числом.
См. также
Примечания
- ^ Когда необходимо различие, можно различать активные и пассивные гравитационные массы.
- ^ Дальтон удобен для выражения масс атомов и молекул.
- ^ Они используются в основном в Соединенных Штатах, за исключением научных контекстов, где вместо них обычно используются единицы СИ.
- ^ Различия между «активной» и «пассивной» гравитационной массой не существует в ньютоновском взгляде на гравитацию в классической механике , и его можно смело игнорировать для многих целей. В большинстве практических приложений предполагается ньютоновская гравитация, поскольку она обычно достаточно точна и проще, чем Общая теория относительности; например, НАСА использует в основном ньютоновскую гравитацию для разработки космических миссий, хотя «точность обычно повышается за счет учета крошечных релятивистских эффектов». www2
.jpl .находится в .gov /основы /bsf3-2 .php Различие между «активным» и «пассивным» очень абстрактно и применяется к приложениям общей теории относительности на уровне аспирантов к определенным проблемам космологии и в других случаях не используется. Тем не менее, в ньютоновской физике существует важное концептуальное различие между «инертной массой» и «гравитационной массой», хотя эти величины идентичны; Концептуальное различие между этими двумя фундаментальными определениями массы сохраняется в целях обучения, поскольку они включают два разных метода измерения. Долгое время считалось аномальным, что два разных измерения массы (инерционное и гравитационное) дали одинаковый результат. Свойство, обнаруженное Галилеем, заключающееся в том, что объекты различной массы падают с одинаковым ускорением (пренебрегая сопротивлением воздуха), показывает, что инерционная и гравитационная массы одинаковы. - ^ Позже было показано, что это постоянное соотношение является прямой мерой активной гравитационной массы Солнца; он имеет единицы измерения куба расстояния на квадрат времени и известен как стандартный гравитационный параметр :
- ↑ В то время, когда Вивиани утверждает, что эксперимент имел место, Галилей еще не сформулировал окончательную версию своего закона свободного падения. Однако он сформулировал более раннюю версию, предсказавшую, что тела из одного и того же материала, проходящие через одну и ту же среду, будут падать с одинаковой скоростью. Видеть Дрейк, С. (1978). Галилей за работой . Издательство Чикагского университета. стр. 19–20 . ISBN 978-0-226-16226-3 .
- ^ Эти два свойства очень полезны, поскольку позволяют обращаться со сферическими коллекциями объектов точно так же, как с большими отдельными объектами.
- ^ В своей первоначальной форме второй закон Ньютона справедлив только для тел постоянной массы.
- ^ Можно провести небольшое различие между «массой покоя» и «инвариантной массой». Для системы из двух или более частиц не требуется, чтобы ни одна из частиц находилась в покое по отношению к наблюдателю, чтобы система в целом покоилась относительно наблюдателя. Чтобы избежать этой путаницы, некоторые источники будут использовать «массу покоя» только для отдельных частиц и «инвариантную массу» для систем.
- ^ Например, ядерная бомба в идеализированном сверхпрочном ящике, стоящая на весах, теоретически не покажет изменения в массе при взрыве (хотя внутренняя часть ящика станет намного жарче). В такой системе масса ящика изменится только в том случае, если будет позволено энергии выходить из ящика в виде света или тепла. Однако в этом случае удаленная энергия унесет с собой связанную с ней массу. Выпуск тепла или радиации из такой системы — это просто способ удалить массу. Таким образом, массу, как и энергию, нельзя уничтожить, а только переместить из одного места в другое.
Ссылки
- ^ Брей, Нэнси (28 апреля 2015 г.). "Наука" . НАСА . Архивировано из оригинала 30 мая 2023 года . Проверено 20 марта 2023 г.
Массу можно понимать как меру инерции, сопротивления объекта, который нужно привести в движение или остановить от движения.
- ^ «Бозон Хиггса» . ЦЕРН . 3 апреля 2024 г. Проверено 9 апреля 2024 г.
- ^ «Новая квантовая теория разделяет гравитационную и инертную массы» . Обзор технологий Массачусетского технологического института . 14 июня 2010 г. Проверено 25 сентября 2020 г.
- ^ фон Клитцинг, Клаус (февраль 2017 г.). «Метрология в 2019 году» (PDF) . Физика природы . 13 (2): 198. arXiv : 1707.06785 . Бибкод : 2017SSPMA..47l9503L . дои : 10.1360/SSPMA2017-00044 . S2CID 133817316 .
- ^ «Проект девятой брошюры SI» (PDF) . МБМВ. 10 ноября 2016 г. стр. 2–9 . Проверено 10 сентября 2017 г.
- ^ В. Риндлер (2006). Относительность: специальная, общая и космологическая . Издательство Оксфордского университета. стр. 16–18. ISBN 978-0-19-856731-8 .
- ^ Кейн, Гордон (4 сентября 2008 г.). «Тайны мессы» . Научный американец . Nature America, Inc., стр. 32–39 . Проверено 5 июля 2013 г.
- ^ Этвос, Р.В.; Пекар, Д.; Фекете, Э. (1922). « Вклад в закон пропорциональности инерции и гравитации » (PDF) . Анналы физики . 68 (9): 11–66. Нагрудный код : 1922АнП...373...11Э . дои : 10.1002/andp.19223730903 .
- ^ Вуазен, Г.; Коньяр, И.; Фрейре, PCC; Векс, Н.; Гиймо, Л.; Девинь, Г.; Крамер, М.; Теро, Г. (июнь 2020 г.). «Улучшенная проверка сильного принципа эквивалентности с пульсаром в тройной звездной системе» . Астрономия и астрофизика . 638 : А24. arXiv : 2005.01388 . Бибкод : 2020A&A...638A..24В . дои : 10.1051/0004-6361/202038104 . S2CID 218486794 . Проверено 4 мая 2022 г.
- ^ Перейти обратно: а б Браун, К.М. (2018). «Доньютоновское значение слова «вес»; комментарий к «Кеплеру и происхождению доньютоновской массы» [Am. J. Phys. 85, 115–123 (2017)]» . Американский журнал физики . 86 (6): 471–74. Бибкод : 2018AmJPh..86..471B . дои : 10.1119/1.5027490 . S2CID 125953814 .
- ^ Дрейк, С. (1979). «Открытие Галилеем закона свободного падения». Научный американец . 228 (5): 84–92. Бибкод : 1973SciAm.228e..84D . doi : 10.1038/scientificamerican0573-84 .
- ^ Галилей, Г. (1632). Диалог о двух главных мировых системах .
- ^ Галилей, Г. (1638). Речи и математические демонстрации вокруг двух новых наук . Том 213. Луи Эльзевир . , переведено на Крю, Х.; де Сальвио, А., ред. (1954). Математические беседы и демонстрации, относящиеся к двум новым наукам . Дуврские публикации . ISBN 978-1-275-10057-2 . Архивировано из оригинала 1 октября 2013 года . Проверено 11 апреля 2012 г. а также доступен в Хокинг, С., изд. (2002). На плечах гигантов . Беговой пресс . стр. 534–535 . ISBN 978-0-7624-1348-5 .
- ^ Ньютон, И. (1729) [1686]. Математические принципы натуральной философии . Перевод Мотта А. Напечатано для Бенджамина Мотта. стр. 1–2.
- ^ Гук, Р. (1674). Попытка доказать движение Земли из наблюдений . Королевское общество .
- ^ Тернбулл, HW, изд. (1960). Переписка Исаака Ньютона, том 2 (1676–1687) . Издательство Кембриджского университета. п. 297.
- ^ Принципы (PDF) . п. 16.
- ^ Уайтсайд, DT, изд. (2008). Математические статьи Исаака Ньютона, том VI (1684–1691) . Издательство Кембриджского университета. ISBN 978-0-521-04585-8 .
- ^ Перейти обратно: а б с д сэр Исаак Ньютон; Северо-Запад Читтенден (1848 г.). Начала Ньютона: Математические принципы естественной философии . Д. Эйди. п. 31 . ISBN 9780520009295 .
- ^ Чук, М. (январь 2003 г.). «Любопытно, что касается астрономии: как измерить массу планеты?» . Спросите астронома . Архивировано из оригинала 20 марта 2003 года . Проверено 12 марта 2011 г.
- ^ Ньютон, Исаак (1728). Трактат о системе мира . Лондон: Ф. Файрам. п. 6 . Проверено 4 мая 2022 г.
- ^ Коэльо, Рикардо Лопес (январь 2010 г.). «О концепции силы: как понимание ее истории может улучшить преподавание физики». Наука и образование . 19 (1): 91–113. Бибкод : 2010Sc&Ed..19...91C . дои : 10.1007/s11191-008-9183-1 . S2CID 195229870 .
- ^ Гиббс, Ивонн (31 марта 2017 г.). «Учителя узнают разницу между массой и весом даже в космосе» . НАСА . Архивировано из оригинала 20 марта 2023 года . Проверено 20 марта 2023 г.
- ^ Хехт, Юджин (январь 2006 г.). «Не существует действительно хорошего определения массы». Учитель физики . 44 (1): 40–45. Бибкод : 2006PhTea..44...40H . дои : 10.1119/1.2150758 .
- ^ Эрнст Мах, «Наука механика» (1919).
- ^ Перейти обратно: а б Ори Белкинд, «Физические системы: концептуальные пути между плоским пространством-временем и материей» (2012) Springer ( глава 5.3 )
- ^ П. В. Бриджмен, Теории Эйнштейна и оперативная точка зрения , в: П. А. Шилпп, изд., Альберт Эйнштейн: философ-ученый , Открытый суд, Ла Саль, штат Иллинойс, Cambridge University Press, 1982, Vol. 2, стр. 335–354.
- ^ Гиллис, Д.А. (1972). «ПДФ» (PDF) . Синтезируйте . 25 : 1–24. дои : 10.1007/BF00484997 . S2CID 239369276 . Архивировано из оригинала (PDF) 26 апреля 2016 года . Проверено 10 апреля 2016 г.
- ^ Анри Пуанкаре. « Классическая механика ». Глава 6 в книге «Наука и гипотеза». Лондон: Издательство Вальтера Скотта (1905): 89–110.
- ^ Тейлор, EF; Уилер, Дж. А. (1992). Физика пространства-времени . У. Х. Фриман. стр. 248–149 . ISBN 978-0-7167-2327-1 .
- ^ Г. Оас (2005). «О злоупотреблении и использовании релятивистской массы». arXiv : физика/0504110 .
- ^ Окунь, Л.Б. (1989). «Концепция массы» (PDF) . Физика сегодня . 42 (6): 31–36. Бибкод : 1989PhT....42f..31O . дои : 10.1063/1.881171 . Архивировано из оригинала (PDF) 22 июля 2011 года.
- ^ Риндлер, В.; Вандик, Массачусетс; Муругесан, П.; Рущин С.; Заутер, К.; Окунь, Л.Б. (1990). «Разоблачение массовых заблуждений» (PDF) . Физика сегодня . 43 (5): 13–14, 115, 117. Бибкод : 1990PhT....43e..13R . дои : 10.1063/1.2810555 . Архивировано из оригинала (PDF) 22 июля 2011 года.
- ^ Сандин, ТР (1991). «В защиту релятивистской массы». Американский журнал физики . 59 (11): 1032. Бибкод : 1991AmJPh..59.1032S . дои : 10.1119/1.16642 .
- ^ Планк, Макс (1907), «О динамике движущихся систем» , труды Королевской прусской академии наук, Берлин , первая половина тома (29): 542–570, Бибкод : 1908AnP...331....1P , дои : 10.1002/andp.19083310602
- Английский перевод из Wikisource: «О динамике движущихся систем» ( см. параграф 16 ).
- ^ Хехт, Юджин (2006). «Не существует действительно хорошего определения массы» (PDF) . Учитель физики . 44 (1): 40–45. Бибкод : 2006PhTea..44...40H . дои : 10.1119/1.2150758 .
- ^ Миснер, CW; Торн, Канзас; Уилер, Дж. А. (1973). Гравитация . У. Х. Фриман. п. 466 . ISBN 978-0-7167-0344-0 .
- ^ Перейти обратно: а б с Лиза Рэндалл, «Искаженные проходы: разгадка тайн скрытых измерений Вселенной» , стр. 286: «Первоначально люди думали о тахионах как о частицах, движущихся со скоростью, превышающей скорость света... Но теперь мы знаем, что тахион указывает на нестабильность теории. к сожалению для любителей научной фантастики, тахионы не являются реальными физическими частицами, встречающимися в природе».
- ^ Типлер, Пол А.; Ллевеллин, Ральф А. (2008). Современная физика (5-е изд.). Нью-Йорк: WH Freeman & Co., с. 54 . ISBN 978-0-7167-7550-8 .
... так что существование частиц v > c ... называемых тахионами ... поставило бы теорию относительности серьезными ... проблемами бесконечных энергий творения и парадоксов причинности.
- ^ Кутасов, Давид; Марино, Маркос и Мур, Грегори В. (2000). «Некоторые точные результаты о тахионной конденсации в теории струнного поля». Журнал физики высоких энергий . 2000 (10): 045. arXiv : hep-th/0009148 . Бибкод : 2000JHEP...10..045K . дои : 10.1088/1126-6708/2000/10/045 . S2CID 15664546 .
- ^ Сен, Ашок (2002). «Вращающийся Тахион». Журнал физики высоких энергий . 2002 (4): 048. arXiv : hep-th/0203211 . Бибкод : 2002JHEP...04..048S . дои : 10.1088/1126-6708/2002/04/048 . S2CID 12023565 .
- ^ Гиббонс, GW (2002). «Космологическая эволюция катящегося тахиона». Физ. Летт. Б. 537 (1–2): 1–4. arXiv : hep-th/0204008 . Бибкод : 2002PhLB..537....1G . дои : 10.1016/s0370-2693(02)01881-6 . S2CID 119487619 .
- ^ Брайан Грин, Элегантная вселенная , Винтажные книги (2000)
- ^ Перейти обратно: а б Ахаронов Ю.; Комар, А.; Сасскинд, Л. (1969). «Сверхсветовое поведение, причинность и нестабильность». Физ. Преподобный . 182 (5): 1400–1403. Бибкод : 1969PhRv..182.1400A . дои : 10.1103/PhysRev.182.1400 .
- ^ Перейти обратно: а б Файнберг, Джеральд (1967). «Возможность частиц быстрее света». Физический обзор . 159 (5): 1089–1105. Бибкод : 1967PhRv..159.1089F . дои : 10.1103/PhysRev.159.1089 .
- ^ Перейти обратно: а б Пескин, Мэн; Шредер, Д.В. (1995). Введение в квантовую теорию поля . Книги Персея.
Внешние ссылки
- Франсиско Флорес (6 февраля 2012 г.). «Эквивалентность массы и энергии» . Стэнфордская энциклопедия философии .
- Гордон Кейн (27 июня 2005 г.). «Тайны мессы» . Научный американец . Архивировано из оригинала 10 октября 2007 года.
- Л. Б. Окунь (2002). «Фотоны, часы, гравитация и концепция массы». Ядерная физика Б: Приложения к сборнику трудов . 110 : 151–155. arXiv : физика/0111134 . Бибкод : 2002НуФС.110..151О . дои : 10.1016/S0920-5632(02)01472-X . S2CID 16733517 .
- Франк Вильчек (13 мая 2001 г.). «Происхождение массы и слабость гравитации» (видео). Видео МТИ.
- Джон Баэз ; и др. (2012). «Изменяется ли масса со скоростью?» .
- Джон Баэз ; и др. (2008). «Какова масса фотона?» .
- Джим Бэгготт (27 сентября 2017 г.). Концепция мессы (видео), опубликованная Королевским институтом на YouTube .

































