Распределение Юла – Саймона

Юл – Саймон

Функция массы вероятности 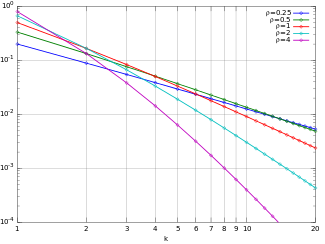PMF Юла – Саймона в логарифмическом масштабе. (Обратите внимание, что функция определяется только при целочисленных значениях k. Соединительные линии не указывают на непрерывность.)
Кумулятивная функция распределения 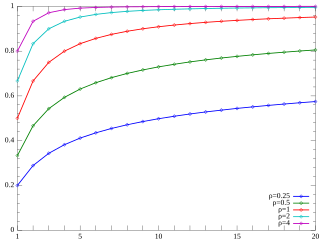Юл – Саймон CMF. (Обратите внимание, что функция определяется только при целочисленных значениях k. Соединительные линии не указывают на непрерывность.)
Параметры	$\rho >0\,$ форма ( настоящая )
Поддерживать	$k\in \{1,2,\dotsc \}$
ПМФ	$\rho \operatorname {B} (k,\rho +1)$
CDF	$1-k\operatorname {B} (k,\rho +1)$
Иметь в виду	${\frac {\rho }{\rho -1}}$ для $\rho >1$
Режим	$1$
Дисперсия	${\frac {\rho ^{2}}{(\rho -1)^{2}(\rho -2)}}$ для $\rho >2$
асимметрия	${\frac {(\rho +1)^{2}{\sqrt {\rho -2}}}{(\rho -3)\rho }}\,$ для $\rho >3$
Избыточный эксцесс	$\rho +3+{\frac {11\rho ^{3}-49\rho -22}{(\rho -4)(\rho -3)\rho }}$ для $\rho >4$
МГФ	не существует
CF	${\frac {\rho }{\rho +1}}{}_{2}F_{1}(1,1;\rho +2;e^{i\,t})e^{i\,t}$

В теории вероятности и статистике распределение Юла-Саймона представляет собой дискретное распределение вероятностей, названное в честь Удного Юла и Герберта А. Саймона . Первоначально Саймон назвал это распределением Йоля .

Функция массы вероятности (pmf) распределения Юла – Саймона ( ρ ) равна

$f(k;\rho )=\rho \operatorname {B} (k,\rho +1),$

для целого числа $k\geq 1$ и настоящий $\rho >0$, где $\operatorname {B}$ это бета-функция . Эквивалентно, PMF можно записать в терминах возрастающего факториала как

$f(k;\rho )={\frac {\rho \Gamma (\rho +1)}{(k+\rho )^{\underline {\rho +1}}}},$

где $\Gamma$ это гамма-функция . Таким образом, если $\rho$ целое число,

$f(k;\rho )={\frac {\rho \,\rho !\,(k-1)!}{(k+\rho )!}}.$

Параметр $\rho$ можно оценить с помощью алгоритма с фиксированной точкой.

Функция массы вероятности f обладает тем свойством, что для достаточно больших k мы имеем

$f(k;\rho )\approx {\frac {\rho \Gamma (\rho +1)}{k^{\rho +1}}}\propto {\frac {1}{k^{\rho +1}}}.$

График распределения Юла – Саймона (1) (красный) и его асимптотический закон Ципфа (синий)

Это означает, что хвост распределения Юла – Саймона является реализацией закона Ципфа : $f(k;\rho )$ можно использовать, например, для моделирования относительной частоты $k$самое частое слово в большом наборе текста, которое, согласно закону Ципфа, обратно пропорционально (обычно небольшой) степени $k$.

возникновение

Распределение Юла-Саймона возникло первоначально как предельное распространение конкретной модели, изученной Удным Юлом в 1925 году для анализа роста числа видов на род в некоторых высших таксонах биотических организмов. Модель Юла использует два связанных процесса Юла, где процесс Юла определяется как непрерывный процесс рождения , который начинается с одного или нескольких человек. Юл доказал, что когда время стремится к бесконечности, предельное распределение числа видов в роде, выбранном равномерно случайным образом, имеет специфическую форму и демонстрирует степенное поведение в своем хвосте. Тридцать лет спустя нобелевский лауреат Герберт А. Саймон предложил дискретную по времени модель предпочтительной привязанности, чтобы описать появление новых слов в большом фрагменте текста. Интересно, что предельное распределение числа вхождений каждого слова при расхождении числа слов совпадает с распределением числа видов, принадлежащих к случайно выбранному роду в модели Юла, при конкретном выборе параметров . Этот факт объясняет обозначение распределения Юла – Саймона, которое обычно присваивается этому предельному распределению. В контексте случайных графов модель Барабаши-Альберта также демонстрирует асимптотическое распределение степеней, которое равно распределению Юла-Саймона в соответствии с конкретным выбором параметров, и при этом представляет степенные характеристики для более общего выбора параметров. То же самое происходит и с другими предпочтительного прикрепления . модели случайного графа

Процесс предпочтительного прикрепления также можно изучать как процесс в урне, в котором шары добавляются к растущему числу урн, при этом каждый шар распределяется по урне с вероятностью, линейной по количеству (шаров), которые уже содержатся в урне.

Распределение также возникает как составное распределение , в котором параметр геометрического распределения рассматривается как функция случайной величины, имеющей экспоненциальное распределение . В частности, предположим, что $W$ следует экспоненциальному распределению с масштабом $1/\rho$ или оцените $\rho$:

$W\sim \operatorname {Exponential} (\rho ),$

с плотностью

$h(w;\rho )=\rho \exp(-\rho w).$

Тогда распределенная переменная Юла–Саймона K имеет следующее геометрическое распределение, зависящее от W :

$K\sim \operatorname {Geometric} (\exp(-W)).$

PMF геометрического распределения равна

$g(k;p)=p(1-p)^{k-1}$

для $k\in \{1,2,\dotsc \}$. Тогда PMF Юла – Саймона представляет собой следующее экспоненциально-геометрическое составное распределение:

$f(k;\rho )=\int _{0}^{\infty }g(k;\exp(-w))h(w;\rho )\,dw.$

Оценка максимального правдоподобия для параметра $\rho$ учитывая наблюдения $k_{1},k_{2},k_{3},\dots ,k_{N}$ является решением уравнения неподвижной точки

$\rho ^{(t+1)}={\frac {N+a-1}{b+\sum _{i=1}^{N}\sum _{j=1}^{k_{i}}{\frac {1}{\rho ^{(t)}+j}}}},$

где $b=0,a=1$ – параметры скорости и формы гамма-распределения до начала $\rho$.

Этот алгоритм разработан Гарсиа путем прямой оптимизации вероятности. Робертс и Робертс

обобщить алгоритм на байесовские настройки с помощью сложной геометрической формулировки, описанной выше. Кроме того, Робертс и Робертс могут использовать структуру максимизации ожиданий (EM), чтобы показать сходимость алгоритма с фиксированной точкой. Более того, Робертс и Робертс вывести сублинейность скорости сходимости для алгоритма с фиксированной точкой. Кроме того, они используют формулировку EM, чтобы получить два альтернативных вывода стандартной ошибки средства оценки из уравнения с фиксированной точкой. Дисперсия $\lambda$ оценщик

$\operatorname {Var} ({\hat {\lambda }})={\frac {1}{{\frac {N}{{\hat {\lambda }}^{2}}}-\sum _{i=1}^{N}\sum _{j=1}^{k_{i}}{\frac {1}{({\hat {\lambda }}+j)^{2}}}}},$

стандартная ошибка — это квадратный корень из величины этой оценки, разделенный на N.

Обобщения

Двухпараметрическое обобщение исходного распределения Юла заменяет бета-функцию неполной бета-функцией . Массовая функция вероятности обобщенного распределения Юла – Саймона ( ρ , α ) определяется как

$f(k;\rho ,\alpha )={\frac {\rho }{1-\alpha ^{\rho }}}\;\mathrm {B} _{1-\alpha }(k,\rho +1),\,$

с $0\leq \alpha <1$. Для $\alpha =0$ обычное распределение Юла–Саймона( ρ ) получается как частный случай. Использование неполной бета-функции приводит к введению экспоненциального среза в верхнем хвосте.

См. также

• Зета-распределение
• Безмасштабная сеть
• Бета-отрицательное биномиальное распределение

Библиография

• Колин Роуз и Мюррей Д. Смит, Математическая статистика в системе Mathematica . Нью-Йорк: Спрингер, 2002, ISBN   0-387-95234-9 . ( См. стр. 107, где это называется «Святочная раздача». )