Оптика

Исследователь, работающий над оптической системой

Оптика — это раздел физики , изучающий поведение и свойства света , включая его взаимодействие с материей и конструкцию инструментов , которые его используют или обнаруживают . ^[1] Оптика обычно описывает поведение видимого , ультрафиолетового и инфракрасного света. Свет — это тип электромагнитного излучения , и другие формы электромагнитного излучения, такие как рентгеновские лучи , микроволны и радиоволны, обладают схожими свойствами. ^[1]

Большинство оптических явлений можно объяснить, используя классическое электромагнитное описание света, однако полное электромагнитное описание света часто трудно применить на практике. Практическая оптика обычно выполняется с использованием упрощенных моделей. Наиболее распространенная из них, геометрическая оптика , рассматривает свет как совокупность лучей , которые движутся по прямым линиям и изгибаются, когда проходят через поверхности или отражаются от них. Физическая оптика — это более полная модель света, которая включает волновые эффекты, такие как дифракция и интерференция , которые невозможно объяснить в геометрической оптике. Исторически сложилось так, что сначала была разработана лучевая модель света, а затем волновая модель света. Прогресс в теории электромагнетизма в 19 веке привел к открытию того, что световые волны на самом деле являются электромагнитным излучением.

Some phenomena depend on light having both wave-like and particle-like properties. Explanation of these effects requires quantum mechanics. When considering light's particle-like properties, the light is modelled as a collection of particles called "photons". Quantum optics deals with the application of quantum mechanics to optical systems.

Optical science is relevant to and studied in many related disciplines including astronomy, various engineering fields, photography, and medicine (particularly ophthalmology and optometry, in which it is called physiological optics). Practical applications of optics are found in a variety of technologies and everyday objects, including mirrors, lenses, telescopes, microscopes, lasers, and fibre optics.

History

Optics began with the development of lenses by the ancient Egyptians and Mesopotamians. The earliest known lenses, made from polished crystal, often quartz, date from as early as 2000 BC from Crete (Archaeological Museum of Heraclion, Greece). Lenses from Rhodes date around 700 BC, as do Assyrian lenses such as the Nimrud lens.^[2] The ancient Romans and Greeks filled glass spheres with water to make lenses. These practical developments were followed by the development of theories of light and vision by ancient Greek and Indian philosophers, and the development of geometrical optics in the Greco-Roman world. The word optics comes from the ancient Greek word ὀπτική, optikē 'appearance, look'.^[3]

Greek philosophy on optics broke down into two opposing theories on how vision worked, the intromission theory and the emission theory.^[4] The intromission approach saw vision as coming from objects casting off copies of themselves (called eidola) that were captured by the eye. With many propagators including Democritus, Epicurus, Aristotle and their followers, this theory seems to have some contact with modern theories of what vision really is, but it remained only speculation lacking any experimental foundation.

Plato first articulated the emission theory, the idea that visual perception is accomplished by rays emitted by the eyes. He also commented on the parity reversal of mirrors in Timaeus.^[5] Some hundred years later, Euclid (4th–3rd century BC) wrote a treatise entitled Optics where he linked vision to geometry, creating geometrical optics.^[6] He based his work on Plato's emission theory wherein he described the mathematical rules of perspective and described the effects of refraction qualitatively, although he questioned that a beam of light from the eye could instantaneously light up the stars every time someone blinked.^[7] Euclid stated the principle of shortest trajectory of light, and considered multiple reflections on flat and spherical mirrors.Ptolemy, in his treatise Optics, held an extramission-intromission theory of vision: the rays (or flux) from the eye formed a cone, the vertex being within the eye, and the base defining the visual field. The rays were sensitive, and conveyed information back to the observer's intellect about the distance and orientation of surfaces. He summarized much of Euclid and went on to describe a way to measure the angle of refraction, though he failed to notice the empirical relationship between it and the angle of incidence.^[8] Plutarch (1st–2nd century AD) described multiple reflections on spherical mirrors and discussed the creation of magnified and reduced images, both real and imaginary, including the case of chirality of the images.

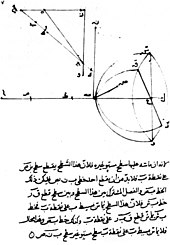
During the Middle Ages, Greek ideas about optics were resurrected and extended by writers in the Muslim world. One of the earliest of these was Al-Kindi (c. 801–873) who wrote on the merits of Aristotelian and Euclidean ideas of optics, favouring the emission theory since it could better quantify optical phenomena.^[9] In 984, the Persian mathematician Ibn Sahl wrote the treatise "On burning mirrors and lenses", correctly describing a law of refraction equivalent to Snell's law.^[10] He used this law to compute optimum shapes for lenses and curved mirrors. In the early 11th century, Alhazen (Ibn al-Haytham) wrote the Book of Optics (Kitab al-manazir) in which he explored reflection and refraction and proposed a new system for explaining vision and light based on observation and experiment.^[11] He rejected the "emission theory" of Ptolemaic optics with its rays being emitted by the eye, and instead put forward the idea that light reflected in all directions in straight lines from all points of the objects being viewed and then entered the eye, although he was unable to correctly explain how the eye captured the rays.^[12] Alhazen's work was largely ignored in the Arabic world but it was anonymously translated into Latin around 1200 A.D. and further summarised and expanded on by the Polish monk Witelo^[13] making it a standard text on optics in Europe for the next 400 years.^[14]

In the 13th century in medieval Europe, English bishop Robert Grosseteste wrote on a wide range of scientific topics, and discussed light from four different perspectives: an epistemology of light, a metaphysics or cosmogony of light, an etiology or physics of light, and a theology of light,^[15] basing it on the works of Aristotle and Platonism. Grosseteste's most famous disciple, Roger Bacon, wrote works citing a wide range of recently translated optical and philosophical works, including those of Alhazen, Aristotle, Avicenna, Averroes, Euclid, al-Kindi, Ptolemy, Tideus, and Constantine the African. Bacon was able to use parts of glass spheres as magnifying glasses to demonstrate that light reflects from objects rather than being released from them.

The first wearable eyeglasses were invented in Italy around 1286.^[16]This was the start of the optical industry of grinding and polishing lenses for these "spectacles", first in Venice and Florence in the thirteenth century,^[17] and later in the spectacle making centres in both the Netherlands and Germany.^[18] Spectacle makers created improved types of lenses for the correction of vision based more on empirical knowledge gained from observing the effects of the lenses rather than using the rudimentary optical theory of the day (theory which for the most part could not even adequately explain how spectacles worked).^[19]^[20] This practical development, mastery, and experimentation with lenses led directly to the invention of the compound optical microscope around 1595, and the refracting telescope in 1608, both of which appeared in the spectacle making centres in the Netherlands.^[21]^[22]

Cover of the first edition of Newton's *Opticks* (1704)

In the early 17th century, Johannes Kepler expanded on geometric optics in his writings, covering lenses, reflection by flat and curved mirrors, the principles of pinhole cameras, inverse-square law governing the intensity of light, and the optical explanations of astronomical phenomena such as lunar and solar eclipses and astronomical parallax. He was also able to correctly deduce the role of the retina as the actual organ that recorded images, finally being able to scientifically quantify the effects of different types of lenses that spectacle makers had been observing over the previous 300 years.^[24] After the invention of the telescope, Kepler set out the theoretical basis on how they worked and described an improved version, known as the Keplerian telescope, using two convex lenses to produce higher magnification.^[25]

Optical theory progressed in the mid-17th century with treatises written by philosopher René Descartes, which explained a variety of optical phenomena including reflection and refraction by assuming that light was emitted by objects which produced it.^[26] This differed substantively from the ancient Greek emission theory. In the late 1660s and early 1670s, Isaac Newton expanded Descartes's ideas into a corpuscle theory of light, famously determining that white light was a mix of colours that can be separated into its component parts with a prism. In 1690, Christiaan Huygens proposed a wave theory for light based on suggestions that had been made by Robert Hooke in 1664. Hooke himself publicly criticised Newton's theories of light and the feud between the two lasted until Hooke's death. In 1704, Newton published Opticks and, at the time, partly because of his success in other areas of physics, he was generally considered to be the victor in the debate over the nature of light.^[26]

Newtonian optics was generally accepted until the early 19th century when Thomas Young and Augustin-Jean Fresnel conducted experiments on the interference of light that firmly established light's wave nature. Young's famous double slit experiment showed that light followed the superposition principle, which is a wave-like property not predicted by Newton's corpuscle theory. This work led to a theory of diffraction for light and opened an entire area of study in physical optics.^[27] Wave optics was successfully unified with electromagnetic theory by James Clerk Maxwell in the 1860s.^[28]

The next development in optical theory came in 1899 when Max Planck correctly modelled blackbody radiation by assuming that the exchange of energy between light and matter only occurred in discrete amounts he called quanta.^[29] In 1905, Albert Einstein published the theory of the photoelectric effect that firmly established the quantization of light itself.^[30]^[31] In 1913, Niels Bohr showed that atoms could only emit discrete amounts of energy, thus explaining the discrete lines seen in emission and absorption spectra.^[32] The understanding of the interaction between light and matter that followed from these developments not only formed the basis of quantum optics but also was crucial for the development of quantum mechanics as a whole. The ultimate culmination, the theory of quantum electrodynamics, explains all optics and electromagnetic processes in general as the result of the exchange of real and virtual photons.^[33] Quantum optics gained practical importance with the inventions of the maser in 1953 and of the laser in 1960.^[34]

Following the work of Paul Dirac in quantum field theory, George Sudarshan, Roy J. Glauber, and Leonard Mandel applied quantum theory to the electromagnetic field in the 1950s and 1960s to gain a more detailed understanding of photodetection and the statistics of light.

Classical optics

Classical optics is divided into two main branches: geometrical (or ray) optics and physical (or wave) optics. In geometrical optics, light is considered to travel in straight lines, while in physical optics, light is considered as an electromagnetic wave.

Geometrical optics can be viewed as an approximation of physical optics that applies when the wavelength of the light used is much smaller than the size of the optical elements in the system being modelled.

Geometrical optics

Geometrical optics, or ray optics, describes the propagation of light in terms of "rays" which travel in straight lines, and whose paths are governed by the laws of reflection and refraction at interfaces between different media.^[35] These laws were discovered empirically as far back as 984 AD^[10] and have been used in the design of optical components and instruments from then until the present day. They can be summarised as follows:

When a ray of light hits the boundary between two transparent materials, it is divided into a reflected and a refracted ray.

The law of reflection says that the reflected ray lies in the plane of incidence, and the angle of reflection equals the angle of incidence.
The law of refraction says that the refracted ray lies in the plane of incidence, and the sine of the angle of incidence divided by the sine of the angle of refraction is a constant: ${\frac {\sin {\theta _{1}}}{\sin {\theta _{2}}}}=n,$ where $n$ is a constant for any two materials and a given colour of light. If the first material is air or vacuum, $n$ is the refractive index of the second material.

The laws of reflection and refraction can be derived from Fermat's principle which states that the path taken between two points by a ray of light is the path that can be traversed in the least time.^[36]

Approximations

Geometric optics is often simplified by making the paraxial approximation, or "small angle approximation". The mathematical behaviour then becomes linear, allowing optical components and systems to be described by simple matrices. This leads to the techniques of Gaussian optics and paraxial ray tracing, which are used to find basic properties of optical systems, such as approximate image and object positions and magnifications.^[37]

Reflections

Reflections can be divided into two types: specular reflection and diffuse reflection. Specular reflection describes the gloss of surfaces such as mirrors, which reflect light in a simple, predictable way. This allows for the production of reflected images that can be associated with an actual (real) or extrapolated (virtual) location in space. Diffuse reflection describes non-glossy materials, such as paper or rock. The reflections from these surfaces can only be described statistically, with the exact distribution of the reflected light depending on the microscopic structure of the material. Many diffuse reflectors are described or can be approximated by Lambert's cosine law, which describes surfaces that have equal luminance when viewed from any angle. Glossy surfaces can give both specular and diffuse reflection.

In specular reflection, the direction of the reflected ray is determined by the angle the incident ray makes with the surface normal, a line perpendicular to the surface at the point where the ray hits. The incident and reflected rays and the normal lie in a single plane, and the angle between the reflected ray and the surface normal is the same as that between the incident ray and the normal.^[38] This is known as the Law of Reflection.

For flat mirrors, the law of reflection implies that images of objects are upright and the same distance behind the mirror as the objects are in front of the mirror. The image size is the same as the object size. The law also implies that mirror images are parity inverted, which we perceive as a left-right inversion. Images formed from reflection in two (or any even number of) mirrors are not parity inverted. Corner reflectors produce reflected rays that travel back in the direction from which the incident rays came.^[39] This is called retroreflection.

Mirrors with curved surfaces can be modelled by ray tracing and using the law of reflection at each point on the surface. For mirrors with parabolic surfaces, parallel rays incident on the mirror produce reflected rays that converge at a common focus. Other curved surfaces may also focus light, but with aberrations due to the diverging shape causing the focus to be smeared out in space. In particular, spherical mirrors exhibit spherical aberration. Curved mirrors can form images with a magnification greater than or less than one, and the magnification can be negative, indicating that the image is inverted. An upright image formed by reflection in a mirror is always virtual, while an inverted image is real and can be projected onto a screen.^[40]

Refractions

Refraction occurs when light travels through an area of space that has a changing index of refraction; this principle allows for lenses and the focusing of light. The simplest case of refraction occurs when there is an interface between a uniform medium with index of refraction $n 1$ and another medium with index of refraction $n 2$ . In such situations, Snell's Law describes the resulting deflection of the light ray:

$n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}$

where $θ 1$ and $θ 2$ are the angles between the normal (to the interface) and the incident and refracted waves, respectively.^[38]

The index of refraction of a medium is related to the speed, $v$ , of light in that medium by $n=c/v,$ where $c$ is the speed of light in vacuum.

Snell's Law can be used to predict the deflection of light rays as they pass through linear media as long as the indexes of refraction and the geometry of the media are known. For example, the propagation of light through a prism results in the light ray being deflected depending on the shape and orientation of the prism. In most materials, the index of refraction varies with the frequency of the light, known as dispersion. Taking this into account, Snell's Law can be used to predict how a prism will disperse light into a spectrum.^[41] The discovery of this phenomenon when passing light through a prism is famously attributed to Isaac Newton.

Some media have an index of refraction which varies gradually with position and, therefore, light rays in the medium are curved. This effect is responsible for mirages seen on hot days: a change in index of refraction air with height causes light rays to bend, creating the appearance of specular reflections in the distance (as if on the surface of a pool of water). Optical materials with varying indexes of refraction are called gradient-index (GRIN) materials. Such materials are used to make gradient-index optics.^[42]

For light rays travelling from a material with a high index of refraction to a material with a low index of refraction, Snell's law predicts that there is no $θ 2$ when $θ 1$ is large. In this case, no transmission occurs; all the light is reflected. This phenomenon is called total internal reflection and allows for fibre optics technology. As light travels down an optical fibre, it undergoes total internal reflection allowing for essentially no light to be lost over the length of the cable.^[43]

Lenses

A ray tracing diagram for a converging lens

A device that produces converging or diverging light rays due to refraction is known as a lens. Lenses are characterized by their focal length: a converging lens has positive focal length, while a diverging lens has negative focal length. Smaller focal length indicates that the lens has a stronger converging or diverging effect. The focal length of a simple lens in air is given by the lensmaker's equation.^[44]

Ray tracing can be used to show how images are formed by a lens. For a thin lens in air, the location of the image is given by the simple equation

${\frac {1}{S_{1}}}+{\frac {1}{S_{2}}}={\frac {1}{f}},$

where $S 1$ is the distance from the object to the lens, $θ 2$ is the distance from the lens to the image, and $f$ is the focal length of the lens. In the sign convention used here, the object and image distances are positive if the object and image are on opposite sides of the lens.^[45]

Incoming parallel rays are focused by a converging lens onto a spot one focal length from the lens, on the far side of the lens. This is called the rear focal point of the lens. Rays from an object at a finite distance are focused further from the lens than the focal distance; the closer the object is to the lens, the further the image is from the lens.

With diverging lenses, incoming parallel rays diverge after going through the lens, in such a way that they seem to have originated at a spot one focal length in front of the lens. This is the lens's front focal point. Rays from an object at a finite distance are associated with a virtual image that is closer to the lens than the focal point, and on the same side of the lens as the object. The closer the object is to the lens, the closer the virtual image is to the lens. As with mirrors, upright images produced by a single lens are virtual, while inverted images are real.^[46]

Lenses suffer from aberrations that distort images. Monochromatic aberrations occur because the geometry of the lens does not perfectly direct rays from each object point to a single point on the image, while chromatic aberration occurs because the index of refraction of the lens varies with the wavelength of the light.^[47]

Physical optics

In physical optics, light is considered to propagate as waves. This model predicts phenomena such as interference and diffraction, which are not explained by geometric optics. The speed of light waves in air is approximately 3.0×10⁸ m/s (exactly 299,792,458 m/s in vacuum). The wavelength of visible light waves varies between 400 and 700 nm, but the term "light" is also often applied to infrared (0.7–300 μm) and ultraviolet radiation (10–400 nm).

The wave model can be used to make predictions about how an optical system will behave without requiring an explanation of what is "waving" in what medium. Until the middle of the 19th century, most physicists believed in an "ethereal" medium in which the light disturbance propagated.^[48] The existence of electromagnetic waves was predicted in 1865 by Maxwell's equations. These waves propagate at the speed of light and have varying electric and magnetic fields which are orthogonal to one another, and also to the direction of propagation of the waves.^[49] Light waves are now generally treated as electromagnetic waves except when quantum mechanical effects have to be considered.

Modelling and design of optical systems using physical optics

Many simplified approximations are available for analysing and designing optical systems. Most of these use a single scalar quantity to represent the electric field of the light wave, rather than using a vector model with orthogonal electric and magnetic vectors.^[50]The Huygens–Fresnel equation is one such model. This was derived empirically by Fresnel in 1815, based on Huygens' hypothesis that each point on a wavefront generates a secondary spherical wavefront, which Fresnel combined with the principle of superposition of waves. The Kirchhoff diffraction equation, which is derived using Maxwell's equations, puts the Huygens-Fresnel equation on a firmer physical foundation. Examples of the application of Huygens–Fresnel principle can be found in the articles on diffraction and Fraunhofer diffraction.

More rigorous models, involving the modelling of both electric and magnetic fields of the light wave, are required when dealing with materials whose electric and magnetic properties affect the interaction of light with the material. For instance, the behaviour of a light wave interacting with a metal surface is quite different from what happens when it interacts with a dielectric material. A vector model must also be used to model polarised light.

Numerical modeling techniques such as the finite element method, the boundary element method and the transmission-line matrix method can be used to model the propagation of light in systems which cannot be solved analytically. Such models are computationally demanding and are normally only used to solve small-scale problems that require accuracy beyond that which can be achieved with analytical solutions.^[51]

All of the results from geometrical optics can be recovered using the techniques of Fourier optics which apply many of the same mathematical and analytical techniques used in acoustic engineering and signal processing.

Gaussian beam propagation is a simple paraxial physical optics model for the propagation of coherent radiation such as laser beams. This technique partially accounts for diffraction, allowing accurate calculations of the rate at which a laser beam expands with distance, and the minimum size to which the beam can be focused. Gaussian beam propagation thus bridges the gap between geometric and physical optics.^[52]

Superposition and interference

In the absence of nonlinear effects, the superposition principle can be used to predict the shape of interacting waveforms through the simple addition of the disturbances.^[53] This interaction of waves to produce a resulting pattern is generally termed "interference" and can result in a variety of outcomes. If two waves of the same wavelength and frequency are in phase, both the wave crests and wave troughs align. This results in constructive interference and an increase in the amplitude of the wave, which for light is associated with a brightening of the waveform in that location. Alternatively, if the two waves of the same wavelength and frequency are out of phase, then the wave crests will align with wave troughs and vice versa. This results in destructive interference and a decrease in the amplitude of the wave, which for light is associated with a dimming of the waveform at that location. See below for an illustration of this effect.^[54]

combined waveform
wave 1
wave 2
	Two waves in phase	Two waves 180° out of phase

When oil or fuel is spilled, colourful patterns are formed by thin-film interference.

Since the Huygens–Fresnel principle states that every point of a wavefront is associated with the production of a new disturbance, it is possible for a wavefront to interfere with itself constructively or destructively at different locations producing bright and dark fringes in regular and predictable patterns.^[55] Interferometry is the science of measuring these patterns, usually as a means of making precise determinations of distances or angular resolutions.^[56] The Michelson interferometer was a famous instrument which used interference effects to accurately measure the speed of light.^[57]

The appearance of thin films and coatings is directly affected by interference effects. Antireflective coatings use destructive interference to reduce the reflectivity of the surfaces they coat, and can be used to minimise glare and unwanted reflections. The simplest case is a single layer with a thickness of one-fourth the wavelength of incident light. The reflected wave from the top of the film and the reflected wave from the film/material interface are then exactly 180° out of phase, causing destructive interference. The waves are only exactly out of phase for one wavelength, which would typically be chosen to be near the centre of the visible spectrum, around 550 nm. More complex designs using multiple layers can achieve low reflectivity over a broad band, or extremely low reflectivity at a single wavelength.

Constructive interference in thin films can create a strong reflection of light in a range of wavelengths, which can be narrow or broad depending on the design of the coating. These films are used to make dielectric mirrors, interference filters, heat reflectors, and filters for colour separation in colour television cameras. This interference effect is also what causes the colourful rainbow patterns seen in oil slicks.^[58]

Diffraction and optical resolution

Diffraction is the process by which light interference is most commonly observed. The effect was first described in 1665 by Francesco Maria Grimaldi, who also coined the term from the Latin diffringere 'to break into pieces'.^[59]^[60] Later that century, Robert Hooke and Isaac Newton also described phenomena now known to be diffraction in Newton's rings^[61] while James Gregory recorded his observations of diffraction patterns from bird feathers.^[62]

The first physical optics model of diffraction that relied on the Huygens–Fresnel principle was developed in 1803 by Thomas Young in his interference experiments with the interference patterns of two closely spaced slits. Young showed that his results could only be explained if the two slits acted as two unique sources of waves rather than corpuscles.^[63] In 1815 and 1818, Augustin-Jean Fresnel firmly established the mathematics of how wave interference can account for diffraction.^[64]

The simplest physical models of diffraction use equations that describe the angular separation of light and dark fringes due to light of a particular wavelength ( $λ$ ). In general, the equation takes the form $m\lambda =d\sin \theta$ where $d$ is the separation between two wavefront sources (in the case of Young's experiments, it was two slits), $θ$ is the angular separation between the central fringe and the $m$ -th order fringe, where the central maximum is $m = 0$ .^[65]

This equation is modified slightly to take into account a variety of situations such as diffraction through a single gap, diffraction through multiple slits, or diffraction through a diffraction grating that contains a large number of slits at equal spacing.^[66] More complicated models of diffraction require working with the mathematics of Fresnel or Fraunhofer diffraction.^[67]

X-ray diffraction makes use of the fact that atoms in a crystal have regular spacing at distances that are on the order of one angstrom. To see diffraction patterns, x-rays with similar wavelengths to that spacing are passed through the crystal. Since crystals are three-dimensional objects rather than two-dimensional gratings, the associated diffraction pattern varies in two directions according to Bragg reflection, with the associated bright spots occurring in unique patterns and $d$ being twice the spacing between atoms.^[68]

Diffraction effects limit the ability of an optical detector to optically resolve separate light sources. In general, light that is passing through an aperture will experience diffraction and the best images that can be created (as described in diffraction-limited optics) appear as a central spot with surrounding bright rings, separated by dark nulls; this pattern is known as an Airy pattern, and the central bright lobe as an Airy disk.^[69] The size of such a disk is given by $\sin \theta =1.22{\frac {\lambda }{D}}$ where $θ$ is the angular resolution, $λ$ is the wavelength of the light, and $D$ is the diameter of the lens aperture. If the angular separation of the two points is significantly less than the Airy disk angular radius, then the two points cannot be resolved in the image, but if their angular separation is much greater than this, distinct images of the two points are formed and they can therefore be resolved. Rayleigh defined the somewhat arbitrary "Rayleigh criterion" that two points whose angular separation is equal to the Airy disk radius (measured to first null, that is, to the first place where no light is seen) can be considered to be resolved. It can be seen that the greater the diameter of the lens or its aperture, the finer the resolution.^[70] Interferometry, with its ability to mimic extremely large baseline apertures, allows for the greatest angular resolution possible.^[56]

For astronomical imaging, the atmosphere prevents optimal resolution from being achieved in the visible spectrum due to the atmospheric scattering and dispersion which cause stars to twinkle. Astronomers refer to this effect as the quality of astronomical seeing. Techniques known as adaptive optics have been used to eliminate the atmospheric disruption of images and achieve results that approach the diffraction limit.^[71]

Dispersion and scattering

Refractive processes take place in the physical optics limit, where the wavelength of light is similar to other distances, as a kind of scattering. The simplest type of scattering is Thomson scattering which occurs when electromagnetic waves are deflected by single particles. In the limit of Thomson scattering, in which the wavelike nature of light is evident, light is dispersed independent of the frequency, in contrast to Compton scattering which is frequency-dependent and strictly a quantum mechanical process, involving the nature of light as particles. In a statistical sense, elastic scattering of light by numerous particles much smaller than the wavelength of the light is a process known as Rayleigh scattering while the similar process for scattering by particles that are similar or larger in wavelength is known as Mie scattering with the Tyndall effect being a commonly observed result. A small proportion of light scattering from atoms or molecules may undergo Raman scattering, wherein the frequency changes due to excitation of the atoms and molecules. Brillouin scattering occurs when the frequency of light changes due to local changes with time and movements of a dense material.^[72]

Dispersion occurs when different frequencies of light have different phase velocities, due either to material properties (material dispersion) or to the geometry of an optical waveguide (waveguide dispersion). The most familiar form of dispersion is a decrease in index of refraction with increasing wavelength, which is seen in most transparent materials. This is called "normal dispersion". It occurs in all dielectric materials, in wavelength ranges where the material does not absorb light.^[73] In wavelength ranges where a medium has significant absorption, the index of refraction can increase with wavelength. This is called "anomalous dispersion".^[73]

The separation of colours by a prism is an example of normal dispersion. At the surfaces of the prism, Snell's law predicts that light incident at an angle $θ$ to the normal will be refracted at an angle $arcsin(sin (θ) / n)$ . Thus, blue light, with its higher refractive index, is bent more strongly than red light, resulting in the well-known rainbow pattern.^[41]

Dispersion: two sinusoids propagating at different speeds make a moving interference pattern. The red dot moves with the phase velocity, and the green dots propagate with the group velocity. In this case, the phase velocity is twice the group velocity. The red dot overtakes two green dots, when moving from the left to the right of the figure. In effect, the individual waves (which travel with the phase velocity) escape from the wave packet (which travels with the group velocity).

Material dispersion is often characterised by the Abbe number, which gives a simple measure of dispersion based on the index of refraction at three specific wavelengths. Waveguide dispersion is dependent on the propagation constant.^[74] Both kinds of dispersion cause changes in the group characteristics of the wave, the features of the wave packet that change with the same frequency as the amplitude of the electromagnetic wave. "Group velocity dispersion" manifests as a spreading-out of the signal "envelope" of the radiation and can be quantified with a group dispersion delay parameter:

$D={\frac {1}{v_{\mathrm {g} }^{2}}}{\frac {dv_{\mathrm {g} }}{d\lambda }}$

where $v g$ is the group velocity.^[75] For a uniform medium, the group velocity is

$v_{\mathrm {g} }=c\left(n-\lambda {\frac {dn}{d\lambda }}\right)^{-1}$

where $n$ is the index of refraction and $c$ is the speed of light in a vacuum.^[76] This gives a simpler form for the dispersion delay parameter:

$D=-{\frac {\lambda }{c}}\,{\frac {d^{2}n}{d\lambda ^{2}}}.$

If $D$ is less than zero, the medium is said to have positive dispersion or normal dispersion. If $D$ is greater than zero, the medium has negative dispersion. If a light pulse is propagated through a normally dispersive medium, the result is the higher frequency components slow down more than the lower frequency components. The pulse therefore becomes positively chirped, or up-chirped, increasing in frequency with time. This causes the spectrum coming out of a prism to appear with red light the least refracted and blue/violet light the most refracted. Conversely, if a pulse travels through an anomalously (negatively) dispersive medium, high-frequency components travel faster than the lower ones, and the pulse becomes negatively chirped, or down-chirped, decreasing in frequency with time.^[77]

The result of group velocity dispersion, whether negative or positive, is ultimately temporal spreading of the pulse. This makes dispersion management extremely important in optical communications systems based on optical fibres, since if dispersion is too high, a group of pulses representing information will each spread in time and merge, making it impossible to extract the signal.^[75]

Polarisation

Polarisation is a general property of waves that describes the orientation of their oscillations. For transverse waves such as many electromagnetic waves, it describes the orientation of the oscillations in the plane perpendicular to the wave's direction of travel. The oscillations may be oriented in a single direction (linear polarisation), or the oscillation direction may rotate as the wave travels (circular or elliptical polarisation). Circularly polarised waves can rotate rightward or leftward in the direction of travel, and which of those two rotations is present in a wave is called the wave's chirality.^[78]

Типичный способ учета поляризации — отслеживать ориентацию вектора электрического поля по мере распространения электромагнитной волны. Вектор электрического поля плоской волны можно произвольно разделить на две перпендикулярные компоненты, обозначенные $x$ и $y$ (где $z$ указывает направление движения). Форма, очерченная в плоскости xy вектором электрического поля, представляет собой фигуру Лиссажу , описывающую состояние поляризации . ^[79] На следующих рисунках показаны некоторые примеры эволюции вектора электрического поля (синий) со временем (вертикальные оси) в определенной точке пространства, а также его $компонентов x$ и $y$ (красный/левый и зеленый/правый). и путь, прослеживаемый вектором на плоскости (фиолетовый): такая же эволюция произойдет, если смотреть на электрическое поле в определенный момент времени при развитии точки в пространстве в направлении, противоположном распространению.

Линейный

Круговой

Эллиптическая поляризация

На крайнем левом рисунке выше $компоненты x$ и $y$ световой волны находятся в фазе. При этом соотношение их сил постоянно, поэтому направление электрического вектора (векторной суммы этих двух составляющих) постоянно. Поскольку кончик вектора очерчивает одну линию на плоскости, этот особый случай называется линейной поляризацией. Направление этой линии зависит от относительных амплитуд двух компонент. ^[80]

На среднем рисунке два ортогональных компонента имеют одинаковые амплитуды и сдвинуты по фазе на 90°. В этом случае один компонент равен нулю, когда другой компонент имеет максимальную или минимальную амплитуду. Существует два возможных фазовых соотношения, которые удовлетворяют этому требованию: $компонент x$ может находиться на 90° впереди компонента $y$ или на 90° позади $компонента y$ . В этом особом случае электрический вектор очерчивает круг на плоскости, поэтому такая поляризация называется круговой поляризацией. Направление вращения в круге зависит от того, какое из двухфазных отношений существует, и соответствует правой круговой поляризации и левой круговой поляризации . ^[81]

Во всех остальных случаях, когда две компоненты либо не имеют одинаковых амплитуд и/или их разность фаз не равна нулю и не кратна 90°, поляризация называется эллиптической поляризацией, поскольку электрический вектор очерчивает эллипс в плоскости ( эллипс поляризации ). ^[82] Это показано на рисунке выше справа. Детальная математика поляризации выполняется с использованием исчисления Джонса и характеризуется параметрами Стокса . ^[83]

Изменение поляризации

Среды, которые имеют разные показатели преломления для разных режимов поляризации, называются двулучепреломляющими . ^[84] Хорошо известные проявления этого эффекта проявляются в оптических волновых пластинах /замедлителях (линейные режимы) и в фарадеевском вращении / оптическом вращении (круговые режимы). ^[85] Если длина пути в двулучепреломляющей среде достаточна, плоские волны будут выходить из материала со значительно другим направлением распространения из-за рефракции. Например, так обстоит дело с макроскопическими кристаллами кальцита , которые представляют зрителю два смещенных, ортогонально поляризованных изображения всего, что рассматривается через них. Именно этот эффект обеспечил первое открытие поляризации Эразмом Бартолином в 1669 году. Кроме того, фазовый сдвиг, а значит и изменение состояния поляризации, обычно зависит от частоты, что в сочетании с дихроизмом часто приводит к появлению ярких цвета и радужные эффекты. В минералогии такие свойства, известные как плеохроизм , часто используются для идентификации минералов с помощью поляризационных микроскопов. Кроме того, многие пластмассы, которые обычно не обладают двойным лучепреломлением, становятся таковыми под воздействием механического напряжения — явления, которое лежит в основе фотоэластичности . ^[86] Недвулучепреломляющие методы для вращения линейной поляризации световых лучей включают использование призматических вращателей поляризации , которые используют полное внутреннее отражение в наборе призм, предназначенных для эффективного коллинеарного прохождения. ^[87]

Среды, которые уменьшают амплитуду определенных мод поляризации, называются дихроичными , а устройства, которые блокируют почти все излучение в одной моде, известны как поляризационные фильтры или просто « поляризаторы ». Закон Малюса, названный в честь Этьена-Луи Малюса , гласит, что, когда идеальный поляризатор помещается в линейно поляризованный луч света, интенсивность $I$ проходящего через него света определяется выражением

$I=I_{0}\cos ^{2}\theta _{\mathrm {i} },$ где $I 0$ — начальная интенсивность, а $θ i$ — угол между начальным направлением поляризации света и осью поляризатора. ^[88]

Луч неполяризованного света можно рассматривать как содержащий однородную смесь линейных поляризаций под всеми возможными углами. Поскольку среднее значение $cos 2 θ$ равен 1/2, коэффициент передачи становится

${\frac {I}{I_{0}}}={\frac {1}{2}}\,.$

На практике некоторая часть света теряется в поляризаторе, и фактическое пропускание неполяризованного света будет несколько ниже, около 38% для поляризаторов типа Polaroid, но значительно выше (>49,9%) для некоторых типов двулучепреломляющих призм. ^[89]

Помимо двойного лучепреломления и дихроизма в протяженных средах, эффекты поляризации могут также возникать на (отражающей) границе раздела между двумя материалами с разными показателями преломления. Эти эффекты рассматриваются уравнениями Френеля . Часть волны передается, а часть отражается, причем соотношение зависит от угла падения и угла преломления. Таким образом, физическая оптика восстанавливает угол Брюстера . ^[90] Когда свет отражается от тонкой пленки на поверхности, интерференция отражений от поверхностей пленки может вызвать поляризацию отраженного и прошедшего света.

Естественный свет

Эффекты поляризационного фильтра на небе на фотографии. Левый снимок сделан без поляризатора. На правом изображении фильтр был настроен так, чтобы устранить определенные поляризации рассеянного синего света неба.

Большинство источников электромагнитного излучения содержат большое количество атомов или молекул, излучающих свет. Ориентация электрических полей, создаваемых этими излучателями, может не коррелировать , и в этом случае свет называется неполяризованным . Если между излучателями существует частичная корреляция, свет частично поляризован . Если поляризация одинакова по всему спектру источника, частично поляризованный свет можно описать как суперпозицию полностью неполяризованного компонента и полностью поляризованного. Тогда можно описать свет в терминах степени поляризации и параметров эллипса поляризации. ^[79]

Свет, отраженный блестящими прозрачными материалами, частично или полностью поляризован, за исключением случаев, когда свет перпендикулярен поверхности. Именно этот эффект позволил математику Этьену-Луи Малюсу провести измерения, которые позволили ему разработать первые математические модели поляризованного света. Поляризация возникает, когда свет рассеивается в атмосфере . Рассеянный свет создает яркость и цвет ясного неба . Этой частичной поляризацией рассеянного света можно воспользоваться, используя поляризационные фильтры для затемнения неба на фотографиях . Оптическая поляризация имеет принципиальное значение в химии из-за кругового дихроизма и оптического вращения ( кругового двойного лучепреломления ), присущих оптически активным ( хиральным ) молекулам . ^[91]

Современная оптика

Современная оптика охватывает области оптической науки и техники, ставшие популярными в 20 веке. Эти области оптической науки обычно связаны с электромагнитными или квантовыми свойствами света, но включают и другие темы. Основная область современной оптики, квантовая оптика , занимается конкретно квантово-механическими свойствами света. Квантовая оптика является не просто теоретической; некоторые современные устройства, например лазеры, имеют принципы работы, основанные на квантовой механике. Детекторы света, такие как фотоумножители и каналтроны , реагируют на отдельные фотоны. Электронные датчики изображения , такие как ПЗС-матрицы , демонстрируют дробовой шум, соответствующий статистике отдельных фотонных событий. Светодиоды и фотоэлектрические элементы тоже невозможно понять без квантовой механики. При изучении этих устройств квантовая оптика часто пересекается с квантовой электроникой . ^[92]

Специализированные области исследований оптики включают изучение того, как свет взаимодействует с конкретными материалами, например, в кристаллооптике и метаматериалах . Другие исследования сосредоточены на феноменологии электромагнитных волн в сингулярной оптике , оптике без изображения , нелинейной оптике , статистической оптике и радиометрии . Кроме того, компьютерные инженеры проявили интерес к интегрированной оптике , машинному зрению и фотонным вычислениям как к возможным компонентам компьютеров «следующего поколения». ^[93]

Сегодня чистая наука оптика называется оптической наукой или оптической физикой, чтобы отличить ее от прикладных оптических наук, которые называются оптической инженерией . Выдающиеся области оптической техники включают светотехнику , фотонику и оптоэлектронику с практическими приложениями, такими как проектирование линз , изготовление и тестирование оптических компонентов и обработка изображений . Некоторые из этих областей пересекаются, с размытыми границами между терминами, которые означают несколько разные вещи в разных частях мира и в разных областях промышленности. Профессиональное сообщество исследователей нелинейной оптики сформировалось за последние несколько десятилетий благодаря достижениям лазерных технологий. ^[94]

Лазеры

Лазер — это устройство, которое излучает свет, разновидность электромагнитного излучения, посредством процесса, называемого вынужденным излучением . Термин «лазер» является аббревиатурой от « Усиление света путем стимулированного излучения » . ^[95] Лазерный свет обычно пространственно когерентен , что означает, что свет либо излучается узким лучом с низкой расходимостью , либо может быть преобразован в него с помощью оптических компонентов, таких как линзы. Поскольку микроволновый эквивалент лазера, мазер , был разработан первым, устройства, излучающие микроволновые и радиочастоты , обычно называются мазерами . ^[96]

Первый работающий лазер был продемонстрирован 16 мая 1960 года Теодором Мейманом в исследовательских лабораториях Хьюза . ^[98] Когда их впервые изобрели, их называли «решением, ищущим проблему». ^[99] С тех пор лазеры превратились в многомиллиардную индустрию, находящую применение в тысячах самых разнообразных приложений. Первым применением лазеров в повседневной жизни населения стал сканер штрих-кодов в супермаркетах , представленный в 1974 году. ^[100] Проигрыватель лазерных дисков , представленный в 1978 году, стал первым успешным потребительским продуктом, включавшим лазер, но проигрыватель компакт -дисков стал первым устройством с лазером, которое стало по-настоящему распространенным в домах потребителей, начиная с 1982 года. ^[101] Эти оптические запоминающие устройства используют полупроводниковый лазер шириной менее миллиметра для сканирования поверхности диска для извлечения данных. Волоконно-оптическая связь использует лазеры для передачи больших объемов информации со скоростью света. Другие распространенные области применения лазеров включают лазерные принтеры и лазерные указки . Лазеры используются в медицине в таких областях, как бескровная хирургия , лазерная хирургия глаза и микродиссекция с лазерным захватом , а также в военных приложениях, таких как системы противоракетной обороны , электрооптические средства противодействия (EOCM) и лидар . Лазеры также используются в голограммах , пузырькограммах , лазерных световых шоу и лазерной эпиляции . ^[102]

Эффект Капицы-Дирака

Эффект Капицы-Дирака приводит к дифракции пучков частиц в результате встречи со стоячей волной света. Свет можно использовать для позиционирования материи с помощью различных явлений (см. оптический пинцет ).

Приложения

Оптика является частью повседневной жизни. Повсеместное распространение зрительных систем в биологии указывает на центральную роль оптики как науки об одном из пяти чувств . Многим людям приносят пользу очки или контактные линзы , а оптика является неотъемлемой частью функционирования многих потребительских товаров, включая фотоаппараты . Радуга и миражи являются примерами оптических явлений. Оптическая связь обеспечивает основу как для Интернета , так и для современной телефонии .

Человеческий глаз

Человеческий глаз функционирует, фокусируя свет на слой фоторецепторных клеток, называемый сетчаткой, который образует внутреннюю оболочку задней части глаза. Фокусировка осуществляется с помощью ряда прозрачных сред. Свет, попадающий в глаз, сначала проходит через роговицу, которая обеспечивает большую часть оптической силы глаза. Затем свет проходит через жидкость сразу за роговицей — переднюю камеру , а затем проходит через зрачок . Затем свет проходит через линзу , которая дополнительно фокусирует свет и позволяет регулировать фокус. Затем свет проходит через основную жидкость глаза — стекловидное тело — и достигает сетчатки. Клетки сетчатки выстилают заднюю часть глаза, за исключением места выхода зрительного нерва; это приводит к слепому пятну .

Существует два типа фоторецепторных клеток: палочки и колбочки, которые чувствительны к различным аспектам света. ^[103] Палочки чувствительны к интенсивности света в широком диапазоне частот, поэтому отвечают за черно-белое зрение . Палочки не присутствуют в ямке, области сетчатки, ответственной за центральное зрение, и не так чувствительны, как колбочки, к пространственным и временным изменениям света. Однако в сетчатке в двадцать раз больше палочек, чем колбочек, поскольку палочки расположены на более широкой площади. Из-за более широкого распространения палочки отвечают за периферическое зрение . ^[104]

Напротив, колбочки менее чувствительны к общей интенсивности света, но бывают трех разновидностей, которые чувствительны к разным диапазонам частот и, таким образом, используются для восприятия цвета и фотопического зрения . Колбочки высоко сконцентрированы в ямке и обладают высокой остротой зрения, что означает, что они обладают лучшим пространственным разрешением, чем палочки. Поскольку колбочки не так чувствительны к тусклому свету, как палочки, большая часть ночного видения ограничивается палочками. Аналогичным образом, поскольку колбочки находятся в ямке, центральное зрение (включая зрение, необходимое для большей части чтения, работы с мелкими деталями, такой как шитье или тщательное изучение объектов) обеспечивается колбочками. ^[104]

Ресничные мышцы вокруг хрусталика позволяют регулировать фокус глаза. Этот процесс известен как аккомодация . Ближняя определяют ближайшее и самое дальнее расстояния от глаза , и дальняя точки на которых объект может быть четко сфокусирован. Для человека с нормальным зрением дальняя точка находится в бесконечности. Расположение точки для близи зависит от того, насколько мышцы могут увеличить кривизну хрусталика и насколько негибким стал хрусталик с возрастом. Оптометристы , офтальмологи и оптики обычно считают, что подходящая точка близи находится ближе, чем обычное расстояние чтения — примерно 25 см. ^[103]

Дефекты зрения можно объяснить с помощью оптических принципов. С возрастом хрусталик становится менее гибким, и точка близи удаляется от глаза — состояние, известное как пресбиопия . Точно так же люди, страдающие дальнозоркостью, не могут уменьшить фокусное расстояние хрусталика настолько, чтобы на сетчатке можно было отобразить близлежащие объекты. И наоборот, люди, которые не могут увеличить фокусное расстояние линзы настолько, чтобы на сетчатке можно было отобразить удаленные объекты, страдают близорукостью и имеют дальнюю точку, которая значительно ближе бесконечности. Состояние, известное как астигматизм, возникает, когда роговица не имеет сферической формы, а более изогнута в одном направлении. Это приводит к тому, что горизонтально вытянутые объекты фокусируются на разных частях сетчатки, чем вертикально вытянутые объекты, что приводит к искажению изображений. ^[103]

Все эти состояния можно исправить с помощью корректирующих линз . При пресбиопии и дальнозоркости собирающая линза обеспечивает дополнительную кривизну, необходимую для приближения ближней точки к глазу, тогда как при близорукости рассеивающая линза обеспечивает кривизну, необходимую для направления дальней точки в бесконечность. Астигматизм корректируется с помощью линзы с цилиндрической поверхностью , которая сильнее изгибается в одну сторону, чем в другую, компенсируя неоднородность роговицы. ^[105]

Оптическая сила корректирующих линз измеряется в диоптриях — величине, равной обратной величине фокусного расстояния, измеренного в метрах; с положительным фокусным расстоянием, соответствующим собирающей линзе, и отрицательным фокусным расстоянием, соответствующим рассеивающей линзе. Для линз, которые также корректируют астигматизм, указаны три числа: одно для сферической оптической силы, одно для цилиндрической оптической силы и одно для угла ориентации астигматизма. ^[105]

Визуальные эффекты

Оптические иллюзии (также называемые зрительными иллюзиями) характеризуются зрительно воспринимаемыми изображениями, отличающимися от объективной реальности. Информация, собранная глазом, обрабатывается в мозгу, чтобы создать восприятие , отличное от отображаемого объекта. Оптические иллюзии могут быть результатом множества явлений, включая физические эффекты, создающие изображения, отличные от создающих их объектов, физиологическое воздействие на глаза и мозг чрезмерной стимуляции (например, яркости, наклона, цвета, движения) и когнитивные иллюзии, при которых глаз и мозг делают неосознанные выводы . ^[106]

Когнитивные иллюзии включают в себя некоторые из них, возникающие в результате бессознательного неправильного применения определенных оптических принципов. Например, иллюзии комнаты Эймса , иллюзии Геринга , Мюллера-Лайера , Орбисона , Понцо , Сандера и Вундта основаны на предположении о видимости расстояния за счет использования сходящихся и расходящихся линий, точно так же, как параллельные световые лучи (или даже любой набор параллельных линий) кажутся сходящимися в бесконечной точке схода в двумерных изображениях с художественной перспективой. ^[107] Это предположение также является причиной знаменитой лунной иллюзии , когда Луна, несмотря на практически одинаковый угловой размер, вблизи горизонта кажется намного больше , чем в зените . ^[108] Эта иллюзия настолько смутила Птолемея , что он ошибочно приписал ее атмосферной рефракции, когда описывал ее в своем трактате «Оптика» . ^[8]

Другой тип оптической иллюзии использует нарушенные закономерности, чтобы заставить разум воспринимать несуществующие симметрии или асимметрии. Примеры включают стену кафе , иллюзии Эренштейна , спираль Фрейзера , Поггендорфа и иллюзии Цёлльнера . Родственными, но не строго иллюзиями, являются закономерности, возникающие из-за наложения периодических структур. Например, прозрачные ткани с сетчатой структурой создают формы, известные как муаровые узоры , а наложение периодических прозрачных узоров, состоящих из параллельных непрозрачных линий или кривых, создает линейные муаровые узоры. ^[109]

Оптические инструменты

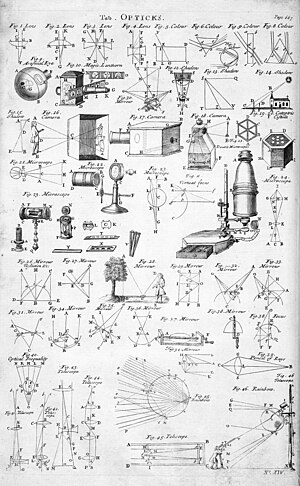
Одиночные линзы имеют множество применений, включая фотографические линзы , корректирующие линзы и увеличительные очки, а одиночные зеркала используются в параболических отражателях и зеркалах заднего вида . Сочетание нескольких зеркал, призм и линз позволяет получить сложные оптические инструменты, имеющие практическое применение. Например, перископ — это просто два плоских зеркала, выровненных таким образом, чтобы можно было видеть вокруг препятствий. Самыми известными сложными оптическими приборами в науке являются микроскоп и телескоп, которые были изобретены голландцами в конце 16 века. ^[110]

Впервые микроскопы были разработаны всего с двумя линзами: объективом и окуляром . Объектив, по сути, представляет собой увеличительное стекло и имеет очень маленькое фокусное расстояние, в то время как окуляр обычно имеет большее фокусное расстояние. Это приводит к созданию увеличенных изображений близких объектов. Обычно используется дополнительный источник освещения, поскольку увеличенные изображения получаются более тусклыми из-за сохранения энергии и распространения световых лучей по большей площади поверхности. Современные микроскопы, известные как составные микроскопы, имеют множество линз (обычно четыре) для оптимизации функциональности и повышения стабильности изображения. ^[111] Немного другая разновидность микроскопа, микроскоп сравнения , рассматривает расположенные рядом изображения, чтобы получить стереоскопическое бинокулярное изображение, которое при использовании людьми кажется трехмерным. ^[112]

Первые телескопы, называемые телескопами-рефракторами, также были разработаны с одним объективом и окуляром. В отличие от микроскопа, объектив телескопа был спроектирован с большим фокусным расстоянием, чтобы избежать оптических аберраций. Объектив фокусирует изображение удаленного объекта в своей фокусной точке, которая настроена так, чтобы находиться в фокусе окуляра с гораздо меньшим фокусным расстоянием. Основной целью телескопа является не обязательно увеличение, а скорее сбор света, который определяется физическим размером объектива. Таким образом, телескопы обычно обозначаются диаметром их объективов, а не увеличением, которое можно изменить путем переключения окуляров. Поскольку увеличение телескопа равно фокусному расстоянию объектива, делённому на фокусное расстояние окуляра, окуляры с меньшим фокусным расстоянием дают большее увеличение. ^[113]

Поскольку изготовление больших линз гораздо сложнее, чем изготовление больших зеркал, большинство современных телескопов являются телескопами-рефлекторами , то есть телескопами, в которых используется главное зеркало, а не объектив. К телескопам-рефлекторам применимы те же общие оптические соображения, что и к телескопам-рефракциям, а именно: чем больше главное зеркало, тем больше света собирается, а увеличение по-прежнему равно фокусному расстоянию главного зеркала, деленному на фокусное расстояние окуляра. . Профессиональные телескопы обычно не имеют окуляров и вместо этого размещают в фокусе инструмент (часто устройство с зарядовой связью). ^[114]

Фотография

Оптика фотографии предполагает как линзы, так и среду, в которой регистрируется электромагнитное излучение, будь то пластинка , пленка или устройство с зарядовой связью. Фотографы должны учитывать взаимность камеры и кадра, которая суммируется соотношением

Экспозиция ∝ Площадь диафрагмы × Время экспозиции × Яркость сцены. ^[115]

Другими словами, чем меньше диафрагма (обеспечивающая большую глубину резкости), тем меньше света попадает, поэтому необходимо увеличить продолжительность времени (что приводит к возможной размытости в случае движения). Примером использования закона взаимности является правило Sunny 16 , которое дает приблизительную оценку настроек, необходимых для оценки правильной экспозиции при дневном свете. ^[116]

Апертура камеры измеряется безразмерным числом, называемым диафрагменным числом или диафрагменным числом. f / #, часто обозначается как $N$ , и задано

f/\#=N={\frac {f}{D}}\

где $f$ - фокусное расстояние, а $D$ - диаметр входного зрачка. По соглашению " f / #» рассматривается как один символ, а конкретные значения f / # записываются путем замены знака числа на значение. Два способа увеличить диафрагму — либо уменьшить диаметр входного зрачка, либо перейти на более длинное фокусное расстояние (в случае зум-объектива это можно сделать, просто отрегулировав объектив). Более высокие числа f также имеют большую глубину резкости из-за того, что объектив приближается к пределу камеры-обскуры, которая способна идеально фокусировать все изображения, независимо от расстояния, но требует очень длительного времени выдержки. ^[117]

Поле зрения, которое обеспечивает объектив, меняется в зависимости от фокусного расстояния объектива. Существует три основные классификации, основанные на соотношении размера диагонали пленки или размера сенсора камеры с фокусным расстоянием объектива: ^[118]

Нормальная линза : угол зрения около 50° (называемый нормальным , потому что этот угол считается примерно эквивалентным человеческому зрению). ^[118]) и фокусное расстояние, примерно равное диагонали пленки или сенсора. ^[119]
Широкоугольный объектив : угол обзора шире 60° и фокусное расстояние короче, чем у обычного объектива. ^[120]
Длиннофокусный объектив : угол обзора уже, чем у обычного объектива. Это любой объектив с фокусным расстоянием, превышающим диагональ пленки или сенсора. ^[121] Наиболее распространенным типом длиннофокусных объективов является телеобъектив , конструкция которого использует специальную телеобъективную группу, которая физически короче его фокусного расстояния. ^[122]

Современные зум-объективы могут обладать некоторыми или всеми этими качествами.

Абсолютное значение требуемого времени экспозиции зависит от того, насколько чувствителен к свету используемый носитель (измеряется светочувствительностью пленки или, для цифровых носителей, квантовой эффективностью ). ^[123] В ранней фотографии использовались носители с очень низкой светочувствительностью, поэтому время выдержки должно было быть большим даже для очень ярких снимков. По мере совершенствования технологий росла и чувствительность пленочных и цифровых фотоаппаратов. ^[124]

Другие результаты физической и геометрической оптики применимы и к оптике камеры. Например, максимальная разрешающая способность конкретной установки камеры определяется пределом дифракции , связанным с размером зрачка и определяемым, грубо говоря, критерием Рэлея. ^[125]

Атмосферная оптика

Красочное небо часто возникает из-за рассеяния света частицами и загрязнениями, как на этой фотографии заката во время лесных пожаров в Калифорнии в октябре 2007 года .

Уникальные оптические свойства атмосферы вызывают широкий спектр впечатляющих оптических явлений. Голубой цвет неба является прямым результатом рэлеевского рассеяния, которое перенаправляет более высокочастотный (синий) солнечный свет обратно в поле зрения наблюдателя. Поскольку синий свет рассеивается легче, чем красный, солнце приобретает красноватый оттенок, когда его наблюдают сквозь плотную атмосферу, например, во время восхода или заката . Дополнительные твердые частицы в небе могут рассеивать разные цвета под разными углами, создавая красочное светящееся небо в сумерках и на рассвете. Рассеяние кристаллов льда и других частиц в атмосфере ответственно за ореолы , послесвечения , короны , солнечные лучи и солнечные собаки . Различия в явлениях такого рода обусловлены разным размером и геометрией частиц. ^[126]

Миражи — это оптические явления, при которых лучи света искривляются из-за тепловых изменений показателя преломления воздуха, создавая смещенные или сильно искаженные изображения удаленных объектов. Другие драматические оптические явления, связанные с этим, включают эффект Новой Земли, когда кажется, что солнце восходит раньше, чем предполагалось, и имеет искаженную форму. Захватывающая форма рефракции возникает при температурной инверсии , называемой Фата Моргана , когда объекты на горизонте или даже за ним, такие как острова, скалы, корабли или айсберги, кажутся вытянутыми и приподнятыми, как «сказочные замки». ^[127]

Радуга — результат сочетания внутреннего отражения и дисперсионного преломления света в каплях дождя. Одиночное отражение от обратной стороны множества капель дождя создает на небе радугу с угловым размером от 40° до 42° с красной внешней стороной. Двойные радуги возникают в результате двух внутренних отражений с угловым размером от 50,5° до 54° с фиолетовым цветом снаружи. Поскольку радугу можно увидеть, когда солнце находится на расстоянии 180° от центра радуги, радуга тем заметнее, чем ближе солнце к горизонту. ^[128]

См. также

Ссылки

^ Перейти обратно: ^а ^б Энциклопедия науки и технологий МакГроу-Хилла (5-е изд.). МакГроу-Хилл. 1993.
^ «Самый старый телескоп в мире?» . Новости Би-би-си . 1 июля 1999 года. Архивировано из оригинала 1 февраля 2009 года . Проверено 3 января 2010 г.
^ Т. Ф. Хоад (1996). Краткий Оксфордский словарь английской этимологии . ISBN 978-0-19-283098-2 .
^ История глаза . Архивировано 20 января 2012 г. в Wayback Machine . Стэнфорд.edu. Проверено 10 июня 2012 г.
^ Т.Л. Хит (2003). Руководство по греческой математике . Публикации Courier Dover. стр. 181–182. ISBN 978-0-486-43231-1 .
^ Уильям Р. Аттал (1983). Визуальное обнаружение формы в трехмерном пространстве . Психология Пресс. стр. 25–. ISBN 978-0-89859-289-4 . Архивировано из оригинала 3 мая 2016 г.
^ Евклид (1999). Элахе Хейрандиш (ред.). Арабская версия оптики Евклида = Китаб Уклидис фи ихтилаф аль-манацир . Нью-Йорк: Спрингер. ISBN 978-0-387-98523-7 .
^ Перейти обратно: ^а ^б Птолемей (1996). А. Марк Смит (ред.). Теория зрительного восприятия Птолемея: английский перевод «Оптики» с введением и комментариями . Издательство ДИАНА. ISBN 978-0-87169-862-9 .
^ Адамсон, Питер (2006). «Аль-Кинди и рецепция греческой философии». В Адамсоне, Питер; Тейлор, Р. Кембриджский спутник арабской философии. Издательство Кембриджского университета. п. 45. ISBN 978-0-521-52069-0 .
^ Перейти обратно: ^а ^б Рашед, Рошди (1990). «Пионер анакластики: Ибн Сахл о горящих зеркалах и линзах». Исида . 81 (3): 464–491. дои : 10.1086/355456 . JSTOR 233423 . S2CID 144361526 .
^
- Хогендейк, Ян П.; Сабра, Абдельхамид И., ред. (2003). Предприятие науки в исламе: новые перспективы . МТИ Пресс. стр. 85–118. ISBN 978-0-262-19482-2 . OCLC 50252039 .
- Дж. Хэтфилд (1996). «Была ли научная революция действительно революцией в науке?». В Ф.Дж. Рагепе; П. Салли; С. Дж. Ливси (ред.). Традиция, передача, трансформация: материалы двух конференций по досовременной науке, состоявшихся в Университете Оклахомы . Издательство «Брилл». п. 500. ИСБН 978-90-04-10119-7 . Архивировано из оригинала 27 апреля 2016 г.
- Надер Эль-Бизри (2005). «Философский взгляд на оптику Альхазена». Арабские науки и философия . 15 (2): 189–218. дои : 10.1017/S0957423905000172 . S2CID 123057532 .
- Надер Эль-Бизри (2007). «В защиту суверенитета философии: критика аль-Багдади геометризации места Ибн аль-Хайсама». Арабские науки и философия . 17 :57–80. дои : 10.1017/S0957423907000367 . S2CID 170960993 .
- Г. Саймон (2006). «Взгляд у Ибн аль-Хайсама». Журнал средневековой истории . 9 : 89–98. дои : 10.1177/097194580500900105 . S2CID 170628785 .
^ Ян П. Ховард; Брайан Дж. Роджерс (1995). Бинокулярное зрение и стереопсис . Издательство Оксфордского университета. п. 7. ISBN 978-0-19-508476-4 . Архивировано из оригинала 6 мая 2016 г.
^ Елена Агацци; Энрико Джаннетто; Франко Джудиче (2010). Представление света в искусстве и науке: теории и практики . В&Р Юнипресс ГмбХ. п. 42. ИСБН 978-3-89971-735-8 . Архивировано из оригинала 10 мая 2016 г.
^ Эль-Бизри, Надер (2010). «Классическая оптика и традиции перспективы, ведущие к Возрождению». В Хендриксе, Джон Шеннон ; Карман, Чарльз Х. (ред.). Ренессансные теории видения (визуальная культура в раннем Новом времени) . Фарнем, Суррей: Ashgate Publishing . стр. 11–30. ISBN 978-1-4094-0024-0 . ; Эль-Бизри, Надер (2014). «Видеть реальность в перспективе: «Искусство оптики» и «Наука живописи» ». В Лупаккини, Росселла; Анджелини, Аннарита (ред.). Искусство науки: от перспективного рисунка к квантовой случайности . Доредрехт: Спрингер. стр. 25–47.
^ DC Линдберг, Теории видения от аль-Кинди до Кеплера , (Чикаго: Чикагский университет, 1976), стр. 94–99.
^ Иларди, Винсент (2007). Видение эпохи Возрождения от очков к телескопам . Филадельфия: Американское философское общество. стр. 4–5. ISBN 978-0-87169-259-7 .
^ «Проект Галилео> Наука> Телескоп», Эл Ван Хелден. Архивировано 20 марта 2012 г. в Wayback Machine . Галилео.rice.edu. Проверено 10 июня 2012 г.
^ Генри К. Кинг (2003). История телескопа . Публикации Courier Dover. п. 27. ISBN 978-0-486-43265-6 . Архивировано из оригинала 17 июня 2016 г.
^ Пол С. Агаттер; Денис Н. Уитли (2008). Размышление о жизни: история и философия биологии и других наук . Спрингер. п. 17. ISBN 978-1-4020-8865-0 . Архивировано из оригинала 16 мая 2016 г.
^ Иларди (2007) , с. 210 .
^ Микроскопы: временная шкала. Архивировано 9 января 2010 г. в Wayback Machine , Нобелевский фонд. Проверено 3 апреля 2009 г.
^ Уотсон, Фред (2007). Звездочёт: Жизнь и времена телескопа . Аллен и Анвин. п. 55. ИСБН 978-1-74175-383-7 . Архивировано из оригинала 8 мая 2016 г.
^ Каспар, Макс (1993) [Впервые опубликовано в 1959 году]. Кеплер . Дуврские публикации. стр. 142–146. ISBN 0-486-67605-6 .
^ Иларди (2007) , с. 244 .
^ Каспар (1993) , стр. 192–202 .
^ Перейти обратно: ^а ^б А. И. Сабра (1981). Теории света от Декарта до Ньютона . Архив Кубка. ISBN 978-0-521-28436-3 .
^ В. Ф. Мэги (1935). Справочник по физике . Издательство Гарвардского университета. п. 309 .
^ Дж. К. Максвелл (1865). «Динамическая теория электромагнитного поля» . Философские труды Лондонского королевского общества . 155 : 459–512. Бибкод : 1865RSPT..155..459C . дои : 10.1098/rstl.1865.0008 . S2CID 186207827 .
^ Твердый подход к сложности интеллектуальной мотивации Планка в отношении кванта, а также его неохотное принятие его последствий см. Х. Краг, Макс Планк: сопротивляющийся революционер. Архивировано 1 апреля 2012 г. в Wayback Machine , Мир физики . Декабрь 2000 года.
^ Эйнштейн, А. (1967). «Об эвристической точке зрения на производство и преобразование света». В Тер Хаар, Д. (ред.). Старая квантовая теория . Пергамон. стр. 91–107 . OCLC 534625 . Эта глава представляет собой английский перевод статьи Эйнштейна 1905 года о фотоэлектрическом эффекте.
^ Эйнштейн, А. (1905). «Об эвристической точке зрения на производство и преобразование света». Анналы физики (на немецком языке). 322 (6): 132–148. Бибкод : 1905АнП...322..132Е . дои : 10.1002/andp.19053220607 .
^ «О строении атомов и молекул» . Философский журнал . 26, серия 6: 1–25. 1913. Архивировано из оригинала 4 июля 2007 года . Знаковая статья, в которой изложена модель атома и молекулярной связи Бора .
^ Р. Фейнман (1985). «Глава 1». КЭД: Странная теория света и материи . Издательство Принстонского университета. п. 6. ISBN 978-0-691-08388-9 .
^ Н. Тейлор (2000). ЛАЗЕР: изобретатель, нобелевский лауреат и тридцатилетняя патентная война . Нью-Йорк: Саймон и Шустер. ISBN 978-0-684-83515-0 .
^ Ариэль Липсон; Стивен Г. Липсон; Генри Липсон (28 октября 2010 г.). Оптическая физика . Издательство Кембриджского университета. п. 48. ИСБН 978-0-521-49345-1 . Архивировано из оригинала 28 мая 2013 года . Проверено 12 июля 2012 г.
^ Артур Шустер (1904). Введение в теорию оптики . Э. Арнольд. п. 41 .
^ Дж. Э. Грейвенкамп (2004). Полевое руководство по геометрической оптике. Полевые руководства SPIE, том. ФГ01 . ШПИОН. стр. 19–20. ISBN 978-0-8194-5294-8 .
^ Перейти обратно: ^а ^б Янг и Фридман (2020) , с. 1109.
^ Янг и Фридман (2020) , стр. 1112–1113.
^ Янг и Фридман (2020) , стр. 1142–1143, 1145.
^ Перейти обратно: ^а ^б Янг и Фридман (2020) , с. 1116.
^ Маршан, EW (1978). Градиентная индексная оптика . Нью-Йорк: Академическая пресса.
^ Янг и Фридман (2020) , стр. 1113–1115.
^ Хехт (2017) , с. 159.
^ Хехт (2017) , с. 165.
^ Янг и Фридман (2020) , с. 1157.
^ Янг и Фридман (2020) , с. 1143,1163,1175.
^ М. В. Кляйн и Т. Е. Фуртак, 1986, Оптика, John Wiley & Sons, Нью-Йорк ISBN 0-471-87297-0 .
^ Максвелл, Джеймс Клерк (1865). «Динамическая теория электромагнитного поля» (PDF) . Философские труды Лондонского королевского общества . 155 : 499. Бибкод : 1865RSPT..155..459C . дои : 10.1098/rstl.1865.0008 . S2CID 186207827 . Архивировано (PDF) из оригинала 28 июля 2011 г. Эта статья сопровождала презентацию Максвелла Королевскому обществу от 8 декабря 1864 года. См. также Динамическую теорию электромагнитного поля .
^ М. Борн и Э. Вольф (1999). Принцип оптики . Кембридж: Издательство Кембриджского университета. ISBN 0-521-64222-1 .
^ Дж. Гудман (2005). Введение в оптику Фурье (3-е изд.). Издательство Робертс и Ко. ISBN 978-0-9747077-2-3 .
^ А. Э. Зигман (1986). Лазеры . Университетские научные книги. ISBN 978-0-935702-11-8 . Глава 16.
^ Янг и Фридман (2020) , стр. 1187–1188.
^ Янг и Фридман (2020) , с. 512, 1189.
^ Янг и Фридман (2020) , стр. 1191–1192.
^ Перейти обратно: ^а ^б П. Харихаран (2003). Оптическая интерферометрия (PDF) (2-е изд.). Сан-Диего, США: Academic Press. ISBN 978-0-12-325220-3 . Архивировано (PDF) из оригинала 6 апреля 2008 г.
^ Э. Р. Гувер (1977). Колыбель величия: национальные и мировые достижения Западного заповедника Огайо . Кливленд: Ассоциация сбережений шейкеров.
^ Янг и Фридман (2020) , стр. 1198–1200.
^ Обер, Дж.Л. (1760). Мемуары по истории науки и изобразительного искусства [ Мемуары по истории науки и изобразительного искусства ] (на французском языке). Париж: Печать. из САС; У Э. Гано. п. 149 .
^ Брюстер, Д. (1831). Трактат по оптике . Лондон: Лонгман, Рис, Орм, Браун и Грин и Джон Тейлор. п. 95 .
^ Гук, Р. (1665). Микрография, или Некоторые физиологические описания мельчайших тел, сделанные с помощью лупы . Лондон: Дж. Мартин и Дж. Аллестри. ISBN 978-0-486-49564-4 .
^ Тернбулл, HW (1940–1941). «Ранние отношения Шотландии с Королевским обществом: И. Джеймс Грегори, FRS (1638–1675)» . Заметки и отчеты Лондонского королевского общества . 3 : 22–38. дои : 10.1098/rsnr.1940.0003 .
^ Ротман, Т. (2003). Все относительно и другие басни в науке и технике . Нью-Джерси: Уайли. ISBN 978-0-471-20257-8 .
^ Хехт (2017) , с. 5.
^ Хехт (2017) , стр. 398–399; Янг и Фридман (2020) , с. 1192.
^ Хехт (2017) , стр. 488–491; Янг и Фридман (2020) , стр. 1224–1225.
^ Лонгхерст, RS (1968). Геометрическая и физическая оптика (2-е изд.). Лондон: Лонгманс. Бибкод : 1967гпо..книга.....Л .
^ Хехт (2017) , с. 497; Янг и Фридман (2020) , стр. 1228–1230.
^ Хехт (2017) , с. 482.
^ Хехт (2017) , с. 485; Янг и Фридман (2020) , с. 1232.
^ Таббс, Роберт Найджел (сентябрь 2003 г.). Удачное воздействие: астрономические изображения атмосферы, ограниченные дифракцией (докторская диссертация). Кембриджский университет. Архивировано из оригинала 5 октября 2008 г.
^ К. Ф. Борен и Д. Р. Хаффман (1983). Поглощение и рассеяние света малыми частицами . Уайли. ISBN 978-0-471-29340-8 .
^ Перейти обратно: ^а ^б Джей Ди Джексон (1975). Классическая электродинамика (2-е изд.). Уайли. п. 286 . ISBN 978-0-471-43132-9 .
^ Хехт (2017) , стр. 202–204.
^ Перейти обратно: ^а ^б Р. Рамасвами; К. Н. Сивараян (1998). Оптические сети: практический взгляд . Лондон: Академическая пресса. ISBN 978-0-12-374092-2 . Архивировано из оригинала 27 октября 2015 г.
^ Бриллюэн, Леон. Распространение волн и групповая скорость . Academic Press Inc., Нью-Йорк (1960)
^ М. Борн и Э. Вольф (1999). Принцип оптики . Кембридж: Издательство Кембриджского университета. стр. 14–24. ISBN 978-0-521-64222-4 .
^ Хехт (2017) , стр. 333–334; Янг и Фридман (2020) , стр. 1083, 1118.
^ Перейти обратно: ^а ^б Хехт (2017) , с. 336.
^ Хехт (2017) , стр. 330–332; Янг и Фридман (2020) , с. 1123.
^ Хехт (2017) , стр. 333–334; Янг и Фридман (2020) , с. 1123.
^ Хехт (2017) , стр. 334–335; Янг и Фридман (2020) , с. 1124.
^ Хехт (2017) , стр. 379–383.
^ Янг и Фридман (2020) , с. 1124.
^ Хехт (2017) , стр. 367, 373.
^ Хехт (2017) , с. 372; Янг и Фридман (2020) , стр. 1124–1125.
^ Ф. Дж. Дуарте (2015). Перестраиваемая лазерная оптика (2-е изд.). Нью-Йорк: CRC. стр. 117–120. ISBN 978-1-4822-4529-5 . Архивировано из оригинала 02 апреля 2015 г.
^ Хехт (2017) , с. 338; Янг и Фридман (2020) , стр. 1119–1121.
^ Хехт (2017) , стр. 339–342.
^ Хехт (2017) , стр. 355–358.
^ Хехт (2017) , стр. 353–356.
^ Уоллс, Дэниел Франк ; Милберн, Дж.Дж. (1994). Квантовая оптика . Спрингер.
^ Маколей, Аластер Д. (16 января 1991 г.). Оптические компьютерные архитектуры: применение оптических концепций к компьютерам следующего поколения . Уайли. ISBN 978-0-471-63242-9 .
^ Шен, Ю.Р. (1984). Принципы нелинейной оптики . Нью-Йорк: Wiley-Interscience. ISBN 978-0-471-88998-4 .
^ «лазер» . Справочник.com. Архивировано из оригинала 31 марта 2008 г. Проверено 15 мая 2008 г.
^ Чарльз Х. Таунс - Нобелевская лекция. Архивировано 11 октября 2008 г. в Wayback Machine . nobelprize.org
^ «Искусственная звезда VLT» . Картинка недели ESO . Архивировано из оригинала 3 июля 2014 года . Проверено 25 июня 2014 г.
^ Ч. Т. Таунс. «Первый лазер» . Чикагский университет. Архивировано из оригинала 17 мая 2008 г. Проверено 15 мая 2008 г.
^ CH Таунс (2003). «Первый лазер» . В Лоре Гарвин ; Тим Линкольн (ред.). Век природы: двадцать одно открытие, изменившее науку и мир . Издательство Чикагского университета. стр. 107–112 . ISBN 978-0-226-28413-2 .
^ Что такое штрих-код? Архивировано 23 апреля 2012 г. на сайте Wayback Machine denso-wave.com.
^ «Как был разработан компакт-диск» . Новости Би-би-си . 17 августа 2007 г. Архивировано из оригинала 7 января 2012 г. Проверено 17 августа 2007 г.
^ Дж. Уилсон и JFB Хоукс (1987). Лазеры: принципы и применение, Международная серия Прентис Холл по оптоэлектронике . Прентис Холл. ISBN 978-0-13-523697-0 .
^ Перейти обратно: ^а ^б ^с Д. Атчисон и Г. Смит (2000). Оптика человеческого глаза . Эльзевир. ISBN 978-0-7506-3775-6 .
^ Перейти обратно: ^а ^б Э. Р. Кандель; Дж. Х. Шварц; ТМ Джесселл (2000). Принципы нейронауки (4-е изд.). Нью-Йорк: МакГроу-Хилл. стр. 507–513 . ISBN 978-0-8385-7701-1 .
^ Перейти обратно: ^а ^б Д. Мейстер. «Дизайн офтальмологических линз» . OptiCampus.com. Архивировано из оригинала 27 декабря 2008 года . Проверено 12 ноября 2008 г.
^ Дж. Брайнер (2 июня 2008 г.). «Ключ ко всем обнаруженным оптическим иллюзиям» . ЖиваяНаука. Архивировано из оригинала 5 сентября 2008 г.
↑ Геометрия точки схода. Архивировано 22 июня 2008 г. в Wayback Machine на сайте Convergence. Архивировано 13 июля 2007 г. в Wayback Machine.
^ «Объяснение лунной иллюзии». Архивировано 4 декабря 2015 г. в Wayback Machine , Дон Маккриди, Университет Висконсин-Уайтуотер.
^ АК Джайн; М. Фигейредо; Дж. Зерубия (2001). Методы минимизации энергии в компьютерном зрении и распознавании образов . Спрингер. ISBN 978-3-540-42523-6 .
^ Янг и Фридман (2020) , стр. 1171–1175.
^ Янг и Фридман (2020) , стр. 1171–1173.
^ ЧП Нотнагл; У. Чемберс; М.В. Дэвидсон. «Введение в стереомикроскопию» . Никон МикроскопияУ. Архивировано из оригинала 16 сентября 2011 г.
^ Янг и Фридман (2020) , с. 1174.
^ Янг и Фридман (2020) , стр. 1175.
^ Сэмюэл Эдвард Шеппард и Чарльз Эдвард Кеннет Мис (1907). Исследования по теории фотографического процесса . Лонгманс, Грин и Ко. р. 214 .
^ Би Джей Зюсс (2003). Освоение черно-белой фотографии . Олворт Коммуникейшнс. ISBN 978-1-58115-306-4 .
^ Эм Джей Лэнгфорд (2000). Базовая фотография . Фокальная пресса. ISBN 978-0-240-51592-2 .
^ Перейти обратно: ^а ^б Уоррен, Брюс (2001). Фотография . Cengage Обучение. п. 71. ИСБН 978-0-7668-1777-7 . Архивировано из оригинала 19 августа 2016 г.
^ Лесли Д. Штробель (1999). Посмотреть технику камеры . Фокальная пресса. ISBN 978-0-240-80345-6 .
^ С. Симмонс (1992). Использование камеры просмотра . Амфотокниги. п. 35. ISBN 978-0-8174-6353-3 .
^ Сидни Ф. Рэй (2002). Прикладная фотографическая оптика: линзы и оптические системы для фотографии, кино, видео, электронного и цифрового изображения . Фокальная пресса. п. 294. ИСБН 978-0-240-51540-3 . Архивировано из оригинала 19 августа 2016 г.
^ Сотрудники Нью-Йорк Таймс (2004). Путеводитель New York Times по основным знаниям . Макмиллан. ISBN 978-0-312-31367-8 .
^ Р. Р. Карлтон; А. Маккенна Адлер (2000). Принципы рентгенографической визуализации: искусство и наука . Томсон Делмар Обучение. ISBN 978-0-7668-1300-7 .
^ У. Кроуфорд (1979). Хранители света: история и рабочее руководство по ранним фотографическим процессам . Доббс Ферри, Нью-Йорк: Морган и Морган. п. 20. ISBN 978-0-87100-158-0 .
^ Дж. М. Коули (1975). Дифракционная физика . Амстердам: Северная Голландия. ISBN 978-0-444-10791-6 .
^ CD Аренс (1994). Метеорология сегодня: введение в погоду, климат и окружающую среду (5-е изд.). Западная издательская компания. стр. 88–89 . ISBN 978-0-314-02779-5 .
^ А. Янг. «Введение в миражи» . Архивировано из оригинала 10 января 2010 г.
^ Янг и Фридман (2020) , стр. 1117–1118.

Цитируемые работы

Хехт, Юджин (2017). Оптика (5-е изд.). Пирсон Образование. ISBN 978-0-133-97722-6 .
Янг, Хью Д.; Фридман, Роджер А. (2020). Университетская физика: расширенная версия с современной физикой (15-е изд.). Пирсон Образование. ISBN 978-1-292-31473-0 .

Дальнейшее чтение

Борн, Макс; Вольф, Эмиль (2002). Принципы оптики . Издательство Кембриджского университета. ISBN 978-1-139-64340-5 .
Фаулз, Грант Р. (1975). Введение в современную оптику (4-е изд.). Эддисон-Уэсли Лонгман.
Липсон, Стивен Г.; Липсон, Генри; Тангхаузер, Дэвид Стефан (1995). Оптическая физика . Издательство Кембриджского университета. ISBN 978-0-521-43631-1 .
Сервей, Раймонд А.; Джуэтт, Джон В. (2004). Физика для ученых и инженеров (6-е, иллюстрированное изд.). Бельмонт, Калифорния: Томсон-Брукс/Коул. ISBN 978-0-534-40842-8 .
Типлер, Пол А.; Моска, Джин (2004). Физика для ученых и инженеров: электричество, магнетизм, свет и элементарная современная физика . Том. 2. У. Х. Фриман. ISBN 978-0-7167-0810-0 .

Внешние ссылки

Соответствующие обсуждения

Оптика в наше время на BBC

Учебники и учебные пособия

Свет и материя - учебник с открытым исходным кодом, содержащий рассмотрение оптики в гл. 28-32
Optics2001 - Библиотека и сообщество оптики.
Фундаментальная оптика - Техническое руководство Меллеса Грио
Физика света и оптика - Университета Бригама Янга Книга для студентов
Оптика для фотоэлектрических систем – пошаговое введение в классическую оптику

Дальнейшее чтение

Оптика и фотоника: физика, улучшающая нашу жизнь по публикациям Института физики

Общества

Европейский консорциум индустрии фотоники – ссылка

[McGrawHill-1] Перейти обратно: ^а ^б Энциклопедия науки и технологий МакГроу-Хилла (5-е изд.). МакГроу-Хилл. 1993.

[2] «Самый старый телескоп в мире?» . Новости Би-би-си . 1 июля 1999 года. Архивировано из оригинала 1 февраля 2009 года . Проверено 3 января 2010 г.

[3] Т. Ф. Хоад (1996). Краткий Оксфордский словарь английской этимологии . ISBN 978-0-19-283098-2 .

[4] История глаза . Архивировано 20 января 2012 г. в Wayback Machine . Стэнфорд.edu. Проверено 10 июня 2012 г.

[5] Т.Л. Хит (2003). Руководство по греческой математике . Публикации Courier Dover. стр. 181–182. ISBN 978-0-486-43231-1 .

[6] Уильям Р. Аттал (1983). Визуальное обнаружение формы в трехмерном пространстве . Психология Пресс. стр. 25–. ISBN 978-0-89859-289-4 . Архивировано из оригинала 3 мая 2016 г.

[7] Евклид (1999). Элахе Хейрандиш (ред.). Арабская версия оптики Евклида = Китаб Уклидис фи ихтилаф аль-манацир . Нью-Йорк: Спрингер. ISBN 978-0-387-98523-7 .

[Ptolemy-8] Перейти обратно: ^а ^б Птолемей (1996). А. Марк Смит (ред.). Теория зрительного восприятия Птолемея: английский перевод «Оптики» с введением и комментариями . Издательство ДИАНА. ISBN 978-0-87169-862-9 .

[9] Адамсон, Питер (2006). «Аль-Кинди и рецепция греческой философии». В Адамсоне, Питер; Тейлор, Р. Кембриджский спутник арабской философии. Издательство Кембриджского университета. п. 45. ISBN 978-0-521-52069-0 .

[j1-10] Перейти обратно: ^а ^б Рашед, Рошди (1990). «Пионер анакластики: Ибн Сахл о горящих зеркалах и линзах». Исида . 81 (3): 464–491. дои : 10.1086/355456 . JSTOR 233423 . S2CID 144361526 .

[11] 
Хогендейк, Ян П.; Сабра, Абдельхамид И., ред. (2003). Предприятие науки в исламе: новые перспективы . МТИ Пресс. стр. 85–118. ISBN 978-0-262-19482-2 . OCLC 50252039 .
Дж. Хэтфилд (1996). «Была ли научная революция действительно революцией в науке?». В Ф.Дж. Рагепе; П. Салли; С. Дж. Ливси (ред.). Традиция, передача, трансформация: материалы двух конференций по досовременной науке, состоявшихся в Университете Оклахомы . Издательство «Брилл». п. 500. ИСБН 978-90-04-10119-7 . Архивировано из оригинала 27 апреля 2016 г.
Надер Эль-Бизри (2005). «Философский взгляд на оптику Альхазена». Арабские науки и философия . 15 (2): 189–218. дои : 10.1017/S0957423905000172 . S2CID 123057532 .
Надер Эль-Бизри (2007). «В защиту суверенитета философии: критика аль-Багдади геометризации места Ибн аль-Хайсама». Арабские науки и философия . 17 :57–80. дои : 10.1017/S0957423907000367 . S2CID 170960993 .
Г. Саймон (2006). «Взгляд у Ибн аль-Хайсама». Журнал средневековой истории . 9 : 89–98. дои : 10.1177/097194580500900105 . S2CID 170628785 .

[12] Хогендейк, Ян П.; Сабра, Абдельхамид И., ред. (2003). Предприятие науки в исламе: новые перспективы . МТИ Пресс. стр. 85–118. ISBN 978-0-262-19482-2 . OCLC 50252039 .

[13] Дж. Хэтфилд (1996). «Была ли научная революция действительно революцией в науке?». В Ф.Дж. Рагепе; П. Салли; С. Дж. Ливси (ред.). Традиция, передача, трансформация: материалы двух конференций по досовременной науке, состоявшихся в Университете Оклахомы . Издательство «Брилл». п. 500. ИСБН 978-90-04-10119-7 . Архивировано из оригинала 27 апреля 2016 г.

[14] Надер Эль-Бизри (2005). «Философский взгляд на оптику Альхазена». Арабские науки и философия . 15 (2): 189–218. дои : 10.1017/S0957423905000172 . S2CID 123057532 .

[15] Надер Эль-Бизри (2007). «В защиту суверенитета философии: критика аль-Багдади геометризации места Ибн аль-Хайсама». Арабские науки и философия . 17 :57–80. дои : 10.1017/S0957423907000367 . S2CID 170960993 .

[16] Г. Саймон (2006). «Взгляд у Ибн аль-Хайсама». Журнал средневековой истории . 9 : 89–98. дои : 10.1177/097194580500900105 . S2CID 170628785 .

[12] Ян П. Ховард; Брайан Дж. Роджерс (1995). Бинокулярное зрение и стереопсис . Издательство Оксфордского университета. п. 7. ISBN 978-0-19-508476-4 . Архивировано из оригинала 6 мая 2016 г.

[13] Елена Агацци; Энрико Джаннетто; Франко Джудиче (2010). Представление света в искусстве и науке: теории и практики . В&Р Юнипресс ГмбХ. п. 42. ИСБН 978-3-89971-735-8 . Архивировано из оригинала 10 мая 2016 г.

[14] Эль-Бизри, Надер (2010). «Классическая оптика и традиции перспективы, ведущие к Возрождению». В Хендриксе, Джон Шеннон ; Карман, Чарльз Х. (ред.). Ренессансные теории видения (визуальная культура в раннем Новом времени) . Фарнем, Суррей: Ashgate Publishing . стр. 11–30. ISBN 978-1-4094-0024-0 . ; Эль-Бизри, Надер (2014). «Видеть реальность в перспективе: «Искусство оптики» и «Наука живописи» ». В Лупаккини, Росселла; Анджелини, Аннарита (ред.). Искусство науки: от перспективного рисунка к квантовой случайности . Доредрехт: Спрингер. стр. 25–47.

[15] DC Линдберг, Теории видения от аль-Кинди до Кеплера , (Чикаго: Чикагский университет, 1976), стр. 94–99.

[16] Иларди, Винсент (2007). Видение эпохи Возрождения от очков к телескопам . Филадельфия: Американское философское общество. стр. 4–5. ISBN 978-0-87169-259-7 .

[17] «Проект Галилео> Наука> Телескоп», Эл Ван Хелден. Архивировано 20 марта 2012 г. в Wayback Machine . Галилео.rice.edu. Проверено 10 июня 2012 г.

[18] Генри К. Кинг (2003). История телескопа . Публикации Courier Dover. п. 27. ISBN 978-0-486-43265-6 . Архивировано из оригинала 17 июня 2016 г.

[19] Пол С. Агаттер; Денис Н. Уитли (2008). Размышление о жизни: история и философия биологии и других наук . Спрингер. п. 17. ISBN 978-1-4020-8865-0 . Архивировано из оригинала 16 мая 2016 г.

[FOOTNOTEIlardi2007[httpsarchiveorgdetailsbub_gb_peIL7hVQUmwCpagen221_210]-20] Иларди (2007) , с. 210 .

[21] Микроскопы: временная шкала. Архивировано 9 января 2010 г. в Wayback Machine , Нобелевский фонд. Проверено 3 апреля 2009 г.

[LZZginzib4C_page_55-22] Уотсон, Фред (2007). Звездочёт: Жизнь и времена телескопа . Аллен и Анвин. п. 55. ИСБН 978-1-74175-383-7 . Архивировано из оригинала 8 мая 2016 г.

[23] Каспар, Макс (1993) [Впервые опубликовано в 1959 году]. Кеплер . Дуврские публикации. стр. 142–146. ISBN 0-486-67605-6 .

[FOOTNOTEIlardi2007[httpsarchiveorgdetailsbub_gb_peIL7hVQUmwCpagen255_244]-24] Иларди (2007) , с. 244 .

[FOOTNOTECaspar1993[httpsarchiveorgdetailskepler00casppage192mode2up_192–202]-25] Каспар (1993) , стр. 192–202 .

[Sabra-26] Перейти обратно: ^а ^б А. И. Сабра (1981). Теории света от Декарта до Ньютона . Архив Кубка. ISBN 978-0-521-28436-3 .

[27] В. Ф. Мэги (1935). Справочник по физике . Издательство Гарвардского университета. п. 309 .

[28] Дж. К. Максвелл (1865). «Динамическая теория электромагнитного поля» . Философские труды Лондонского королевского общества . 155 : 459–512. Бибкод : 1865RSPT..155..459C . дои : 10.1098/rstl.1865.0008 . S2CID 186207827 .

[29] Твердый подход к сложности интеллектуальной мотивации Планка в отношении кванта, а также его неохотное принятие его последствий см. Х. Краг, Макс Планк: сопротивляющийся революционер. Архивировано 1 апреля 2012 г. в Wayback Machine , Мир физики . Декабрь 2000 года.

[30] Эйнштейн, А. (1967). «Об эвристической точке зрения на производство и преобразование света». В Тер Хаар, Д. (ред.). Старая квантовая теория . Пергамон. стр. 91–107 . OCLC 534625 . Эта глава представляет собой английский перевод статьи Эйнштейна 1905 года о фотоэлектрическом эффекте.

[AnnPhysik322132-31] Эйнштейн, А. (1905). «Об эвристической точке зрения на производство и преобразование света». Анналы физики (на немецком языке). 322 (6): 132–148. Бибкод : 1905АнП...322..132Е . дои : 10.1002/andp.19053220607 .

[32] «О строении атомов и молекул» . Философский журнал . 26, серия 6: 1–25. 1913. Архивировано из оригинала 4 июля 2007 года . Знаковая статья, в которой изложена модель атома и молекулярной связи Бора .

[33] Р. Фейнман (1985). «Глава 1». КЭД: Странная теория света и материи . Издательство Принстонского университета. п. 6. ISBN 978-0-691-08388-9 .

[34] Н. Тейлор (2000). ЛАЗЕР: изобретатель, нобелевский лауреат и тридцатилетняя патентная война . Нью-Йорк: Саймон и Шустер. ISBN 978-0-684-83515-0 .

[35] Ариэль Липсон; Стивен Г. Липсон; Генри Липсон (28 октября 2010 г.). Оптическая физика . Издательство Кембриджского университета. п. 48. ИСБН 978-0-521-49345-1 . Архивировано из оригинала 28 мая 2013 года . Проверено 12 июля 2012 г.

[36] Артур Шустер (1904). Введение в теорию оптики . Э. Арнольд. п. 41 .

[37] Дж. Э. Грейвенкамп (2004). Полевое руководство по геометрической оптике. Полевые руководства SPIE, том. ФГ01 . ШПИОН. стр. 19–20. ISBN 978-0-8194-5294-8 .

[FOOTNOTEYoungFreedman20201109-38] Перейти обратно: ^а ^б Янг и Фридман (2020) , с. 1109.

[FOOTNOTEYoungFreedman20201112–1113-39] Янг и Фридман (2020) , стр. 1112–1113.

[FOOTNOTEYoungFreedman20201142–1143,_1145-40] Янг и Фридман (2020) , стр. 1142–1143, 1145.

[FOOTNOTEYoungFreedman20201116-41] Перейти обратно: ^а ^б Янг и Фридман (2020) , с. 1116.

[42] Маршан, EW (1978). Градиентная индексная оптика . Нью-Йорк: Академическая пресса.

[FOOTNOTEYoungFreedman20201113–1115-43] Янг и Фридман (2020) , стр. 1113–1115.

[FOOTNOTEHecht2017159-44] Хехт (2017) , с. 159.

[FOOTNOTEHecht2017165-45] Хехт (2017) , с. 165.

[FOOTNOTEYoungFreedman20201157-46] Янг и Фридман (2020) , с. 1157.

[FOOTNOTEYoungFreedman20201143,1163,1175-47] Янг и Фридман (2020) , с. 1143,1163,1175.

[48] М. В. Кляйн и Т. Е. Фуртак, 1986, Оптика, John Wiley & Sons, Нью-Йорк ISBN 0-471-87297-0 .

[49] Максвелл, Джеймс Клерк (1865). «Динамическая теория электромагнитного поля» (PDF) . Философские труды Лондонского королевского общества . 155 : 499. Бибкод : 1865RSPT..155..459C . дои : 10.1098/rstl.1865.0008 . S2CID 186207827 . Архивировано (PDF) из оригинала 28 июля 2011 г. Эта статья сопровождала презентацию Максвелла Королевскому обществу от 8 декабря 1864 года. См. также Динамическую теорию электромагнитного поля .

[Born_and_Wolf-50] М. Борн и Э. Вольф (1999). Принцип оптики . Кембридж: Издательство Кембриджского университета. ISBN 0-521-64222-1 .

[51] Дж. Гудман (2005). Введение в оптику Фурье (3-е изд.). Издательство Робертс и Ко. ISBN 978-0-9747077-2-3 .

[52] А. Э. Зигман (1986). Лазеры . Университетские научные книги. ISBN 978-0-935702-11-8 . Глава 16.

[FOOTNOTEYoungFreedman20201187–1188-53] Янг и Фридман (2020) , стр. 1187–1188.

[FOOTNOTEYoungFreedman2020512,_1189-54] Янг и Фридман (2020) , с. 512, 1189.

[FOOTNOTEYoungFreedman20201191–1192-55] Янг и Фридман (2020) , стр. 1191–1192.

[interferometry-56] Перейти обратно: ^а ^б П. Харихаран (2003). Оптическая интерферометрия (PDF) (2-е изд.). Сан-Диего, США: Academic Press. ISBN 978-0-12-325220-3 . Архивировано (PDF) из оригинала 6 апреля 2008 г.

[57] Э. Р. Гувер (1977). Колыбель величия: национальные и мировые достижения Западного заповедника Огайо . Кливленд: Ассоциация сбережений шейкеров.

[FOOTNOTEYoungFreedman20201198–1200-58] Янг и Фридман (2020) , стр. 1198–1200.

[59] Обер, Дж.Л. (1760). Мемуары по истории науки и изобразительного искусства [ Мемуары по истории науки и изобразительного искусства ] (на французском языке). Париж: Печать. из САС; У Э. Гано. п. 149 .

[60] Брюстер, Д. (1831). Трактат по оптике . Лондон: Лонгман, Рис, Орм, Браун и Грин и Джон Тейлор. п. 95 .

[61] Гук, Р. (1665). Микрография, или Некоторые физиологические описания мельчайших тел, сделанные с помощью лупы . Лондон: Дж. Мартин и Дж. Аллестри. ISBN 978-0-486-49564-4 .

[62] Тернбулл, HW (1940–1941). «Ранние отношения Шотландии с Королевским обществом: И. Джеймс Грегори, FRS (1638–1675)» . Заметки и отчеты Лондонского королевского общества . 3 : 22–38. дои : 10.1098/rsnr.1940.0003 .

[63] Ротман, Т. (2003). Все относительно и другие басни в науке и технике . Нью-Джерси: Уайли. ISBN 978-0-471-20257-8 .

[FOOTNOTEHecht20175-64] Хехт (2017) , с. 5.

[FOOTNOTEHecht2017398–399YoungFreedman20201192-65] Хехт (2017) , стр. 398–399; Янг и Фридман (2020) , с. 1192.

[FOOTNOTEHecht2017488–491YoungFreedman20201224–1225-66] Хехт (2017) , стр. 488–491; Янг и Фридман (2020) , стр. 1224–1225.

[phyoptics-67] Лонгхерст, RS (1968). Геометрическая и физическая оптика (2-е изд.). Лондон: Лонгманс. Бибкод : 1967гпо..книга.....Л .

[FOOTNOTEHecht2017497YoungFreedman20201228–1230-68] Хехт (2017) , с. 497; Янг и Фридман (2020) , стр. 1228–1230.

[FOOTNOTEHecht2017482-69] Хехт (2017) , с. 482.

[FOOTNOTEHecht2017485YoungFreedman20201232-70] Хехт (2017) , с. 485; Янг и Фридман (2020) , с. 1232.

[71] Таббс, Роберт Найджел (сентябрь 2003 г.). Удачное воздействие: астрономические изображения атмосферы, ограниченные дифракцией (докторская диссертация). Кембриджский университет. Архивировано из оригинала 5 октября 2008 г.

[72] К. Ф. Борен и Д. Р. Хаффман (1983). Поглощение и рассеяние света малыми частицами . Уайли. ISBN 978-0-471-29340-8 .

[J286-73] Перейти обратно: ^а ^б Джей Ди Джексон (1975). Классическая электродинамика (2-е изд.). Уайли. п. 286 . ISBN 978-0-471-43132-9 .

[FOOTNOTEHecht2017202–204-74] Хехт (2017) , стр. 202–204.

[optnet-75] Перейти обратно: ^а ^б Р. Рамасвами; К. Н. Сивараян (1998). Оптические сети: практический взгляд . Лондон: Академическая пресса. ISBN 978-0-12-374092-2 . Архивировано из оригинала 27 октября 2015 г.

[76] Бриллюэн, Леон. Распространение волн и групповая скорость . Academic Press Inc., Нью-Йорк (1960)

[77] М. Борн и Э. Вольф (1999). Принцип оптики . Кембридж: Издательство Кембриджского университета. стр. 14–24. ISBN 978-0-521-64222-4 .

[FOOTNOTEHecht2017333–334YoungFreedman20201083,_1118-78] Хехт (2017) , стр. 333–334; Янг и Фридман (2020) , стр. 1083, 1118.

[FOOTNOTEHecht2017336-79] Перейти обратно: ^а ^б Хехт (2017) , с. 336.

[FOOTNOTEHecht2017330–332YoungFreedman20201123-80] Хехт (2017) , стр. 330–332; Янг и Фридман (2020) , с. 1123.

[FOOTNOTEHecht2017333–334YoungFreedman20201123-81] Хехт (2017) , стр. 333–334; Янг и Фридман (2020) , с. 1123.

[FOOTNOTEHecht2017334–335YoungFreedman20201124-82] Хехт (2017) , стр. 334–335; Янг и Фридман (2020) , с. 1124.

[FOOTNOTEHecht2017379–383-83] Хехт (2017) , стр. 379–383.

[FOOTNOTEYoungFreedman20201124-84] Янг и Фридман (2020) , с. 1124.

[FOOTNOTEHecht2017367,_373-85] Хехт (2017) , стр. 367, 373.

[FOOTNOTEHecht2017372YoungFreedman20201124–1125-86] Хехт (2017) , с. 372; Янг и Фридман (2020) , стр. 1124–1125.

[87] Ф. Дж. Дуарте (2015). Перестраиваемая лазерная оптика (2-е изд.). Нью-Йорк: CRC. стр. 117–120. ISBN 978-1-4822-4529-5 . Архивировано из оригинала 02 апреля 2015 г.

[FOOTNOTEHecht2017338YoungFreedman20201119–1121-88] Хехт (2017) , с. 338; Янг и Фридман (2020) , стр. 1119–1121.

[FOOTNOTEHecht2017339–342-89] Хехт (2017) , стр. 339–342.

[FOOTNOTEHecht2017355–358-90] Хехт (2017) , стр. 355–358.

[FOOTNOTEHecht2017353–356-91] Хехт (2017) , стр. 353–356.

[92] Уоллс, Дэниел Франк ; Милберн, Дж.Дж. (1994). Квантовая оптика . Спрингер.

[93] Маколей, Аластер Д. (16 января 1991 г.). Оптические компьютерные архитектуры: применение оптических концепций к компьютерам следующего поколения . Уайли. ISBN 978-0-471-63242-9 .

[94] Шен, Ю.Р. (1984). Принципы нелинейной оптики . Нью-Йорк: Wiley-Interscience. ISBN 978-0-471-88998-4 .

[95] «лазер» . Справочник.com. Архивировано из оригинала 31 марта 2008 г. Проверено 15 мая 2008 г.

[96] Чарльз Х. Таунс - Нобелевская лекция. Архивировано 11 октября 2008 г. в Wayback Machine . nobelprize.org

[97] «Искусственная звезда VLT» . Картинка недели ESO . Архивировано из оригинала 3 июля 2014 года . Проверено 25 июня 2014 г.

[98] Ч. Т. Таунс. «Первый лазер» . Чикагский университет. Архивировано из оригинала 17 мая 2008 г. Проверено 15 мая 2008 г.

[99] CH Таунс (2003). «Первый лазер» . В Лоре Гарвин ; Тим Линкольн (ред.). Век природы: двадцать одно открытие, изменившее науку и мир . Издательство Чикагского университета. стр. 107–112 . ISBN 978-0-226-28413-2 .

[100] Что такое штрих-код? Архивировано 23 апреля 2012 г. на сайте Wayback Machine denso-wave.com.

[BBC6950933-101] «Как был разработан компакт-диск» . Новости Би-би-си . 17 августа 2007 г. Архивировано из оригинала 7 января 2012 г. Проверено 17 августа 2007 г.

[102] Дж. Уилсон и JFB Хоукс (1987). Лазеры: принципы и применение, Международная серия Прентис Холл по оптоэлектронике . Прентис Холл. ISBN 978-0-13-523697-0 .

[eyeoptics-103] Перейти обратно: ^а ^б ^с Д. Атчисон и Г. Смит (2000). Оптика человеческого глаза . Эльзевир. ISBN 978-0-7506-3775-6 .

[Kandel-104] Перейти обратно: ^а ^б Э. Р. Кандель; Дж. Х. Шварц; ТМ Джесселл (2000). Принципы нейронауки (4-е изд.). Нью-Йорк: МакГроу-Хилл. стр. 507–513 . ISBN 978-0-8385-7701-1 .

[lensdesign-105] Перейти обратно: ^а ^б Д. Мейстер. «Дизайн офтальмологических линз» . OptiCampus.com. Архивировано из оригинала 27 декабря 2008 года . Проверено 12 ноября 2008 г.

[106] Дж. Брайнер (2 июня 2008 г.). «Ключ ко всем обнаруженным оптическим иллюзиям» . ЖиваяНаука. Архивировано из оригинала 5 сентября 2008 г.

[107] Геометрия точки схода. Архивировано 22 июня 2008 г. в Wayback Machine на сайте Convergence. Архивировано 13 июля 2007 г. в Wayback Machine.

[108] «Объяснение лунной иллюзии». Архивировано 4 декабря 2015 г. в Wayback Machine , Дон Маккриди, Университет Висконсин-Уайтуотер.

[109] АК Джайн; М. Фигейредо; Дж. Зерубия (2001). Методы минимизации энергии в компьютерном зрении и распознавании образов . Спрингер. ISBN 978-3-540-42523-6 .

[FOOTNOTEYoungFreedman20201171–1175-110] Янг и Фридман (2020) , стр. 1171–1175.

[FOOTNOTEYoungFreedman20201171–1173-111] Янг и Фридман (2020) , стр. 1171–1173.

[112] ЧП Нотнагл; У. Чемберс; М.В. Дэвидсон. «Введение в стереомикроскопию» . Никон МикроскопияУ. Архивировано из оригинала 16 сентября 2011 г.

[FOOTNOTEYoungFreedman20201174-113] Янг и Фридман (2020) , с. 1174.

[FOOTNOTEYoungFreedman20201175-114] Янг и Фридман (2020) , стр. 1175.

[115] Сэмюэл Эдвард Шеппард и Чарльз Эдвард Кеннет Мис (1907). Исследования по теории фотографического процесса . Лонгманс, Грин и Ко. р. 214 .

[116] Би Джей Зюсс (2003). Освоение черно-белой фотографии . Олворт Коммуникейшнс. ISBN 978-1-58115-306-4 .

[117] Эм Джей Лэнгфорд (2000). Базовая фотография . Фокальная пресса. ISBN 978-0-240-51592-2 .

[Bruce_Warren,_Photography,_page_71-118] Перейти обратно: ^а ^б Уоррен, Брюс (2001). Фотография . Cengage Обучение. п. 71. ИСБН 978-0-7668-1777-7 . Архивировано из оригинала 19 августа 2016 г.

[119] Лесли Д. Штробель (1999). Посмотреть технику камеры . Фокальная пресса. ISBN 978-0-240-80345-6 .

[120] С. Симмонс (1992). Использование камеры просмотра . Амфотокниги. п. 35. ISBN 978-0-8174-6353-3 .

[121] Сидни Ф. Рэй (2002). Прикладная фотографическая оптика: линзы и оптические системы для фотографии, кино, видео, электронного и цифрового изображения . Фокальная пресса. п. 294. ИСБН 978-0-240-51540-3 . Архивировано из оригинала 19 августа 2016 г.

[122] Сотрудники Нью-Йорк Таймс (2004). Путеводитель New York Times по основным знаниям . Макмиллан. ISBN 978-0-312-31367-8 .

[123] Р. Р. Карлтон; А. Маккенна Адлер (2000). Принципы рентгенографической визуализации: искусство и наука . Томсон Делмар Обучение. ISBN 978-0-7668-1300-7 .

[124] У. Кроуфорд (1979). Хранители света: история и рабочее руководство по ранним фотографическим процессам . Доббс Ферри, Нью-Йорк: Морган и Морган. п. 20. ISBN 978-0-87100-158-0 .

[125] Дж. М. Коули (1975). Дифракционная физика . Амстердам: Северная Голландия. ISBN 978-0-444-10791-6 .

[autogenerated1-126] CD Аренс (1994). Метеорология сегодня: введение в погоду, климат и окружающую среду (5-е изд.). Западная издательская компания. стр. 88–89 . ISBN 978-0-314-02779-5 .

[127] А. Янг. «Введение в миражи» . Архивировано из оригинала 10 января 2010 г.

[FOOTNOTEYoungFreedman20201117–1118-128] Янг и Фридман (2020) , стр. 1117–1118.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

[68]

[69]

[70]

[71]

[72]

[73]

[74]

[75]

[76]

[77]

[78]

[79]

[80]

[81]

[82]

[83]

[84]

[85]

[86]

[87]

[88]

[89]

[90]

[91]

[92]

[93]

[94]

[95]

[96]

[97]

[98]

[99]

[100]

v т и Основные разделы физики
Divisions	Pure Applied Engineering
Approaches	Experimental Theoretical Computational
Classical	Classical mechanics Newtonian Analytical Celestial Continuum Acoustics Classical electromagnetism Classical optics Ray Wave Thermodynamics Statistical Non-equilibrium
Modern	Relativistic mechanics Special General Nuclear physics Quantum mechanics Particle physics Atomic, molecular, and optical physics Atomic Molecular Modern optics Condensed matter physics
Interdisciplinary	Astrophysics Atmospheric physics Biophysics Chemical physics Geophysics Materials science Mathematical physics Medical physics Ocean physics Quantum information science
Related	History of physics Nobel Prize in Physics Philosophy of physics Physics education Timeline of physics discoveries

v т и о стекле Темы науки
Basics	Glass Glass transition Supercooling
Formulation	AgInSbTe Bioglass Borophosphosilicate glass Borosilicate glass Ceramic glaze Chalcogenide glass Cobalt glass Cranberry glass Crown glass Flint glass Fluorosilicate glass Fused quartz GeSbTe Gold ruby glass Lead glass Milk glass Phosphosilicate glass Photochromic lens glass Silicate glass Soda–lime glass Sodium hexametaphosphate Soluble glass Tellurite glass Thoriated glass Ultra low expansion glass Uranium glass Vitreous enamel Wood's glass ZBLAN
Glass-ceramics	Bioactive glass CorningWare Glass-ceramic-to-metal seals Macor Zerodur
Preparation	Annealing Chemical vapor deposition Glass batch calculation Glass forming Glass melting Glass modeling Ion implantation Liquidus temperature sol–gel technique Viscosity Vitrification
Optics	Achromat Dispersion Gradient-index optics Hydrogen darkening Optical amplifier Optical fiber Optical lens design Photochromic lens Photosensitive glass Refraction Transparent materials
Surface modification	Anti-reflective coating Chemically strengthened glass Corrosion Dealkalization DNA microarray Hydrogen darkening Insulated glazing Porous glass Self-cleaning glass sol–gel technique Tempered glass
Diverse topics	Conservation and restoration of glass objects Glass-coated wire Safety glass Glass databases Glass electrode Glass fiber reinforced concrete Glass ionomer cement Glass microspheres Glass-reinforced plastic Glass cloth Glass-to-metal seal Porous glass Pre-preg Prince Rupert's drops Radioactive waste vitrification Windshield Glass fiber