Двойное пространство

В математике любое векторное пространство $V$ имеет соответствующее двойственное векторное пространство (или просто двойственное пространство ), состоящее из всех линейных форм на $V,$ вместе со структурой векторного пространства поточечного сложения и скалярного умножения на константы.

Двойственное пространство, определенное выше, определено для всех векторных пространств, и во избежание двусмысленности его также можно назвать алгебраическим дуальным пространством .При определении топологического векторного пространства существует подпространство двойственного пространства, соответствующее непрерывным линейным функционалам , называемое непрерывным двойственным пространством .

Двойные векторные пространства находят применение во многих разделах математики, в которых используются векторные пространства, например, в тензорном анализе с конечномерными векторными пространствами.Применительно к векторным пространствам функций (которые обычно являются бесконечномерными) двойственные пространства используются для описания мер , распределений и гильбертовых пространств . Следовательно, двойственное пространство является важным понятием в функциональном анализе .

Ранние термины для дуального включают полярный Раум [Hahn 1927], espace conjugué , присоединенное пространство [Alaoglu 1940] и транспоньерный Raum [Schauder 1930] и [Banach 1932]. Термин «двойной» принадлежит Бурбаки в 1938 году.

Алгебраическое двойственное пространство

Учитывая любое векторное пространство $V$ над полем $F$, (алгебраическое) двойственное пространство $V^{*}$ (альтернативно обозначается $V^{\lor }$ или $V'$) определяется как набор всех линейных отображений $\varphi :V\to F$ ( линейные функционалы ). Поскольку линейные карты являются гомоморфизмами векторного пространства , двойственное пространство можно обозначить $\hom(V,F)$. Двойное пространство $V^{*}$ сам становится векторным пространством над $F$ при наличии сложения и скалярного умножения, удовлетворяющего:

${\begin{aligned}(\varphi +\psi )(x)&=\varphi (x)+\psi (x)\\(a\varphi )(x)&=a\left(\varphi (x)\right)\end{aligned}}$

для всех $\varphi ,\psi \in V^{*}$, $x\in V$, и $a\in F$.

Элементы алгебраического дуального пространства $V^{*}$ иногда называют ковекторами , одноформами или линейными формами .

Сопряжение функционала $\varphi$ в двойном пространстве $V^{*}$ и элемент $x$ из $V$ иногда обозначается скобкой: $\varphi (x)=[x,\varphi ]$или $\varphi (x)=\langle x,\varphi \rangle$. Это спаривание определяет невырожденное билинейное отображение $\langle \cdot ,\cdot \rangle :V\times V^{*}\to F$ называется естественным спариванием .

Конечномерный случай

См. Также: Двойная основа

Если $V$ конечномерна, то $V^{*}$ имеет ту же размерность, что и $V$. Учитывая основу $\{\mathbf {e} _{1},\dots ,\mathbf {e} _{n}\}$ в $V$, можно построить конкретный базис в $V^{*}$, называемый двойным базисом . Этот двойственный базис представляет собой множество $\{\mathbf {e} ^{1},\dots ,\mathbf {e} ^{n}\}$ линейных функционалов на $V$, определяемый соотношением

$\mathbf {e} ^{i}(c^{1}\mathbf {e} _{1}+\cdots +c^{n}\mathbf {e} _{n})=c^{i},\quad i=1,\ldots ,n$

при любом выборе коэффициентов $c^{i}\in F$. В частности, если, в свою очередь, каждый из этих коэффициентов будет равен одному, а другие коэффициенты равны нулю, получим систему уравнений

$\mathbf {e} ^{i}(\mathbf {e} _{j})=\delta _{j}^{i}$

где $\delta _{j}^{i}$ — символ дельты Кронекера . Это свойство называется свойством биортогональности .

показывать Доказательство

Consider $\{\mathbf {e} _{1},\dots ,\mathbf {e} _{n}\}$ the basis of V. Let $\{\mathbf {e} ^{1},\dots ,\mathbf {e} ^{n}\}$ be defined as the following: $\mathbf {e} ^{i}(c^{1}\mathbf {e} _{1}+\cdots +c^{n}\mathbf {e} _{n})=c^{i},\quad i=1,\ldots ,n$. These are a basis of $V^{*}$ because: The $\mathbf {e} ^{i},i=1,2,\dots ,n,$ are linear functionals, which map $x,y\in V$ such as $x=\alpha _{1}\mathbf {e} _{1}+\dots +\alpha _{n}\mathbf {e} _{n}$ and $y=\beta _{1}\mathbf {e} _{1}+\dots +\beta _{n}\mathbf {e} _{n}$ to scalars $\mathbf {e} ^{i}(x)=\alpha _{i}$ and $\mathbf {e} ^{i}(y)=\beta _{i}$. Then also, $x+\lambda y=(\alpha _{1}+\lambda \beta _{1})\mathbf {e} _{1}+\dots +(\alpha _{n}+\lambda \beta _{n})\mathbf {e} _{n}$ and $\mathbf {e} ^{i}(x+\lambda y)=\alpha _{i}+\lambda \beta _{i}=\mathbf {e} ^{i}(x)+\lambda \mathbf {e} ^{i}(y)$. Therefore, $\mathbf {e} ^{i}\in V^{*}$ for $i=1,2,\dots ,n$. Suppose $\lambda _{1}\mathbf {e} ^{1}+\cdots +\lambda _{n}\mathbf {e} ^{n}=0\in V^{*}$. Applying this functional on the basis vectors of $V$ successively, lead us to $\lambda _{1}=\lambda _{2}=\dots =\lambda _{n}=0$ (The functional applied in $\mathbf {e} _{i}$ results in $\lambda _{i}$). Therefore, $\{\mathbf {e} ^{1},\dots ,\mathbf {e} ^{n}\}$ is linearly independent on $V^{*}$. Lastly, consider $g\in V^{*}$. Then $g(x)=g(\alpha _{1}\mathbf {e} _{1}+\dots +\alpha _{n}\mathbf {e} _{n})=\alpha _{1}g(\mathbf {e} _{1})+\dots +\alpha _{n}g(\mathbf {e} _{n})=\mathbf {e} ^{1}(x)g(\mathbf {e} _{1})+\dots +\mathbf {e} ^{n}(x)g(\mathbf {e} _{n})$ and $\{\mathbf {e} ^{1},\dots ,\mathbf {e} ^{n}\}$ generates $V^{*}$. Hence, it is a basis of $V^{*}$.

Например, если $V$ является $\mathbb {R} ^{2}$, пусть его базис выбран как $\{\mathbf {e} _{1}=(1/2,1/2),\mathbf {e} _{2}=(0,1)\}$. Базисные векторы не ортогональны друг другу. Затем, $\mathbf {e} ^{1}$ и $\mathbf {e} ^{2}$ являются одноформами (функциями, отображающими вектор в скаляр) такими, что $\mathbf {e} ^{1}(\mathbf {e} _{1})=1$, $\mathbf {e} ^{1}(\mathbf {e} _{2})=0$, $\mathbf {e} ^{2}(\mathbf {e} _{1})=0$, и $\mathbf {e} ^{2}(\mathbf {e} _{2})=1$. (Примечание: верхний индекс здесь представляет собой индекс, а не показатель степени.) Эту систему уравнений можно выразить с использованием матричной записи как

${\begin{bmatrix}e^{11}&e^{12}\\e^{21}&e^{22}\end{bmatrix}}{\begin{bmatrix}e_{11}&e_{21}\\e_{12}&e_{22}\end{bmatrix}}={\begin{bmatrix}1&0\\0&1\end{bmatrix}}.$

Решение неизвестных значений в первой матрице показывает, что двойственный базис $\{\mathbf {e} ^{1}=(2,0),\mathbf {e} ^{2}=(-1,1)\}$. Потому что $\mathbf {e} ^{1}$ и $\mathbf {e} ^{2}$ являются функционалами, их можно переписать как $\mathbf {e} ^{1}(x,y)=2x$ и $\mathbf {e} ^{2}(x,y)=-x+y$.

В общем, когда $V$ является $\mathbb {R} ^{n}$, если $E=[\mathbf {e} _{1}|\cdots |\mathbf {e} _{n}]$ представляет собой матрицу, столбцы которой являются базисными векторами и ${\hat {E}}=[\mathbf {e} ^{1}|\cdots |\mathbf {e} ^{n}]$ - матрица, столбцы которой являются двойственными базисными векторами, тогда

${\hat {E}}^{\textrm {T}}\cdot E=I_{n},$

где $I_{n}$ - единичная матрица порядка $n$. Свойство биортогональности этих двух базисных наборов позволяет любой точке $\mathbf {x} \in V$ быть представленным как

$\mathbf {x} =\sum _{i}\langle \mathbf {x} ,\mathbf {e} ^{i}\rangle \mathbf {e} _{i}=\sum _{i}\langle \mathbf {x} ,\mathbf {e} _{i}\rangle \mathbf {e} ^{i},$

даже если базисные векторы не ортогональны друг другу. Строго говоря, приведенное выше утверждение имеет смысл только тогда, когда внутренний продукт $\langle \cdot ,\cdot \rangle$ и соответствующее спаривание двойственности вводятся, как описано ниже в § Билинейные произведения и двойственные пространства .

В частности, $\mathbb {R} ^{n}$ можно интерпретировать как пространство столбцов $n$ вещественных чисел пространство строк , его двойственное пространство обычно записывается как $n$ реальные цифры. Такой ряд действует на $\mathbb {R} ^{n}$ как линейный функционал путем обычного умножения матриц . Это связано с тем, что функционал отображает каждое $n$-вектор $x$ в действительное число $y$. Тогда, рассматривая этот функционал как матрицу $M$, и $x$ как $n\times 1$ матрица и $y$ а $1\times 1$ матрица (тривиально, действительное число) соответственно, если $Mx=y$ тогда, по соображениям размерности, $M$ должно быть $1\times n$ матрица; то есть, $M$ должен быть вектором-строкой.

Если $V$ состоит из пространства геометрических векторов на плоскости, то кривые уровня элемента $V^{*}$ образуют семейство параллельных прямых в $V$, поскольку диапазон является одномерным, поэтому каждая точка в диапазоне кратна любому одному ненулевому элементу.Итак, элемент $V^{*}$ можно интуитивно представить как определенное семейство параллельных линий, покрывающих плоскость. Чтобы вычислить значение функционала по заданному вектору, достаточно определить, на какой из прямых лежит этот вектор. Неформально это «подсчитывает», сколько линий пересекает вектор.В более общем смысле, если $V$ — векторное пространство любой размерности, то множества уровня линейного функционала в $V^{*}$ являются параллельными гиперплоскостями в $V$, и действие линейного функционала на вектор можно визуализировать в терминах этих гиперплоскостей.

Бесконечномерный случай

Если $V$ не конечномерен, но имеет базис $\mathbf {e} _{\alpha }$ индексируется бесконечным множеством $A$, то та же конструкция, что и в конечномерном случае, дает линейно независимые элементы $\mathbf {e} ^{\alpha }$ ( $\alpha \in A$) двойственного пространства, но они не составят основу.

Например, рассмотрим пространство $\mathbb {R} ^{\infty }$, элементами которого являются последовательности действительных чисел, содержащие только конечное число ненулевых элементов, базис которых индексируется натуральными числами. $\mathbb {N}$. Для $i\in \mathbb {N}$, $\mathbf {e} _{i}$ – это последовательность, состоящая из всех нулей, кроме $i$-я позиция, то есть 1.Двойное пространство $\mathbb {R} ^{\infty }$ (изоморфен) $\mathbb {R} ^{\mathbb {N} }$, пространство всех последовательностей действительных чисел: каждая действительная последовательность $(a_{n})$ определяет функцию, в которой элемент $(x_{n})$ из $\mathbb {R} ^{\infty }$ отправляется на номер

$\sum _{n}a_{n}x_{n},$

что является конечной суммой, поскольку существует лишь конечное число ненулевых $x_{n}$. Размерность ​ ​ $\mathbb {R} ^{\infty }$ счетно бесконечно , тогда как $\mathbb {R} ^{\mathbb {N} }$ не имеет счетного базиса.

Это наблюдение распространяется на любые бесконечномерное векторное пространство $V$ над любым полем $F$: выбор основы $\{\mathbf {e} _{\alpha }:\alpha \in A\}$ идентифицирует $V$ с пространством $(F^{A})_{0}$ функций $f:A\to F$ такой, что $f_{\alpha }=f(\alpha )$ отличен от нуля только для конечного числа $\alpha \in A$, где такая функция $f$ отождествляется с вектором

$\sum _{\alpha \in A}f_{\alpha }\mathbf {e} _{\alpha }$

в $V$ (сумма конечна в силу предположения о $f$и любой $v\in V$ можно записать таким образом однозначно по определению базиса).

Двойное пространство $V$ тогда может быть отождествлено с пространством $F^{A}$ всех из функций $A$ к $F$: линейный функционал $T$ на $V$ однозначно определяется значениями $\theta _{\alpha }=T(\mathbf {e} _{\alpha })$ это принимается на основе $V$и любая функция $\theta :A\to F$ (с $\theta (\alpha )=\theta _{\alpha }$) определяет линейный функционал $T$ на $V$ к

$T\left(\sum _{\alpha \in A}f_{\alpha }\mathbf {e} _{\alpha }\right)=\sum _{\alpha \in A}f_{\alpha }T(e_{\alpha })=\sum _{\alpha \in A}f_{\alpha }\theta _{\alpha }.$

Опять же, сумма конечна, поскольку $f_{\alpha }$ отличен от нуля только для конечного числа $\alpha$.

Набор $(F^{A})_{0}$ может быть отождествлено (по существу по определению) с прямой суммой бесконечного числа копий $F$ (рассматривается как одномерное векторное пространство над собой), индексируемое $A$, т.е. существуют линейные изоморфизмы

$V\cong (F^{A})_{0}\cong \bigoplus _{\alpha \in A}F.$

С другой стороны, $F^{A}$ является (опять же по определению) прямым продуктом бесконечного числа копий $F$ индексируется $A$, и поэтому идентификация

$V^{*}\cong \left(\bigoplus _{\alpha \in A}F\right)^{*}\cong \prod _{\alpha \in A}F^{*}\cong \prod _{\alpha \in A}F\cong F^{A}$

является частным случаем общего результата, связывающего прямые суммы ( модулей ) с прямыми произведениями.

Если векторное пространство не является конечномерным, то его (алгебраическое) двойственное пространство всегда имеет большую размерность (как кардинальное число ), чем исходное векторное пространство. Это контрастирует со случаем непрерывного дуального пространства, обсуждаемым ниже, которое может быть изоморфно исходному векторному пространству, даже если последнее бесконечномерно.

Доказательство этого неравенства между размерностями вытекает из следующего.

Если $V$ представляет собой бесконечномерную $F$-векторном пространстве арифметические свойства кардинальных чисел подразумевают, что

$\mathrm {dim} (V)=|A|<|F|^{|A|}=|V^{\ast }|=\mathrm {max} (|\mathrm {dim} (V^{\ast })|,|F|),$

где мощности обозначены как абсолютные значения . За то, что доказал это $\mathrm {dim} (V)<\mathrm {dim} (V^{*}),$ достаточно доказать, что $|F|\leq |\mathrm {dim} (V^{\ast })|,$ что можно сделать с помощью аргумента, подобного диагональному аргументу Кантора . Точная размерность двойственного дается теоремой Эрдеша-Капланского .

Билинейные произведения и двойственные пространства

Если V конечномерен, то V изоморфен V ^∗ . вообще говоря, нет естественного изоморфизма . Но между этими двумя пространствами, Любая билинейная форма ⟨·,·⟩ на V дает отображение V в его двойственное пространство через

$v\mapsto \langle v,\cdot \rangle$

где правая часть определяется как функционал на V, переводящий каждый w ∈ V в ⟨ v , w ⟩ . Другими словами, билинейная форма определяет линейное отображение

$\Phi _{\langle \cdot ,\cdot \rangle }:V\to V^{*}$

определяется

$\left[\Phi _{\langle \cdot ,\cdot \rangle }(v),w\right]=\langle v,w\rangle .$

Если билинейная форма невырождена , то это изоморфизм на подпространство V ^∗ .Если V конечномерно, то это изоморфизм на все V ^∗ . Обратно, любой изоморфизм $\Phi$ из V в подпространство V ^∗ (соответственно все V ^∗ если V конечномерно) определяет единственную невырожденную билинейную форму $\langle \cdot ,\cdot \rangle _{\Phi }$ on V by

$\langle v,w\rangle _{\Phi }=(\Phi (v))(w)=[\Phi (v),w].\,$

Таким образом, существует взаимно однозначное соответствие между изоморфизмами V подпространству (соответственно всем) V. ^∗ и невырожденные билинейные формы на V .

Если векторное пространство V находится над комплексным полем, то иногда более естественно рассматривать полуторалинейные формы вместо билинейных.В этом случае данная полуторалинейная форма ⟨·,·⟩ определяет изоморфизм V с комплексно-сопряженным сопряженным пространством

$\Phi _{\langle \cdot ,\cdot \rangle }:V\to {\overline {V^{*}}}.$

Сопряженное двойственное пространство ${\overline {V^{*}}}$ можно отождествить с множеством всех аддитивных комплекснозначных функционалов f : V → C таких, что

$f(\alpha v)={\overline {\alpha }}f(v).$

Инъекция в дабл-дуал

Существует естественный гомоморфизм $\Psi$ от $V$ в двойной двойной $V^{**}=\{\Phi :V^{*}\to F:\Phi \ \mathrm {linear} \}$, определяемый $(\Psi (v))(\varphi )=\varphi (v)$ для всех $v\in V,\varphi \in V^{*}$. Другими словами, если $\mathrm {ev} _{v}:V^{*}\to F$ это карта оценки, определяемая $\varphi \mapsto \varphi (v)$, затем $\Psi :V\to V^{**}$ определяется как карта $v\mapsto \mathrm {ev} _{v}$. Эта карта $\Psi$ всегда инъективен ; и это всегда изоморфизм , если $V$ является конечномерным. Действительно, изоморфизм конечномерного векторного пространства с его двойным двойником является архетипическим примером естественного изоморфизма .Бесконечномерные гильбертовы пространства изоморфны не своим двойным алгебраическим двойникам, а своим непрерывным двойным двойникам.

Транспонирование линейной карты

Основная статья: Транспонирование линейной карты

Если f : V → W — линейное отображение , то транспонирование (или двойственное ) f ^∗ : В ^∗ → V ^∗ определяется

$f^{*}(\varphi )=\varphi \circ f\,$

для каждого $\varphi \in W^{*}$. Полученный функционал $f^{*}(\varphi )$ в $V^{*}$ называется откатом ​ $\varphi$ вдоль $f$.

Следующее тождество справедливо для всех $\varphi \in W^{*}$ и $v\in V$:

$[f^{*}(\varphi ),\,v]=[\varphi ,\,f(v)],$

где скобка [·, ·] слева — это естественное спаривание V с двойственным к нему пространством, а справа — естественное спаривание W с двойственным к нему пространством. Это тождество характеризует транспонирование, и формально аналогично определению сопряженного .

Присваивание f ↦ f ^∗ производит инъективное линейное отображение между пространством линейных операторов из V в W и пространством линейных операторов из W ^∗ to V ^∗ ; этот гомоморфизм является изоморфизмом тогда и только тогда, когда W конечномерно.Если V = W , то пространство линейных отображений на самом деле является алгеброй относительно композиции отображений , и тогда присваивание является антигомоморфизмом алгебр, а это означает, что ( fg ) ^∗ = г ^∗ ж ^∗ . Таким образом, на языке теории категорий взятие двойственного векторного пространства и транспонирования линейных отображений является контравариантным функтором из категории векторных пространств над F в себя.Можно определить ( f ^∗ ) ^∗ с f, используя естественную инъекцию в двойной дуал.

Если линейное отображение f представлено матрицей A относительно двух базисов V и W , то f ^∗ представлена ​​транспонированной матрицей A ^Т относительно двойственных базисов W ^∗ и В. ^∗ , отсюда и название.Альтернативно, поскольку f представлено как A, действующее слева на вектор-столбцы, f ^∗ представлена ​​той же матрицей, действующей справа на векторы-строки.Эти точки зрения связаны каноническим скалярным произведением на R ^н , который идентифицирует пространство векторов-столбцов с двойственным пространством векторов-строок.

Факторпространства и аннуляторы

Позволять $S$ быть подмножеством $V$.Уничтожитель ​ ​ $S$ в $V^{*}$, обозначенный здесь $S^{0}$, представляет собой набор линейных функционалов $f\in V^{*}$ такой, что $[f,s]=0$ для всех $s\in S$.То есть, $S^{0}$ состоит из всех линейных функционалов $f:V\to F$ такое, что ограничение на $S$ исчезает: $f|_{S}=0$.В конечномерных векторных пространствах аннулятор двойствен (изоморфен) ортогональному дополнению .

Аннулятор подмножества сам по себе является векторным пространством.Аннулятором нулевого вектора является все дуальное пространство: $\{0\}^{0}=V^{*}$, а аннулятор всего пространства — это как раз нулевой ковектор: $V^{0}=\{0\}\subseteq V^{*}$.Более того, отнесение аннулятора к подмножеству $V$ обращает включения, так что если $\{0\}\subseteq S\subseteq T\subseteq V$, затем

$\{0\}\subseteq T^{0}\subseteq S^{0}\subseteq V^{*}.$

Если $A$ и $B$ представляют собой два подмножества $V$ затем

$A^{0}+B^{0}\subseteq (A\cap B)^{0}.$

Если $(A_{i})_{i\in I}$ любое семейство подмножеств $V$ индексируется $i$ принадлежность к некоторому набору индексов $I$, затем

$\left(\bigcup _{i\in I}A_{i}\right)^{0}=\bigcap _{i\in I}A_{i}^{0}.$

В частности, если $A$ и $B$ являются подпространствами $V$ затем

$(A+B)^{0}=A^{0}\cap B^{0}$

и

$(A\cap B)^{0}=A^{0}+B^{0}.$

Если $V$ конечномерен и $W$ является векторным подпространством , то

$W^{00}=W$

после идентификации $W$ со своим образом во втором дуальном пространстве при изоморфизме двойной двойственности $V\approx V^{**}$. В частности, образование аннулятора представляет собой связность Галуа на решетке подмножеств конечномерного векторного пространства.

Если $W$ является подпространством $V$ тогда факторпространство $V/W$ является векторным пространством само по себе и поэтому имеет двойственное пространство. По первой теореме об изоморфизме функционал $f:V\to F$ факторы через $V/W$ тогда и только тогда, когда $W$ в ядре находится $f$. Таким образом, существует изоморфизм

$(V/W)^{*}\cong W^{0}.$

Как частное следствие, если $V$ является прямой суммой двух подпространств $A$ и $B$, затем $V^{*}$ представляет собой прямую сумму $A^{0}$ и $B^{0}$.

Размерный анализ

Дуальное пространство аналогично пространству «отрицательных» измерений. Проще всего, поскольку вектор $v\in V$ можно использовать в паре с ковектором $\varphi \in V^{*}$ по естественному спариванию $\langle x,\varphi \rangle :=\varphi (x)\in F$ чтобы получить скаляр, ковектор может «отменить» размерность вектора, аналогично уменьшению дроби . Таким образом, хотя прямая сумма $V\oplus V^{*}$ это ⁠ $2n$⁠ -мерное пространство (если ⁠ $V$⁠ это ⁠ $n$⁠ -мерный), ⁠ $V^{*}$⁠ ведет себя как ⁠ $(-n)$⁠ -мерное пространство в том смысле, что его размеры можно сократить по сравнению с размерами ⁠ $V$⁠ . Это формализуется сжатием тензора .

Это возникает в физике посредством анализа размерностей , где двойственное пространство имеет обратные единицы. При естественном спаривании эти единицы сокращаются, и результирующее скалярное значение, как и ожидалось, является безразмерным . Например, в (непрерывном) анализе Фурье или, в более широком смысле, частотно-временном анализе : задано одномерное векторное пространство с единицей времени ⁠ $t$⁠ , двойственное пространство имеет единицы частоты : появления в единицу времени (единицы ⁠ $1/t$⁠ ). Например, если время измеряется в секундах , соответствующей двойной единицей является обратная секунда : в течение 3 секунд событие, которое происходит 2 раза в секунду, происходит в общей сложности 6 раз, что соответствует $3s\cdot 2s^{-1}=6$. Аналогично, если основное пространство имеет длину, двойственное пространство имеет обратную длину .

Непрерывное двойное пространство

При работе с векторными пространствами непрерывные топологическими линейные функционалы из пространства в базовое поле $\mathbb {F} =\mathbb {C}$ (или $\mathbb {R}$) особенно важны.Это порождает понятие «непрерывного дуального пространства» или «топологического дуального пространства», которое является линейным подпространством алгебраического дуального пространства. $V^{*}$, обозначенный $V'$.Для любого конечномерного нормированного векторного пространства или топологического векторного пространства, такого как евклидово n- пространство , непрерывное двойственное и алгебраически двойственное пространство совпадают.Однако это неверно для любого бесконечномерного нормированного пространства, как показано на примере разрывных линейных отображений .Тем не менее, в теории топологических векторных пространств термины «непрерывное дуальное пространство» и «топологическое дуальное пространство» часто заменяются на «дуальное пространство».

Для топологического векторного пространства $V$ его сплошное двойственное пространство , или топологическое дуальное пространство , или просто двойное пространство (в смысле теории топологических векторных пространств) $V'$ определяется как пространство всех непрерывных линейных функционалов $\varphi :V\to {\mathbb {F} }$.

Важными примерами непрерывных двойственных пространств являются пространство компактных тестовых функций. ${\mathcal {D}}$ и его двойственность ${\mathcal {D}}',$ пространство произвольных распределений (обобщенных функций); пространство произвольных пробных функций ${\mathcal {E}}$ и его двойственность ${\mathcal {E}}',$ пространство компактных дистрибутивов; и пространство быстро убывающих пробных функций ${\mathcal {S}},$ пространство Шварца и его двойственное ${\mathcal {S}}',$ пространство умеренных распределений (медленно растущих распределений) в теории обобщенных функций .

Характеристики

Если X — Хаусдорфа векторное пространство (TVS), то непрерывное двойственное пространство к X идентично непрерывному двойственному пространству пополнения X топологическое .

Топологии на двойственном

Основные статьи: Полярная топология и Двойная система

Существует стандартная конструкция введения топологии на непрерывном двойственном $V'$ топологического векторного пространства $V$. Исправить коллекцию ${\mathcal {A}}$ ограниченных подмножеств ​ $V$.Это дает топологию на $V$ равномерной сходимости на множествах из ${\mathcal {A}},$ или, что то же самое, топология, порожденная полунормами вида

$\|\varphi \|_{A}=\sup _{x\in A}|\varphi (x)|,$

где $\varphi$ является непрерывным линейным функционалом на $V$, и $A$ пробегает по классу ${\mathcal {A}}.$

Это означает, что сеть функционалов $\varphi _{i}$ стремится к функциональному $\varphi$ в $V'$ тогда и только тогда, когда

${\text{ for all }}A\in {\mathcal {A}}\qquad \|\varphi _{i}-\varphi \|_{A}=\sup _{x\in A}|\varphi _{i}(x)-\varphi (x)|{\underset {i\to \infty }{\longrightarrow }}0.$

Обычно (но не обязательно) класс ${\mathcal {A}}$ должно удовлетворять следующим условиям:

• Каждая точка $x$ из $V$ принадлежит некоторому множеству $A\in {\mathcal {A}}$:

  ${\text{ for all }}x\in V\quad {\text{ there exists some }}A\in {\mathcal {A}}\quad {\text{ such that }}x\in A.$

• Каждые два комплекта $A\in {\mathcal {A}}$ и $B\in {\mathcal {A}}$ содержатся в некотором множестве $C\in {\mathcal {A}}$:

  ${\text{ for all }}A,B\in {\mathcal {A}}\quad {\text{ there exists some }}C\in {\mathcal {A}}\quad {\text{ such that }}A\cup B\subseteq C.$

• ${\mathcal {A}}$ замыкается относительно операции умножения на скаляры:

  ${\text{ for all }}A\in {\mathcal {A}}\quad {\text{ and all }}\lambda \in {\mathbb {F} }\quad {\text{ such that }}\lambda \cdot A\in {\mathcal {A}}.$

Если эти требования выполняются, то соответствующая топология на $V'$ это Хаусдорф и множества

$U_{A}~=~\left\{\varphi \in V'~:~\quad \|\varphi \|_{A}<1\right\},\qquad {\text{ for }}A\in {\mathcal {A}}$

сформировать свою местную базу.

Вот три наиболее важных особых случая.

• Сильная топология на $V'$ — топология равномерной сходимости на ограниченных подмножествах в $V$ (так вот ${\mathcal {A}}$ можно выбрать как класс всех ограниченных подмножеств в $V$).

Если $V$ является нормированным векторным пространством (например, банаховым или гильбертовым пространством ), то сильная топология на $V'$ нормировано (фактически банахово пространство, если поле скаляров полно), с нормой

$\|\varphi \|=\sup _{\|x\|\leq 1}|\varphi (x)|.$

• Топология стереотипа на $V'$ — топология равномерной сходимости на вполне ограниченных множествах в $V$ (так вот ${\mathcal {A}}$ можно выбрать как класс всех вполне ограниченных подмножеств в $V$).
• Слабая топология на $V'$ — топология равномерной сходимости на конечных подмножествах в $V$ (так вот ${\mathcal {A}}$ можно выбрать как класс всех конечных подмножеств в $V$).

Каждый из этих трех вариантов топологии на $V'$ приводит к варианту свойства рефлексивности для топологических векторных пространств:

• Если $V'$ наделено сильной топологией , то соответствующее понятие рефлексивности является стандартным: рефлексивные в этом смысле пространства называются просто рефлексивными .
• Если $V'$ наделено стереотипно-двойственной топологией, то соответствующая рефлексивность представлена ​​в теории стереотипных пространств : рефлексивные в этом смысле пространства называются стереотипными .
• Если $V'$ наделен слабой топологией , то соответствующая рефлексивность представлена ​​в теории дуальных пар : рефлексивными в этом смысле пространствами являются произвольные (хаусдорфовы) локально выпуклые пространства со слабой топологией.

Примеры

Пусть 1 < p < ∞ — действительное число, и рассмотрим банахово пространство ℓ ^п всех последовательностей a = ( an _для ), которых

$\|\mathbf {a} \|_{p}=\left(\sum _{n=0}^{\infty }|a_{n}|^{p}\right)^{\frac {1}{p}}<\infty .$

Определим число q как 1/ p + 1/ q = 1 . Тогда непрерывный двойственный к ℓ ^п естественно отождествляется с ℓ ^д : задан элемент $\varphi \in (\ell ^{p})'$, соответствующий элемент ℓ ^д это последовательность $(\varphi (\mathbf {e} _{n}))$ где $\mathbf {e} _{n}$ обозначает последовательность, n -й член которой равен 1, а все остальные равны нулю. Обратно, учитывая элемент a = ( a _n ) ∈ ℓ ^д , соответствующий непрерывный линейный функционал $\varphi$ где ℓ ^п определяется

$\varphi (\mathbf {b} )=\sum _{n}a_{n}b_{n}$

для всех б знак равно ( б _п ) ∈ ℓ ^п (см. неравенство Гёльдера ).

Аналогично, непрерывный двойник ℓ ¹ естественно отождествляется с ℓ ^∞ (пространство ограниченных последовательностей).Более того, непрерывные двойственные банаховы пространства c (состоящие из всех сходящихся последовательностей с нормой супремума ) и c ₀ (последовательности, сходящиеся к нулю) естественным образом отождествляются с ℓ ¹ .

По теореме о представлении Рисса непрерывное двойственное гильбертово пространство снова является гильбертовым пространством, которое антиизоморфно исходному пространству.Это приводит к появлению обозначений брекета, используемых физиками в математической формулировке квантовой механики .

По теореме о представлении Рисса–Маркова–Какутани непрерывное двойственное пространство некоторых пространств непрерывных функций можно описать с помощью мер.

Транспонирование непрерывной линейной карты

См. Также: Транспонирование линейной карты и Двойная система § Транспонирование.

Если T : V → W — непрерывное линейное отображение между двумя топологическими векторными пространствами, то (непрерывное) транспонирование T′ : W′ → V′ определяется той же формулой, что и раньше:

$T'(\varphi )=\varphi \circ T,\quad \varphi \in W'.$

Результирующий функционал T′ ( φ ) находится в V′ . Назначение T → T' создает линейное отображение между пространством непрерывных линейных отображений из V в W и пространством линейных отображений из W' в V' .Если T и U — составные непрерывные линейные отображения, то

$(U\circ T)'=T'\circ U'.$

Когда V и W — нормированные пространства, норма транспонирования в L ( W′ , V′ ) равна норме транспонирования T в L ( V , W ) .Некоторые свойства транспозиции зависят от теоремы Хана-Банаха .Например, ограниченное линейное отображение T имеет плотный образ тогда и только тогда, когда транспонирование T' инъективно.

Когда T — компактное линейное отображение между двумя банаховыми пространствами V и W , тогда транспонирование T компактно.Это можно доказать с помощью теоремы Арсела–Асколи .

Когда V — гильбертово пространство, существует антилинейный изоморфизм i _V из V на его непрерывное двойственное пространство V' .Для каждого ограниченного линейного отображения T на V транспонирующий и сопряженный операторы связаны соотношением

$i_{V}\circ T^{*}=T'\circ i_{V}.$

Когда T является непрерывным линейным отображением между двумя топологическими векторными пространствами V и W , тогда транспонирование T' является непрерывным, когда W' и V' оснащены «совместимыми» топологиями: например, когда для X = V и X = W , оба двойственных X' имеют сильную топологию β ( X' , X ) равномерной сходимости на ограниченных множествах X , или оба имеют слабую ∗ топологию σ ( X' , X ) поточечной сходимости X. на Транспонирование T' непрерывно от β ( W' , W ) до β ( V' , V ) или от σ ( W' , W ) до σ ( V' , V ) .

Аннигиляторы

Предположим, что W — замкнутое линейное подпространство нормированного пространства V , и рассмотрим аннулятор W в V′ ,

$W^{\perp }=\{\varphi \in V':W\subseteq \ker \varphi \}.$

Тогда двойник фактора V / W   можно отождествить с W ^⊥ , а двойственный к W можно отождествить с фактором V′ / W ^⊥ . Действительно, пусть P обозначает каноническую сюръекцию из V на фактор V / W   ; тогда транспонирование P′ является изометрическим изоморфизмом из ( V / W )′ в V′ с диапазоном, равным W ^⊥ .Если j обозначает карту вставки из W в V , то ядро ​​транспонирования j' является аннулятором W :

$\ker(j')=W^{\perp }$

следует и из теоремы Хана–Банаха , что j′ индуцирует изометрический изоморфизм В' / Вт ^⊥ → W′ .

Дополнительные свойства

Если двойственное нормированное пространство V сепарабельно , то сепарабельно пространство V. и само Обратное неверно: например, пробел ℓ ¹ отделим, но его двойственный ℓ ^∞ нет.

Двойной двойной

Это естественное преобразование сложения векторов из векторного пространства в его двойное двойное пространство. ⟨ x ₁ , x ₂ ⟩ обозначает упорядоченную пару двух векторов. Сложение + переводит x ₁ и x ₂ в x ₁ + x ₂ . Добавление +′, индуцированное преобразованием, можно определить как $[\Psi (x_{1})+'\Psi (x_{2})](\varphi )=\varphi (x_{1}+x_{2})=\varphi (x)$ для любого $\varphi$ в двойственном пространстве.

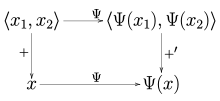
По аналогии со случаем алгебраического двойного двойного оператора всегда существует естественно определенный непрерывный линейный оператор Ψ : V → V′′ из нормированного пространства V в его непрерывный двойной двойственный оператор V′′ , определяемый формулой

$\Psi (x)(\varphi )=\varphi (x),\quad x\in V,\ \varphi \in V'.$

Как следствие теоремы Хана-Банаха , это отображение на самом деле является изометрией , что означает ‖ Ψ( x ) ‖ = ‖ x ‖ для всех x ∈ V .Нормированные пространства, для которых отображение Ψ является биекцией , называются рефлексивными .

Когда V является топологическим векторным пространством , тогда Ψ( x ) по-прежнему можно определить по той же формуле для каждого x ∈ V , однако возникает несколько трудностей.Во-первых, когда V не является локально выпуклым , непрерывное двойственное отображение может быть равно {0}, а отображение Ψ тривиально.Однако если V хаусдорфово в и локально выпукло, отображение Ψ инъективно из V алгебраическое двойственное V ′ ^∗ непрерывного двойственного, опять же как следствие теоремы Хана – Банаха.

Во-вторых, даже в локально выпуклой постановке на непрерывном двойственном V'' можно определить несколько топологий естественного векторного пространства , так что непрерывный двойной двойственный V'' не определяется как множество однозначно. Утверждение, что Ψ отображается из V в V′′ или, другими словами, что Ψ( x ) непрерывно на V′ для каждого x ∈ V , является разумным минимальным требованием к топологии V′ , а именно, что оценочные отображения

$\varphi \in V'\mapsto \varphi (x),\quad x\in V,$

быть непрерывным для выбранной топологии на V' . Далее, существует еще выбор топологии на V′′ , и непрерывность Ψ зависит от этого выбора.Как следствие, определение рефлексивности в этой системе является более сложным, чем в нормированном случае.

См. также

• Ковариантность и контравариантность векторов
• Двойной модуль
• Двойная норма
• Двойственность (математика)
• Двойственность (проективная геометрия)
• Двойственность Понтрягина
• Обратная решетка - двупространственный базис в кристаллографии.

Библиография

• Экслер, Шелдон Джей (2015). Линейная алгебра сделана правильно (3-е изд.). Спрингер . ISBN  978-3-319-11079-0 .
• Бурбаки, Николя (1989). Элементы математики, Алгебра I. Спрингер-Верлаг. ISBN  3-540-64243-9 .
• Бурбаки, Николя (2003). Элементы математики, Топологические векторные пространства . Спрингер-Верлаг.
• Халмос, Пол Ричард (1974) [1958]. Конечномерные векторные пространства (2-е изд.). Спрингер . ISBN  0-387-90093-4 .
• Кацнельсон, Ицхак ; Кацнельсон, Йонатан Р. (2008). (Краткое) Введение в линейную алгебру . Американское математическое общество . ISBN  978-0-8218-4419-9 .
• Ланг, Серж (2002), Алгебра , Тексты для выпускников по математике , том. 211 (пересмотренное третье издание), Нью-Йорк: Springer-Verlag, ISBN.  978-0-387-95385-4 , МР   1878556 , Збл   0984.00001
• Ту, Лоринг В. (2011). Введение в многообразия (2-е изд.). Спрингер . ISBN  978-1-4419-7400-6 .
• Мак Лейн, Сондерс ; Биркгоф, Гаррет (1999). Алгебра (3-е изд.). Издательство AMS Челси. ISBN  0-8218-1646-2 . .
• Миснер, Чарльз В .; Торн, Кип С .; Уиллер, Джон А. (1973). Гравитация . У. Х. Фриман. ISBN  0-7167-0344-0 .
• Наричи, Лоуренс; Бекенштейн, Эдвард (2011). Топологические векторные пространства . Чистая и прикладная математика (Второе изд.). Бока-Ратон, Флорида: CRC Press. ISBN  978-1584888666 . OCLC   144216834 .
• Рудин, Уолтер (1973). Функциональный анализ . Международная серия по чистой и прикладной математике. Том. 25 (Первое изд.). Нью-Йорк, штат Нью-Йорк: McGraw-Hill Science/Engineering/Math . ISBN  9780070542259 .
• Рудин, Уолтер (1991). Функциональный анализ . Международная серия по чистой и прикладной математике. Том. 8 (Второе изд.). Нью-Йорк, штат Нью-Йорк: McGraw-Hill Science/Engineering/Math . ISBN  978-0-07-054236-5 . OCLC   21163277 .
• Робертсон, AP; Робертсон, В. (1964). Топологические векторные пространства . Издательство Кембриджского университета.
• Шефер, Гельмут Х. (1966). Топологические векторные пространства . Нью-Йорк: Компания Macmillan.
• Шефер, Хельмут Х .; Вольф, Манфред П. (1999). Топологические векторные пространства . ГТМ . Том. 8 (Второе изд.). Нью-Йорк, Нью-Йорк: Springer New York Выходные данные Springer. ISBN  978-1-4612-7155-0 . OCLC   840278135 .
• Тревес, Франсуа (2006) [1967]. Топологические векторные пространства, распределения и ядра . Минеола, Нью-Йорк: Dover Publications. ISBN  978-0-486-45352-1 . OCLC   853623322 .

Внешние ссылки

• Вайсштейн, Эрик В. «Двойное векторное пространство» . Математический мир .